
1
Całkowanie funkcji niewymiernych
Całki z funkcji niewymiernych sprowadzamy do całek z funkcji wymiernych.
dx
d
cx
b
ax
x
R
n
+
+
,
d
c
b
a
bc
ad
,
,
,
0
∧
≠
−
- liczby rzeczywiste
R
– funkcja wymierna dwu zmiennych
( )
( )
( )
y
x
W
y
x
P
y
x
R
,
,
,
=
a
c
t
d
t
b
x
d
cx
b
ax
t
d
cx
b
ax
t
n
n
n
n
−
−
=
+
+
=
+
+
=
(
)
(
)
(
)
(
)
(
)
dt
a
c
t
bc
ad
nt
dx
dt
a
c
t
d
t
b
c
nt
a
ct
d
nt
dx
n
n
n
n
n
n
n
2
1
2
1
1
−
−
=
−
−
−
−
−
=
−
−
−
(
)
dx
c
bx
ax
x
R
+
+
2
,
R
– funkcja wymierna dwu zmiennych
0
0
4
2
≠
∧
≠
−
a
ac
b
1)
0
>
a
pierwsze podstawienie Eulera
t
a
b
c
t
x
xt
a
t
c
bx
x
a
t
c
bx
ax
2
2
2
2
2
+
−
=
−
=
+
−
=
+
+
(
)
(
)
(
)
(
)
dt
t
a
b
c
a
tb
t
a
dx
dt
t
a
b
c
t
a
t
a
b
t
dx
2
2
2
2
2
2
2
2
2
2
2
2
+
+
+
=
+
−
−
+
=
Inne podstawienia:
x
a
t
c
bx
ax
+
=
+
+
2
,
t
x
a
c
bx
ax
−
=
+
+
2
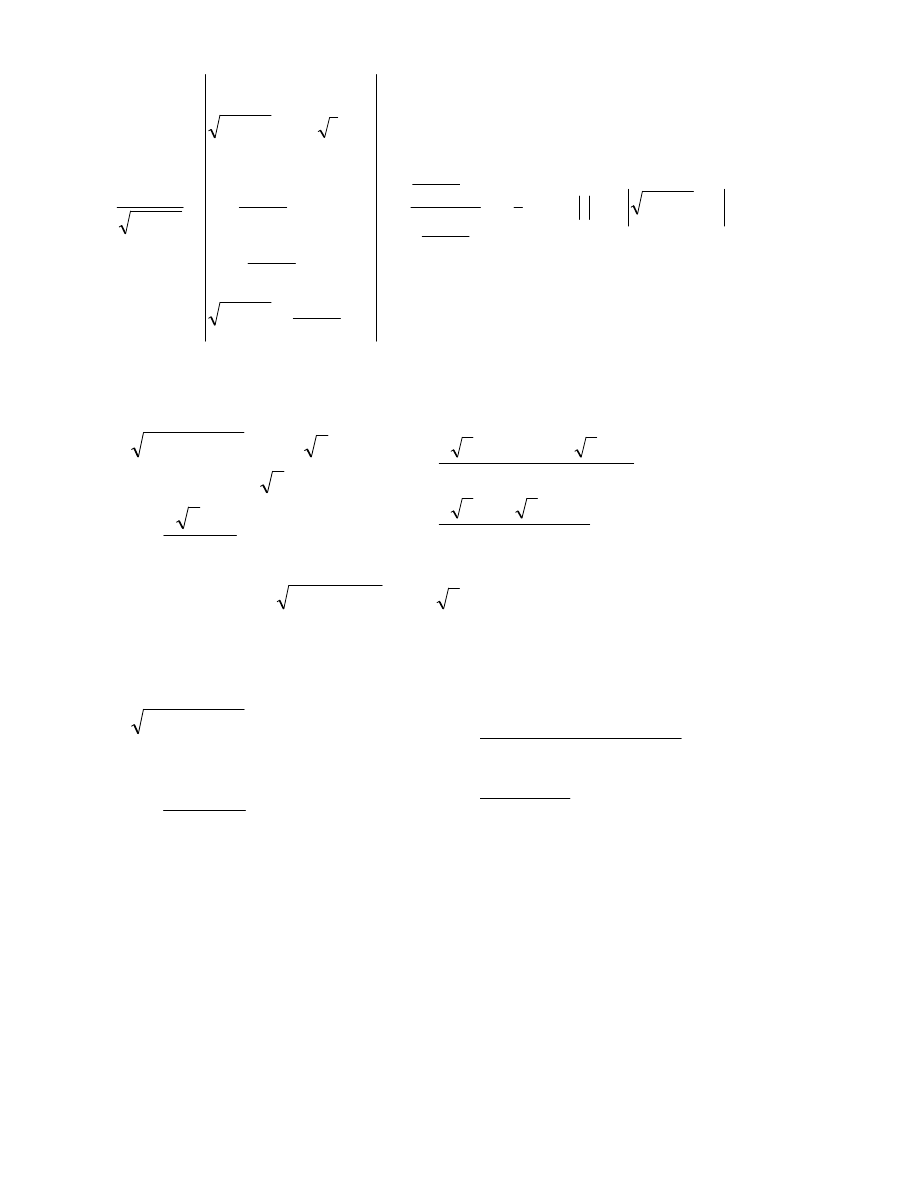
2
Przykład
C
x
k
x
t
dt
t
t
k
t
dt
t
k
t
t
k
t
k
x
dt
t
k
t
dx
t
k
t
x
x
tx
t
k
x
x
t
k
x
k
x
dx
+
+
±
=
=
=
±
±
=
±
=
±
±
=
=
+
−
=
±
−
=
±
=
±
2
2
2
2
2
2
2
2
2
2
2
2
2
2
ln
ln
1
2
2
2
2
2
2
1
2)
0
>
c
drugie podstawienie Eulera
2
2
2
2
2
t
a
b
t
c
x
t
c
xt
b
ax
c
xt
c
bx
ax
−
−
=
−
=
+
+
=
+
+
(
)
(
)
(
)
(
)
dt
t
a
tb
a
c
t
c
dx
dt
t
a
b
t
c
t
t
a
c
dx
2
2
2
2
2
2
2
2
2
2
−
−
+
=
−
−
+
−
=
Inne podstawienia:
c
xt
c
bx
ax
−
=
+
+
2
3)
0
0
<
∧
<
c
a
trzecie podstawienie Eulera
(
(
)(
)
2
1
2
2
1
:
,
0
x
x
x
x
a
c
bx
ax
R
x
x
zał
−
−
=
+
+
∈
∃
>
∆
(
)
(
)(
)
(
)
2
1
2
2
2
1
2
2
1
1
2
t
a
x
t
ax
x
x
x
t
x
x
x
x
a
x
x
t
c
bx
ax
−
−
=
−
=
−
−
−
=
+
+
(
) (
)
(
)
(
)
(
)
dt
a
t
x
x
ta
dx
dt
a
t
x
t
ax
t
a
t
tx
dx
2
2
1
2
2
2
1
2
2
2
1
2
2
2
−
−
=
−
−
+
−
=
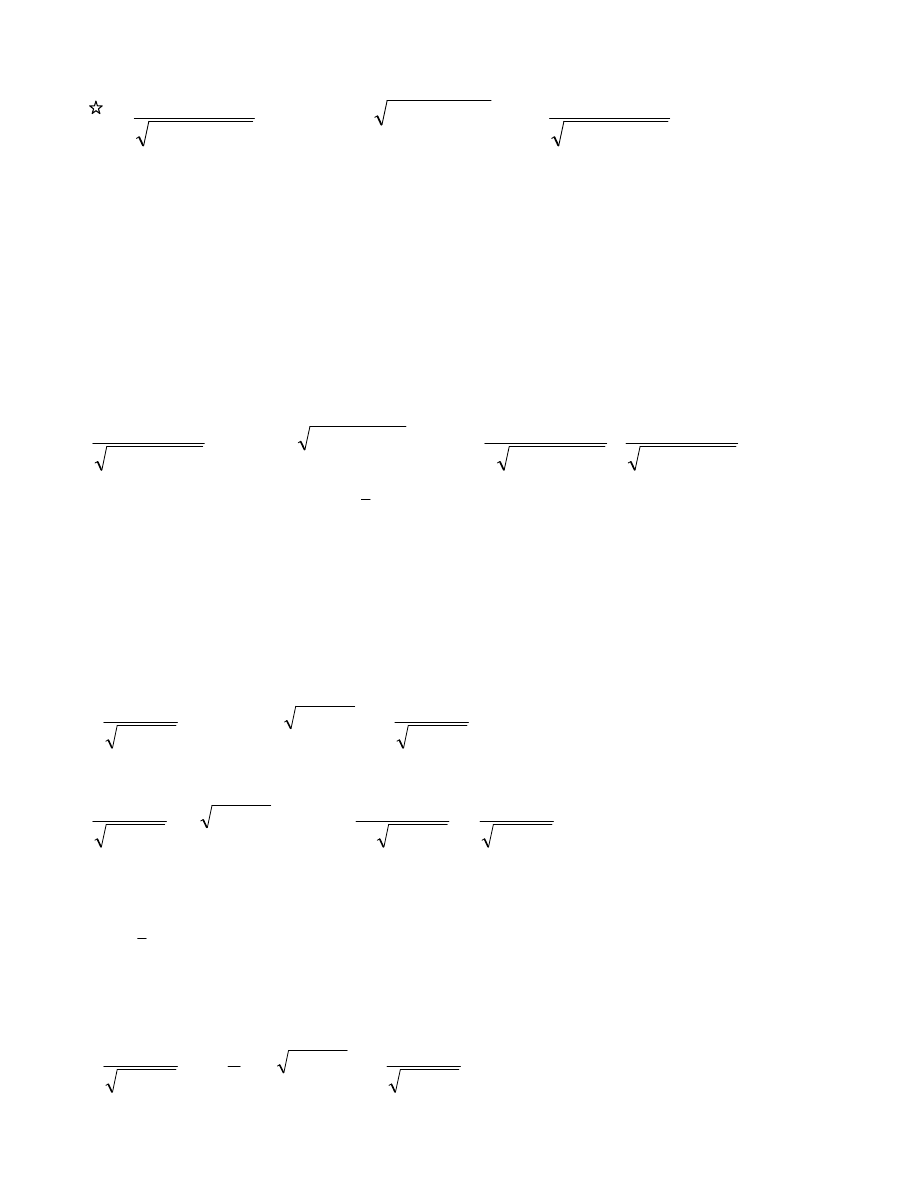
3
Wzór Abela
( )
( )
+
+
⋅
+
+
+
⋅
=
+
+
−
c
bx
ax
dx
k
c
bx
ax
x
W
dx
c
bx
ax
x
W
n
n
2
2
1
2
,
gdzie
n
W
,
1
−
n
W
– wielomiany stopnia odpowiednio
n
i
1
−
n
,
R
k
∈
Dane:
W
n
,a ,b, c
Szukane:
( )
?
?,
1
=
=
−
k
x
W
n
Metoda współczynników nieoznaczonych
Po zró niczkowaniu to samo ci we wzorze Abela otrzymujemy:
( )
( )
( )
c
bx
ax
k
c
bx
ax
b
ax
x
W
c
bx
ax
x
W
c
bx
ax
x
W
n
n
n
+
+
+
+
+
+
+
+
+
⋅
′
=
+
+
−
−
2
2
1
2
1
2
2
2
( )
( )
(
)
( )(
)
k
b
ax
x
W
c
bx
ax
x
W
x
W
n
n
n
+
+
+
+
+
⋅
′
=
−
−
2
1
2
1
2
1
Powy sza to samo jest to samo ci wielomianów, zatem jest ona spełniona gdy współczynniki
przy odpowiednich pot gach wielomianu po prawej stronie i po lewej stronie to samo ci s sobie
równe. St d łatwo wyznaczy współczynniki wielomianu
W
n
oraz stał
k
.
Przykład
(
)
−
+
−
+
=
−
−
2
2
2
2
4
4
4
8
x
x
dx
k
x
x
B
Ax
dx
x
x
x
nast pnie ró niczkuj c to równanie otrzymujemy:
(
)
2
2
2
2
2
4
1
4
2
2
4
4
4
8
x
x
k
x
x
x
B
Ax
x
x
A
x
x
x
−
+
−
⋅
−
+
+
−
=
−
−
(
)
(
)(
)
k
x
B
Ax
x
x
A
x
+
−
+
+
−
=
−
2
4
8
2
2
z czego łatwo jest wyliczy :
=
=
=
2
3
2
1
k
B
A
czyli:
−
+
−
+
=
−
−
2
2
2
2
4
2
4
3
2
4
8
x
x
dx
x
x
x
dx
x
x
x
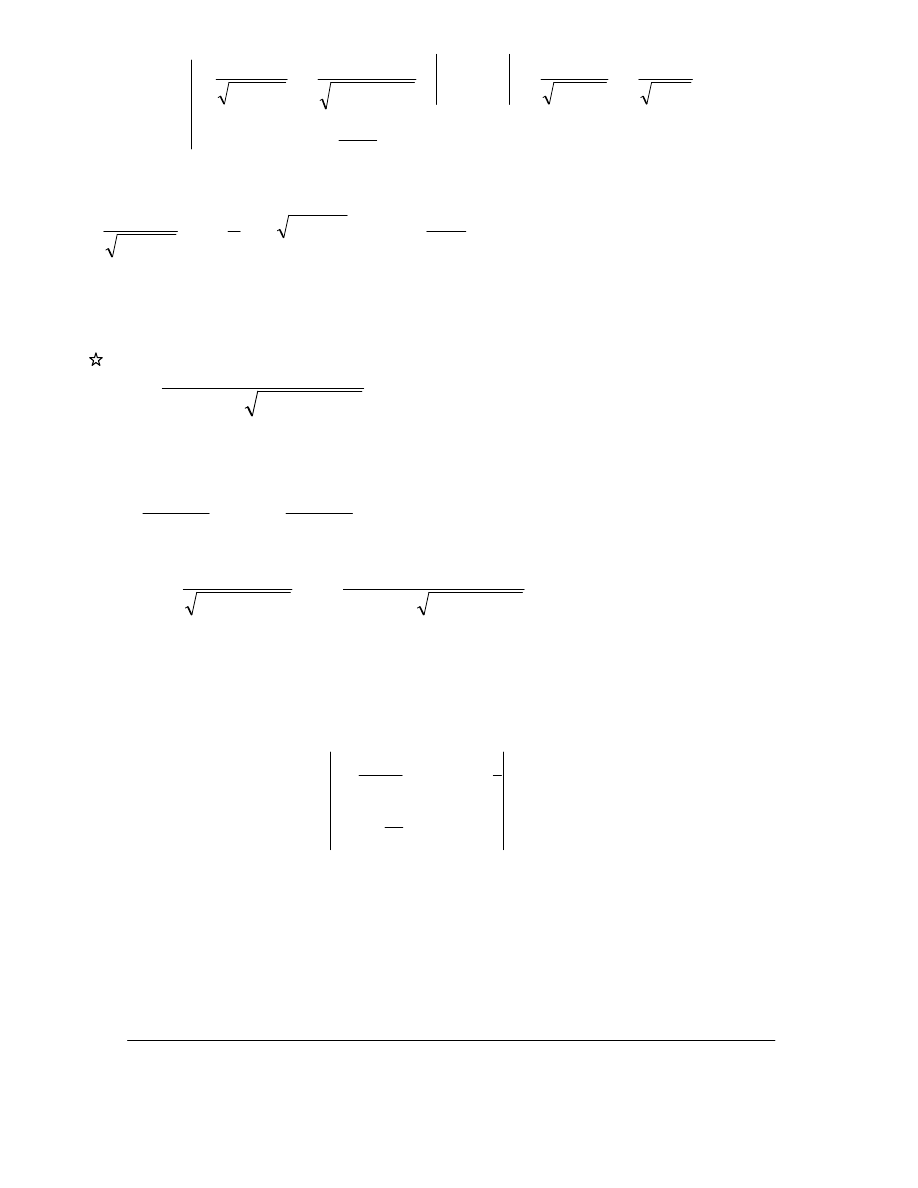
4
(
)
C
x
t
t
dx
t
dx
dt
dx
t
x
x
dx
x
x
dx
+
−
=
=
=
−
=
−
=
=
=
−
=
−
−
=
−
2
2
arcsin
arcsin
1
4
4
2
2
2
2
2
4
4
2
2
2
2
C
x
x
x
x
dx
x
x
x
+
−
+
−
+
=
−
−
2
2
arcsin
2
4
3
2
4
8
2
2
2
( )
(
)
+
+
⋅
−
=
dx
c
bx
ax
x
x
W
I
k
n
2
α
N
k
R
∈
∈ ,
α
Je eli
k
n
≥
( )
(
)
( )
( )
(
)
k
k
n
x
x
R
x
P
x
x
W
α
α
−
+
=
−
( )
( )
(
)
+
+
⋅
−
+
+
+
=
dx
c
bx
ax
x
x
R
dx
c
bx
ax
x
P
I
k
2
2
α
gdzie pierwsz całk rozwi zujemy metod współczynników nieoznaczonych, a drug – w
nast puj cy sposób (przypadek
n<k
)
Je eli
k
n
<
Stosujemy podstawienie
dt
t
dx
t
x
x
t
2
1
1
1
−
=
=
−
−
=
α
α
a nast pnie rozwi zujemy całk metod
współczynników nieoznaczonych.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron