
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
Macierzowa metoda przemieszczeń
materiały do wykładu nr 1

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
2
Macierzowa metoda przemieszczeń
Dyskretyzacja ustroju konstrukcyjnego
Dyskretyzacja
ustroju polega na wyborze punktów nazywanych węzłami,
co prowadzi do podziału na elementy
• W wyniku dyskretyzacji układ zostaje podzielony na elementy
• Elementy opisujemy w lokalnych układach współrzędnych

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
3
Macierzowa metoda przemieszczeń
Określenie liczby niewiadomych wiąże się z podziałem konstrukcji na elementy.
Niewiadome zestawiamy w wektor przemieszczeń węzłowych układu q.
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
4
Macierzowa metoda przemieszczeń
Stan przemieszczenia ustroju będziemy opisywać poprzez uogólnione przemieszczenia
węzłów konstrukcji (przesunięcia i obroty).
Liczba stopni swobody węzła:
• liczba przemieszczeń pojedynczego węzła układu
• zależy od przyjętego modelu układu (rodzaju konstrukcji)
Układ belkowy
Rama płaska

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
5
Macierzowa metoda przemieszczeń
Kratownica przestrzenna
Kratownica płaska
Rama przestrzenna
Ruszt załamany w planie

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
6
Macierzowa metoda przemieszczeń
Macierz sztywności i podatności układu
Dla dowolnego układu można określić wektor uogólnionych przemieszczeń
węzłowych q oraz odpowiadający mu wektor obciążeń węzłowych R
Między elementami wektorów q i R istnieje zależność:
Kq = R

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
7
Macierzowa metoda przemieszczeń
Metody wyznaczania macierzy K oraz F
a) Macierz K można wyznaczyć metodą jednostkowych stanów przemieszczeń

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
8
Macierzowa metoda przemieszczeń
Metody wyznaczania macierzy K oraz F
a) Macierz K można wyznaczyć metodą jednostkowych stanów przemieszczeń

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
9
Macierzowa metoda przemieszczeń
Metody wyznaczania macierzy K oraz F
b) Macierz F można wyznaczyć metodą jednostkowych stanów obciążeń

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
10
Macierzowa metoda przemieszczeń
Własności macierzy K oraz F
1. Jeżeli
det( )
0
K
1
F = K
det( )
0
F
1
K = F
2. Warunek det(K) ≠ 0 jest warunkiem wystarczającym geometrycznej
niezmienności układu.
Jeżeli macierz K jest osobliwa, to układ jest geometrycznie zmienny,
a macierz F nie istnieje.
3. Jeżeli przemieszczenia w wektorze q są liniowo zależne, to macierz F jest
osobliwa, a macierz K nie istnieje

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
11
Macierzowa metoda przemieszczeń
Własności macierzy K oraz F
4. Macierze K i F są symetryczne.
Symetria macierzy K wynika z twierdzenia o wzajemności reakcji,
symetria macierzy F wynika z twierdzenia o wzajemności przemieszczeń.
5. Macierze K i F są jądrami form kwadratowych, poprzez które wyraża się
energia potencjalna odkształcenia sprężystego układu:
1
1
2
2
T
T
p
E
q Kq
R FR
Jeżeli E
p
> 0
, to układ jest geometrycznie niezmienny, zaś macierze K i F są
dodatnio określone

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
12
Macierzowa metoda przemieszczeń
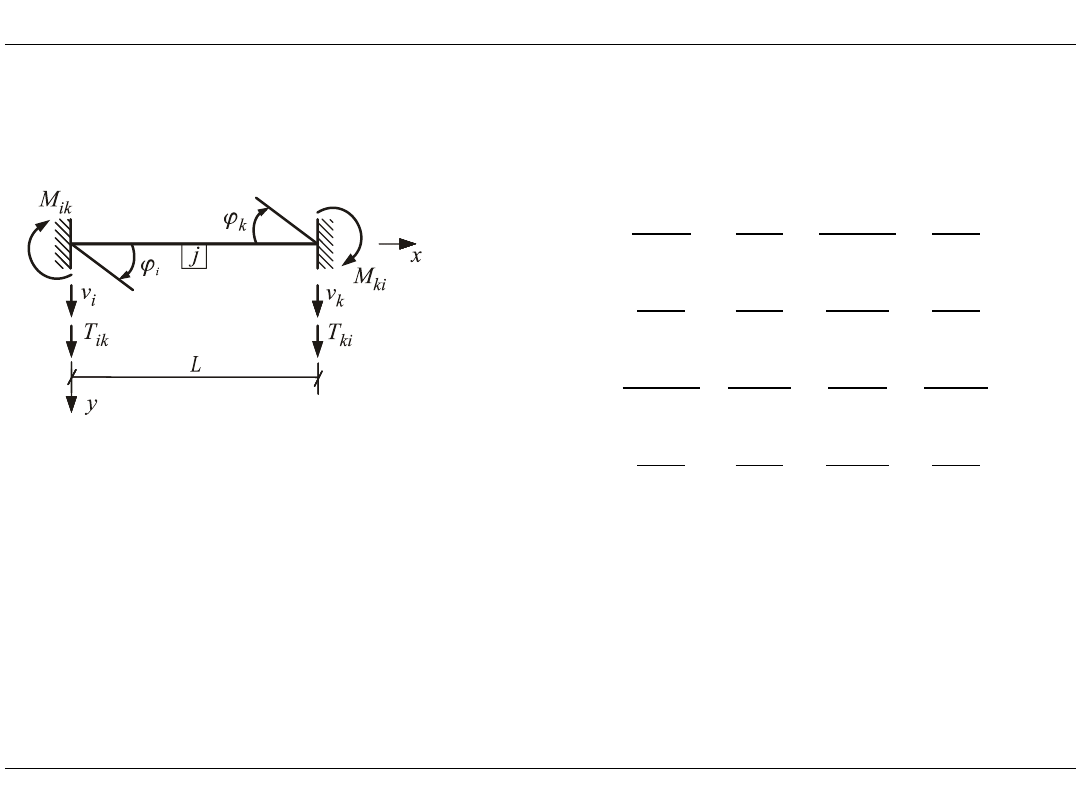
Macierz sztywności elementu belkowego
Element belkowy
T
j
i
i
k
k
v
v
D
T
j
ik
ik
ki
ki
T
M
T
M
S
el
j
k
el
j
j
j
S
k D
Dla każdego elementu j można zapisać zależności przywęzłowych sił
i przywęzłowych przemieszczeń, tzn. utworzyć macierz sztywności elementu

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
13
Macierzowa metoda przemieszczeń
Macierz sztywności elementu belkowego
Element belkowy – cechy:
posiada 2 stopnie swobody w węźle
założenie podłużnej nieodkształcalności
tylko do układów o ortogonalnej siatce prętów
prawidłowa dyskretyzacja musi zapewnić zgodność przemieszczeń
elementowych z przemieszczeniami globalnymi
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
14
Macierzowa metoda przemieszczeń
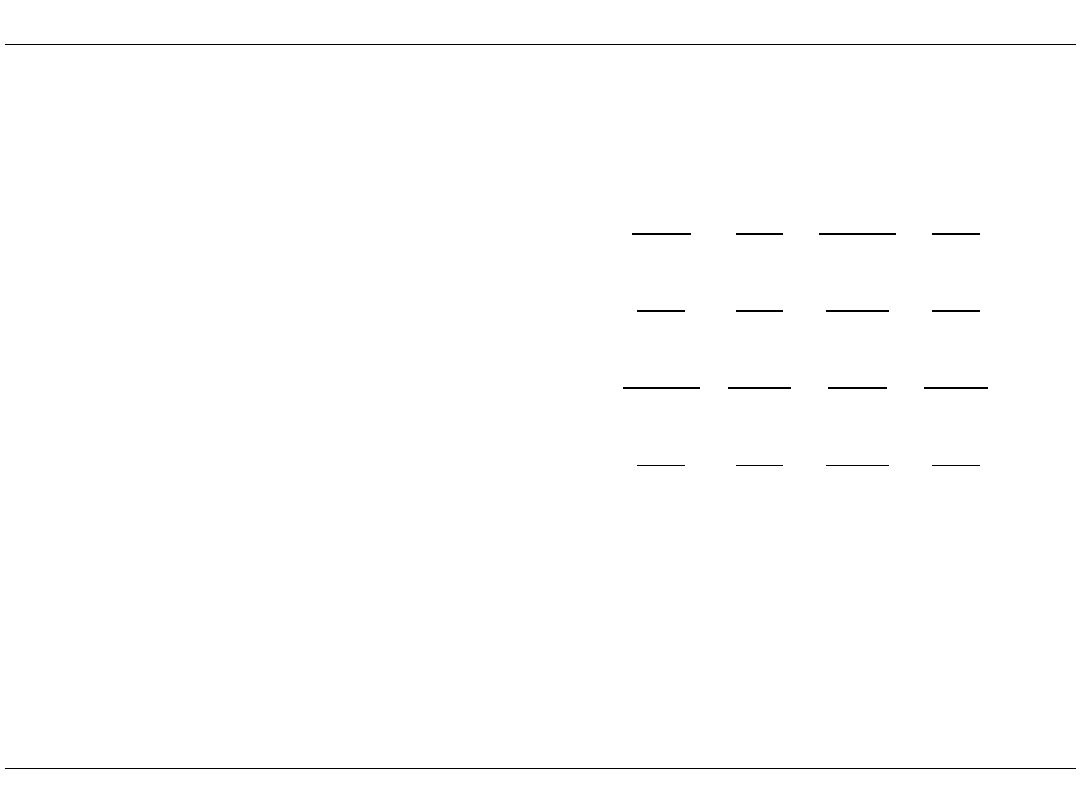
Macierz sztywności elementu belkowego
W celu wyznaczenia macierzy sztywności elementu k
j
el
na kierunkach wektora
D
j
zakładamy więzy i rozpatrujemy stany jednostkowych przemieszczeń
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
ik
i
ik
i
ki
k
ki
k
EI
EI
EI
EI
L
L
L
L
T
v
EI
EI
EI
EI
M
L
L
L
L
T
v
EI
EI
EI
EI
M
L
L
L
L
EI
EI
EI
EI
L
L
L
L
Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
15
Macierzowa metoda przemieszczeń
Macierz sztywności elementu belkowego
W celu wyznaczenia macierzy sztywności elementu k
j
el
na kierunkach wektora
D
j
zakładamy więzy i rozpatrujemy stany jednostkowych przemieszczeń
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
ik
i
ik
i
ki
k
ki
k
EI
EI
EI
EI
L
L
L
L
T
v
EI
EI
EI
EI
M
L
L
L
L
T
v
EI
EI
EI
EI
M
L
L
L
L
EI
EI
EI
EI
L
L
L
L

Metody Obliczeniowe
Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o , s e m e s t r 5 , r o k a k a d e m i c k i 2 0 1 3 / 1 4
Magdalena Rucka
16
Macierzowa metoda przemieszczeń
Podsumowanie
Dyskretyzacja
układu:
Podział układu na zbiór węzłów i elementów
Opis zależności teoretycznych przez:
a) wielkości globalne odniesione do węzłów:
- wektor przemieszczeń węzłowych q
- wektor obciążeń węzłowych R
b) wielkości odniesione do przekrojów przywęzłowych elementów:
- wektor przemieszczeń przywęzłowych D
j
- wektor sił przywęzłowych S
j
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron