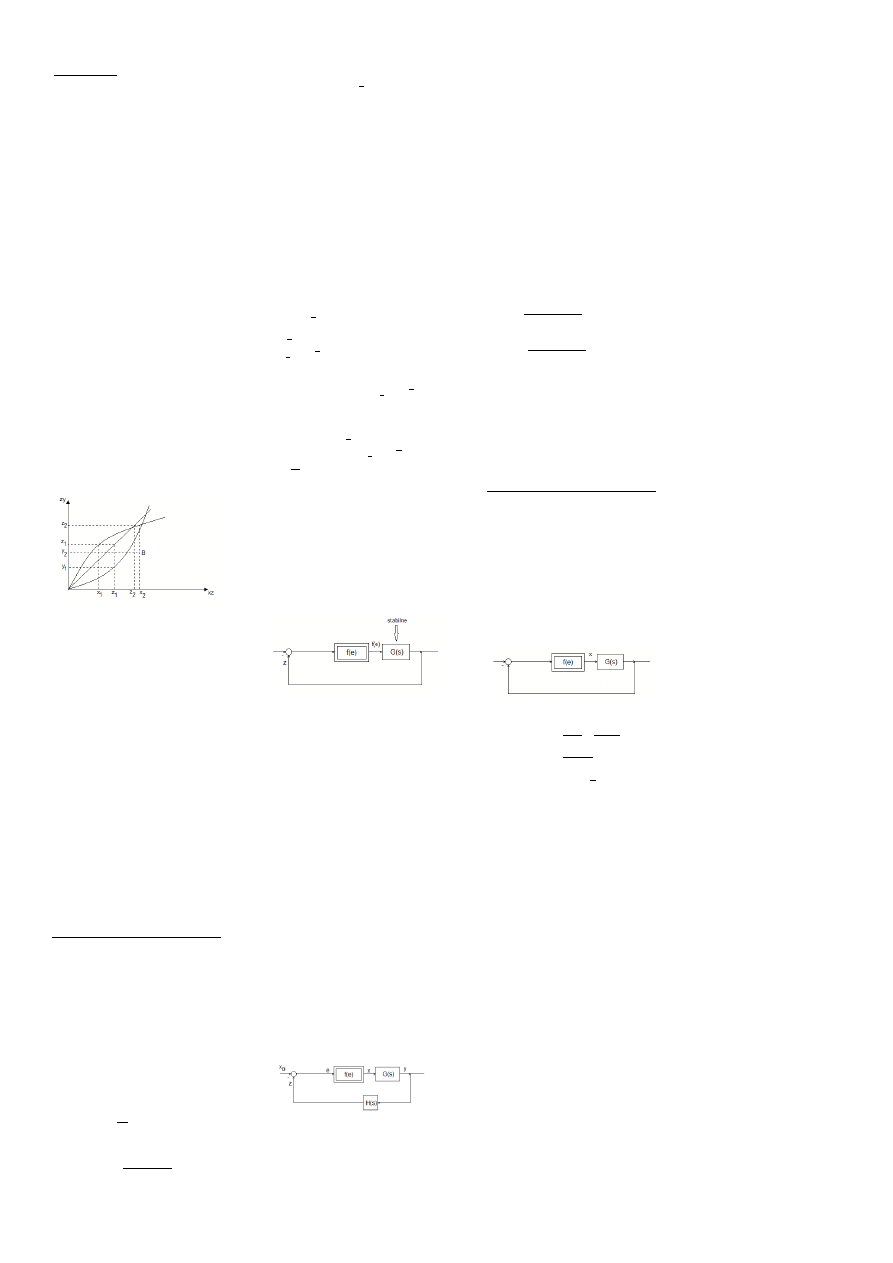
Nieliniowe układy regulacji 
Układ nieliniowy- nazywa się układy regulacji 
opisane nieliniowymi równaniami 
różniczkowymi lub algebraicznymi 
Jeżeli chociaż jeden z elementów układu jest 
nieliniowy to cały układ jest nieliniowy. 
W układach nieliniowych nie obowiązuje 
zasada superpozycji. 
Mówi ona że odpowiedź układu na 
wymuszenie będące kombinacją liniowej 
odpowiedzi na każde z wymuszeo 
oddzielnie. 
 
Układ może byd nieliniowy statycznie lub 
dynamicznie –  
To znaczy jego char. Statyczna określająca  
wsp. wzmocnienia może nie byd linią prostą 
lub przebieg zjawisk dynamicznych może 
mied zależnośd nieliniową. 
 
Procedury wyznaczania charakterystyk 
zastępczych: 
1.Wykreślamy we wspólnym układzie 
współrzędnych  charakter  f

1

 i f

2

. 

2. Rysujemy prostą P nachyloną  pod 
kątem45

0

 do przenoszenia sygnału”   

dla wyznaczania kolejnych  punktów char. 
Wypadkowej należy: 
3. Przyjąc jakąś wartośd sygnału 
wejściowego np. x

1

. 

4. odczytad wartośd na wyjściu np. =1 (człon 
f

1

)

. 

5. Podad tę wartośd  na drugi element  i 
odczytad odpowiedz y

1

. 

6. Przecięcie x

1

 i y

1

 wyznacza 1 punkt 

charakter. Wypadkowej P

1

 

Inne punkty powtarzająd procedurę 
UWAGA: przestawienie kolejności członów 
zamienia chraterystykę. 
 

 

 
Stabilnośd nieliniowych UAR: 
Def. (wg LAPUNOWA) Punkt równowagi x

o

 

układu sterowania w n-wymiarowej 
przestrzeni stanu nazywamy stabilnym jeżeli 
dla dowolnego otoczenia ε  stanu 
równowagi można dobrad takie otoczenie η 
tego punktu, że cała trajektoria 
rozpoczynająca się z η bęzie zawierała się 
wewnątrz  obszau ε 
 
1.Punkt równowagi jest wyłączony z 𝑥   =
0 nie ma ruchu 
2. Układ sterowania opisany jest w 
otoczeniu punktu równowagi układem 
równao 
Xi=f(x1,x2,x3,…,xn) n- rząd układó  
Trajektoria – krzywa stanu po której pousza 
się układ  
3.η- otoczenie (obszar) warunków 
początkowych może mied dowolny krztałt 
4.η- jeśli jest ograniczone to stabilnośd 
będzie lokalna, jeśli nieograniczone stab. 
globalna 
 
Badanie stabilności UAR: 
1.metoda Lapunowa 
- pośrednia 
-bezpośrednia 
2.Kryteium Popowa 

1.Metoda Lapunowa – Polega ona na 
badaniu stabilności punktów równowagi 
układu nieliniowego przez badanie jego 
przybliżeo liniowych w tych punktach. 
Jeżeli dokona się przesunięcia początku 
układu wsp. stanu do punktu równowagi 
rozwiązanie będze funkcją określającą  
współrzędne stanu (fi) w szeregu Taylora  
To odrzucid częśd nieliniową (resztą) to układ 
sterowania w otoczeniu punktu równowagi 
będzie sopisany: 

𝑥 

1

= 𝑎

11

𝑥

1

+ 𝑎

12

𝑥

2

+ ⋯ 𝑎

1𝑛

𝑥

𝑛

 

: 

𝑥 

1

= 𝑎

𝑖1

𝑥

1

+ 𝑎

𝑖2

𝑥

2

+ ⋯ 𝑎

𝑖𝑛

𝑥

𝑛

 

: 

𝑥 

0

= 𝑎

𝑛1

𝑥

1

+ 𝑎

𝑛2

𝑥

2

+ ⋯ 𝑎

𝑛𝑛

𝑥

𝑛

 

Te same co 𝑥 

0

= 𝐴𝑥 Jest to przybliżenie 

liniowe  
Z Taylora wylicza się współrzędne i, j=1,2 
…n 

𝑎

𝑖𝑗

=

𝜕𝑓𝑖(𝑥

1

… 𝑥

𝑛

)

𝜕𝑥

𝑗

 

Tw. Jeżeli przybliżenie liniowe(2) lub (3) jest 
stabilne asymptotycznie to układ nieliniowy 
jest stabilny  w punkcie 𝑥 = 0. 
Jeżeli przybliżenie liniowe(2) lub (3) jest 
niestabilne asymptotycznie to układ w 
punkcie równowagi jest niestabilny . 
UWAGI: 
1.Tą metodą niemożna zbadad czy układ 
nieliniowy jest  stab. Czy też nie w punkcie 
równowagi jeżeli przybliżenie liniwe jest 
stabilne ale nie asymptotycznie. 
2.ta metoda określa stabilnośd  lokalną  i nie 
daje odpowiedzi jak duży jest obszar 
stabilności. 
Metoda Lapunowa 2 
Polega na rozpatrywaniu pełnego opisu 
układu nieliniowego, doborze i dodaniu 
pewnej funkcji zwanej f. LAPUNOWA. 
Tw. Jeżeli w Obsza że D zawierającym 
początek układu wsp. stanu układu 
sterowania i będącego pnktem równowagi 
istnieje skalarna funkcja 𝑉(𝑥

1

, 𝑥

2

. . 𝑥

𝑛

 ) 

Od wsp. stanu dodatnio określone tzn: 
a) 

  𝑉(𝑥)

𝑥𝜖𝐷

𝜖𝐶

1   -funkcja ciągłą wraz z 1                                  

pochodną 

b)V(0)=0 
c)  

   𝑉(𝑥)

𝑥𝜖𝐷

𝑥 ≠0

> 0  (dodatnio określona) 

i taka że jej pochodna względem czasu jest 
ujemnie określona w tym obszarze tzn. 
spełnia warunek a) i b) oraz  

   𝑉(𝑥)

𝑥𝜖𝐷

𝑥 ≠0

< 0 

to układ nieliniowy opisany w przestrzeni 
stanu jest stabilny asymptotycznie w 
obszarze D. 
Jeżeli pochodna 𝑉 (𝑥) jest ujemnie pół 
określona w obszarze tj.  

   𝑉(𝑥)

𝑥𝜖𝐷

𝑥 ≠0

≤

0^𝑉(0) = 0 
To układ nieliniowy jest w obszarze D 
stabilny ale niekoniecznie asymptotycznie. 
Funkcję Lapunowa przyjmuje się taka aby 
spełniała w/w założenia. Nie jest to łatwe ,  
najczęściej przyjmuje się formą kwadratową. 
 
 
Metoda POPOWA: 
Wykorzystuje się do badania układów 
sterowania ze stabilnymi częściami 
liniowymi i statycznym elementem 
nieliniowym 
 

 

 
 
TW. Jeżeli w G(s) wszystkie bieguny mają 
części rzeczywiste ujemna to VAR jak na 
rysunku zawierający statyczny element 
nieliniowy spełniający warunek 1 
Jest  stabilny asymptotycznie w obszarze 
nieograniczonym pod warunkiem, że wykres 
zmodyfikowanej charakterystyki A-F 
G(jω)= V(ω)+jV(ω)  V(ω)=P(ω) 
G(jω)=P(ω)+jQ(ω)  V(ω)=ωQ(ω) 
Częśd liniowa leży na prawo od co najmniej 
jednej prostej przechodzącej przez punkt 
U=-1/k, V=0 
Jeżeli częśd liniowa ma 1 biegun zerowy to 
musi byd spełniony dodatkowy. 
 
 
 
Operatorowa metoda kolejnych przybliżeń: 

Metoda pozwala w uproszczony sposób 
analizowad pracę układu zwierającego 
jednoznaczną i niejednoznaczną nieliniowośd 
statyczną. Polega na wyznaczaniu kolejnych 
przybliżeo przebiegu uchybu 
uwzględniających coraz wpływ nieliniowości. 

Punktem wyjścia rozważao jest schemat 
blokowy układu regulacji: 

 

 

 

 

Dane: 
x

o

 

f(e) 
G(s) 
H(s) 
Założenie: 
f(e) – powinna dad przekształcid się do 
struktury zawierającej człon proporcjonalny 
f(e)=f

1

(e)+ke (nie zawsze się da) 

Korzystając z teorii przekształceo Laplace’a z 
definicji transmitancji można napisad 
𝑌 𝑠  = 𝑘𝐸 𝑠  + 𝐿 𝑡

1

 𝑒   

𝐸 𝑠  = 𝑋𝑜 𝑠  ∗ 𝑍 𝑠  
Transf. uchybu 
𝐸 𝑠  − 𝑋𝑜 𝑠  − 𝑌 𝑠 𝐻 𝑠 
= 𝑋𝑜 𝑠  − 𝑋𝑜 𝑠 𝐺 𝑠 𝐻 𝑠 
= 𝑋𝑜 𝑠  − 𝐺 𝑠 𝐻 𝑠  𝐾𝐸 𝑠  + 𝐿[𝑓

1

(𝑒)  

𝐸 𝑠  = 𝐸𝑜 𝑠  + 𝐵 𝑒  
𝐸𝑜 𝑠  −  𝑜𝑑 𝑙𝑖𝑛𝑖𝑜𝑤𝑜ś𝑐𝑖 
𝐵 𝑒  −  𝑝𝑜𝑝𝑟𝑎𝑤𝑘𝑎 

𝐸𝑜 𝑠  =

1

1 + 𝐾𝐺 𝑠 𝐻 𝑠 

𝑋𝑜 𝑠  

 

𝐵 𝑒  = −

𝐺 𝑠 𝐻 𝑠 

1 + 𝐾𝐺 𝑠 𝐻 𝑠 

𝑋𝑜 𝑠     𝐿 𝑓

1

 𝑒   

Eo(s) – transformata Laplace’a uchybu 
zlinearyzowanego, tzw zerowe przybliżenie 
przebiegu uchybu 
𝐸

1

 𝑠  = 𝐸𝑜 𝑠  + 𝐵 𝑒

𝑜

  

𝐸

𝑧

 𝑠  = 𝐸𝑜 𝑠  + 𝐵 𝑒

1

  

𝐸

𝑛

 𝑠  = 𝐸

𝑛

 𝑠  + 𝐵 𝑒

𝑛−1

  

Procedura jest przerywana, jeżeli przebieg 
kolejnego przybliżenia niewiele różni się od 
poprzedniego 

 

 

Metoda funkcji opisujących    

Metod częstotliw.  Nie można stosowad do 
układów nieliniowych, gdyż nie ma dla niech 
związków funkcyjnych pomiędzy 
przebiegami czasowymi  a char. 
Częstotliwościowymi. Przy założeniu, że 
częśd liniowa układu regulacji  jest filtrem 
dolnoprzepustowym(tłumi wyższe charm) 
można opisad własności dynamicznie członu 
nieliniowego, przy pomocy tak jakby 
odpowiednika transmitancji widmowej tzw 
FUNKCJI OISUJĄCEJ 

 

Przybliżenie funkcji opisującej 
Funkcja opisująca. 

𝐽 𝐴, 𝜔  ≝

𝐵𝑒

𝑗𝜑

𝐴

=

𝐵 + 𝑗𝐶

𝐴

 

 

𝐵 𝐵

2

+ 𝐶

2

 

𝜑 = 𝑎𝑟𝑐𝑡𝑔

𝐶
𝐵

 

 
Funkcja opisująca 𝐽 𝐴, 𝜔  członu 
nieliniowego nazywamy stosunek wartości 
zespolonej amplitudy 1 Harmonicznej 
odpowiedzi wywołanej wymuszenie 
sinusoidalnym w stanie ustalonym do 
wartości zespolonej amplitudy tego 
wymuszenia to  B, C , 1-harn. 
e(t)=Asin𝜑          𝜑 = 𝜔𝑡 

  

  
 jeżeli  e(t) będzie sinusoidalne to na wyjściu 
członu o char. statycznej f(e) sygnał będzie 
okresowy ale nie sinusoidalny.