1

Konrad Weinreb

ZADANIA ZE STANÓW USTALONYCH SYMETRYCZNYCH

MASZYN ELEKTRYCZNYCH

1. TRANSFORMATORY

1.1. Transformator jednofazowy o danych : S

N

= 10kVA, U

1N

= 500V, U

2N

= U

20

= 220V,

u

k

= 4,5%, P

wN

= 100W, P

Fe

= 120W, I

0

= 5% I

N

ma uzwojenie wykonane z miedzi. Po napra-

wie zastąpiono uzwojenie miedziane uzwojeniem aluminiowym o tych samych wymiarach.
Zakładając równość strat znamionowych przed i po remoncie wyznaczyć dla tego transforma-
tora: nowe parametry schematu zastępczego, nową moc znamionową S

x

, nowy prąd znamio-

nowy I

1x

oraz nowe napięcie zwarcia u

k

. Konduktywność: miedzi -

γ

Cu

= 57MS/m, alumi-

nium -

γ

Al

= 34,8MS/m.

1.2. Transformator jednofazowy ma liczby zwojów N

1

= 400, N

2

= 200, zaś jego parametry

wynoszą: L

σ

1

= 0,01H, L

σ

2

= 0,0025H, L

m

= 0,75H, R

1

= 0,6

Ω

, R

2

= 0,15

Ω

. Określić napięcie

po stronie wtórnej, jeżeli po stronie pierwotnej przyłożono napięcie sinusoidalnie zmienne o
wartości skutecznej 220V i częstotliwości f = 50Hz oraz gdy strona wtórna jest: a) rozwarta,
b) obciążona rezystancją R = 8

Ω

, c) obciążona impedancją o charakterze indukcyjnym i war-

tości Z = 8

Ω

, cos

ϕ

= 0,6.

1.3.

Transformator jednofazowy o danych: S

N

= 5kVA, U

1N

= 500V, U

2N

= 220V, u

k

= 10%,

P

wN

= 250W zasila element grzejny o danych znamionowych: P

N

= 5kW, U

N

= 220V. O ile

zmieniła się moc grzejnika przy zasilaniu z tego transformatora? Wskazówka: przy oblicze-
niach przyjąć schemat zastępczy transformatora z pominięciem prądu biegu jałowego czyli
parametrów gałęzi poprzecznej.

1.4.

Transformator trójfazowy ma dane: S

N

= 1000kVA, U

1N

= 110kV, U

2N

= 6kV, Yy0,

u

k

= 9,5%, P

wN

= 4kW, P

Fe

= 5kW, I

0

= 1,5% I

N

. Zakładając

2

1

σ

σ

X

X

′

=

oraz

2

1

R

R

′

=

wyzna-

czyć parametry schematu zastępczego transformatora.

1.5.

Transformator 3-fazowy o danych: S

N

= 1000kVA, U

1N

= 60kV, U

2N

= 6kV, Yd5,

u

k

= 8%, P

wN

= 5kW jest zasilony z sieci trójfazowej o napięciu U = 60kV. Na linii U = 6kV

nastąpiło zwarcie trójfazowe w odległości dziesięciu kilometrów od stacji transformatorowej.
Przyjmując reaktancję fazową linii równą 0,4

Ω

/km obliczyć ustalony prąd zwarcia I

kx

po stro-

nie 60kV.

1.6.

Transformator o połączeniu uzwojeń Yd5 ma dane znamionowe: S

N

= 200kVA,

U

1N

= 20kV, U

2N

= 400V, u

k

= 6%, P

wN

= 4kW, f

N

= 50Hz. Transformator ten zasila odbiornik

połączony w gwiazdę o stałej impedancji o charakterze pojemnościowym i danych znamio-
nowych: P

N

= 200kW, U

N

= 400V,

6

0,

cos

=

N

ϕ

. Pomijając prąd biegu jałowego określić prąd

przewodowy strony pierwotnej oraz napięcie fazowe na odbiorniku, jeśli napięcie zasilające
transformator wynosi dokładnie 20kV. Obliczyć procentową zmienność napięcia po stronie
wtórnej. Jak zmieni się moc czynna pobierana przez odbiornik w stosunku do mocy znamio-
nowej odbiornika?

1.7.

Obliczyć prądy fazowe transformatora po stronie pierwotnej i wtórnej, jeżeli jest on

obciążony symetrycznie impedancjami o charakterze indukcyjnym i wartościach fazowych

2

Z = 2,5

Ω

, przy cos

ϕ

= 0,8. Transformator ma układ i grupę połączeń Yy0, impedancje połą-

czone są w trójkąt. Dane transformatora: L

σ

1

= 0,01H, L

σ

2

= 0,05mH, L

m

= 7,5H, R

1

= 0,3

Ω

,

R

2

= 1,5m

Ω

, U

1ph

= 6000/ 3 V, U

2ph

= 400/ 3 V. Jak zmienią się prądy w transformatorze,

jeśli obciążenie będzie miało charakter pojemnościowy o tych samych wartościach liczbo-
wych? Wskazówka: przy zmianie symetrycznych impedancji fazowych z połączenia w trójkąt
(

∆

) na połączenie w gwiazdę (Y) spełniona jest zależność Z

∆

= 3Z

Y

.

ROZWIĄZANIA ZADAŃ I ODPOWIEDZI DO ROZDZIAŁU 1

1.1. Prąd znamionowy strony pierwotnej (zasilanej) transformatora wynosi:

A

U

S

I

N

N

N

20

500

10000

1

1

=

=

=

Wszystkie obliczenia zostaną przeprowadzone dla przypadku, gdy schemat zastępczy odpo-
wiada sprowadzeniu strony wtórnej transformatora na stronę pierwotną. Sposób obliczeń nie
ulega zmianie przy przeciwnym podejściu. Parametry gałęzi poprzecznej schematu zastęp-
czego transformatora oblicza się z danych opisujących stan jałowy pracy. Napięcie znamio-
nowe strony wtórnej (odbierającej moc) jest równe napięciu zmierzonemu na zaciskach trans-
formatora w stanie jałowym.

Rezystancja reprezentująca straty w rdzeniu:

Ω

=

=

=

)

3

(

,

2083

120

500

2

2

1

Fe

N

Fe

P

U

R

,

stąd prąd w tej rezystancji:

A

R

U

I

Fe

N

Fe

24

,

0

1

=

=

.

Prąd biegu jałowego:

A

I

I

N

1

%

5

1

0

=

=

.

Prąd magnesujący:

A

I

I

I

Fe

m

971

,

0

2

2

0

=

−

=

.

Reaktancja główna:

Ω

=

=

05

,

515

1

m

N

m

I

U

X

.

Parametry gałęzi podłużnej schematu zastępczego transformatora oblicza się z danych opisu-
jących stan zwarcia.

Rezystancja zwarcia:

Ω

=

=

=

25

,

0

20

100

2

2

1N

wN

kCu

I

P

R

.

Impedancja zwarcia:

Ω

=

⋅

=

=

125

,

1

20

500

045

,

0

%

100

1

1

N

N

k

kCu

I

U

u

Z

,

stąd reaktancja zwarcia:

Ω

=

−

=

0968

,

1

2

2

kCu

kCu

kCu

R

Z

X

.

Z tematu zadania wynika, że pomimo przezwojenia, wartość reaktancji głównej, reaktancji
rozproszeń oraz rezystancji odpowiadającej stratom w rdzeniu nie zmieniają się. Przekładnia
napięciowa transformatora jest równa stosunkowi napięć znamionowych przy spełnieniu wa-

runku, że jest

≥

1:

273

,

2

20

1

2

1

=

=

=

U

U

U

U

K

N

N

N

Z warunku równości wymiarów geometrycznych uzwojeń przed i po remoncie wynika nastę-
pująca relacja ich rezystancji:

Al

Cu

kCu

kAl

R

R

γ

γ

=

,

3

stąd:

Ω

=

⋅

=

4095

,

0

8

,

34

57

25

,

0

kAl

R

.

Ponieważ reaktancja zwarcia nie zmieniła się, to:

Ω

=

=

097

,

1

kCu

kAl

X

X

Impedancja zwarcia dla uzwojenia aluminiowego wynosi:

Ω

=

+

=

171

,

1

2

2

kAl

kAl

kAl

X

R

Z

Z warunku wartości strat znamionowych w uzwojeniach przed i po remoncie:

AlN

CuN

P

P

∆

=

∆

wynika zależność:

2

1

2

1

N

kCu

x

kAl

I

R

I

R

=

i dalej:

A

I

R

R

I

N

kAl

kCu

x

627

,

15

20

781

,

0

1

1

=

⋅

=

=

.

Moc pozorna znamionowa w nowych warunkach wyniesie:

7,813

1

1

=

=

x

N

x

I

U

S

kVA

.

Nowe procentowe napięcie zwarcia będzie równe:

%

66

,

3

%

100

1

1

=

=

N

x

kAl

kx

U

I

Z

u

Odpowiedź: W wyniku przezwojenia uległy zmianie jedynie wartości rezystancji uzwojeń:

=

′

=

Al

Al

R

R

2

1

0,2047

Ω

. Wartości pozostałych parametrów schematu zastępczego pozostają

bez zmian. Nowa moc znamionowa transformatora wynosi 7,813kVA, nowy prąd znamiono-
wy płynący po stronie górnego napięcia jest równy 15,627A, zaś nowe procentowe napięcie
zwarcia wynosi 3,66%.

1.2.

Odpowiedź: a) U

2

= 108,55V, b) U

2

= 102,87V, c) U

2

= 91,87V.

1.3. Element grzejny ma charakter rezystancyjnym o wartości:

Ω

=

=

=

68

,

9

5000

220

2

2

N

N

L

P

U

R

Z danych tematu zadania (pytamy się o moc grzejnika) wynika, że wygodniej jest rozpatry-
wać schemat zastępczy transformatora od strony odbiornika (wtórnej).
Stąd obliczamy parametry schematu zastępczego transformatora sprowadzone na stronę wtór-
ną.

Prąd znamionowy -

A

U

S

I

N

N

N

727

,

22

220

5000

2

2

=

=

=

.

Rezystancja zwarcia -

Ω

=

=

=

484

,

0

727

,

22

250

2

2

2 N

wN

k

I

P

R

.

Impedancja zwarcia -

Ω

=

⋅

=

=

968

,

0

727

,

22

220

1

,

0

%

100

2

2

N

N

k

k

I

U

u

Z

.

Reaktancja zwarcia -

Ω

=

−

=

8383

,

0

2

2

k

k

k

R

Z

X

.

Interesuje nas jedynie moduł wartości skutecznej prądu, a nie jego faza.
Zatem nie znając fazy napięcia strony wtórnej możemy przyjąć, że jest równa zero.

V

e

U

U

j

N

N

220

0

2

2

=

=

.

4

Wartość prądu płynącego przez odbiornik wyniesie wtedy:

A

j

j

Z

U

I

I

k

N

L

773

,

1

5

,

21

8383

,

0

164

,

10

220

2

2

−

=

+

=

=

=

, I

L

= 21,57A.

Moc pobierana przez odbiornik wynosi:

W

I

R

P

L

L

L

4504

2

≅

=

.

Oznacza to, że odbiornik pobiera moc czynną mniejszą od znamionowej. Jest to spowodowa-
ne spadkiem napięcia na transformatorze.
Różnica wynosi:

∆

P

L

= P

N

– P

L

= 496W.

Odpowiedź: Moc grzejnika zasilanego z transformatora zmniejszyła się w stosunku do mocy
znamionowej o 496W.

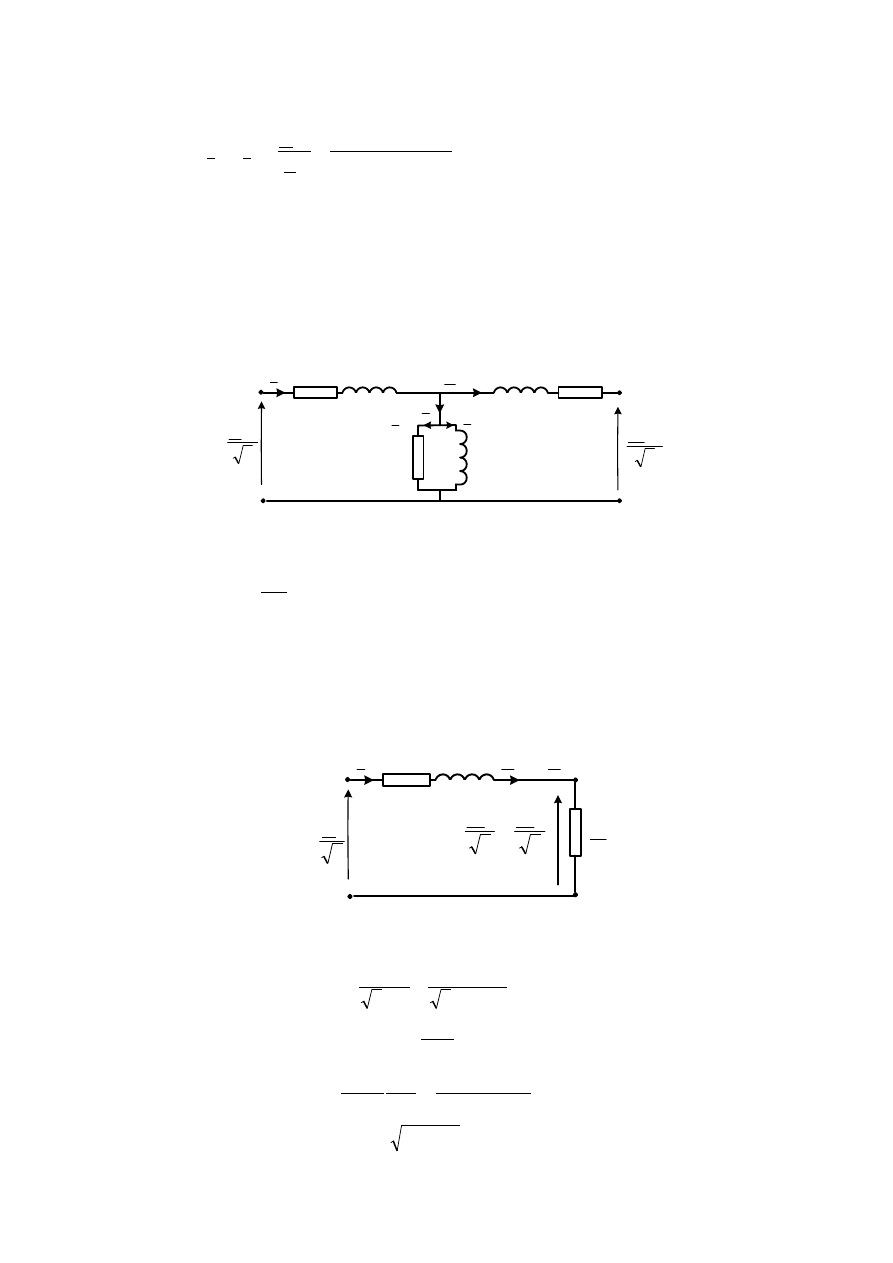
1.4. Schemat zastępczy fazowy transformatora ma postać:

1

I

1

R

1

σ

jX

2

σ

X

j

′

2

r

I

′

3

1N

U

Fe

R

m

jX

0

I

Fe

I

m

I

3

2 N

U

′

2

R

′

gdzie:

=

′

=

2

1

R

R

24,2

Ω

,

=

′

=

2

1

σ

σ

X

X

574,24

Ω

,

=

m

X

855,6k

Ω

,

=

Fe

R

2,42M

Ω

.

1.5. I

kx

= 50,453 A,

24

,

5

1

=

N

kx

I

I

.

1.6. Na podstawie danych przyjmujemy do obliczeń uproszczony schemat zastępczy fazowy
transformatora, z pominięciem gałęzi poprzecznej. Układ „transformator-odbiornik” rozpatru-
jemy od strony zasilania, sprowadzając układ połączeń transformatora do zastępczego układu

Yy

, co przy skojarzeniu odbiornika w gwiazdę pozwala w prosty sposób połączyć oba sche-

maty, jak na rysunku poniżej:

1

I

k

R

k

jX

L

r

I

I

′

=

′

2

3

1

U

3

3

2

L

U

U

′

=

′

L

Z

′

Parametry zwarciowe transformatora dla tego zastępczego układu połączeń można wyznaczyć
z formuł:

A

U

S

I

N

N

N

77

,

5

20000

3

200000

3

1

1

≅

⋅

=

=

,

Ω

=

=

40

3

2

1N

wN

k

I

P

R

,

Ω

=

⋅

=

=

120

200000

20000

06

,

0

%

100

2

2

1

N

N

k

k

S

U

u

Z

Ω

≅

−

=

14

,

113

2

2

k

k

k

R

Z

X

,

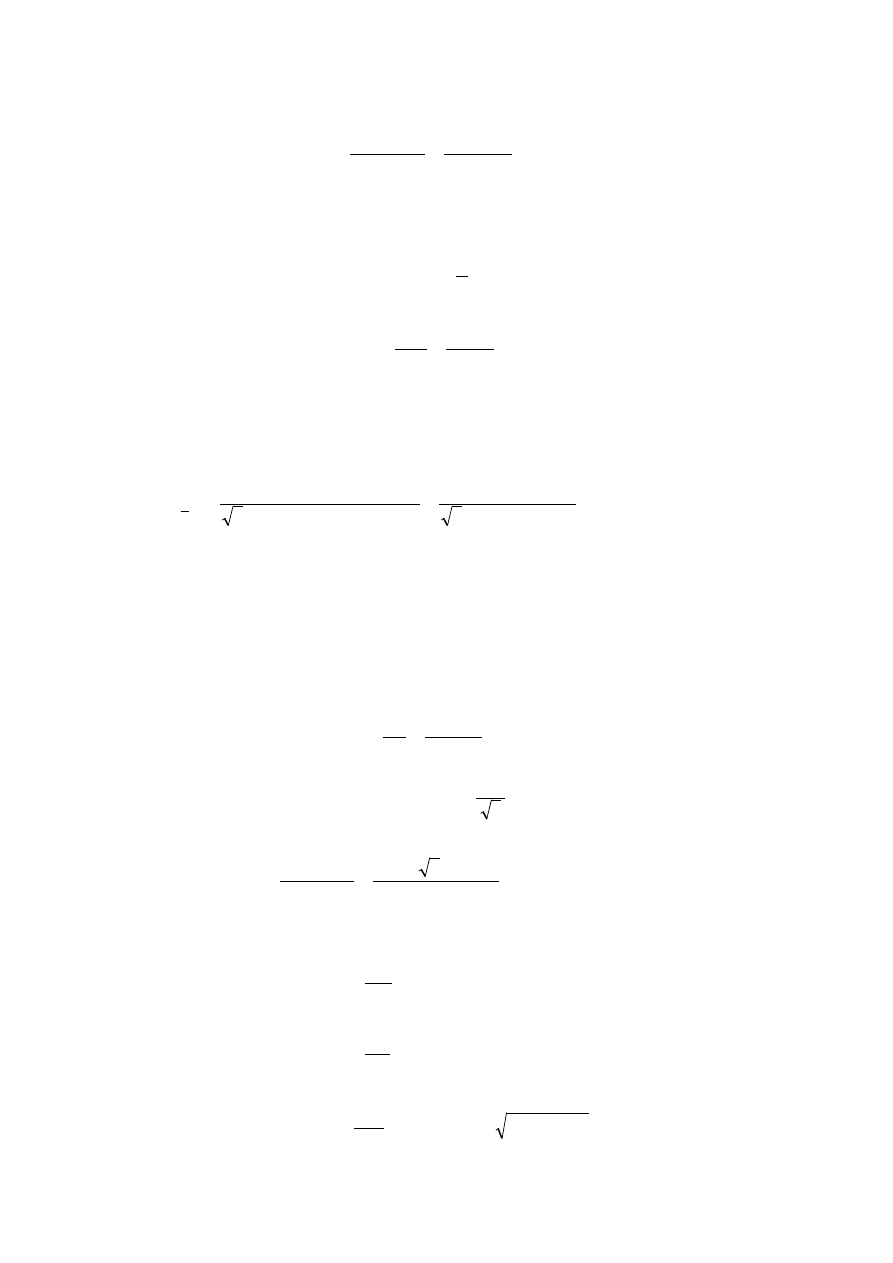
5

Impedancję fazową odbiornika można wyznaczyć z zależności:

Ω

=

⋅

=

=

48

,

0

200000

6

,

0

400

cos

2

2

N

N

N

L

P

U

Z

ϕ

,

Ω

=

=

288

,

0

cos

N

L

L

Z

R

ϕ

,

Ω

=

=

384

,

0

sin

N

L

L

Z

X

ϕ

.

W postaci zespolonej impedancja ta jest równa:

=

−

=

L

L

L

jX

R

Z

0,288 – j0,384 (

Ω

).

Parametry te są sprowadzone na stronę górnego napięcia transformatora poprzez uwzględnie-
nie przekładni napięciowej:

50

400

20000

2

1

=

=

=

N

N

U

U

K

Zatem:

Ω

=

=

′

720

2

L

L

R

K

R

,

Ω

=

=

′

960

2

L

L

X

K

X

.

Prąd pobierany z sieci ma wartość:

)

(

55

,

7

78

,

6

)

86

,

846

760

(

3

20000

)]

(

)

[(

3

1

1

A

j

j

X

X

j

R

R

U

I

L

k

L

k

N

x

+

=

−

=

′

−

+

′

+

=

.

Zatem: I

1x

= 10,15A.

Odpowiadający mu prąd przewodowy po stronie odbiornika wynosi:

A

I

K

I

x

x

46

,

507

15

,

10

50

1

2

=

⋅

=

⋅

=

.

Moc czynna pobierana przez odbiornik w tym stanie pracy wynosi:

W

I

R

P

x

L

x

222494

)

46

,

507

(

288

,

0

3

3

2

2

2

=

⋅

⋅

=

=

i jest większa od mocy znamionowej:

112

,

1

200000

222494

=

=

N

x

P

P

razy.

Napięcie fazowe na odbiorniku jest równe:

V

I

Z

U

U

x

L

x

phx

58

,

243

3

2

2

=

⋅

=

=

.

Zmienność napięcia strony wtórnej transformatora wynosi zatem:

%

47

,

5

0547

,

0

400

58

,

243

3

400

2

2

2

−

=

−

=

⋅

−

=

−

=

∆

N

x

N

U

U

U

u

Zmienność napięcia przy znamionowym napięciu zasilania można również wyznaczyć z za-
leżności:

)

sin

cos

(

%

%

2

2

%

L

XN

L

RN

N

x

u

u

I

I

U

ϕ

ϕ

+

=

∆

lub równoważnej

)

sin

cos

(

%

%

1

1

%

L

XN

L

RN

N

x

u

u

I

I

U

ϕ

ϕ

+

=

∆

gdzie:

100

%

N

wN

RN

S

P

u

=

,

2

%

2

%

%

RN

k

XN

u

u

u

−

=

.

6

W funkcjach kąta

L

ϕ

należy uwzględnić charakter obciążenia (dla obciążenia pojemnościo-

wego kąt jest ujemny).

Tu:

675

,

288

2

=

N

I

A,

,

758

,

1

2

2

=

N

x

I

I

,

2

%

=

RN

u

657

,

5

%

=

XN

u

.

stąd:

%

85

,

5

%

−

=

∆

u

.

Napięcie fazowe na obciążeniu wyznaczone ze zmienności napięcia wynosi:

4

,

244

3

400

0585

,

1

3

)

100

1

(

2

%

=

⋅

=

∆

−

=

N

phx

U

u

U

V

Pomimo uproszczonej metody wyznaczania napięcia można przyjąć, że otrzymany wynik
niewiele różni się od uzyskanego z dokładnych obliczeń.

Odpowiedź: Prąd przewodowy strony pierwotnej obciążonego transformatora wynosi
10,15A, napięcie fazowe na odbiorniku jest równe 243,58V i

wzrosło w stosunku do znamio-

nowego o 5,47%. Stąd też moc czynna pobierana przez odbiornik zwiększyła się w stosunku
do jego mocy znamionowej 1,112 razy.

1.7. Dla obciążenia o charakterze indukcyjnym prądy fazowe transformatora wynoszą:

=

1

I

18,93A,

=

2

I

270,15A.

Dla obciążenia o charakterze pojemnościowym prądy fazowe transformatora wynoszą:

=

1

I

17,96A,

=

2

I

281,85A.

2. PRACA RÓWNOLEGŁA TRANSFORMATORÓW

2.1.

Dwa transformatory o danych: A) S

N

= 4MVA, U

1N

= 30kV, U

2N

= 6,3kV, f

N

= 50Hz,

u

k

= 6,5%, P

wN

= 30kW, Yd11; B) S

N

= 2MVA, U

1N

= 30kV, U

2N

= 6,3kV, f

N

= 50Hz, u

k

= 10%,

P

wN

= 18kW, Yd11 są po stronie 1 zasilone znamionowo , a po stronie 2 połączone równolegle

i obciążone impedancją o charakterze indukcyjnym i wartości fazowej Z

L

= 6

Ω

, przy

cos

ϕ

L

= 0,8, połączoną w gwiazdę. Obliczyć prądy obu transformatorów po stronie 2. Jaką

największą moc pozorną

max

S

może przesłać układ bez przeciążenia transformatorów? Jak

zmienią się te prądy, gdy transformator A będzie miał przekładnię 30kV/6,5kV (dla uprosz-
czenia pominąć zmianę impedancji zwarcia wynikłej ze zmiany przekładni). Podać wartość
prądu wyrównawczego

∆

I, jaki płynąłby po stronie 2 w przypadku odłączenia obciążenia.

2.2.

Trzy transformatory o danych: A) S

N

= 2000kVA, K = 30kV/6,3kV, Dy11, u

k

= 7%,

P

wN

= 20kW;

B) S

N

= 4000kVA,

K = 30kV/6,3kV,

Dy11,

u

k

= 6,3%,

P

wN

= 30,2kW;

C) S

N

= 8000kVA, K = 30kV/6,3kV, Dy11, u

k

= 7,5%, P

wN

= 65kW pracują równolegle. Obli-

czyć jaką maksymalną moc S

max

można obciążyć transformatory, aby prąd żadnego nie prze-

kroczył wartości nominalnej. Określić maksymalny kąt rozsunięcia fazowego

α

max

między

prądami przewodowymi w tych transformatorach.

2.3.

Dwa transformatory o danych: A) S

N

= 6,3MVA, U

1N

= 30kV, U

2N

= 6,3kV, f

N

= 50Hz,

u

k

= 7%, P

wN

= 94,5kW, Dy0; B) S

N

= 2,5MVA, U

1N

= 30kV, U

2N

= 6,3kV, f

N

= 50Hz,

u

k

= 10%, P

wN

= 25kW, Dy0 zasilone znamionowo, pracują równolegle. Obliczyć ich prądy i

napięcia na zaciskach wtórnych, gdy wspólne szyny obciążono prądem odpowiadającym su-

7

mie arytmetycznej mocy znamionowej obu transformatorów , przy indukcyjnym charakterze
obciążenia i

8

,

0

cos

=

ϕ

.

2.4.

Transformator 3-fazowy ma dane katalogowe:

S

N

= 2

MVA, U

1N

= 60

kV, U

2N

= 6,3

kV,

Yd5, u

k

= 8%,

P

wN

= 10

kW. Transformator jest połączony na wspólnych szynach z drugim o

danych:

S

N

= 3

MVA, U

1N

= 110

kV, U

2N

= 6,3

kV, Yd5, u

k

= 10%,

P

wN

= 15

kW, zasilonym z

sieci o napięciu 115

kV. Obliczyć prąd wyrównawczy

∆

I na biegu jałowym po stronie 6kV.

Wskazówka: Przyjąć, że fazy napięć sieci 60

kV i 115kV są ze sobą zgodne.

2.5.

Dwa transformatory trójfazowe mają dane znamionowe:

A) S

N

= 400

kVA, U

1N

= 3

kV,

U

2N

= 0,4

kV, Dy11, u

k

= 5%,

B) S

N

= 200

kVA, U

1N

= 3

kV, U

2N

= 0,4

kV, Yy0, u

k

= 5%. Obli-

czyć prąd wyrównawczy

∆

I po stronie niskiego napięcia w przypadku pracy równoległej tych

transformatorów.

2.6.

Dwa transformatory

Yy0 o danych znamionowych: A) S

N

= 600

kVA, U

1N

= 3

kV,

U

2N

= 0,4

kV, u

k

= 5%,

P

wN

= 12

kW; B) S

N

= 250

kVA, U

1N

= 3

kV, U

2N

= 0,4

kV, u

k

= 4,1%,

P

wN

= 6

kW pracują równolegle zasilanie z sieci sztywnej o napięciu U = 2,5kV. Transformato-

ry te są obciążone 3-fazowym symetrycznym odbiornikiem o charakterze indukcyjnym połą-
czonym w gwiazdę, o danych:

I = 1000A przy

8

,

0

cos

=

ϕ

. Obliczyć moc odbiornika

P i sto-

pień obciążenia w stosunku do obciążenia znamionowego obu transformatorów.

ROZWIĄZANIA ZADAŃ I ODPOWIEDZI DO ROZDZIAŁU 2

2.1. W analizie pracy równoległej transformatorów wygodnie jest rozważać schemat zastęp-
czy transformatora przy sprowadzeniu parametrów schematu na stronę obciążenia. Z warun-
ków zadania wynika, że schematy zastępcze dla fazy reprezentowane będą jedynie przez pa-
rametry gałęzi podłużnych, tzn. parametry zwarciowe. Ponieważ interesują nas prądy płynące
przez obciążenie i prądy przewodowe stron wtórnych transformatorów, w obliczeniach
wprowadzamy, niezależnie od realnego układu połączeń, równoważne w wymienionym
aspekcie połączenie faz

Yy .

I tak dla transformatora:

A)

A

U

S

I

NA

NA

NA

57

,

366

6300

3

4000000

3

2

2

=

⋅

=

=

,

0744

,

0

403121

30000

3

2

2

=

=

=

NA

wNA

kA

I

P

R

Ω

,

645

,

0

4000000

6300

065

,

0

%

100

2

2

2

=

⋅

=

=

NA

NA

kA

kA

S

U

u

Z

Ω

,

641

,

0

2

2

=

−

=

kA

kA

kA

R

Z

X

Ω

,

641

,

0

0744

,

0

j

Z

kA

+

=

(

Ω

).

B)

A

U

S

I

NB

NB

NB

29

,

183

6300

3

2000000

3

2

2

=

⋅

=

=

,

1786

,

0

100786

18000

3

2

2

=

=

=

NB

wNB

kB

I

P

R

Ω

,

9845

,

1

2000000

6300

1

,

0

%

100

2

2

2

=

⋅

=

=

NB

NB

kB

kB

S

U

u

Z

Ω

,

9764

,

1

2

2

=

−

=

kB

kB

kB

R

Z

X

Ω

,

9764

,

1

1786

,

0

j

Z

kB

+

=

(

Ω

).

Impedancja fazowa obciążenia przy połączeniu w gwiazdę ma wartość:

Ω

+

=

+

⋅

=

+

=

j3,6

4,8

j0,6)

(0,8

6

)

sin

(cos

L

L

L

L

j

Z

Z

ϕ

ϕ

.

8

Aby przedstawić schemat zastępczy opisujący pracę transformatorów na wspólny odbiór
sprawdzamy, czy oba transformatory mają równe napięcia po stronie wtórnej co do amplitudy
i fazy. Ponieważ transformatory mają ten sam układ i grupę połączeń oraz równe napięcia
strony pierwotnej i napięcia strony wtórnej (co oznacza równość przekładni napięciowych

B

A

K

K

=

, powyższe wymaganie jest spełnione:











=

∧

=

⇒

=

⇒

=

B

A

B

A

j

B

j

A

B

A

U

U

e

U

e

U

U

U

B

A

α

α

α

α

2

2

2

2

2

2

W zadaniu napięcia te mają wartość znamionową i dla uproszczenia analizy przyjmujemy ich
fazy za równe zeru (przy

B

A

α

α

=

wartość fazy napięcia strony wtórnej transformatora nie

ma wpływu na wartości skuteczne prądów, gdyż o nich decydują impedancje układu i moduł
napięcia) :

N

j

N

B

A

U

e

U

U

U

2

0

2

2

2

=

=

=

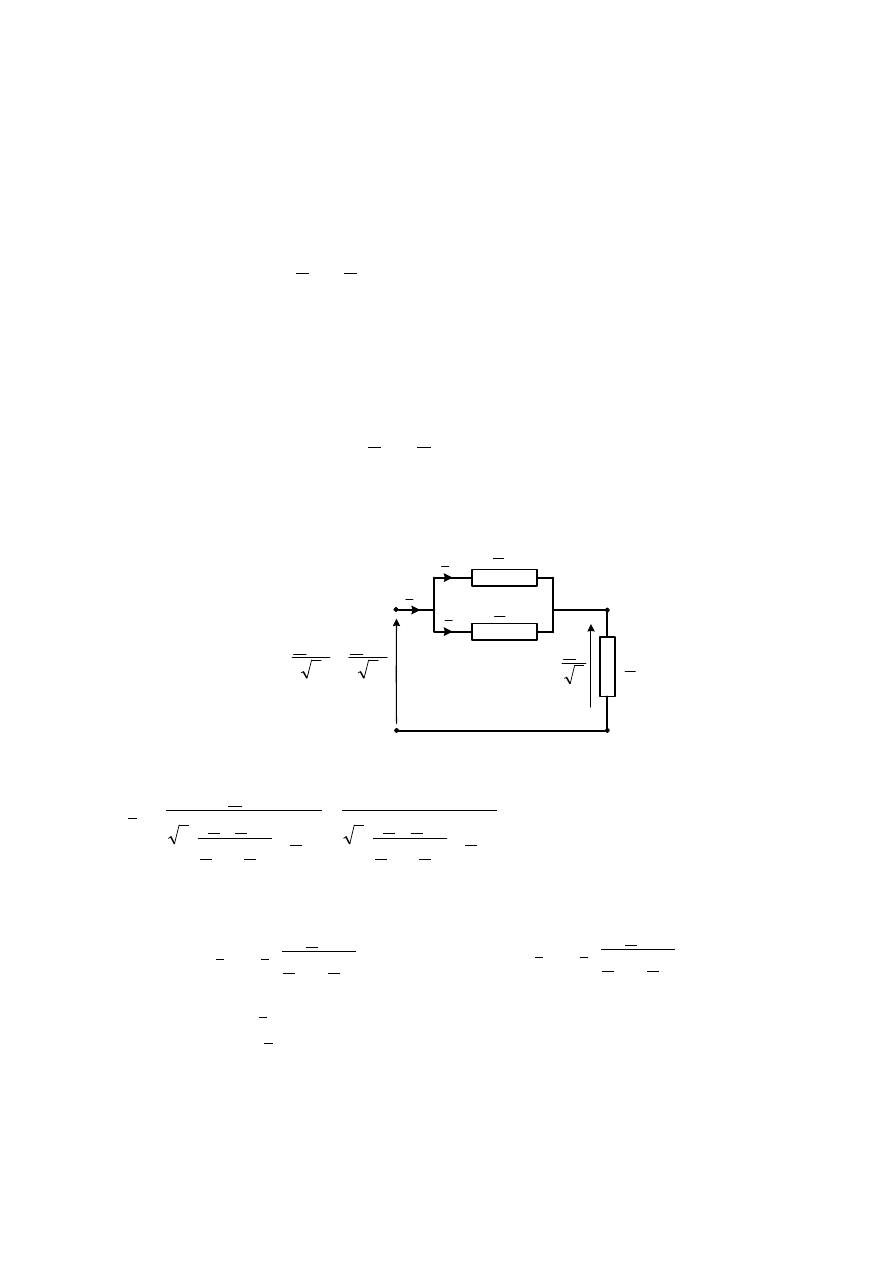
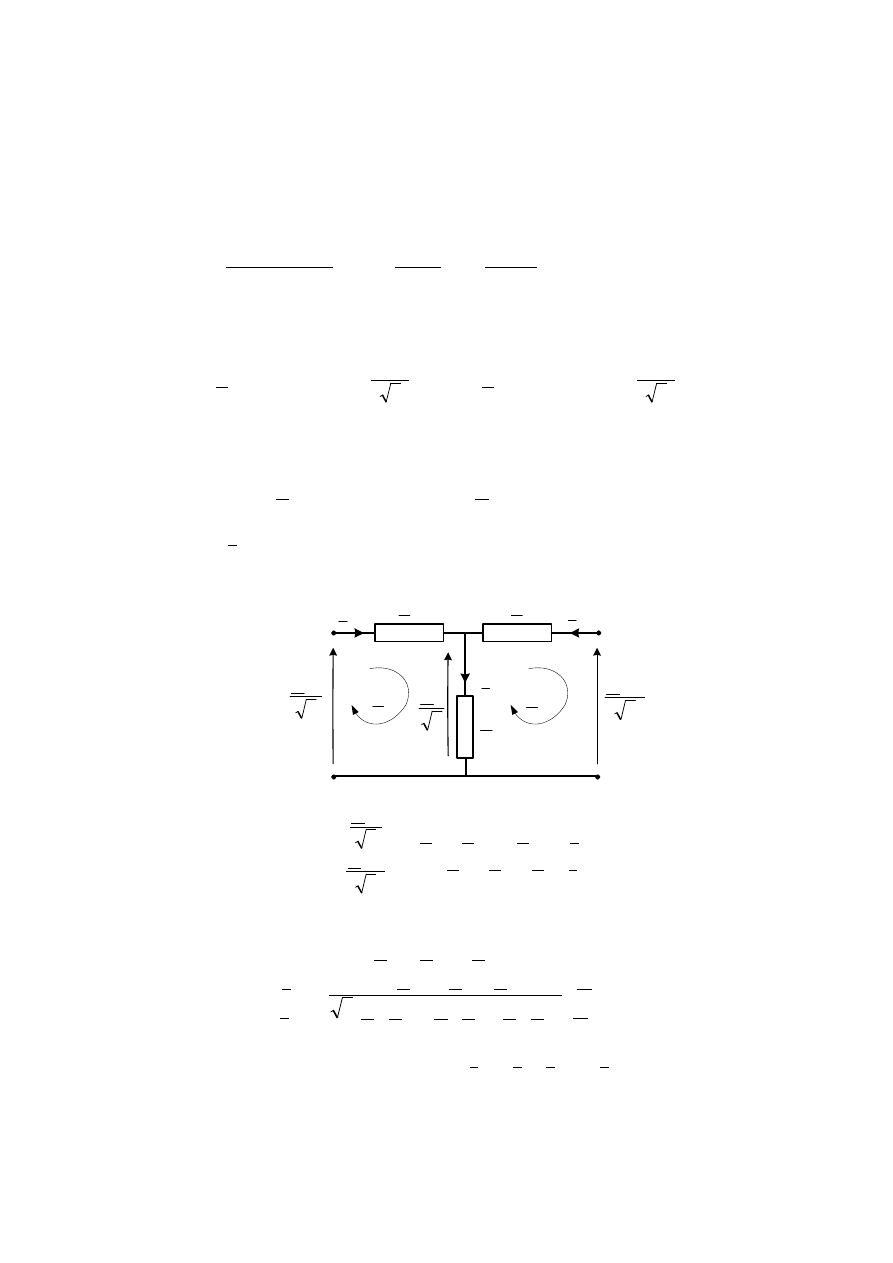
Stosując zasadę superpozycji można w tym przypadku pracy równoległej transformatorów
przypisać schemat zastępczy, w którym ich impedancje zwarciowe są połączone ze sobą rów-
nolegle.

L

I

3

3

2

2

NB

NA

U

U

=

3

L

U

L

Z

A

I

2

B

I

2

kA

Z

kB

Z

Zatem prąd obciążenia wyznaczony jest przez zależność:

=













+

+

=













+

+

=

L

kB

kA

kB

kA

N

L

kB

kA

kB

kA

N

L

Z

Z

Z

Z

Z

U

Z

Z

Z

Z

Z

U

I

3

3

2

2

438,77 – j369,24

A,

L

I

= 573,46

A.

Z rozpływu prądów wynika, że:

kB

kA

kB

L

A

Z

Z

Z

I

I

+

=

2

oraz

kB

kA

kA

L

B

Z

Z

Z

I

I

+

=

2

A

j

I

A

6

276

87

332

2

,

,

−

=

,

A

I

A

79

432

2

,

=

.

A

j

I

B

62

,

92

91

,

105

2

−

=

,

A

I

B

7

,

140

2

=

.

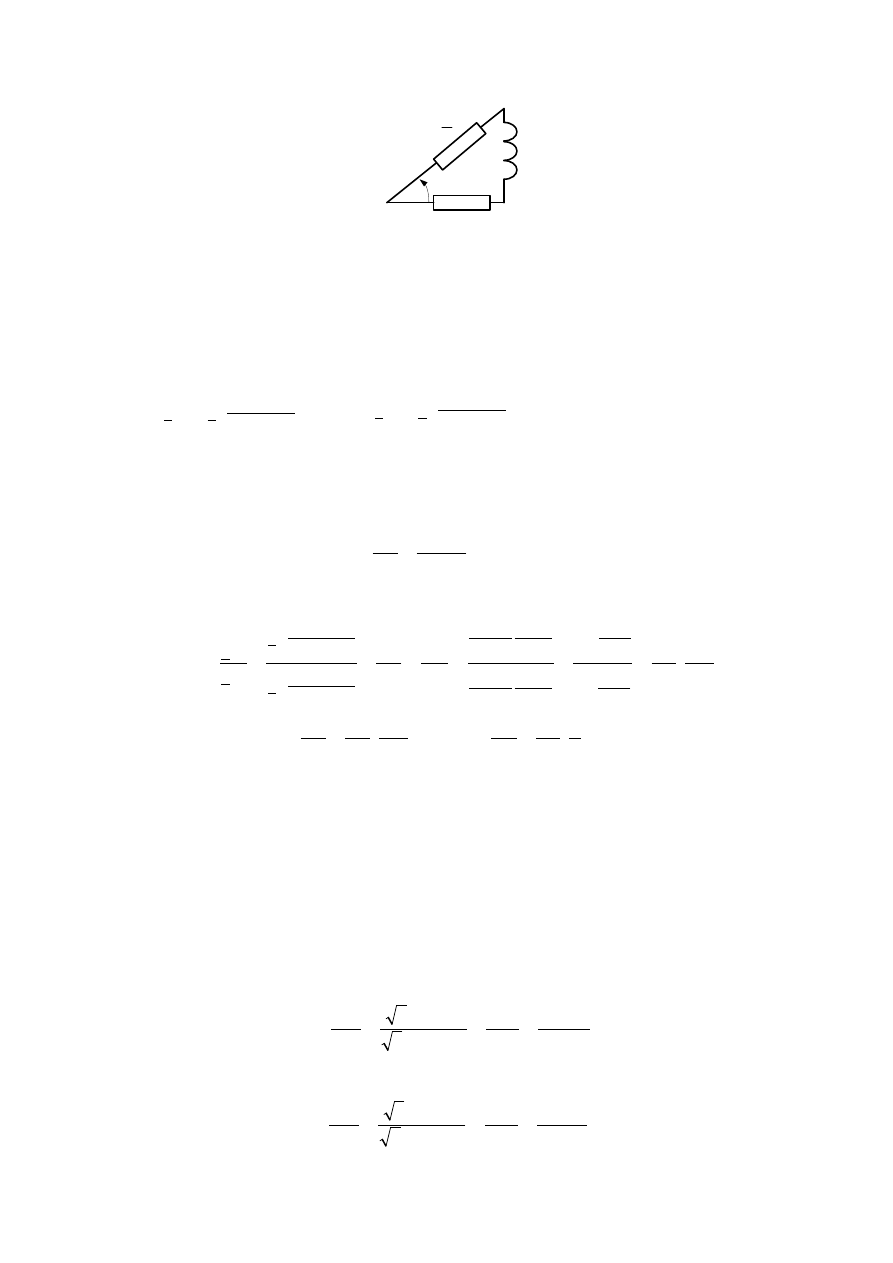
Ostatnie obliczenia można uprościć przez wprowadzenie dla impedancji zwarciowych, w
miejsce liczb zespolonych, ich modułów. Jest to uzasadnione wtedy, gdy trójkąty impedancji
zwarciowych dla obu transformatorów będą podobne.

9

k

Z

k

jX

k

R

k

ϕ

Dla danych tego zadania można przyjąć to uproszczenie, gdyż kąty pomiędzy częścią czynną
a modułem impedancji (kąty zwarciowe) wynoszą odpowiednio: dla transformatora

A -

ϕ

kA

= 83,38

°

, dla transformatora

B -

ϕ

kB

= 84,84

°

.

Kąt przesunięcia między prądami przewodowymi transformatorów wynosi zatem:

∆

ϕ

=

ϕ

kA

-

ϕ

kB

= -1,46

°

Oznacza to, że można przyjąć, że trójkąty impedancji są podobne.

Stąd:

kB

kA

kB

L

A

Z

Z

Z

I

I

+

≅

2

oraz

kB

kA

kA

L

B

Z

Z

Z

I

I

+

≅

2

Zatem ostatecznie:

I

2A

= 432,8

A,

I

2B

= 140,66

A.

Wyniki uzyskane tą drogą nieznacznie różnią się od wyników z obliczeń dokładnych.
Wyznaczony stąd stosunek prądów strony wtórnej obu transformatorów wynosi:

08

,

3

66

,

140

8

,

432

2

2

=

=

B

A

I

I

.

Powyższy rozkład prądów można wyznaczyć bezpośrednio z danych znamionowych:

NB

NA

kA

kB

NA

N

kA

NB

N

kB

NA

NA

kA

NB

NB

kB

kA

kB

B

A

kB

kA

kA

L

kB

kA

kB

L

B

A

S

S

u

u

S

U

u

S

U

u

S

U

u

S

U

u

Z

Z

I

I

Z

Z

Z

I

Z

Z

Z

I

I

I

⋅

=

=

=

=

=

+

+

≅

2

2

2

2

2

2

2

2

2

2

2

2

%

100

%

100

NB

NA

kA

kB

B

A

S

S

u

u

I

I

⋅

=

2

2

,

tu:

08

,

3

2

4

5

,

6

10

2

2

=

⋅

=

B

A

I

I

.

Z powyższej zależności, określającej rozkład prądu obciążenia na poszczególne transformato-
ry wynikają wnioski:

•

przy równych mocach znamionowych (

NB

NA

S

S

=

) stosunek prądów stron wtórnych trans-

formatorów jest odwrotnie proporcjonalny do stosunku ich napięć zwarcia - bardziej bę-
dzie obciążony transformator o mniejszym napięciu zwarcia;

•

przy równych napięciach zwarcia transformatorów (

kB

kA

u

u

=

) stosunek prądów stron

wtórnych transformatorów jest wprost proporcjonalny do stosunku ich mocy znamiono-
wych.

Stwierdzamy, że transformator

A jest przeciążony w stosunku do mocy znamionowej:

18

1

57

366

69

432

3

3

2

2

2

2

2

2

,

,

,

=

=

=

=

=

AN

A

AN

NA

A

NA

AN

A

A

I

I

I

U

I

U

S

S

k

.

Transformator

B jest niedociążony w stosunku:

77

0

29

183

66

140

3

3

2

2

2

2

2

2

,

,

,

=

=

=

=

=

BN

B

BN

NB

B

NB

BN

B

B

I

I

I

U

I

U

S

S

k

.

10

Moc przesyłana do obciążenia jest sumą mocy obu transformatorów.

BN

B

AN

A

B

A

S

k

S

k

S

S

S

+

=

+

=

Aby obliczyć maksymalną dopuszczalną wartość tej mocy, gdy prąd każdego z transformato-
rów nie przekracza wartości znamionowej, należy zmniejszyć jej wartość o krotność przecią-
ż

enia transformatora

A.

Zatem:

3

5

18

1

2

77

0

4

,

,

,

max

≅

⋅

+

=

+

=

+

=

A

BN

B

AN

A

BN

B

AN

A

k

S

k

S

k

S

k

S

k

S

MVA.

Po zmianie przekładni dla transformatora

A każda z impedancji zwarciowych będzie zasilana

przez inne źródła napięcia, czyli:

kA

Z

przez

3

6500

2

=

A

U

oraz

kB

Z

przez

3

6300

2

=

B

U

W dalszej analizie przyjmujemy, że fazy napięć zasilania są te same (z uwagi na te same
układy i grupy połączeń) i są równe zeru:

A

j

A

A

U

e

U

U

2

0

2

2

=

=

oraz

B

j

B

B

U

e

U

U

2

0

2

2

=

=

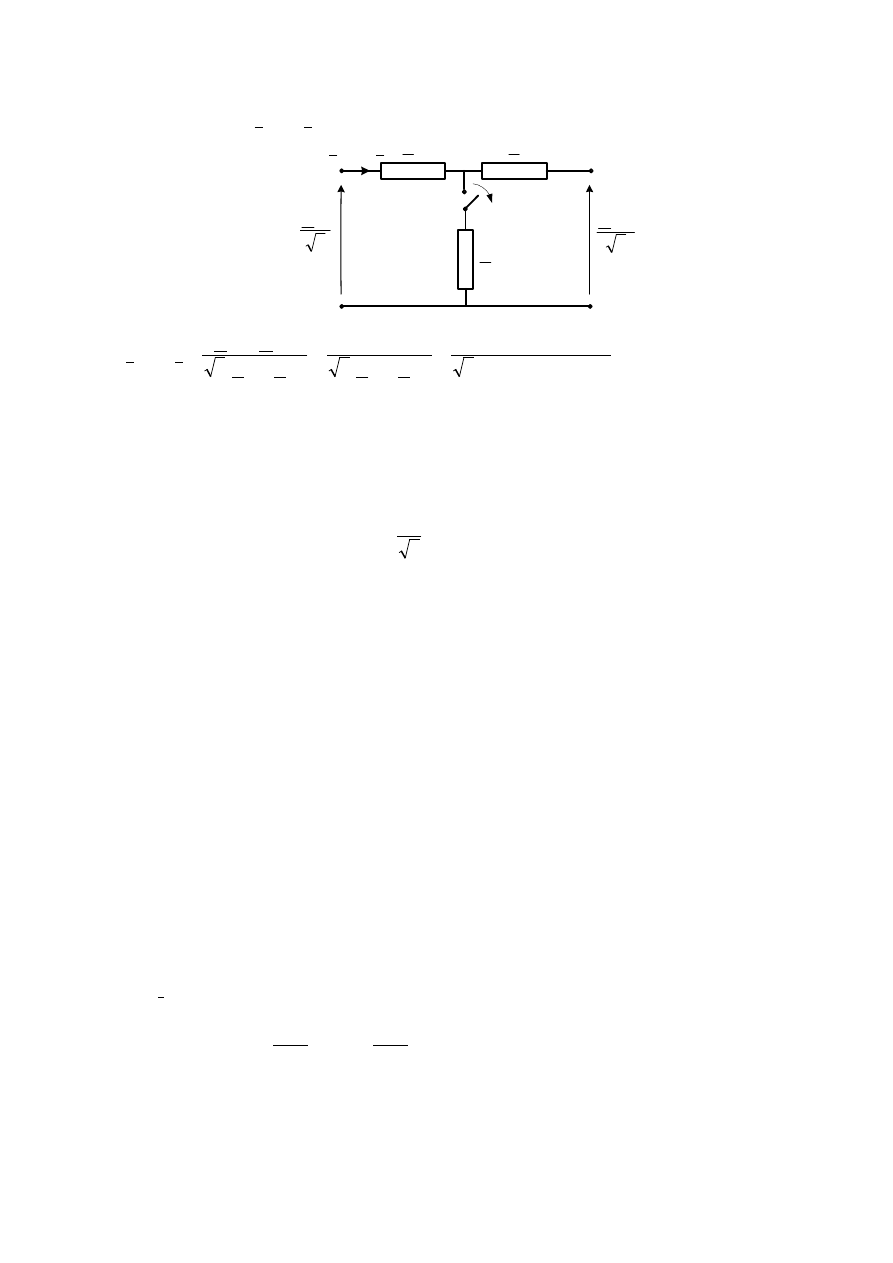
Prąd obciążenia

L

I

jest sumą geometryczną prądów przewodowych stron wtórnych obu trans-

formatorów i aby go wyliczyć należy rozwiązać dwuoczkowy układ aktywny, przedstawiony
na schemacie poniżej.

L

I

3

L

U

L

Z

A

I

2

B

I

2

kA

Z

kB

Z

3

2 A

U

3

2 NB

U

I

I

II

I

























+

−

−

+

=

























II

I

L

kB

L

L

L

kA

NB

A

I

I

Z

Z

Z

Z

Z

Z

U

U

3

3

2

2

Stąd wartości zespolone prądów oczkowych wynoszą:













+

+













+

+

=













NB

A

L

kB

L

kA

kB

kA

L

kA

L

L

L

kB

II

I

U

U

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

Z

I

I

2

2

)

(

3

czyli wartości zespolone prądów stron wtórnych:

I

A

I

I

=

2

,

II

B

I

I

−

=

2

.

Ostatecznie uzyskuje się następujące wartości skuteczne prądów stron wtórnych:

I

2A

= 475,2A,

I

2B

= 120,6A.

11

Prąd wyrównawczy

I

I

w

∆

=

można wyznaczyć ze schematu:

L

Z

kA

Z

kB

Z

3

2 A

U

3

2 NB

U

I

I

w

∆

=

708

,

43

225

,

4

)

6174

,

2

253

,

0

(

3

200

)

(

3

)

(

3

2

2

2

2

j

j

Z

Z

U

U

Z

Z

U

U

I

I

kB

kA

BN

A

kB

kA

BN

A

w

−

=

+

⋅

=

+

−

=

+

−

=

∆

=

(A)

Stąd:

∆

I = 43,92A.

Jest to prąd przewodowy i fazowy zastępczego układu połączeń Yy transformatorów i jedno-

cześnie prąd przewodowy strony wtórnej rzeczywistego układu połączeń Yd .
Prąd wyrównawczy płynący w fazie strony wtórnej obu transformatorów połączonej w trój-
kąt, przy odłączeniu obciążenia jest równy:

35

,

25

3

=

∆

I

A

.

Wnioski końcowe: Różnica napięć zwarcia wpływa na przeciążenie transformatora A i niedo-
ciążenie transformatora B w przypadku, gdy mają jednakowe przekładnie. W celu poprawnej
eksploatacji, należy zatem zmniejszyć obciążenie do wartości limitowanej przez znamionowe
obciążenie transformatora A. Po zmianie przekładni transformatora A w układzie można do-
datkowo wyodrębnić prąd wyrównawczy, który płynąc od źródła o wyższym napięciu zwięk-
szył przeciążenie transformatora B.

Odpowiedź: Prądy transformatorów po stronie wtórnej wynoszą odpowiednio: I

2A

= 432,8A,

I

2B

= 140,66A. Układ może przesłać bez przeciążenia transformatorów maksymalną moc:

S

max

= 5,085MVA. Po zmianie przekładni prądy transformatorów przyjmują wartości:

I

2A

= 475,2A, I

2B

= 120,6A. W przypadku odłączenia obciążenia w fazie strony wtórnej każde-

go z transformatorów popłynie prąd wyrównawczy równy 25,35A.

2.2. S

max

= 12,66MVA,

α

max

= 2,6

°

.

2.3. I

2A

= 175,6A, I

2B

= 631,85A, U

2

= 5951V.

2.4. Prąd wyrównawczy ma charakter indukcyjny i wartości

∆

I

= 56,8A oraz kąt przesunięcia

fazowego względem napięcia strony wtórnej

α

= - 86,74

°

.

2.5.

∆

I

= 515,65 – j1924,5 (A),

∆

I

= 1992A.

2.6. P

L

= 442730W,

,

77

,

0

2

2

=

AN

A

I

I

.

94

,

0

2

2

=

BN

B

I

I

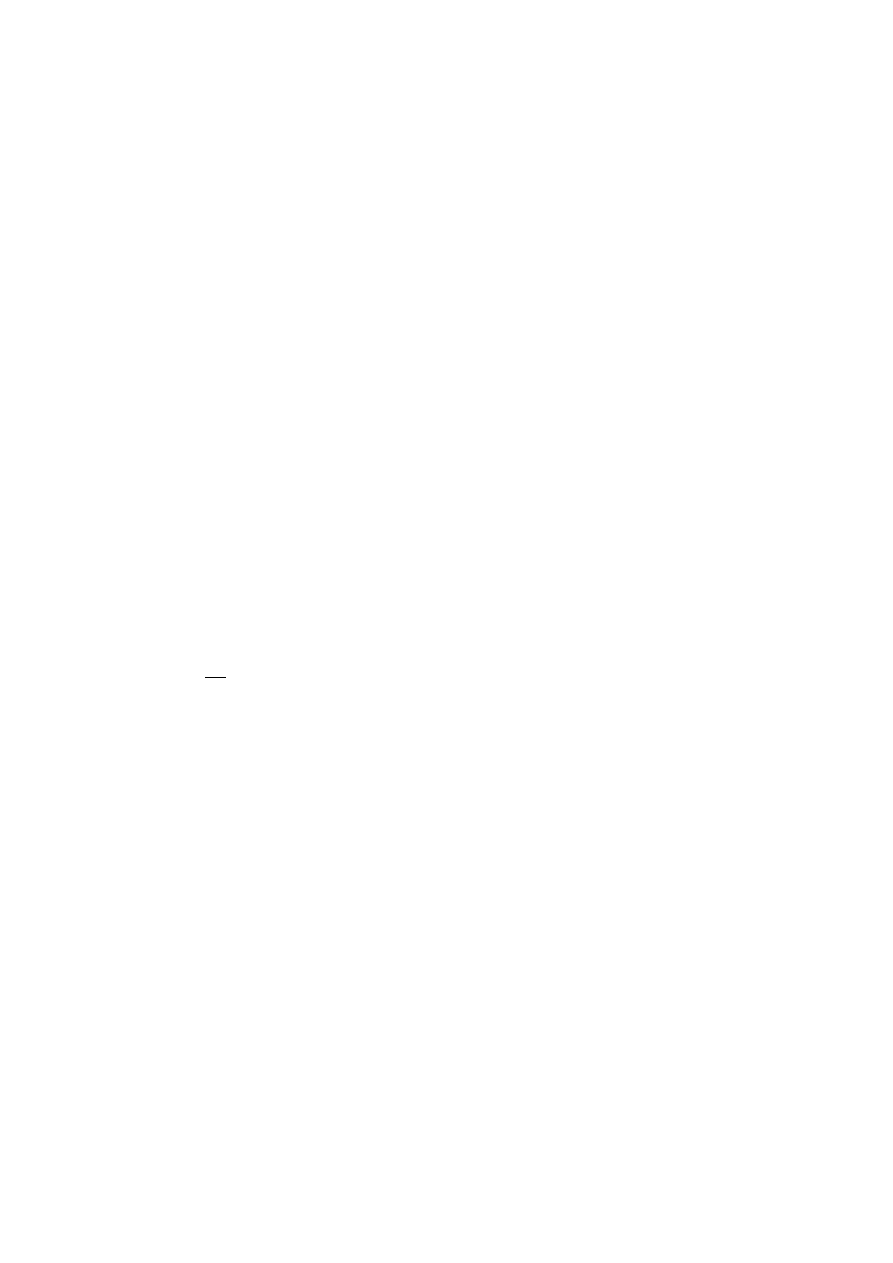
12

3. MASZYNY INDUKCYJNE (ASYNCHRONICZNE) TRÓJFAZOWE

3.1. Dla 4-biegunowego trójfazowego silnika indukcyjnego o danych: P

N

= 37kW, U

N

= 440V,

f

N

= 50Hz, t

b

= 2,5 i moment rozruchowy - T

1

= 1,6T

N

określić wartości s

b

, s

N

, T

N

.

Uwaga: w obliczeniach pominąć rezystancję stojana i straty mechaniczne.

3.2. Określić moment rozruchowy T

1

i maksymalny T

b

oraz moc strat mechanicznych silnika

indukcyjnego pierścieniowego o danych znamionowych: P

N

= 45kW, U

N

= 380V(Y),

I

sN

= 88A, n

N

= 970/min. Dane wirnika:

r

U

1

= 160V(Y), I

rN

= 184A, R

r

= 0,0142Ω/fazę. Prąd

zwarcia I

k

wynosi 5I

sN

. Wskazówka: w obliczeniach pominąć rezystancję stojana - R

s

= 0

i straty w żelazie - ∆P

Fe

= 0 oraz założyć równość reaktancji rozproszenia stojana i reaktancji

rozproszenia wirnika, sprowadzonej na stronę stojana (

r

s

X

X

σ

σ

′

=

).

3.3. Silnik indukcyjny ma obroty synchroniczne n

s

= 1500/min dla f

N

=

50Hz, U

N

= 500V(∆),

cosφ

N

= 0,876, s

N

= 0,02, η

N

= 0,9, ∆P

m

= 200W i parametry schematu zastępczego: R

s

= 0,

Ω

=

′

7

,

0

r

R

, X

m

/X

σ

s

= 25,

Ω

=

′

=

5

,

3

r

s

X

X

σ

σ

. Obliczyć s

b

, T

b

, n

N

, P

N

, I

N

.

3.4. Silnik indukcyjny 3-fazowy ma dane znamionowe: P

N

= 350kW, U

N

= 500V(Y),

cosφ

N

= 0,88, η

N

= 0,9, n

N

= 980/min, t

b

= 2,3, P

ws

= 1kW, ∆P

m

= 0,5%P

N

, P

ad

= 0,5%P

N

,

I

0

= 40%I

N

. Wyznaczyć parametry schematu zastępczego, przy założeniu

r

s

X

X

σ

σ

′

=

.

3.5. Silnik indukcyjny ma następujące parametry fazowego schematu zastępczego:

Ω

=

′

=

5

,

3

r

s

X

X

σ

σ

, R

s

= 0,4Ω,

Ω

=

′

7

,

0

r

R

, X

m

/X

σ

s

= 25, R

Fe

= 150Ω, p = 2 przy f = 50Hz. Za-

kładając, że U

N

= 500V(∆) i s

N

= 0,02 oraz ∆P

m

= 0 obliczyć :

a) P

N

, η

N

, I

N

, cosφ

N

, t

b

;

b) T

1

, I

1

, i

1

=

N

I

I

1

- wartości rozruchowe po przyłączeniu silnika do sieci.

3.6. Silnik indukcyjny pierścieniowy ma dane znamionowe: P

N

= 190kW, U

N

= 500V(Y),

r

U

1

= 400V(Y), f

N

= 50Hz, p = 2, t

b

= 2,3, n

N

= 1480/min.

a) Dobrać wartość rezystancji dodatkowej dołączonej do uzwojenia wirnika tak, aby moment
rozruchowy był równy maksymalnemu (R

rd

wyrazić w Ω),

b) Ile będzie wynosił względny prąd rozruchowy początkowy i

1

przy tej rezystancji?

3.7. Silnik indukcyjny o danych: P

N

= 100kW, U

N

= 500V(∆), cosφ

N

= 0,88, η

N

= 0,93,

n

N

= 980/min, P

ws

= 1000W, ∆P

m

= 0,5%P

N

, P

ad

= 0,5%P

N

, I

0

= 40%I

N

, t

b

= 2,1. Silnik ten

zasilono z sieci o napięciu międzyfazowym 220V, przy połączeniu faz stojana w trójkąt. Obli-
czyć prąd pobierany z sieci i moment przy postoju.

3.8. Silnik indukcyjny 3-fazowy ma dane: P

N

= 10kW, U

N

= 380V(Y), cosφ

N

= 0,85, η

N

= 0,9,

n

N

= 1460/min,

1

i

= 4.

a) Wyznaczyć parametry uproszczonego schematu zastępczego przy pominięciu gałęzi po-
przecznej i dobrać rezystancję rozruchową

rd

R

′

tak, aby moment T

l

= T

N

(przy s

b

< 1).

b) Obliczyć ustalone obroty n, gdy

rd

R

′

pozostanie w obwodzie wirnika, zaś moment obciąże-

nia wynosi T = 0,4T

N

.

3.9. Silnik indukcyjny o danych: n

s

= 1500/min, U

N

= 500V(Y) ma parametry schematu za-

stępczego:

Ω

=

′

=

5

,

3

r

s

X

X

σ

σ

,

r

R

′

= 0,7Ω, R

s

= 0 (w schemacie zastępczym pominąć gałąź

13

poprzeczną). Silnik ten zasilany jest z sieci trójfazowej o napięciu międzyfazowym 300V
i częstotliwości f = 40Hz. Obliczyć w tych warunkach T

bx

, s

bx

oraz ustalone obroty przy ob-

ciążeniu momentem obrotowym T = 0,4T

bN

.

3.10. Silnik indukcyjny dźwigowy o danych: P

N

= 100kW, n

N

= 1470/min, U

N

= 500V(Y),

t

b

= 2,5, U

lr

= 300V(Y), napędza wciągarkę.

a) Dobrać wartość oporników rozruchowych, przy których silnik ten, obciążony T = 0,9T

N

,

pracuje z prędkością 0,6n

N

.

b) Obliczyć prędkość maszyny przy hamowaniu prądnicowym z pozostawionym z punktu a)
oporem rozruchowym, gdy maszyna napędzana jest momentem T = 500Nm (w obliczeniach
pominąć rezystancję stojana i prąd biegu jałowego).

3.11. Silnik indukcyjny o danych: P

N

= 25kW, U

N

= 380V, cosφ

N

= 0,85, n

N

= 960/min,

t

b

= 2,5, (przyjąć R

s

= 0, a w schemacie zastępczym silnika pominąć gałąź poprzeczną). Obli-

czyć moment znamionowy i poślizg krytyczny. Obliczyć moment jakim można obciążyć sil-
nik, aby przy napięciu U = 220V osiągnął prędkość n = n

N

. Ile wtedy wyniesie współczynnik

mocy - cosφ?

3.12. Silnik indukcyjny pierścieniowy ma dane: U

N

= 380V(Y), obroty synchroniczne

n

s

= 1500/min, f

sN

= 50Hz, p = 2, t

b

= 2,1, X

k

= 7Ω,

r

R

′

= 0,7Ω. Silnik zasilono, przy niezmie-

nionym układzie połączeń stojana, napięciem U

s

= 220V, i obciążono momentem T = 0,5T

N

,

zaś do obwodu dołączono opór dodatkowy do każdej fazy równy R

rd

= 4R

r

. Obliczyć ustalone

obroty w nowych warunkach pracy.

3.13. Silnik indukcyjny o danych: P

N

= 50kW, U

N

= 380V(∆), cosφ

N

= 0,86, η

N

= 0,88,

n

N

= 970/min, T

b

/T

N

= 2,1 , pracuje zasilany napięciami przewodowymi 380V, przy połącze-

niu uzwojenia stojana w gwiazdę. Ile wynosi moment początkowy przy symetrycznym dołą-
czeniu do wirnika oporu dodatkowego R

rd

= 10R

r

? Obliczyć obroty wirnika przy obciążeniu

go momentem T = 0,4T

b

(T

b

w nowych warunkach pracy).

3.14. Silnik indukcyjny pierścieniowy o danych: P

N

= 50kW, U

N

= 380V(∆), cosφ

N

= 0,86,

η

N

= 0,88 , n

N

= 970/min, T

b

/T

N

= 2,1 ma włączony w celach regulacji prędkości opornik do-

datkowy o wartości rezystancji fazy R

rd

= 8R

r

. Obliczyć straty mocy wydzielonej w uzwoje-

niu wirnika i w oporze dodatkowym, przy obciążeniu T = T

N

.

3.15. Silnik indukcyjny ma dane znamionowe: P

N

= 26,5kW, U

N

= 380V(∆), n

N

= 735/min,

t

b

= 1,9, I

sN

= 56A, U

1r

= 300V(Y). Dobrać wartość opornika dodatkowego, aby przy obciąże-

niu momentem T = 0,8T

N

silnik miał prędkość n = 0,6n

s

.

3.16. Silnik indukcyjny pierścieniowy o danych: P

N

= 2500kW, U

N

= 6000V(Y),

U

1r

= 1000V(Y), f

s

= 50Hz, t

b

= 2,1, p = 2, n

N

= 1480/min. W wyniku dołączenia do każdej

fazy wirnika rezystancji dodatkowej obroty silnika, przy obciążeniu momentem znamiono-
wym wynoszą 1400/min. Określić wartość tej rezystancji w Ω oraz rozdział mocy traconej w
wirniku i na rezystancjach dodatkowych.

3.17. Silnik indukcyjny ma dane znamionowe: P

N

= 250kW, U

N

= 380V(∆), cosφ

N

= 0,88,

η

N

= 0,94 , t

b

= 2,5 , n

N

= 710/min,

r

s

R

R

′

=

7

,

0

(w schemacie zastępczym silnika pominąć gałąź

poprzeczną). Obliczyć indukcyjność dławika, jaki trzeba włączyć szeregowo w przewody
zasilające uzwojenie stojana, aby ograniczyć prąd rozruchowy do 3I

N

. Ile będzie wynosił

wówczas moment rozruchowy w stosunku do znamionowego? Jak zmieni się poślizg przy

14

obciążeniu znamionowym, gdyby dławik nie został wyłączony? Wskazówka: w obliczeniach
momentu stosować wzory uproszczone, nie uwzględniając R

s

.

3.18. Silnik indukcyjny ma dane: U

N

= 380V(Y), C

s

= 0,97, n

N

= 1450/min, f

N

= 50Hz,

Ω

=

′

=

5

,

3

r

s

X

X

σ

σ

,

Ω

=

′

1

,

0

r

R

. Silnik pracuje zasilany z sieci trójfazowej o napięciu między-

fazowym 220V, przy f = 40Hz. Obliczyć: T

b

, s

b

i obroty silnika przy obciążeniu momentem

T

= 0,5T

N

w podanych warunkach.

3.19. Silnik indukcyjny pierścieniowy ma dane: P

N

= 100kW, U

N

= 500V(Y), n

N

= 720/min,

t

b

= 2,2, η

N

= 0,91, cosφ

N

= 0,85, f

sN

= 50Hz, U

1r

= 250V(Y). Silnik pracuje zasilany napięciem

znamionowym U

N

przy f = 60Hz. Obliczyć nową przeciążalność momentem - t

bx

. Dobrać opór

R

rd

dołączony do wirnika tak, aby w nowych warunkach silnik obciążony momentem równym

0,75T

N

wirował z prędkością obrotową 600/min. Obliczyć prąd pobierany z sieci.

3.20. Silnik indukcyjny pierścieniowy ma dane znamionowe: P

N

= 190kW, U

N

= 500V(Y),

U

1r

= 400V(Y), f

N

= 50Hz, p = 2, t

b

= 2,3, n

N

= 1480/min, I

sN

= 264A. Silnik pracuje w warun-

kach zmienionych: U = 380V(∆),

N

f

f

2

,

1

=

, T = 0,8T

N

. Dobrać wartość rezystancji dodatko-

wej dołączonej do fazy wirnika tak, aby obroty wirnika wynosiły 1450/min (R

rd

wyrazić w

Ω

). Obliczyć straty mocy w obwodach wirnika w tym stanie pracy. Straty mechaniczne pomi-

nąć.

3.21. Silnik indukcyjny pierścieniowy ma dane znamionowe: P

N

= 190kW, U

N

= 500V(Y),

p

= 2, U

1r

= 400V(Y), f

N

= 50Hz, t

b

= 2,3, n

N

= 1480/min, I

sN

= 264A, I

rN

= 310A. Silnik pracu-

je w sieci f = 60Hz. Obliczyć prędkość silnika przy obciążeniu momentem znamionowym,
jeśli napięcie zasilania nie uległo zmianie. Oszacować prąd stojana w tym stanie pracy.

3.22. Silnik indukcyjny pierścieniowy ma dane znamionowe: P

N

= 190kW, U

N

= 500V(Y),

p

= 2, U

1r

= 400V(Y), f

N

= 50Hz, t

b

= 2,3, n

N

= 1480/min, I

sN

= 264A, I

rN

= 310A. Silnik pracu-

je w nowych warunkach, gdy: U = U

N

, f = 1,2 f

N

. Obliczyć jakim momentem można obciążyć

silnik, aby poślizg pozostał znamionowy. Oszacować prąd stojana w tym stanie pracy.

ROZWIĄZANIA ZADAŃ I ODPOWIEDZI DO ROZDZIAŁU 3

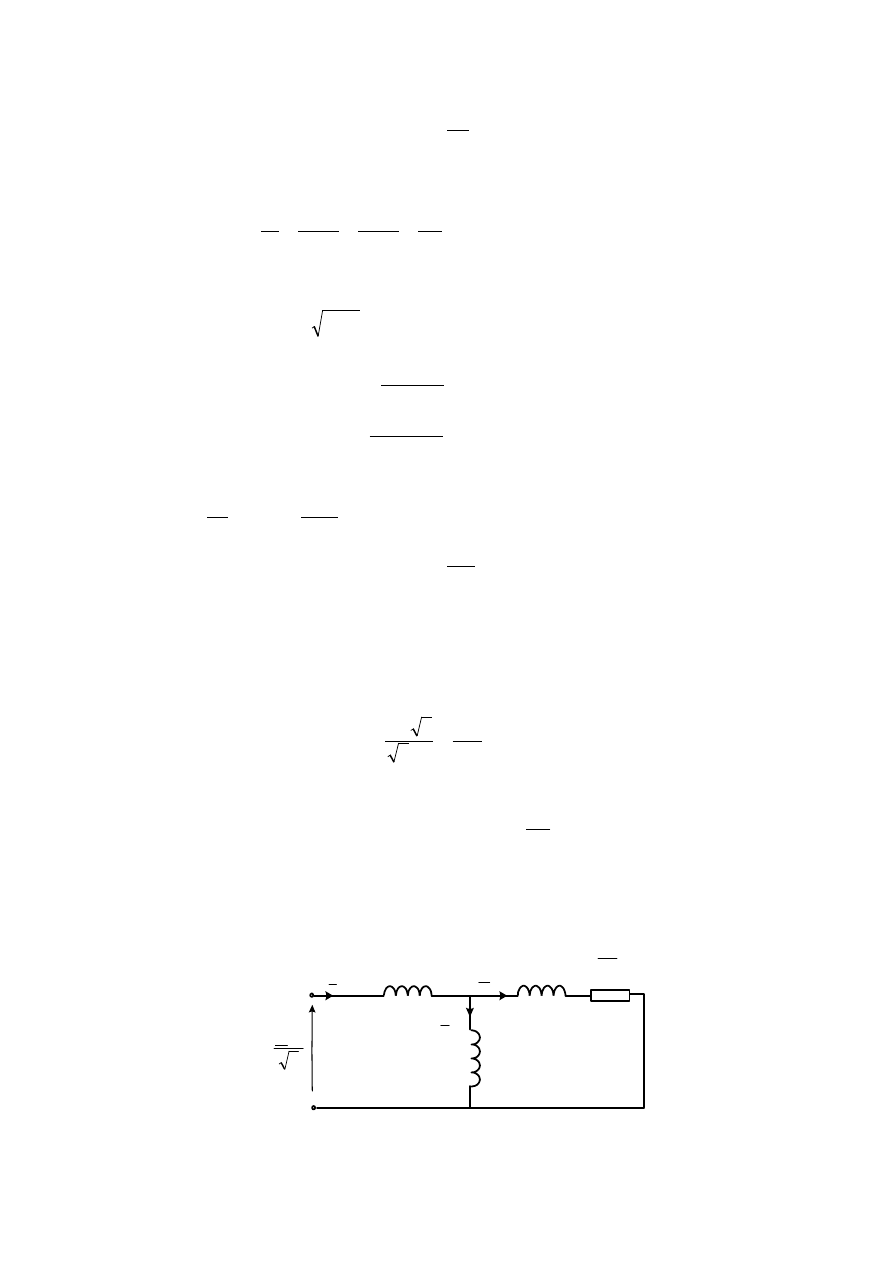
3.1.

Wyrażenie na moment elektromagnetyczny silnika indukcyjnego (wzór Klossa) dla

przyjętych założeń ma postać:

s

s

s

s

T

T

b

b

b

e

+

=

2

Jeśli określimy przeciążalność chwilową momentem jako:

T

T

t

b

=

,

gdzie w warunkach pracy stabilnej zachodzi równość: T = T

e

,

to z rozwiązania wyrażenia na moment otrzymamy związek między poślizgiem krytycznym
i poślizgiem w danym stanie pracy:

)

1

(

2

−

±

=

t

t

s

s

b

lub

)

1

(

2

−

±

=

t

t

s

s

b

15

Przeciążalność znamionowa jest równa:

N

b

b

T

T

t

=

, gdzie T

N

jest znamionowym momentem

obrotowym.

W zadaniu:

5625

,

1

6

,

1

5

,

2

6

,

1

5

,

2

6

,

1

1

=

=

=

=

=

N

N

N

b

b

T

T

T

t

T

T

t

, dla

1

1

=

=

s

s

stąd:

362

,

0

=

b

s

(drugi wynik: s

b

= 2,762 odrzucamy)

076

,

0

)

1

(

2

≅

−

±

=

b

b

b

N

t

t

s

s

(drugi wynik s

N

= 1,734 odrzucamy).

Wyrażenie na poślizg ma postać:

s

s

p

s

ω

ω

Ω

−

=

,

dla wartości znamionowych:

s

N

s

N

p

s

ω

ω

Ω

−

=

.

Tu liczba par biegunów: p = 2.

Stąd:

21

,

145

)

1

(

2

)

1

(

=

−

=

−

=

Ω

N

N

N

s

N

s

p

f

s

p

π

ω

rad/s.

Znamionowy moment obrotowy wynosi:

Nm

P

T

N

N

N

255

8

,

254

≅

=

Ω

=

.

Odpowiedź:

,

362

,

0

=

b

s

076

,

0

=

N

s

,

Nm

T

N

255

≅

.

3.2. Przekładnia napięciowa jest liczona jako stosunek napięć fazowych stojana do wirnika:

375

,

2

160

380

3

3

1

=

=

=

r

N

U

U

K

Rezystancja fazy wirnika sprowadzona na stronę stojana:

Ω

=

=

′

0801

,

0

2

r

r

R

K

R

,

prąd fazowy wirnika po sprowadzeniu ma wartość:

A

K

I

I

rN

rN

47

,

77

=

=

′

Ponieważ w znamionowym stanie pracy wartości fazowe prądu wirnika

rN

I

′

i prądu stojana

sN

I

są różne, w analizie schematu zastępczego należy uwzględnić gałąź poprzeczną. Jest ona

reprezentowana przez reaktancję główną

m

X

.

N

r

s

R

′

sN

I

s

jX

σ

3

sN

U

m

I

m

jX

r

X

j

σ

′

rN

I

′

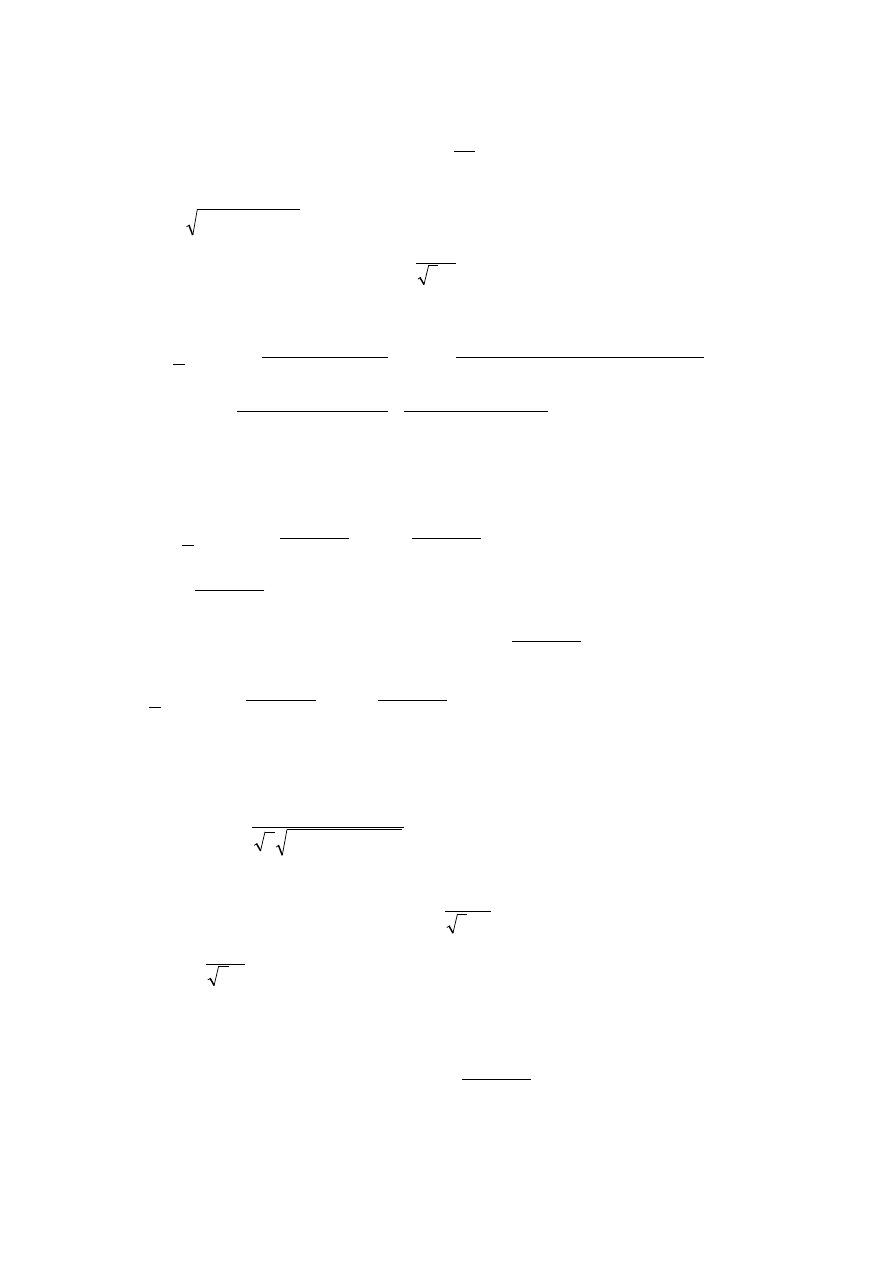
16

Zakładamy dla uproszczenia, że w znamionowym stanie pracy prąd wirnika jest w fazie

z napięciem na gałęzi poprzecznej (ponieważ

r

N

r

X

s

R

σ

′

>>

′

) i wyprzedza prąd magnesowania

w tej gałęzi (

)

m

I

o 90

0

.

Stąd:

A

I

I

I

rN

sN

m

7

,

41

)

(

)

(

2

2

=

′

−

=

i dalej szacunkowa wartość reaktancji głównej wynosi:

Ω

=

=

26

,

5

3

m

sN

m

I

U

X

W stanie zwarcia wypadkowa impedancja fazowa ma postać:

2

2

2

2

2

2

2

2

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)]

(

)[

(

)

(

)

(

r

m

r

r

m

r

m

r

m

r

m

r

r

m

s

r

m

r

r

m

r

r

r

m

s

r

m

r

r

r

m

s

k

X

X

R

X

X

X

jX

X

X

R

X

R

R

jX

jX

X

X

R

X

X

j

R

X

j

R

jX

jX

X

X

j

R

X

j

R

jX

jX

Z

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

′

+

+

′

′

+

′

+

′

+

+

′

′

+

′

+

=

=

′

+

+

′

′

+

−

′

′

+

′

+

=

′

+

+

′

′

+

′

+

=

Jeśli uwzględnimy, że

r

m

R

X

′

>>

(patrz obliczenia wyżej) to impedancję można

zapisać jako:

)

(

)

(

2

2

r

r

s

r

r

r

r

m

m

r

r

m

m

s

k

X

C

X

j

R

C

X

X

X

X

j

R

X

X

X

jX

Z

σ

σ

σ

σ

σ

σ

′

+

+

′

=

′

′

+

+

′













′

+

+

≅

gdzie:

r

m

m

r

X

X

X

C

σ

′

+

=

.

W temacie zadania przyjęto:

s

r

X

X

σ

σ

=

′

, stąd

m

s

m

s

r

X

X

X

C

C

+

=

=

σ

oraz

k

r

s

k

r

r

r

r

m

m

r

r

m

m

s

k

jX

R

C

jX

R

C

X

X

X

X

j

R

X

X

X

jX

Z

+

′

=

+

′

=

′

′

+

+

′













′

+

+

=

2

2

2

)

(

)

(

σ

σ

σ

σ

,

gdzie:

r

s

s

k

X

X

C

X

σ

σ

′

+

=

.

Prąd zwarcia:

A

I

I

sN

k

440

5

=

=

.

Jednocześnie:

2

2

)

(

)

(

3

k

r

s

sN

k

X

R

C

U

I

+

′

=

.

Uwzględniając, że

2

2

)

(

r

s

k

R

C

X

′

>>

przyjmujemy wartość prądu zwarcia za równą:

k

sN

k

X

U

I

3

≅

,

stąd:

Ω

≅

=

498

,

0

3

k

sN

k

I

U

X

.

Aby obliczyć wartości reaktancji rozproszeń

s

r

X

X

σ

σ

=

′

oraz współczynnika

s

C należy roz-

wiązać równanie kwadratowe ze względu na

s

X

σ

:

s

s

m

s

m

r

s

s

k

X

X

X

X

X

X

X

C

X

σ

σ

σ

σ

σ

+

+

=

′

+

=

,

stąd:

0

)

2

(

)

(

2

=

−

−

+

m

k

s

k

m

s

X

X

X

X

X

X

σ

σ

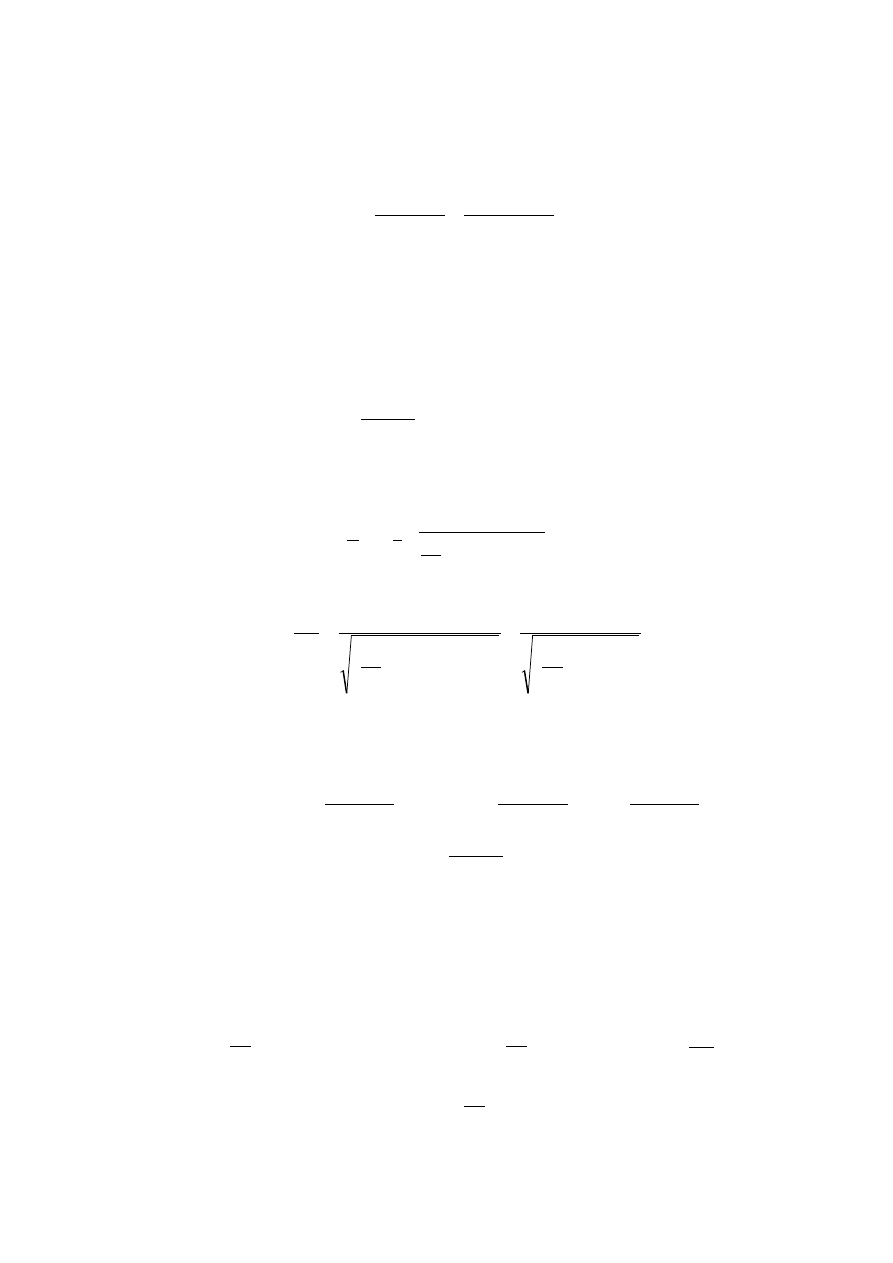
17

Uwzględniając wyznaczone wcześniej przybliżone wartości indukcyjności głównej

Ω

=

26

,

5

m

X

i indukcyjności zwarcia

Ω

=

498

,

0

k

X

otrzymujemy:

0

62

,

2

02

,

10

)

(

2

=

−

+

s

s

X

X

σ

σ

Stąd:

Ω

=

′

=

255

,

0

r

s

X

X

σ

σ

oraz

954

,

0

255

,

0

26

,

5

26

,

5

=

+

=

+

=

m

s

m

s

X

X

X

C

σ

.

Dla dokładniejszego wyznaczenia wartości reaktancji

m

X ,

s

X

σ

i dalej współczynnika

s

C nale-

ż

y uwzględnić w gałęzi wirnika rezystancję

r

R

′

.

Analizę przeprowadzimy dla znamionowych warunków pracy.

Dla rozważanego silnika przyjmujemy wartość obrotów synchronicznych równą:
n

s

= 1000/min.

Poślizg znamionowy wynosi:

03

,

0

=

−

=

s

N

s

N

n

n

n

s

.

Zależność między znamionowymi wartościami prądów stojana i wirnika wyznaczymy na
podstawie schematu zastępczego z dzielnika prądów:

(

)

m

r

N

r

m

sN

rN

X

X

j

s

R

jX

I

I

+

′

+

′

=

′

σ

i przy założeniu równości reaktancji rozproszeń -

r

s

X

X

σ

σ

′

=

przyjmuje postać:

(

)

2

2

2

2

)

(

s

N

r

m

m

r

N

r

m

sN

rN

X

s

R

X

X

X

s

R

X

I

I

+













′

=

+

′

+













′

=

′

σ

(1)

gdzie:

m

r

s

X

X

X

+

′

=

σ

.

Jednocześnie można zapisać:

=

+

+

=

+

′

+

=

′

+

+

=

′

+

=

m

s

m

s

s

m

r

m

r

s

r

m

s

m

s

r

s

s

k

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

C

X

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

'

s

m

s

s

X

X

X

X

σ

σ

+

=

stąd:

(

) (

)(

)

2

2

m

s

m

s

m

s

m

s

s

m

s

s

s

s

k

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

−

=

+

−

=

+

=

+

=

σ

σ

σ

czyli:

s

k

s

m

X

X

X

X

−

=

2

2

(2)

Po uwzględnieniu zależności (2) w równaniu (1), po wprowadzeniu parametru

k

X , otrzymu-

jemy równanie kwadratowe z niewiadomą

s

X :

2

2

2

2

2

s

N

r

m

X

k

s

R

k

X

+













′

=

czyli

2

2

2

2

2

s

N

r

s

k

s

X

k

s

R

k

X

X

X

+













′

=

−

, gdzie:

sN

rN

I

I

k

′

=

,

i dalej:

0

)

1

(

2

2

2

2

=













′

+

+

−

N

r

s

k

s

s

R

k

X

X

X

k

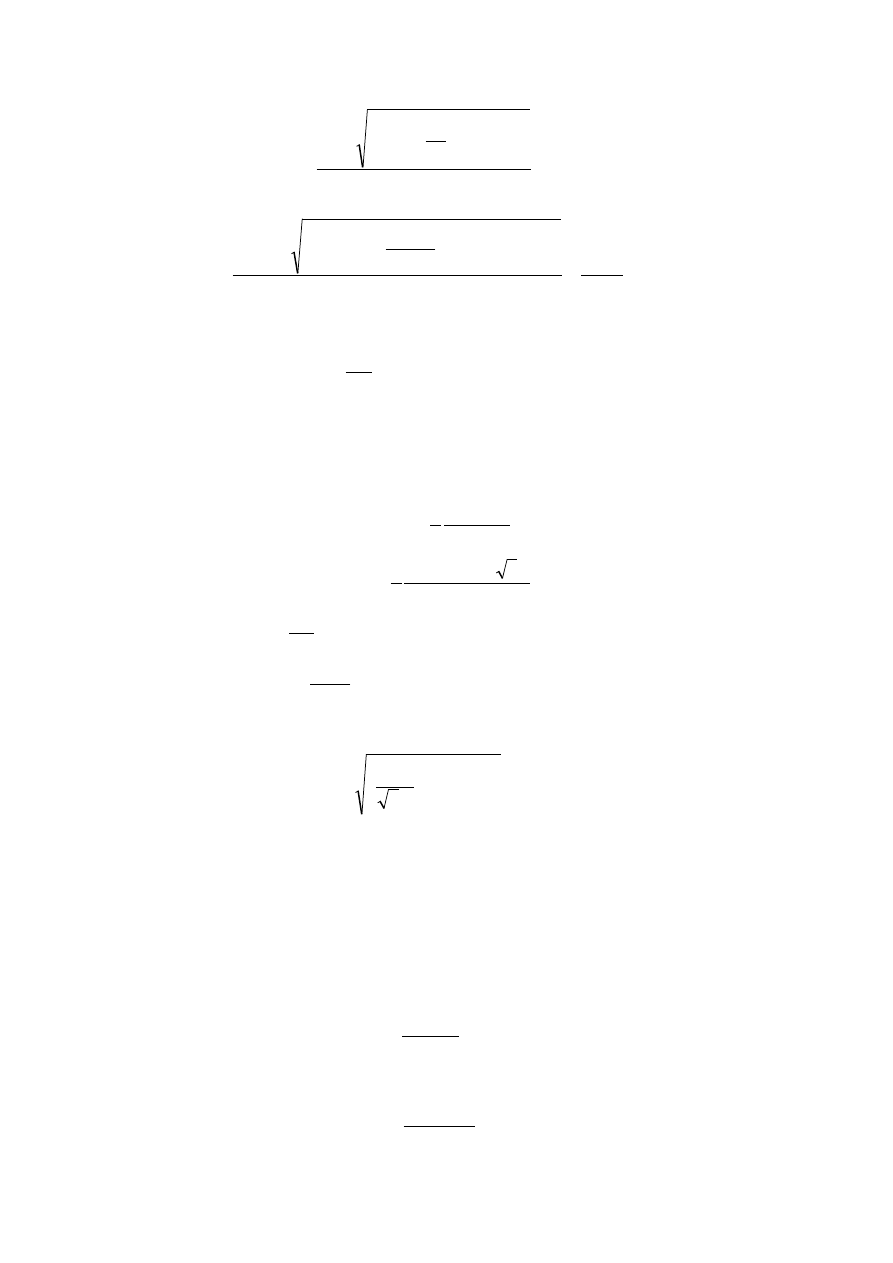
18

Stąd:

(

)

(

)

2

2

2

2

2

1

2

1

4

k

k

k

s

R

X

X

X

N

r

k

k

s

−

−













′

+

+

=

(

)

(

)

Ω

=

=

−

−













+

+

=

184

,

6

45

,

0

783

,

2

88

,

0

1

2

88

,

0

1

88

,

0

03

,

0

0801

,

0

4

498

,

0

498

,

0

2

2

2

2

2

s

X

.

Wyznaczone wartości reaktancji wynoszą:

s

X = 6,184Ω,

m

X = 5,93Ω.

Wtedy stała

s

C jest równa:

959

,

0

=

=

s

m

s

X

X

C

,

natomiast reaktancje rozproszenia, przy założeniu

r

s

X

X

σ

σ

′

=

, wynoszą:

Ω

=

−

=

′

=

254

,

0

m

s

r

s

X

X

X

X

σ

σ

Na podstawie znamionowej wartości prędkości obrotowej przyjmujemy p = 3.
Wyrażenie na moment krytyczny ma postać:

(

)

k

s

sph

s

b

X

U

C

p

T

ω

2

2

3

=

Zatem:

(

)

Nm

T

b

1273

498

,

0

100

3

/

380

959

,

0

2

3

3

2

≅

⋅

⋅

⋅

=

π

Poślizg krytyczny:

161

,

0

=

′

=

k

r

b

X

R

s

.

Moment rozruchowy:

Nm

s

s

T

T

b

b

b

l

399

1

2

2

≅

+

=

.

Powtórzenie powyższego cyklu obliczeń dla poprawionej wartości reaktancji zwarcia, równej:

(

)

Ω

≅

′

−















=

493

,

0

3

2

2

r

s

k

sN

k

R

C

I

U

X

,

prowadzi do otrzymania końcowych wyników:

,

959

,

0

≅

s

C

,

2516

,

0

=

′

=

r

s

X

X

σ

σ

,

1625

,

0

=

b

s

Nm

T

b

1286

=

,

Nm

T

l

407

=

.

Zauważmy, że przeprowadzona korekta poprawia wyniki w zakresie nie przekraczającym 2%.
Biorąc pod uwagę dokładność samego modelu matematycznego można uznać, że nie była ona
konieczna. Również uproszczona procedura wyznaczenia reaktancji i stałej

s

C (pominięcie

wpływu rezystancji wirnika) daje wyniki zbliżone do obliczeń dokładnych.
Wyznaczmy teraz znamionowy moment elektromagnetyczny ze wzoru:

Nm

s

s

s

s

T

T

b

N

b

N

b

eN

459

2

2

2

≅

+

=

Całkowitą moc mechaniczną wytwarzaną przez maszynę możemy obliczyć ze wzoru:

(

)

46643

1

=

−

=

p

s

T

P

N

s

eN

mN

ω

W,

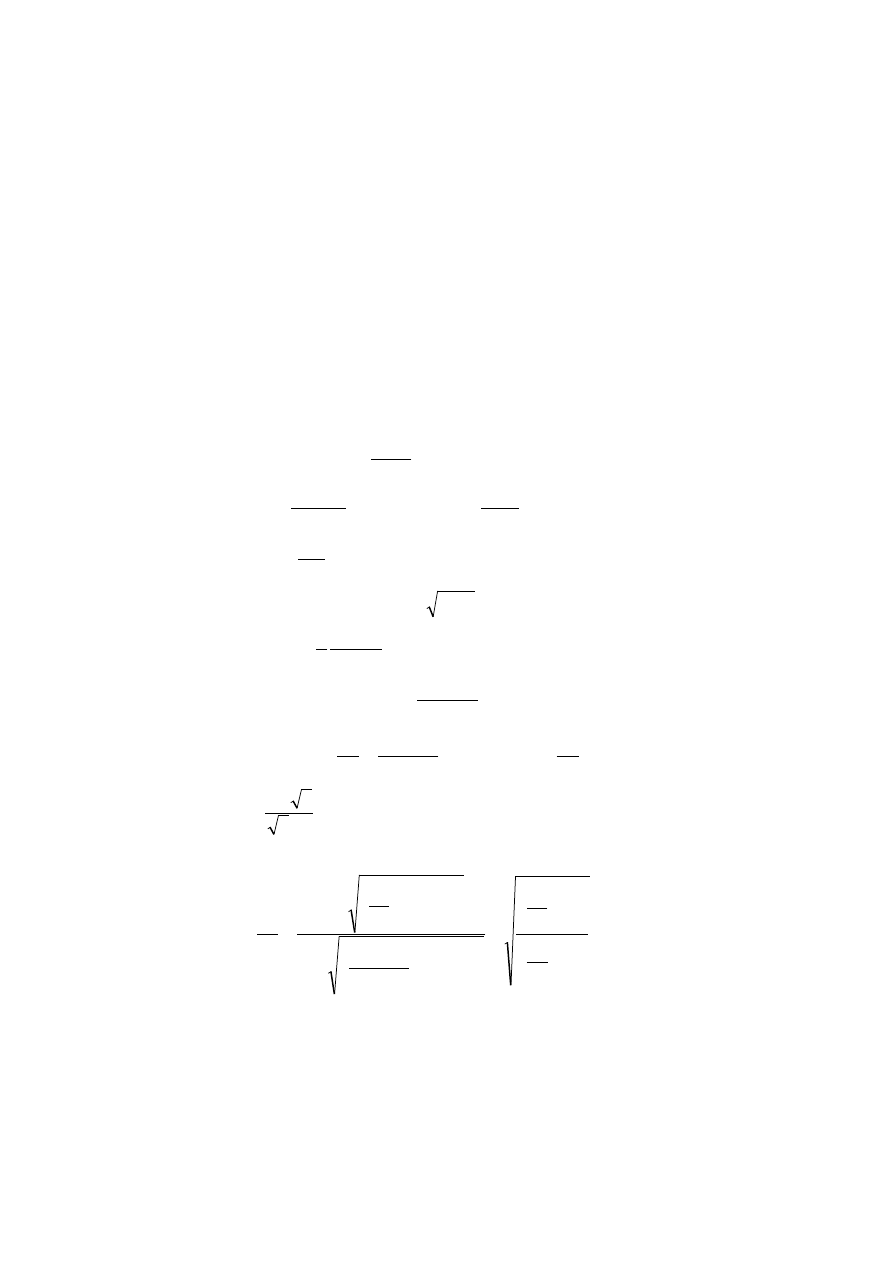
19

stąd moc strat mechanicznych:

W

P

P

P

N

mN

m

1643

=

−

=

∆

.

Odpowiedź: Moment rozruchowy silnika ma wartość: T

l

= 407Nm, moment maksymalny jest

równy: T

b

= 1286Nm, moc strat mechanicznych wynosi:

1643

=

−

=

∆

N

mN

m

P

P

P

Nm.

3.3.

,

102

,

0

=

b

s

Nm

T

b

322

=

,

1470

=

N

n

/min,

,

3

,

120 Nm

T

N

=

,

5

,

18 kW

P

N

=

,

1

,

27 A

I

N

=

3.4. R

s

= 1,28mΩ,

Ω

=

′

m

R

r

12

,

Ω

=

43

,

1

m

X

, R

Fe

= 8,86Ω,

.

0705

,

0

Ω

=

′

=

r

s

X

X

σ

σ

3.5. a)

A

I

N

55

,

30

=

,

88

,

0

cos

=

N

ϕ

,

kW

P

N

7

,

18

=

,

802

,

0

=

N

η

,

.

6

,

2

≅

b

t

b)

Nm

T

4

,

62

1

=

,

A

I

125

1

=

,

.

4

1

≅

i

3.6. Przy rozwiązywaniu zadania posługujemy się uproszczonym schematem zastępczym
silnika pomijając parametry gałęzi poprzecznej i rezystancję stojana, stąd stała

1

=

s

C

.

Ad a) Prędkość synchroniczna

1500

60

=

=

p

f

n

N

s

/min,

)

3

(

01

,

0

=

−

=

s

N

s

N

n

n

n

s

,

s

rad

n

N

N

/

99

,

154

30

=

=

Ω

π

,

Nm

P

T

N

N

N

1230

1226

≅

=

Ω

=

,

Nm

T

t

T

N

b

b

2820

=

=

,

(

)

0583

,

0

1

2

≅

−

+

=

b

b

N

b

t

t

s

s

,

Ω

=

=

282

,

0

)

(

2

3

2

b

s

sph

k

T

U

p

X

ω

,

Ω

=

=

′

0165

,

0

k

b

r

X

s

R

.

Nowa wartość poślizgu krytycznego:

1

=

′

+

′

=

k

rd

r

bx

X

R

R

s

Ponieważ

k

X nie zmienia się:

r

rd

r

b

bx

R

R

R

s

s

′

′

+

′

=

, stąd













−

′

=

′

1

b

bx

r

rd

s

s

R

R

,

Ω

=

′

266

,

0

rd

R

.

Przy przekładni:

25

,

1

3

3

1

=

=

r

N

U

U

K

otrzymujemy:

Ω

≅

17

,

0

rd

R

Ad b) Wartość stosunkowa prądu przy zahamowanym wirniku, gdy s

x

= 1:

( )

( )

3

17

,

3

1

1

1

2

2

2

2

2

2

≅

=

+













+













=

+













′

+

′

+













′

=

=

bx

N

b

k

x

rd

r

sph

k

N

r

sph

N

l

l

s

s

s

X

s

R

R

U

X

s

R

U

I

I

i

Odpowiedź: a) Szukana wartość rezystancji dodatkowej dołączonej do fazy wirnika wynosi:

Ω

≅

17

,

0

rd

R

; b) Wartość stosunkowa prądu przy zahamowanym wirniku

3

17

,

3

1

≅

=

i

.

3.7.

Prąd przewodowy pobierany z sieci ma wartość

A

I

s

2

,

250

=

, moment elektromagne-

tyczny wytwarzany przez silnik przy postoju wynosi

Nm

T

3

,

59

1

=

.

20

3.8.

a) Parametry uproszczonego schematu zastępczego silnika wynoszą:

,

707

,

0

Ω

=

s

R

,

231

,

0

Ω

=

′

r

R

.

3

,

1

Ω

=

′

=

s

s

X

X

σ

σ

Szukana rezystancja rozruchowa dołączona do obwodu wir-

nika, przy połączeniu faz w gwiazdę, ma wartość fazową:

Ω

=

267

,

0

rd

R

; b) n = 1479/min.

3.9.

,

95

,

63

Nm

T

bx

=

,

125

,

0

=

bx

s

4

,

1137

=

n

/min.

3.10. ad a) Na podstawie danych znamionowych przyjmujemy: p = 2. Obroty synchroniczne
wynoszą:

1500

=

s

n

/min, zaś obroty silnika, n = 0,6,

882

1470

6

,

0

=

⋅

=

N

n

/min.

Poślizg w tych warunkach jest równy:

412

,

0

1500

882

1500

=

−

=

−

=

s

s

n

n

n

s

.

Przeciążalność momentem dla zadanego obciążenia jest równa:

)

7

(

,

2

9

,

0

9

,

0

=

=

=

b

N

b

bx

t

T

T

t

.

Poślizg krytyczny w tych warunkach wynosi:

(

)

212

,

2

1

2

=

−

+

=

bx

bx

bx

t

t

s

s

.

Moment krytyczny znamionowy wynosi:

Nm

n

P

t

P

t

T

N

N

b

N

N

b

b

1624

1470

100000

30

5

,

2

30

=

⋅

⋅

⋅

=

=

Ω

=

π

π

.

Reaktancję zwarcia wyznaczamy ze wzoru na moment krytyczny, kładąc

1

=

s

C

:

(

)

Ω

=

⋅

⋅













⋅

=

=

49

,

0

1624

100

2

3

500

3

2

2

3

2

2

π

ω

b

s

sph

s

k

T

U

C

p

X

.

Poślizg znamionowy wynosi:

02

,

0

1500

1470

1500

=

−

=

−

=

s

N

s

N

n

n

n

s

.

Poślizg krytyczny znamionowy jest równy:

(

)

0958

,

0

1

2

=

−

+

=

b

b

N

b

t

t

s

s

.

Rezystancję fazową wirnika wyliczamy ze wzoru na poślizg krytyczny:

Ω

=

=

′

04695

,

0

k

b

r

X

s

R

.

Rezystancja fazowa opornika dodatkowego sprowadzona na stronę stojana ma wartość wyni-
kłą ze wzoru na poślizg krytyczny w nowych warunkach pracy:

k

rd

r

bx

X

R

R

s

′

+

′

=

.

Stąd:

Ω

=

′

−

=

′

0369

,

1

r

k

bx

rd

R

X

s

R

.

Po uwzględnieniu przekładni:

)

6

(

,

1

300

500

3

3

1

=

=

=

r

N

U

U

K

,

otrzymamy wartość rezystancji dodatkowej dla fazy wirnika:

Ω

=

′

=

373

,

0

2

K

R

R

d

rd

.

Ad b) Nowa przeciążalność momentem wynosi:

248

,

3

500

1624

=

=

=

T

T

t

b

bxx

.

Przy pracy prądnicowej poślizg krytyczny ma ujemną wartość równą, przy pominięciu wpły-
wu rezystancji stojana, poślizgowi – s

bx

z części a) zadania.

21

Zatem:

bx

bxx

s

s

−

=

.

Poślizg odpowiadający ustalonej pracy maszyny przy hamowaniu prądnicowym wynosi:

(

)

349

,

0

1

2

−

=

−

−

−

=

bxx

bxx

bx

xx

t

t

s

s

.

Stąd ustalone obroty mają wartość:

(

)

(

)

2024

349

,

0

1

1500

1

=

+

=

−

=

xx

s

s

n

n

/min.

Odpowiedź: a) Szukana wartość rezystancji dodatkowej dołączonej do fazy wirnika wynosi:

Ω

=

373

,

0

rd

R

; b) Ustalone obroty przy hamowaniu prądnicowym wynoszą:

2024

=

n

/

min.

3.11.

,

36

,

83

Nm

T

=

.

85

,

0

cos

=

ϕ

3.12.

=

n

1187/

min.

3.13.

728

=

n

/

min,

.

333

Nm

T

l

≅

3.14. Straty mocy wydzielonej w uzwojeniu wirnika wynoszą:

.

1545

W

P

r

≅

∆

Straty mocy

wydzielonej w oporze dodatkowym wynoszą:

.

12370

W

P

rd

≅

∆

3.15. Szukana rezystancja rozruchowa dołączona do obwodu wirnika, przy połączeniu faz w
gwiazdę, ma wartość fazową:

Ω

=

525

,

1

rd

R

.

3.16. Rezystancja fazowa wirnika dodatkowego ma wartość:

.

0198

,

0

Ω

=

rd

R

Straty mocy

wydzielonej w uzwojeniu wirnika wynoszą:

.

33780

W

P

r

=

∆

Straty mocy wydzielonej w opo-

rze dodatkowym wynoszą:

.

135130

W

P

rd

=

∆

3.17. Indukcyjność dławika ma wartość fazową:

),

(

136

,

0

Y

mH

L

d

=

stosunek momentu

rozruchowego do znamionowego wyniesie wtedy:

.

64

,

0

1

1

=

=

N

T

T

t

Poślizg, przy znamiono-

wym obciążeniu i załączonym dławiku, wzrośnie o

.

0025

,

0

=

∆

s

3.18.

,

230

Nm

T

b

≅

,

127

,

0

=

b

s

1153

=

n

/

min.

3.19. Nowa przeciążalność momentem wyniesie:

,

53

,

1

=

bx

t

rezystancja fazowa opornika

dodatkowego ma wartość:

.

185

,

0

Ω

=

rd

R

Prąd pobierany z sieci ma wartość:

.

9

,

111

A

I

s

=

3.20. Rezystancja fazowa opornika dodatkowego ma wartość:

.

092

,

0

Ω

≅

rd

R

Straty mocy

wydzielonej w obwodach wirnika wynoszą:

.

35945

W

P

P

rd

r

=

∆

+

∆

3.21. Wskazówka: w rozwiązaniu zastosować uproszczoną procedurę wyznaczenia reaktan-
cji zwarcia i stałej

s

C , przy pominięciu wpływu rezystancji wirnika, jak w zadaniu 3.2.

Odpowiedź:

1769

=

n

/

min,

.

291

A

I

s

≅

3.22. Wskazówka: w rozwiązaniu zastosować uproszczoną procedurę wyznaczenia reaktan-
cji zwarcia i stałej

s

C , przy pominięciu wpływu rezystancji wirnika, jak w zadaniu 3.2.

Odpowiedź:

,

1000

Nm

T

≅

.

236

A

I

s

≅

22

4. MASZYNY SYNCHRONICZNE CYLINDRYCZNE

Uwaga: We wszystkich zadaniach w rozdziałach 4 i 5 przyjmujemy sprawność maszyny

1

=

η

(pomijamy wszelkie straty mocy czynnej). Ponadto zakładamy liniową zależność indu-

kowanej w tworniku siły elektromotorycznej

f

E od prądu wzbudzenia

f

I , czyli:

f

f

kI

E

=

.

4.1. Silnik synchroniczny o danych:

P

N

= 1MW, U

N

= 6

kV(

∆

),

x

d

=

x

q

= 1,6, I

fN

= 100A,

cos

ϕ

N

= 0,8

cap

, pracuje w warunkach znamionowych. Obliczyć

I

aN

,

ϑ

LN

, E

fN

, I

f0

.

4.2. Silnik synchroniczny ma dane znamionowe:

P

N

= 3 MW, U

N

= 6

kV(Y), cos

ϕ

N

= 0,8

cap

,

Ω

N

= 314rad/s i parametry X

d

= X

q

= 15

Ω

.

a) Obliczyć przeciążalność znamionową tego silnika i zapas kąta mocy ∆

ϑ

L

przy zmianie

prądu wzbudzenia do wartości, przy której

fN

f

E

E

9

,

0

=

.

b) Obliczyć prąd sieci (stojana) i współczynnik mocy przy tym wzbudzeniu, gdy moment
obciążenia jest znamionowy oraz gdy wynosi 0,8 momentu znamionowego.

4.3. Silnik synchroniczny cylindryczny o danych:

P

N

= 16kW, U

N

= 500

V(Y), X

d

= 6

Ω

,

cos

ϕ

N

= 0,8

cap

, zasilany jest napięciem znamionowym i obciążony tak, aby przy

cos

ϕ

N

= 0,9

cap

pobierał prąd znamionowy. Jak należy zmienić wzbudzenie, aby przy obciąże-

niu momentem równym połowie poprzedniej wartości moc bierna pobierana pozostała taka
sama? Obliczyć prąd fazowy, jaki wtedy popłynie.

4.4. Silnik synchroniczny cylindryczny o danych:

P

N

= 1MW, U

N

= 5

kV (Y), I

fN

= 450A,

I

f0

= 200

A, cos

ϕ

N

= 0,8

cap

,

x

d

= 1,5 pracuje przy obciążeniu równym 0,5T

N

i wzbudzeniu

0,8

I

fN

. Oblicz wartość prądu fazowego i cos

ϕ

.

4.5. Silnik synchroniczny cylindryczny o danych:

P

N

= 1 MW, U

N

= 6

kV (Y), I

fN

= 500 A,

cos

ϕ

N

= 0,8

cap

,

x

d

=

x

q

= 1,2,

Ω

N

= 314 rad/s ma kompensować moc bierną Q = 900 kVar. Jak

dużym momentem można go obciążyć, aby prąd wzbudzenia nie przekroczył wartości zna-
mionowej? Ile w tych warunkach będzie wynosił prąd pobierany przez silnik z sieci?

4.6. Silnik synchroniczny cylindryczny o danych:

P

N

= 10 MW, U

N

= 6

kV (Y), I

fN

= 450A,

I

f0

= 200

A, cos

ϕ

N

= 0,8

cap

,

x

d

= 1,5. Obliczyć prąd wzbudzenia, aby przy znamionowym ob-

ciążeniu kąt mocy wynosił 60

°

. Jaki będzie wtedy cos

ϕ

?

4.7. Silnik synchroniczny cylindryczny o danych:

P

N

= 160 kW, U

N

= 6

kV (Y), X

d

= 60

Ω

,

cos

ϕ

N

= 0,8

cap

, zasilany jest napięciem znamionowym i wzbudzany tak, aby przy

cos

ϕ

= 0,9

cap

pobierał prąd znamionowy. Jak należy zmienić wzbudzenie, aby przy obciąże-

niu mocą czynną, równą połowie poprzedniej wartości, moc bierna pobierana przez silnik
pozostała niezmieniona? Ile w tych warunkach będzie wynosił prąd stojana?

4.8. Prądnica synchroniczna o danych:

S

N

= 2

MVA, U

N

= 6,3

kV(Y), cos

ϕ

N

= 0,9

ind

i parame-

trach

X

d

= X

q

= 20

Ω

, zasila odbiornik trójfazowy o danych znamionowych:

LN

P = 1MW,

1

cos

=

LN

ϕ

,

=

LN

U

6

kV.

a) Jak powinna być wzbudzona prądnica, aby napięcie na jej zaciskach było równe

=

x

U

6

kV(Y)?

b) Jaki jest prąd zwarcia symetrycznego tej prądnicy przy takim wzbudzeniu?

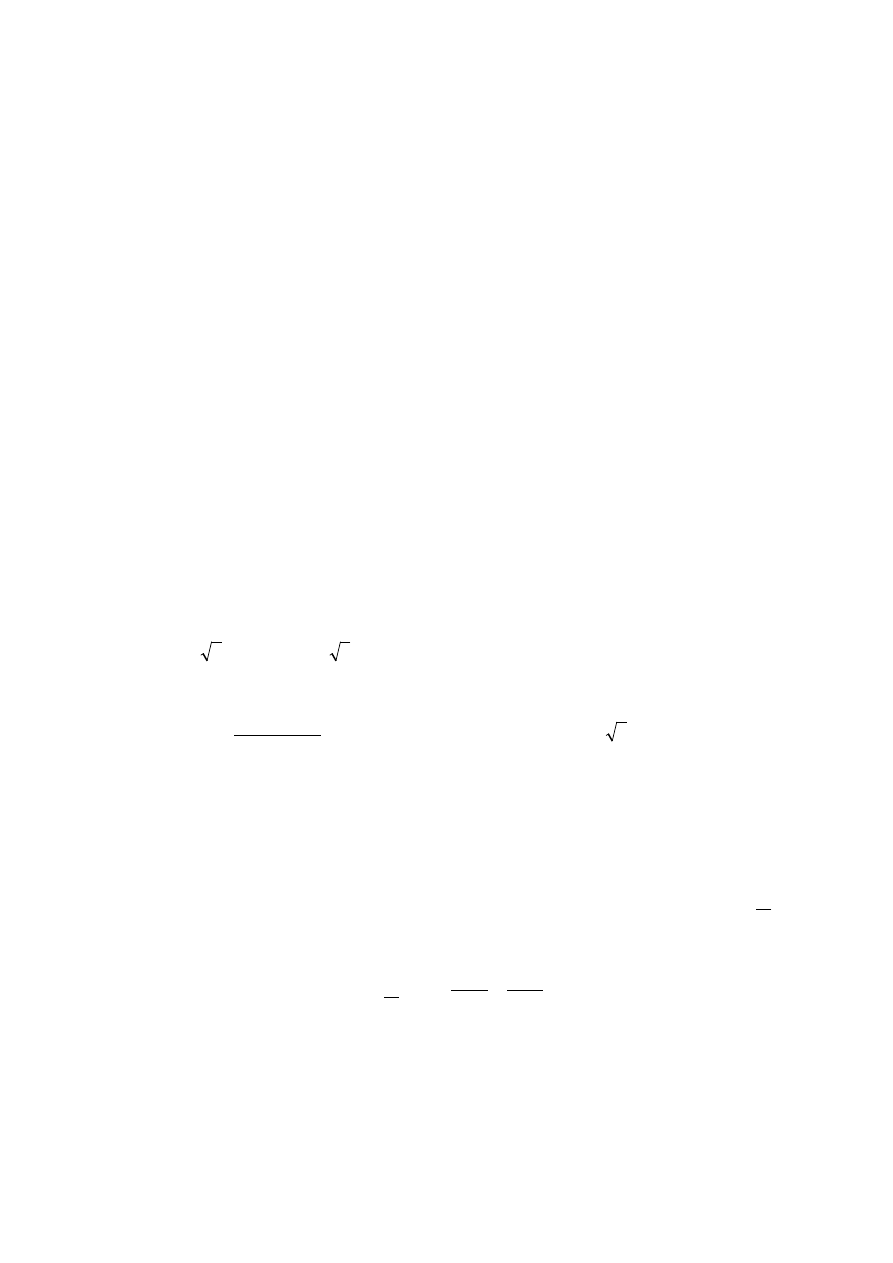
23

4.9. Generator synchroniczny cylindryczny ma dane:

S

N

= 1,25

MVA, U

N

= 6

kV (Y), x

d

= 1,5,

Ω

N

= 314

rad/s. Pracując samotnie generator ma napięcie znamionowe na zaciskach stojana,

przy obciążeniu prądem równym 2/3 znamionowej wartości prądu stojana i cos

ϕ

= 0,9

ind

.

Obliczyć ustaloną zmianę napięcia stojana po odłączeniu obciążenia.

4.10. Generator synchroniczny cylindryczny o danych:

S

N

= 120

MVA, U

N

= 13,5

kV(Y),

x

d

= x

q

= 1,5,

I

fN

= 500A, I

f0

= 280

A,

Ω

N

= 314

rad/s pracuje napędzany momentem

T = 2

.

10

5

Nm, podłączony do sieci 12kV, przy I

f

= 350A (praca na sieć sztywną). Obliczyć

moc czynną i bierną oddawaną do sieci, prąd twornika i cos

ϕ

w nowych warunkach pracy.

4.11. Generator synchroniczny cylindryczny o danych:

S

N

= 12,5

MVA, U

N

= 10,5

kV(Y),

cos

ϕ

N

= 0,8

ind

,

f

N

= 50

Hz, X

d

= 17,9

Ω

, napędzany z prędkością znamionową, pracuje na od-

biór o

cos

ϕ

= 0,75

ind

. Obliczyć dopuszczalną moc czynną

P wydawaną przez generator pra-

cujący przy

U = 9800V, gdy I

a

≤

I

aN

oraz

I

f

≤

I

fN

.

4.12. Generator synchroniczny cylindryczny o danych:

S

N

= 31,25

MVA, U

N

= 6,3

kV(Y),

f

N

= 50

Hz, x

d

= 1,97, I

fN

= 492A, cos

ϕ

N

= 0,8

ind

pracuje na sieć

U = 6000V, f = 50 Hz obcią-

ż

ony prądem

I = 2000A i wydaje moc P = 18MW. Obliczyć prąd wzbudzenia generatora.

ROZWIĄZANIA ZADAŃ I ODPOWIEDZI DO ROZDZIAŁU 4

4.1.

Moc znamionowa silnika jest mocą czynną mechaniczną. Pomijając wszelkie straty

przy przetwarzaniu energii przyjmujemy, że jest ona równa znamionowej mocy elektrycznej
pobieranej z sieci zasilającej. Przy połączeniu uzwojenia stojana w trójkąt:

N

aphN

aN

N

aphN

aphN

N

aN

aN

N

N

N

N

I

U

I

U

I

U

I

U

P

ϕ

ϕ

ϕ

ϕ

cos

3

cos

3

cos

3

cos

3

=

=

=

=

Stąd prąd fazowy stojana (twornika) jest równy:

A

U

P

I

N

aN

N

aphN

44

,

69

cos

3

=

=

ϕ

, a prąd przewodowy -

A

I

I

aphN

aN

1

,

120

3

=

=

.

W dalszych analizach można pominąć indeks „

a” w opisie prądu i napięcia stojana.

W maszynach cylindrycznych zachodzi równość reaktancji synchronicznych:

q

d

X

X

=

, stąd

w opisie maszyny stosuje się reaktancję w osi podłużnej -

d

X .

W warunkach znamionowych pracy (

tylko wtedy!) wprowadza się do zależności wartości

względne reaktancji, zapisanej małą literą -

d

x albo równoważnie poprzez podkreślenie -

d

X

.

Pozwala to uprościć obliczenia. Reaktancja względna jest bezwymiarowa i jest równa warto-
ś

ci reaktancji odniesionej do znamionowej wartości impedancji fazowej maszyny -

phN

Z

.

phN

d

phN

phN

d

d

d

Z

X

U

I

X

X

x

=

=

=

Wykres wskazowy silnika synchronicznego cylindrycznego przedstawia zależności pomiędzy
wartościami skutecznymi

fazowymi napięć i prądów i dla warunków znamionowych ma po-

stać (odpowiada mu schemat zastępczy, na którym dla przejrzystości zapisu pomija się zwy-
kle indeks „

ph”) jak niżej:

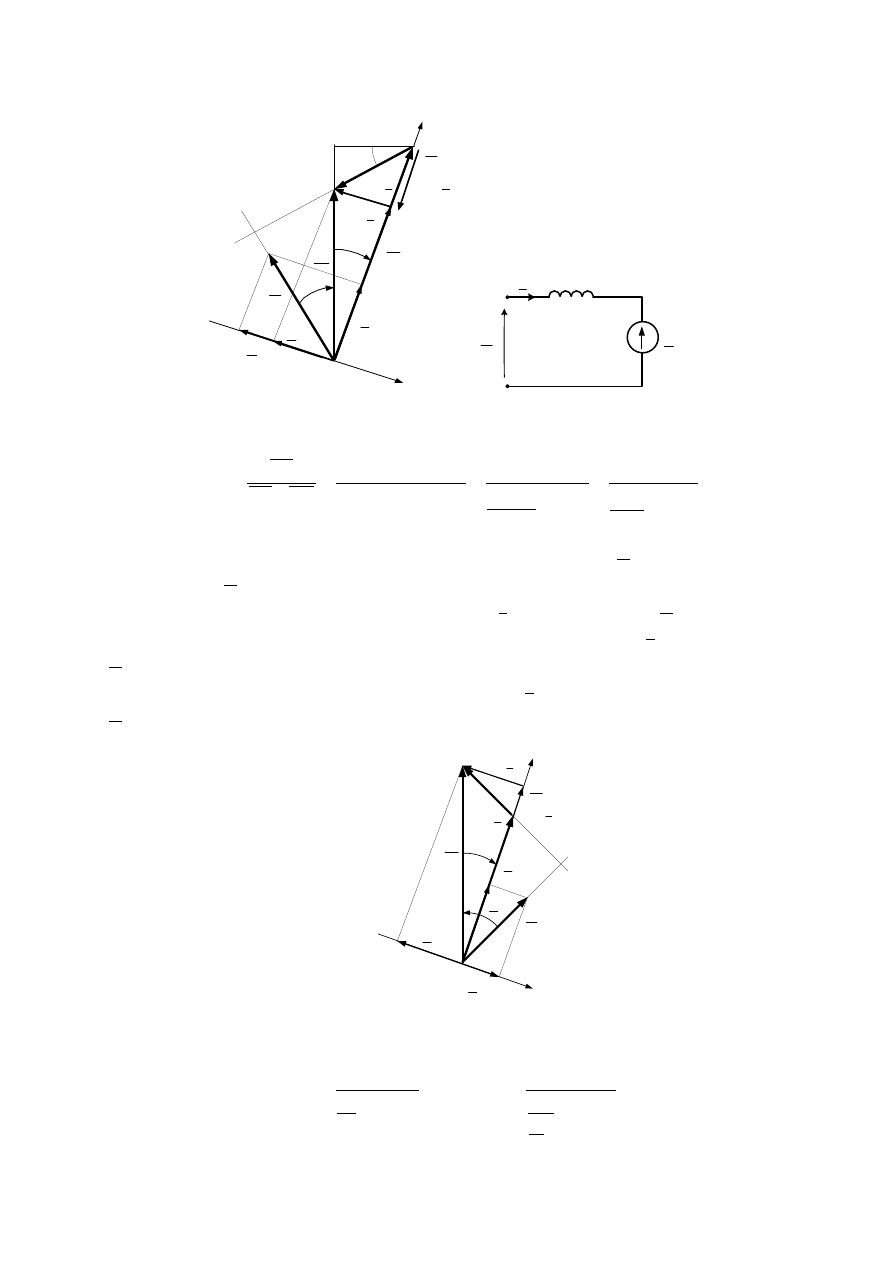
24

q

U

I

d

I

q

I

d

U

q

U

d

d

d

I

jX

q

d

I

jX

I

jX

d

f

E

I

X

d

ϕ

ϕ

L

ϑ

O

A

B

C

D

ϕ

cos

U

d

jX

I

f

E

Tangens kąta mocy, wyznaczony z trójkąta prostokątnego ∆

OCB, jest równy:

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϑ

sin

cos

sin

cos

sin

cos

+

=

+

=

+

=

+

=

I

X

U

I

X

U

I

X

U

I

X

AC

OA

CB

tg

d

ph

d

ph

ph

d

ph

ph

d

L

Kąt mocy

L

ϑ

jest kątem skierowanym,

zawsze od wskazu napięcia

U

do wskazu siły elek-

tromotorycznej

f

E - dla silnika w prawo, dla prądnicy w lewo. Kąt przesunięcia fazowego -

ϕ

jest kątem skierowanym,

zawsze od wskazu prądu

I

do wskazu napięcia

U

. Dla silnika, w

którym

U

E

f

>

ϑ

cos

, zwanego silnikiem przewzbudzonym wskaz prądu

I

wyprzedza wskaz

U

i silnik pobiera z sieci moc bierną pojemnościową. Jest to ważna zaleta jego pracy. Dla

silnika niedowzbudzonego

U

E

f

<

ϑ

cos

i wskaz prądu

I

jest opóźniony względem wskazu

U

i silnik pobiera z sieci moc bierną indukcyjną. Wtedy wykres wskazowy ma postać:

q

ϕ

ϑ

U

I

d

I

d

U

q

U

d

f

E

q

I

d

d

I

jX

q

d

I

jX

I

jX

d

Wprowadzając do wzoru dla warunków znamionowych względną wartość reaktancji otrzy-
mamy wzór na

LN

tg

ϑ

:

N

d

N

LN

x

tg

ϕ

ϕ

ϑ

sin

1

cos

+

=

lub

N

d

N

LN

X

tg

ϕ

ϕ

ϑ

sin

1

cos

+

=

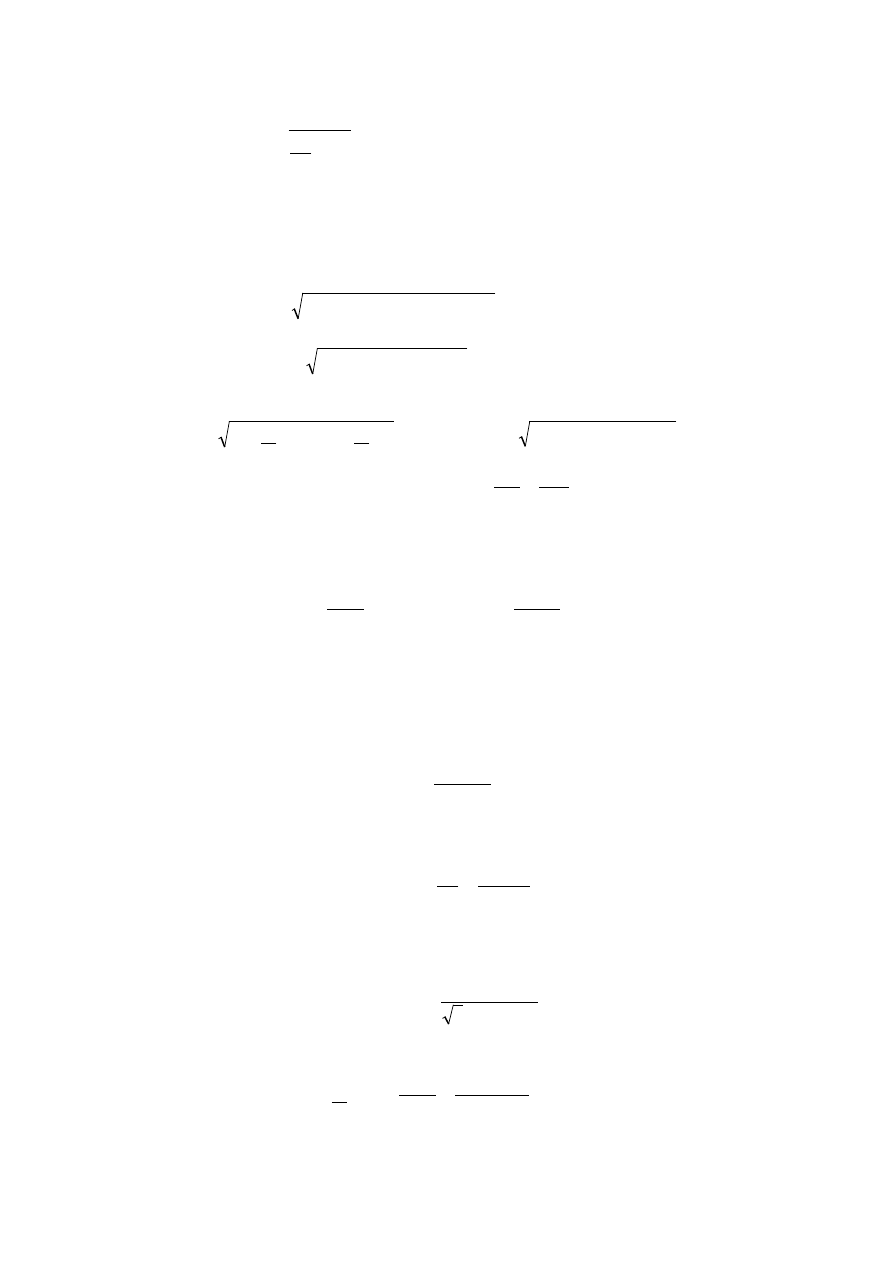
25

Tu:

653

,

0

6

,

0

6

,

1

1

8

,

0

=

+

=

LN

tg

ϑ

, stąd

9

0

33

0

′

=

LN

ϑ

.

Wartość siły elektromotorycznej można wyznaczyć na podstawie analizy trójkąta prostokąt-
nego ∆

OCB, na wykresie wskazowym napięć silnika:

2

2

2

)

cos

(

)

sin

(

)

(

ϕ

ϕ

I

X

I

X

U

E

d

d

f

+

+

=

i dalej

]

)

(cos

)

[(sin

)

(

sin

2

)

(

2

2

2

2

2

ϕ

ϕ

ϕ

+

+

+

=

I

X

I

UX

U

E

d

d

f

czyli

2

2

)

(

sin

2

I

X

I

UX

U

E

d

d

f

+

+

=

ϕ

.

W warunkach znamionowych pracy można wprowadzić wartości względne reaktancji, przez

co otrzymamy:

2

)

(

sin

2

1

d

N

d

phN

fN

x

x

U

E

+

+

=

ϕ

,

lub w innym zapisie:

2

)

(

sin

2

1

d

N

d

phN

fN

X

X

U

E

+

+

=

ϕ

, tu:

V

E

fN

14040

)

6

,

1

(

6

.

0

6

,

1

2

1

6000

2

=

+

⋅

⋅

+

=

.

Zakładamy liniowość obwodu magnetycznego, stąd:

fN

fx

fN

fx

E

E

I

I

=

W szczególności dla

0

f

I

wartość

0

f

E

jest równa znamionowemu napięciu fazowemu tworni-

ka

phN

U

, zatem:

fN

phN

fN

f

E

U

I

I

=

0

tu:

A

I

f

72

,

42

14040

6000

100

0

=

⋅

=

Odpowiedź:

A

I

aN

1

,

120

=

,

9

0

33

0

′

=

LN

ϑ

,

V

E

fN

14040

=

,

A

I

f

72

,

42

0

=

4.2. Ad a) Moment elektromagnetyczny silnika synchronicznego cylindrycznego (z bieguna-
mi utajonymi) w ustalonym stanie pracy wyraża się wzorem:

L

d

N

f

ph

e

X

E

U

T

ϑ

sin

3

Ω

=

Przeciążalność znamionową silnika definiujemy jako iloraz momentu maksymalnego i zna-
mionowego:

LN

N

b

N

T

T

t

ϑ

sin

1

=

=

Dla wyznaczenia poszukiwanej przeciążalności niezbędne jest wyliczenie znamionowego
kąta mocy

LN

ϑ

. Dla silnika synchronicznego, połączonego w gwiazdę, obowiązuje związek:

N

N

N

aN

phN

U

P

I

I

ϕ

cos

3

=

=

,

zatem względna wartość reaktancji wynosi:

5625

,

1

cos

2

=

=

=

=

N

N

N

q

phN

phN

d

d

d

U

P

X

U

I

X

X

x

ϕ

.

Stąd znamionowy kąt mocy ma wartość, obliczoną ze wzoru na tangens kąta mocy:

26

573

,

0

6

,

0

5625

,

1

1

8

,

0

tg

arc

=

























+

=

L

ϑ

rad

Wobec powyższego przeciążalność znamionowa wynosi:

8446

,

1

)

573

,

0

sin(

1

=

=

N

t

Zapas kąta mocy dla silnika synchronicznego określony jest wzorem:

Lx

Lb

Lx

ϑ

ϑ

ϑ

−

=

∆

gdzie:

Lb

ϑ

– kąt mocy, przy którym moment wytwarzany przez maszynę synchroniczną osiąga

wartość maksymalną;

Lx

ϑ

– kąt mocy danego punktu pracy, dla którego określamy zapas kąta

mocy.
W przypadku maszyny synchronicznej cylindrycznej powyższy wzór przyjmie postać:

Lx

Lx

ϑ

π

ϑ

−

=

∆

2

Z warunków zadania wynika, że wartość napięcia indukowanego zmniejszyła się do poziomu
0,9

E

fN

. Stąd też konieczne staje się wyliczenie znamionowej wartości tego napięcia. Na pod-

stawie wyrażenia na znamionową wartość momentu (mocy) możemy napisać, przy założeniu,
ż

e straty mocy mechaniczne są równe zeru,

0

=

∆

m

P

:

LN

d

fN

N

N

N

N

X

E

U

T

P

ϑ

sin

3

=

Ω

=

,

stąd:

V

U

X

P

E

LN

N

d

N

fN

7987

sin

3

≅

=

ϑ

.

Znając wartość znamionową napięcia indukowanego możemy określić wartość kąta mocy

ϑ

Lx

w nowych warunkach pracy:

6024

,

0

9

,

0

3

sin

=

=

fN

N

d

N

Lx

E

U

X

P

ϑ

,

stąd:

∆

ϑ

Lx

= 0,9243

rad

Ad b) Prąd stojana, gdy nie znamy wartości

ϕ

cos

wyznaczamy z wykresu wskazowego.

Dla poprawnego narysowania wykresu sprawdzamy zależność

U

E

f

>

ϑ

cos

.

Ponieważ dla przypadku znamionowego zasilania uzwojeń stojana, przy obniżonym prądzie
wzbudzenia:

6024

,

0

sin

=

Lx

ϑ

, stąd

3

6000

2

,

6375

)

6024

,

0

(

1

7987

2

>

=

−

.

Oznacza to, że silnik jest przewzbudzony i można w dalszej analizie posługiwać się wykre-
sem wskazowym z zadania 4.1.

Prąd stojana wyznaczamy z trójkąta ∆

OAB, korzystając z twierdzenia cosinusów:

L

f

f

d

UE

E

U

I

X

ϑ

cos

2

)

(

)

(

)

(

2

2

2

−

+

=

,

stąd

L

f

f

d

UE

E

U

X

I

ϑ

cos

2

)

(

)

(

1

2

2

−

+

=

,

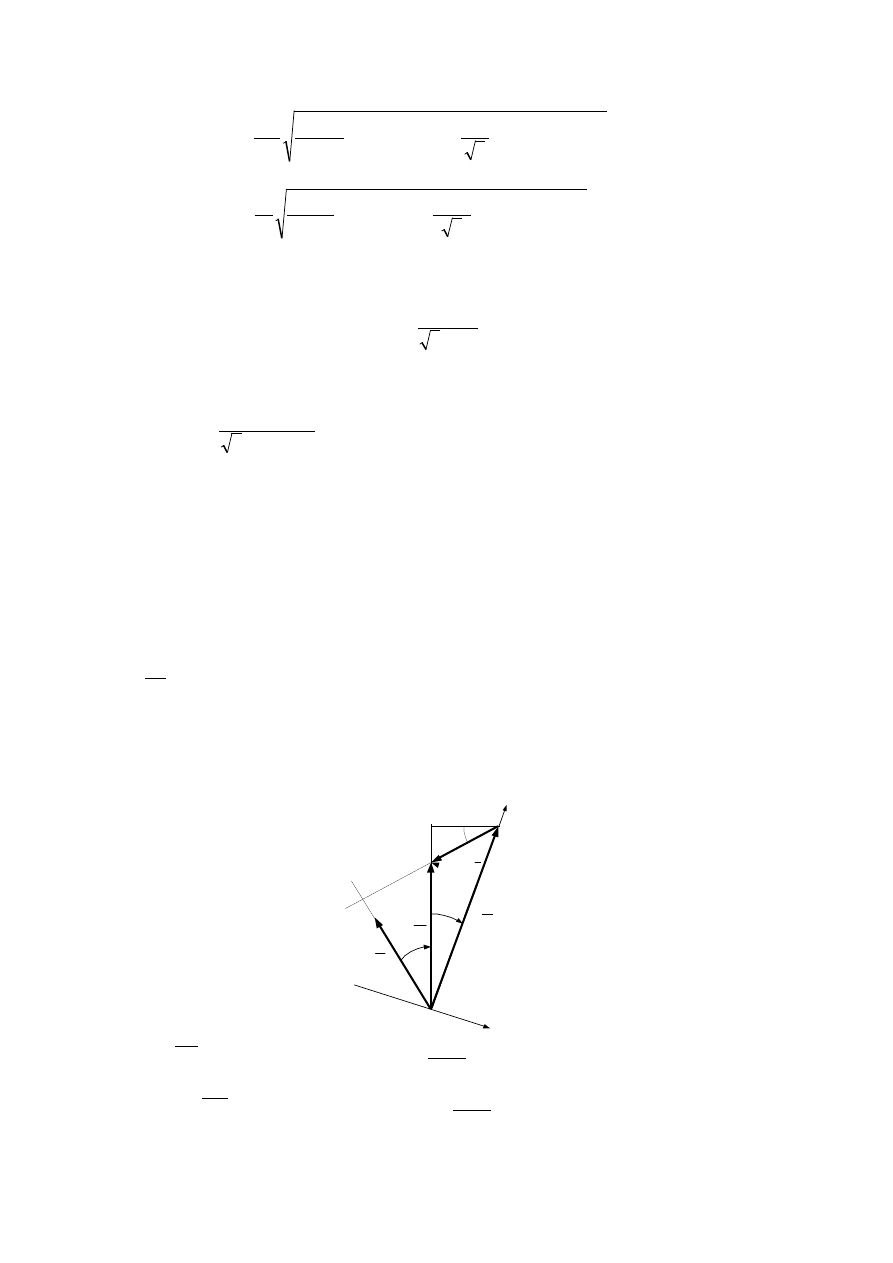
27

tu:

Lx

fN

N

fN

N

d

x

E

U

E

U

X

I

ϑ

cos

)

9

,

0

(

3

2

)

9

,

0

(

3

)

(

1

2

2

−

+

=

,

A

I

x

05

,

326

7982

,

0

3

,

7188

3

6000

2

3

,

7188

3

6000

15

1

2

2

≅

⋅

⋅

−

+

=

.

Współczynnik mocy można teraz wyliczyć z wyrażenia na moc czynną w układach trójfazo-
wych:

885

,

0

3

cos

≅

=

x

N

N

x

I

U

P

ϕ

Dla przypadku, gdy obciążenie wynosi 0,8 obciążenia znamionowego, przy pozostawionej
wartości prądu wzbudzenia, można zapisać:

4819

,

0

6024

,

0

8

,

0

sin

8

,

0

9

,

0

3

8

,

0

sin

=

⋅

=

=

=

Lx

fN

N

d

N

Lxx

E

U

X

P

ϑ

ϑ

, stąd

8762

,

0

cos

=

Lxx

ϑ

.

Postępując analogicznie jak uprzednio otrzymuje się następujące wyniki:

A

I

xx

4

,

298

=

,

7739

,

0

cos

=

xx

ϕ

.

Odpowiedź: Znamionowa przeciążalność silnika wynosi 1,84. Zapas kąta mocy przy zna-
mionowym obciążeniu i obniżonym prądzie wzbudzenia do poziomu 0,9 znamionowego prą-
du wzbudzenia wynosi 0,9243. Wartość prądu stojana i współczynnik mocy w tych warun-
kach wynoszą odpowiednio 326

A i 0,885. Przy obciążeniu zmniejszonym do poziomu 0,8

obciążenia znamionowego wielkości te przyjmują wartości odpowiednio 298,4

A i 0,7739.

4.3.

96

,

0

=

f

x
f

I

I

,

I

a

= 14,5

A

4.4.

I

a

= 88,5

A, cos

ϕ

cap

= 0,6524

4.5.

W stanie znamionowym silnik jest przewzbudzony i odpowiada mu wykres wskazowy:

q

U

I

d

I

jX

d

ϕ

ϕ

L

ϑ

O

A

B

C

D

P

~

Q

~

f

E

Odcinek

P

U

P

X

I

X

I

X

CB

ph

d

ph

d

d

~

3

cos

cos

=

=

=

=

ϕ

ϕ

jest proporcjonalny do mocy czynnej,

zaś odcinek

Q

U

Q

X

I

X

I

X

AC

ph

d

ph

d

d

~

3

sin

sin

=

=

=

=

ϕ

ϕ

- do mocy biernej silnika.

28

Ponieważ prąd wzbudzenia pozostaje znamionowy, siłę elektromotoryczną można wyznaczyć
ze wzoru:

V

x

x

U

E

d

N

d

phN

fN

5

,

6823

2

,

1

6

,

0

2

,

1

2

1

3

6000

)

(

sin

2

1

2

2

=

+

⋅

⋅

+

=

+

+

=

ϕ

.

W nowych warunkach siła elektromotoryczna będzie zależna od nieznanego prądu I i nowe-
go kąta

ϕ

:

ϕ

ϕ

ϕ

sin

3

2

)

(

3

)

(

)

cos

(

)

sin

(

)

(

2

2

2

2

2

I

X

U

I

X

U

I

X

I

X

U

E

d

N

d

N

d

d

phN

fN

+

+

=

+

+

=

czyli:

Q

X

I

X

U

E

d

d

N

fN

3

2

)

(

3

)

(

)

(

2

2

2

+

+

=

.

Wartość reaktancji w

Ω

jest równa:

N

N

N

d

phN

phN

d

d

P

U

x

I

U

x

X

ϕ

cos

2

⋅

=

⋅

=

Tu:

Ω

=

⋅

⋅

⋅

=

56

,

34

10

1

8

,

0

6000

2

,

1

6

2

d

X

.

Zatem prąd fazowy stojana ma wartość:

A

X

Q

X

U

E

I

d

d

N

fN

6

,

107

56

,

34

1

,

3718

3

2

3

)

(

)

(

2

2

=

=

+

−

−

=

.

Dalej wyznaczamy nowy

ϕ

cos .

Z mocy biernej obliczamy wartość:

A

U

Q

U

Q

I

N

phN

6

,

86

10

6

3

10

900

3

3

sin

3

3

=

⋅

⋅

⋅

=

=

=

ϕ

,

805

,

0

6

,

107

6

,

86

sin

sin

=

=

=

I

I

ϕ

ϕ

, stąd:

593

,

0

805

,

0

1

cos

2

=

−

=

ϕ

Moc czynna silnika:

kW

I

U

P

N

4

,

663

5933

,

0

6

,

107

6000

3

cos

3

=

⋅

⋅

⋅

=

=

ϕ

Zatem maksymalny moment obciążenia maszyny wynosi:

Nm

P

T

N

7

,

2112

314

663400

=

=

Ω

=

.

Odpowiedź: T = 2112,7Nm, I

a

= 107,6A.

4.6. I

f

= 277,1A, cos

ϕ

cap

= 0,969

4.7. E

f

= 7104V, E

fx

= 0,9756E

f

, I

ax

= 12,04A

4.8. W analizie zależności napięciowo - prądowych dla pracy generatora synchronicznego
korzystnie jest przyjąć źródłowy (prądnicowy) sposób strzałkowania. Oznacza to, że

prąd

fazowy

I

płynie od prądnicy do odbiornika (przy pracy samotnej generatora), albo do

sieci zasilającej (przy współpracy generatora z siecią). Konsekwencją takiego kierunku
prądu jest postać wykresu wskazowego generatora, spełniająca przy tym wszystkie zasady
zapisu napięć i prądów za pomocą metody symbolicznej na płaszczyźnie zespolonej.
Przypadek pracy samotnej generatora synchronicznego na dowolną impedancję

L

Z

przedsta-

wia schemat poniżej.

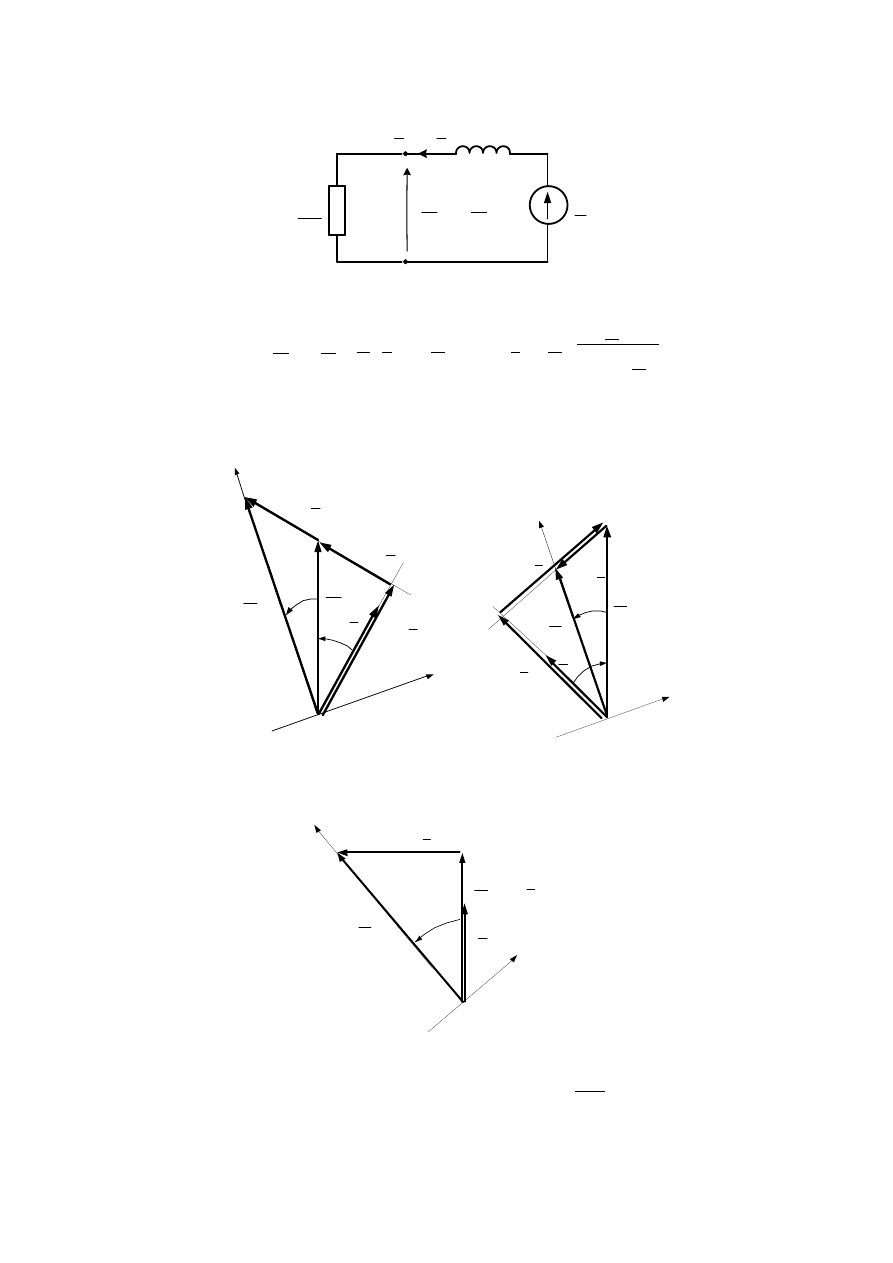
29

d

jX

f

E

L

Z

U

U

L

=

I

I

L

=

Napięcie na fazie odbiornika jest zarazem napięciem fazowym stojana generatora, a jego war-
tość może się zmieniać, zgodnie z zależnością:

L

d

L

f

d

f

L

L

L

Z

jX

Z

E

I

jX

E

I

Z

U

U

+

=

−

=

=

=

)

(

Przedstawiony poniżej wykres wskazowy na rysunku z lewej strony opisuje generator obcią-
ż

ony impedancją o charakterze indukcyjnym, wykres na rysunku z prawej strony opisuje ge-

nerator obciążony impedancją o charakterze pojemnościowym.

q

ϕ

d

I

I

R

L

I

jX

L

I

jX

d

f

E

L

ϑ

U

q

d

L

ϑ

ϕ

U

I

I

R

L

I

jX

L

−

f

E

I

jX

d

W warunkach zadania obciążenie generatora jest czysto rezystancyjne czyli prąd fazowy sto-
jana jest w fazie z napięciem fazowym na odbiorniku (czyli z napięciem fazowym generato-
ra). Wtedy wykres wskazowy przybiera wtedy postać:

I

R

U

L

=

I

I

jX

d

d

q

L

ϑ

f

E

Ad a) Biorąc pod uwagę dane rezystancja fazowa odbiornika (przyjmujemy, że jest on połą-

czony podobnie jak uzwojenie stojana w gwiazdę) wynosi:

Ω

=

=

36

2

P

U

R

L

L

.

Prąd fazowy stojana jest równy prądowi fazowemu odbiornika i wyznaczony na podstawie
wykresu wskazowego w nowych warunkach wynosi:

30

A

R

U

R

U

I

L

x

L

225

,

96

36

3

6000

3

=

⋅

=

⋅

=

=

.

Odpowiada mu wartość fazowa siły elektromotorycznej:

V

I

X

R

E

d

L

f

8

,

3962

225

,

96

182

,

41

2

2

=

⋅

=

⋅

+

=

.

Ad b) Prąd zwarcia symetrycznego można obliczyć ze wzoru:

A

X

E

X

R

E

I

d

f

d

L

f

k

1

,

198

20

8

,

3962

)

0

(

2

2

=

=

=

+

=

=

.

Odpowiedź: a) Prądnica powinna być tak wzbudzona, aby wartość fazowa napięcia induko-
wanego wynosiła 3962,8V; b) Prąd zwarcia symetrycznego przy wzbudzeniu wyliczonym w
punkcie a) wyniesie 198A.

4.9. Napięcie międzyfazowe stojana wzrośnie o

V

U

a

4168

=

∆

.

4.10. Prąd fazowy stojana znamionowy wyznaczamy z mocy pozornej:

A

U

S

I

I

N

N

phN

N

5132

13500

3

10

120

3

6

=

⋅

⋅

=

=

=

.

Wartość reaktancji

d

X w

Ω

wyznaczamy jak w zadaniu 4.5:

Ω

≅

⋅

⋅

=

⋅

=

28

,

2

5132

3

13500

5

,

1

phN

phN

d

d

I

U

x

X

.

Wartość siły elektromotorycznej w nowych warunkach pracy wynika ze związku (jak w za-
daniu 4.1):

V

I

I

U

I

I

I

I

U

I

I

E

E

f

fx

phN

fN

fx

f

fN

phN

fN

fx

fN

fx

9743

280

350

3

13500

0

0

≅

=

=

⋅

=

=

.

Moment napędzający jest równoważny momentowi maszyny, zgodnie zależnością:

Lx

d

N

fx

x

Lx

d

N

fx

phx

x

X

E

U

X

E

U

T

ϑ

ϑ

sin

3

sin

3

Ω

=

Ω

=

Stąd nowa wartość kąta mocy wynosi:

707

,

0

9743

12000

3

28

,

2

314

10

2

3

sin

5

=

⋅

⋅

⋅

⋅

⋅

=

Ω

=

fx

x

d

N

x

Lx

E

U

X

T

ϑ

, czyli:

0

45

=

Lx

ϑ

.

Dla tej wartości kąta:

707

,

0

cos

=

Lx

ϑ

.

Analizowany generator

współpracuje z siecią, przez co napięcie na zaciskach stojana jest

stałe i

równe napięciu sieci. Nową wartość prądu fazowego stojana wyznaczymy z wykresu

wskazowego generatora na podstawie znajomości składowych prądu w osiach „d-q” (Uwaga:
analiza dotyczy modułów napięć, równym długościom odcinków na wykresie wskazowym).
Wykres wskazowy wyznaczamy przy założeniu źródłowego sposóbu strzałkowania (prąd
stojana płynie z generatora do sieci) – jak w zadaniu 4.8.

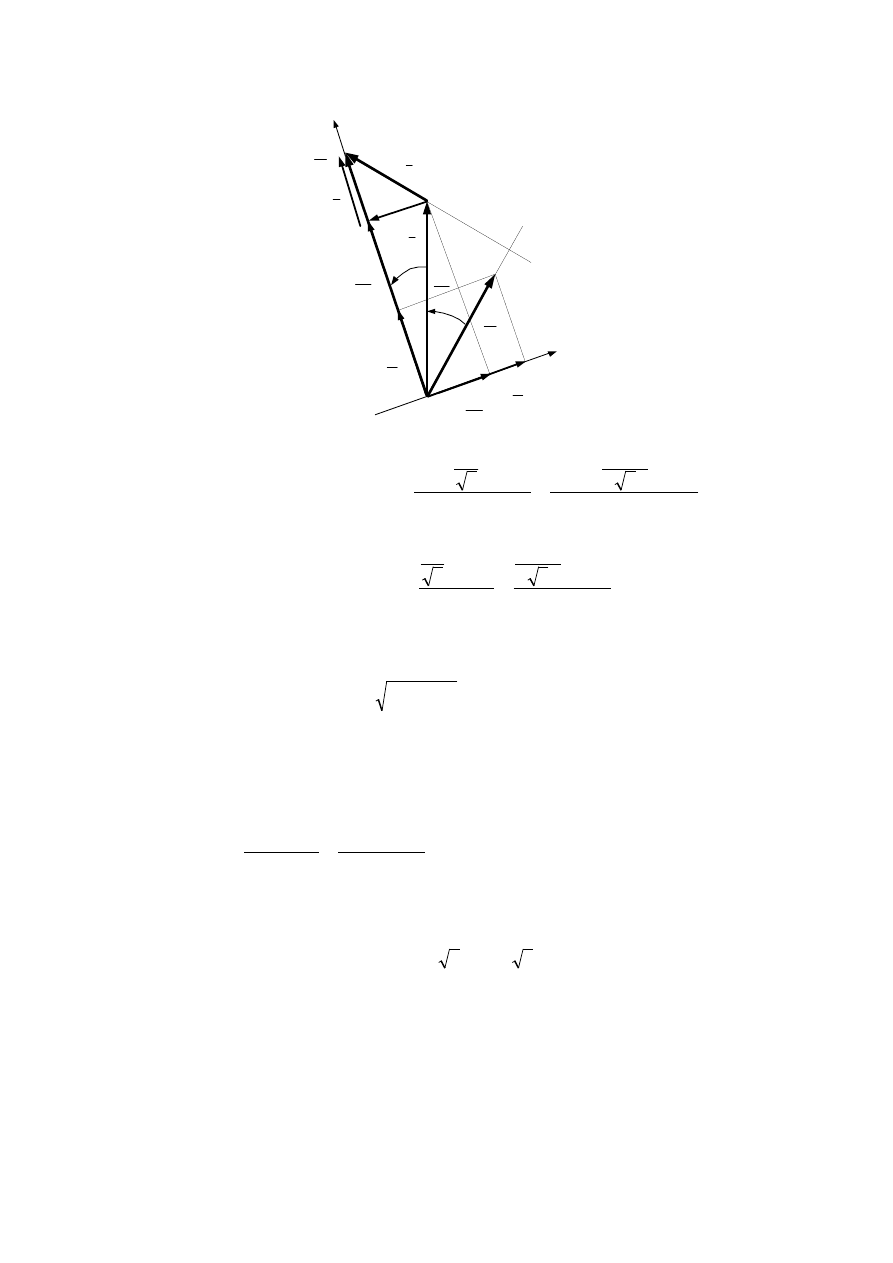
31

q

d

d

I

jX

q

d

I

jX

ϕ

U

I

d

I

jX

d

f

E

L

ϑ

d

U

d

I

q

I

q

U

A

X

U

E

I

U

E

I

X

d

Lx

x

fx

dx

Lx

phx

fx

dx

d

2125

28

,

2

707

,

0

3

12000

9743

cos

3

cos

≅

⋅

−

=

−

=

⇒

−

=

ϑ

ϑ

A

X

U

I

U

I

X

d

Lx

x

qx

Lx

phx

qx

d

2148

28

,

2

707

,

0

3

12000

sin

3

sin

≅

⋅

=

=

⇒

=

ϑ

ϑ

Stąd prąd oddawany do sieci ma wartość skuteczną:

kA

A

I

I

I

I

qx

dx

phx

x

02

,

3

3021

2

2

≅

=

+

=

=

.

Nowy współczynnik mocy wyznaczamy z zależności (patrz rozwiązanie zadania 4.5):

Lx

fx

x

x

d

E

I

X

ϑ

ϕ

sin

cos

=

Stąd:

1

3020

28

,

2

707

,

0

9743

sin

cos

=

⋅

⋅

=

=

x

d

Lx

fx

x

I

X

E

ϑ

ϕ

Zatem generator wydziela moc bierną

0

=

Q

.

Moc czynna przesyłana do sieci wynosi:

MW

I

U

P

x

x

x

77

,

62

3020

12000

3

3

=

⋅

⋅

=

=

.

Odpowiedź: Dla zmienionych warunków szukane wartości są odpowiednio równe:

MW

P

77

,

62

=

,

0

=

Q

,

kA

I

a

02

,

3

=

,

1

cos

=

ϕ

.

4.11.

.

75

,

8

MW

P

=

4.12.

,

6

,

370

A

I

f

=

lub 223A.

32

5. MASZYNY SYNCHRONICZNE WYDATNOBIEGUNOWE

5.1.

Silnik synchroniczny z wydatnymi biegunami o danych: P

N

= 6,7MW, U

N

= 6kV(Y),

cos

ϕ

N

= 0,9

cap

, n

N

= 1000/min, X

d

= 9,42

Ω

, X

q

= 7,54

Ω

jest obciążony mocą czynną znamio-

nową. Ile powinna wynosić wartość napięcia indukowanego E

f

, aby silnik ten kompensował

moc bierną indukowaną Q = 2MVAr. Jaka będzie wartość I

ax

prądu pobieranego z sieci w tych

warunkach i ile będzie wynosił współczynnik mocy cos

ϕ

?

5.2.

Silnik synchroniczny ma dane znamionowe: P

N

= 2,2MW, U

N

= 6 kV(Y), I

N

= 280A,

I

fN

= 360A oraz parametry X

d

= 17,5

Ω

, X

q

= 12,5

Ω

. Silnik zasilono napięciem

x

U = 5,5kV. Jak

należy zmienić wzbudzenie, aby przy obciążeniu momentem znamionowym uzyskać współ-
czynnik mocy cos

ϕ

x

= 1. Przyjąć liniową charakterystykę magnesowania silnika.

5.3.

Silnik synchroniczny o danych znamionowych: P

N

= 250kW, U

N

= 6kV(Y), I

fN

= 25A,

cos

ϕ

N

= 0,8

cap

, n

N

= 750/min, f

N

= 50Hz i parametrach x

d

= 1,2 , x

q

= 0,8 zasilono z sieci

o napięciu 5kV. Obliczyć maksymalny moment, jakim można obciążyć silnik, aby nie wypadł
on z synchronizmu po przerwaniu obwodu wzbudzenia. Jaki prąd będzie pobierany przez ten
silnik, gdy obciąży się go momentem o wartości równej połowie wartości momentu uprzednio
obliczonego? Określić wartość współczynnika mocy dla tego przypadku.

5.4.

Generator synchroniczny wydatnobiegunowy ma dane znaionowe: S

N

= 2,75MVA,

U

N

= 6kV(Y), I

fN

= 360A, I

f

0

= 198A, X

d

= 12,5

Ω

, X

q

= 7,5

Ω

. Obciążony jest on impedancją:

Z = 7,5(0,8

−

j0,6)

Ω

/fazę (Y). Jak należy wzbudzić generator, aby napięcie na zaciskach

osiągnęło wartość znamionową?

ROZWIĄZANIA ZADAŃ I ODPOWIEDZI DO ROZDZIAŁU 5

5.1. Dla silnika synchronicznego z wydatnymi biegunami można narysować wykres wska-
zowy (i odpowiadający mu schemat zastępczy), który dla warunków zadania ma postać:

U

I

d

I

q

I

d

U

q

U

d

ϕ

ϕ

L

ϑ

O

A

B

C

D

E

F

d

q

I

jX

d

d

I

jX

q

q

I

jX

I

jX

q

q

f

E

U

q

jX

I

d

q

d

I

X

X

j

)

(

−

f

E

Napięcie i prąd stojana oraz siła elektromotoryczna są tu wielkościami fazowymi, przy czym
dla uproszczenia zapisu pominięto w ich opisie indeks „ph”.

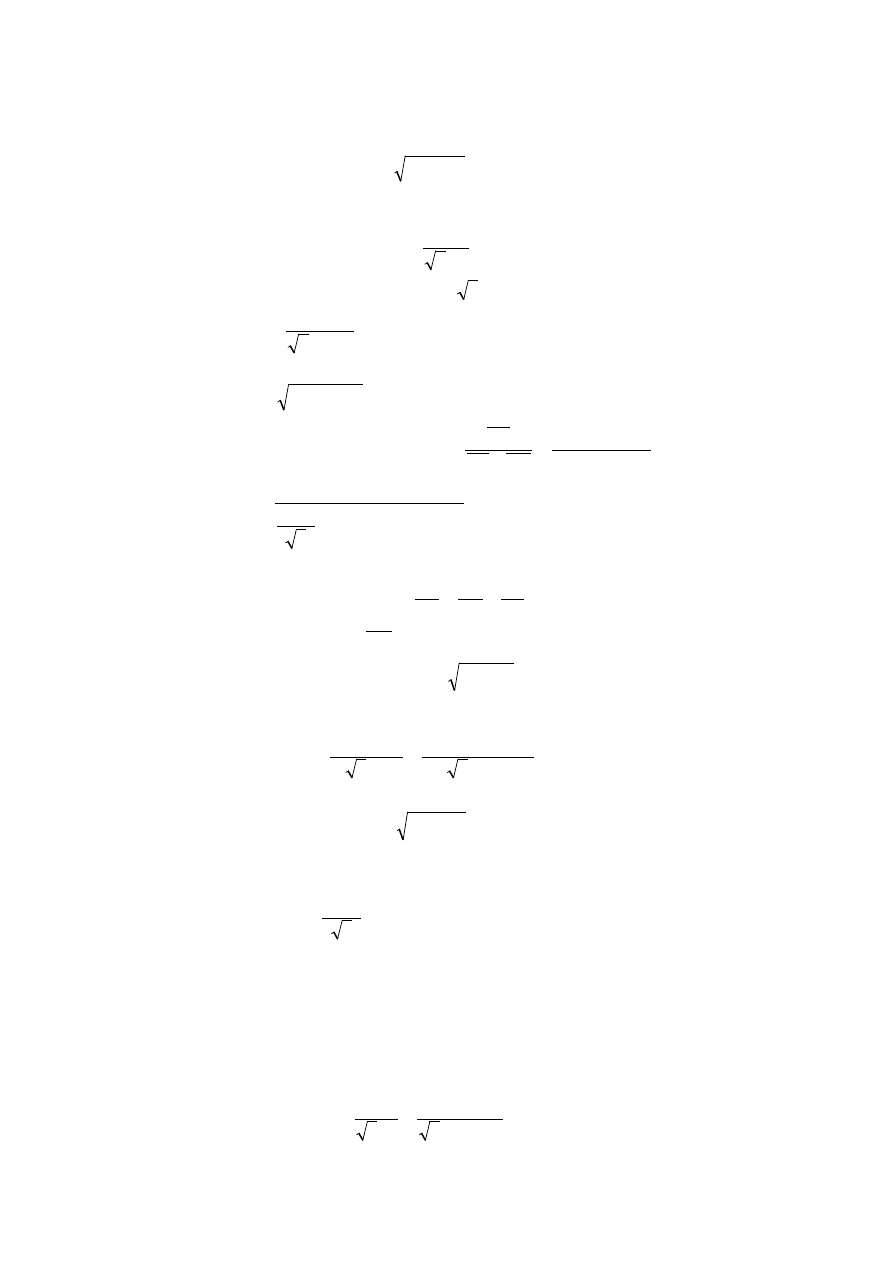
33

Zauważmy, że przy pominięciu strat mocy czynnej (

1

=

η

) moc pozorna silnika w zadanych

warunkach pracy będzie wynosiła:

7

2

2

≅

+

=

Q

P

S

N

x

MVA.

Prąd fazowy pobierany z sieci będzie miał zatem wartość:

8

,

672

3

=

=

=

N

x

x

ax

U

S

I

I

A.

Ponieważ moc bierna wyraża się wzorem:

x

ax

N

I

U

Q

ϕ

sin

3

=

zatem:

286

,

0

3

sin

=

=

ax

N

x

I

U

Q

ϕ

,

stąd:

9582

,

0

cos

1

cos

2

=

−

=

x

x

ϕ

ϕ

.

Aby wyznaczyć kąt mocy zauważmy, że:

ϕ

ϕ

ϑ

sin

cos

I

X

U

I

X

AC

OA

CB

tg

q

q

L

+

=

+

=

i dalej:

989

,

0

286

,

0

8

,

672

54

,

7

3

6000

9582

,

0

8

,

672

54

,

7

=

⋅

⋅

+

⋅

⋅

=

Lx

tg

ϑ

zatem:

ϑ

Lx

= 0,78rad.

Z wykresu wskazowego wynika, że:

d

d

L

f

I

X

U

FE

OF

OE

E

+

=

+

=

=

ϑ

cos

q

q

L

I

X

U

AF

=

=

ϑ

sin

2

2

q

d

I

I

I

+

=

Na podstawie danych zadania otrzymamy:

A

X

U

I

q

Lx

N

qx

1

,

323

54

,

7

3

)

78

,

0

sin(

6000

3

sin

=

⋅

⋅

=

=

ϑ

A

I

I

I

qx

ax

dx

1

,

590

2

2

=

−

=

Wobec powyższego wartość siły elektromotorycznej wynosi:

8

,

8021

1

,

590

42

,

9

)

78

,

0

cos(

3

6000

=

⋅

+

⋅

=

fx

E

V.

Odpowiedź: Aby silnik kompensował moc bierną o wartości 2MVAr, wartość siły elektromo-
torycznej winna wynosić 8021,8V. W tych warunkach prąd pobierany z sieci będzie równy
672,8A, a współczynnik mocy cosφ

x

= 0,9582

cap

.

5.2. W warunkach znamionowych obciążenia, przy

1

cos

=

x

ϕ

prąd pobierany przez silnik z

sieci i jednocześnie prąd fazowy silnika wynosi:

A

U

P

I

x

N

231

10

5

,

5

3

10

2

,

2

3

3

6

≅

⋅

⋅

⋅

=

=

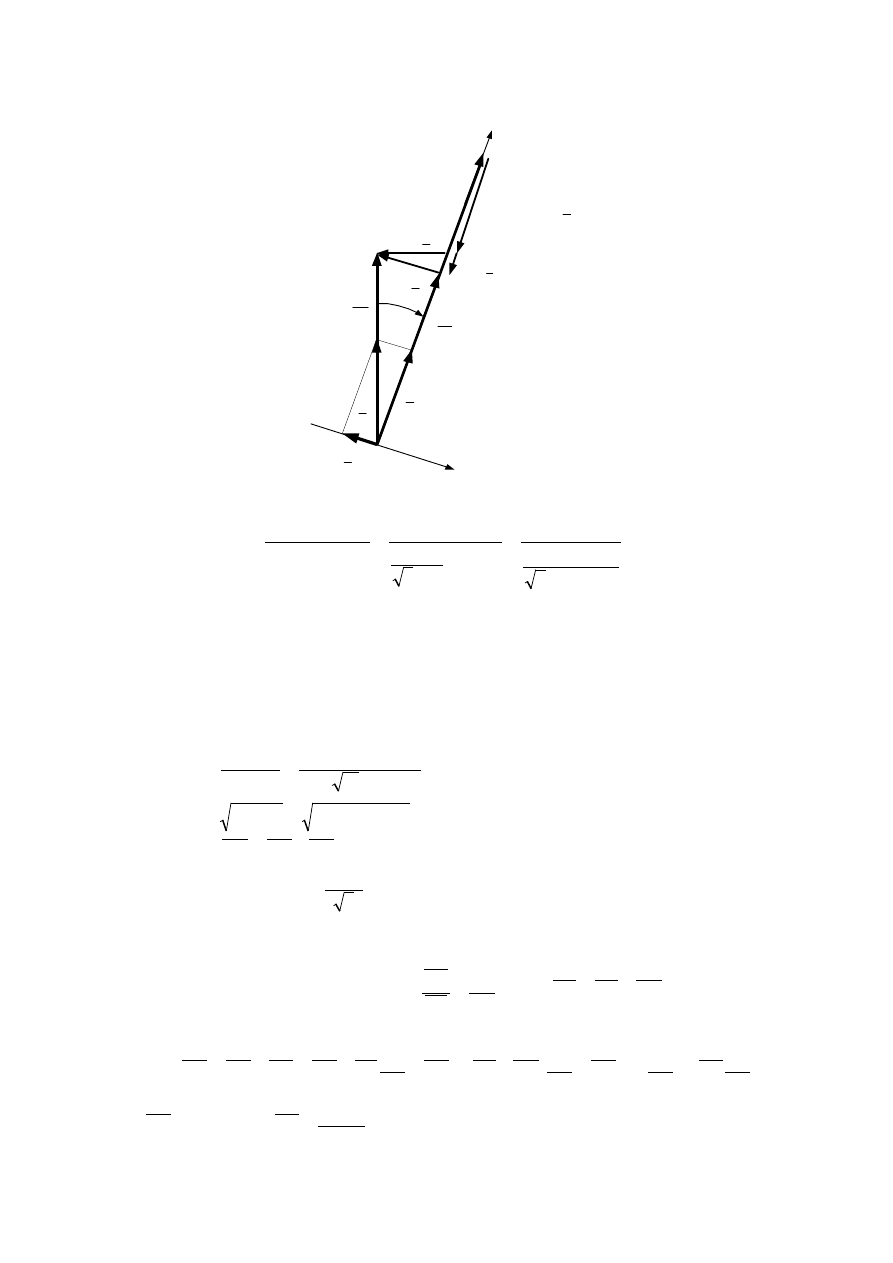
34

Wykres wskazowy prądów i napięć przybiera postać:

d

L

ϑ

d

q

d

I

X

X

j

)

(

−

I

jX

q

q

I

d

I

q

I

U

q

U

d

q

I

jX

q

q

I

jX

O

A

B

C

D

Obliczony z wykresu wskazowego kąt mocy w zadanych warunkach pracy wynosi:

909

,

0

5

,

12

231

3

10

5

,

5

1

sin

3

cos

sin

cos

3

=

⋅

⋅

⋅

=

+

=

+

=

x

q

x

x

x

q

x

q

L

I

X

U

I

X

U

I

X

tg

ϕ

ϕ

ϕ

ϕ

ϑ

stąd:

7378

,

0

=

L

ϑ

rad .

Nową wartość siły elektromotorycznej

f

E można wyznaczyć trzema sposobami:

Sposób pierwszy - z wykresu wskazowego z wykorzystaniem składowych prądów i napięć sil-
nika we współrzędnych „d-q”

Z analizy wykresu wynika równość:

q

q

L

I

X

U

=

ϑ

sin

stąd:

9

,

170

5

,

12

3

)

7378

,

0

sin(

5500

sin

≅

⋅

=

=

q

L

q

X

U

I

ϑ

A,

i dalej:

4

,

155

9

,

170

231

2

2

2

2

=

−

≅

−

=

q

d

I

I

I

A.

Wartość

CD

OC

OD

E

f

+

=

=

,

stąd:

5069

4

,

155

5

,

17

)

7378

,

0

cos(

3

5500

cos

≅

⋅

+

=

+

=

d

d

L

f

I

X

U

E

ϑ

V.

Sposób drugi - z wykresu wskazowego przez analizę trygonometryczną jego składowych

Porównajmy relacje pomiędzy odcinkami:

q

d

X

X

CB

CD

=

oraz

OC

OB

CB

−

=

Ponieważ:

q

d

q

d

q

d

q

d

f

X

X

OB

X

X

OC

X

X

OC

OB

OC

X

X

CB

OC

CD

OC

OD

E

+















−

=

−

+

=

+

=

+

=

=

1

)

(

zaś:

L

U

OC

ϑ

cos

=

, a

L

U

OB

ϑ

cos

=

,

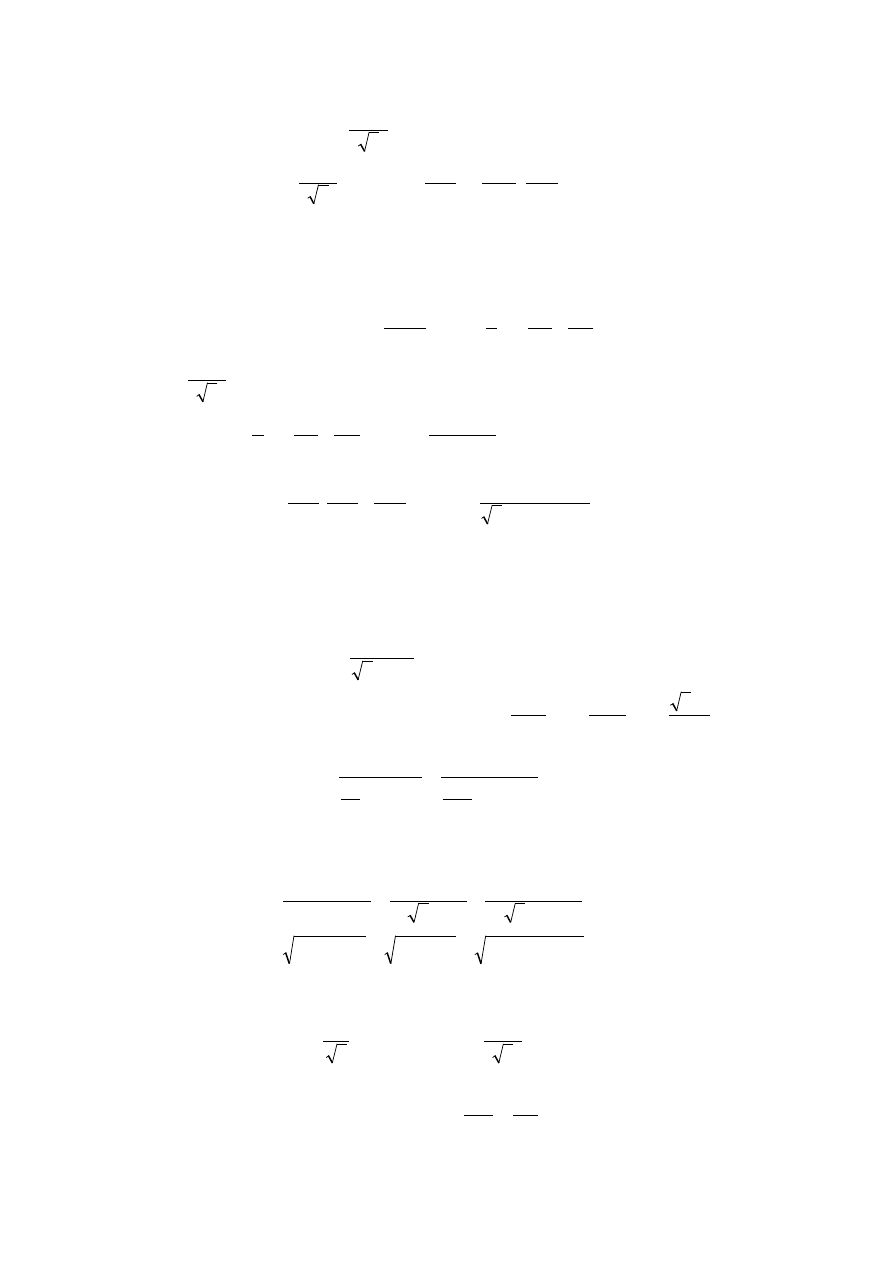
35

po podstawieniu danych ( tu

3

5500

=

U

V oraz

74

,

0

cos

=

L

ϑ

) otrzymujemy:

5068

)

5

,

12

5

,

17

74

,

0

1

5

,

12

5

,

17

1

74

,

0

(

3

5500

=

⋅

+













−

⋅

⋅

=

f

E

V.

Sposób trzeci - ze wzoru na moc (moment) silnika

Silnik obciążony jest znamionowo, lecz zmieniły się wartości napięcia, siły elektromotorycz-
nej i kąta mocy.

L

d

q

L

d

f

N

N

N

X

X

U

X

UE

T

P

ϑ

ϑ

2

sin

)

1

1

(

2

3

sin

3

2

−

+

=

Ω

=

tu:

3

5500

=

U

V oraz

6726

,

0

sin

=

L

ϑ

,

9955

,

0

2

sin

=

L

ϑ

.

Zatem:

L

d

L

d

q

N

f

U

X

X

X

U

P

E

ϑ

ϑ

sin

3

2

sin

)

1

1

(

2

3

2















−

−

=

, a po podstawieniu danych:

5069

10

6726

,

0

5

,

5

3

5

,

17

9955

,

0

)

5

,

17

1

5

,

12

1

(

2

5

,

5

2

,

2

3

2

=

⋅

⋅

⋅













⋅

−

−

=

f

E

V.

Dla wyznaczenia prądu wzbudzenia w nowych warunkach pracy należy określić znamionową
wartość siły elektromotorycznej.
Wybierając pierwszy z przedstawionych powyżej sposobów analizy wyznaczamy wartości
znamionowe:

współczynnika mocy -

756

,

0

3

cos

=

=

N

N

N

N

I

U

P

ϕ

względną wartość reaktancji w osi poprzecznej -

01

,

1

3

≅

=

=

=

N

N

q

phN

phN

q

phN

q

q

U

I

X

U

I

X

Z

X

x

tangens kąta mocy -

46

,

0

6545

,

0

01

,

1

1

756

,

0

sin

1

cos

≅

+

=

+

=

N

q

N

LN

x

tg

ϕ

ϕ

ϑ

stąd:

431

,

0

=

LN

ϑ

rad.

Zatem:

A

X

U

X

U

I

LN

q

LN

N

q

LN

phN

qN

8

,

115

5

,

12

3

sin

6000

3

sin

sin

≅

⋅

⋅

=

=

=

ϑ

ϑ

ϑ

A

I

I

I

I

I

qN

N

qN

phN

dN

9

,

254

8

,

115

280

2

2

2

2

2

2

=

−

=

−

=

−

=

Wobec powyższego znamionowa wartość napięcia indukowanego wyniesie:

V

I

X

U

I

X

U

E

dN

d

LN

N

dN

d

LN

phN

fN

7608

9

,

254

5

,

17

)

431

,

0

cos(

3

6000

cos

3

cos

≅

⋅

+

=

+

=

+

=

ϑ

ϑ

Przy założeniu liniowości obwodu magnetycznego pomiędzy siłą elektromotoryczną i prądem

wzbudzenia zachodzi relacja proporcjonalności:

fN

fx

fN

fx

I

I

E

E

=

.

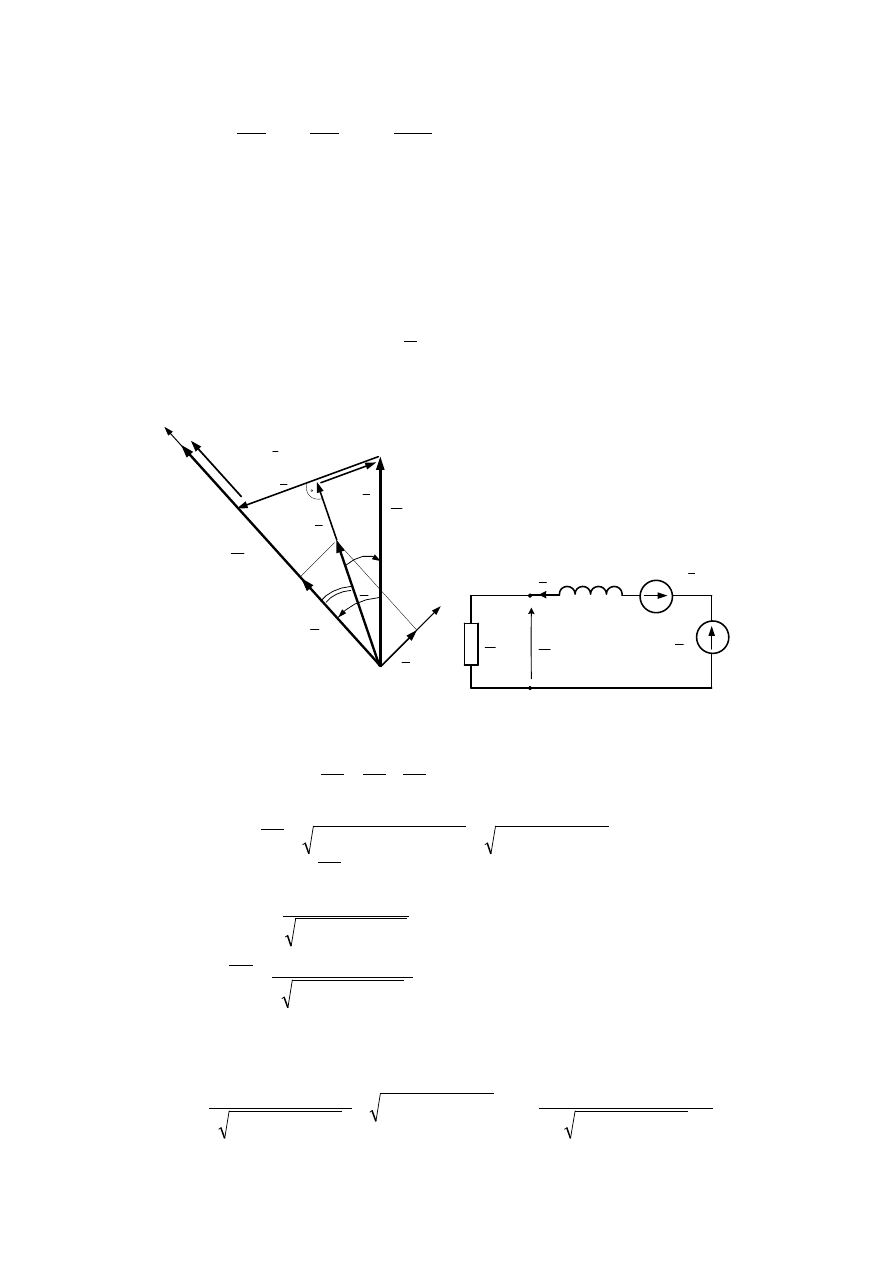
36

Zatem:

8

,

239

7608

5069

360

=

⋅

=

=

=

fN

f

fN

fN

fx

fN

fx

E

E

I

E

E

I

I

A.

Odpowiedź: Należy obniżyć wzbudzenie do poziomu ok. 240A.

5.3.

6

,

576

=

T

Nm,

A

I

a

7

,

21

=

, przy cosφ

ind

= 0,1205.

5.4. Prąd wzbudzenia znamionowy ma większą wartość niż prąd wzbudzenia jałowy

0

f

fN

I

I

>

, zatem generator pracuje w warunkach przewzbudzenia.

Impedancja fazowa obciążenia wynosi:

5

,

4

6

j

jX

R

Z

−

=

−

=

(Ω).

Ponieważ zachodzi zależność:

q

X

X

<

, pracę samotną generatora ilustruje orientacyjny wy-

kres wskazowy i odpowiadający mu schemat fazowy układu „generator-obciążenie”:

U

q

d

L

ϑ

ϕ

Ψ

d

I

q

I

I

R

I

jX

−

I

jX

q

I

f

E

O

A

d

q

d

I

X

X

j

)

(

−

B

d

q

d

I

X

X

j

)

(

−

f

E

Z

U

I

q

jX

Aby wyznaczyć wartość prądu wzbudzenia

f

I w tym stanie pracy, należy wyznaczyć wartość

siły elektromotorycznej

f

E .

Z wykresu wynika, że:

AB

OA

OB

E

f

+

=

=

,

gdzie:

I

X

X

R

I

X

X

RI

OA

q

q

⋅

−

+

=

−

+

=

2

2

2

2

)

(

]

)

[(

)

(

,

d

q

d

I

X

X

AB

)

(

−

=

, zaś

Ψ

=

sin

I

I

d

i jednocześnie:

2

2

)

(

sin

X

X

R

X

X

q

q

−

+

−

=

Ψ

,

zatem:

I

X

X

R

X

X

X

X

AB

q

q

d

q

⋅

−

+

−

−

=

2

2

)

(

)

)(

(

.

Uwzględniając powyższe zależności otrzymamy:

I

X

X

R

X

X

X

X

R

I

X

X

R

X

X

R

X

X

X

X

E

q

d

q

q

q

q

d

q

f

⋅

−

+

−

−

+

=

⋅

















−

+

+

−

+

−

−

=

2

2

2

2

2

2

2

)

(

)

)(

(

)

(

)

(

)

)(

(

37

Napięcie na zaciskach generatora jest jednocześnie napięciem na impedancji obciążenia. Aby
osiągnęło wartość znamionową w zadanym układzie połączeń, prąd fazowy obciążenia winien
być równy:

462

5

,

7

3

6000

3

≅

⋅

=

=

Z

U

I

N

A.

Wtedy:

V

E

f

4132

462

)

5

,

4

5

,

7

(

6

)

5

,

4

5

,

12

)(

5

,

4

5

,

7

(

6

2

2

2

=

⋅

−

+

−

−

+

=

.

Przyjmujemy dalej, że:

0

f

f

phN

f

I

I

U

E

=

.

Zatem:

236

6000

3

4132

198

3

0

≅

⋅

⋅

=

⋅

=

N

f

f

f

U

E

I

I

A.

Odpowiedź: Generator należy wzbudzić prądem o wartości:

A

I

f

236

=

.

6. MASZYNY KOMUTATOROWE PRĄDU STAŁEGO

Uwaga: w analizie wszystkich przedstawionych zadań przyjęto liniową charakterystykę ma-
gnesowania silnika, pominięto oddziaływanie uzwojenia biegunów pomocniczych oraz nie
uwzględniono strat w żelazie, strat komutacyjnych i strat dodatkowych.

6.1. Silnik obcowzbudny prądu stałego o danych znamionowych: P

N

= 30kW, U

N

= 220V,

n

N

= 1200/min ma rezystancję twornika R

a

= 0,06

Ω

i jest wzbudzony znamionowo. Obliczyć

rezystancję rozruchową R

d

taką, aby prąd maksymalny nie przekraczał 2,2I

N

przy znamiono-

wym napięciu U

N

= 220V. Obliczyć obroty, przy których ma nastąpić przełączenie, przyjmu-

jąc prąd minimalny I

a

= I

N

. Wskazówka: przyjąć straty mechaniczne za równe zeru

−

∆

P

m

= 0.

6.2. Silnik obcowzbudny prądu stałego o danych znamionowych: P

N

= 5kW, U

N

= 200V,

n

N

= 1400/min ma rezystancję twornika R

a

= 0,06

Ω

, a straty mechaniczne

∆

P

mN

= 150W. Ob-

liczyć napięcie zasilania, aby przy znamionowym wzbudzeniu i momencie obciążenia
T

x

= 20Nm uzyskać obroty wirnika n

x

= 1000/min. Wskazówka: przyjąć, że straty mechanicz-

ne są wprost proporcjonalne do prędkości obrotowej.

6.3. Silnik obcowzbudny prądu stałego o danych znamionowych: P

N

= 55kW, U

N

= 400V,

I

N

= 152A,

Ω

N

=120rad/s ma twornik zasilony napięciem U = 200V. Jak należy zmienić stru-

mień wzbudzenia

Ψ

, aby prędkość pozostała znamionowa, przy momencie obciążenia

N

T

T

5

,

0

=

. Wskazówka: przyjąć, że straty mechaniczne są równe zeru -

∆

P

m

= 0.

6.4. Silnik bocznikowy prądu stałego o danych: P

N

= 20kW, U

N

= 220V, n

N

= 1450/min,

η

N

= 0,85, R

a

= 0,145

Ω

, R

f

= 88

Ω

został zasilony napięciem U = 180V i obciążony momen-

tem T = 0,8T

N

.

a) Obliczyć ustalone obroty dla tych warunków pracy.
b) Obliczyć wartość R

d

rozrusznika, jaki należy dołączyć do obwodu twornika, aby dla zna-

mionowej wartości zasilania prąd rozruchowy pobierany z sieci był równy 2I

N

.

38

6.5. Silnik bocznikowy prądu stałego o danych znamionowych: P

N

= 15kW, U

N

= 220V,

I

N

= 81A,

Ω

N

= 100 rad/s, R

a

= 0,14

Ω

, R

f

= 110

Ω

.

a) Obliczyć ustalone obroty, jakie osiągnie silnik, gdy napięcie zasilania zostanie obniżone
do 0,5U

N

, zaś moment obciążenia pozostanie znamionowy.

b) Obliczyć ustalone obroty, gdy napięcie zasilania i obciążenie pozostaną znamionowe, zaś
w obwód twornika włączona jest rezystancja dodatkowa R

d

= 0,36

Ω

.

Założyć, że straty mechaniczne są wprost proporcjonalne do prędkości obrotowej.

6.6. Silnik szeregowy o danych: P

N

= 5,1kW, U

N

= 220V, n

N

= 1800/min, I

N

= 24A zasilono

napięciem U

x

= 120V i obciążono momentem T

x

= 0,7T

N

.

Obliczyć ustalone obroty n

x

oraz

prąd silnika I

x

. Wskazówka: przyjąć, że straty mechaniczne są równe zeru -

∆

P

m

= 0.

6.7. Silnik szeregowy o danych: P

N

= 23kW, U

N

= 220V, n

N

= 660/min, I

N

= 120A,

R

a

+R

f

= 0,175

Ω

jest obciążony momentem znamionowym. Obliczyć ustalone obroty n, jeśli

napięcie na zaciskach silnika spadnie do wartości 0,5U

N

. Wskazówka: przyjąć, że straty

mechaniczne są stałe.

6.8. Silnik szeregowy obciążony wiruje z prędkością n

1

= 1200/min, przy zasilaniu napięciem

U = 230V i prądzie I = 16,3A. Moment obciążenia zmienia się proporcjonalnie do

ω

1,8

. Jakie

powinny być wartości prądu I

x

i napięcia U

x

, aby prędkość tego silnika wynosiła

n

2

= 1750/min ? Rezystancja obwodu szeregowego wynosi R = 1

Ω

.

6.9. Silnik szeregowy o danych: I

N

= 105A, U

N

= 220V, n

N

= 1450/min, R

a

= 0,1

Ω

,

R

f

= 0,05

Ω

. Do obwodu twornika dołączono szeregowo opór R

d

= 0,7

Ω

, uzwojenie wzbudze-

nia zbocznikowano rezystancją R

b

= 0,05

Ω

, a napięcie zasilania obniżono do wartości 0,8U

N

.

Obliczyć ustalone obroty, jakie osiągnie silnik, gdy dla tych warunków obciąży się go mo-
mentem znamionowym.

6.10. Silnik prądu stałego obcowzbudny z dozwojeniem szeregowym zgodnym o danych:
P

N

= 125kW, U

N

= 440V, I

N

= 312A, n

N

= 1500/min,

5

,

2

0

=

Ψ

=

Ψ

N

Vs/rad (od prądu wzbu-

dzenia obcego, w stanie znamionowym), R

a

+ R

s

= 126m

Ω

pracuje przy obciążeniu momen-

tem T = 500Nm. Obliczyć o ile ulegną zmianie obroty tego silnika, jeśli jego dozwojenie sze-
regowe będzie przeciwne. Obliczyć wartość prądu twornika w tych warunkach. Przyjąć li-
niową charakterystykę magnesowania silnika.

6.11. Silnik bocznikowy z dozwojeniem szeregowym zgodnym o danych: P

N

= 22kW,

U

aN

= 200V, I

aN

= 119A, I

fN

= 2,5A, n

N

= 785/min, R

a

= 0,12

Ω

,

f

a

M = 0,845H/rad (indukcyj-

ność rotacji związana ze wzbudzeniem bocznikowym) jest zasilany napięciem U

a

= 180V

i obciążony połową momentu znamionowego. Pomijając straty mechaniczne, obliczyć ustalo-
ne obroty n silnika.

6.12. Silnik uniwersalny o danych parametrach: R

a

= 0,5

Ω

, R

f

= 0,5

Ω

,

f

a

M = 0,15H/rad,

f

a

L

L

+

= 0,2H obciążony jest momentem T = 0,2Nm. Obliczyć obroty silnika przy:

a) zasilaniu napięciem stałym U = 220V,
b) zasilaniu napięciem przemiennym o wartości skutecznej U = 220V i f = 50Hz.

39

6.13. Prądnica prądu stałego obcowzbudna ma dane parametry: R

a

= 0,2

Ω

, I

f

= 1A,

f

a

M = 2,5H/rad,

Ω

= 100rad/s. Przy założeniu, że szczotki są w strefie neutralnej obliczyć:

moc P oddawaną przez prądnicę, prąd wzbudzenia I

f

oraz napięcie na zaciskach prądnicy U

a

,

gdy obciążona jest rezystancją R = 40

Ω

.

ROZWIĄZANIA ZADAŃ I ODPOWIEDZI DO ROZDZIAŁU 6

6.1. Bilans mocy silnika w znamionowych warunkach pracy, przy uwzględnieniu w stratach
mocy jedynie strat w rezystancji twornika, ma postać:

2

aN

a

N

aN

aN

I

R

P

I

U

+

=

stąd z równania kwadratowego wyliczamy nieznany prąd znamionowy twornika:

0

30000

220

06

,

0

2

=

+

−

aN

aN

I

I

8

,

3524

=

aN

I

A - ten wynik odrzucamy, przyjmujemy wartość

85

,

141

=

aN

I

A.

Zgodnie z tematem zadania maksymalny prąd przy rozruchu wyniesie

312

2

,

2

=

⋅

=

aN

l

I

I

A.

Odpowiada mu sumaryczna rezystancja w obwodzie twornika:

Ω

=

=

=

+

705

,

0

312

220

l

aN

d

a

I

U

R

R

stąd:

Ω

=

645

,

0

d

R

.

Równanie napięciowe silnika prądu stałego można zapisać jako:

a

a

a

I

R

U

E

−

=

.

Siła elektromotoryczna indukowana w tworniku od prądu wzbudzenia ma równoważne posta-
cie:

n

c

c

I

M

E

f

f

a

Φ

=

ΦΩ

=

ΨΩ

=

Ω

=

30

π

.

Uwzględniając zapis E w równaniu napięć otrzymujemy podstawową zależność pomiędzy
prędkością kątową (obrotami wirnika), a wielkościami elektrycznymi silnika:

Φ

−

=

Ψ

−

=

−

=

=

Ω

c

I

R

U

I

R

U

I

M

I

R

U

n

a

a

a

a

a

a

f

f

a

a

a

a

30

π

.

Podczas rozruchu chwili wyłączenia rezystancji dodatkowej przy znamionowym prądzie
twornika, odpowiadać będzie prędkość kątowa

x

Ω

:

N

aN

d

a

aN

x

I

R

R

U

Ψ

+

−

=

Ω

)

(

.

W znamionowym stanie pracy prędkość kątowa

N

Ω

spełnia zależność:

N

aN

a

aN

N

I

R

U

Ψ

−

=

Ω

.

Nieznane obroty można wyznaczyć dwoma sposobami.

40

Sposób pierwszy - przez proporcję: porównanie nowego i poprzedniego stanów pracy.

W tym przypadku nieznane obroty wynoszą:

aN

a

aN

aN

d

a

aN

N

x

N

x

I

R

U

I

R

R

U

n

n

−

+

−

=

Ω

Ω

=

)

(

,

i dalej:

681

1400

85

,

141

06

,

0

220

85

,

141

705

,

0

220

)

(

=

⋅

⋅

−

⋅

−

=

⋅

−

+

−

=

N

aN

a

aN

aN

d

a

aN

x

n

I

R

U

I

R

R

U

n

/min.

Sposób drugi - przez wyznaczenie strumienia wzbudzenia (indukcyjności rotacji).

Z równania dla stanu znamionowej pracy silnika wyznaczamy:

1,683

30

=

−

=

Ω

−

=

Φ

=

Ψ

=

N

aN

a

aN

N

aN

a

aN

N

N

fN

f

a

n

I

R

U

I

R

U

c

I

M

π

Vs/rad.

Zatem obroty w stanie przełączenia będą równe:

681

)

(

30

=

Ψ

+

−

=

N

aN

d

a

aN

x

I

R

R

U

n

π

/min.

Odpowiedź: Wartość rezystancji dodatkowej, jaką należy włączyć w obwód twornika wynosi
0,645

Ω

. Obroty wirnika, przy których ma nastąpić przełączenie, wynoszą 681/min.

6.2. Wskazówka: ponieważ straty mechaniczne są proporcjonalne do obrotów silnika, mo-

ment strat mechanicznych ma stałą wartość -

N

m

N

m

m

n

P

P

T

∆

⋅

=

Ω

∆

=

π

30

. Przy stałej znamionowej

wartości strumienia wzbudzenia momenty elektromagnetyczne rozwijane przez silnik w obu

analizowanych stanach pracy pozostają w proporcji:

aN

ax

aN

N

ax

N

m

N

m

x

I

I

I

I

T

T

T

T

=

Ψ

Ψ

=

+

+

.

Odpowiedź:

7

,

142

≅

a

U

V.

6.3.

N

Ψ

≅

Ψ

423

0,

.

6.4. Równania napięciowe silnika bocznikowego prądu stałego mają postać:

a

a

f

f

a

a

a

a

I

R

I

M

I

R

E

U

+

Ω

=

+

=

,

f

f

a

f

I

R

U

U

=

=

Prąd silnika, pobierany z sieci, wynosi przy tym:

f

a

I

I

I

+

=

Znamionowy prąd silnika wyznaczamy z relacji mocy elektrycznej i mechanicznej:

N

N

N

N

I

U

P

η

=

, stąd:

107

≅

=

N

N

N

N

U

P

I

η

A.

Znamionowa wartość prądu wzbudzenia wynosi:

5

,

2

=

=

f

N

fN

R

U

I

A.

Zatem:

5

,

104

=

−

=

fN

N

aN

I

I

I

A, oraz

54

,

0

≅

Ω

−

=

fN

N

aN

a

aN

f

a

I

I

R

U

M

H/rad.

Ad a) Znamionowy moment obrotowy wyznaczamy z zależności:

7

,

131

=

Ω

=

N

N

N

P

T

Nm,

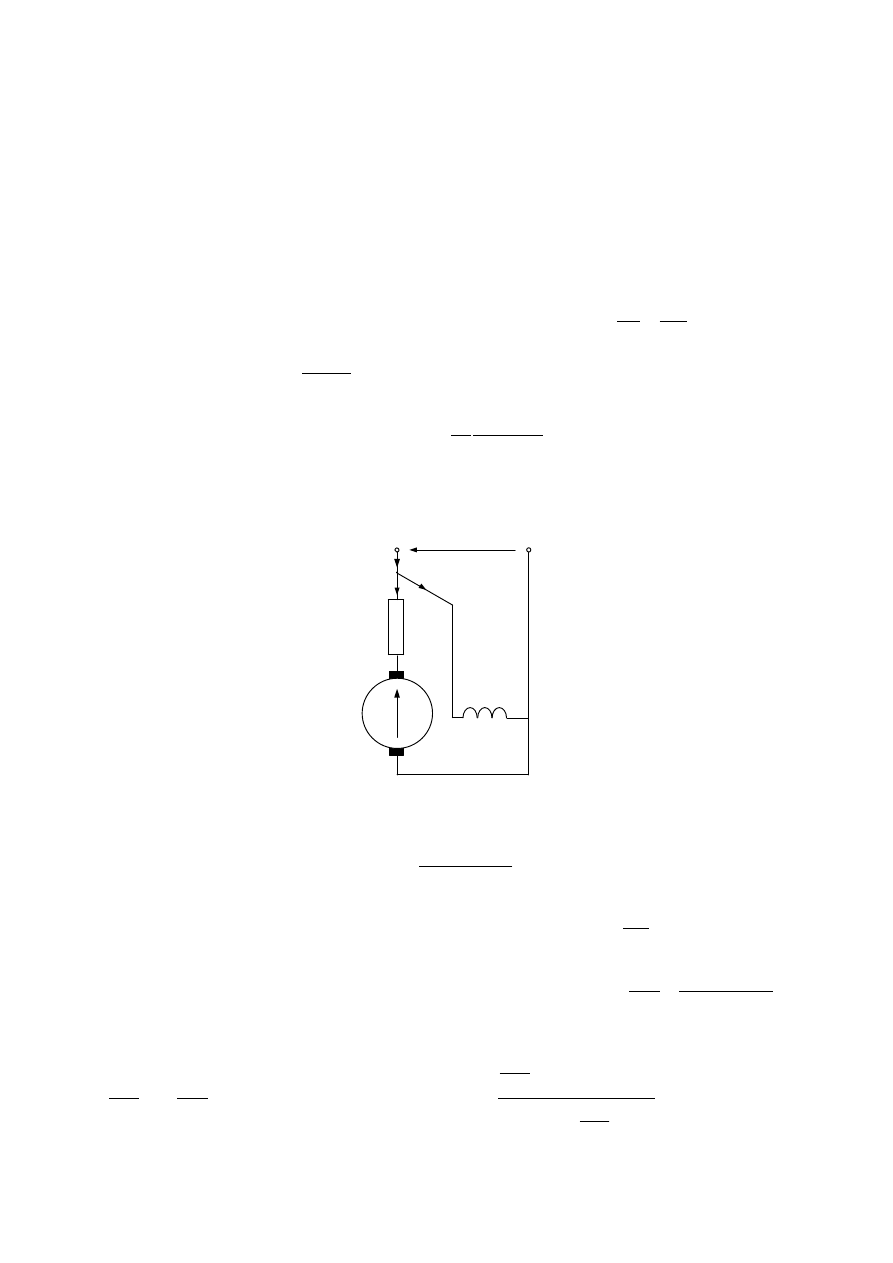
41

natomiast wartość znamionowa momentu elektromagnetycznego jest równa:

141

=

=

aN

fN

f

a

eN

I

I

M

T

Nm,

stąd moment strat mechanicznych wynosi:

3

,

9

=

−

−

N

eN

m

T

T

T

Nm.

Przyjmując, jak w zadaniu 6.2, stałą wartość momentu strat mechanicznych możemy określić
całkowity moment obciążenia w nowych warunkach pracy:

7

,

114

8

,

0

=

+

=

m

N

x

T

T

T

Nm.

W nowych warunkach pracy prąd wzbudzenia przyjmie wartość:

04

,

2

88

180

≅

=

=

f

fx

R

U

I

A,

zaś prąd twornika:

1

,

104

≅

=

fx

f

a

x

ax

I

M

T

I

A.

Ostatecznie prędkość obrotowa wyniesie:

5

,

1429

30

≅

−

=

fx

f

a

ax

a

x

I

M

I

R

U

n

π

/min.

Ad b) Schemat połączeń silnika bocznikowego w warunkach przeprowadzania rozruchu opo-
rowego

przedstawia się następująco:

d

R

f

R

a

R

f

a

U

U

=

a

I

A1

A2

E1

E2

f

I

I

E

Dla zatrzymanej maszyny

)

0

(

=

E

całkowita rezystancja mierzona z zacisków twornika wyra-

zi się wzorem:

f

d

a

f

d

a

w

R

R

R

R

R

R

R

+

+

+

=

)

(

.

Ponadto uwzględniamy ograniczenie prądu pobieranego z sieci:

w

N

N

R

U

I

=

2

.

Z powyższych zależności wyznaczamy wartość rezystancji rozrusznika:

f

d

a

f

d

a

N

N

R

R

R

R

R

R

I

U

+

+

+

=

)

(

2

i dalej:

f

d

f

a

f

a

N

N

d

N

N

R

R

R

R

R

R

I

U

R

I

U

+

=

+

+

)

(

2

2

, stąd:

895

,

0

2

)

(

2

=

−

−

+

=

N

N

f

f

a

f

a

N

N

d

I

U

R

R

R

R

R

I

U

R

Ω

.

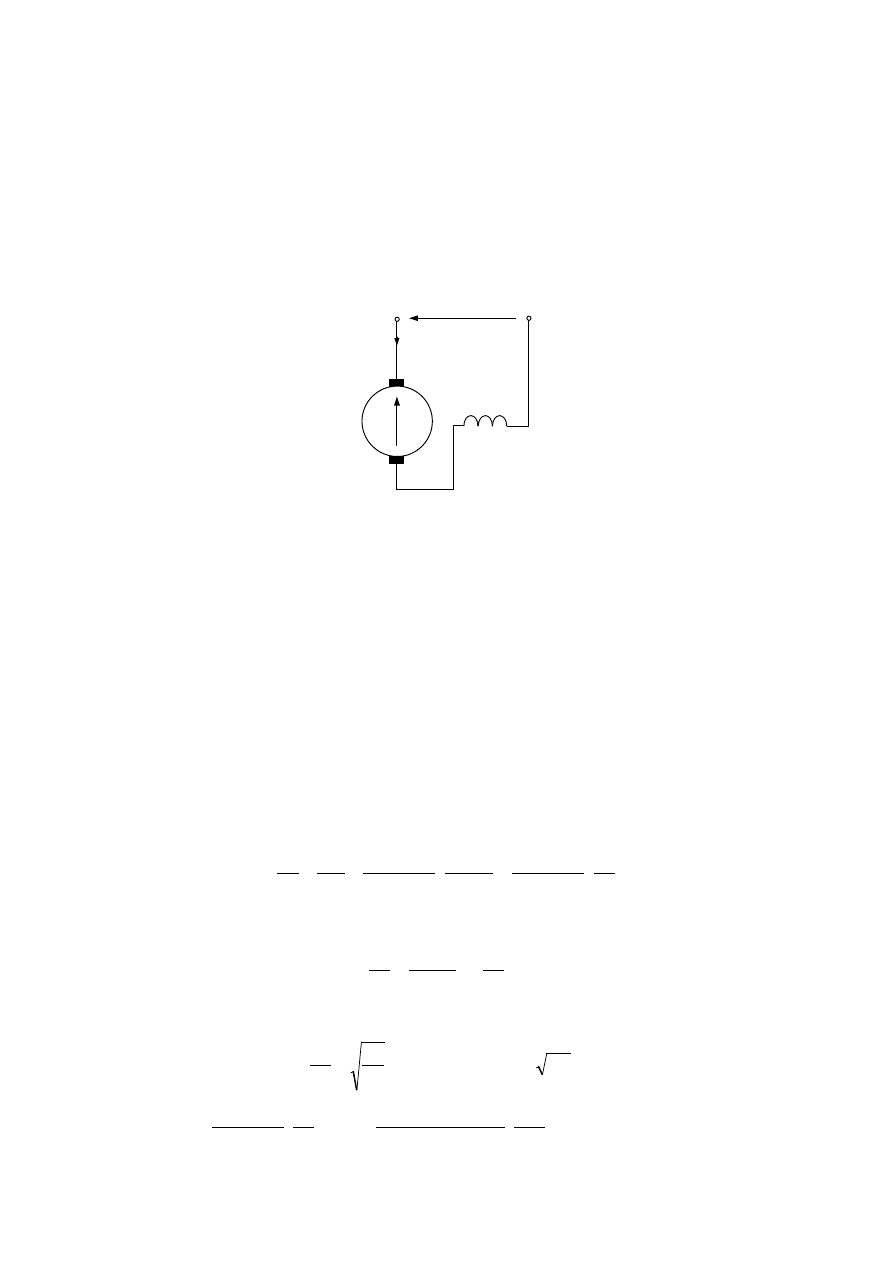
42

Odpowiedź: ad a) Ustalona prędkość obrotowa wynosi 1429,5/min.

ad b) Wartość rezystancji rozruchowej ma być równa 0,895

Ω

.

6.5. Ad a)

800

≅

x

n

/min, ad b)

821

≅

x

n

/min

-1

.

6.6. Schemat silnika szeregowego przedstawia rysunek poniżej:

E

f

R

a

R

U

I

A1

A2

D1

D2

Równanie napięć silnika szeregowego prądu stałego ma postać:

RI

I

M

RI

E

U

f

a

+

Ω

=

+

=

gdzie:

f

a

R

R

R

+

=

Uproszczony bilans mocy, uwzględniający jako jedyne straty mocy - straty mocy w rezystan-
cjach uzwojeń, można zapisać jako:

N

N

N

N

P

RI

I

U

=

−

2

Stąd:

3125

,

0

=

R

Ω

.

Pierwszy sposób wyznaczenia nowych obrotów:

Z porównania równania napięć w nowym i poprzednim stanie pracy silnika otrzymujemy
związek pomiędzy prędkościami obrotowymi silnika:

x

N

N

N

x

x

x

f

a

N

f

a

N

N

x

x

N

x

N

x

I

I

RI

U

RI

U

I

M

I

M

RI

U

RI

U

n

n

⋅

−

−

=

⋅

−

−

=

Ω

Ω

=

Analogiczne porównujemy momenty elektromagnetyczne wytworzone przez silnik:

2

2

2













=

=

N

x

N

f

a

x

f

a

N

x

I

I

I

M

I

M

T

T

.

Z warunków zadania wynikają wartości:

N

x

N

x

T

T

I

I

=

, stąd:

1

,

20

7

,

0

24

≅

=

x

I

A

oraz

1151

1

,

20

24

24

3125

,

0

220

1

,

20

3125

,

0

120

1800

≅

⋅

⋅

−

⋅

−

⋅

=

⋅

−

−

⋅

=

x

N

N

N

x

x

N

x

I

I

RI

U

RI

U

n

n

/min.

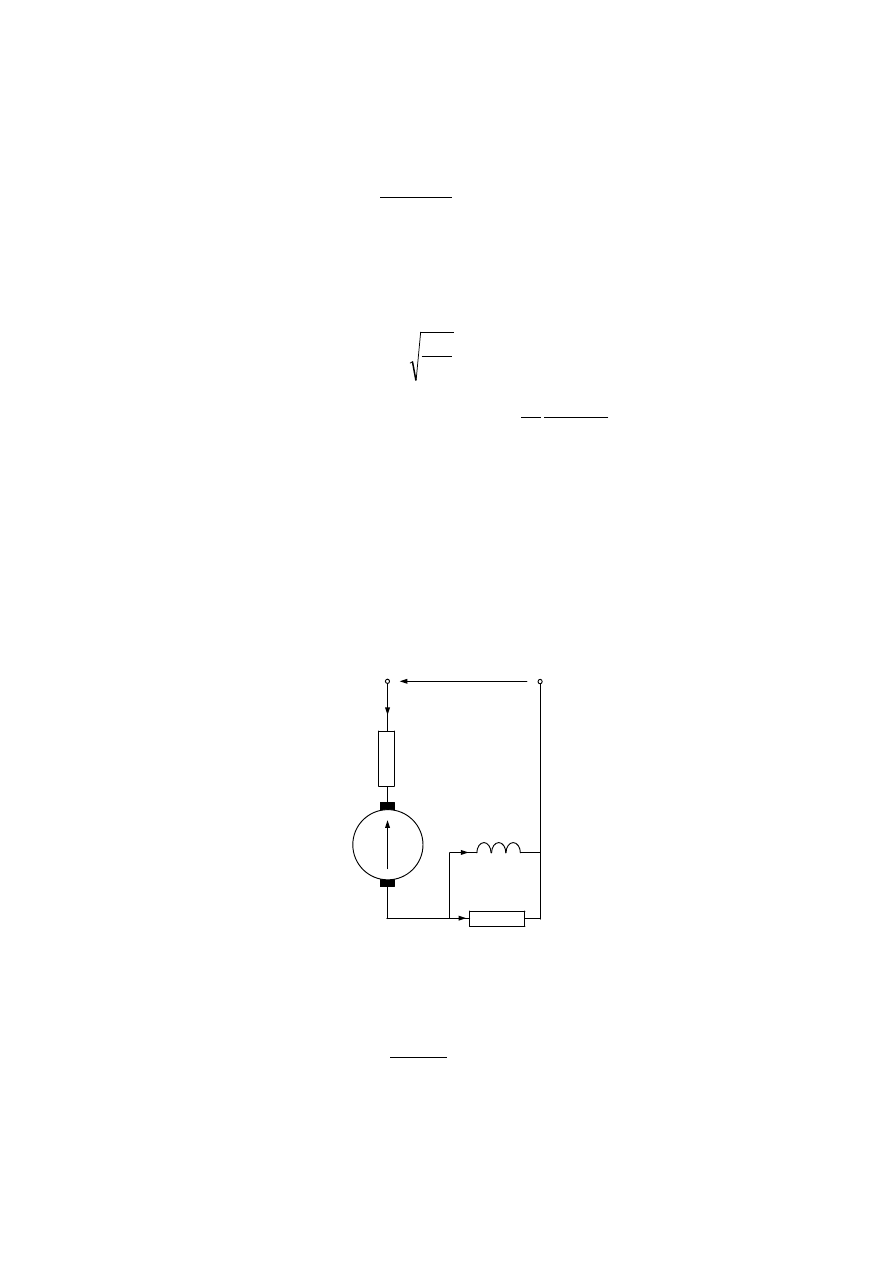
43

Drugi sposób wyznaczenia nowych obrotów:

Na podstawie równania napięć można teraz wyznaczyć współczynnik

f

a

M :

047

,

0

≅

Ω

−

=

N

N

N

N

f

a

I

RI

U

M

H/rad.

Znamionowy moment elektromagnetyczny ma wartość:

27

2

≅

=

N

f

a

eN

I

M

T

Nm.

Moment obciążenia wynosi:

94

,

18

7

,

0

=

=

N

x

T

T

Nm, zatem prąd silnika w nowych warunkach

pracy jest równy:

1

,

20

≅

=

f

a

x

x

M

T

I

A.

Prędkość obrotowa w nowych warunkach wyniesie:

1151

30

≅

−

=

x

f

a

x

x

x

I

M

RI

U

n

π

/min.

Odpowiedź: Prędkość obrotowa silnika w nowych warunkach pracy wyniesie 1151/min,
a pobierany prąd z sieci będzie równy 20,1A.

6.7.

295

=

n

/min.

6.8.

9

,

22

=

x

I

A,

5

,

460

=

x

U

V.

6.9. Schemat silnika szeregowego można przedstawić jak na rysunku poniżej:

d

R

a

R

A1

A2

I

b

R

f

R

f

I

b

I

U

E

D1

D2

W stanie znamionowym silnik wytwarza moment elektromagnetyczny równy:

2

N

f

a

N

I

M

T

=

.

W nowym stanie pracy zmienia się relacja pomiędzy prądem wzbudzenia i prądem twornika.
Zgodnie z dzielnikiem prądów zachodzi:

b

f

b

x

fx

R

R

R

I

I

+

=

, tu

x

fx

I

I

5

,

0

=

.

Formuła na moment elektromagnetyczny wyraża się wtedy zależnością:

x

fx

f

a

x

I

I

M

T

=

, tu

2

5

,

0

x

f

a

x

I

M

T

=

.

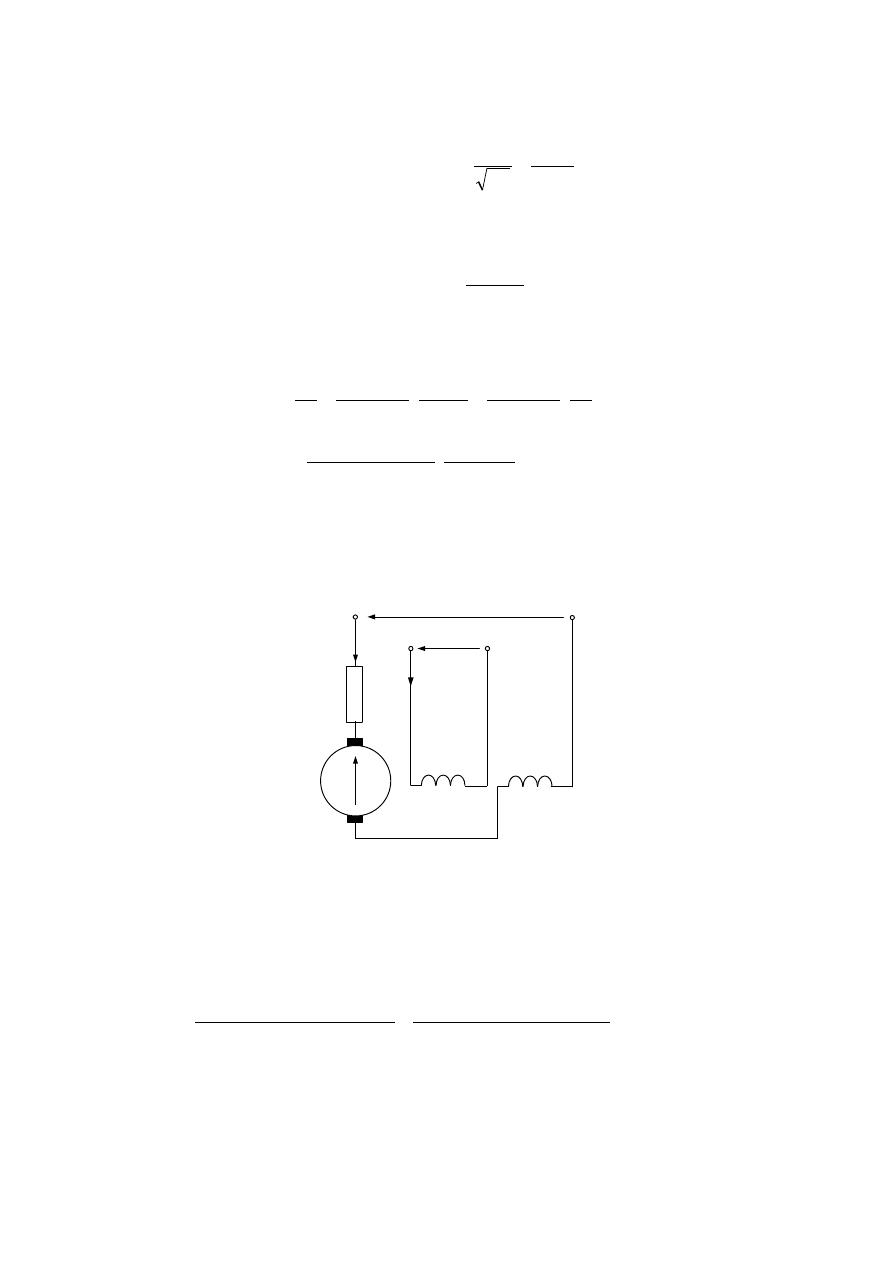
44

Ponieważ nowy moment równy jest znamionowemu -

N

x

T

T

=

, otrzymujemy:

2

2

5

,

0

N

f

a

x

f

a

I

M

I

M

=

, stąd

5

,

148

707

,

0

105

5

,

0

=

=

=

N

x

I

I

A.

Rezystancja wypadkowa silnika w stanie znamionowym wynosi:

15

,

0

=

+

=

f

a

R

R

R

Ω

.

Rezystancja wypadkowa silnika w nowym stanie pracy jest równa:

825

,

0

=

+

⋅

+

+

=

b

f

b

f

a

d

w

R

R

R

R

R

R

R

Ω.

Z porównania równania napięć w nowym i poprzednim stanie pracy silnika otrzymujemy
związek pomiędzy prędkościami obrotowymi silnika:

fx

N

N

N

x

w

x

fx

f

a

N

f

a

N

N

x

w

x

N

x

I

I

RI

U

I

R

U

I

M

I

M

RI

U

I

R

U

n

n

⋅

−

−

=

⋅

−

−

=

,

stąd:

537

5

,

148

5

,

0

105

105

15

,

0

220

5

,

148

825

,

0

176

1450

≅

⋅

⋅

⋅

−

⋅

−

⋅

=

x

n

/min.

Odpowiedź:

537

=

x

n

/min.

6.10. Schemat silnika obcowzbudnego z dozwojeniem szeregowym można przedstawić jak
na rysunku poniżej:

d

R

f

R

a

R

a

I

A1

A2

f

I

s

R

F1

F2

f

U

a

U

D1

D2

E

Równanie napięć tego silnika ma postać:

a

s

a

a

s

a

a

I

R

R

I

M

U

)

(

)

(

0

+

+

+

Ψ

Ω

=

,

gdzie:

s

R - rezystancja dozwojenia szeregowego,

s

a

M - indukcyjność rotacji związana z do-

zwojeniem szeregowym.

Stąd w stanie znamionowym (w warunkach zadania wartość

N

Ψ

=

Ψ

0

nie zmienia się):

4

-

10

1,63

312

50

50

5

,

2

312

126

,

0

440

)

(

⋅

=

⋅

⋅

−

⋅

−

=

Ω

Ω

Ψ

−

+

−

=

π

π

aN

N

N

N

aN

s

a

aN

s

a

I

I

R

R

U

M

H/rad.

Wyrażenie na moment elektromagnetyczny silnika z dozwojeniem szeregowym zgodnym
można zapisać jako:

2

0

a

s

a

a

e

I

M

I

T

+

Ψ

=

,

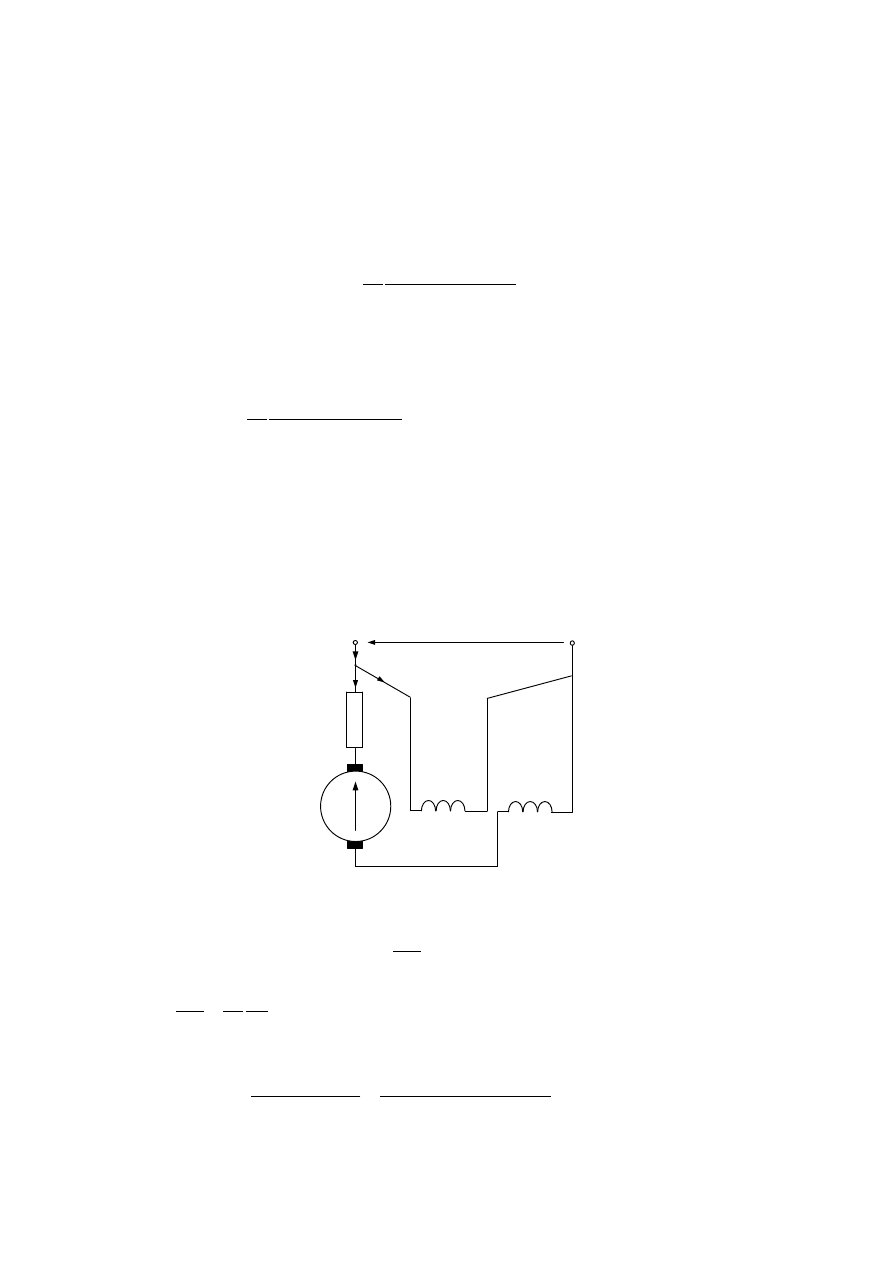
45

stąd możemy wyznaczyć wartość prądu twornika, przy obciążeniu momentem

500

=

T

Nm,

z poniższego równania kwadratowego:

0

500

5

,

2

000163

,

0

1

2

1

=

−

+

a

a

I

I

Wynosi ona:

≅

1

a

I

197,5A.

Dla takiego przypadku prędkość obrotowa będzie wynosiła:

≅

+

Ψ

+

−

=

1

0

1

1

)

(

30

a

s

a

a

s

a

aN

I

M

I

R

R

U

n

π

1566/min.

W przypadku dozwojenia przeciwnego otrzymujemy odpowiednio:

2

0

a

s

a

a

e

I

M

I

T

−

Ψ

=

,

i dalej:

0

500

5

,

2

000163

,

0

2

2

2

=

+

−

a

a

I

I

, skąd:

≅

2

a

I

202,7A,

wobec czego:

≅

−

Ψ

+

−

=

2

0

2

2

)

(

30

a

s

a

a

s

a

aN

I

M

I

R

R

U

n

π

1606/min.

Przyrost obrotów wyniesie zatem:

40

1

2

=

−

=

∆

n

n

n

/min.

Odpowiedź: Prędkość obrotowa wzrośnie wskutek zmiany dozwojenia szeregowego ze
zgodnego na przeciwne z 1566/min do 1606/min. Prąd twornika w nowych warunkach będzie
miał wartość 202,7A.

6.11. Schemat silnika bocznikowego z dozwojeniem szeregowym zgodnym można przedsta-
wić jak na rysunku poniżej:

d

R

f

R

a

R

f

a

U

U

=

a

I

A1

A2

E1

E2

f

I

I

D1

D2

s

R

E

Przy pominięciu strat mechanicznych moment elektromagnetyczny równa się momentowi
obciążenia silnika. W stanie znamionowym pracy otrzymujemy:

2

aN

s

a

aN

fN

f

a

N

N

N

eN

I

M

I

I

M

P

T

T

+

=

Ω

=

=

,

tu:

62

,

267

30

=

=

Ω

=

N

N

N

N

N

n

P

P

T

π

Nm, stąd indukcyjność rotacji „dozwojenie szeregowe - twor-

nik” wynosi:

001146

,

0

119

119

5

,

2

845

,

0

62

,

267

2

2

=

⋅

⋅

−

=

−

=

aN

aN

fN

f

a

N

s

a

I

I

I

M

T

M

H/rad.

46

Nieznaną wartość rezystancji dozwojenia szeregowego wyznaczamy dla stanu znamionowe-
go, przekształcając formułę:

aN

s

a

fN

f

a

aN

s

a

aN

N

I

M

I

M

I

R

R

U

n

+

+

−

=

)

(

30

π

do postaci:

(

)

a

aN

aN

s

a

fN

f

a

N

aN

s

R

I

I

M

I

M

n

U

R

−

+

−

=

30

π

.

Stąd:

007

,

0

=

s

R

Ω

.

Moment silnika w nowych warunkach pracy wynosi:

2

5

,

0

ax

s

a

ax

fx

f

a

N

x

I

M

I

I

M

T

T

+

=

=

,

gdzie nowy prąd wzbudzenia:

aN

ax

fN

f

ax

fx

U

U

I

R

U

I

=

=

, tu:

25

,

2

200

180

5

,

2

=

⋅

=

fx

I

A.

Po podstawieniu pozostałych danych otrzymujemy równanie kwadratowe:

0

81

,

133

9

,

1

001146

,

0

2

=

−

+

ax

ax

I

I

Wyznaczona stąd wartość prądu twornika (drugie rozwiązanie ma wartość ujemną) wynosi:

66

,

67

=

ax

I

A.

Szukane obroty wirnika obliczamy z zależności:

ax

s

a

fx

f

a

ax

s

a

ax

x

I

M

I

M

I

R

R

U

n

+

+

−

=

)

(

30

π

tu:

7

,

827

66

,

67

001146

,

0

25

,

2

845

,

0

66

,

67

127

,

0

180

30

=

⋅

+

⋅

⋅

−

=

π

x

n

/min.

Odpowiedź: W nowych warunkach pracy silnik osiągnie ustalone obroty równe 827,7/min.

6.12. Ad a) Przy zasilaniu napięciem stałym równania silnika uniwersalnego stają się równa-
niami silnika szeregowego ( patrz schemat silnika w zadaniu 6.6).

I

M

RI

U

f

a

−

=

Ω

1

oraz

2

I

M

T

f

a

=

,

zatem:

f

a

M

T

I

=

, stąd:

f

a

f

a

f

a

M

R

T

M

U

I

M

RI

U

−

=

−

=

Ω

1

.

Tu:

5

,

1263

15

,

0

1

2

,

0

15

,

0

220

1

=

−

⋅

=

Ω

rad/s,

czyli:

12066

30

1

=

Ω

=

N

n

π

/min.

47

Ad b) Pracę silnika uniwersalnego w ustalonym stanie pracy, przy zasilaniu napięciem sinuso-
idalnym, opisują formuły:

•

równanie napięć zapisane dla wartości skutecznych zespolonych prądu i napięcia:

I

M

I

L

j

I

R

U

f

a

Ω

+

+

=

0

ω

czyli:

I

L

j

I

M

R

U

f

a

0

)

(

ω

+

Ω

+

=

•

wartość średnia momentu elektromagnetycznego:

2

I

M

T

f

a

ś

r

=

gdzie:

f

a

R

R

R

+

=

,

f

a

L

L

L

+

=

,

f

π

ω

2

0

=

.

Moduły wartości skutecznych prądu i napięcia wiąże zależność:

I

L

M

R

U

f

a

⋅

+

Ω

+

=

2

0

2

)

(

)

(

ω

,

stąd wyznaczamy wartość prędkości kątowej wirnika:

f

a

M

R

L

I

U

−

−













=

Ω

2

0

2

2

)

(

ω

.

Ponieważ skuteczna wartość prądu twornika wynosi:

155

,

1

=

=

=

f

a

f

a

ś

r

M

T

M

T

I

A,

szukana wartość prędkości jest równa:

1192

15

,

0

1

)

2

,

0

100

(

155

,

1

220

2

2

2

=

−

⋅

−













=

Ω

π

rad/s.

czyli:

11384

2

=

n

/min.

Odpowiedź: Ad a) Przy zasilaniu napięciem stałym obroty silnika wyniosą

12066

1

=

n

/min.

Ad b) Przy zasilaniu napięciem przemiennym obroty silnika wyniosą

11384

2

=

n

/min.

6.13. Równanie prądnicy dla stanu ustalonego ma postać:

a

a

a

f

f

a

I

R

U

I

M

+

=

Ω

,

jednocześnie:

a

a

RI

U

=

,

zatem:

a

a

f

f

a

I

R

R

I

M

)

(

+

=

Ω

,

stąd:

22

,

6

=

a

I

A.

Moc oddawaną przez prądnicę można wyliczyć z zależności:

1547

2

≅

=

a

RI

P

W.

Napięcie na zaciskach prądnicy jest równe spadkowi napięcia na rezystancji obciążenia i wy-
nosi:

249

≅

=

a

a

RI

U

V.

Odpowiedź: Moc oddawana przez prądnicę wynosi 1547W, prąd twornika 6,2A, natomiast
napięcie na zaciskach prądnicy jest równe 249V.