WYKŁAD 6
2. ELEMENTY GEOMETRII ANALITYCZNEJ I
WEKTOROWEJ
2.1. Wstęp: metoda współrzędnych
W geometrii analitycznej badamy obiekty geometryczne metodą
analityczną. Najbardziej znaną metodą tego typu jest metoda współrzędnych
oparta na układzie współrzędnych.
2A1
(
Definicja: układ współrzędnych). Układ Oxyz współrzędnych w
przestrzeni składa się z trzech (zwykle wzajemnie prostopadłych) prostych Ox,
Oy, Oz
z jednostkami mierzenia i ustalonymi kierunkami, przecinających się w
jednym punkcie O. Proste Ox, Oy, Oz nazywamy osiami
, płaszczyzny xOy, xOz,
yOz
płaszczyznami, punkt O początkiem układu współrzędnych. Zwykle
korzysta się z orientacji układu prawoskrętnego, tzn. jeżeli prawą rękę
umieścimy tak, aby kciuk wskazywał dodatnią część osi Oz, to zgięte palce
wskażą kierunek obrotu od osi Ox do osi Oy.
W metodzie współrzędnych każdemu punktowi M przestrzeni odpowiada
uporządkowana trójka (
,
,
M
M
M
x
y
z
) liczb rzeczywistych (współrzędnych tego
punktu) i na odwrót. Wtedy geometryczne obiekty opisujemy przez warunki
(równania, nierówności lub ich układy), które spełniają współrzędne punktów
zawartych w geometrycznych obiektach. Odpowiednie równania nazywamy
równaniami tych obiektów.
Podobnie definiujemy układ współrzędnych na płaszczyźnie.
2A2
2.1. Równanie
(
Przykłady).
2
2
2
(
)
(
)
(
)
0
M
M
M
x
x
y
y
z
z
−
+
−
+ −
=
opisuje punkt
(
,
,
)
M
M
M
M x
y
z
o współrzędnych
,
,
M
M
M
x
y
z
w przestrzeni;
2.2.
Układ nierówności
1,
0,
0
x
y
x
y
+ ≤
≥
≥
opisuje trójkąt OAB o wierzchołkach O(0,0), A(1,0), B(0,1) na płaszczyźnie.
W geometrii analitycznej rozpatrujemy dwa podstawowych problemy: opisanie
obiektów równaniami otrzymanymi z własności tych obiektów i na odwrót,
badanie własności geometrycznych obiektów przez ich równania.
2.2. Wektory
Pod pojęciem wektora (odcinka skierowanego) a
w przestrzeni (lub na
płaszczyźnie) rozumiemy wyłącznie wektor swobodny, tzn. zbiór wszystkich
wektorów zaczepionych w różnych punktach, które mają ten sam kierunek,
zwrot oraz długość. Wektor tego zbioru o początku w punkcie O będziemy
nazywali reprezentantem wektora
a
. Jeżeli A jest końcem tego reprezentanta, to
wektor
a
można utożsamiać z wektorem OA
wodzącym punktu A i z jego
współrzędnymi. Mamy zatem
a
=
OA
=
(
,
,
)
A
A
A
x
y z
=
(
,
,
)
a
a
a
x y z
,
gdzie liczby rzeczywiste
,
,
a
a
a
x y z
są współrzędnymi wektora a
.
Wektor
0
(0,0,0)
=
nazywamy wektorem zerowym, wektor
(
,
,
)
a
a
a
a
x
y
z
− = −
−
−
wektorem przeciwnym do wektora
a
.
Podobnie definiujemy wektory na płaszczyźnie.
2A+B3
,
a b
(W
ektory współliniowe). Wektory
są współliniowe (równoległe), co
oznaczamy
||
a b
, gdy istnieje jedna lub dwie równoległe proste, w których
zawarte są te wektory. Stąd mamy warunek współliniowości:
||
lub
a
a
a
b
b
b
x
y
z
a b
a
b
b
a
x
y
z
⇔
=
=
⇔ = λ
= λ
, gdzie
λ
jest liczbą .
2A+B4
, ,
a b c
(
Wektory współpłaszczyznowe). Wektory
są współpłaszczyznowe,
gdy są zawarte w jednej lub równoległych płaszczyznach. Warunek
0
a
a
a
b
b
b
c
c
c
x
y
z
x
y
z
x
y
z
=
jest warunkiem współpłaszczyznowości wektorów , ,
a b c
.
2A5
a
(Definicja:
długość wektora). Długość wektora a
jest określona
wzorem
2
2
2
.
a
a
a
a
x
y
z
=
+
+
2A+B6
b
P a
(Definicja: rzut wektora). Rzut
wektora
a
na wektor
b
określamy
wzorem
cos (
)
b
P a
a
a b
=
, gdzie
(
)
a b
oznacza kąt między wektorami a
i
b
.
Uwaga
. Współrzędne wektora są jego rzutami na osie układu współrzędnych.
2B7 (
Ćwiczenie). Podać własności długości oraz rzutów wektorów.
2A8
(1,0,0)
i
=
(Definicja: wersory
). Każdy wektor o długości 1 nazywamy wersorem.
Najbardziej znany są wersory
,
(0,1,0)
j
=
,
(0,0,1)
k
=
położone
odpowiednio na osiach Ox, Oy, Oz
układu współrzędnych.
2A+B9
1:
λ
(
Podział odcinka w podanym stosunku). Niech C będzie punktem
podziału odcinka AB w stosunku
, gdzie
0
λ
> , tzn. CB
AC
λ
=
. Wtedy
współrzędne tego punktu wyrażają się wzorami:
,
,
.
1
1
1
A
B
A
B
A
B
C
C
C
x
x
y
y
z
z
x
y
z
λ
λ
λ
λ
λ
λ
+
+
+
=
=
=
+
+
+
W postaci wektorowej mamy
1
(
)
OC
OA OB
λ
λ
=
+
. Punkt C
jest środkiem odcinka AB w szczególnym
przypadku gdy
1
λ
= .
Ćwiczenie (B+C). Określić podział odcinka w podanym stosunku dla λ∈ .
2A+B10
a b
(Iloczyn skalarny). Iloczyn skalarny
wektorów
( ,
,
)
a
a
a
a
x y z
=
i
( ,
,
)
b
b
b
b
x y z
=
określamy wzorem
cos (
)
a b
a b
a b
= ⋅ ⋅
.
Przykłady:
1,
0
i i
j
j
k k
i
j
j k
i k
=
=
=
=
=
=
(tu i dalej wektory
, ,
i j k
oznaczają wersory odpowiednio na osiach Ox, Oy, Oz. .
Własności iloczynu skalarnego:
1)
a b
b a
=
; 2)
(
)
(
)
(
)
a
b
a b
a
b
α
α
α
=
=
; 3)
2
a a
a
=
;
4)
(
)
a
b
c
a c
b c
+
=
+
; 5) a b
a b
≤ ⋅
;
6)
0
a b
=
⇔
wektory
i
a b
są prostopadłe (tu
, ,
a b c
są wektorami,
α
∈
).
Stąd mamy wzór do obliczania iloczynu skalarnego:
a
b
a
b
a
b
a b
x x
y y
z z
=
+
+
.
2A+B11
( ,
,
)
a
a
a
a
x y z
=
(Iloczyn wektorowy). Niech wektory
,
( ,
,
)
b
b
b
b
x y z
=
,
( ,
, )
c
c
c
c
x y z
=
tworzą układ o orientacji zgodnej z orientacją układu
współrzędnych tzn.
0
a
a
a
b
b
b
c
c
c
x
y
z
x
y
z
x
y
z
>
. Wtedy wektor
c
nazywamy iloczynem
wektorowym uporządkowanej pary wektorów
i
a b
, co oznaczamy
c
a b
= ×
,
jeżeli spełnione są warunki:
1) wektor
c
jest prostopadły do płaszczyzny rozpiętej na wektorach
i
a b
;

2) długość c
wektora
c
jest równa polu równoległoboku rozpiętego na
wektorach
i
a b
:
sin (
)
c
a b
a b
= ⋅ ⋅
;
3) orientacja wektorów
, ,
a b c
jest zgodna z orientacja układu współrzędnych
Oxyz.
Przykłady:
0,
,
,
i i
j
j
k
k
i
j
k
j i j k
i
k
j k i
j
i k
× = × = × =
× = = − ×
× = = − ×
× = = − ×
.
Własności iloczynu wektorowego:
1)
a b
b a
× = − ×
; 2)
(
)
(
)
(
)
a
b
a b
a
b
α
α
α
× =
× = ×
; 3)
0
a a
× =
;
4)
(
)
,
(
)
a
b
c
a c
b c
a
b
c
a b
a c
+ × = × + ×
× +
= × + ×
; 5) a b
a b
× ≤ ⋅
;
6)
0
a b
× =
⇔
wektory
||
a b
⇔
wektory
i
a b
s
ą równoległe (tu
, ,
a b c
są
wektorami,
α
∈).
Stąd mamy wzór do obliczania iloczynu wektorowego:
def
a
a
a
a
a
a
b
b
b
b
b
b
a
a
a
b
b
b
i
j
k
y
z
x
z
x
y
c
a b
i
j
k
y
z
x
z
x
y
x
y
z
x
y
z
= × =
⋅ −
⋅ +
⋅
=
,
gdzie pierwszy „wyznacznik” obliczamy przez rozwinięcie względem
pierwszego wiersza.
2A+B12
( , , ) lub
a b c
a b c
(Iloczyn mieszany). Iloczyn mieszany
wektorów
( ,
,
)
a
a
a
a
x y z
=
,
( ,
,
)
b
b
b
b
x y z
=
,
( ,
, )
c
c
c
c
x y z
=
określamy wzorem
def
( , , )
(
)
a b c
a b c
a b
c
=
×
=
.
Własności iloczynu mieszanego:
1)
a b c
b c a
c a b
b a c
c b a
a c b
=
=
= −
= −
= −
;
2) interpretacja geometryczna iloczynu mieszanego: iloczyn mieszany
a b c
wektorów
, ,
a b c
jest równy (z dokładnością do znaku) objętości
równoległościanu D rozpiętego na tych wektorach: D abc
=
;
3)
0
a b c
= ⇔
wektory
, ,
a b c
są współpłaszczyznowe;
4) wzór do obliczania iloczynu mieszanego:
a
a
a
b
b
b
c
c
c
a b c
x
y
z
x
y
z
x
y
z
=
, skąd można otrzymać inne własności iloczynu mieszanego.
2B+C13
(
Ćwiczenie: zastosowania rachunku wektorowego). Podać przykłady:
środek masy i momenty bezwładności układu punktów materialnych, moment
siły itd.
Podobnie rozpatrujemy rachunek wektorowy na płaszczyźnie.
Zbiór reprezentantów wszystkich wektorów przestrzeni przez współrzędne tych
reprezentantów można utożsamiać z
3
i ogólniej przestrzeń
n
utożsamiamy
z przestrzenią wektorową n-wymiarową, której elementy będziemy nazywali
wektorami (n-wektorami kolumnowymi). Przy oznaczaniu tych wektorów
strzałki będziemy opuszczali.
2A+B14
n
(
Współrzędne wektora w bazie). Bazą przestrzeni
nazywamy zbiór
n
liniowo niezależnych wektorów tej przestrzeni. Wtedy każdy wektor
przestrzeni można zapisać jako kombinację liniową wektorów bazy.
Współczynniki tej kombinacji (to jest rozwinięcia wektora w bazie) dla danego
wektora są wyznaczone jednoznacznie i nazywa się współrzędnymi wektora w
tej bazie. Wektory tworzą bazę standardową (kanoniczną) jeżeli macierz o
kolumnach, kt
órych elementy są odpowiednio współrzędnymi tych wektorów
jest jednostkowa. Współrzędne wektora w podanej bazie obliczamy jako
współczynniki odpowiedniej kombinacji liniowej w rozwinięciu wektora w tej
bazie, co sprowadza się do rozwiązywania pewnego układa Cramera.
2.3. Płaszczyzna w przestrzeni
Niech w przestrzeni
3
będzie ustalony układ współrzędnych Oxyz. Wtedy
równanie (przy dodatkowych założeniach)
(
)
0
,
,
=
z
y
x
F
jest równaniem powierzchni w tej przestrzeni. Powie
rzchnię tę określamy jako
zbiór punktów
( , , )
M x y z w
3
, których współrzędne
, ,
x y z
spełniają to
równanie. Najprostszą powierzchnią jest płaszczyzna, którą można określić
różnymi sposobami. W zależności od sposobów rozpatrujemy różne równania
płaszczyzny.
2A+B15
15.1. Równanie normalne p
łaszczyzny
(
Równania płaszczyzny).
π
przechodzącej przez punkt
(
)
0
0
0
0
,
,
z
y
x
M
i prostopadłej do wektora
(
)
, ,
0
n
A B C
=
≠
.
Wektor
(
)
, ,
0
n
A B C
=
≠
nazywamy wektorem normalnym
płaszczyzny
π
jeżeli
jest on prostopadły do tej płaszczyzny tzn. do dowolnego wektora zawartego w
tej płaszczyźnie. Jeżeli wektor
n
jest wektorem normalnym
π
to i wektor
(
)
C
B
A
n
⋅
⋅
⋅
=
⋅
λ
λ
λ
λ
,
,
będzie normalnym wektorem płaszczyzny
π
. Niech
(
)
z
y
x
M
,
,
będzie dowolnym punktem płaszczyzny
π
. Wtedy wektor
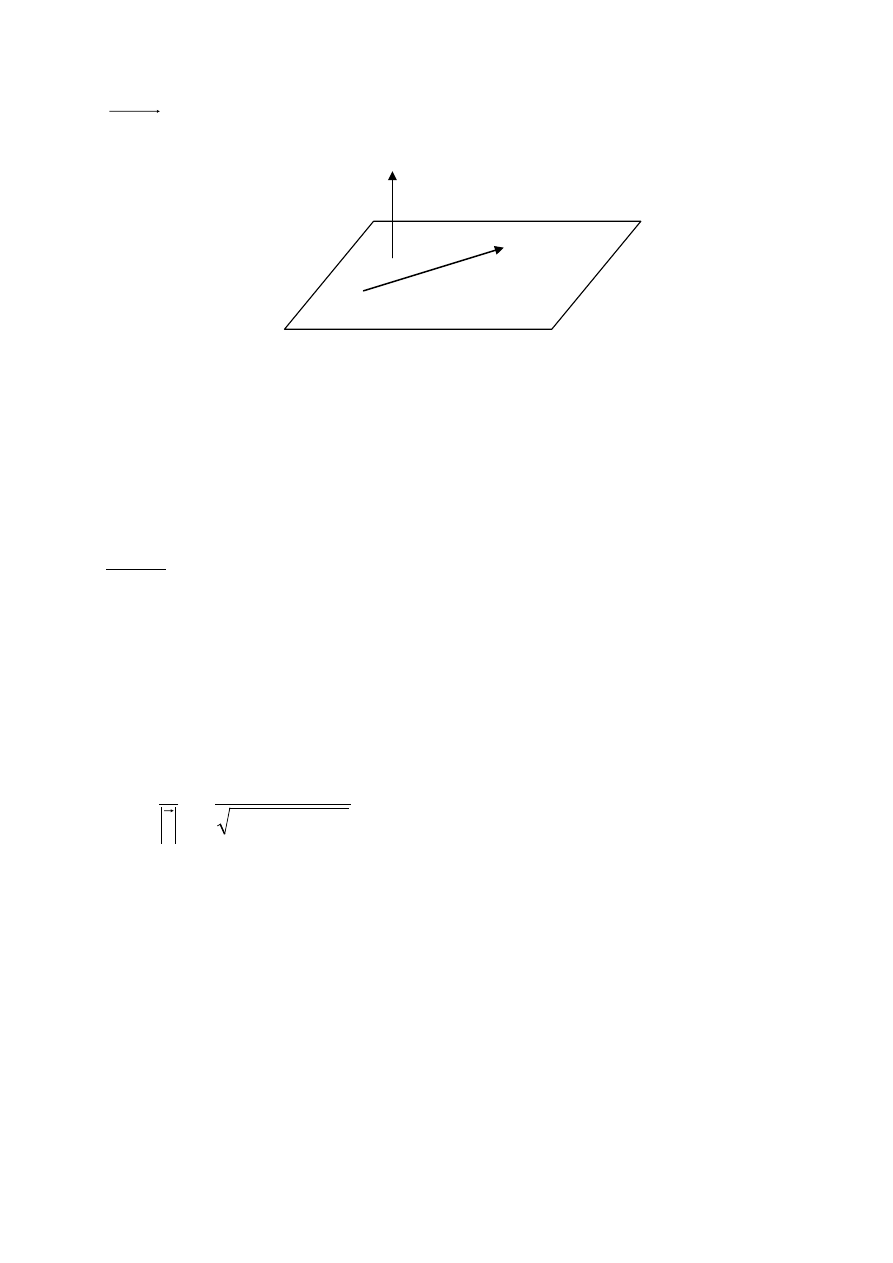
(
)
0
0
0
0
,
,
z
z
y
y
x
x
M
M
−
−
−
=
jest
prostopadły do wektora
(
)
C
B
A
n
,
,
=
skąd
biorąc pod uwagę 2A+B10 otrzymamy równanie płaszczyzny
π
(rys. 1)
(
)
C
B
A
n
,
,
=
π
(
)
z
y
x
M
,
,
(
)
0
0
0
0
,
,
z
y
x
M
Rys. 1.
Płaszczyzna o równaniu
(
) (
) (
)
0
0
0
0
=
−
+
−
+
−
z
z
C
y
y
B
x
x
A
.
przechodzącej przez punkt
(
)
0
0
0
0
,
,
z
y
x
M
i prostopadłej do wektora n :
π
:
(
) (
) (
)
0
0
0
0
=
−
+
−
+
−
z
z
C
y
y
B
x
x
A
, (1)
gdzie
2
2
2
0
A
B
C
+
+
≠ .
Uwaga
, ,
A B C
. Przy dowolnych
, gdzie
2
2
2
0
A
B
C
+
+
≠
, równanie (1) określa
pęk płaszczyzn przechodzących przez punkt
(
)
0
0
0
0
,
,
z
y
x
M
.
Następnie niech
0
,
r r
będą wektorami wodzącymi punktów odpowiednio
(
)
0
0
0
0
,
,
z
y
x
M
,
(
)
z
y
x
M
,
,
. Wtedy mamy równanie normalne p
łaszczyzny
π
w
postaci wektorowej:
π
: n
(
)
0
o
r
r
−
=
. (2)
W równaniu (2) wektor normalny
(
)
, ,
n
A B C
=
zastąpimy wersorem n
µ
gdzie
2
2
2
1
1
C
B
A
n
+
+
±
=
±
=
µ
i znak wybieramy przeciwny do wyrazu wolnego
D. Wtedy otrzymamy
równanie normalne płaszczyzny
π
:
0
cos
cos
cos
=
−
+
+
p
z
y
x
γ
β
α
, (3)
gdzie
γ
β
α
,
,
są kątami między normalnym wektorem i wersorami odpowiednio
na osiach Ox, Oy, Oz oraz p
jest odległością początku układu współrzędnych od
polszczyzny.
15.2. Równanie ogólne p
łaszczyzny
π
.
Oznaczamy
(
)
0
0
0
Cz
By
Ax
D
+
+
−
=
. Wtedy równanie (1) p
łaszczyzny
π
przyjmuje postać
π
:
0
=
+
+
+
D
Cz
By
Ax
, (4)

która jest prostopadła do wektora
(
)
, ,
0
n
A B C
=
≠
(normalnego wektora
p
łaszczyzny).
Twierdzenie. Przy
ustalonym układzie współrzędnych Oxyz w przestrzeni
3
liniowe równanie (4) przedstawia płaszczyznę i na odwrót każdą
płaszczyznę w tej przestrzeni można opisać przez równanie (4).
Przykłady:
1)
0
A
= czyli
0
=
+
+
D
Cz
By
−
równanie płaszczyzny równoległej do osi Ox
(wektor normalny
(
)
0, ,
0
n
B C
=
≠
jest prostopadły do osi Ox: n Ox
⊥
);
2)
0
=
B
czyli
0
Ax
Cz
D
+
+ =
−
równanie płaszczyzny równoległej do osi Oy
(
(
)
,0,
n
A
C
=
Oy
⊥
);
3)
0
=
C
czyli
0
=
+
+
D
By
Ax
−
równanie płaszczyzny równoległej do osi Oz
(
(
)
, ,0
n
A B
=
⊥ Oz);
4)
0
=
D
czyli
0
=
+
+
Cz
By
Ax
−
równanie płaszczyzny przechodzących przez
początek układu współrzędnych;
5)
0
=
= B
A
czyli
0
=
+ D
Cz
−
równanie płaszczyzny prostopadłej do osi Oz
(równoległej do płaszczyzny Oxy :
(
)
C
n
,
0
,
0
=
||
Oz
);
6)
0
=
= C
A
czyli
0
=
+ D
By
−
równanie płaszczyzny prostopadłej do osi Oy
(
równoległej do płaszczyzny Oxz);
7)
0
=
= C
B
czyli
0
=
+ D
Ax
−
równanie płaszczyzny prostopadłej do osi Ox
(
równoległej do płaszczyzny Oyz);
8)
0
=
= D
A
czyli
0
=
+ Cz
By
−
równanie płaszczyzny przechodzącej przez oś
Ox ;
9)
0
=
= D
B
czyli
0
=
+ Cz
Ax
−
równanie płaszczyzny przechodzącej przez oś
Oy ;
10)
0
=
C
czyli
0
=
+ By
Ax
−
równanie płaszczyzny przechodzącej przez oś
Oz
;
11)
0
=
=
=
D
B
A
czyli
0
=
Cz
(
)
0
=
z
−
równanie płaszczyzny pokrywającej
się z płaszczyzną Oxy ;
12)
0
=
=
=
D
C
A
czyli
0
=
+ D
By
(
)
0
=
y
−
równa
nie płaszczyzny
pokrywającej się z płaszczyzną
Oxz
;
13)
0
=
=
=
D
C
B
czyli
0
=
+ D
Ax
(
)
0
=
x
−
równanie płaszczyzny
pokrywającej się z płaszczyzną Oyz.
15.3.
Równanie odcinkowe płaszczyzny
π
.
Jeżeli
0,
0,
0 oraz D
0
A
B
C
≠
≠
≠
≠
, równanie (4) można sprowadzić do
postaci
π
:
1
=
+
+
c
z
b
y
a
x
, (5)
gdzie
A
D
a
−
=
,
B
D
b
−
=
,
C
D
c
−
=
. (5) jest wtedy równaniem płaszczyzny
odcinającej na osiach układu współrzędnych odcinki (zorientowane) o
długościach odpowiednio , , ,
a b c .
15.4.
Równanie płaszczyzny
π
przechodzącej przez trzy niewspółliniowe punkty
(
)
1
1
1
1
,
,
z
y
x
M
,
(
)
2
2
2
2
,
,
z
y
x
M
,
(
)
3
3
3
3
,
,
z
y
x
M
.
Nich
(
)
z
y
x
M
,
,
będzie dowolnym punktem płaszczyzny
π
. Wtedy wektory
(
)
1
1
1
1
,
,
z
z
y
y
x
x
M
M
−
−
−
=
,
(
)
1
2
1
2
1
2
2
1
,
,
z
z
y
y
x
x
M
M
−
−
−
=
,
(
)
1
3
1
3
1
3
3
1
,
,
z
z
y
y
x
x
M
M
−
−
−
=
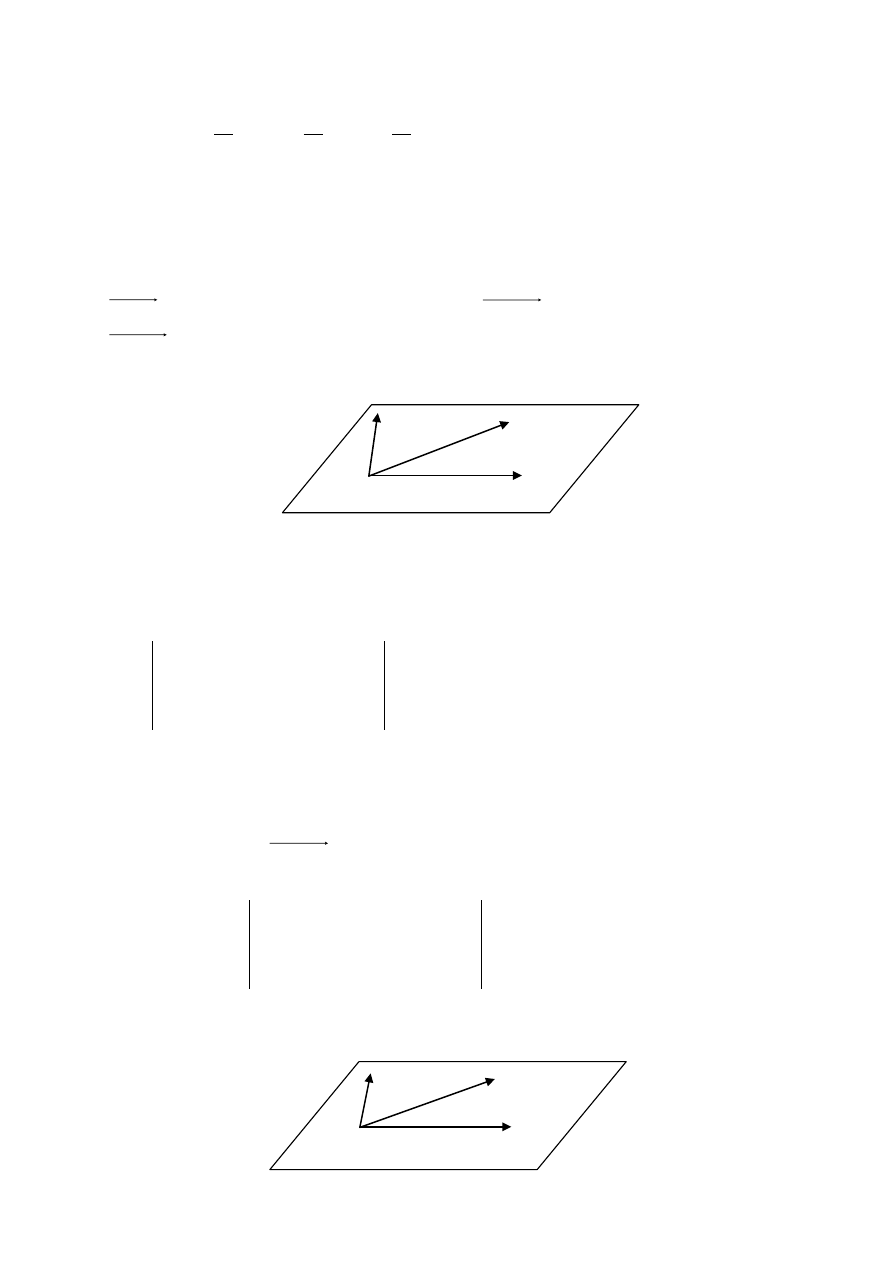
są współpłaszczyznowe (rys. 2)..
2
M
M
π
1
M
3
M
Rys. 2. Płaszczyzna przechodząca przez trzy niewspółliniowe punkty.
Korzystając z warunku współpłaszczyznowości wektorów otrzymamy
równanie tej płaszczyzny
0
1
3
1
3
1
3
1
2
1
2
1
2
1
1
1
=
−
−
−
−
−
−
−
−
−
z
z
y
y
x
x
z
z
y
y
x
x
z
z
y
y
x
x
.
(6)
15.5.
Równanie płaszczyzny
π
przechodzącej przez dwa punkty
(
)
1
1
1
1
,
,
z
y
x
M
,
(
)
2
2
2
2
,
,
z
y
x
M
i równoległej do wektora
(
)
3
2
1
,
,
a
a
a
a
=
.
Jeżeli wektory
a
i
(
)
1
2
1
2
1
2
2
1
,
,
z
z
y
y
x
x
M
M
−
−
−
=
nie są współliniowe (rys.
3) to otrzymujemy równanie tej płaszczyzny:
π
:
0
3
2
1
1
2
1
2
1
2
1
1
1
=
−
−
−
−
−
−
a
a
a
z
z
y
y
x
x
z
z
y
y
x
x
(7)
2
M
M
π
1
M
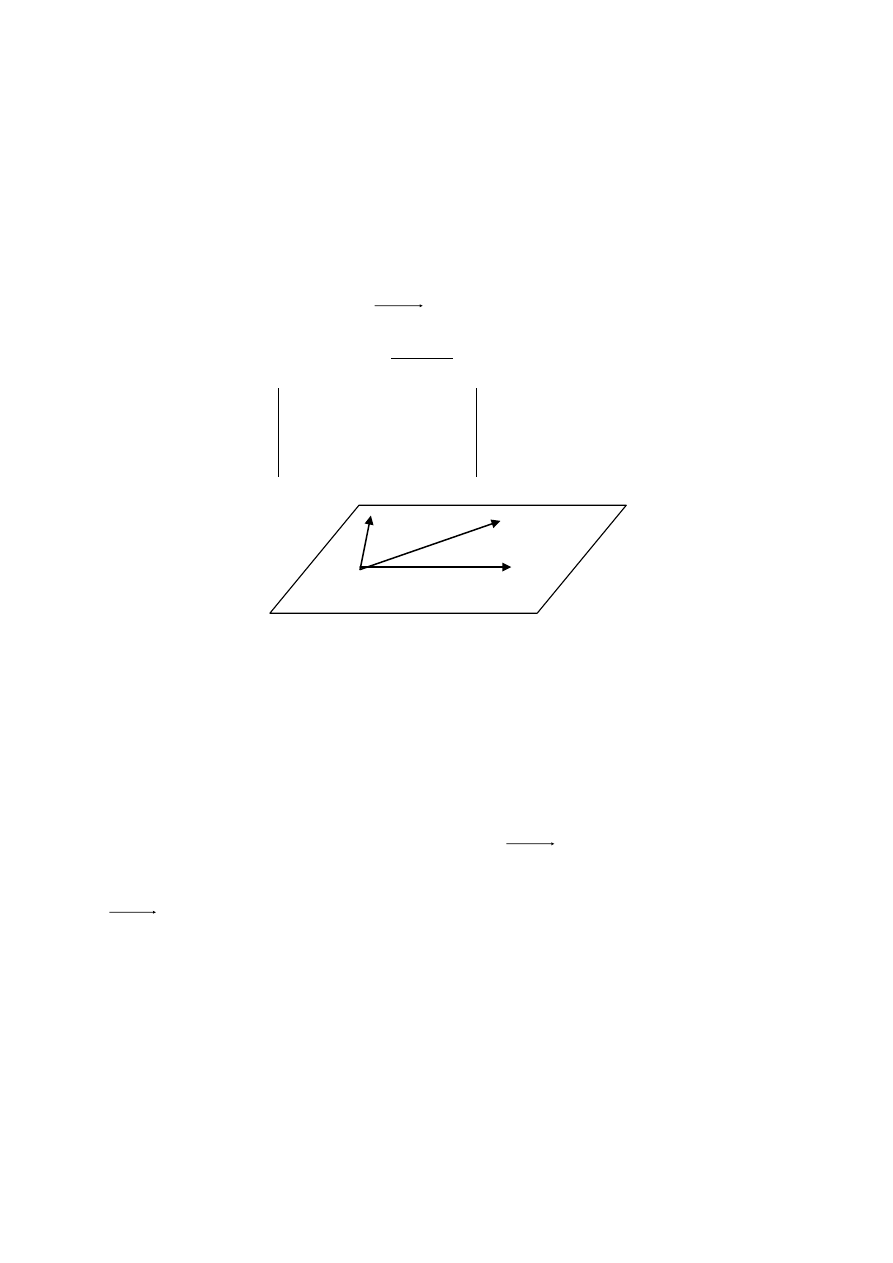
a
Rys.3. Płaszczyzna równoległa do wektora
a
i przechodzą przez
punkty
1
M
,
2
M
.
15.6.
Równanie płaszczyzny
π
przechodzącej przez punkt
(
)
1
1
1
1
,
,
z
y
x
M
i
równoległej do dwu niewspółliniowych wektorów
(
)
1
2
3
,
,
a
a a a
=
,
(
)
1
2
3
,
,
b
b y z
=
.
Niech punkt
(
)
z
y
x
M
,
,
należy do płaszczyzny
π
. Wtedy wektory (rys. 4)
(
)
3
2
1
,
,
a
a
a
a
=
,
(
)
1
2
3
,
,
b
b y z
=
,
(
)
1
1
1
1
,
,
z
z
y
y
x
x
M
M
−
−
−
=
są
współpłaszczyznowe. Z warunku 2A+B4
współpłaszczyznowości otrzymamy
π
:
0
3
2
1
3
2
1
1
1
1
=
−
−
−
b
b
b
a
a
a
z
z
y
y
x
x
(8)
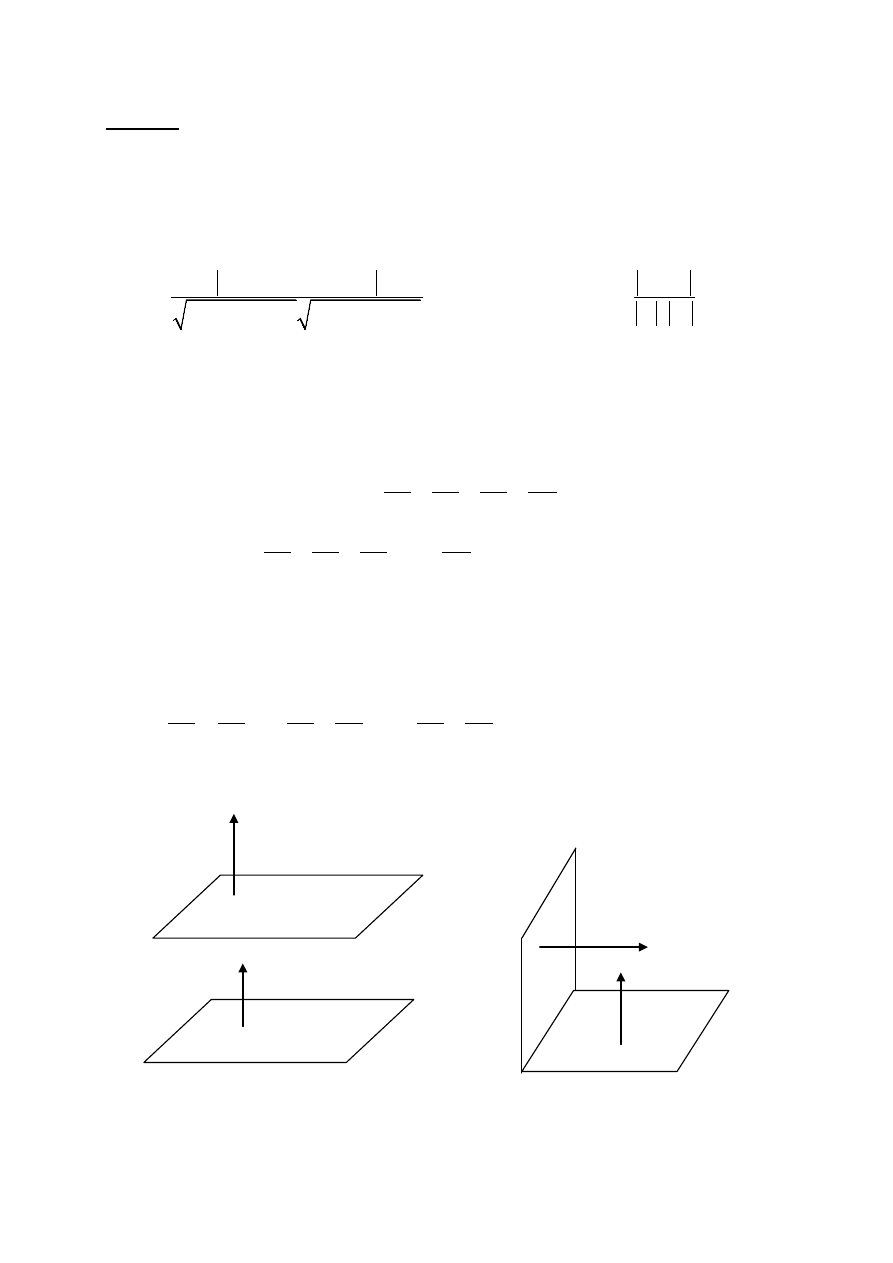
A M
π
a
1
M
B
b
Rys.4.
Płaszczyzna przechodzą przez punkt
1
M
i r
ównoległa do dwu
niewspółliniowych wektorów
a
i
b
.
15.7.
Równanie parametryczne płaszczyzny
π
.
Niech dowolny punkt
(
)
z
y
x
M
,
,
o wektorze wodzącym
r
należy do
płaszczyzny
π
przechodzącej przez punkt
(
)
1
1
1
1
,
,
z
y
x
M
i rozpiętej na
niewspółliniowych wektorach
(
)
3
2
1
,
,
a
a
a
a
=
,
(
)
1
2
3
,
,
b
b y z
=
. Wtedy wektory
a
i
b
tworzą bazę w
π
wektor
0
r
r
−
(
)
1
1
1
1
,
,
z
z
y
y
x
x
M
M
−
−
−
=
o
wektorze wodzącym
0
r
możemy przedstawić jako kombinację liniową
b
v
a
u
M
M
+
=
1
tych wektorów (równanie wektorowe)
π
:
0
r
r
ua
vb
=
+
+
czyli w rozwiniętej formie (równanie parametryczne
)
π
:
1
1
1
1
2
2
1
3
3
,
,
,
x
x
ua
vb
y
y
ua
vb
z
z
ua
vb
= +
+
= + +
= +
+
(9)
gdzie u i v
są parametrami.
2A+B16
Kąt między płaszczyznami nazywamy kąt ostry między wektorami normalnymi
tych płaszczyzn. Przyjmujemy, że kąt między płaszczyznami równoległymi jest
równy
(W
zajemnie położenie dwu płaszczyzn).
0.
Kąt między płaszczyznami
1
2
, i
π
π o wektorach normalnych odpowiednio
1
1
1
1
( ,
,
)
n
A B C
=
i
2
2
2
2
(
,
,
)
n
A B C
=
wyraża się wzorem
1
2
1
2
1
2
2
2
2
2
2
2
1
1
1
2
2
2
cos
A A
B B
C C
A
B
C
A
B
C
+
+
ϕ =
+
+
+
+
lub
1
2
1
2
1
2
( ,
)
arccos
.
n
n
n
n
π π
=
⋅
(10)
Stąd mamy
Twierdzenie. Nich
1
π :
0
1
1
1
1
=
+
+
+
D
z
C
y
B
x
A
,
2
π :
0
2
2
2
2
=
+
+
+
D
z
C
y
B
x
A
.
Wtedy
1.
1
π pokrywa się z
2
π
⇔
λ
=
=
=
=
1
2
1
2
1
2
1
2
D
D
C
C
B
B
A
A
.
2.
1
π
2
π
⇔
1
2
1
2
1
2
1
2
D
D
C
C
B
B
A
A
≠
=
=
=
λ
tzn.
1
2
n
n
(rys. 8).
3.
Płaszczyzny
1
π i
2
π są nierównolegle
⇔
4.
1
2
1
2
B
B
A
A ≠
lub
1
2
1
2
C
C
B
B ≠
, lub
1
2
1
2
C
C
A
A ≠
.
5.
1
π ⊥
2
π (rys. 9)
⇔
1
n
⊥
2
n
⇔
0
2
1
2
1
2
1
=
+
+
C
C
B
B
A
A
.
1
n
1
π
2
π
2
n
2
n
2
π
1
π
1
n
Rys. 8.
1
π
2
π . Rys. 9.
1
π ⊥
2
π .
2A+B17
Odległość punktu
(O
dległość punktu od płaszczyzny).
0
0
0
0
( ,
,
)
M
x y z
=
od płaszczyzny :
0,
Ax
By
Cz
D
π
+
+
+ =
gdzie
2
2
2
0
A
B
C
+
+
≠ ,
wyraża się wzorem (A):
0
0
0
0
2
2
2
(
, )
.
Ax
By
Cz
D
d M
A
B
C
+
+
+
=
+
+
π
Odległość punktu M od płaszczyzny
π
jest równa długości odcinka
0
0
'
M M
,
gdzie
'
P
jest rzutem prostokątnym punktu M na płaszczyznę
π
.
Odległość między płaszczyznami równoległymi
1
π i
2
π o równaniach
1
1
2
2
:
0,
:
0
Ax
By
Cz
D
Ax
By
Cz
D
π
π
+
+
+
=
+
+
+
=
wyraża się wzorem (B):
1
2
1
2
2
2
2
( ,
)
.
D
D
d
A
B
C
π π
−
=
+
+
2A+B18
Rzutem prostokątnym punktu
(Definicja:
rzut punktu na płaszczyznę).
M
na płaszczyznę
π
nazywany punkt
'
M tej
płaszczyzny spełniający warunek:
'
.
MM
⊥
π
2.4. Prosta w przestrzeni
2A+B19
Równanie parametryczne prostej. Równanie prostej
(Równania prostej).
l
przechodzącej przez
punkt
0
0
0
0
( ,
,
)
P
x y z
=
o wektorze wodzącym
0
r
i wyznaczonej przez niezerowy
wektor kierunku
( , , )
v
a b c
=
ma postać:
0
:
, gdzie
l r
r
tv
t
= +
∈
lub po rozpisaniu na współrzędne:
0
0
0
: ( , , )
( ,
,
)
( , , ), gdzie
.
l
x y z
x y z
t a b c
t
=
+
∈
Powyższą zależność nazywany równaniem parametrycznym prostej w postaci
wektorowej. Inny zapis tego równania ma
postać
0
0
0
,
:
, gdzie .
,
x
x
at
l
y
y
bt
t
z
z
ct
=
+
= +
∈
= +
Uwaga.
t
Powyższe równania będą przedstawiały półproste lub odcinek, gdy
parametr
będzie
przebiegał
odpowiednio
przedziały
(
, ], [ , ) lub [ , ].
β
α
α β
−∞
∞
Równanie kierunkowe prostej. Równanie prostej
l
przechodzącej przez punkt
0
0
0
0
( ,
,
)
P
x y z
=
i wyznaczonej przez niezerowy wektor kierunku
( , , )
v
a b c
=
ma
postać

0
0
0
:
.
x
x
y
y
z
z
l
a
b
c
−
−
−
=
=
Ten sposób zapisu równania parametrycznego prostej nazywamy jej równaniem
kierunkowym.
Uwaga (B)
. Aby nie ograniczyć zakresu stosowania równania kierunkowego
prostej przyjmujemy, że w mianownikach powyższych ułamków mogą wystąpić
zera.
Równanie krawędziowe prostej. Prostą l , która jest częścią wspólną dwóch
nierównoległych płaszczyzn
1
1
1
1
1
:
0,
A x
B y
C z
D
π
+
+
+
=
2
2
2
2
2
:
0
A x
B y
C z
D
π
+
+
+
=
, będziemy zapisywać w postaci:
1
1
1
1
2
2
2
2
0,
:
0.
A x
B y
C z
D
l
A x
B y
C z
D
+
+
+
=
+
+
+
=
Ten sposób zapisu prostej nazywamy jej równaniem krawędziowym.
Uwaga.
1
1
1
1
2
2
2
2
0,
:
0.
A x
B y
C z
D
l
A x
B y
C z
D
+
+
+
=
+
+
+
=
Wektor kierunkowy prostej
ma postać
1
1
1
2
2
2
(
,
,
) (
,
,
).
v
A B C
A B C
=
×
2A+B20
Rzutem prostokątnym punktu
(
Rzut punktu na prostą).
P
na prostą l nazywamy punkt '
P tej prostej
spełniający warunek:
'
.
PP
l
⊥
Uwaga.
W podobny sposób definiuje się rzut ukośny punktu na płaszczyznę lub
na prostą w kierunku ustalonego wektora.
2A+B21
Kątem nachylenia prostej
(K
ąt nachylenia prostej do płaszczyzny).
l
do płaszczyzny
π
nazywamy kąt
,
2
π
ϕ
α
= − gdzie
α
jest kątem ostrym między wektorem normalnym
n
płaszczyzny
π
i
wektorem kierunkowym
v
prostej
l
. Jeżeli prosta jest równoległa do
płaszczyzny, to przyjmujemy, ze kąt jej nachylenia do tej płaszczyzny jest
równy
0.
Kąt nachylenia prostej
l
o wektorze kierunkowym
v
do płaszczyzny
π
o
wektorze normalnym
n
wyraża się wzorem:
( , )
arcsin
.
n v
l
n v
π
=
⋅
2A+B22 (K
ąt między prostymi).
Kątem między prostymi nazywamy kąt ostry utworzony przez wektory
kierunkowe tych prostych. Przyjmujemy, że kąt między prostymi równoległymi
jest równy 0 .
Kąt między prostymi
1
2
,
l l
o wektorach kierunkowych odpowiednio
1
2
i
v
v
wyraża się wzorem
1
2
( , )
arccos
.
n v
l l
n v
=
⋅
2A+B+C23
(
)
(
)
1
1
1
1
2
2
2
2
, ,
,
, ,
v
a b c
v
a b c
=
=
(W
zajemnie położenie dwu prostych). Niech
będą wektorami kierunkowymi prostych
1
l
i
2
l
przechodzących odpowiednio przez punkty
(
)
1
1
1
1
,
,
z
y
x
M
i
(
)
2
2
2
2
,
,
M
x y z
.
Wtedy
23.1(A).
1
2
l
l
⇔
1
2
v
v
1
1
1
2
2
2
a
b
c
a
b
c
⇔
=
=
.
23.2(A).
1
2
l
l
⊥ ⇔
1
2
v
v
⊥
1 2
1 2
1 2
0
a a
b b
c c
⇔
+
+
=
.
23.3(B).
1
l
i
2
l
są zawarte w jednej płaszczyźnie
π ⇔
2
1
2
1
2
1
1
1
1
2
2
2
0
x
x
y
y
z
z
a
b
c
a
b
c
−
−
−
= .
23.4(C).
1
l
i
2
l
są skośne
⇔
2
1
2
1
2
1
1
1
1
2
2
2
0
x
x
y
y
z
z
a
b
c
a
b
c
−
−
−
≠ .
2A+B24
(
)
0
0
0
0
,
,
z
y
x
M
(O
dległość punktu od prostej). Odległość punktu
od
prostej o równaniu
1
1
1
x
x
y
y
z
z
a
b
c
−
−
−
=
=
obliczamy ze wzoru
( )
1
0
r
r
v
d
v
−
×
=
,
gdzie
(
)
, ,
v
a b c
=
,
0
r
i
1
r
są wektorami wodzącymi odpowiednio punktów
(
)
0
0
0
0
,
,
z
y
x
M
,
(
)
1
1
1
1
,
,
M
x y z
(rys. 10).
Odległość d jest równa wysokości równoległoboku rozpiętego na wektorach
0
1
r
r
−
i
v
.

a
0
M
0
1
r
r
−
d
0
r
1
M
1
r
O
Rys. 10.
Odległość punktu od prostej.
2B+C25
25.1. Odległość między równoległymi prostymi
(O
dległość między prostymi).
1
l
:
1
1
1
1
1
1
x
x
y
y
z
z
a
b
c
−
−
−
=
=
i
2
l
:
2
2
2
2
2
2
x
x
y
y
z
z
a
b
c
−
−
−
=
=
wyraża się wzorem
( )
2
1
1
1
r
r
v
d
v
−
×
=
( )
2
1
2
2
r
r
v
v
−
×
=
.
25.2.
Odległość między prostymi skośnymi
1
l
i
2
l
wyraża się wzorem
( )
2
1
1
2
1
2
r
r v v
d
v
v
−
=
×
, gdzie
(
)
1
1
1
1
, ,
v
a b c
=
,
(
)
2
2
2
2
, ,
v
a b c
=
;
2
r
i
1
r
są wektorami
wodzącymi odpowiednio punktów
(
)
2
2
2
2
,
,
M
x y z
i
(
)
1
1
1
1
,
,
M
x y z .
Uwaga. Wiemy z 2A+B15
3
że równanie liniowe (4) w przestrzeni
określa
płaszczyznę. Analogiczne równanie liniowe
0
Ax
By
C
+
+ = , gdzie
2
2
0
A
B
+
≠ ,
określa prostą na płaszczyźnie. Więcej informacji o geometrii
an
alitycznej w płaszczyźnie
2
można przeczytać w skrypcie
Tereza Jurlewicz, Zbigniew Skoczylas. Algebra liniowa 1, GiS, Wrocław,
2002, s. 148-159.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron