Paulina Szewczyk 221218 pon 15:15
04.05.2015
Ćwiczenie nr. 44
Pomiar zależności oporu metali i półprzewodników od temperatury
I.
Cel ćwiczenia
Celem ćwiczenia jest pomiar oporu elektrycznego metalu i półprzewodnika
w funkcji temperatury oraz wyznaczenie temperaturowego współczynnika
oporu metalu i szerokości pasma wzbronionego półprzewodnika.
II.
Wstęp teoretyczny
Ciała stałe pod względem własności elektrycznych dzielimy na przewodniki,
półprzewodniki i izolatory. To co je zasadniczo różni to koncentracja
swobodnych elektronów, które są nośnikami prądu. Mówiąc swobodny
elektron mamy na myśli to, że nie jest on związany z konkretnym atomem,
lecz może poruszać się w całej sieci krystalicznej. O takim swobodnym
elektronie mówimy, że znajduje się w paśmie przewodnictwa.
III.
Wyniki pomiarów i obliczenia
1)
Wyniki pomiarów
Lp.
R1 [Ω]
R2 [Ω]
R3 [Ω]
R4 [Ω]
t [
C
o
]
T [K]
1
91,1
52,1
29,3
111,7
31,4
304,55
2
78,6
47,8
25,4
113,4
39,6
312,75
3
66,3
42,3
21,2
115,2
47,5
320,65
4
55,5
34,7
16,3
117,6
55
328,15
5
43,8
29,9
13,3
119,7
63
336,15
6
36,8
25,5
10,9
122
71
344,15
7
31,4
22,2
8,9
124,2
79
352,15
8
25,5
18,8
7,2
126,7
87
360,15
Lp.
Ln
R
1
Ln
R
2
Ln
R
3
1000/T
1
4,51
3,95
3,38
3,28
2
4,36
3,87
3,23
3,2
3
4,19
3,74
3,05
3,12
4
4,02
3,55
2,79
3,05
5
3,78
3,4
2,59
2,97
6
3,61
3,24
2,39
2,91
7
3,45
3,1
2,19
2,84
8
3,24
2,93
1,97
2,78
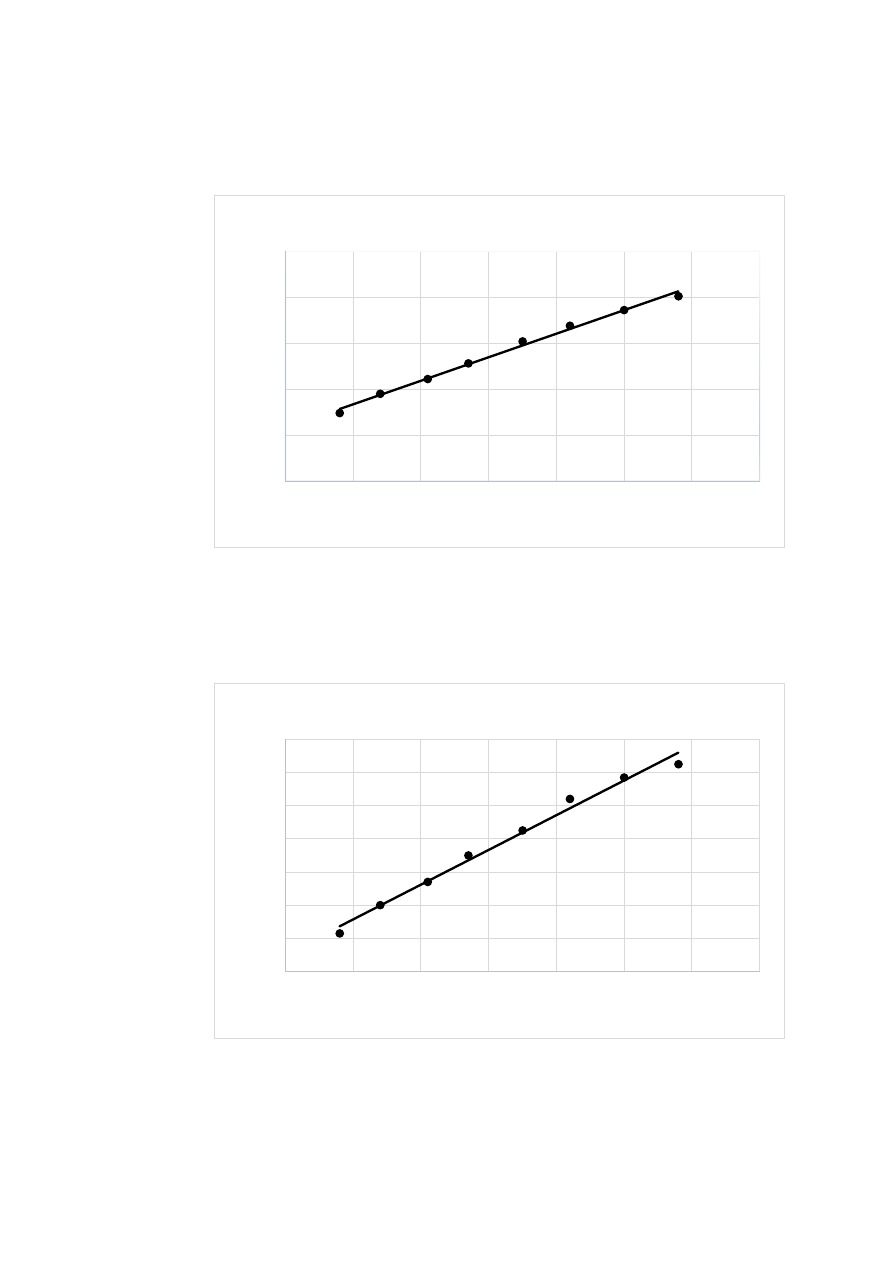
2) Obliczenia i wykresy
Wykres 1. Wykres LnR=f(1000/T) dla R1
Wykres 2. Wykres LnR=f(1000/T) dla R2
2,5
3
3,5
4
4,5
5
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
Ln
R1
1000/T
LnR1=f(1000/T)
2,7
2,9
3,1
3,3
3,5
3,7
3,9
4,1
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
Ln
R2
1000/T
LnR2=f(1000/T)
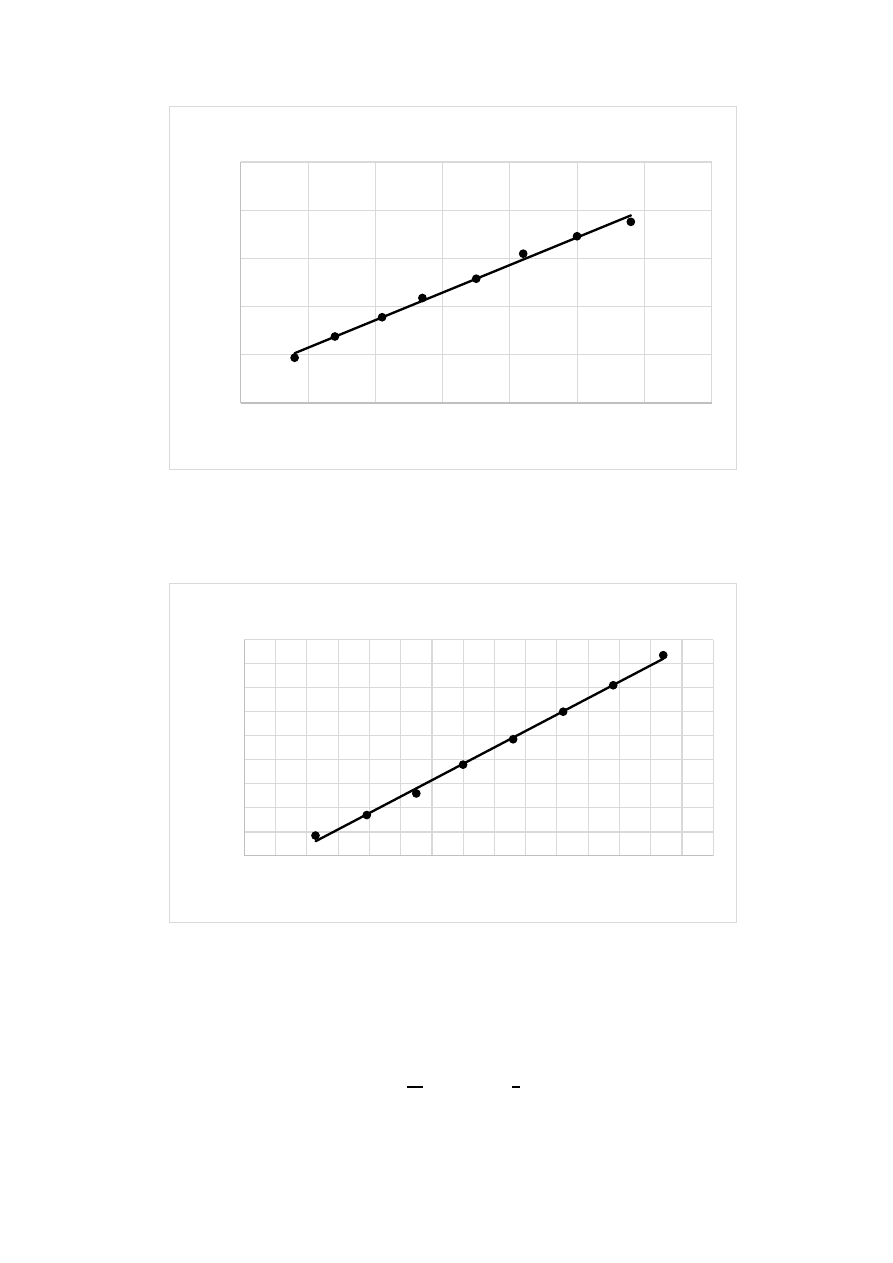
Wykres 3. Wykres LnR=f(1000/T) dla R3
Wykres 4. Wykres R=f(t) dla R4
Porównując równanie wyznaczonej prostej y = ax + b z równaniem na opór
metalu w funkcji temperatury
R(t) = R
0
∗ α ∗ t + R
0
można zauważyć, że
zmienna x odpowiada temperaturze t, więc z porównania wynika że a = R
0
∗ α
i
b = R
0
stąd otrzymujemy α =
a
R
0
, czyli
α =
a
b
.
α = (0,0026±0,00021) 1/K
1,5
2
2,5
3
3,5
4
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
Ln
R3
1000/T
LnR3=f(1000/T)
110
112
114
116
118
120
122
124
126
128
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
R [
Ω
]
t [C]
R=f(t)
△ α = ±α {
∆a
a
+
∆b
b
}
△ α = 0,00021
Opór półprzewodnika opisany jest równaniem R = R
0
∗ e
Eg
2∗K∗T
po
zlogarytmowaniu otrzymujemy
lnR = 10
−3
∗
E
g
2∗K
∗
1000
T
+ lnR
o
Porównując równanie wyznaczonej prostej y=Ax+B zauważając że 1000/T
odpowiada zmiennej x, szerokość pasma wzbronionego możemy obliczyć ze
wzoru
10
−3
∗
E
g
2k
= A, czyli E
g
= 2000 ∗ k ∗ A
k = 1,3806 10-23 J/K -
stała Boltzmanna
∆E
g
= ± {
∆k
k
+
∆A
A
}
R1
R2
R3
(0,44
±0,001) eV
(0,36
±0,001) eV
(0,49
±0,001) eV
IV.
Wnioski
Błędy pomiarowe mogło spowodować wiele czynników takich jak niedokładność
przyrządów pomiarowych, czy niedokładne odczytywanie wartości z termometru
przy ich szybkiej zmianie. Wykresy za równo dla półprzewodników jak i dla metalu
mają postać linii prostych.