1.1 Wyjaśnić pojęcia: automatyka, automatyzacja,
teoria sterowania, sterowanie ręczne, sterowanie
automatyczne.
1.2 Scharakteryzować krótko historię rozwoju
automatyki.
1.3 Wyjaśnić istotę sterowania w układzie
zamkniętym i w układzie otwartym.
1.4 Czym różni się sterowanie od regulacji?
1.5 Omówić wady i zalety sterowania w układzie
otwartym i zamkniętym.
1.6 Wyjaśnić pojęcia: sygnał wejściowy, sygnał
wyjściowy, sygnał uchybu, regulator, człon
wykonawczy, obiekt sterowania, sprzężenie
zwrotne, przewodnik pomiarowy.
2.1 Przedstawić istotę oraz podstawowe właściwości
ciągłego przekształcenia Laplace`a
2.2 przedstawić sposób wyznaczania oryginału
transformaty Laplace`a na podstawie:
-metod rozkładu na ułamki proste
-metody residuów
-rozkładu sygnału wejściowego na składniki.
2.3 Omówić problem dyskretyzacji sygnału
ciągłego.
2.4

Scharakteryzować strukturę układu

dyskretnego.
2.5 Podać przykłady kwantyzacji oraz próbkowania
sygnału.
2.6 Jaką funkcję w układzie sterowania spełnia
impulsator (przewodnik analogowo-cyfrowy)?
2.7 Jaką funkcję w układzie sterowania spełnia
ekstrapolator (przewodnik cyfrowo-analogowy)?
2.8 Narysować przykładowe widmo ciągłego i
dyskretnego sygnału harmonicznego.
2.9

Sformułować twierdzenia Shannona-

Kotielnikowa.
2.10 Podać istotę i podstawowe właściwości
dyskretnego przekształcenia.
2.11 Omówić metody odwrotnego przekształcenia.
3.1 Wymienić podstawowe formy opisu układu
dynamicznego.
3.2 Przedstawić opis układu za pomocą równań
różniczkowych.
3.3 Przedstawić opis układu za pomocą równań
różnicowych.
3.4 Scharakteryzować opis układu ciągłego i
dyskretnego za pomocą transmitancji operatorowej.
3.5 Scharakteryzować opis układu ciągłego i
dyskretnego za pomocą transmitancji widmowej.
3.6 Co to jest charakterystyka statyczna układu?
Podaj sposób jej wyznaczania na podstawie
eksperymentu, równania różniczkowego i
transmitancji operatorowej
3.7 Przedstawić opis układu ciągłego za pomocą
równań stanu.
3.8 Przedstawić opis układu dyskretnego za pomocą
równań stanu.
3.9 Wyprowadzić związek między równaniami stanu
a transmitancją dla układu ciągłego i dyskretnego.
3.10 Omówić podstawowe charakterystyki czasowe
układu ciągłego i dyskretnego
3.11 Analityczne i eksperymentalne wyznaczanie
charakterystyk częstotliwościowych.
4.1 Wymienić i omówić standardowe sygnały
wymuszające.
4.2

Scharakteryzować klasyczne metody analizy.

4.3

Omówić operatorowe metody analizy.

4.4 Jakie są podstawowe zasady budowy
schematów blokowych?
4.5 Podstawowe metody przekształcenia schematów
blokowych – omówić i podać przykłady.
4.6

Wyprowadzić zależności określające

transmitancje ciągłego i dyskretnego układu:
otwartego, zamkniętego oraz uchybową.
4.7 Omówić metody dyskretnej aproksymacji

układów ciągłych
4.8

Wymienić i podać interpretacje fizyczną

podstawowych parametrów członów dynamicznych.
Oblicz parametry dla zadanej postaci transmitancji

układu
4.9 Przedstawić problem wyznaczania uchybu

ustalonego
4.10 Omówić podstawowe człony dynamiczne

(proporcjonalny, inercyjny pierwszego rzędu,
całkujące, różniczkujące, inercyjne drugiego rzędu i

opóźniający )
4.11

Zapisać transmitancje układu ciągłego bez zer

i z zerami w przestrzeni stanów
4.12

zapisać transmitancje układu dyskretnego bez

zer i z zerami w przestrzeni stanów.
4.13

co to są wartości własne układu ?

4.14

odpowiedz czasowa układu swobodnego i

wymuszonego, opisanego równaniami stanu

5.1

Wyjaśnij pojęcia: układ stabilny

asymptotycznie, stabilny nieasymptotycznie,
stabilny globalnie, stabilny lokalnie i niestabilny
5.2 Co to jest punkt (stanu) równowagi
5.3 Podać warunek konieczny i wystarczający
stabilności asymptotycznej układu ciągłego
5.4 Algebraiczne kryteria stabilności ciągłych
układów dynamicznych
5.5 Częstotliwościowe kryteria stabilności ciągłych
układów dynamicznych
5.6 Podać warunek konieczny i wystarczający
stabilności asymptotycznej układu dyskretnego
6.1 Przedstawić istotę problemu układu regulacji
6.2

Napisać transmitancje oraz narysować

charakterystyki skokowe i częstotliwościowe
podstawowych regulatorów analogowych
6.3 Napisać równania podstawowych regulatorów
dyskretnych
6.4 Wymienić metody zwiększenia dokładności
statycznej układu
6.5 Synteza układów regulacji bazująca na
rozkładzie

pierwiastków

równania

charakterystycznego
6.6 Scharakteryzować metody czasowe syntezy
ciągłych i dyskretnych układów regulacji (zasada
zieglera-nicholsa)

6.7 Scharakteryzować metody przestrzeni stanów
syntezy układów ciągłych
6.8 Przedstawić sposób wyznaczania transmitancji
regulatora dla zadanej transmitancji dyskretnego
układu zamkniętego

6.9 scharakteryzować metody przestrzeni stanów
syntezy układów dyskretnych
1.1.
Automatyka - dziedzina nauki i techniki zajmujaca
się teorią i praktyczną realizacją nadzoru i
sterowania obiektami technologicznymi bez udziału
lub z ograniczonym udziałem człowieka. W
automatyce mozemy wydzielić 3 podstawowe
działy:
- podstawy teoretyczne automatyki
- budowa elementów i urządzeń automatyki
- zastosowanie automatyki w różnych dziedzinach
techniki
Automatyzacja to znaczne ograniczenie lub
zastąpienie (proces zastępowania) ludzkiej pracy
fizycznej i umysłowej przez pracę maszyn
działających na zasadzie samoregulacji i
wykonujących określone czynności bez udziału
człowieka. Również zastosowanie maszyn do pracy
niemożliwej do wykonania w inny sposób.
Teoria sterowania jest działem nauki i techniki
zajmującym się zachowaniem układów
dynamicznych w czasie. Sterowaniem obiektu
nazywa się oddziaływanie za pomocą sygnałów
wejściowych na proces zachodzący w obiekcie, tak
aby sygnał wyjściowy miał pożądaną wartość lub
przebieg czasowy. Inaczej mówiąc, jest to więc
celowe oddziaływanie na obiekt za pośrednictwem
wielkości wejściowych, aby jego wielkości wyjściowe
przyjęły określoną postać lub wartość
Sterowanie ręczne - sterowanie prowadzone przez
człowieka, na strumień wyjściowy (zmianę jego
wartości) wpływa człowiek
Sterowanie automatyczne

- sterowanie

prowadzone przez specjalne urządzenie sterujące
(realizowane przez układ sterujący), na strumień
wyjściowy (zmianę jego wartości) wpływa
urządzenie sterujące
1.3
Sterowanie w układzie otwartym – na obiekt
sterowania oddziałujemy wielkością sterującą
zmienianą w świadomy sposób, tak aby wielkość
wyjściowa przyjmowała określona wartość. Wielkość
wyjściowa nie wpływa na wielkość wejściową.
Ponieważ na obiekt mogą działać zakłócenia
(wielkości podlegające zmianom przypadkowym),
dlatego też wartość wyjściowa pod wpływem tych
zakłóceń (zewnętrznych) często odchyla się od
wartości żądanej. Ze względu na oddziaływanie
jednokierunkowe w torze sterowania, wielkość
sterująca powinna być dostosowana do zakłóceń jak
i do wielkości wyjściowej. Np. Sygnał radiowy
Sterowanie w układzie zamkniętym

–

Urządzenie sterujące wyznacza wartości sygnału
sterującego na podstawie wartości sygnału
wejściowego i wyjściowego. Np. Pływakowy
regulator poziomu wody.
1.4
Ze sterowaniem mamy do czynienia w układzie
otwartym, z regulacją zaś w układzie zamkniętym,
gdzie układ podlega samoregulacji.
1.5
Układ zamknięty jest o wiele praktyczniejszy i
lepszy od układu otwartego. Sterowanie w układzie
otwartym jest fatalne, wiąże się to z tym że brak
jest sprzężenia zwrotnego (występuje ono w
układzie zamkniętym). W układzie otwartym na
obiekt sterowania mogą działać zakłócenia, dlatego
wielkość wyjściowa często odchyla się znacznie od
wartości żądanej. Natomiast w układzie zamkniętym
wielkość wyjściowa jest ściśle wyznaczona przez
wartość sygnału wejściowego.
1.6
Sygnał wejściowy – strumień materiałowy,
energetyczny lub informacyjny, którego natężenie
możemy zmieniać, mogący wpływać na procesy
fizyczne zachodzące w obiekcie
Sygnał wyjściowy - strumień materiałowy,
energetyczny lub informacyjny będący wynikiem
przetwarzania w obiekcie strumieni wejściowych.
Sygnał uchybu (błąd regulacji) - róznica
sygnałów e(t): zadanego w(t) i regulowanego y(t),
porównanych na wejściu regulatora. Na podstawie
wartości sygnału błędu e(t), regulator wytwarza
odpowiedni sygnał sterujący u(t), tak aby wartość
błedu była możliwie bliska zeru. (Inaczej mówiąc
jest to różnica sygnału wejściowego i wyjściowego)
Regulator – urządzenie przetwarzające sygnał
uchybu na sygnał sterujący obiektem
Człon wykonawczy – przetwarza sygnał wyjściowy
z regulatora na sygnał o naturze fizycznej,
przystosowany do sterowania obiektem..
Obiekt sterowania - urządzenie, w którym
zachodzi proces technologiczny, czyli czynność lub
zespół czynności, polegających na przetwarzaniu
pewnych wielkości fizycznych z danej formy na inną.
Z punktu widzenia automatyki obiekt lub proces w
nim zachodzący są więc pojęciami prawie
równoznacznymi. Obiekty można dzielić tak jak
procesy. Obiekt jest to element dla króego
budowany jest układ sterowania powiązany z
otoczeniem przez oddziaływania, którymi
wprowadza się lub wyprowadza różnorodne
strumienie.
Sprzężenie zwrotne

– wartość sygnału

wyjściowego, mająca wpływ na sygnał sterujący.
Przetwornik pomiarowy – przetwarza wielkość
regulowaną na wielkość odpowiednią dla danego
elementu regulacyjnego.

2.1

Przekształcenie Laplace’a
F(s)=L[f(t)]=

0

∫

∞

f(t)e

-st

dt

stosowane jest w celu usystematyzowania
rozwiązywania równań różniczkowych.
Przekształcenie Laplace'a:
Zalety:
- włącza automatycznie warunki początkowe
- rozwiązanie uzyskuje się przez proste operacje
algebraiczne
- umożliwia proste ujęcie nieciągłych sygnałów
wejściowych
- rozwiązania ogólne i szczególne uzyskuje się
jednocześnie.
Właściwości:
- liniowość
L[a

1

f

1

(t)+a

2

f

2

(t)]=a

1

F

1

(s)+a

2

F

2

(s)

- przesunięcie w dziedzinie zmiennej rzeczywistej
L[f(t-t

0

)*1(t-t

0

)]=e

-st0

F(s)

- różniczkowanie w dziedzinie zmiennej rzeczywistej
L[d

n

f(t)/dt

n

]=s

n

F(s)-∑(k=0..n-1) s

n-k-1

f

(k)

(0

+

), a gdy

n=1 to:
L[df(t)/dt]=sF(s)-f(0

+

)

- transformata funkcji okresowej
jeśli f(t)=f(t+kT), k=1, 2, 3,…
oraz F

T

(s)=

0

∫

T

f(t)e

-st

dt to:

L[f(t)]= F

T

(s)/1-e

-sT

- wartość końcowa
lim

t->0

f(t)= lim

s->0

sF(s)

- wartość początkowa
lim

t->∞

f(t)= lim

s->∞

sF(s)

2.2.
Wyznacz. oryginału transformaty:
• metoda rozkładu na uł. Proste
• metoda residuów
• rozkładu sygnału wejściowego na składniki
2.3.
Dyskretyzacja sygnału:
Jest to przekształcenie sygnału ciągłego w
dyskretny. Rozróżnia się dyskretyzację w poziomie
(kwantowanie) (występuje w układach
przekaźnikowych) i dyskretyzację sygnału w czasie
(próbkowanie). Układy dyskretne (cyfrowe) mogą
być układami liniowymi lub nieliniowymi (jeśli
występuje proces kwantyzacji). Są układami
regulacji automatycznej, w których informacja jest
przekazywana tylko w dyskretnych chwilach,
zwanych chwilami impulsowania (próbkowania).
Przedstawienie sygnału ciągłego w postaci ciągu
impulsów jest nazywane modulacją impulsową i w
teorii jest realizowane za pomocą impulsatora.
2.4.
Struktura układu dyskretnego:
(elementy układu regulacji)
• impulsator - element przetwarzający sygnał ciągły
e(t) na impulsy e*(t)
• regulator impulsowy - przetwarza ciąg impulsów
e*(t) w ciąg impulsów u*(t)
• ekstrapolator - ciąg impulsów u*(t) jest
zastępowany np. funkcją schodkową u(t)
(elementy układu o charakterze aplikacyjnym)
• przetwornik A/C – przetwornik analogowo-
cyfrowy, próbkując cyklicznie sygnał uchybu e(t)
przetwarza go na sygnał cyfrowy (binarny) e*(t),
• regulator cyfrowy - urzadzenie mikroprocesorowe,
które w wyniku cyklicznego przetworzenia sygnału
e*(t) wyznacza potrzebną wartość sygnału
sterującego u*(t)
• przetwornik C/A przekształca wprowadzaną
cyklicznie wartość sygnału sterującego u*(t) na
schodkowy sygnał sterujący u(t)
• proces – obiekt regulacji o charakterze ciągłym
2.5.
a) Przykład kwantylizacji sygnału

b) Przykład próbkowania sygnału

2.6.
Impulsator w układzie sterowania jego funkcję
spełnia przetwornik analogowo-cyfrowy. Ze względu
na trudny opis matematyczny takiego impulsatora
stosuje się pewien idealny jego model, zwany
impulsatorem idealnym. W modelu tym każdy z
impulsów rzeczywistych jest zastąpiony przez
impuls o nieskończenie małej szerokości,
nieskończenie dużej wysokośći i o powierzchni
jednostkowej pomnożonej przez wartość funkcji w
chwilach próbkowania.
2.7.
W każdym dyskretnym układzie sterowania
występuje przynajmniej 1 ekstrapolator. W
układzie praktycznym funkcję tę spełnia przetwornik
cyfrowo-analogowy. Jego zadaniem jest
aproksymacja sygnału między kolejnymi próbkami,
zwykle funkcją stałą. W procesie ekstrapolacji
można uwzględniać jedynie przeszłe i bieżące
wartości dyskretne sygnału (ze względu na
realizowalność fizyczną).
2.8.
Widmo sygnału impulsowego jest sumą wielokrotnie
powtórzonego sygnału ciągłego, przesuniętego o
wielokrotność w

i

=2pi/T

a) widmo częstotliwościowe sygnału ciągłego

b) widmo częstotliwościowe dyskretnego sygnału
harmonicznego (próbkowanego)

2.9.
Twierdzenia Shannona-Kotielnikowa:
Sygnał ciągły może być ponownie odtworzony z
sygnału dyskretnego, jeśli był próbkowany z
częstotliwością co najmniej dwa razy większą od
granicznej częstotliwości swego widma.
2.10
Przekształcenia dyskretne transformaty Z:
Służą do opisu i analizy układów dyskretnych.
Stanowią odpowiednik przekształcenia Laplace'a w
analizie układów ciągłych. Przekształceniem Z
dyskretnej funkcji czasu f*(t) jest przekształcenie
operatorowe:
Z [f*(t)] = Z [f(kT)] = F(z)
określone wzorem:
F(z) = ∑ f(kT)z

-k

.

Transformaty Z istnieją dla funkcji dyskretnych,
które rosną nie szybciej od funkcji wykładniczych.
Właściwości:
- liniowość
Z[af

1

(kT)+bf

2

(kT)]=aF

1

(z)+bF

2

(z)

- przesunięcie w dziedzinie czasu
Z[f(kT+mT)*1(kT)]=z

m

[F(z)- ∑(n=0..m-1) f(nT)z

-n

]

- transformata różnicy
Z[∆f(k)]=(z-1)F(z)-zf(0), Gdzie ∆f(k)= f[(k+1)T-
f(kT) różnica 1 rz
- wartość końcowa
lim

k->∞

f(kT)= lim

z->1

(z-1)F(z)

2.11.
Odwrotne przekształcenie Z:
Jest to proces wyznaczania wartości dyskretnych
funkcji f(kT) na podstawie znajomości transformaty
F(z).
Z

-1

[F(z)] = f(kT), k=0, 1, 2, ...

Odwrotne przekształcenie Z można zrealizować
metodami:
• rozkładu na ułamki proste
• szeregu potęgowego
• residuów.
3.1.
Formy opisu układu dynamicznego:
• równania różnicowe
• transmitancje (operatorowe, widmowe)
• równania stanów
• charakterystyki czasowe lub częstotliwościowe
3.2.
Równania różniczkowe:
Równanie różniczkowe zwyczajne, opisujące ciągły,
jednowymiarowy obiekt sterowania o stałych
skupionych ma ogólną postać:
F=(y,y’,…,y

(n)

,u,u’,…u

(m)

,z,z’,…, z

(k)

,t)=0

Gdzie: y–sygnał wy, u–sygnał we z – zakłócenia
Równanie to w przypadku ogólnym opisuje
jednowymiarowy obiekt nieliniowy i niestacjonarny.
Gdy obiekt jest stacjonarny, w równaniu nie
występuje bezpośrednio zależność od czasu
(współczynniki równania są stałe). Natomiast, gdy
obiekt jest linowy, równanie to jest liniową
kombinacją sygnałów i ich pochodnych. W
przypadku ciągłego i stacjonarnego układu liniowego
równanie można zapisać w postaci:
a

n

d

n

y(t)/dt

n

+...+ a

1

dy(t)/dt+ a

0

dy(t) =

b

m

d

m

u(t)/dt

m

+...+

b

1

du(t)/dt+

b

0

u(t)+

c

k

d

k

z(t)/dt

k

+...+c

1

dz(t)/dt+ c

0

z(t)

Zależnie od warunków pracy rozróżnia sie 4
przypadki:
1) Na obiekt działa zarówno sygnał sterujący u(t),
jak i sygnał (lub sygnały) zakłucający z(t)
2) Na obiekt działa tylko sygnał sterujący
(zakłócenie = 0)
3) Na obiekt działa tylko zakłócenie (sygnał
sterujący = 0)
4) Na obiekt nie działają żadne sygnały zewnętrzne.
3.4.
a) Transmitancja operatorowa układu ciągłego
to wielkość określona jako stosunek transformaty
Laplace’a Y(s) sygnału wyjściowego obiektu do
transformaty U(s) sygnału wejściowego (przy
zerowych warunkach początkowych).
G(s) = Y(s) / U(s)
Dla układów opisanych liniowymi równaniami
różniczkowymi o stałych współczynnikach
transmitancja jest funkcją wymierną zmiennej
zespolonej s, (iloraz 2 wielomianów o postaci):
G(s) = L(s) / M(s) = b

m

s

m

+.+b

1

s+b

0

/a

n

s

n

+.+a

1

s+a

0

Pierwiastki licznika to tzw. zera, a mianownika to
bieguny transmitancji.
Gdy układ posiada r wejść oraz m wyjść definiuje
się wówczas macierz transmitancji:
[G

11

(s) G

12

(s) … G

1r

(s)]

G(s) = [G

21

(s) G

22

(s) … G

2r

(s)]

[G

m1

(s) G

m2

(s) … G

mr

(s)]

gdzie:
G

ij

(s)=Y

i

(s)/U

j

(s), i=1..m, j=1..r

Zaletą zapisu przy pomocy macierzy transmitancji
jest to, że transmitancje stanowiące elementy tej
macierzy reprezentują właściwości dynamiczne
poszczególnych części układu. Wadą natomiast jest
ujęcie wszystkich własności dynamicznych w

określonych przypadkach. (np. poszczególne we
oddziałują na wy obiektu)
Opis w przestrzeni stanów pozwala na pełniejsze
przedstawienie zjawisk dynamicznych oraz stwarza
dogodne warunki do obliczeń.
b)

Transmitancja operatorowa układu

dyskretnego
to wielkość określona jako stosunek dyskretnej
transformaty Laplace’a Y(z) sygnału wyjściowego
obiektu do transformaty U(z) sygnału wejściowego
(przy zerowych warunkach początkowych).
G(z) = Y(z) / U(z)
Dla dyskretnych układów opisanych liniowymi
równaniami

różniczkowymi

o

stałych

współczynnikach transmitancja jest funkcją
wymierną zmiennej zespolonej z, (iloraz 2
wielomianów o postaci):
G(z) = L(z) / M(z)
Pierwiastki licznika to tzw. zera, a mianownika to
bieguny transmitancji.
Gdy układ dyskretny posiada p wejść oraz q wyjść
definiuje się wówczas macierz transmitancji:
[G

11

(z) G

12

(z) … G

1p

(z)]

G(z) = [G

21

(z) G

22

(z) … G

2p

(z)]

[G

q1

(z) G

q2

(z) … G

qp

(z)]

gdzie:
G

ij

(z)=Y

i

(z)/U

j

(z)

Transformatę sygnału wyjściowego można zapisać
jako:
Y(z) = G(z)U(z)
Gdy:
[U

1

(z)] [Y

1

(z)]

U(z)=[ . . . ] Y(z)= [ . . . ]
[Up(z)] [Y

1

(z)]

3.5.
Transmitancją widmową G(jw) liniowego
układu stacjonarnego nazywa się iloraz wartości
zespolonej wartości zespolonej odpowiedzi Y(jw)
wywołanej wymuszeniem harmonicznym do
wartości zespolonej U(jw) tego wymuszenia:
G(jw)=Y(jw) / U(jw)
Transmitancję widmową wyznacza się z
transmitancji operatorowej:
G(jw)=G(s) |

s=jw

Wynika to z faktu, że przekształcenie Fouriera dla
s=jw jest szczególnym przypadkiem przekształcenia
Laplace’a. Transmitacja widmowa (odpowiadająca
transmitacji operatorowej) ma postac:
G(z) = b

m

(jw)

m

+.+b

1

(jw)+b

0

/a

n

(jw)

n

+.+a

1

(jw)+a

0

Równanie to możemy przedstawić w postaci:
a) jako iloraz 2 wielkości zespolonych:
b)

jako suma składnika rzeczywistego

rzeczywistego urojonego (post algebraiczna)
c) w postaci wykładniczej
d) w postaci trygonometrycznej.
Dyskretną transmitancją widmową nazywa się
zależność:
G(jwp)=Y(jwp) / U(jwp)
Ze względu na to ze jest to wielkość zespolona
otrzymujemy:
G(jwp)=P(wp) / jQ(wp) gdzie:
P(wp)=Re[G(jwp)], Q=Im[G(jwp)]
Między dyskretną transmitancją widmową a
dyskretną transmitancją zachodzi zależność:
G(jwp)=G(z) |

z=e

jwp

Dyskretna transmitancja widmowa jest funkcją
okresową pulsacji w

p

o okresie 2 pi

G(jwp+2npi)=G((jwp) n=0,1,2,…
Macierz dyskretnych transmitancji widmowych
układu wielowymiarowego jest definiowana
identycznie jak macierz układu ciągłego.
3.6
Charakterystyka statyczna układu jest to
zależność sygnału wyjściowego od wejściowego
(istotna właściwość obiektu w stanie ustalonym).
a)

Eksperymentalnie punkt leżący na

charakterystyce statycznej wyznacza się
wprowadzając na wejście obiektu stały sygnał i
mierząc w stanie ustalonym jego wyjście.
Dokonując pomiaru dla różnych (ale stałych)
wartości sygnału wejściowego, otrzyma się zbiór
punktów, który po odpowiedniej aproksymacji
stanowi chartka. statyczną.
b) Z równania różniczkowego wyznacza się tą
charakterystykę w ten sposób, że porównujemy
wszystkie pochodne do zera.
c) Charakterystykę statyczną z transmitancji
operatorowej wyznacza się przyjmując s=0.
y= (b

0

/a

0

)*u

a jej współczynnik nazywany jest współczynnikiem
wzmocnienia.
3.7.
Równania stanu układu są układem n równań
różniczkowych pierwszego rzędu (w ogólnym
przypadku

nieliniowych

niestacjonarnych).

Równania te uzupełniają równania we, które są
równaniami algebraicznymi (pokazują w jaki sposób
wektor zmiennych stanu x(t) i sterowanie u(t)
oddziałują

na

wy

y(t):

Postać

wektorowo-maciwrzowa:

x'(t)=A(x)+Bu(t)
y(t)=Cx(t)+Du(t)

gdzie:

x

-

n-wymiarowy

wektor

stanu

u(t)

-

r-wymiarowy

wektor

ster.

y(t)

-

m-wymiarowy

wektor

wy

A - nxn-wymiarowa macierz stanu
B - nxr-wymiarowa macierz sterowań (wejść)
C

-

mxn-wymiarowa

macierz

wy

D - mxr-wymiarowa macierz transmitancyjna
(bezpośredniego oddziaływania we na wy)
Gdy układ jest jednowymiarowy (r,m=1) w
powyższych równaniach należy zastąpić
wielkościami skalarnymi u(t) oraz y(t). Macierze B i
C przedstawić odpowiednio nx1 oraz 1xn.
3.8
Równania stanów układów dyskretnych:

Mamy dane równanie stanu układu ciągłego o
postaci:
x'(t)=A

c

(x)+B

c

u(t)

y(t)=C

c

x(t)+D

c

u(t)

Dla warunku początkowego x(t

0

)=x(kT) w chwili

t=(k+1)T równanie ma postać:
X(k+1)=e

AcT

x(k)+

kT

∫

(k+1)T

e

Ac[(k+1)T-t]

B

c

u(t) dt

Zakładając, że dyskretyzacja układu ciągłego jest
dokonywana poprzez wprowadzenie do układu
impulsatora i ekstrapolatora zerowego rzędu, w
wyniku czego sygnał u(t) jest wielowymiarową
funkcją schodkową więc mamy:
x(k+1)=Ax(k)+Bu(k)
y(k)=Cx(k)+Du(k) gdzie:
A=exp(A

c

T)≈I+A

c

T+A

c

2

T

2

+...

B=A

c

-1

[exp(A

c

T)-I]B

c

C=C

c

D=D

c

W przypadku gdy okres próbkowania T jest mały, to
pomija się rozwinięcia w szereg potęgowy exp(A

c

T)

z czego wynik
A=I+ A

c

T B= B

c

T

Identyczne zależności możemy otrzymać
zas™epując pochodną

poprzez różnicę

wyprzedzoną:
x’(t)|

t=k

=1/T [x(k+1)-x(k)]

co daje nam po przekształceniach
x(k+1)= [I+ A

c

T]x(k)+B

c

Tu(k)

3.9
a) Mając równania stanu możemy wyznaczyć
transmitancję operatorową (układu ciągłego)
przedstawioną

wzorem

(dla

warunków

początkowych równych 0 x(0)=0)
sX(s)=AX(s)+BU(s)
Y(s)=CX(s)+DU(s), gdzie:
X(s), U(s), Y(s) są transformatami Laplace’a
wektorów x(t), u(t), y(t)
Wtedy otrzymujemy:
sX(s)-AX(s)=BU(s)
oraz [sI-A]X(s)=BU(s)
następnie wyznaczamy X(s) (założenie istnieje
macierz odwrotna, det<>0 tzw macierz nieosobliwa)
X(s)=[sI-A]

-1

BU(s)

Gdzie po podstawieniu otrzymujemy:
Y(s)=(C[sI-A]

-1

B+D)U(s)

Z czego wynika macierz transm.
G(s)=Y(s) / U(s) = C[sI-A]

-1

B+D

b) Analogicznie jak w układach ciągłych, można
wyznaczyć związek miedzy równaniami stanu a
transmitancją dyskretną. W tym celu należy do
równań zastosować przekształcenie Z (przy
zerowych warunkach początkowych):
zX(z)=AX(z)+BU(z)
Y(z)=CX(z)+DU(z), gdzie:
X(z), U(z), Y(z) są transformatami Z wektorów x(t),
u(t), y(t)
Wtedy otrzymujemy:
zX(z)-AX(z)=BU(z)
oraz [zI-A]X(z)=BU(z)
następnie wyznaczamy X(z) (założenie istnieje
macierz odwrotna, det<>0 tzw macierz nieosobliwa)
X(z)=[sI-A]

-1

BU(z)

Gdzie po podstawieniu otrzymujemy:
Y(z)=(C[zI-A]

-1

B+D)U(z)

Z czego wynika macierz transm.
G(z)=Y(z) / U(z) = C[zI-A]

-1

B+D

4.1
Skok jednostkowy 1(t)
Przy stosowaniu tego typu sygnału założono, że
czas jego narastania jest równy zeru, co jest tylko
przybliżeniem sygnału rzeczywistego, jednak w
wielu przypadkach jest to założenie dopuszczalne.
Impuls (funkcja) Diraca ρ(t).
Impuls Diraca jest definiowany jako impuls o
nieskończenie wielkiej amplitudzie i nieskończenie
małym czasie trwania oraz o polu równym jedności.
Funkcje potęgowe
Funkcje te można przedstawić w postaci
u(t)=U0t do n*1(t) n=1,2,…
Wymienione funkcje wykorzystuje się głownie do
analizy układów śledzących.
Funkcja harmoniczna
Najczęściej stosuje się sygnał sinusoidalny o postaci
u(t)=U0sinωt . Na tego typu sygnale bazują głównie
częstotliwościowe metody analizy.
4.4
Ogólne zasady postępowania przy budowie
schematu blokowego można sprowadzić do
następującej procedury :
a) dodać transformaty laplace’a układu równań
różniczkowych,
b) ustalić sygnał wejściowy i wyjściowy układu,
c) na podstawie układu równań operatorowych
narysować schemat blokowy.
4.5
znane są następujące sposoby przekształcenia
(uproszczenia) schematów blokowych
- metoda przekształcenia układu równań
opisujących układ. Stosuje się najczęściej na etapie
budowy schematu blokowego i nie będzie szerzej
analizowana.
- metoda krok po kroku poprzez kolejne
dokonywanie prostych przekształceń schematu.
Pozwala zarówno przekształcić, jak i uproszczać
schemat blokowy. Stosuje się ją do przekształcenia
dowolnie skomplikowanych schematów. Metoda ta
ma istne zalety gdyż:
- nie wymaga określenia klasy schematu, a więc ma
zastosowanie do wszystkich schematów układów
liniowych,
- umożliwia dokonywanie kontroli poprawności
każdego kroku, a więc zapewnia poprawny wynik
przekształceń
4.6
Transmitancja układu otwartego
Go(s)=G(s)H(s)=Lo(s)/Mo(s)
Transmitancja układu zamkniętego
Gz(s)=Y(s)/U(s)=G(s)/1±G(s)H(s)=Lz(s)/Mz(s)

1

1

K

U

e

u

=

2

2

K

U

e

u

=

Transmitancja uchybowa
Gu(s)=E(s)/U(s)=1/1±G(s)H(s)
4.7
Metoda 1 (w oparciu o tablice transformat)
W tabelach transformat Z często jest podane
zestawienie transmitancji G(s) i odpowiadających im
dyskretnych transmitancji G(z). Jeżeli natomiast w
tabelach są podane tylko transformaty dyskretne
F(z) dla funkcji ciągłych f(t) lub funkcji dyskretnych
f(kT), to chcąc wyznaczyć dla danej transmitancji
G(s) transmitancję G(z) należy postępować
następująco:
-Wyznaczyć charakterystykę impulsowa g(t)
g(t)=α do -1[G(s)]
-Wyznaczyć dyskretną charakterystykę impulsową
g(kT)=g(t)|t=kT (*)
-Dla wyznaczonej charakterystyki g(t) lub g(kT)
odczytać transmitancję G(z)
Metoda 2 (bazująca na wyznaczaniu charakterystyki
impulsowej)
Dyskretną charakterystykę impulsową g(kT), dla
danej transmitancji G(s), wyznacza się zgodnie z
zależnością *. Poszukiwana transmitancja dyskretna
G(z)określona jest zależnością G(z) = Z[g(kT)]
4.9 przedstawic problem wyznaczania uchybu
ustalonego
Uchyb w stanie ustalonym dla układu ciągłego :

e

u

=

)

(

1

)

(

0

lim

)

(

0

lim

)

(

lim

0

s

G

s

U

s

s

s

sE

s

t

e

t

+

→

=

→

=

∞

→

1. Wymuszenie w postaci sygnalu skokowego –
u(t)=U

0

1(t)

Gdy k = 0 e

u

=

0

0

0

0

1

)

(

1

0

lim

K

U

s

G

U

s

+

=

+

→

Gdy k > 0 e

u

=0

2. Wymuszenie w postaci sygnalu liniowego – u(t) =
U

1

(t)1(t)

Gdy k = 0 e

u

-> nieskończoności!

Gdy k = 1
Gdy k > 1 e

u

= 0

3. wymuszenie w postaci sygnalu parabolicznego –
u(t) = U

2

t

2

1(t)

Gdy k = 0 e

u

-> nieskończoności!

Gdy k = 1
Gdy k >2 e

u

= 0

Uchyb ustalony układu dyskretnego

e

u

=

4.10
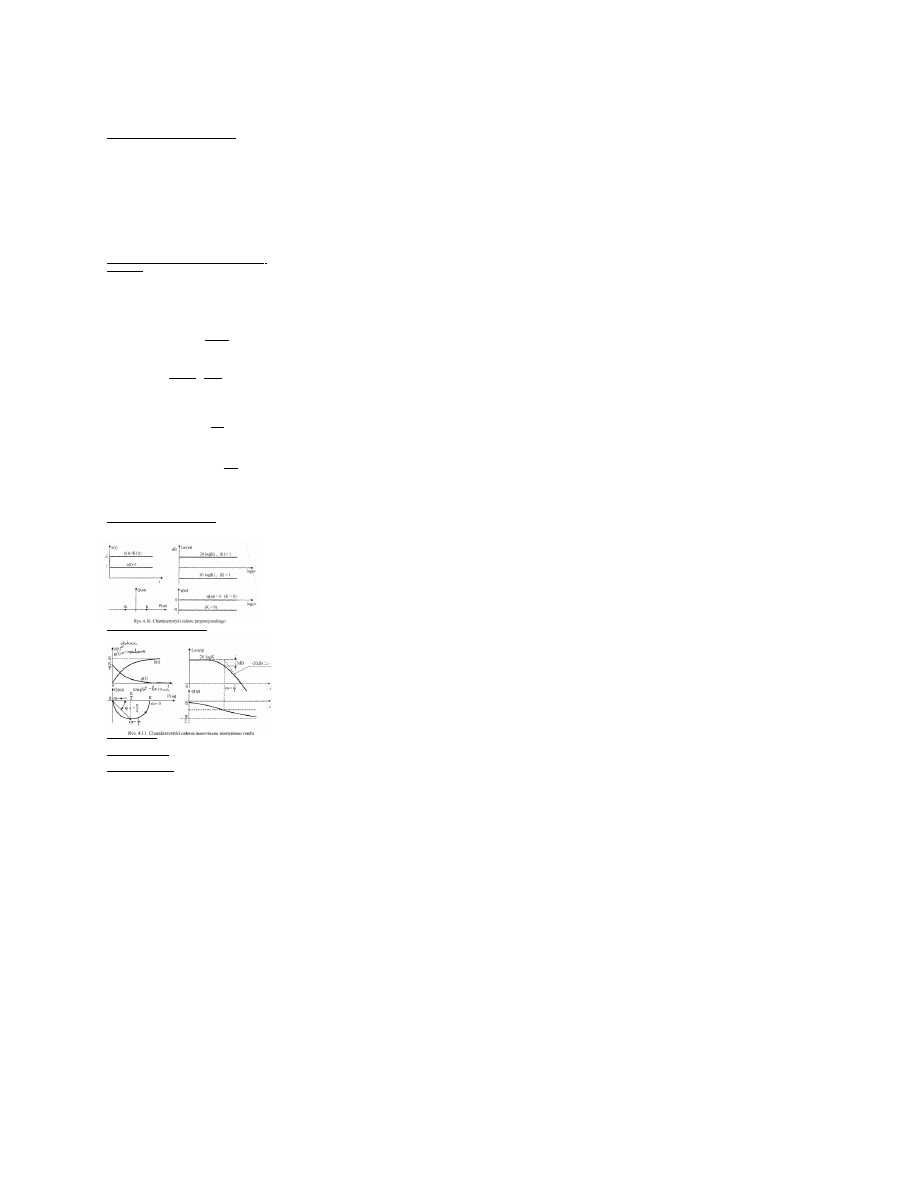
Człon proporcjonalny (bezinercyjny)
Równanie i transmitancja
y(t)=Ku(t) G(s)=K

Człon inercyjny pierwszego rzędu
T*Dy(t)/(dt+y(t))=Ku(t) G(s)=K/Ts+1

Człony całkujące
dy(t)/dt=Ku(t) G(s)=K/s=1/sTi
Człony różniczkujące
y(t)=K*du(t)/dt G(s)=Ks
Człony drugiego rzędu
G(s)=K/(T*T*s*s+2ETs+1)
Człon opóźniający
G(s)=Ke do -sTo
5.1.
układ jest stabilny asymptotycznie - gdy

spełniony zostanie następujący warunek konieczny i
dostateczny: wszystkie rzeczywiste pierwiastki

równania charakterystycznego (bieguny
transmitancji lub wartości własne macierzy stanu)

lub wszystkie części rzeczywiste pierwiastków
zespolonych muszą być ujemne, czyli pierwiastki te

muszą leżeć w lewej półpłaszczyźnie zmiennej
zespolonej.

układ jest stabilny nieasymptotycznie - gdy
oprócz pierwiastków leżących w lewej

półpłaszczyźnie występują:
- jeden pierwiastek rzeczywisty równy zeru

- pojedyncze pary pierwiastków urojonych,
- żaden z pierwiastków nie znajduje się w prawej

półpłaszczyźnie, natomiast na osi urojonej
występują pierwiastki pojedyncze, w tym co

najwyżej jeden rzeczywisty równy zeru.
Układ jest stabilny globalnie, gdy jest stabilny

dla dowolnych warunków początkowych.
Układ jest stabilny lokalnie, gdy jest stabilny dla

warunków początkowych leżących w pobliżu
stanu równowagi

Układ Jest niestabilny, jeśli co najmniej jeden
pierwiastek znajduje się w prawej półpłaszczyźnie

zmiennej zespolonej s.
5.2.

Stan równowagi jest to stan, do którego wraca
układ po ustaniu działania wymuszenia (do stanu,

w jakim znajdował się przed zmianą wymuszenia).
Punkt – nazwa w przestrzeni stanów.

5.3.
Układ jest stabilny, gdy spełniony zostanie warunek

konieczny i dostateczny: wszystkie pierwiastki

)

(

)

1

(

1

lim

)

(

lim

z

E

z

z

kT

e

k

−

→

=

→

równania charakterystycznego (bieguny
transmitancji lub wartości własne macierzy stanu)

lub
wszystkie części rzeczywiste pierwiastków

zespolonych muszą być ujemne, czyli pierwiastki te
muszą leżeć w lewej półpłaszczyźnie zmiennej

zespolonej.
5.4.

Kryteria algebraiczne pozwalają stwierdzić, czy
liniowy układ jednowymiarowy jest stabilny

asymptotycznie, na podstawie wartości
współczynników równania charakterystycznego., bez

jego
rozwiązywania.

Warunkiem koniecznym, ale niewystarczającym
stabilności asymptotycznej układu jest, aby jego

równanie charakterystyczne miało wszystkie
współczynniki ao, a1,…, an jednego znaku i

niezerowe.
Warunki dostateczne: (Kryterium Hurtwitza) to

warunki, które powinny być spełnione, aby
Równanie charakterystyczne układu miało wyłącznie

pierwiastki w lewej półpłaszczyźnie zmiennej
zespolonej s. Aby było to możliwe muszą być

spełnione warunki: 1 warunek konieczny stabilności
(wszystkie współczynniki są większe od zera); 2

podwyznaczniki Δi, jako minory główne
wyznacznika Δn, są większe od zera (warunek

dostateczny) Δi>0, i=2,3,…,n-1
5.5.

Częstotliwościowe kryteria stabilności:
● kryterium Nyquista – najczęściej stosowane,

pozwala ono badać stabilność układu zamkniętego
na podstawie przebiegu charakterystyki

częstotliwościowej układu otwartego, którą można
wyznaczyć zarówno analitycznie, jak i

doświadczalnie, umożliwia ona także ocenę
odległości układu

od graniczy stabilności.
● kryterium logarytmiczne – badania stabilności

układu w oparciu o logarytmiczną charakterystykę
amplitudową i fazowa lub logarytmiczną

charakterystykę amplitudowo- fazową.
5.6.

Warunek konieczny i wyst. Układu
dyskretnego:

Układ dyskretny jest stabilny jeśli dyskretne
wartości składowych przejściowych są ograniczone

dla dowolnej chwili czasu. Jeżeli ponadto te
dyskretne wartości składowych przejściowych kT->8

maleją do zera, to układ taki jest stabilny
asymptotycznie.

6.1.
1. Synteza jest rozważana wyłącznie w

kategoriach dynamiki układu(dokładność
dynamiczna,

zapas stabilności, charakter lub czas trwania
procesu przejściowego itp.). Rozwiązując zadanie

syntezy należy dysponować następującymi danymi:
a) modelem matematycznym obiektu (lub

wielkościami charakteryzującymi pośrednio jego
dynamikę)

b) celem sterowanie,
c) informacjami o ograniczeniach sygnałów

występujących w układzie
d) wskaźnikiem jakości,

e) założeniami o typie algorytmu regulacji
6.2.
a) Regulator typu P (proporcjonalny)
Regulator ten charakteryzuje się tym, że jego
sygnał wyjściowy u(t) jest proporcjonalny do
wejściowego(wejściowego). Transmitancja wynosi:
G(s)=U(s)/E(s)=kp
przy czym kp jest współczynnikiem
wzmocnienia(proporcjonalności).
b) Regulator typu I (całkujący) Transmitancja ma
postać:
G(s)= kp/s=1/sTi, Ti=1/kp
przy czym kp jest współczynnikiem wzmocnienia, Ti
to czas po upływie którego amplituda odpowiedzi
skokowej jest równa amplitudzie wymuszającego
sygnału skokowego.
c) Regulator typu PI (proporcjonalno-całkujący)
W regulatorze typu PI sygnał wejściowy jest
proporcjonalny do sumy sygnału wejściowego i jego
całki. Transmitancja natomiast opisana jest
wzorem:
G(s)=kp(1+1/Tis)
Gdzie Ti jest nazywane czasem zdwojenia regulatora
Charakterystyka:
a)skokowa

b) częstotliwościowa

d)Regulator typu PD (proporcjonalno-
różniczkujący)

W regularnym regulatorze typu PD sygnał wyjściowy
jest proporcjonalny do sygnału wejściowego i
pochodnej tego sygnału. Transmitancja wynosi:
G(s)=kp(1+Tds), gdzie stała Td jest nazywana
czasem wyprzedzenia. Praktyczna realizacja
takiego regulatora PD jest często niemożliwa, ze
względu na nieuniknioną inercję części
różniczkującej, dlatego stosuje się model
matematyczny rzeczywistego regulatora typu PD w
postaci transmitancji:
G(s)=kp(1+ Tds/Ts+1)
Charakterystyka regulatora PD idealnego (linia
przerywana) rzeczywistego(linia ciągła)
a) skokowa

b)częstotliwościowa

d) regulator typu PID (proporcjonalno-całkująco-
różn.)
W idealnym regulatorze PID sygnał wyjściowy
związany jest z sygnałem wejściowym.
Transmitancja idealnego i rzeczywistego regulatora
PID mają odpowiednio postać:
G(s)=kp(1+1/Tis+Tds),
G(s)=kp(1+1/Tis+Tds/Ts+1),
Charakterystyka regulatora PID idealnego (linia
przerywana) rzeczywistego(linia ciągła)
a) skokowa

b) czestotliwosciowa

6.3.
Regulatory dyskretne
Dyskretne wersje klasycznych regulatorówciągłych
otrzymuje się poprzez aproksymację ich
równania wyrażenia, w których całkowanie
zastąpiono sumowaniem, a różniczkowanie –
różnicą
pierwszego rzedu. I tak równania różnicowe mają
postać:
● Regulator typu P u(kT)=kpe(kT)
● Regulator typu I
u(kT)=T/Ti i=0Σke(iT)
● Regulator typu PI
u(kT)=kp(e(kT)+ T/Ti i=0Σke(iT)
● Regulator typu PD
u(kT)=
kp(e(kT)+Td/T[e(kT)-e(k-1)T)]
● Regulator typu PID
u(kT)=kp(e(kT)+T/Ti i=0Σke(iT) +Td/T[e(kT)-e(k-
1)T)]
6.4
- zwiększenie wartości współczynnika wzmocnienia
Wzrost współczynnika układu otwartego wpływa na
zmniejszenie wartości uchybu statycznego. Jednak
wzrost współczynnika wzmocnienia układu
otwartego jest ograniczony stabilnością układu
zamkniętego. Przy pewnej określonej wartości tego

współczynnika w układzie zanika tłumienie i układ
zbliża się do granicy stabilności. Dalszy wzrost
współczynnika może spowodować niestabilność
układu. Ze względu na dokładność statyczną
współczynnik wzmocnienia powinien być więc jak
największy, a ze względu na stabilność- możliwie
mały. Występuje zatem przeciwieństwo między
wymaganiami dokładności statycznej i stabilności.
- podwyższenie rzędu astatyzmu
Uchyb ustalony doprowadza się do wartości równej
zeru przez zastosowanie modyfikacji, po której
układ regulacji stanie się astatyczny odpowiedniego
rzędu. W tym celu należy do układu wprowadzić
człony całkujące, których liczbę i miejsce
usytuowania dobiera się w taki sposób, aby uchyb
ustalony był równy zeru. Niestety ten sposób
likwidacji uchybu ustalonego ma zasadniczą wadę-
wprowadzenie członów całkujących może
spowodować utratę stabilności.
6.5
Synteza układów regulacji bazująca na rozkładzie
pierwiastków równania. Badanie rozkładu
pierwiastków równania charakterystycznego układu
regulacji umożliwia bardziej precyzyjne określenie
własności procesów przejściowych niż badanie
charakterystyk częstotliwościowych. Jednak metody
syntezy oparte na analizie rozkładu biegunów
transmitancji są mniej ogólne, choćby z tego
powodu że dotyczą zwykle transmitancji o postaci
funkcji wymiernych. Warunkami syntezy najczęściej
są:1)algebraiczne kryteria stabilności 2)zadanie
położenie biegunów i ewentualnie zer
transmitancji.3)zadana postać transmitancji układu.
Algebraiczne kryteria stabilności stosuje się do
syntezy układów regulacji, od których wymaga się
tylko spełnienia warunku stabilności. Parametry
regulatora można określić z warunku zadanego
położenia biegunów lub zadanej postaci
transmitancji. W tym przypadku określa się
strukturę układu regulacji i typ regulatora, a
następnie wyznacza transmitancję układu
zamkniętego z regulatorem. Problem syntezy
upraszcza się jeżeli układ regulacji z regulatorem
jest opisany transmitancją drugiego rzędu. Wtedy
parametry regulatora najwygodniej jest obliczyć z
zadanej wartości współczynnika tłumienia i pulsacji
drgań własnych nietłumionych.
6.6
Metoda Zieglera-Nicholasa stała się standardową
procedurą doboru parametrów regulatora. W wielu
przypadkach zapewnia dobra jakość regulacji.
Pomimo dużej popularności tej metody
otrzymywane w wyniku jej zastosowania wartości
parametrów należy traktować jedynie jako pierwsze
racjonalne przybliżenie. Procedura doboru wartości
parametrów regulatora:
a)regulator zainstalowany w układzie regulacji
należy nastawić na działanie P i zwiększyć
stopniowo jego wzmocnienie k

p

, doprowadzając

układ do granicy stabilności,
b) w stanie wzbudzonym oscylacji zmierzyć ich
okres T

os

oraz odczytać wartość współczynnika

wzmocnienia k

p

=k

kr,

c)zależnie od typu regulatora należy przyjąć:
dla P k

p

=0,5k

kr

dla PI k

p

=0,45k

kr

, T

i

=0,85T

os

dla PID k

p

=0,6k

kr

, T

i

=0,5T

os

, T

d

=0,125T

os

6.7
Metody przestrzeni stanów syntezy układów ciągłych
Sposób rozwiązywania problemu syntezy w oparciu
o metody przestrzeni stanów, także i struktura
układu sterowania są uzależnione od możliwości
pomiaru zmiennych stanu. W przypadku dostępności
pomiarowej pełnego wektora stanu obiektu, zadanie
syntezy polega na wyznaczeniu elementów
proporcjonalnego regulatora wielowymiarowego,
umieszczonego w torze sprzężenia zwrotnego od
wektora stanu obiektu do wejścia układu
sterowania. Składowe wektora powinny być tak
dobrane, aby macierz stanu układu z regulatorem
posiadała wartości własne o pożądanych
wartościach. Natomiast w przypadku możliwości
pomiaru tylko części zmiennych stanu jest
niezbędne zastosowanie w układzie sterowania tzw.
obserwatora stanu, który na podstawie pomiaru
wejścia i części zmiennych stanu obiektu odtwarza
pozostała niemierzalną część wektora stanu.
6.8
Celem syntezy jest wyznaczenie transmitancji
regulatora dyskretnego
Gr(z)=Lr(z)/Mr(z)
W przypadku, gdy dana jest transmitancja
dyskretna obiektu wraz ekstrapolatorem
G(z)=L(z)/M(z) *
I żądana transmitancja układu zamkniętego
Gz(z)=Lz(z)/Mz(z) **
Rozwiązując zależność określającą dyskretną
transmitancję zastępczą układu (przyjęto regulator
w torze głównym)
Gz(z)=Gr(z)G(z)/1+Gr(z)G(z)
Wzglendem poszukiwanej transmitancji Gr(z),
otrzymano
Gr(z)=Gz(z)/G(z)[1-Gz(z)] ***
Lub po uwzględnieniu zależności *, **
Gr(z)=M(z)L(z)/L(z)[Mz(z)-Lz(z)] ****
Na podstawie równań *** lub **** Można
wyznaczyć równanie różnicowe, według którego
regulator (mikroprocesora) oblicza wartości sygnału
sterującego obiektem w kolejnych chwilach
próbkowania. Gdyby wyznaczona transmitancja
regulatora nie była realizowana fizycznie (stopień
wielomianu licznika większy od stopnia wielomianu
w mianowniku), wówczas należy zmienić warunek
syntezy, czyli postać transmitancji Gz(z).
W dyskretnym układzie regulacji o równaniu
charakterystycznym w postaci
Mz(z)=z(do potęgi)n=0

Czas trwania procesu przejściowego jest skończony i
jest najkrótszy z możliwych.
Układ regulacji spełniający ten warunek jest
nazywany układem czasooptymalnym.
6.9
Klasyczne metody projektowania polegają w
większości przypadków na kompromisie między
wymaganiami stabilności a wymaganiami
dokładności statycznej. W układach
jednowymiarowych do syntezy układów regulacji
można zastosować metody czasowe i
częstotliwościowe, znane dla układów liniowych.
Metody częstotliwościowe stosuje się wtedy, gdy
dysponuje się wyznaczoną eksperymentalnie
charakterystyką częstotliwościową obiektu oraz gdy
wymagania sformułowane są w postaci parametrów
procesu przejściowego, pasma przenoszonych
częstotliwości lub zapasu stabilności. Poza
metodami syntezy znanymi dla układów ciągłych, w
układach dyskretnych są stosowane specyficzne dla
tych układów metody.