Automatyka i Robotyka

2011/12

Fizyka 1

Materiały do wykładu 2

14 10 2011

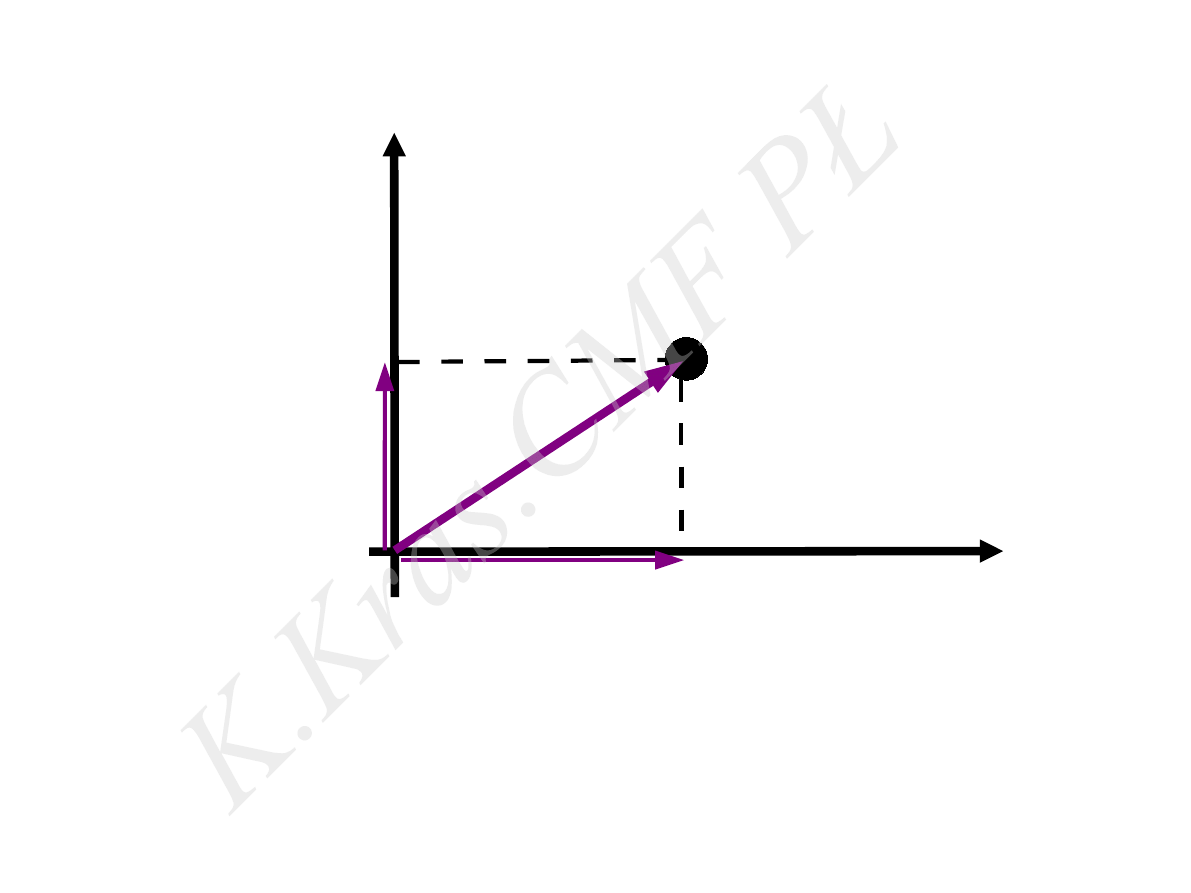
y

x

⃗r (t)

⃗

r

x

(

t )

⃗

r

y

(

t)

wektor położenia

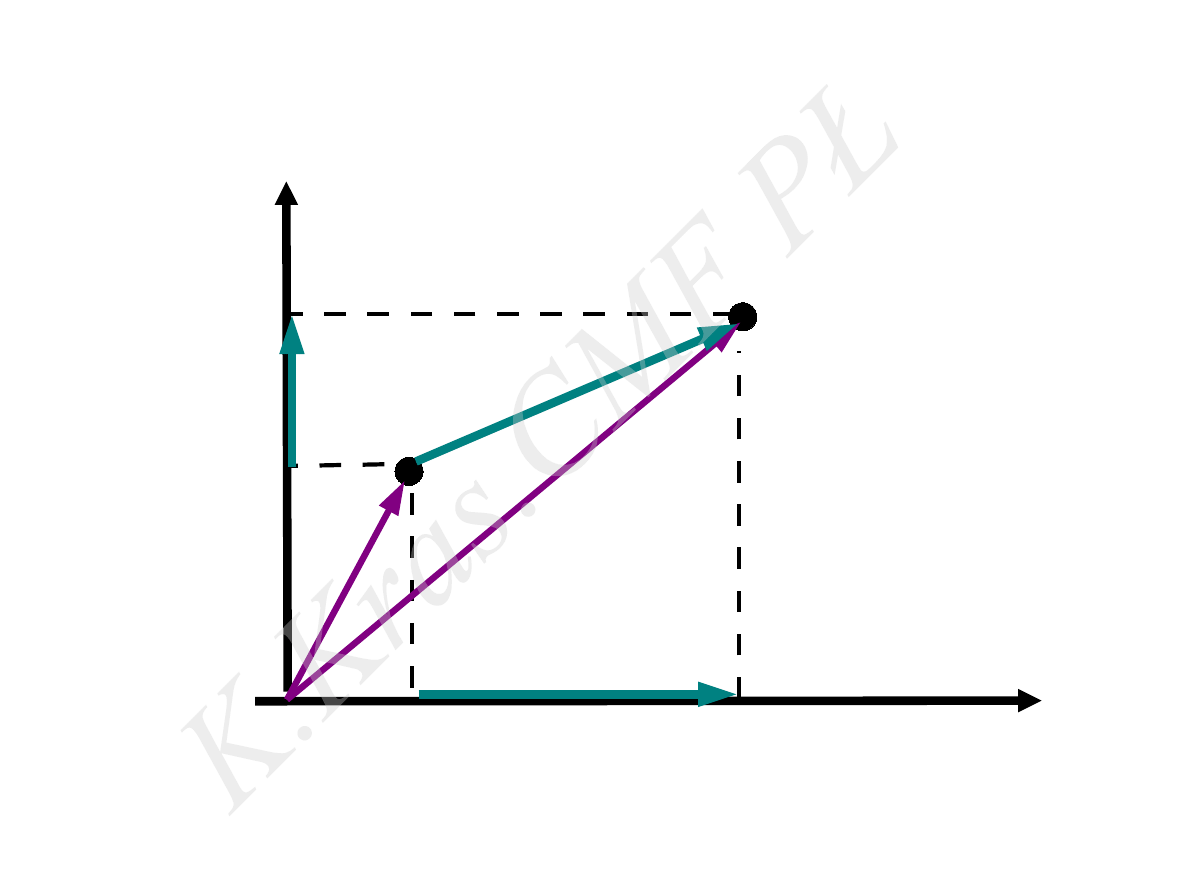
y

x

⃗

r

1

(

t)

⃗

r

2

(

t+Δ t)

⃗

Δ

r

⃗

Δ

r

x

⃗

Δ

r

y

wektor przemieszczenia

⃗

V =

d ⃗r

d t

=

d ⃗

r

x

dt

+

d ⃗

r

y

dt

+

d ⃗

r

z

dt

=

dx

dt

⃗i + dy

dt

⃗j + dz

dt

⃗k

⃗

V = ⃗

V

x

+ ⃗

V

y

+ ⃗

V

z

=

V

x

⃗i + V

y

⃗j + V

z

⃗k

⃗

V = lim

Δ

t →0

Δ ⃗r

Δ

t

=

⃗

dr

d t

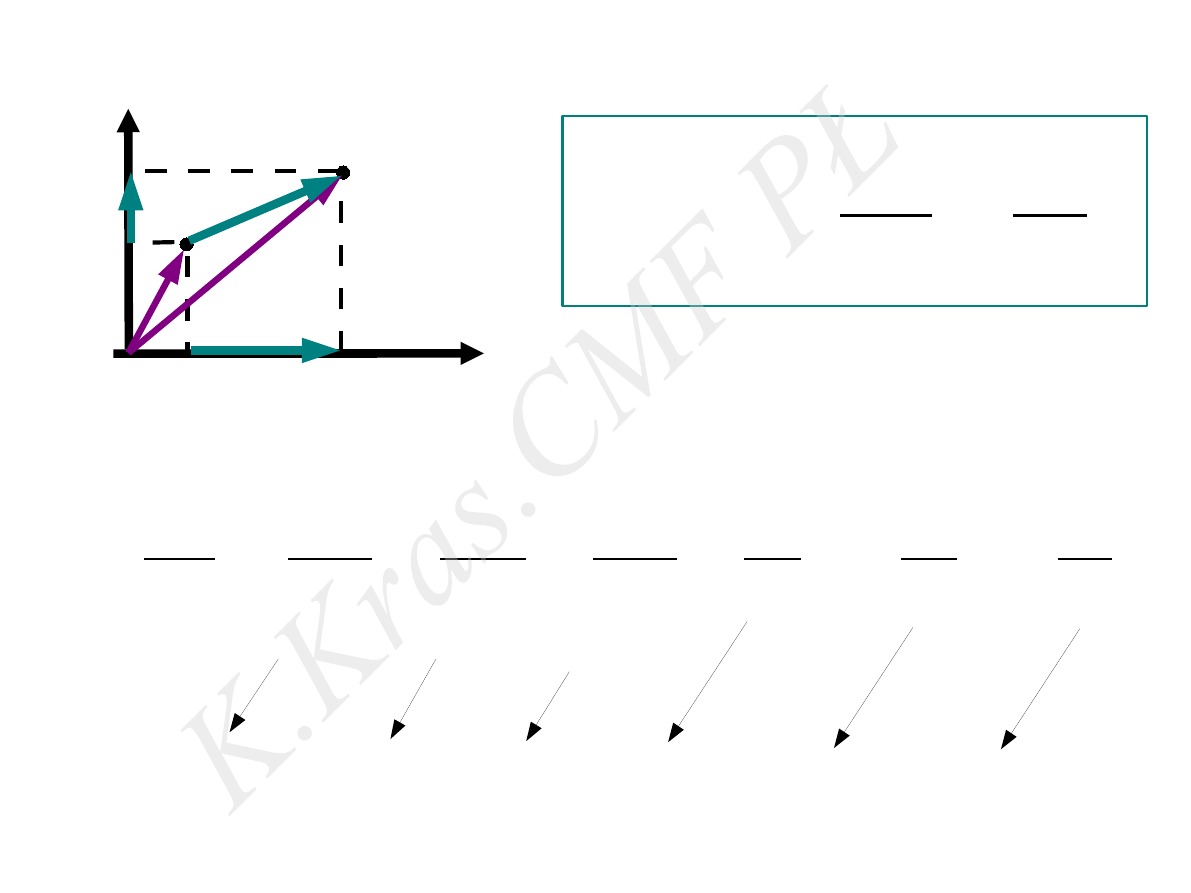
wektor prędkości

y

x

⃗

r

1

(

t)

⃗

r

2

(

t+Δ t)

⃗

Δ

r

⃗

Δ

r

x

⃗

Δ

r

y

⃗

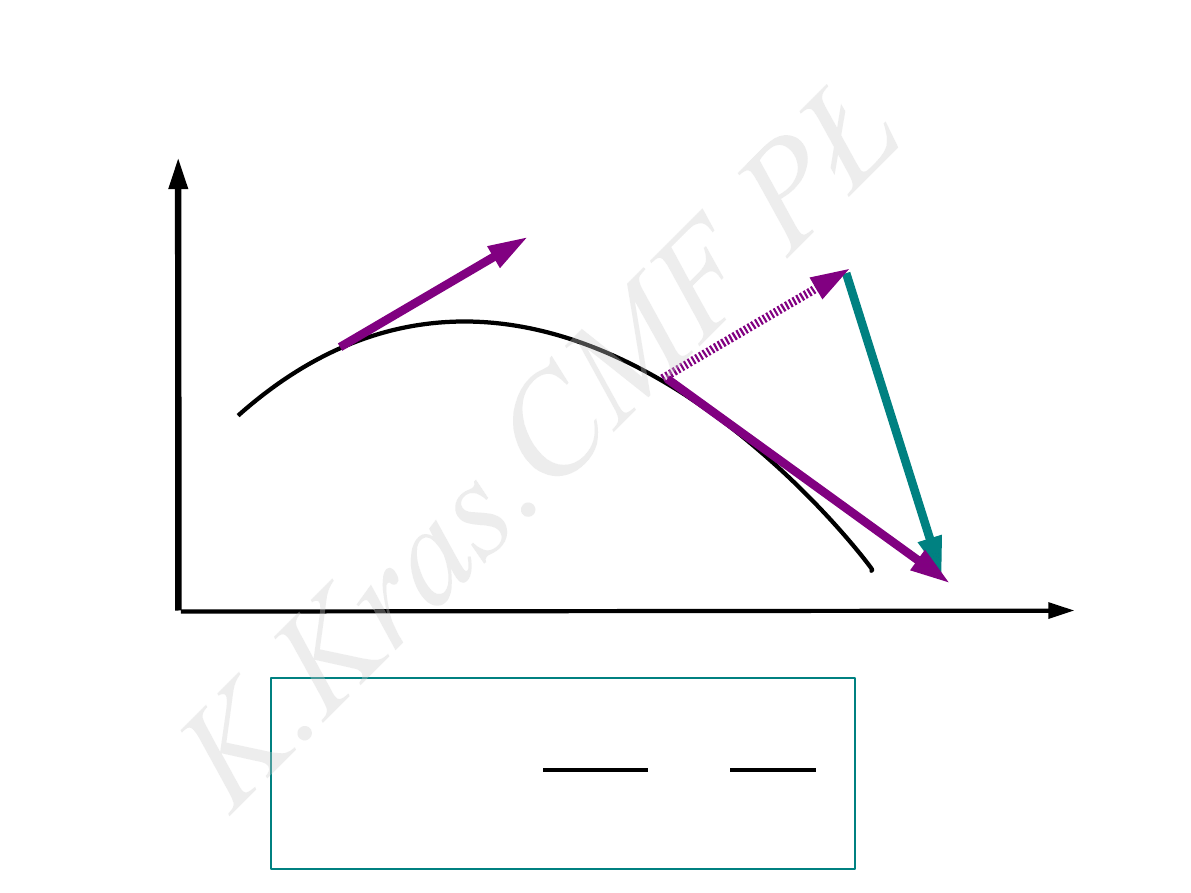
V (t )

⃗

V (t+Δ t)

Δ ⃗

V

⃗a = lim

Δ

t → 0

Δ ⃗

V

Δ

t

=

⃗

dV

d t

y

x

wektor przyspieszenia

I zasada dynamiki

Ciało trwa w spoczynku

lub w ruchu jednostajnym prostoliniowym,

dopóki nie zadziała na niego siła, która

zmusi go do zmiany tego stanu

Układ odniesienia, względem którego

ciało

swobodne

spoczywa lub porusza się ruchem

jednostajnym prostoliniowym

to

układ inercjalny

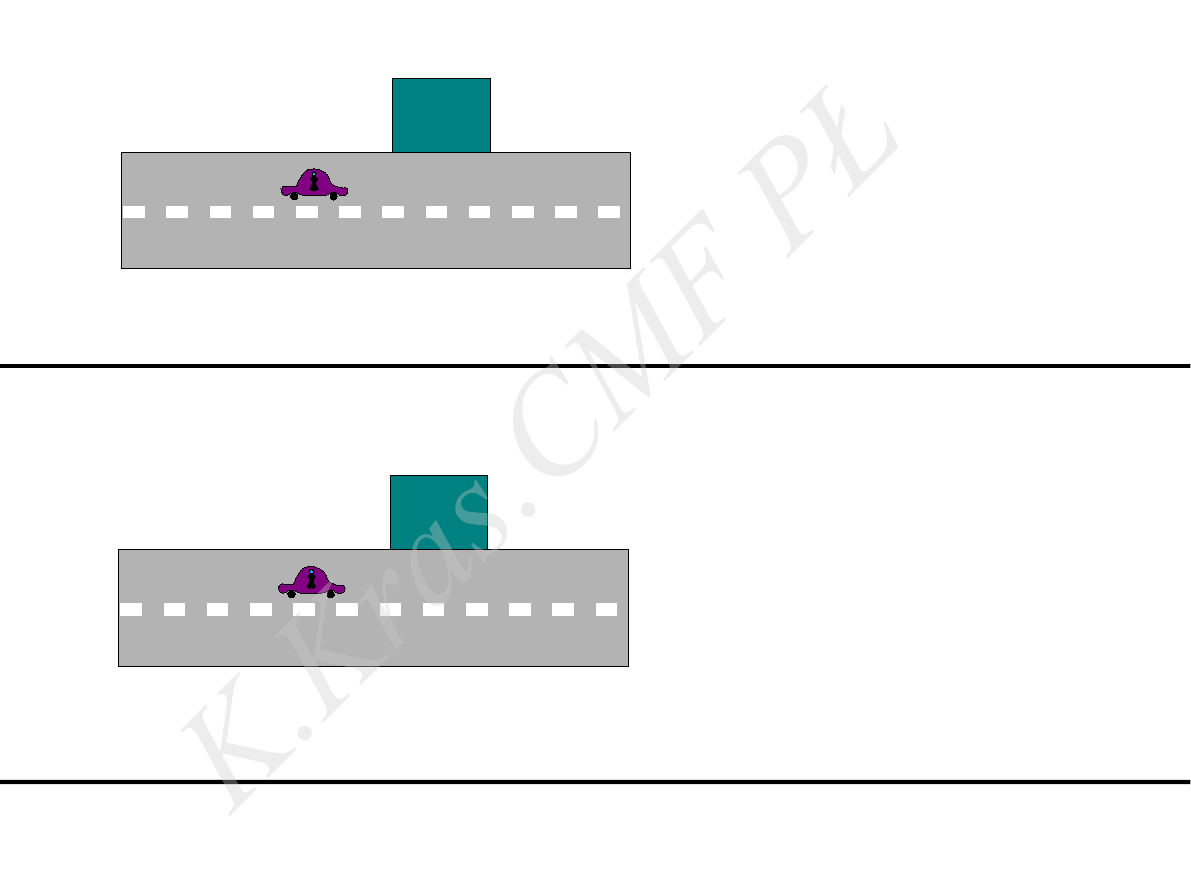
obiekt obserwowany –

dom

układ odniesienia -

samochód

siły( poziome), działające na dom –

brak

t =t

1

t =t

2

>

t

1

układ inercjalny

⃗

V =0

⃗

V =0

wynik obserwacji:

obiekt spoczywa

I zasada dynamiki

- spełniona

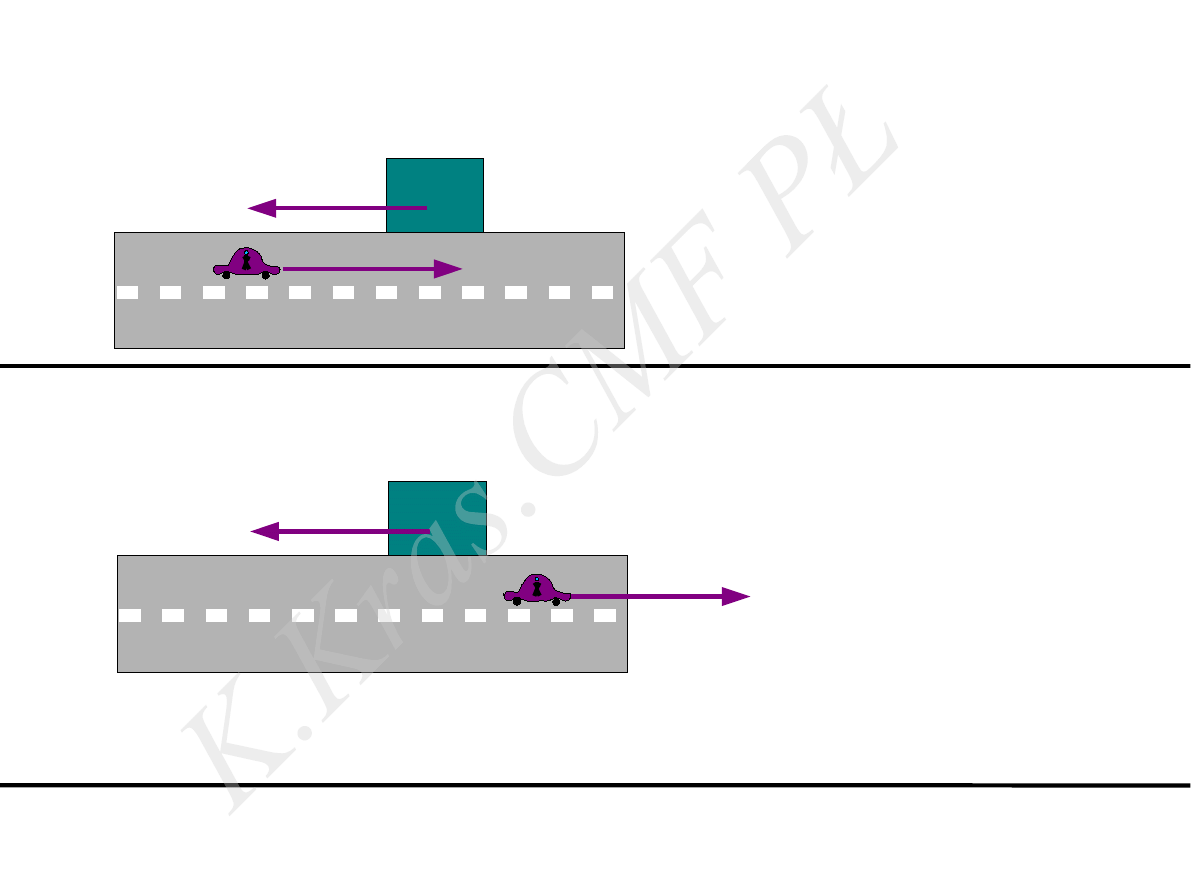
stała prędkość

układ inercjalny

t =t

1

t =t

2

>

t

1

⃗

V ≠0

⃗

V ≠0

obiekt obserwowany –

dom

układ odniesienia -

samochód

siły( poziome), działające na dom –

brak

wynik obserwacji:

obiekt porusza się ruchem

jednostajnym prostoliniowym

I zasada dynamiki

- spełniona

stała prędkość

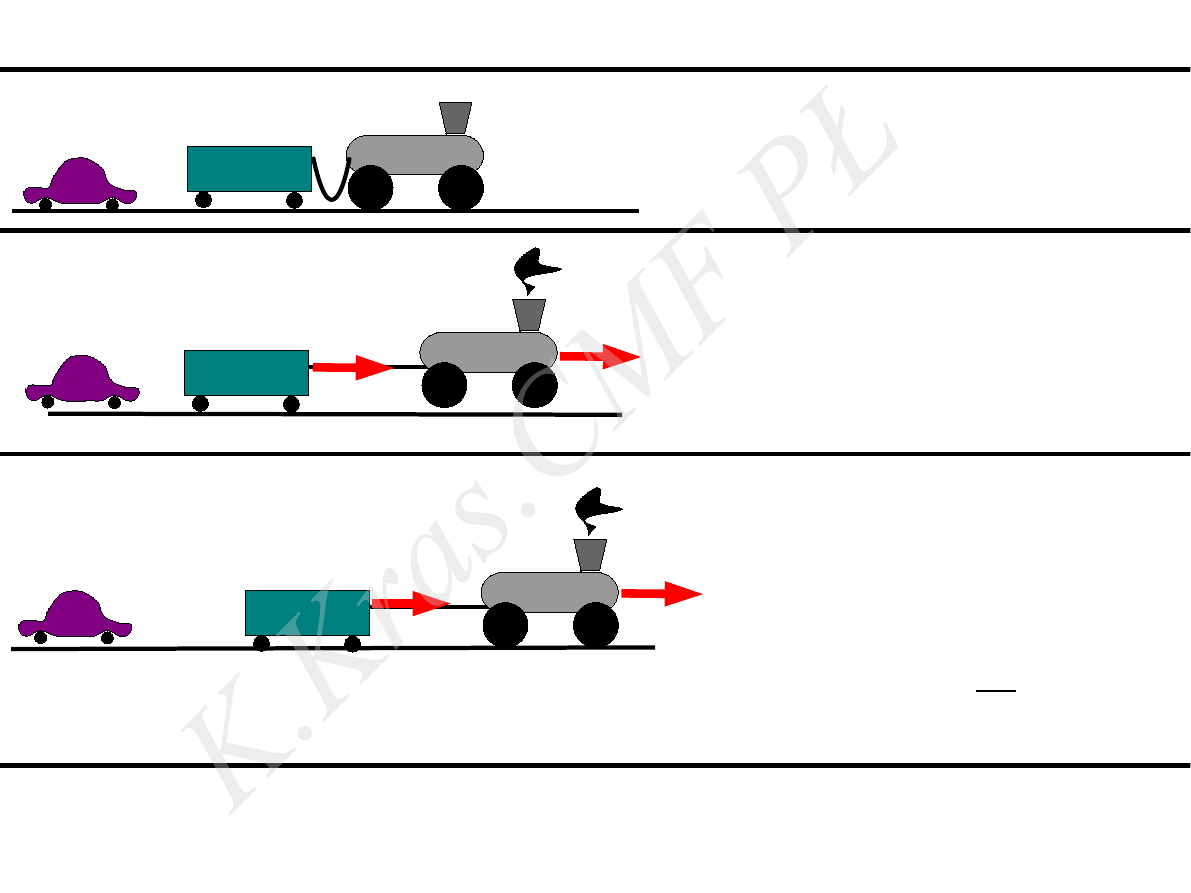
m

układ odniesienia -

samochód

, obiekt obserwowany -

wagon

⃗b =

⃗

F

m

przyspieszenie wagonu

względem

samochodu

⃗

F ≠0

m

⃗b

⃗

F ≠0

m

⃗a

⃗b

siła( pozioma), działająca na wagon –

działa

wynik obserwacji:

obiekt porusza się

z przyspieszeniem

układ inercjalny

II zasada dynamiki

-

spełniona

II zasada dynamiki

d ⃗p

d t

= ⃗

F

dla m = const.

d ⃗p

d t

=

d (m ⃗

V )

d t

=

m

d ⃗

V

d t

=

m⃗a = ⃗F

⃗

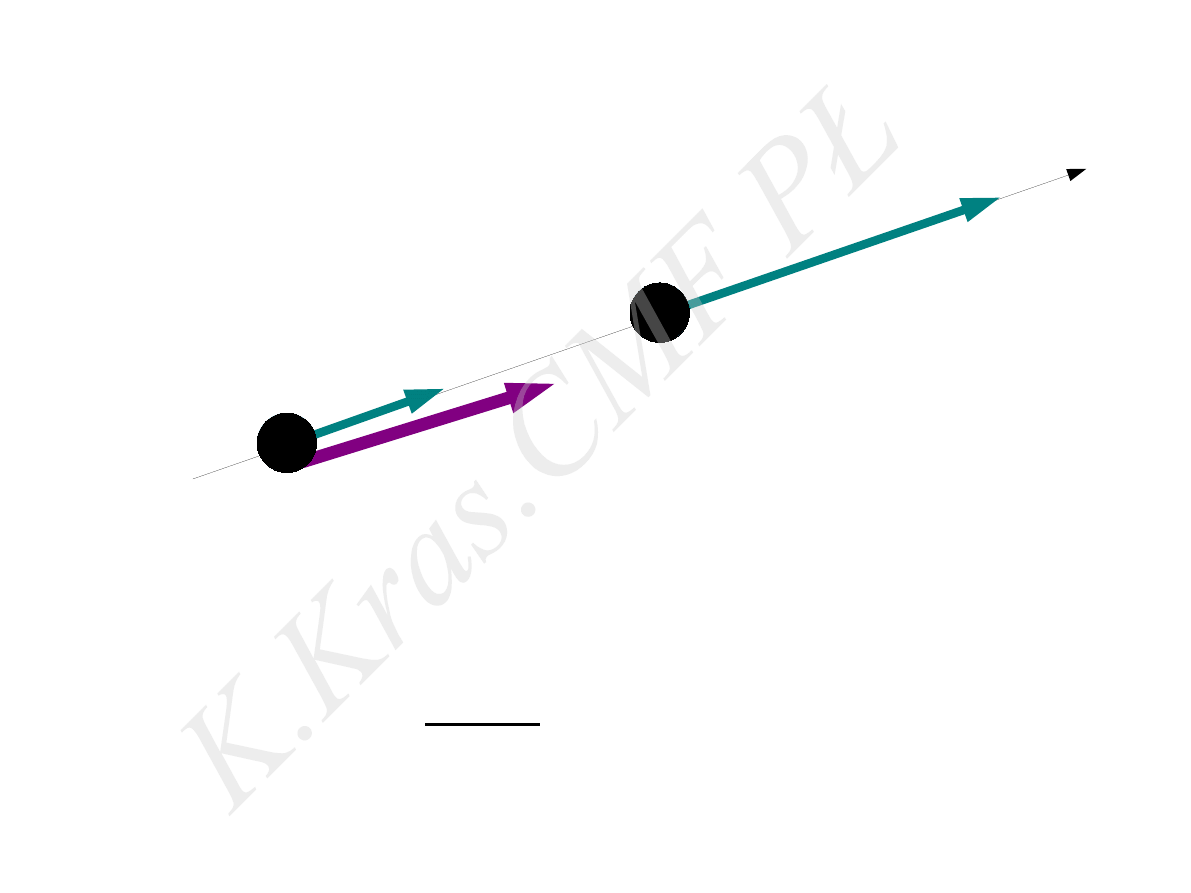
F ≠0 ⇒

d ⃗p

dt

≠

0 ⇒ ⃗p≠const

⃗p

⃗p

⃗

F

II zasada dynamiki

⃗

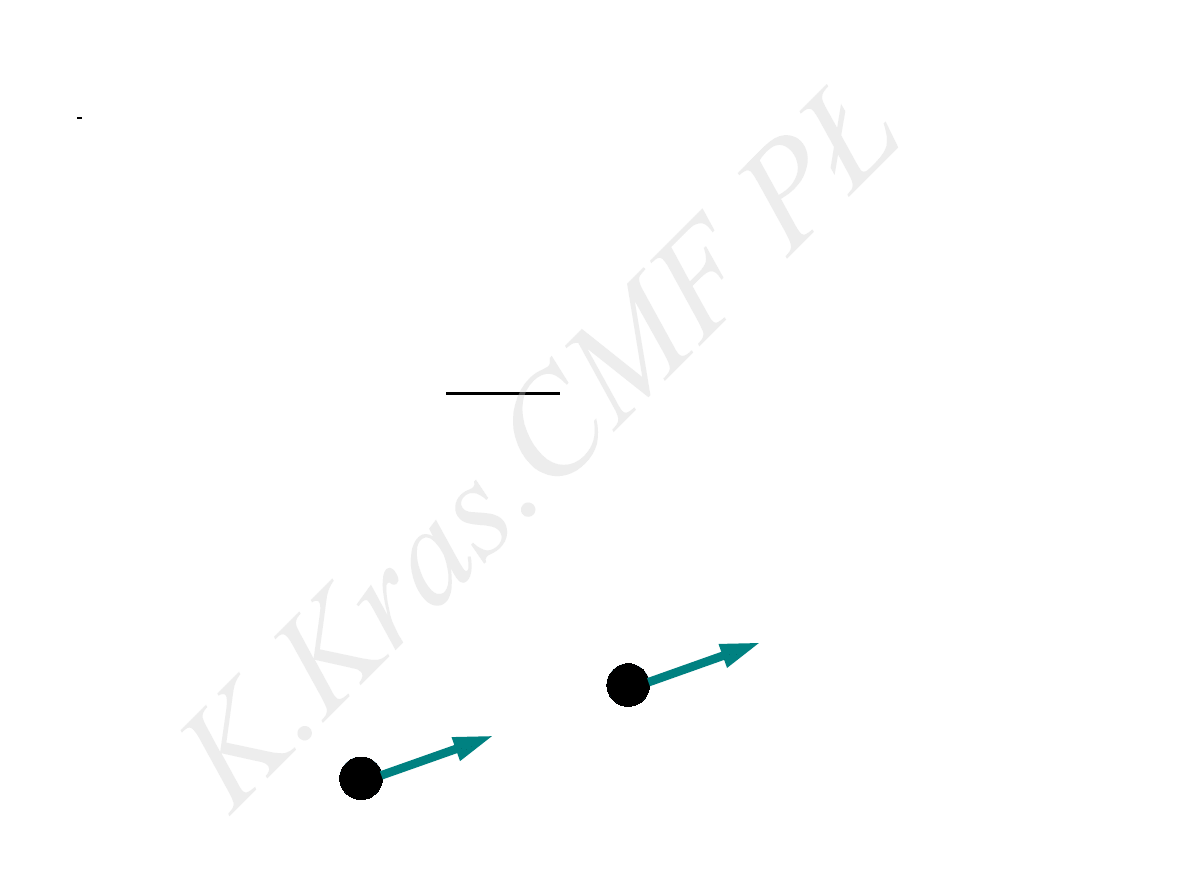
F =0 ⇒

d ⃗p

dt

=

0 ⇒ ⃗p=const

zasada zachowania pędu

⃗p

⃗p

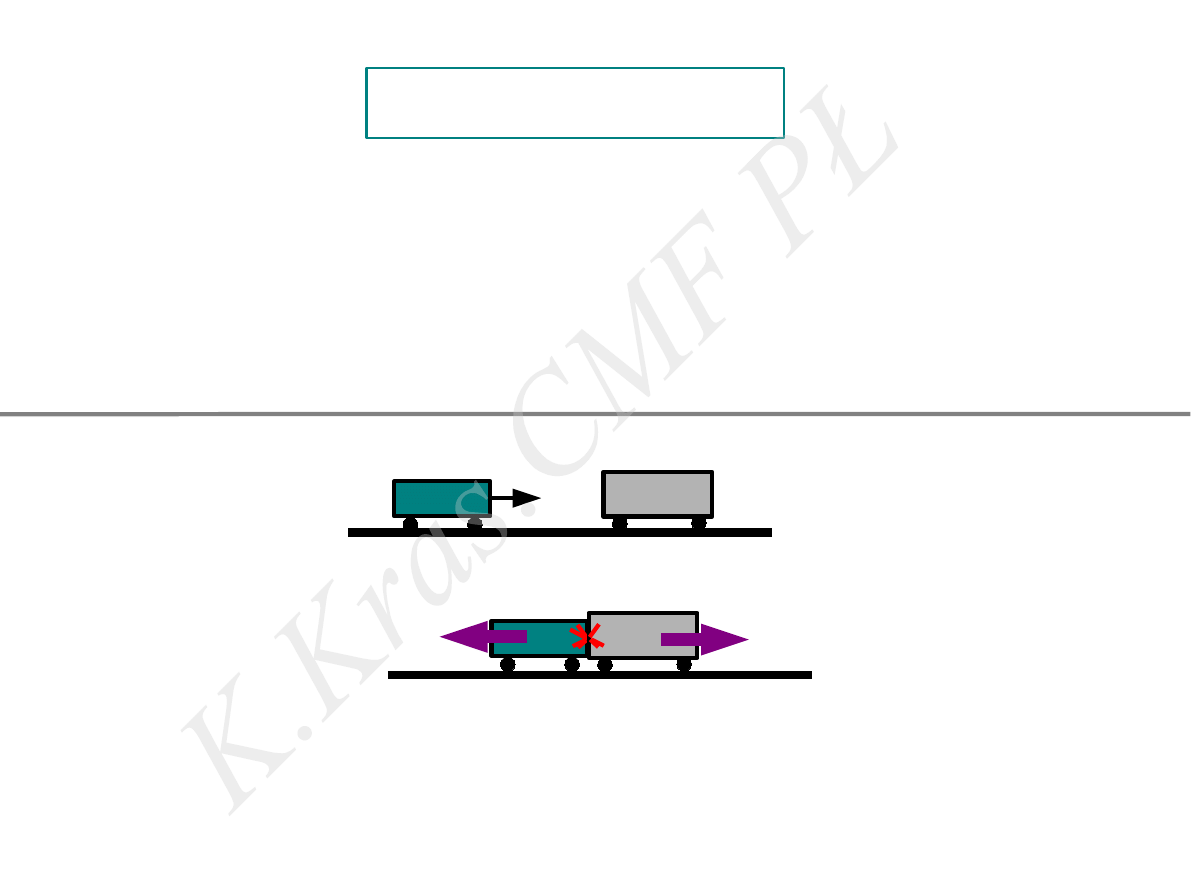
III zasada dynamiki

⃗

F

i j

= − ⃗

F

j i

V

⃗

F

21

⃗

F

12

1

2

1

2

1

⃗

F

21

= − ⃗

F

12

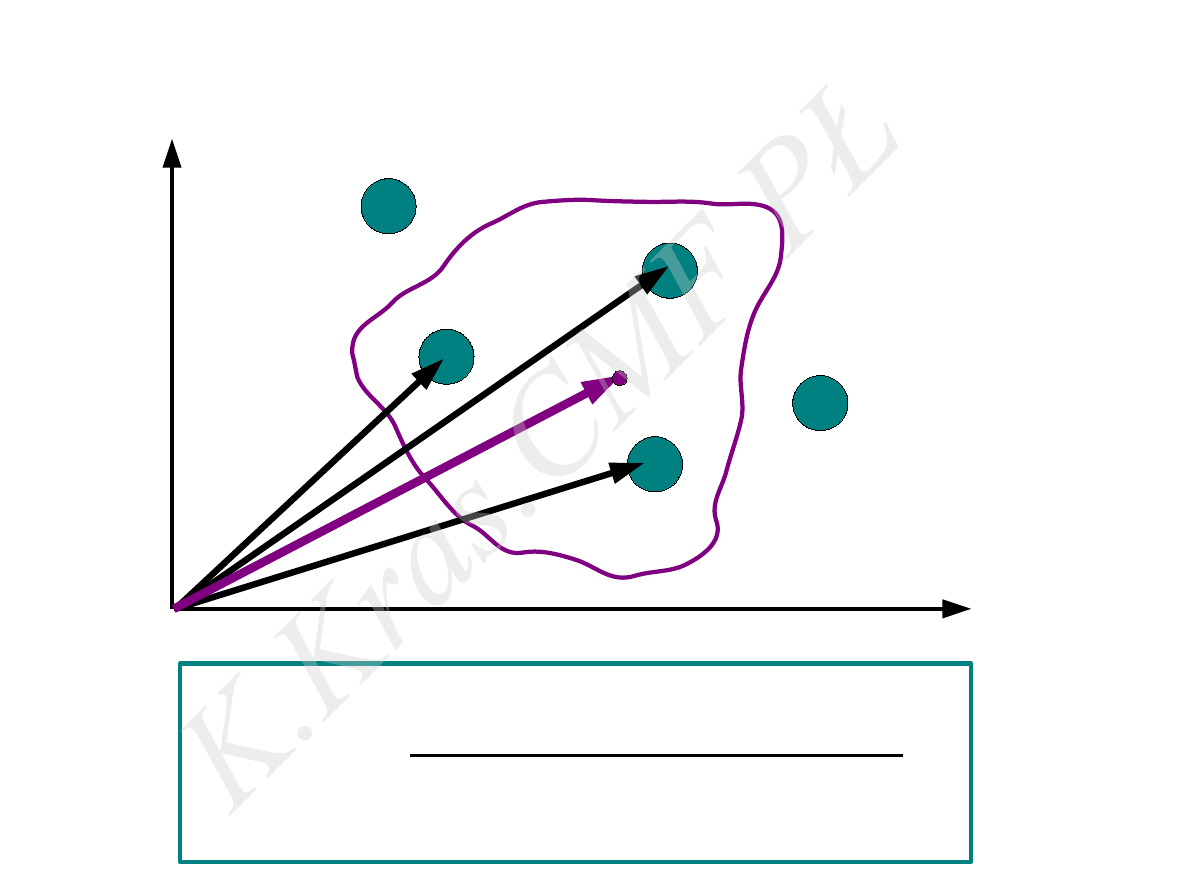
x

y

⃗

r

1

⃗

r

2

⃗

r

3

m

1

m

2

m

3

środek masy układu punktów materialnych

⃗

R

środek
masy

⃗

R =

m

1

⃗

r

1

+

m

2

⃗

r

2

+

m

3

⃗

r

3

m

1

+

m

2

+

m

3

d

d t

⃗

R =

d

d t

(

m

1

⃗

r

1

+

m

2

⃗

r

2

+

m

3

⃗

r

3

m

1

+

m

2

+

m

3

)

⃗

V

u

=

m

1

⃗

V

1

+

m

2

⃗

V

2

+

m

3

⃗

V

3

m

1

+

m

2

+

m

3

M

u

=

m

1

+

m

2

+

m

3

ruch środka masy układu

prędkość środka masy układu

masa układu

⃗

P

u

=

M

u

⃗

V

u

=

m

1

⃗

V

1

+

m

2

⃗

V

2

+

m

3

⃗

V

3

pęd środka masy układu ciał

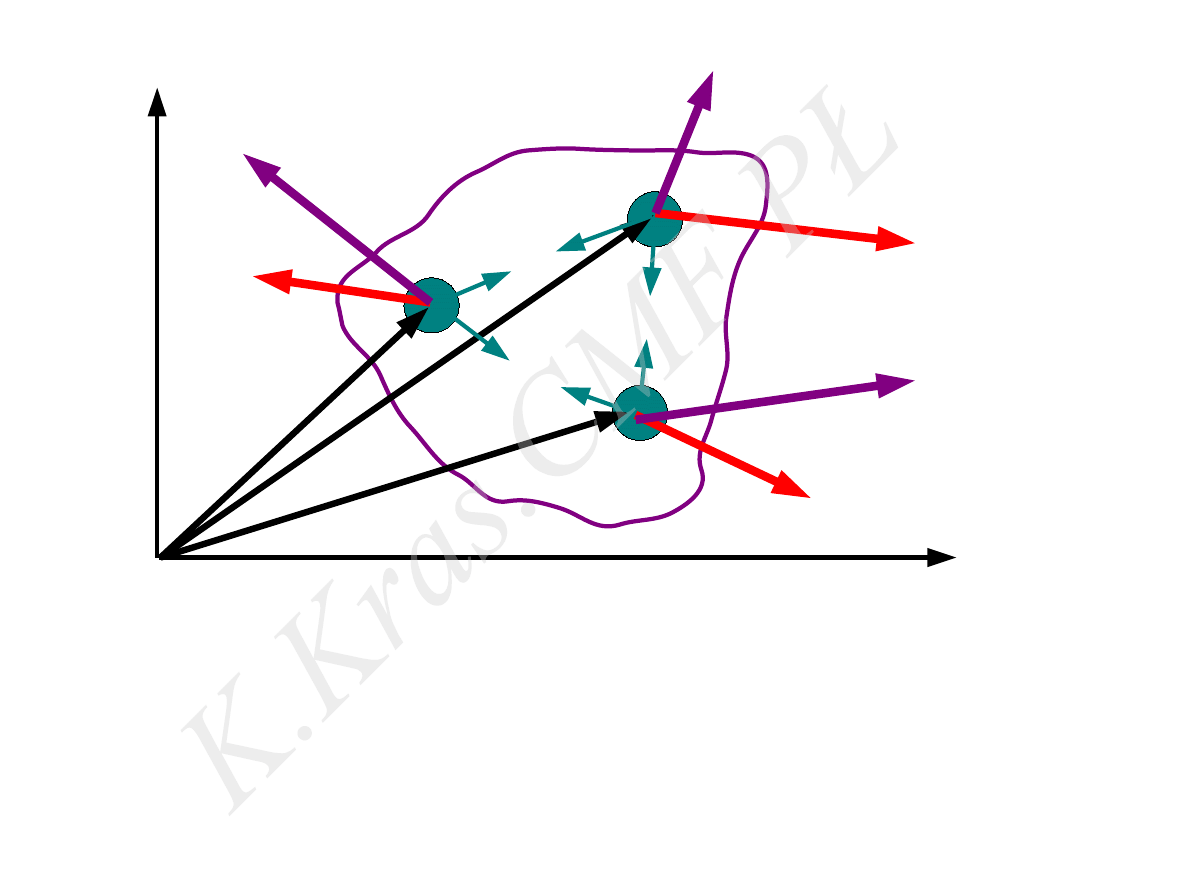
x

y

m

1

m

2

m

3

⃗

F

21

⃗

F

12

⃗

F

31

⃗

F

23

⃗

F

13

⃗

F

32

⃗

F

z1

⃗

F

z2

⃗

F

z3

⃗

p

3

⃗

p

2

⃗

p

1

⃗

F

12

, ⃗

F

13

, ⃗

F

21

, ⃗

F

23

, ⃗

F

31

, ⃗

F

32

siły wewnętrzne układu

⃗

P

u

= ⃗

p

1

+ ⃗

p

2

+ ⃗

p

3

⃗

F

z1

, ⃗

F

z2

, ⃗

F

z3

siły zewnętrzne

pęd układu

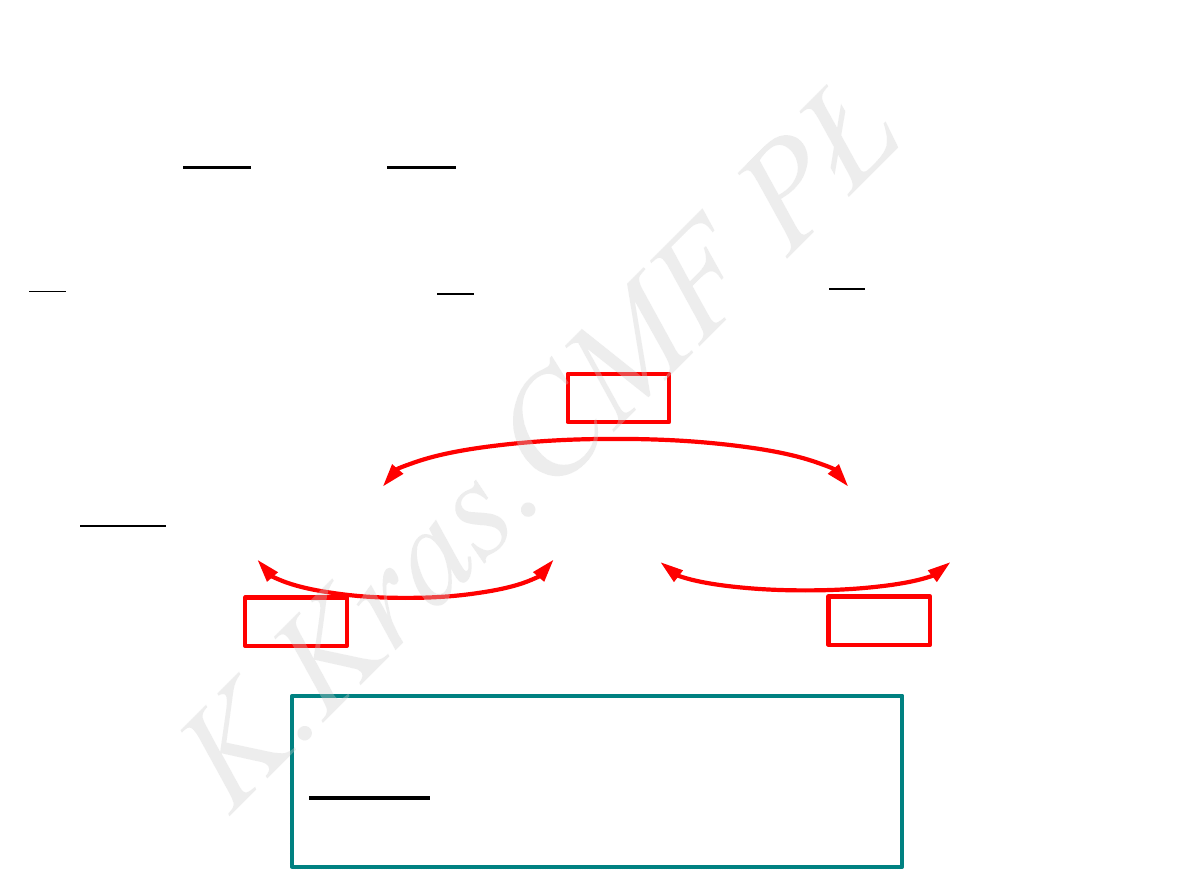
ruch środka masy układu ciał

d

d t

⃗

P

u

=

d

d t

(

m

1

⃗

V

1

+

m

2

⃗

V

2

+

m

3

⃗

V

3

)

d

d t

(

m

1

⃗

V

1

)

= ⃗

F

21

+ ⃗

F

31

+ ⃗

F

z1

d

d t

(

m

2

⃗

V

2

)

= ⃗

F

12

+ ⃗

F

32

+ ⃗

F

z2

d

d t

(

m

3

⃗

V

3

)

= ⃗

F

13

+ ⃗

F

23

+ ⃗

F

z3

d ⃗

P

u

d t

= ⃗

F

21

+ ⃗

F

31

+ ⃗

F

z1

+ ⃗

F

12

+ ⃗

F

32

+ ⃗

F

z2

+ ⃗

F

13

+ ⃗

F

23

+ ⃗

F

z3

Σ=

0

d ⃗

P

u

d t

= ⃗

F

z1

+ ⃗

F

z2

+ ⃗

F

z3

Σ=

0

Σ=

0

zasada zachowania pędu układu ciał

układ odosobniony

∑

i=1

i=n

⃗

F

zi

=

0 ⇒

d ⃗

P

u

d t

=

0 ⇒ ⃗

P

u

=

const

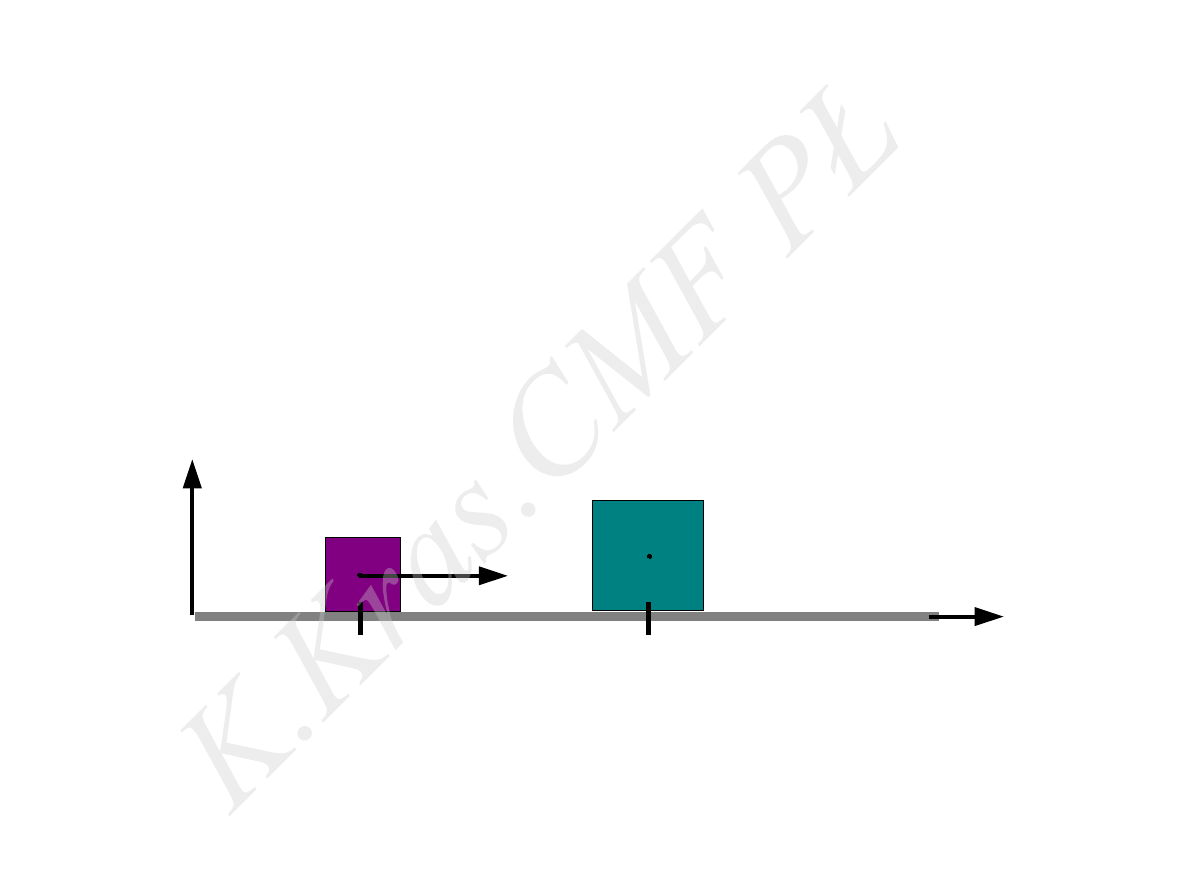
x

y

m

M

⃗

V

0

0

l

Przykład 1.

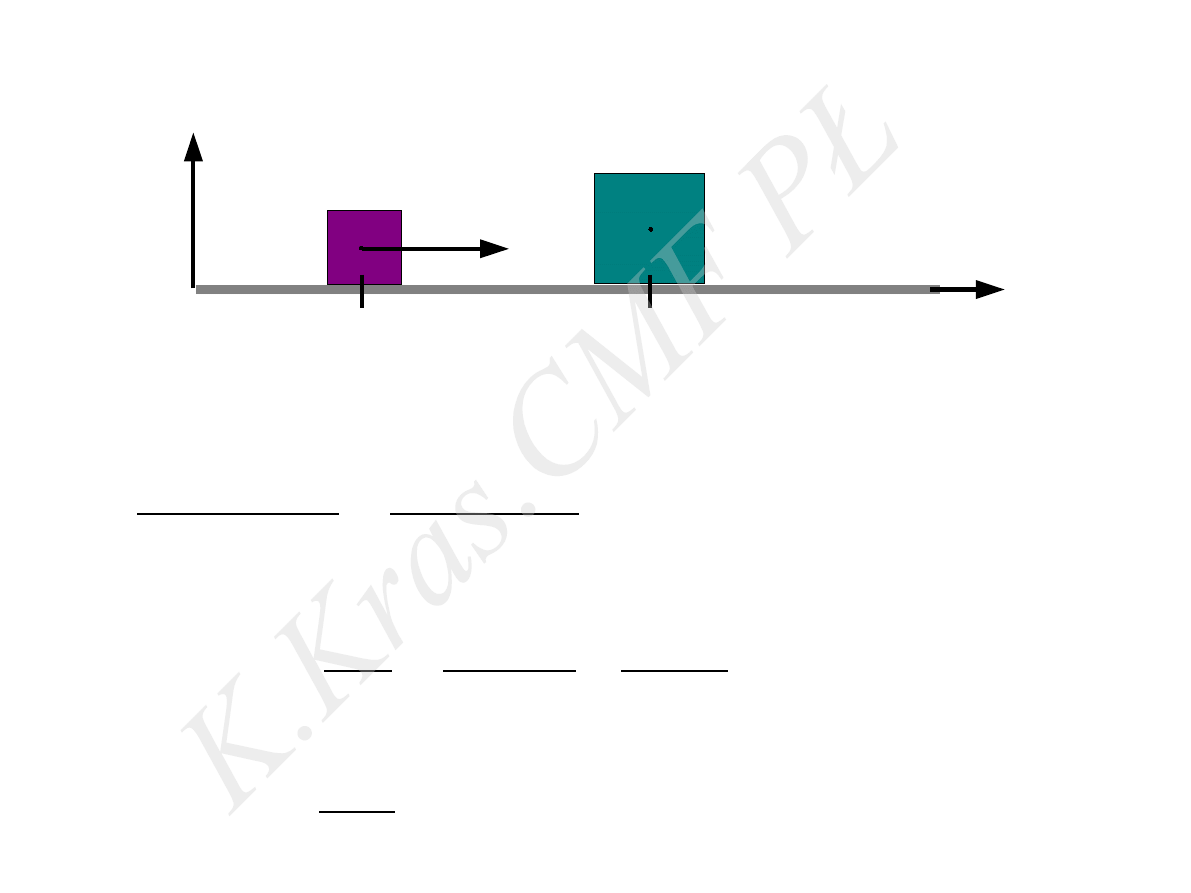
x

y

m

M

⃗

V

0

0

l

Przed zderzeniem.

x

m

=

V

0

t

x

M

=

l

x

u

=

m x

m

+

M x

M

m+M

=

m V

0

t+M l

m+M

V

u

=

d x

u

dt

=

m V

0

+

0

m+M

=

m V

0

m+M

prędkość środka masy
układu przed zderzeniem

a

u

=

d V

u

dt

=

0

przyspieszenie środka masy
układu przed zderzeniem

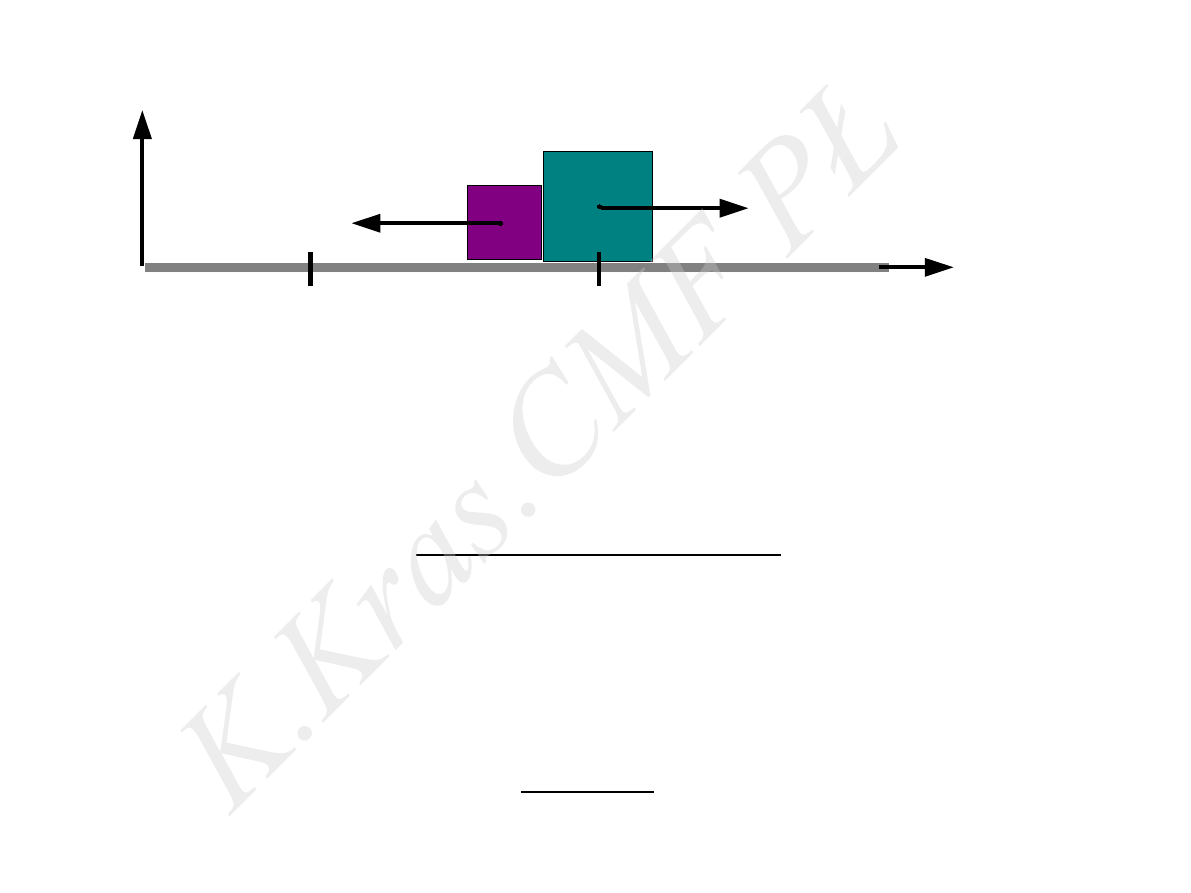
x

y

m

M

⃗

F

0

l

Zderzenie

⃗

F

τ−

czas zderzenia

m V

0

+Δ

p

m

=

m V

k

m V

0

−

F τ = m V

k

M 0+Δ p

M

=

M V

k

M 0+F τ = M V

k

m V

0

=

M 0 = m V

k

+

M V

k

= (

m+M )V

k

V

k

=

mV

0

(

m+M )

prędkość ciał po zderzeniu

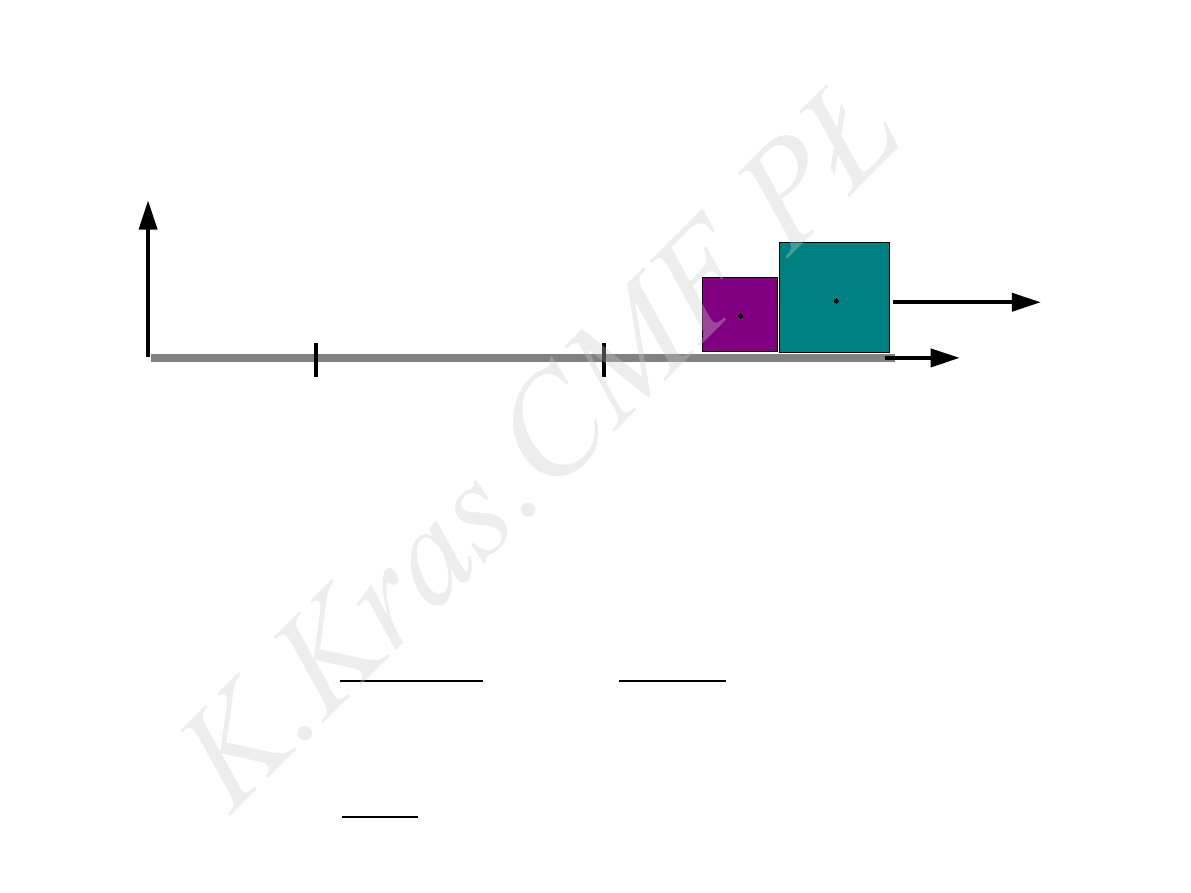
x

y

m

M

⃗

V

k

0

l

Po zderzeniu

x

m+M

=

l+V

k

t

V

u

=

d ( x

m+ M

)

dt

=

V

k

=

mV

0

m+M

prędkość środka masy
układu po zderzeniu

a

u

=

d V

u

dt

=

0

przyspieszenie środka masy
układu po zderzeniu

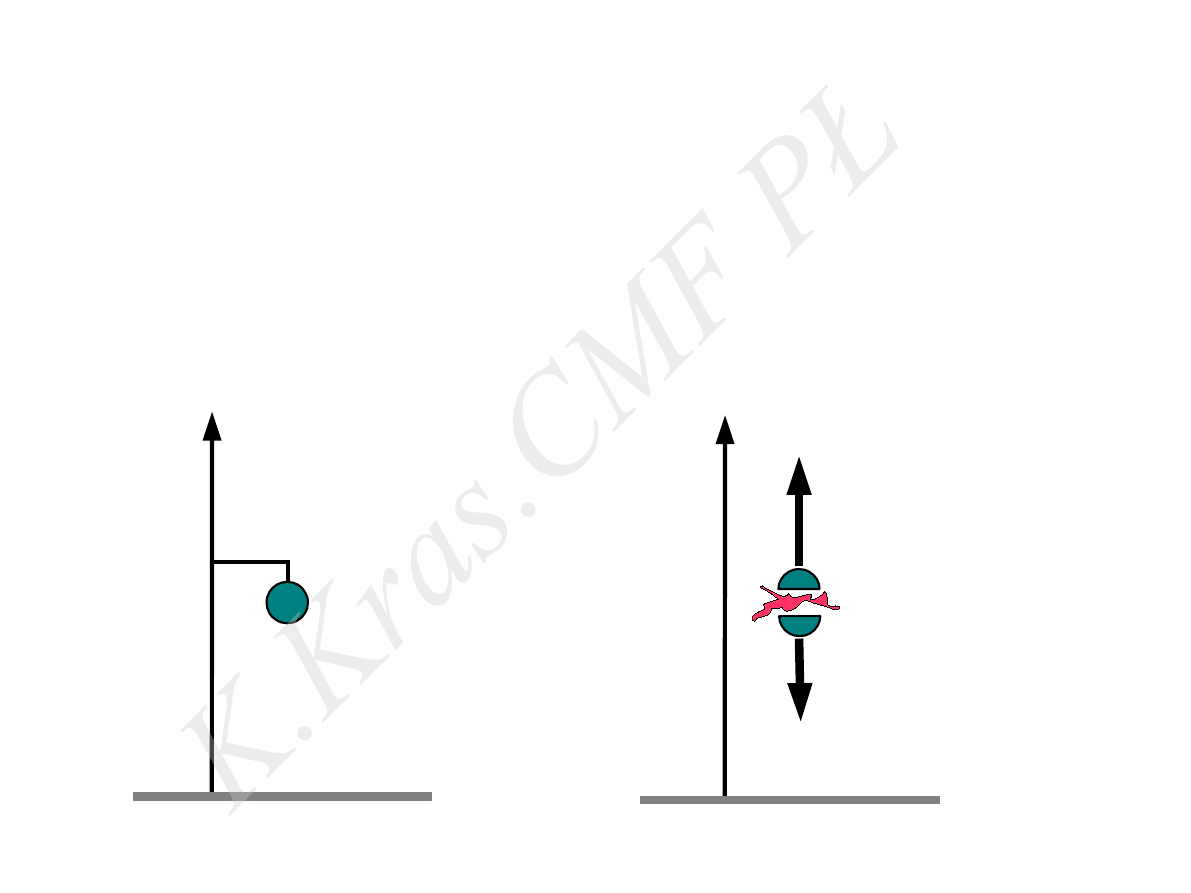
y

h

0

y

h

0

V

1

V

2

Przykład 2

.

m

1

m

2

m

1

+

m

2

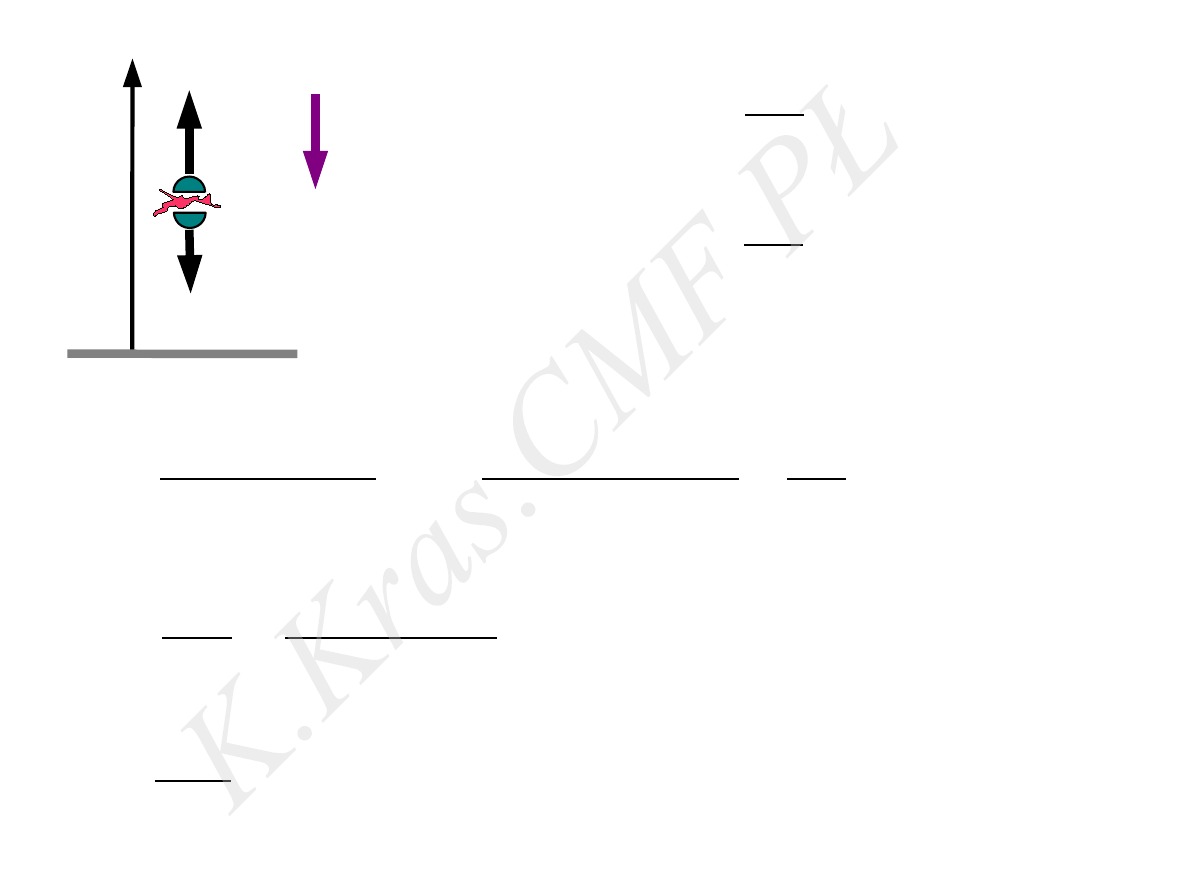
y

h

0

V

1

V

2

m

1

m

2

y

1

=

h+V

1

t−

g t

2

2

y

2

=

h−V

2

t−

g t

2

2

y

u

=

m

1

y

1

+

m

2

y

2

m

1

+

m

2

=

h+

(

m

1

V

1

−

m

2

V

2

)

t

m

1

+

m

2

−

g t

2

2

V

u

=

d y

u

dt

=

m

1

V

1

−

m

2

V

2

m

1

+

m

2

−

g t

a

u

=

d V

u

dt

= −

g

prędkość środka masy układu

przyspieszenie środka masy układu

⃗g

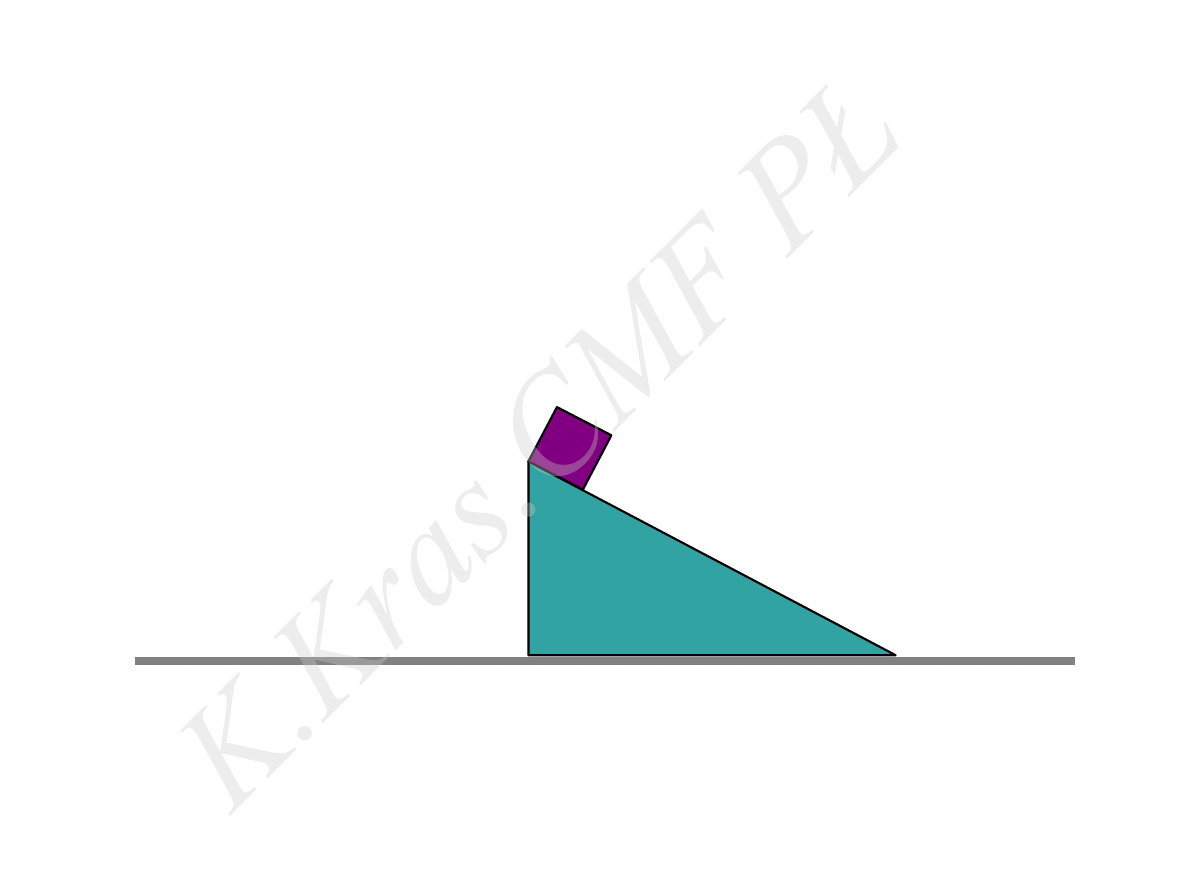
M

m

Przykład 3

.

l

⃗

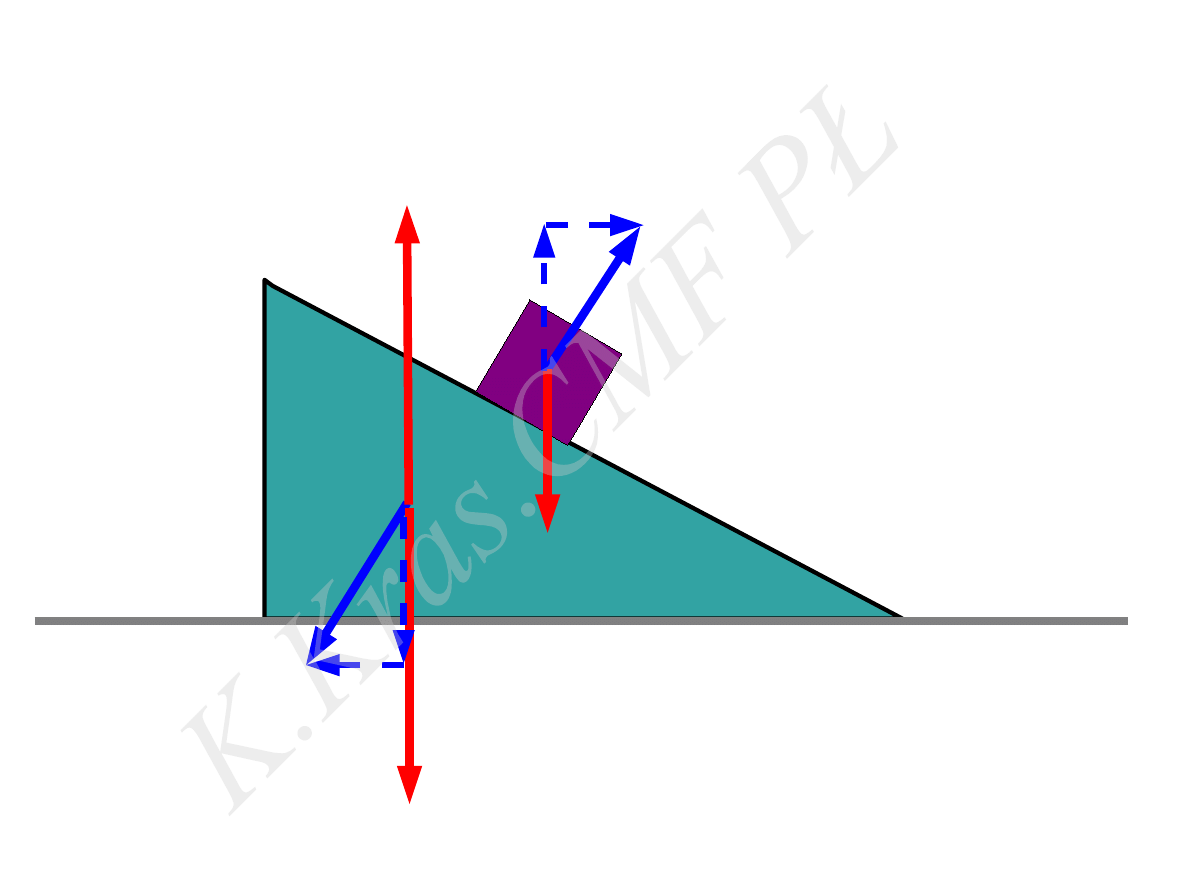
R

1

⃗

R

1

⃗

mg

⃗

R

2

⃗

Mg

siły wewnętrzne

siły zewnętrzne

układ: m i M

l

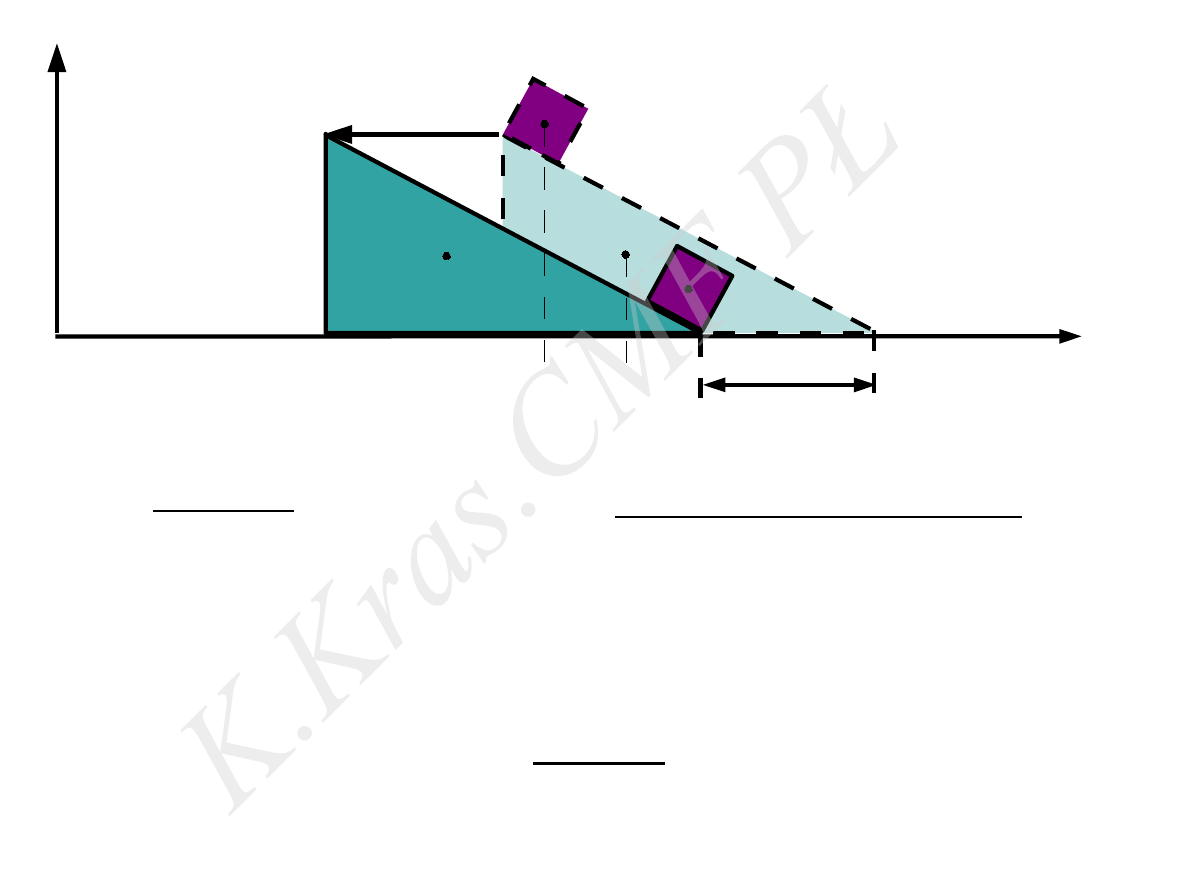
M

m

x

y

M

m

a

b

l

s

M

x

ś0

=

ma+Mb

m+M

0

x

śk

=

m(a+l−s

M

)+

M (b−s

M

)

m+M

x

ś0

=

x

śk

s

M

=

m

m+M

l

s

M

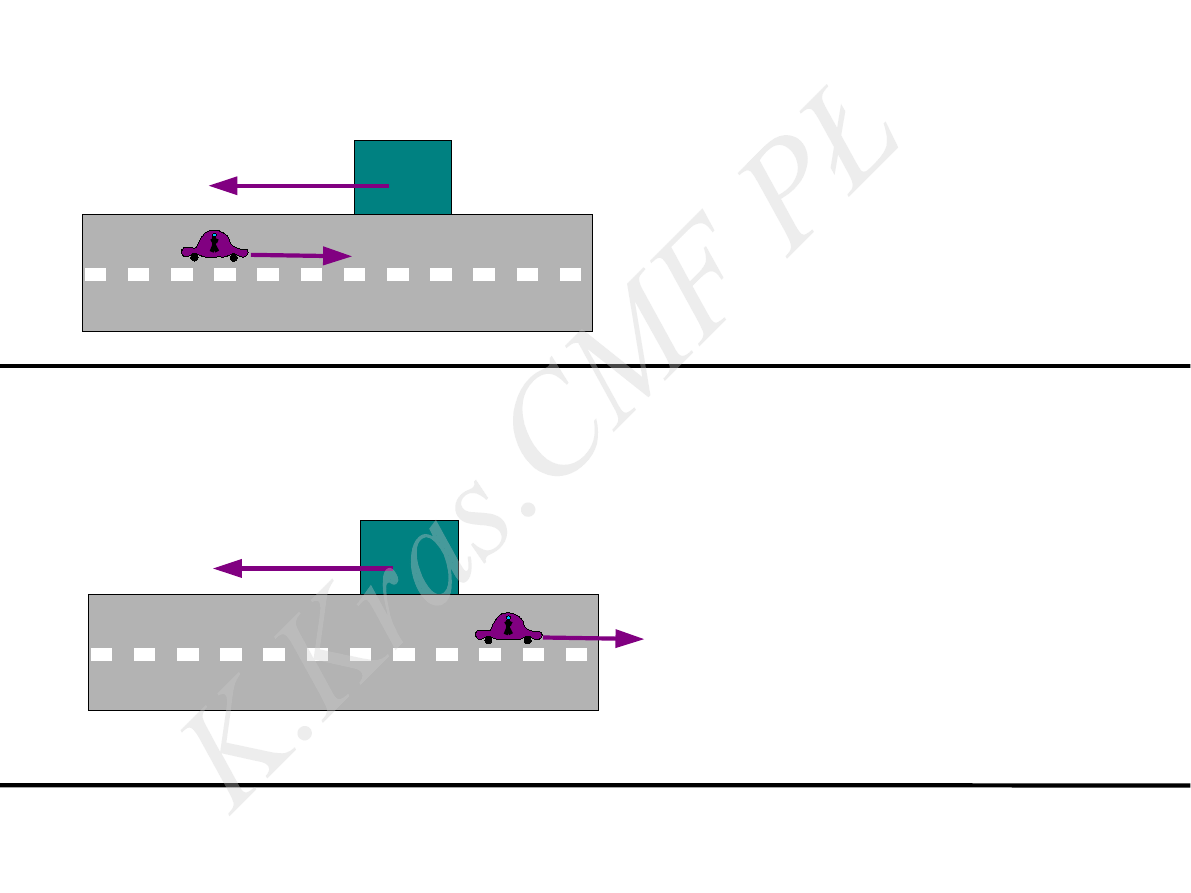
układ nieinercjalny

przyspieszenie

przyspieszenie

t =t

1

t =t

2

>

t

1

obiekt obserwowany –

dom

układ odniesienia -

samochód

siły( poziome), działające na dom –

brak

wynik obserwacji:

obiekt porusza się

z przyspieszeniem

⃗b ≠0

⃗b ≠0

I zasada dynamiki –

NIE spełniona

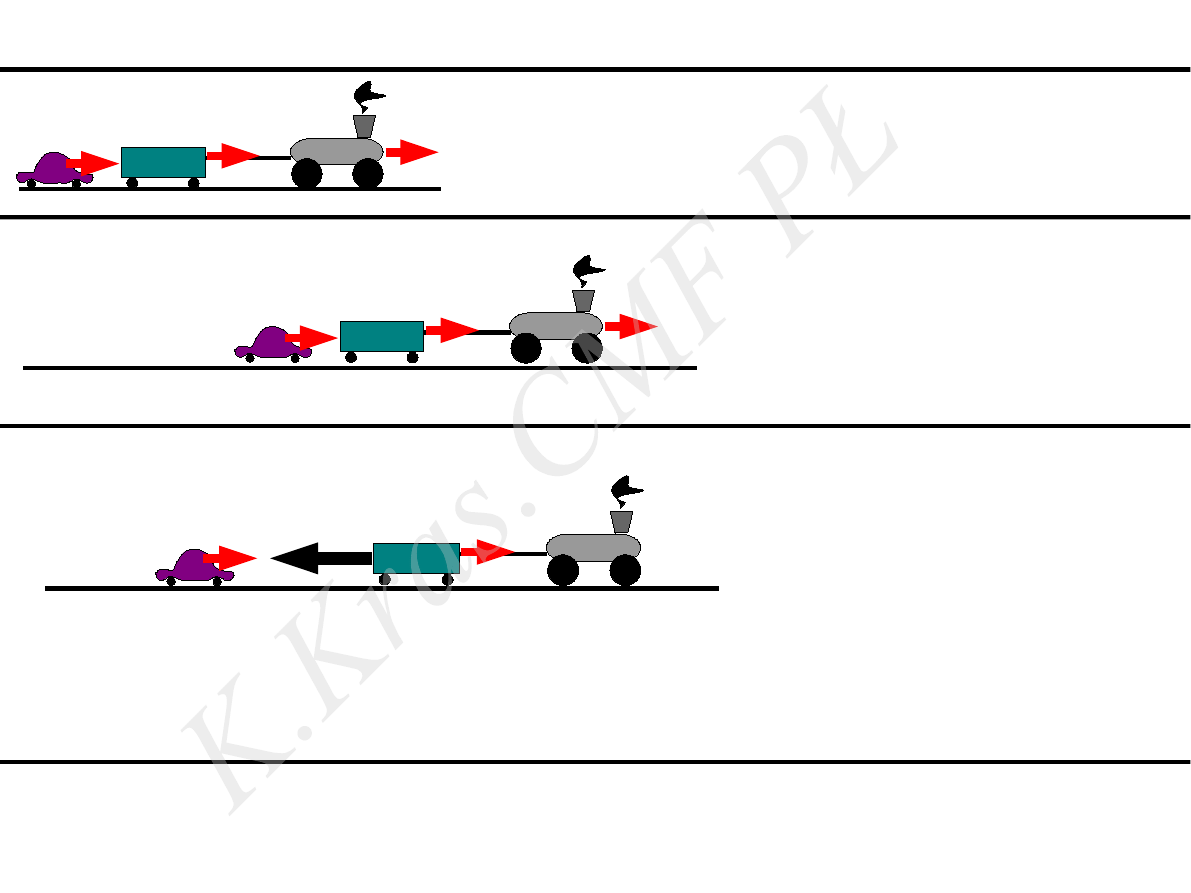
układ odniesienia -

samochód

, obiekt obserwowany -

wagon

⃗b

m

⃗b

⃗b

m

⃗b

⃗b

siła( pozioma), działająca na wagon

– działa

wynik obserwacji:

obiekt spoczywa

II zasada dynamiki –

NIE spełniona

układ nieinercjalny

⃗

F

m

⃗

B =−m ⃗b

⃗b

⃗

F

⃗

F

B - siła bezwładności

⃗

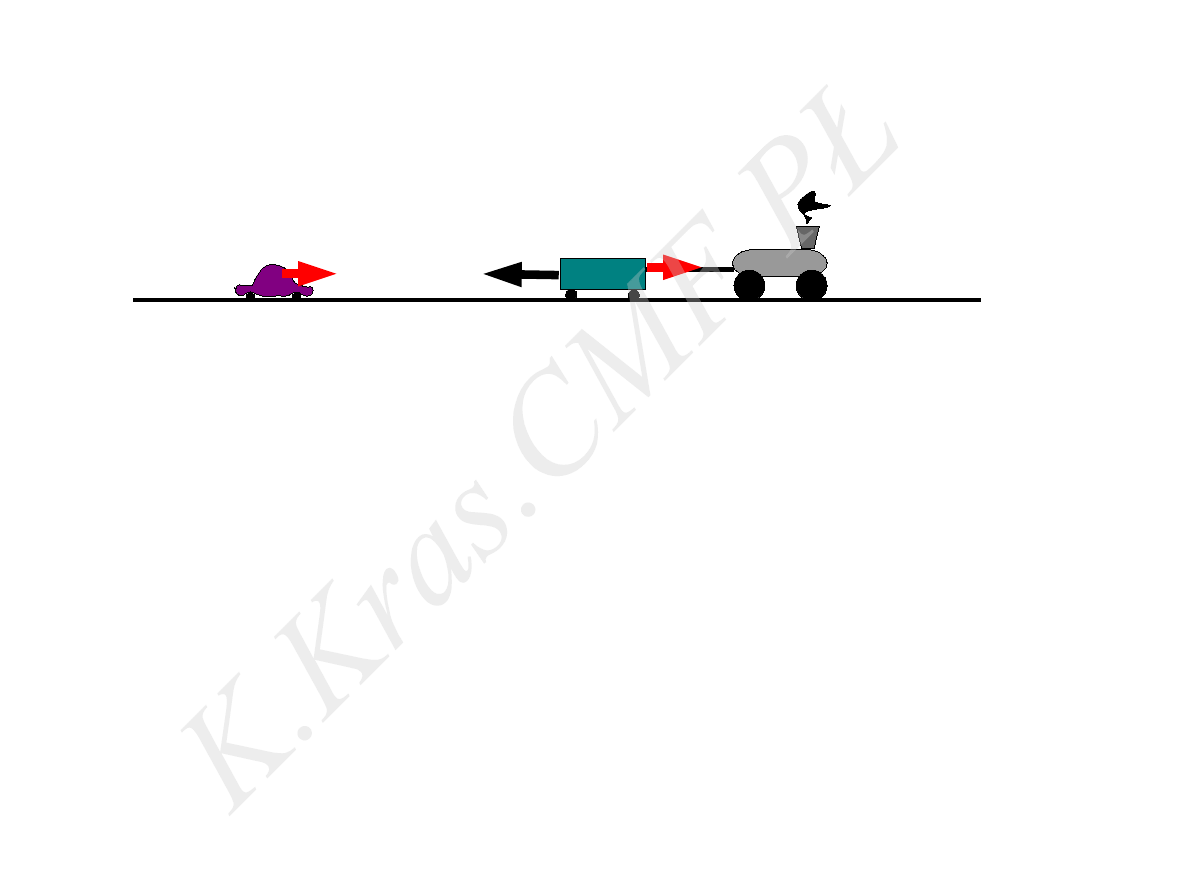
F

m

⃗

B =−m ⃗b

m⃗a = ⃗F +⃗B = 0

⃗a = 0

⃗b

⃗a = przyspieszenie wagonu wzgl. samochodu

układ nieinercjalny

m a = F −B = 0

dynamiczne równanie ruchu wagonu względem samochodu