STATYSTYKA MATEMATYCZNA

Ć

WICZENIA 3

ESTYMACJA PRZEDZIAŁOWA

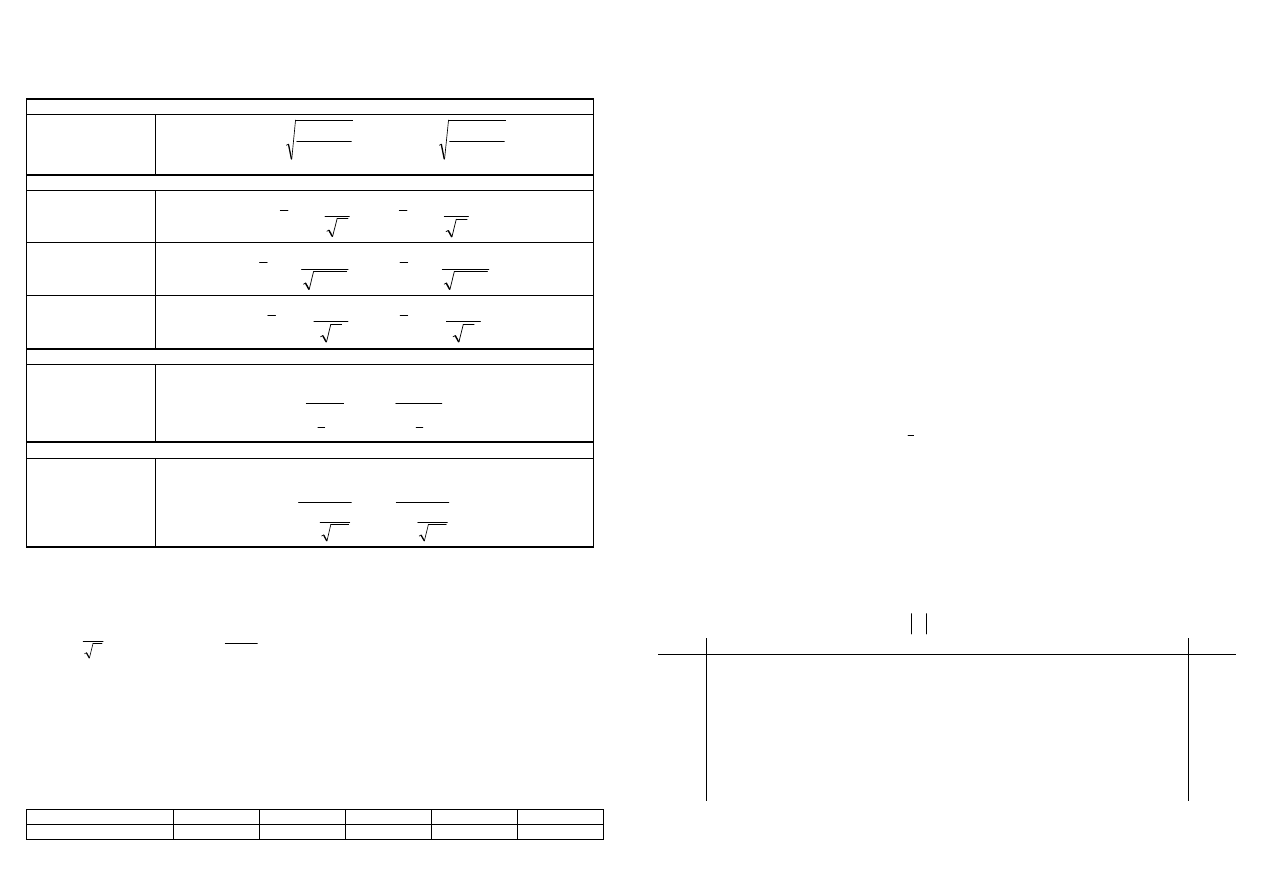
Przedział ufności dla frakcji

Rozkład Bernoulliego,
przy wnioskowaniu na

podstawie tzw. dużej

próby (n>10)













−

+

≤

≤

−

−

n

w

w

u

w

p

n

w

w

u

w

)

1

(

)

1

(

α

α

Przedział ufności dla średniej

- rozkład Normalny,

- znane σ

-liczebność dowolna













+

≤

≤

−

n

u

x

m

n

u

x

σ

σ

α

α

- rozkład Normalny,

- nieznane σ

-mała próba (n<30)













−

+

≤

≤

−

−

1

)

(

1

)

(

n

x

S

t

x

m

n

x

S

t

x

α

α

- rozkład dowolny

- nieznane σ

-mała duża (n≥30)













+

≤

≤

−

n

x

S

u

x

m

n

x

S

u

x

)

(

)

(

α

α

Przedział ufności dla wariancji

Mała próba (n<30)





















≤

≤

−

−

−

2

1

,

2

1

2

2

2

1

,

2

2

n

n

nS

nS

α

α

χ

σ

χ

Przedział ufności dla odchylenia standardowego

Duża próba (n≥30)

( )

( )























−

≤

≤

+

n

u

x

S

n

u

x

S

2

1

2

1

α

α

σ

Estymacja punktowa polega na uznaniu za wartość parametru oceny jego estymatora z próby losowej.
Ocena wielkości błędu estymatora, to odchylenie standardowe estymatora noszące nazwę średniego błędu
szacunku (estymacji) D(T

n

)

Miarą jakości wnioskowania statystycznego za pomocą wybranego estymatora jest tzw. błąd względny V(T

n

)

n

T

T

D

n

n

=

)

(

ˆ

n

n

n

T

T

D

T

V

)

(

ˆ

)

(

ˆ

=

Zadanie 1.
Spośród mieszkańców pewnego miasta wylosowano próbę losową prostą o liczebności 4000 osób i określono
wśród nich liczbę osób, które nie tylko mieszkają w tym mieście, ale również urodziły się w nim. Na postawie
próby losowej stwierdzono, że takich osób było 520.
Przyjmując współczynnik ufności 0,95 zbuduj przedział ufności dla osób mieszkających w tym mieście i w nim
urodzonych.

Zadanie 2.
Poniższy szereg rozdzielczy przedstawia strukturę 1000 losowo wybranych mieszkań na osiedlu Ursynów
w Warszawie według liczy izb.
Liczba izb w mieszkaniu

2

3

4

5

6 i więcej

Liczba mieszkań

96

288

404

168

44

Na podstawie powyższych danych:

Oszacować przedział ufności dla odsetka mieszkań 3-izbowych w populacji wszystkich mieszkań na
Ursynowie. Przyjąć współczynnik ufności na poziomie 0,90.

Zadanie 3.
W grupie 900 losowo wybranych pracowników przedsiębiorstwa, średnia liczba dni nieobecności w pracy w
1994 r. wynosiła 25, a odchylenie standardowe 3 dni.
Przyjmując współczynnik ufności na poziomie 0,90, oszacować średnią absencję w pracy wśród ogółu
pracowników.

Zadanie 4.
Na podstawie informacji o czasie przepisywania na komputerze jednej strony przez 10 losowo wybranych
maszynistek, określono, że średni czas przepisywania jednej strony wyniósł 6 minut, a odchylenie standardowe
1,5 minuty. Wiedząc, że rozkład czasu przepisywania jednej strony tekstu przez wszystkie maszynistki jest
rozkładem normalnym oraz przyjmując poziom ufności 0,90 oszacować przedział ufności dla nieznanego czasu
przepisywania na komputerze jednej strony tekstu przez wszystkie maszynistki.

Zadanie 5.
Na podstawie losowej próby 20 tabliczek czekolady otrzymano średnią wagę równą 120g. Wiedząc że rozkład
wagi wszystkich produkowanych tabliczek czekolady jest rozkładem normalnym z odchyleniem standardowym
σ

=20, oszacować przedział ufności dla średniej wagi wszystkich produkowanych tabliczek czekolady. Przyjąć

poziom ufności 0,95.

Zadanie 6.
Na podstawie losowej próby 200 tabliczek czekolady otrzymano średnią wagę równą 95 g oraz odchylenie
standardowe 10 g. Przyjmując współczynnik ufności na poziomie 0,90, oszacować przedziałowo

a)

wariancję wagi wszystkich produkowanych tabliczek czekolady.

b)

odchylenie standardowe wszystkich produkowanych tabliczek czekolady

Zadanie 7.
W celu porównania osiągniętych wyników sportowych w skoku w dal zawodnika wylosowano 8 wyników
skoków. Otrzymano następujące rezultaty:

cm

m

x

10

s

,

2

,

4

=

=

. Przyjmując współczynnik ufności 0,9

oszacować przedziałowo:

a)

nieznaną wariancję skoków w dal zawodnika.

b)

Odchylenie standardowe skoków w dal zawodnika.

Zakładamy, że rozkład skoków zawodnika jest zgodny z rozkładem normalnym.

Zadanie 8.
Ocenić przedziałowo zróżnicowanie (odchylenie standardowe) średnicy pni drzew w całym lesie. W 64-
elementowej próbie losowej prostej złożonej z pni drzew wybranych z tego lasu otrzymano średnią 37,3 cm
oraz

)

(

5

,

13

cm

s

=

. Zakładamy, że rozkład średnicy pni drzew w lesie jest zgodny z rozkładem normalnym.

Poziom ufności 0,9.

Rozkład normalny

α

α

=

≥

)

(

u

U

P

α

αα

α

0,00

0,01

0,02

0,03

0,04

0,05

0,06

0,07

0,08

0,09

α

αα

α

0,0

∝

2,576

2,326

2,170

2,054

1,960

1,881

1,812

1,751

1,695

0,0

0,1

1,644

1,598

1,555

1,514

1,476

1,440

1,405

1,372

1,341

1,311

0,1

0,2

1,281

1,254

1,227

1,200

1,175

1,150

1,126

1,103

1,080

1,058

0,2

0,3

1,036

1,015

0,994

0,974

0,954

0,935

0,915

0,896

0,878

0,860

0,3

0,4

0,842

0,324

0,806

0,789

0,772

0,755

0,739

0,722

0,706

0,690

0,4

0,5

0,674

0,659

0,643

0,628

0,613

0,598

0,583

0,568

0,553

0,539

0,5

0,6

0,524

0,510

0,496

0,482

0,468

0,454

0,440

0,426

0,412

0,400

0,6

0,7

0,385

0,372

0,358

0,345

0,332

0,319

0,305

0,292

0,279

0,266

0,7

0,8

0,253

0,240

0,228

0,215

0,202

0,189

0,176

0,164

0,151

0,138

0,8

0,9

0,126

0,113

0,100

0,088

0,075

0,063

0,050

0,038

0,025

0,013

0,9