Pomiar lepkości cieczy

1

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

Ćwiczenie 2

POMIAR LEPKOŚCI CIECZY

2.1. Wprowadzenie

Cieczą lepką nazywany płyn, który charakteryzuje się następującymi własnościami:

- jest nieściśliwy,
- przewodzi ciepło,
- przynajmniej jedna ze składowych niediagonalnych t

ij

/i

¹j/ tensora naprężeń jest różna od zera.

Z kursu mechaniki płynów wiadomo, że składowe niediagonalne tensora naprężeń

przedstawiają naprężenia styczne. Wynika stąd, że: lepkością /tarciem wewnętrznym/

nazywamy zdolność cieczy do przenoszenia naprężeń stycznych w czasie rucha względnego

sąsiednich warstw cieczy.

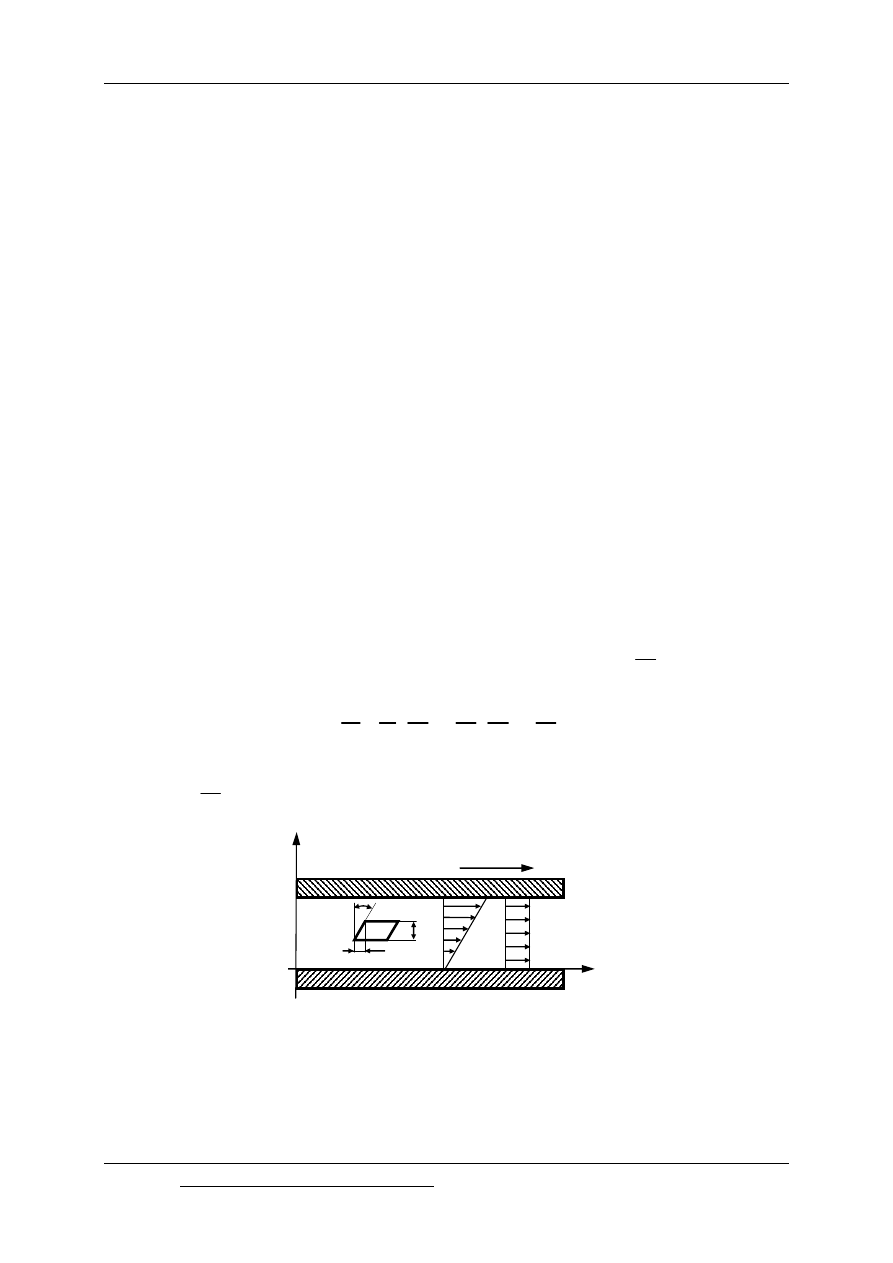
Zależność naprężeń stycznych, w jednowymiarowym przepływie, od prędkości

odkształcenia podaje prawo tarcia wewnętrznego Newtona (hipoteza Newtona), zgodnie

z którą naprężenie styczne

t jest proporcjonalne do gradientu prędkości

dv
dy

lub do prędkości

odkształcenia postaciowego

d

d dx

d dx

dv

dt

dt dy

dy dt

dy

æ

ö

g

æ

ö

g =

»

=

=

ç

÷

ç

÷

è

ø

è

ø

&

. Zatem

dv
dy

t = h

= h× g

&

(2.1)

y

x

v

v(y)

t(y)

dy

g

dx

Rys. 2.1. Rozkład prędkości i naprężeń stycznych w jednowymiarowym przepływie płynu

Współczynnik proporcjonalności

h jest miarą lepkości i nazywa się dynamicznym,

współczynnikiem lepkości. Ciecze, w których naprężenia styczne opisane są z dostateczną

dokładnością za pomocą prawa tarcia wewnętrznego Newtona, nazywamy cieczami

newtonowskimi.

2

Pomiar lepkości cieczy

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

Dalsze rozważania dotyczyć będą wyłącznie lepkości cieczy newtonowskich.

Lepkość cieczy newtonowskich jest funkcją ciśnienia i temperatury. Wzrost ciśnienia

w cieczy powoduje wzrost jej lepkości, ale jest on znaczący dopiero przy ciśnieniach

większych od 10

7

[N/m

2

], natomiast ze wzrostem temperatury lepkość cieczy maleje.

Zależność lepkości cieczy od ciśnienia i temperatury można przedstawić za pomocą wzoru:

(

)

(

)

0

0

exp

p

t t

h = h ×

a × D - b -

(2.2)

gdzie:

h

0

- lepkość w temperaturze t

0

przy ciśnieniu atmosferycznym,

a - piezometryczny współczynnik lepkości,

Dp - przyrost ciśnienia,

b - termiczny współczynnik lepkości,

t - temperatura cieczy.

Współczynnik

a i b można łatwo wyliczyć na podstawie danych tabelarycznych lub

znaleźć ich wartości w monografiach specjalistycznych.

2.1.1. Jednostki dynamicznego współczynnika lepkości

1)

w układzie SI

[ ]

2

N s

1

m

×

é

ù

h = ê

ú

ë

û

2)

w układzie CGS

[

] [ ]

1

2

g

N s

1 Poise

1 P

1

10

cm s

m

-

×

é

ù

é

ù

=

=

=

ê

ú

ê

ú

×

ë

û

ë

û

Jednostka pochodna:

[

] [ ]

[ ]

2

3

2

N s

1 centi Poise

1 cP

10

P

10

m

-

-

×

é

ù

=

=

=

ê

ú

ë

û

2.1.2. Kinematyczny współczynnik lepkości

W dynamice płynów znaczną rolę odgrywa współczynnik będący ilorazem

dynamicznego współczynnika lepkości

h i gęstości płynu r. Tę nową wielkość:

h

n =

r

(2.3)

nazywa się kinematycznym współczynnikiem lepkości cieczy.

Pomiar lepkości cieczy

3

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

Jednostki kinematycznego współczynnika lepkości:

1)

w układzie SI:

[ ]

2

m

1

s

é

ù

n = ê ú

ë

û

2)

w układzie CGS:

[

] [ ]

2

2

4

cm

m

1 Stokes

1 St

1

10

s

s

-

é

ù

é

ù

=

=

=

ê

ú

ê

ú

ë

û

ë

û

Jednostka pochodna:

[

] [ ]

[ ]

2

2

6

m

1 centiStokes

1 cSt

10

St

10

s

-

-

é

ù

=

=

=

ê

ú

ë

û

2.1.3. Skale lepkości względnej

W przemyśle i handlu często stosuje się następujące skale tzw. lepkości względnej:

a) skala Englera /stosowana w Europie/,

b) skala Redwooda /używana w Wielkiej Brytanii/,

c) skala Saybolta /stosowana w USA/.

Skala Englera

Lepkość w stopniach Englera [

°E] wylicza się za stosunku czasu wypływu 200 [cm

3

]

badanej cieczy w dowolnie ustalonej temperaturze z wiskozymetru Englera do czasu

wypływu 200 [cm

3

] wody destylowanej w temperaturze 20 [°C].

Skala Redwooda Admiliraty

Mierzymy czas /w sekundach/ wypływu 50 [cm

3

] płynu o temperaturze 32 [°F] (0 [

°C])

z wiskozymetru Redwooda. Lepkość wyrażamy w sekundach uniwersalnych Redwooda /RA/.

Skala Saybolta

Mierzymy czas (w sekundach) wypływu 60 [cm

3

] płynu badanego w temperaturze 60

[°F] (15.5 [°C]). Lepkość wyraża się w sekundach uniwersalnych Saybolta /SSU/.

Kinematyczny współczynnik lepkości można w przybliżeniu wyrazić ze skali lepkości

względnej za pomocą wzoru empirycznego:

2

B

cm

A t

t

s

é

ù

n = × -

ê

ú

ë

û

gdzie:

A i B - stałe odpowiadające danemu typowi wiskozymetru,

t - czas wypływu w [s] z danego wiskozymetru.

4

Pomiar lepkości cieczy

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

Tablica 2.1. Stałe A i B odpowiadające danemu typowi wiskozymetru

Typ wiskozymetru

A

B

Saybolta uniwersalny

0.0022

1.80

Redwooda

0.0026

1.72

Redwooda Admirality

0.0270

20.00

Englera

0.00147

3.74

2.2. Przyrządy do pomiaru lepkości /wiskozymetry, lepkościomierze/

2.2.1. Wiskozymetry, których zasada działania oparta jest na wykorzystaniu prawa

Hagena-Poiseuille’a
W ruchu laminarnym cieczy odbywającym się w prostoosiowym przewodzie

o przekroju kołowym natężenie przepływu jest wprost proporcjonalne do spadku ciśnienia

i czwartej potęgi średnicy przewodu, a odwrotnie proporcjonalne do dynamicznego

współczynnika lepkości i długości przewodu. Powyższe stanowi treść prawa Hagena-

Poiseuille’a, które można zapisać w postaci:

4

4

p d

p d

Q

128

L 128

L

p× D ×

p× D ×

=

=

×h×

×n×r×

(2.4)

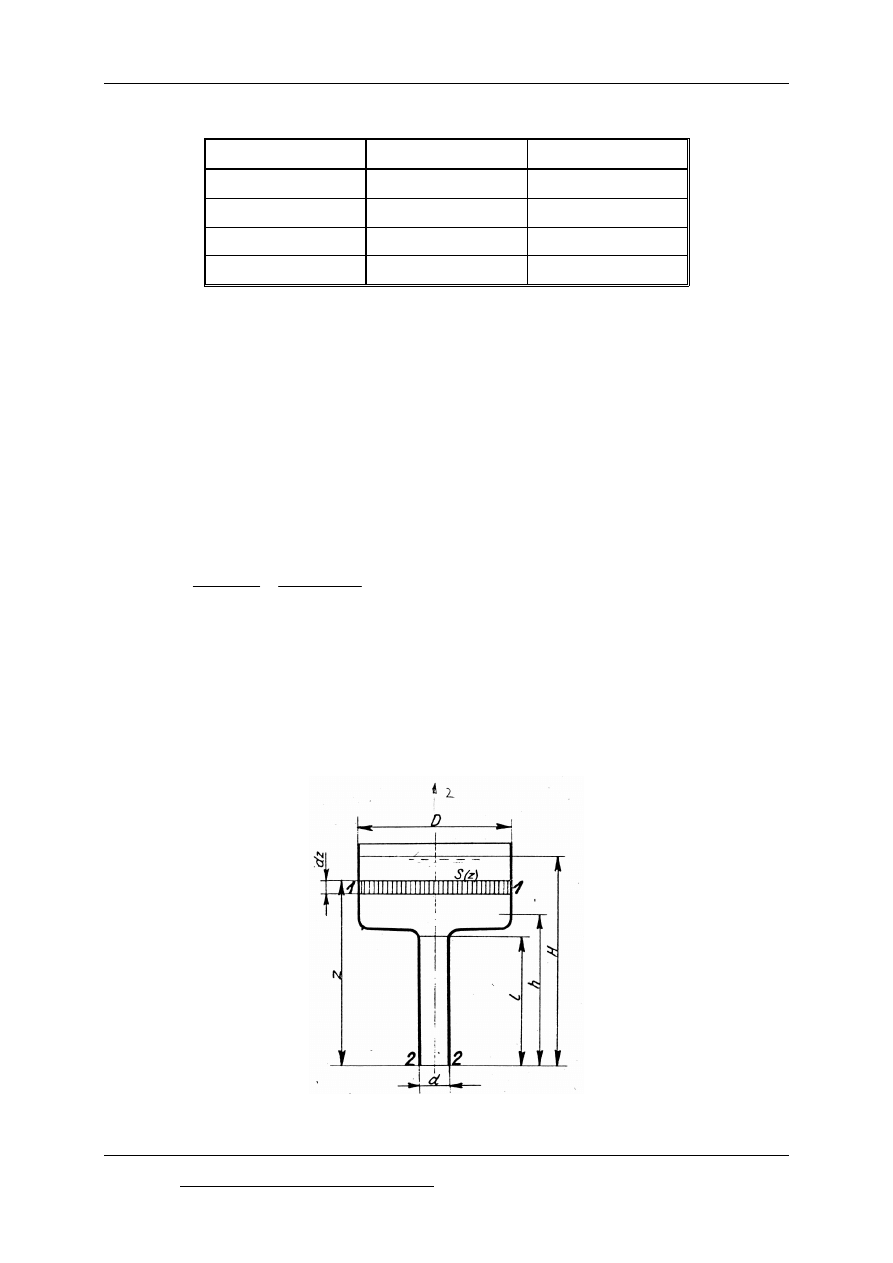
Załóżmy, że wiskozymetr składa się z naczynia w kształcie walca o średnicy D,

połączonego w środku dna z pionową kapilarą o długości L i średnicy d (rys.2.1). Brzegi

połączenia są zaokrąglone. Będziemy poszukiwać zależności między kinematycznym

współczynnikiem lepkości a czasem, po upływie którego poziom cieczy opadnie z wysokości

H do wysokości h.

Rys. 2.2 Schemat wiskozymetru, którego zasada działania oparta jest na wykorzystaniu prawa
Hagena-Poiseuille’a

Pomiar lepkości cieczy

5

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

Równanie ciągłości dla przekrojów 1-1 i 2-2 ma postać:

2

2

D

d

dz

v dt

4

4

p×

p×

-

= m ×

× ×

gdzież

m - współczynnik poprawkowy natężenia wypływu,

v - średnia prędkość przepływu.

Przekształcając równanie ciągłości otrzymujemy:

2

2

D

dz

dt

d v

= -

m ×

Założymy, że ruch cieczy w kapilarze jest laminarny. Średnia prędkość przepływu

cieczy w ruchu laminarnym wynika z prawa Hagena-Poiseuille’a i wynosi:

2

2

4 Q

p d

v

d

32

L

×

D ×

=

=

p×

×n ×r×

Ponieważ nad zwierciadłem cieczy panuje ciśnienie atmosferyczne, a ciecz wypływa

do atmosfery, różnica ciśnień równa jest ciśnieniu hydrostatycznemu:

p

g z

D = r× ×

Ostatecznie średnia prędkość przepływu laminarnego w kapilarze wyniesie:

2

g d z

v

32

L

r× × ×

=

×n ×r×

Podstawiając wzór na v do przekształconego równania ciągłości, mamy:

2

4

32

L D dz

dt

g d

z

×n × ×

= -

m × ×

Całkując powyższe równanie oraz zamieniając granice całkowania, otrzymamy:

h

H

2

2

4

4

H

h

32

L D

dz

32

L D

H

t

dt

ln

g d

z

g d

h

- ×n × ×

×n × ×

=

=

=

m × ×

m × ×

ò

ò

Ostatecznie kinematyczny współczynnik lepkości jest równy:

4

2

g d

t

H

32 L D ln

h

m × ×

n =

×

× ×

×

(2.5)

Ponieważ w znanych konstrukcjach wiskozymetrów wielkości: d, L, D, H, i h są

ustalonymi parametrami konstrukcyjnymi, zatem można napisać:

2

m

C t

s

é

ù

n = ×

ê

ú

ë

û

(2.6)

6

Pomiar lepkości cieczy

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

gdzie:

C – oznacza stałą wiskozymetru

4

2

2

2

g d

m

C

H

s

32 L D ln

h

é

ù

m × ×

=

ê

ú

ë

û

× ×

×

(2.7)

Przytoczone wyżej rozważania są obarczone błędem wynikającym z pominięcia strat

energii na wejściu i wyjściu z kapilary oraz strat energii wynikających z tarcia cieczy o ściany

naczynia wypływowego.

W oparciu o powyższą zasadę działają wiskozymetry: Englera, Saybolta, Redwooda,

Parmena, Vogel-Ossaga Pinkiewicza, Wolarowicza oraz Ubbelohdego.

Poniżej przedstawiono budowę i sposób pomiaru lepkości za pomocą wiskozymetru

Ubbelohdego.

Wiskozymetr Ubbelohdego, z wiszącym meniskiem, składa się z kompletu kapilar

i metalowej oprawy. Kapilary wykonane są z bezbarwnego, jednorodnego, wolnego od skaz

i zgrubień szkła kwarcowego. Kapilary powinny być odprężone. Przy pomiarach seryjnych

należy stosować kapilary o takich średnicach, aby czas wypływu badanej cieczy wynosił co

najmniej 120 [s], a przy wzorcowaniu kapilar - co najmniej 200 [s]. Górna granica dla czasu

wypływu nie jest normowana, ze względów praktycznych jednak nie powinna przekraczać

1500 [s]. Najczęściej używane kapilary podano w tablicy 2.2.

Tablica 2.2. Najczęściej używane kapilary

Numer

kapilary

Wewnętrzna średnica

kapilary [mm]

Zakres lepkości

[cSt]

Czas wypływu [s]

Stała C kapilary

1

0.63

±0.02

1,2

¸15

12O

¸1500

0.01

1A

0.95

±0.03

6

¸75

120

¸1500

0.05

2

1.10

±0.03

12

¸150

120

¸1500

0.10

3

1.96

¸0.04

120

¸1500

120

¸1500

1.00

4

3.58

¸0.08

1200

¸15000

120

¸1500

10.00

Uwaga: Wartości podane w tablicy 2.2 należy traktować wyłącznie jako orientacyjne.

Wzorcowanie kapilar [PN/C-04013]

Kapilara nr 1

Zmierzyć czas wypływu wody destylowanej z badanej kapilary w lepkościomierzu

Ubbelohdego w temperaturze 20 i 37,8 [°C]. Obliczyć stałą B z zależności:

Pomiar lepkości cieczy

7

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

(

)

1

2

2

1

1 2

2

2

2

1

t t

B

t

t

t

t

×

=

n × - n

-

(2.8)

gdzie:

t

1

- czas wypływu wody w temperaturze 20 [

°C] w [s],

t

2

- czas wypływu wody w temperaturze 37,8 [

°C] w [s],

n

1

- kinematyczny współczynnik lepkości wody w temperaturze 20[°C],

n

1

= 1.007 [cSt],

n

2

- kinematyczny współczynnik lepkości wody w temperaturze 37,8 [

°C], n

2

= 0,689 [cSt].

Stałą C obliczyć według wzoru:

1

1

1

B
t

C

t

n +

=

Po podstawieniu (2.8) wzór przyjmie postać:

2

2

1 1

2

2

2

1

t

t

C

t

t

n × - n

=

-

(2.9)

Kapilary nr 1A, 2, 3, 4

Dla tych kapilar stała B = 2.8. Zmierzyć czas wypływu oleju wzorcowego z badanej

kapilary. Olej wzorcowy (dostarczany przez Główny Urząd Miar) należy dobrać tak, aby jego

czas wypływu wynosił co najmniej 200 [s].

Stałą C należy obliczyć z zależności:

w

B

t

C

t

n +

=

gdzie:

n

w

- kinematyczny współczynnik lepkości oleju wzorcowego [cSt],

t - czas wypływu oleju wzorcowego [s].

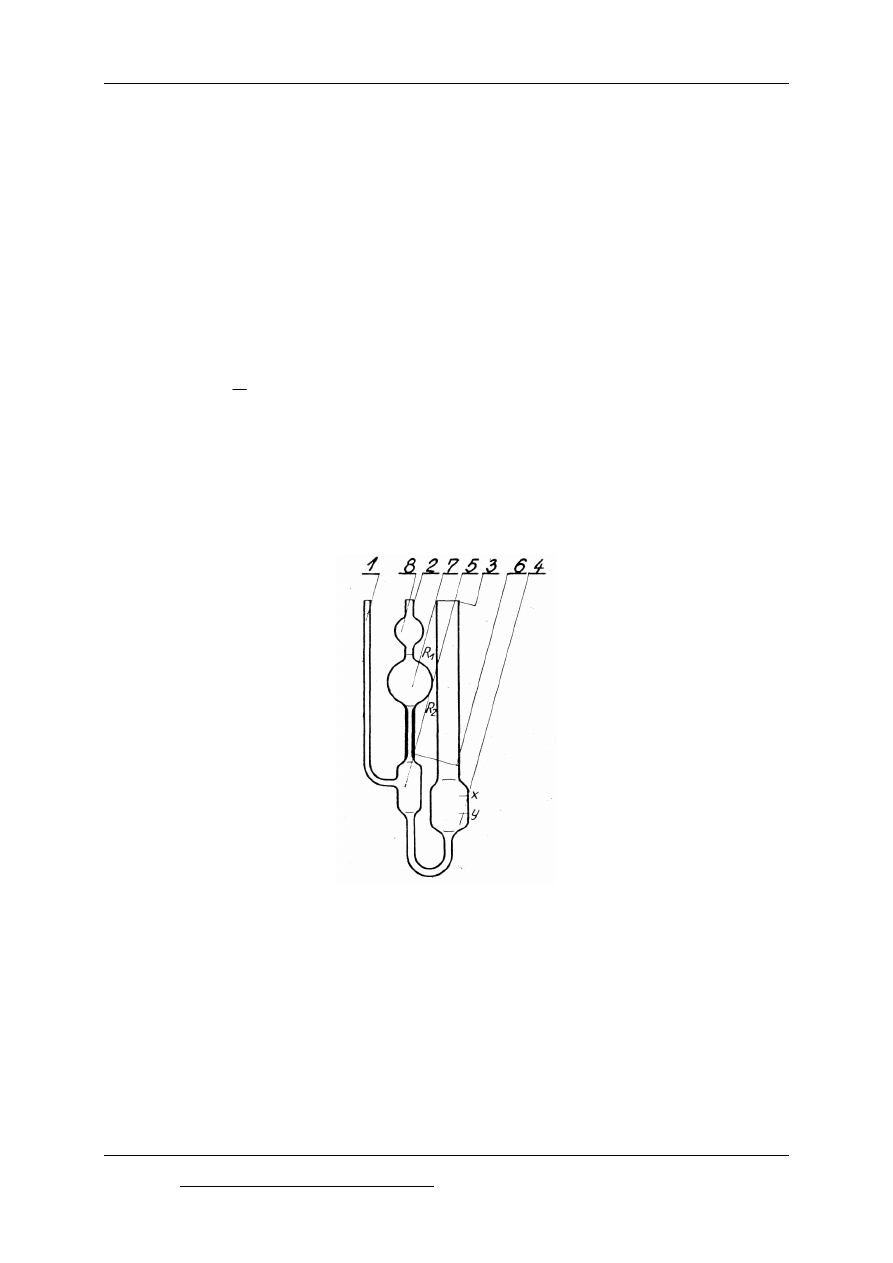
Opis pomiaru (rys. 2. 2)

Kapilarę (6) wymyć benzenem lub benzyną, a następnie eterem etylowym lub

naftowym i wysuszyć w suszarce. Do rurki (3) przyrządu wlać po przesączeniu badaną ciecz

tak, aby poziom cieczy znajdował się pomiędzy kreskami x i y rozszerzenia (4). Umieścić

przyrząd w obudowie metalowej i włożyć do ultratermostatu. Po 20 minutach wyjąć

wiskozymetr i umieścić w statywie. Zamknąć szczelnie rurkę (1) i wciągnąć ciecz przez

zassanie do rurki (2) ponad górną kreskę R

1

, najwyżej jednak do połowy rozszerzenia (8).

Należy przy tym uważać, aby nie powstały przy zasysaniu pęcherzyki powietrza w cieczy.

8

Pomiar lepkości cieczy

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

Następnie rurkę (1) połączyć z atmosferą i zmierzyć stoperem czas przepływu cieczy o

objętości zawartej między górną kreską R

1

a dolną R

2

rozszerzenia (7) kapilary, przy czym za

poziom cieczy przyjmujemy dolny menisk. W przypadku wytworzenia się w rozszerzeniu (5)

piany należy usunąć ją przez łagodne stukanie w rurkę 1, a pomiar trzeba powtórzyć.

Jeżeli czas wypływu jest krótszy niż 120 [s], należy wybrać kapilarę o niższej stałej C,

a sam pomiar powtórzyć. Kinematyczny współczynnik lepkości w temperaturze pomiaru

oblicza się według wzoru:

- przy wzorcowaniu kapilar i pomiarach rozjemczych:

B

C t

t

n = × +

- przy pomiarach seryjnych, oraz gdy n ³ 20 [cSt], z zależności:

C t

n = ×

Przeprowadza się z reguły dwa pomiary (różnica pomiędzy nimi nie powinna przekraczać

0.2 %), a za wynik ostateczny należy przyjąć średnią arytmetyczną.

Rys. 2.3 Wiskozymetr Ubbelohdego, z wiszącym meniskiem

2.2.2. Wiskozymetry, których zasada działania oparta jest na wykorzystaniu wzoru Stokesa

Jedną z uproszczonych, zlinearyzowanych form równania Naviera-Stokesa

zaproponował Stokes w następującej postaci:

( )

( )

2

grad p

v

= h×Ñ r

(2.10)

Wyszedł on z założenia, że dla przypadku powolnego ruchu ciała w cieczy o dużej

lepkości (małe liczby Reynoldsa), siły wywołane lepkością są znacznie większe niż siły

Pomiar lepkości cieczy

9

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

bezwładności, wobec czego te ostatnie można pominąć. Ponadto założono, że:

r = const.,

h = const. oraz ruch jest ustalony. Równanie (2.10) wraz z równaniem ciągłości, w układzie

współrzędnych kartezjańskich, stanowi układ zamknięty, ponieważ zawiera on cztery

równania i cztery funkcje niewiadome (p, v

x

, v

y

, v

z

).

Rozwiązując ten układ równań dla przypadku opływu kuli strumieniem jednorodnym

płynu, w nieskończoności, określił Stokes pole prędkości i ciśnień, a na tej podstawie

otrzymał wzór na opór kuli:

P 6

v R

¥

= × p×h×

×

(2.11)

zwany wzorem Stokesa. Wzór (2.11) uzależnia siłę oporu P od dynamicznego współczynnika

lepkości cieczy

h , prędkości opadania kuli v

¥

i jej promienia R.

Grupa wiskozymetrów, w których elementem roboczym jest opadająca kula, znajduje

coraz szersze zastosowanie. Na powyższej zasadzie działają wiskozymetry Gardnera

i Höpplera.

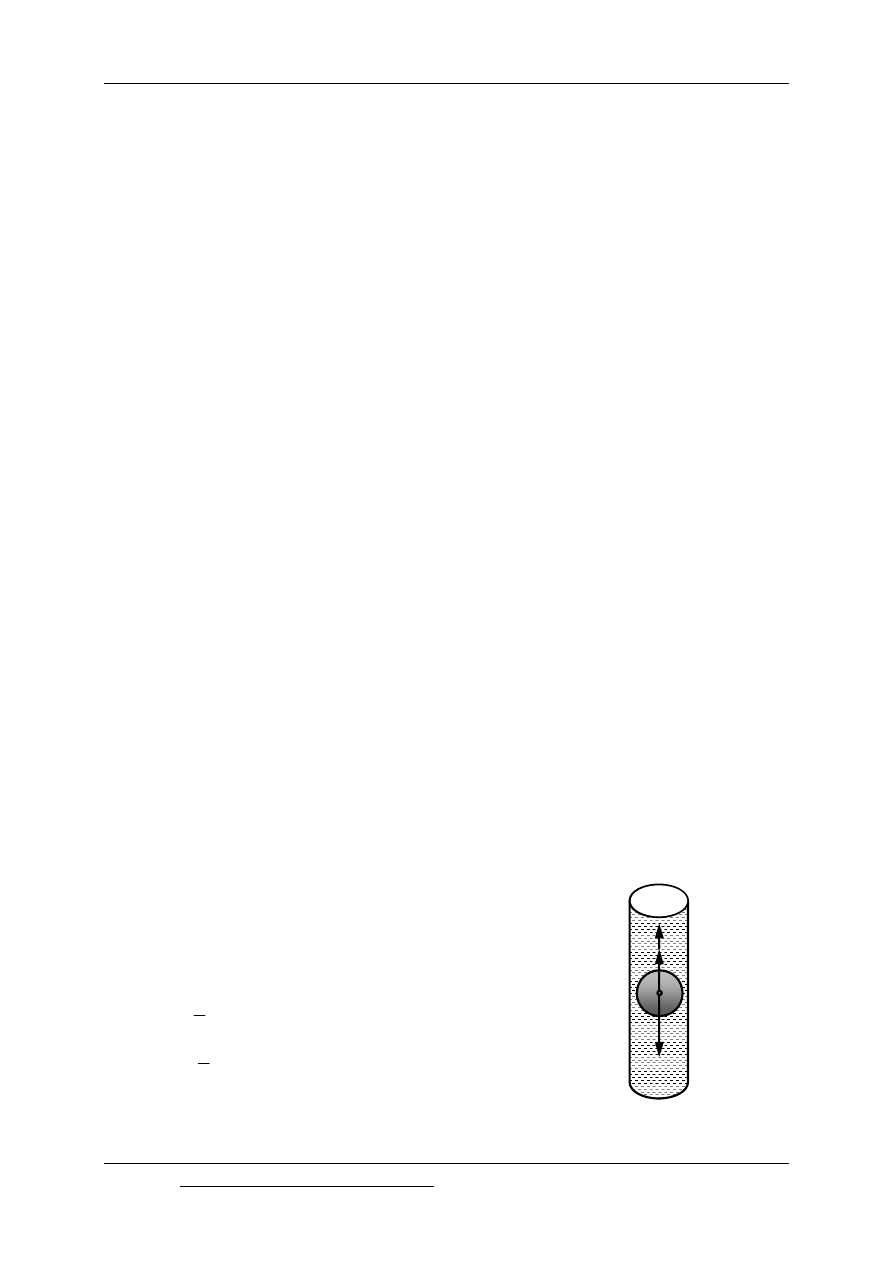
Przystępując do analizy sił działających na opadającą w cieczy kulkę, należy pamiętać,

że wzór Stokesa obowiązuje w przypadku, gdy obszar cieczy otaczającej kulkę jest

nieograniczony, ruch jest laminarny (Re≤0,3) i ustalony. W konsekwencji należy zachować

następujące warunki:

- kulka powinna być gładka, mieć prawidłową budowę, poruszać się w dostatecznej

odległości od dna i ścian naczynia,

- ciecz powinna być jednorodna, uboczne ruchy cieczy /konwekcja, ruch pęcherzyków

gazu/ nie są dopuszczalne,

- pomiędzy kulką i cieczą nie może występować poślizg.

Na kulkę opadającą jednostajnie w cieczy oprócz siły oporu działają jeszcze siła ciężkości

G i siła wyporu hydrostatycznego W. Wynika stąd warunek /siły działające mają ten sam

kierunek/ równowagi:

G W P 0

-

- =

gdzie:

3

k

3

c

4

G

R

g

3

4

W

R

g

3

P 6

v R

= × p×

×r ×

= × p×

×r ×

= × p×h× ×

G

W

P

Rys. 2.4 Siły działające na kulę

swobodnie opadającą w płynie

10

Pomiar lepkości cieczy

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

Po podstawieniu i przekształceniach otrzymuje się wzór pozwalający na obliczenie

dynamicznego współczynnika lepkości:

(

)

2

k

c

2 R

g

9 v

×

× r - r ×

h =

×

Wyrażając prędkość opadania kulki v za pomocą ilorazu drogi opadania s i czasu

opadania t, otrzymujemy:

(

)

(

)

2

k

c

k

c

2 R g

t C

t

9 s

×

×

h =

r - r × = × r - r ×

×

gdzie:

C – stała wiskozymetru

2

2 R g

C

9 s

×

×

=

×

Biorąc pod uwagę fakt, ze obszar płynu w wiskozymetrze typu Höpplera jest

ograniczony, kula doznaje rotacji, a rura spadowa jest pochylona /

a = 15°/ wprowadza się

dodatkowo współczynnik poprawkowy k

1

. Wytwórnie wiskozymetrów podają wartości

stałych dla kul stosowanych w danym rozwiązaniu, przy czym stała dla kuli jest równa

K = k

1

·C. Ostatecznie wartość dynamicznego współczynnika lepkości cieczy /badanego za

pomocą wiskozymetru Höpplera/ obliczamy ze wzoru:

(

)

k

c

K

t

h = × r - r ×

(2.12)

gdzie:

K - stała wiskozymetru [m

2

/s

2

],

r

k

- gęstość materiału kulki [kg/m

3

],

r

c

-.gęstość cieczy [kg/m

3

],

t - czas opadania kulki [s].

W przypadku, gdy wytwórnia nie podała wartości stałej kulki lub też istnieje

podejrzenie, że kulka nie pochodzi z danego kompletu, należy wyznaczyć wartość stałej, za

pomocą pomiaru lepkości oleju wzorcowego. Czynność ta jest niezbędna w przypadku

pomiarów rozjemczych. Wiskozymetr Höpplera pozwala na pomiar lepkości w zakresie

h = 6·10

-4

¸80 [N·s/m

2

], dla przedziału temperatur cieczy - 60

¸150 [°C]. Błąd pomiaru waha

się w granicach ±0.5

¸2 % mierzonej wartości.

Poniżej omówimy budowę i metodykę pomiaru lepkości przy zastosowaniu

wiskozymetru Höpplera.

Pomiar lepkości cieczy

11

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

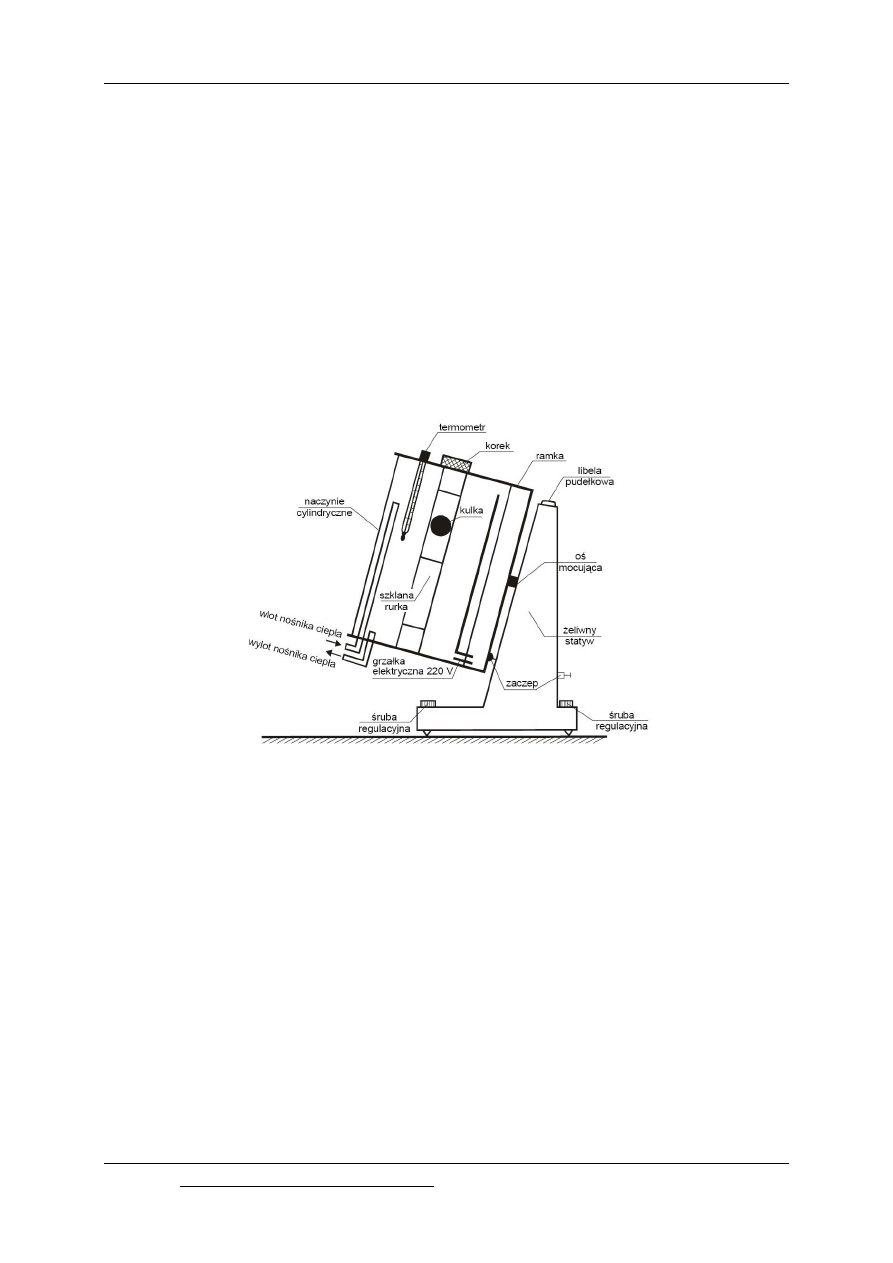
Przed przystąpieniem do pomiaru należy sprawdzić ustawienie poziomicy przyrządu.

Ciecz dokładnie przefiltrować. Napełnić rurę spadową badaną cieczą, około 25 [mm] poniżej

jej górnej krawędzi. Następnie pincetką włożyć odpowiednią kulkę tak, by nie tworzyły się na

jej powierzchni pęcherzyki powietrza (a gdyby powstały, to przez wciśnięcia pałeczką

szklaną usunąć je). Zamknięcie rury spadowej dokonuje się za pomocą wydrążonego czopu;

lekko naciskając go nakręca się pokrywę. Czopów gumowych używa się do wody i benzyny,

a do cieczy rozpuszczających gumę stosuje się czopy metalowe.

Połączyć wiskozymetr z ultratermostatem. Przyrząd jest przygotowany do pomiaru. Czas

opadania kulki pomiędzy kreskami zaznaczonymi na rurze spadowej mierzymy sekundomierzem.

Wykonać trzy pomiary i obliczyć średni czas opadania jako średnią arytmetyczną.

Rys. 2.5 Wiskozymetr Höpplera

2.2.3. Wiskozymetry ultradźwiękowe

W środowisku o dużej lepkości amplituda drgań swobodnych ciała stopniowo

zmniejsza się i to tym bardziej, im większy jest opór wewnętrzny.

Mierząc współczynnik tłumienia fali ultradźwiękowej można wnioskować o lepkości cieczy.

Na tej zasadzie oparta jest budowa większości wiskozymetrów ultradźwiękowych.

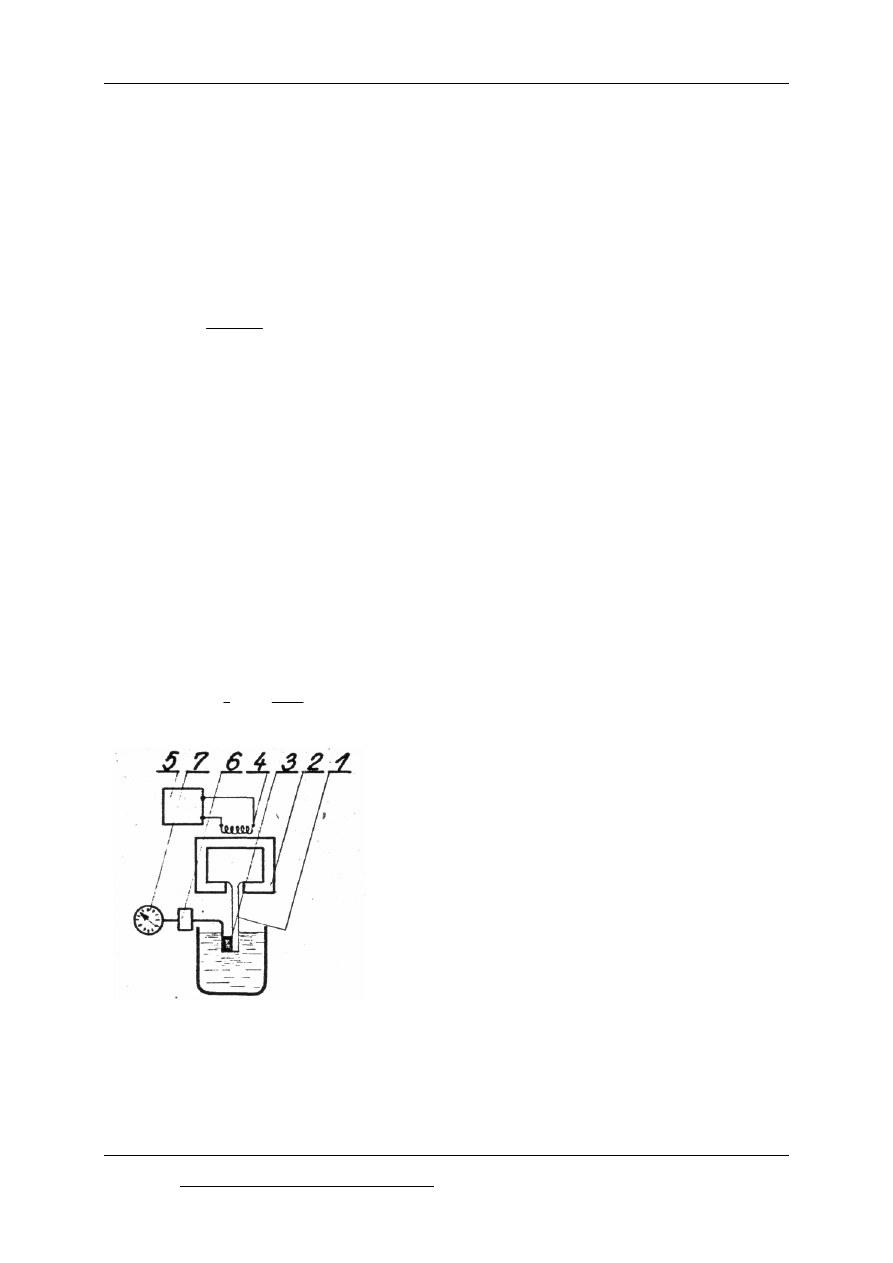
Zasada działania:

Na drgającym końcu twornika 1 elektromagnesu zasilanego z generatora wysokiej

częstotliwości (5) zamocowany jest element piezoelektryczny (3) sporządzony z kwarcowej

lub tytanowo-barowej płytki o średnicy 4

¸5 [mm]. Razem z twornikiem drga również płytka

z częstotliwością 400

¸700 [Hz], w wyniku czego na jej powierzchni tworzy się zmienne

napięcie. Im większą jest lepkość cieczy, tym bardziej zmniejsza się amplituda drgań płytki,

12

Pomiar lepkości cieczy

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

co z kolei wywołuje odkształcenie elementu piezoelektrycznego, a w następstwie tego

i zmianę wartości napięcia między jej płaszczyznami. Tą zmianę napięcia po wzmocnieniu

mierzy się za pomocą przyrządu pomiarowego, którego skala może być wzorcowana

w jednostkach lepkości.

Zależność dynamicznego współczynnika lepkości od tłumienia /absorpcji/ fali

ultradźwiękowej została przedstawiona wzorem:

3

2

2

a

K

f

a ×r×

h =

p ×

gdzie:

h - dynamiczny współczynnik lepkości,

K - stała zależna od przyjętego układu jednostek,

a - współczynnik tłumienia fali ultradźwiękowej,

r - gęstość cieczy,

f - częstotliwość drgań płytki piezoelektrycznej,

a - prędkość rozchodzenia się fali ultradźwiękowej.

Wiskozymetry ultradźwiękowe mogą być wykorzystane do ciągłego pomiaru lepkości

cieczy bezpośrednio w liniach technologicznych. Zakres pomiarowy tych wiskozymetrów

wynosi:

4

2

2

N s

10 : 10

m

-

×

é

ù

h =

ê

ú

ë

û

Rys. 2.6 Schemat wiskozymetru ultradźwiękowego:

1 - twornik elektromagnesu, 2 -rdzeń elektromagnesu,

3 -płytka piezoelektryczna, 4 – uzwojenie wzbudzenia

elektromagnesu, 5 – generator wysokiej częstotliwości,

6 – wzmacniacz, 7 – przyrząd pomiarowy

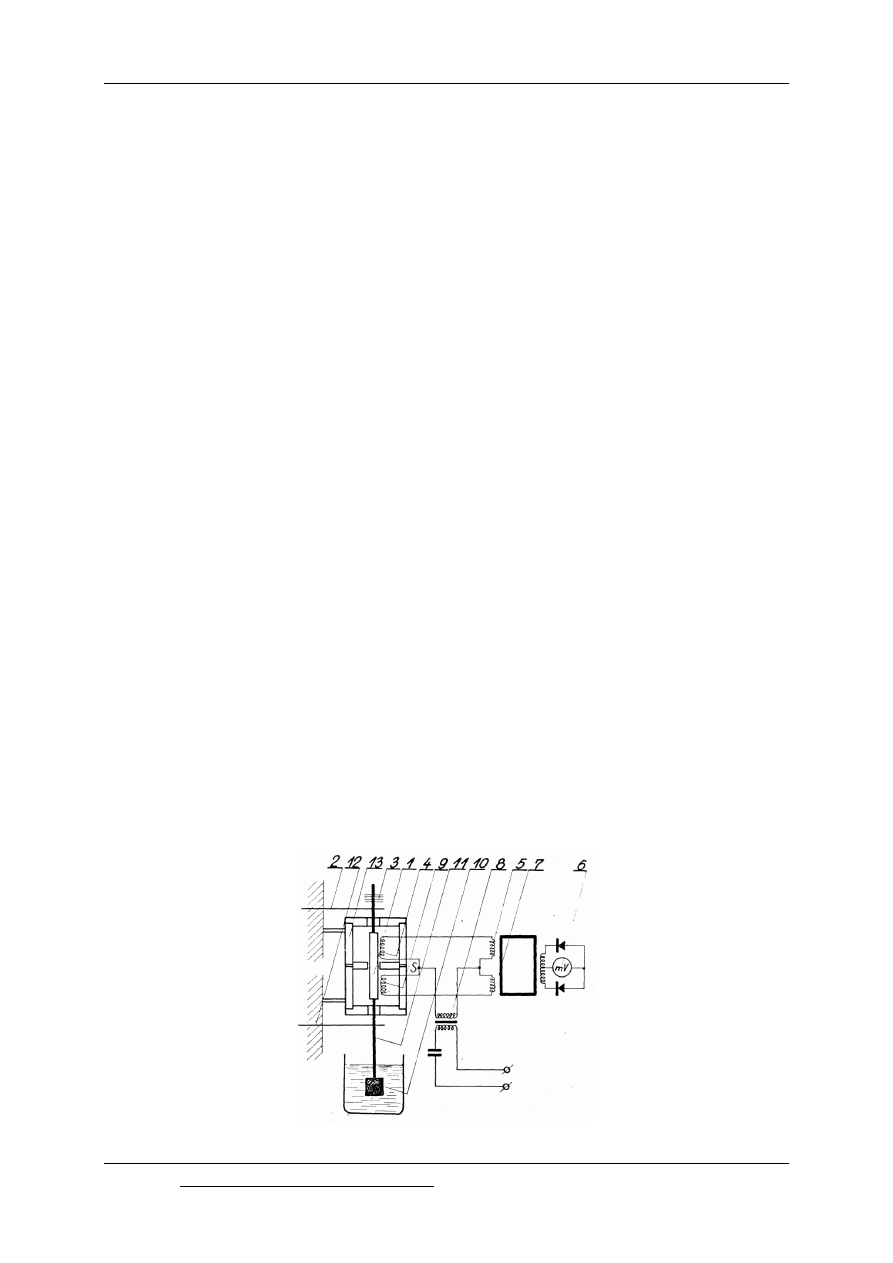
2.2.4. Wiskozymetry wibracyjne

W wiskozymetrach wibracyjnych miarą lepkości jest czas niezbędny do odpowiedniego

zmniejszenia amplitudy wahań czujnika pomiarowego, zanurzonego w badanej cieczy. Na

rys.2.6 przedstawiono schemat elektrycznego wiskozymetru wibracyjnego. Do rdzenia (1)

Pomiar lepkości cieczy

13

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

wykonanego z miękkiej stali i umocowanego na taśmach (2) i (12) za pomocą trzpienia (11)

przymocowana jest nasadka (l0). Materiał nasadki zależny jest od własności cieczy i jej

temperatury. Rdzeń umieszczony jest w układzie elektromagnetycznym, składającym się ze

stałego magnesu (13) i cewek (4) i (9) o jednakowej charakterystyce. Cewki te połączone są w

ten sposób, ze wytwarzane przez nie strumienie magnetyczne sumują się. Przy przepływie

prądu zmiennego przez cewki powstaje zmienne pole magnetyczne, które współdziała z polem

stałym magnesów i daje okresową siłę działającą na rdzeń. Jeżeli prąd w cewkach będzie tak

skierowany, że namagnesowany nim rdzeń ma biegun północny N w górze, a południowy S na

dole, to rdzeń współdziałając z magnesem będzie przesuwać się w dół. Po zmianie kierunku

prądu w cewkach rdzeń przemieszczać się będzie do góry. Jak widać, rdzeń, a razem z nim

nasadka będą wykonywać ruchy drgające. Największa czułość i najmniejszy błąd przyrządu

wystąpią wówczas, gdy częstotliwość własna drgań ruchomych części wiskozymetru będzie

równa częstotliwości zakłócającej siły.

Tę równość osiąga się przez odpowiedni dobór masy rdzenia (1), nasadki (l0),

sztywności sprężynujących taśm. Masę ruchomych części przyrządu reguluje się nakrętkami

(3). Amplituda drgań wymuszonych zalety od wielkości strat energii wibrujących ruchomych

części przyrządu przy stałości wszystkich. innych warunków. Te straty zależne są od lepkości

cieczy odkształcenia sprężystych taśm i od sił tarcia o powietrze. Dwie ostatnie wielkości

strat w określonych warunkach są stosunkowo małe i dlatego można określić lepkość cieczy

na podstawie wielkości amplitudy wahań rdzenia. Wartość amplitudy drgań rdzenia

przekształca się w proporcjonalną do niej wartość natężenia lub napięcia prądu, które

wskazuje miliwoltomierz (6). Osiąga się to za pomocą cewek (4) i (9), które mają jednakową

liczbę zwojów i są zasilane ze stabilizatora napięcia przez zwoje transformatora różnicowego

(5) i (7). Przyrząd wzorcuje się cieczami o znanej lepkości.

Rys. 2.7. Schemat elektrycznego wiskozymetru wibracyjnego

14

Pomiar lepkości cieczy

download: http://www.mech.pk.edu.pl/~m52/pdf/[2_opis].pdf

2.3. Opis ćwiczenia

W ćwiczeniu należy przeprowadzić pomiar lepkości cieczy za pomocą wiskozymetru

Höpplera i Ubbelohdego, zgodnie z wytycznymi, podanymi w p. 2.2.1. i 2.2.2. instrukcji. Przy

pomiarze lepkości cieczy za pomocą wiskozymetru Ubbelohdego należy zmierzyć co

najmniej dwukrotnie czas wypływu cieczy i obliczyć czas średni wypływu z dwóch

pomiarów, dla których różnica wartości jest mniejsza niż 0.2 %. Obliczyć kinematyczny

współczynnik lepkości badanej cieczy oraz dynamiczny współczynnik lepkości. Wyniki

przedstawić w jednostkach SI.

Przy pomiarze lepkości cieczy za pomocą wiskozymetru Höpplera zmierzyć

trzykrotnie czas opadania kulki pomiędzy dwiema skrajnymi kreskami i do obliczeń przyjąć

ich średnią arytmetyczną. Obliczyć dynamiczny współczynnik lepkości; wynik przedstawić

w jednostkach układu SI.

2.4. Literatura

[1] Considine D. M., Boss D. S.: Handbook of Applied Instrumentation. Mc Graw-Hill, New

York 1964.

[2] Prosnak W. J.: Mechanika płynów. T.I. PWN, Warszawa 1970.

[3] Carr A., Parrent D., Pecki S.: Chem. lng. Progr. Ser. 51/91/, 1955.

[4] Bennett C. O., Myers J. E.: Przenoszenie pędu, ciepła i masy. WNT, Warszawa 1967.