Z. Kąkol-Notatki do Wykładu z Fizyki
24-1
Wykład 24
24. Drgania elektromagnetyczne
24.1 Wstęp
Przypomnienie: masa M na sprężynie, bez oporów. Równanie ruchu
kx
t
x
M
−
=
2
2
d
d
Rozwiązania
x = Acos
ωt
v
= dx/dt = A
ωsinωt
a = d
2
x/dt
2
= – A
ω
2
cos
ωt
przy warunku
ω = (k/M)
1/2
.
24.2 Obwód LC
Rozpatrzmy obwód złożony z szeregowo połączonych indukcyjności L i pojemności
C. Opór omowy jest równy zeru (R = 0). Załóżmy, że w chwili początkowej na
kondensatorze C jest nagromadzony ładunek q
m
, a prąd przez cewkę jest równy zeru.
Energia zawarta w kondensatorze
W
C
= q
m
2
/(2C)
(24.1)
jest maksymalna, a energia w cewce
W
L
= LI
2
/2
(24.2)
jest równa zeru.
Po zamknięciu obwodu, kondensator rozładowuje się przez cewkę. W obwodzie płynie
prąd I = dq/dt. W miarę jak maleje ładunek na kondensatorze maleje też energia zawarta
w polu elektrycznym kondensatora, a rośnie energia pola magnetycznego, które pojawia
się w cewce w miarę narastania w niej prądu.
Wreszcie gdy ładunek spadnie do zera cała energia jest przekazana do pola
magnetycznego cewki. Prąd w cewce indukcyjnej ma maksymalną wartość. Ten prąd
ładuje kondensator (przeciwnie) więc energia jest ponownie przekazywana do
kondensatora. Stan końcowy jest taki jak początkowy tylko kondensator jest
naładowany odwrotnie. Sytuacja powtarza się. Mamy więc do czynienia z oscylacjami
ładunku (prądu).
Z. Kąkol-Notatki do Wykładu z Fizyki
24-2
Opis ilościowy
Z prawa Kirchoffa
U
L
+ U
C
= 0
0
d
d
=
+
C
q
t
I
L
(24.3)
Ponieważ I = dq/dt więc
C
q
t
q
L
−
=
2
2
d
d
(24.4)
To jest równanie analogiczne do przypomnianego równania dla sprężyny, przy czym
następujące wielkości są analogiczne
q
↔ x, L ↔ M, 1/C ↔ k
Tak więc możemy napisać rozwiązanie tego równania
q = q
m
cos
ωt
I = dq/dt = q
m
ωsinωt = I
m
sin
ωt
ω = (1/LC)
1/2
(24.5)
gdzie I
m
= q
m
ω
U
L
= - LdI/dt = – LI
m
ωcosωt
U
C
= q/c = (q
m
/C)cos
ωt
Ponieważ
LI
m
ω = Lq
m
ω
2
= Lq
m
(1/LC) = q
m
/C
widać, że
amplitudy napięć są takie same
.
24.3 Obwód szeregowy RLC
Dotychczas rozważaliśmy obwód zwierający indukcyjność L oraz pojemność C.
Tymczasem każdy obwód ma pewien opór R, przykładowo jest to opór drutu z którego
nawinięto cewkę. Obecność oporu w obwodzie powoduje straty energii w postaci
wydzielającego się ciepła. Energia zawarta w obwodzie maleje i otrzymujemy drgania
tłumione analogiczne do drgań tłumionych sprężyny opisanych w wykładzie 12, przy
czym współczynnik tłumienia 1/2
τ jest równy R/2L.
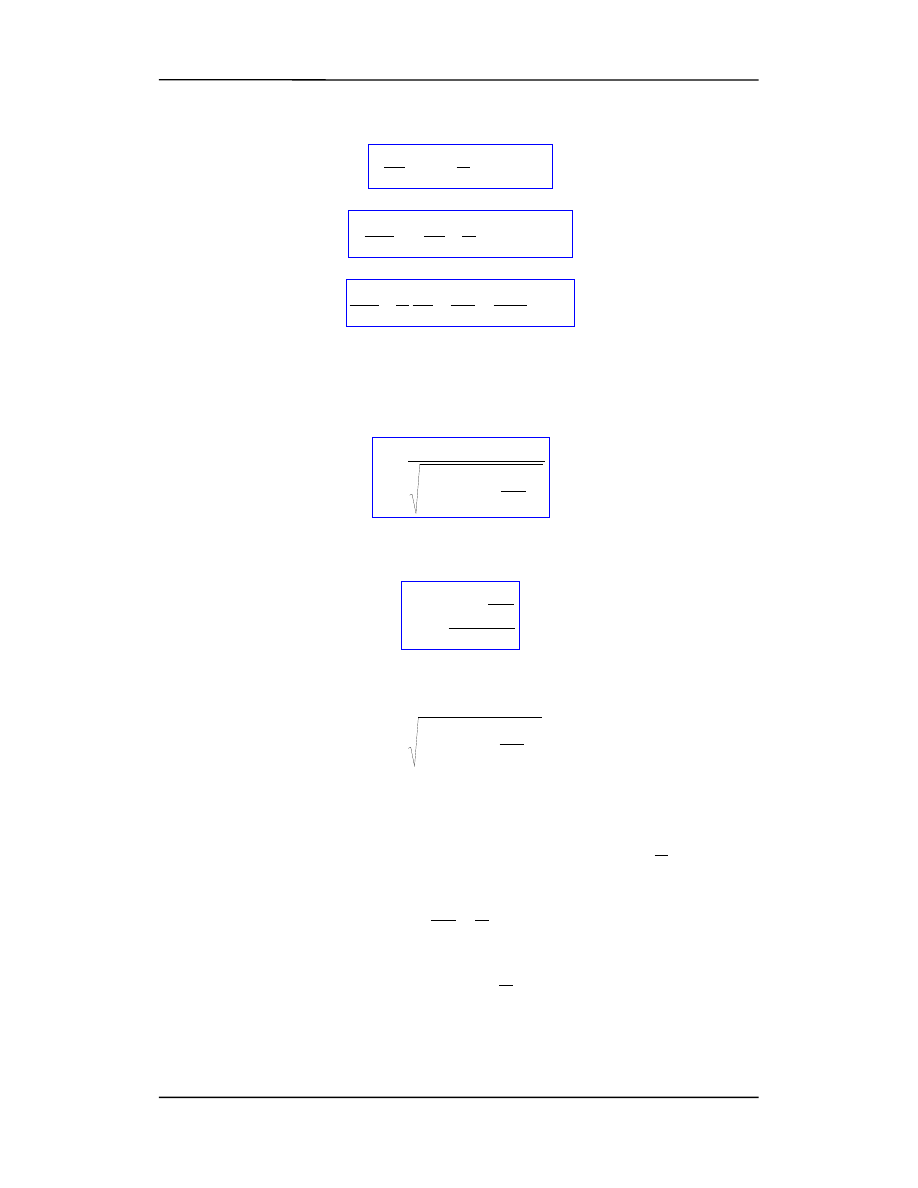
Drgania w obwodzie RLC można podtrzymać jeżeli obwód będziemy zasilać
napięciem sinusoidalnie zmiennym
t
U
t
U
ω
sin
)
(
0
=
Z. Kąkol-Notatki do Wykładu z Fizyki
24-3
Prawo Kirchhoffa dla obwodu zawierającego elementy R, L, C oraz źródło SEM ma
postać
t
U
C
q
RI
t
I
L
ω
sin
d
d
0
=
+
+
(24.6)
różniczkując po dt
t
U
C
I
t
I
R
t
I
L
ω
ω
cos
d
d
d
d
0
2
2
=
+
+
(24.7)
albo
t
L
U
LC
I
t
I
L
R
t
I
ω
ω
cos
d
d
d
d
0
2
2
=
+
+
(24.8)
To jest równanie analogiczne do omawianego dla oscylatora wymuszonego przy R/L
↔
1/
τ, 1/LC
↔
ω
0
2
oraz
ωU
0
/L
↔
α
0
.
Rozwiązanie ma więc analogiczną postać
)
sin(
0
ϕ
ω
−
=
t
I
I
.
Amplituda wynosi więc
2
2
0
0
1
−
+
=
C
L
R
V
I
ω
ω
(24.9)
a między napięciem i natężeniem prądu istnieje różnica faz, dana równaniem
R
C
L
ω
ω
ϕ
1
−
=
tg
(24.10)
Wyrażenie (24.9) ma postać prawa Ohma przy czym stała proporcjonalności pomiędzy
U
0
i I
0
2
2
1
−
+
=
C
L
R
Z
ω
ω
(24.11)
pełni analogiczną rolę jak opór R w prawie Ohma. Wielkość Z nazywamy
impedancją
(
zawadą
) obwodu.
Gdy zmienne sinusoidalne napięcie przyłożymy do kondensatora to
C
q
U
=
Stąd
C
I
t
U
=
d
d
co dla U=U
0
sin
ωt daje
C
I
t
U
=
ω
ω
cos
0
Stąd
)
90
sin(
cos
0
0
o
+
=
=
t
CU
t
CU
I
ω
ω
ω
ω
Z. Kąkol-Notatki do Wykładu z Fizyki
24-4
R
(X
L
- X
C
)
Z
ϕ
Widać, że
prąd wyprzedza napięcie
na kondensatorze o 90
°
.
Maksymalny prąd I
0
= U
0
/(
ωC) a stała proporcjonalności 1/ωC pełniąca rolę
analogiczną do oporu w obwodzie prądu stałego nazywamy
reaktancją pojemnościową
.
X
C
= 1/
ωC
(24.12)
Jeżeli generator prądu zmiennego podłączymy do cewki indukcyjnej to analogicznie
można pokazać, że
)
90
sin(
cos
0
0
o
−
=
−
=
t
L
U
t
L
U
I
ω
ω
ω
ω
Prąd
pozostaje za napięciem
o 90
°
, a
reaktancja indukcyjna
ma wartość
X
L
=
ωL
(24.12)
Zauważmy, że w obwodzie RLC, pomimo połączenia szeregowego oporów omowego,
pojemnościowego i indukcyjnego ich opór zastępczy (zawada) nie jest prostą sumą tych
oporów. Wynika to właśnie z
przesunięć fazowych
.
Trzeba je uwzględnić przy dodawaniu napięć.
U = U
R
+ U
C
+ U
L
czyli
U = I
0
Rsin
ωt - X
C
I
0
cos
ωt + X
L
I
0
cos
ωt
(na kondensatorze U pozostaje za I, na cewce U wyprzedza I)
Stąd
t
X
X
t
R
I
U
C
L
ω
ω
cos
)
(
sin
0
0
−
+
=
Mamy teraz dodać sinus i cosinus graficznie tak jak na rysunku obok Możemy przy tym
skorzystać z wyrażenia (24.10) według, którego tg
ϕ = (X
L
- X
C
)/R
.Relacja ta jest pokazana na rysunku poniżej
Zauważmy, ze przeciwprostokątna trójkąta na rysunku jest równa zawadzie
Z = (R
2
+ (X
L
- X
C
)
2
)
1/2
.
Z. Kąkol-Notatki do Wykładu z Fizyki
24-5
24.3.1 Rezonans
Drgania ładunku, prądu i napięcia w obwodzie odbywają się z częstością zasilania
ω.
Amplituda tych drgań zależy od
ω i osiąga maksimum dla pewnej charakterystycznej
wartości tej częstości. Przypomnijmy, że zjawisko to nazywamy
rezonansem
. Dla
małego oporu R czyli dla małego tłumienia warunek rezonansu jest spełniony gdy
LC
1
0
=
=
ω
ω
(24.13)
Natężenie prądu osiąga wtedy wartość maksymalną równą
R
U
I
0
0
=
(24.14)
Widzimy, że natężenie prądu w obwodzie jest takie, jak gdyby nie było w nim ani
pojemności ani indukcyjności, a zawada wynosiła R.
Przykład
Drgania wymuszone w obwodzie można także wywołać bez włączania bezpośredniego
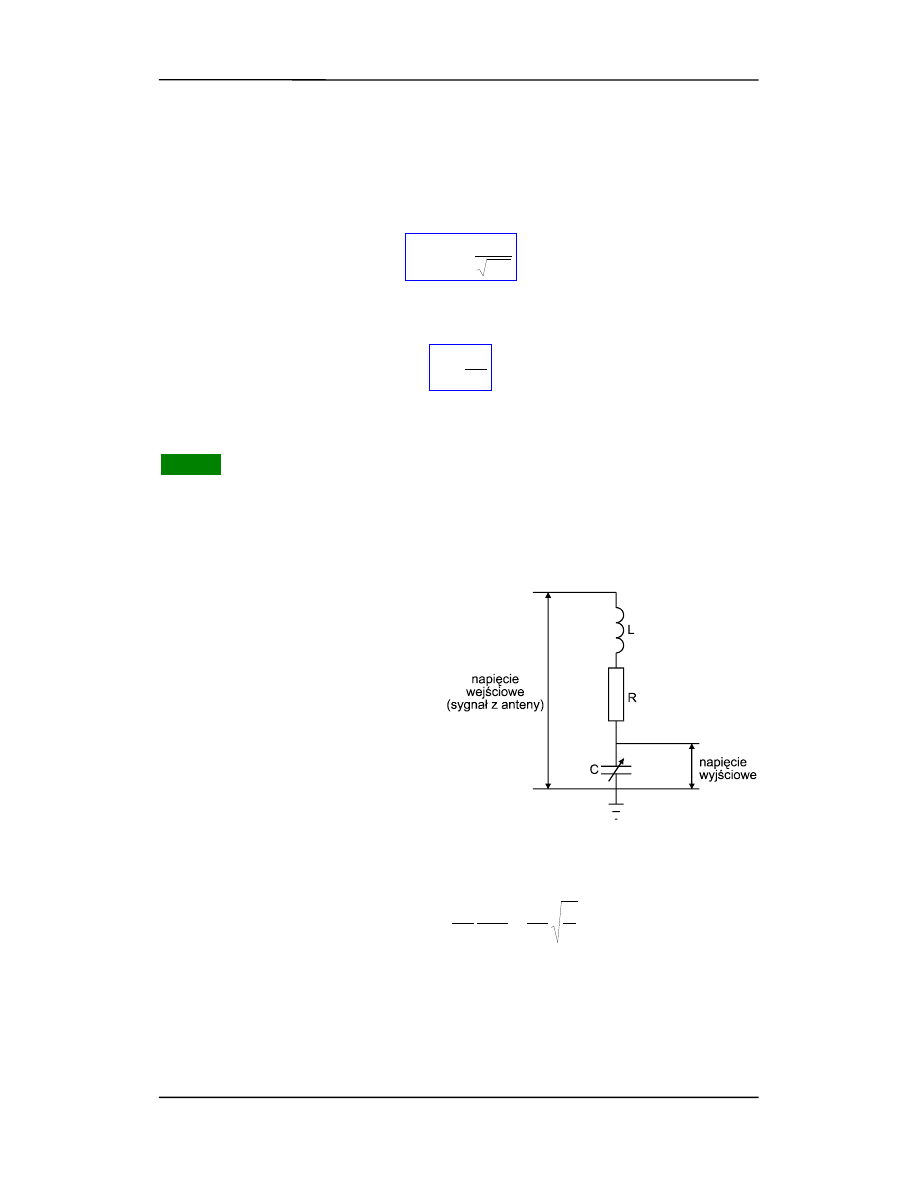
źródła SEM w postaci generatora. Przykładem może być układ RLC w obwodzie
wejściowym radioodbiornika (telewizora) pokazany na rysunku poniżej. Układ ten jest
zasilany sygnałem z anteny.
W
układzie
dostrojenie
do
częstotliwości danej radiostacji jest
osiągane przez dobranie pojemności.
W ten sposób jest spełniony warunek
rezonansu
dla
tej
częstotliwości.
Przyjmijmy, że w pokazanym układzie
R = 10
Ω
, a L = 1
µ
H. Sprawdźmy, jaka
powinna być pojemność C aby uzyskać
dostrojenie odbiornika (rezonans) do
stacji "Jazz Radio", która w Krakowie
nadaje na częstotliwości 101 MHz?
Korzystając
z
warunku
(24.13)
otrzymujemy C = 2.48 pF.
W warunkach rezonansu napięcie na
kondensatorze (w obwodzie RLC) jest równe
C
L
R
U
C
R
U
X
I
U
C
rez
C
0
0
0
0
,
1
=
=
=
ω
Jeżeli sygnał wejściowy z anteny ma amplitudę 100
µ
V to napięcie na kondensatorze
przy częstotliwości rezonansowej ma wartość 6.35 mV. Dla porównania napięcie na
kondensatorze przy tych samych ustawieniach R, L, C i sygnale o tej samej amplitudzie
ale o częstotliwości 96.0 MHz (radio "RMF") wynosi 1 mV.
Z. Kąkol-Notatki do Wykładu z Fizyki
24-6
24.3.2 Moc w obwodzie prądu zmiennego
W obwodzie prądu przemiennego moc dana analogicznym wyrażeniem jak dla
prądu stałego
)
(
)
(
)
(
t
I
t
U
t
P
=
(24.15)
ale wartość jej zmienia się bo zmienne jest napięcie i natężenie prądu. Dlatego też w
przypadku prądu zmiennego posługujemy się
wartościami średnimi
. Zgodnie z naszymi
obliczeniami moc w obwodzie RLC w dowolnej chwili t wynosi
)
sin(
sin
)
(
)
(
)
(
0
0
ϕ
ω
ω
−
=
=
t
t
I
U
t
I
t
U
t
P
Korzystając ze wzoru na sinus różnicy kątów otrzymujemy
)
sin
2
sin
2
1
cos
(sin
)
sin
cos
cos
(sin
sin
)
(
2
0
0
0
0
ϕ
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
t
t
I
U
t
t
t
I
U
t
P
−
=
−
=
gdzie skorzystaliśmy z relacji
2
2 t
t
t
ω
ω
ω
sin
cos
sin
=
. Moc średnia jest więc dana
wyrażeniem
)
sin
2
sin
2
1
cos
sin
(
2
0
0
ϕ
ω
ϕ
ω
t
t
I
U
P
−
=
Ponieważ
1
2
2
=
+
t
t
ω
ω
cos
sin
to
2
1
2
2
=
=
t
t
ω
ω
cos
sin
(wykresy sinus i cosinus są
takie same, jedynie przesunięte o
π/2). Ponadto
0
2
=
t
ω
sin
bo funkcja sinus jest na
przemian dodatnia i ujemna. Uwzględniając, ponadto że U
0
= ZI
0
oraz, że (zgodnie z
rysunkiem na stronie 24-4)
Z
R
=
ϕ
cos
otrzymujemy wyrażenie na moc średnią
2
2
)
(
cos
2
2
0
0
0
0
0
R
I
Z
R
I
ZI
I
U
P
=
=
=
ϕ
(24.16)
Jak widzimy, średnia moc zależy od przesunięcia faz. Przypomnijmy, że dla prądu
stałego P = I
2
R. Z porównania tych dwóch wyrażeń dochodzimy do wniosku, że moc
średnia wydzielana przy przepływie prądu zmiennego o amplitudzie I
0
jest taka sama jak
prądu stałego o natężeniu
2
0
I
I
sk
=
(24.17)
Tę wielkość nazywamy
wartością skuteczną prądu zmiennego
. Analogicznie
definiujemy
skuteczną wartością napięcia prądu zmiennego
2
0
U
U
sk
=
(24.18)
Z. Kąkol-Notatki do Wykładu z Fizyki
24-7
Mierniki prądu zmiennego (np. amperomierze i woltomierze) odczytują właśnie
wartości skuteczne. Wartość napięcia 220 V w naszej sieci domowej to wartość
skuteczna.
Obliczyliśmy moc średnią wydzielaną w całym obwodzie. Porównajmy ją teraz ze
średnią mocą traconą na oporze R
2
2
0
2
2
0
2
R
I
R
t
I
R
t
I
P
R
=
=
=
ω
sin
)
(
Widzimy, że
cała moc wydziela się na oporze R
, a to oznacza, że
na kondensatorze i
cewce nie ma strat mocy
. Zwróćmy uwagę, że ten wniosek pozostaje w zgodności
z naszymi wcześniejszymi obliczeniami. Gdy w obwodzie znajduje się tylko pojemność
lub indukcyjność (nie ma oporu omowego) to przesuniecie fazowe jest równe
π/2, a
ponieważ cos(
π/2) = 0 to zgodnie z równaniem (24.16) średnia moc jest równa zeru.
Jednocześnie zauważmy, że moc chwilowa zmienia się z czasem; raz jest dodatnia
(energia jest gromadzona w polu elektrycznym kondensatora lub magnetycznym cewki),
a raz ujemna (zgromadzona moc jest oddawana do układu).
Omawiane obwody, w których elementy R, L, C stanowiły odrębne części nazywamy
obwodami o elementach skupionych
. W praktyce jednak mamy do czynienia
z elementami, które mają złożone własności. Przykładem może tu być cewka, która
oprócz indukcyjności L ma zawsze opór R oraz pojemność międzyzwojową C. Mamy
wtedy do czynienia z
obwodami o elementach rozłożonych
.