PRZEGLĄD BUDOWLANY

9/2006

16

KONSTRUKCJE–ELEMENTY–MATERIAŁY

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

Streszczenie

W artykule przedstawiono autor-

ski model numeryczny i związany

z nim pakiet programów do symu-

lacji temperatur twardnienia, skur-

czu oraz stanu naprężenia i wytę-

żenia w betonowych konstrukcjach

masywnych. Możliwości wykorzy-

stania opracowanego modelu

do analiz masywnych konstruk-

cji betonowych zaprezentowano

na przykładzie bloku o wymiarach

4 x 4 x 4 m. Przedstawiono wybra-

ne wyniki obliczeń temperatur

twardnienia oraz wytężenia bloku.

1. Wprowadzenie

Zasadniczym obciążeniem beto-

nowych konstrukcji masywnych

w okresie ich wznoszenia są

zmiany temperatury i skurczu

twardniejącego betonu, określa-

ne jako oddziaływania pośrednie.

Zmiany temperatury w masywach

betonowych są związane z egzo-

termicznym charakterem proce-

su hydratacji cementu. Wskutek

wydzielanego w tym procesie

ciepła, następuje wzrost tempe-

ratury betonu. Chłodzenie warstw

powierzchniowych konstrukcji

oraz stosunkowo niska wartość

współczynnika przewodnictwa

cieplnego powodują zróżnicowa-

nie temperatur pomiędzy warstwa-

mi powierzchniowymi a wnętrzem

konstrukcji. Powstające nielinio-

we i niestacjonarne pola tempera-

tur generują w konstrukcji naprę-

żenia własne (związane z więzami

wewnętrznymi konstrukcji, które

wynikają z nierównomiernego roz-

grzania) i naprężenia wymuszone

(związane z ograniczeniem swo-

body odkształceń konstrukcji).

Naprężenia te, często o znacz-

nych wartościach mogą być przy-

czyną powstawania zarysowań

warstw przypowierzchniowych

konstrukcji w fazie wzrostu tem-

peratur twardnienia oraz – znacz-

nie rzadziej – zarysowań we wnę-

trzu konstrukcji w fazie studzenia.

Powstające w tym samym czasie

odkształcenia skurczowe dodat-

kowo zwiększają ryzyko zaryso-

wania.

Naprężenia wywołane niestacjo-

narnymi polami temperatury i wil-

gotności w elementach betono-

wych i żelbetowych są jakościowo

rozpoznane, jednak ich ilościo-

we określenie przysparza sporo

trudności. Wiąże się to z silną

nieliniowością oraz ze złożonym

charakterem zagadnienia. Należy

pamiętać, że wspomniane pola

termiczno-wilgotnościowe gene-

rują powstanie naprężeń w mate-

riale o nie w pełni ukształtowanej

strukturze, który doznaje szybkich

zmian własności mechanicznych.

Dodatkowo, zadanie komplikuje

się dla elementów pracujących

w przestrzennym stanie napręże-

nia, gdy stosowany jest bardziej

złożony model materiałowy niż

model liniowo-sprężysty.

Do niedawna, przy ograniczonym

dostępie do komputerów poszu-

kiwano przede wszystkim uprosz-

czonych rozwiązań analitycz-

nych tego zagadnienia. Ostatnie

lata, związane z dynamicznym

rozwojem metod numerycznych

oraz powszechnym dostępem

do dobrej klasy komputerów PC

stwarzają nowe możliwości roz-

wiązań.

2. Opis modelu numerycznego

Masywy betonowe są szczegól-

nym rodzajem konstrukcji – w fazie

ich wznoszenia źródłem obciążeń

jest materiał, z którego wykona-

na jest konstrukcja. Ocena ryzyka

powstania rys nie sprowadza się

więc tylko do określenia stanu

naprężenia i wytężenia, koniecz-

ne jest też ustalenie obciążeń.

Jak wspomniano w poprzednim

rozdziale, zasadniczymi obciąże-

niami konstrukcji masywnych są

obciążenia termiczno-skurczowe.

Wartość i rozkład tych obciążeń

w czasie twardnienia betonu zale-

żą od wymiarów elementu oraz

licznych czynników technologicz-

no-materiałowych [1], dlatego mu-

szą być one ustalane indywidual-

nie dla każdej analizowanej kon-

strukcji.

Kompleksowa analiza masywnych

konstrukcji betonowych powinna

obejmować wyznaczenie tempe-

ratur twardnienia, odkształceń

skurczowych oraz stanu napręże-

nia i wytężenia. Poniżej przedsta-

wiono krótki opis modelu nume-

rycznego oraz pakietu programów

do numerycznej symulacji opisy-

wanych zjawisk. Szczegółowy

opis modelu jest dostępny w pra-

Wykorzystanie metod komputerowych

w przewidywaniu ryzyka zarysowania

konstrukcji masywnych

Dr inż. Barbara Klemczak, Politechnika Śląska

PRZEGLĄD BUDOWLANY

9/2006

KONSTRUKCJE–ELEMENTY–MATERIAŁY

17

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

cach [2, 3, 4]. Analiza konstruk-

cji masywnej prowadzona jest

w następujących krokach:

1. Blok danych wejściowych

Generacja modelu numeryczne-

go, utworzenie tablicy parame-

trów materiałowych do obliczeń

pól temperatury, pól wilgotności

oraz stanu naprężenia – program

MAFEM3D

2. Wyznaczenie pól termicznych

Obliczenie rozkładu temperatur

w całym okresie twardnienia beto-

nu programem POLTEM, określe-

nie odkształceń termicznych

3. Wyznaczenie pól wilgotności

Obliczenie rozkładu wilgotności

w całym okresie twardnienia beto-

nu programem POLWIL, określe-

nie odkształceń skurczowych

4. Wyznaczenie stanu napręże-

nia i wytężenia

Odczytanie odkształceń termicz-

nych i skurczowych w poszcze-

gólnych krokach czasowych, obli-

czenie stanu naprężenia i wytęże-

nia w całym okresie twardnienia

betonu zmodyfikowanym progra-

mem MAFEM

5. Prezentacja wyników obliczeń

– program MAFEM3D

Program do generacji modelu

numerycznego określa współ-

rzędne węzłów analizowanego

elementu w globalnym układzie

współrzędnych oraz tworzy tabli-

cę parametrów materiałowych

do obliczeń pól temperatury, pól

wilgotności oraz stanu napręże-

nia. Weryfikacją programu jest

graficzna prezentacja węzłów siat-

ki elementu.

Przy wyznaczaniu pól termiczno-

-wilgotnościowych przyjęto zało-

żenie upraszczające o rozprzęże-

niu równań przewodnictwa ciepl-

nego i dyfuzji wilgoci. Uzależnienie

tych pól wynika jedynie z przyjęcia

w równaniu dyfuzji wilgoci funkcji

gęstości ciepła hydratacji cementu

jako funkcji temperatury. W pierw-

szej kolejności wyznaczane są

pola temperatur, a następnie pola

wilgotności. Do rozwiązania rów-

nania przewodnictwa cieplnego

i równania dyfuzji wilgoci wykorzy-

stano metodę elementów skoń-

czonych. Układ równań algebra-

icznych określających temperatu-

rę i wilgotność w poszczególnych

węzłach elementu (przestrzenne-

go lub płaskiego) sformułowa-

no stosując zasadę residualną

Galerkina. Do rozwiązania nielinio-

wego zadania MES wykorzystano

algorytm przyrostowo-iteracyjny.

Program POLTEM (pola tempera-

tur) i POLWIL (pola wilgotności)

został opracowany w kompilatorze

FORTRAN POWER STATION v.5

.

Weryfikację programu przeprowa-

dzono poprzez porównanie wyni-

ków obliczeń z wynikami badań

doświadczalnych [3] oraz dostęp-

nymi w literaturze wynikami obli-

czeń i pomiarów pól temperatury

i wilgotności [2].

W celu określenia stanu napręże-

nia i odkształcenia opracowano

lepko-sprężysto-plastyczny model

materiałowy betonu twardniejące-

go. Przyjęto, że beton jest ośrod-

kiem ciągłym o właściwościach

zależnych od czasu lub od czasu

i temperatury, a określenie naprę-

żenie odnosi się do naprężeń

typu makro. W proponowanym

modelu uwzględniono zmienność

parametrów mechanicznych oraz

odkształcenia pełzania twardnie-

jącego betonu. Wprowadzono

również kinematyczne prawo osła-

bienia oraz anizotropię odkształ-

ceniową. Jako powierzchnię gra-

niczną przyjęto zmodyfikowaną

3-parametrową powierzchnię Will-

ama-Warnke. Do prowadzenia

analiz numerycznych z wykorzy-

staniem opracowanego modelu

przystosowano program MAFEM,

którego autorem jest prof. dr inż.

S. Majewski [4]. Do prezentacji

wyników obliczeń wykorzystano

program MAFEM3D autorstwa

dr. inż. Wandzika.

Przedstawiony pakiet programów

może być stosowany do prowa-

dzenia analiz elementów płaskich

i przestrzennych. W opracowa-

nych programach możliwa jest

pełna swoboda kształtowania

danych wejściowych do obliczeń

a więc przyjmowania parametrów

cieplno-wilgotnościowych i wła-

sności mechanicznych betonu.

Programy umożliwiają również

wprowadzenie współpracy podło-

ża gruntowego czy też obciążenia

zmiennego. Analizy tego typu były

wcześniej prezentowane [5, 6].

3. Przykład analizy konstrukcji

masywnej

W celu prezentacji możliwości

wykorzystania opracowanego mo-

delu numerycznego w analizie

konstrukcji masywnych wykonano

obliczenia temperatur twardnienia

oraz stanu naprężenia w masyw-

nym bloku betonowym o wymia-

rach 4 x 4 x 4m. Pola wilgotności,

mające mniejsze znaczenie w ele-

mentach masywnych [7, 8] nie były

w tym przypadku analizowane.

Założono, że blok został wykonany

z betonu o następującym składzie:

cement CEM II BS 32,5R w ilości

350 kg/m

3

, kruszywo 2–16 mm

– 953 kg/m

3

, piasek 812 kg/m

3

,

woda 175 l/m

3

. W pierwszej kolej-

ności, wykorzystując program

POLTEM

porównano rozkład i war-

tości temperatur w analizowanym

bloku, w zależności od:

•

zastosowanej izolacji termicznej

oraz czasu usunięcia tej izolacji,

•

warunków prowadzenia robót

betonowych, a więc temperatury

początkowej mieszanki betonowej

i temperatury otoczenia.

W obliczeniach temperatur tward-

nienia betonu przyjęto średnie

wartości współczynników termofi-

zycznych [7]: współczynnik prze-

wodzenia ciepła λ=1,75 W/(m·K),

ciepło właściwe c

b

=1,0 J/(kg·K).

Ciepło uwodnienia cementu przy-

jęto równe Q

∞

=300 J/g, a funkcję

gęstości ciepła hydratacji przyjęto

zgodnie z pracą [8].

Jako podstawę założono, że na po-

wierzchniach zewnętrznych bloku

ułożone jest deskowanie drew-

niane grubości 2,5 cm przez

cały analizowany okres, to jest

PRZEGLĄD BUDOWLANY

9/2006

18

KONSTRUKCJE–ELEMENTY–MATERIAŁY

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

20 dni od chwili zabetonowania.

W obliczeniach deskowanie zosta-

ło uwzględnione poprzez reduk-

cję współczynnika odpływu ciepła

z powierzchni betonu z pierwot-

nej wartości α

p

=10,7 W/(m

2

·K)

do wartości α

pz

=4,57 W/(m

2

·K)

[1, 8]. W przypadku dodatkowe-

go uwzględnienia izolacji termicz-

nej (styropian o grubości 5 cm

oraz 10 cm) współczynnik odpły-

wu ciepła z powierzchni betonu

wynosił odpowiednio α

pz

=0,68

W/(m

2

·K) i α

pz

=0,37 W/(m

2

·K).

Założono, że temperatura począt-

kowa T

p

mieszanki jest równa

temperaturze otoczenia T

z

i wyno-

si 20°C. Rozkład temperatury

we wnętrzu bloku oraz na jego

bocznej powierzchni, obliczony

przy powyższych założeniach

przedstawiono na rysunku 1.

Korzystny wpływ zastosowania

izolacji termicznej na bocznych

powierzchniach bloku, polegający

na znacznym zmniejszeniu różnicy

temperatur wnętrze – powierzch-

nia widoczny jest również na ry-

sunku 2.

Rysunki 3 i 4 przedstawiają rozkła-

dy temperatur twardnienia beto-

nu przy założeniu rozdeskowania

(lub usunięcia izolacji termicz-

nej) bloku po 3, 5 lub 7 dniach

od momentu zabetonowania.

Przy analizie warunków prowa-

dzenia robót betonowych, wyzna-

czono temperatury twardnienia

bloku 4 x 4 x 4 m dla temperatury

otoczenia wynoszącej odpowied-

nio: 0, 5, 10, 15, 20, 25 i 30°C.

Temperaturę początkową mie-

szanki przyjmowano równą tem-

peraturze otoczenia, jak również

zakładano obniżenie temperatury

początkowej betonu o 5°C oraz

10°C w stosunku do temperatury

otoczenia. Dla niskich temperatur

zewnętrznych (0°C, 5°C) zbadano

również rozkład temperatur tward-

nienia w przypadku, gdy tempe-

ratura początkowa mieszanki jest

wyższa od temperatury zewnętrz-

nej. Prezentację wyników obliczeń

ograniczono do przedstawienia

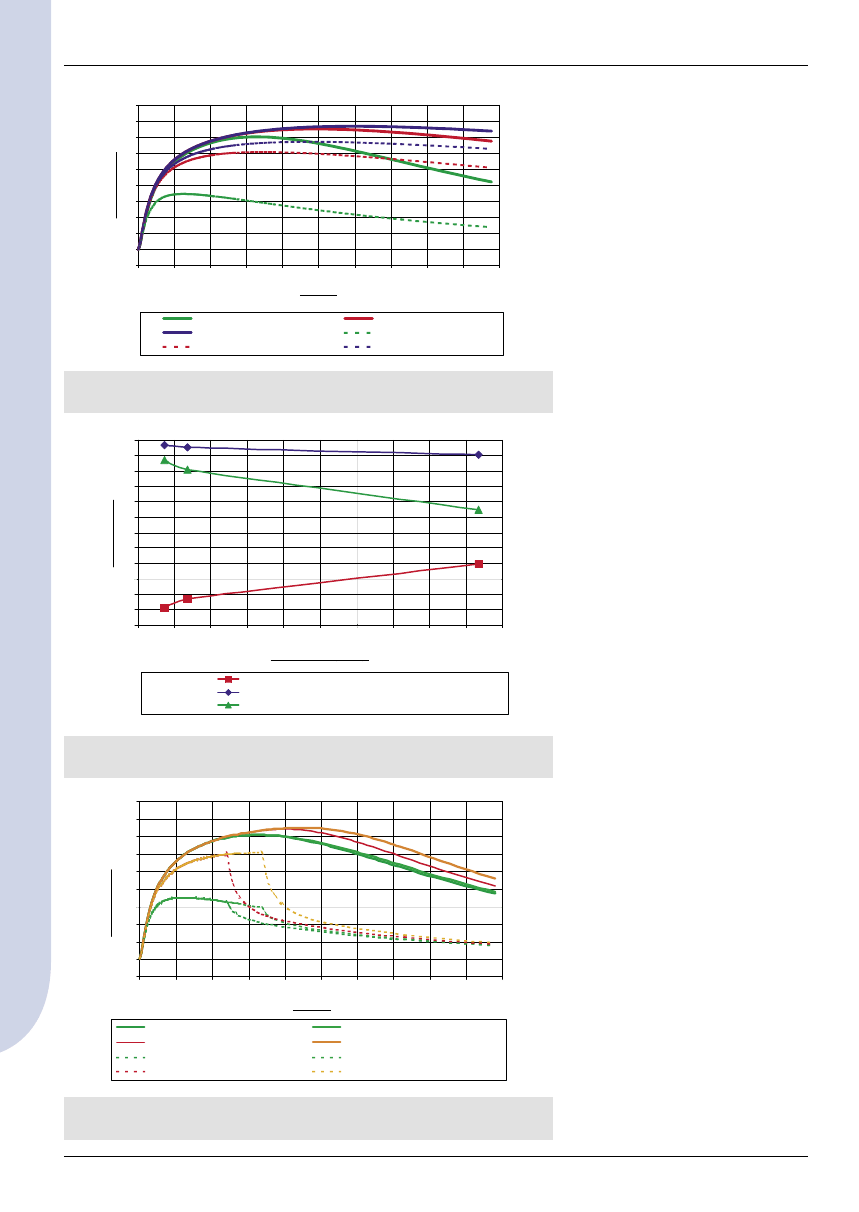
Rys. 1. Rozkład temperatur twardnienia betonu w bloku 4 x 4 x 4 m przy zasto-

sowaniu różnej izolacji termicznej

15

20

25

30

35

40

45

50

55

60

65

0

2

4

6

8

10

12

14

16

18

20

Czas, dni

,

ar

ut

ar

ep

me

T

o

C

wnętrze – deskowanie

wnętrze – styropian 5 cm

wnętrze – styropian 10 cm

powierzchnia – deskowanie

powierzchnia – styropian 5 cm

powierzchnia – styropian 10 cm

Rys. 2. Wpływ wartości współczynnika odpływu ciepła z powierzchni betonu

na temperatury twardnienia betonu w bloku 4 x 4 x 4 m

0

5

10

15

20

25

30

35

40

45

50

55

60

0

0,5

1

1,5

2

2,5

3

3,5

4

4,5

5

współczynnik a

p

, W/m

2

K

,

ar

ut

ar

ep

me

T

o

C

maks. różnica temperatur wnętrze – powierzchnia
maks. temperatura wnętrza
maks. temperatura powierzchni

15

20

25

30

35

40

45

50

55

60

65

0

2

4

6

8

10

12

14

16

18

20

Czas, dni

,

ar

ut

ar

ep

me

T

o

C

wnętrze – deskowanie – 5 dni

wnętrze – deskowanie – 7 dni

wnętrze – styropian 5 cm – 5 dni

wnętrze – styropian 5 cm – 7 dni

powierzchnia – deskowanie – 5 dni

powierzchnia – deskowanie – 7 dni

powierzchnia – styropian 5 cm – 5 dni

powierzchnia – styropian 5 cm – 7 dni

Rys. 3. Rozkład temperatur twardnienia betonu w bloku 4 x 4 x 4 m w zależno-

ści od czasu rozdeskowania (lub usunięcia izolacji termicznej)

PRZEGLĄD BUDOWLANY

9/2006

KONSTRUKCJE–ELEMENTY–MATERIAŁY

19

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

wartości maksymalnych różnic

temperatury wnętrze–powierzch-

nia (rys. 5).

Przedstawiany pakiet programów

umożliwia również analizę zmian

temperatury w dowolnym prze-

kroju konstrukcji. Przykładowy,

przekrojowy rozkład temperatur

twardnienia w 6 dniu dojrzewania

bloku 4 x 4 x 4 m jest widoczny

na rysunku 6.

Wyznaczone pola termiczne

w konstrukcji masywnej są pod-

stawą do określenia generowa-

nego w wyniku działania tych

pól stanu naprężenia i wytężenia

oraz ewentualnego zarysowania.

Do obliczeń przyjęto następujące

wartości wytrzymałości dla beto-

nu 28-dniowego: f

cm

=28 MPa,

f

ctm

=2,21 MPa. Moduł sprężysto-

sci betonu 28-dniowego przyjęto

równy 29 GPa. Funkcję opisującą

rozwój własności mechanicznych

przyjęto zgodnie z zaleceniami

CEB FIP MC 90 [9]. Wpływ pod-

wyższonych temperatur twardnie-

nia na rozwój parametrów mecha-

nicznych uwzględniono poprzez

wprowadzenie ekwiwalentnego

czasu dojrzewania do funkcji

określających zmiany własności

mechanicznych w czasie tward-

nienia.

Wyniki uzyskane w trakcie obli-

czeń programem MAFEM pozwa-

lają na dokładną analizę stanu

naprężenia w czasie twardnienia

betonu dla poszczególnych obsza-

rów bloków. Program do graficz-

nej prezentacji wyników obliczeń

MAFEM3D

umożliwia przegląda-

nie w każdym kroku obliczenio-

wym rozkładów 6 składowych

stanu naprężenia w poszczegól-

nych płaszczyznach bloku, rozkła-

dów i kierunków naprężeń głów-

nych oraz rozkładu wytężenia.

Można również tworzyć wykresy

przekrojowe oraz wykresy obrazu-

jące zmiany w czasie poszczegól-

nych naprężeń.

Analiza konstrukcji w proponowa-

nym modelu materiałowym odby-

wa się w przestrzeni naprężeń

wyznaczonej przez trzy zmienne:

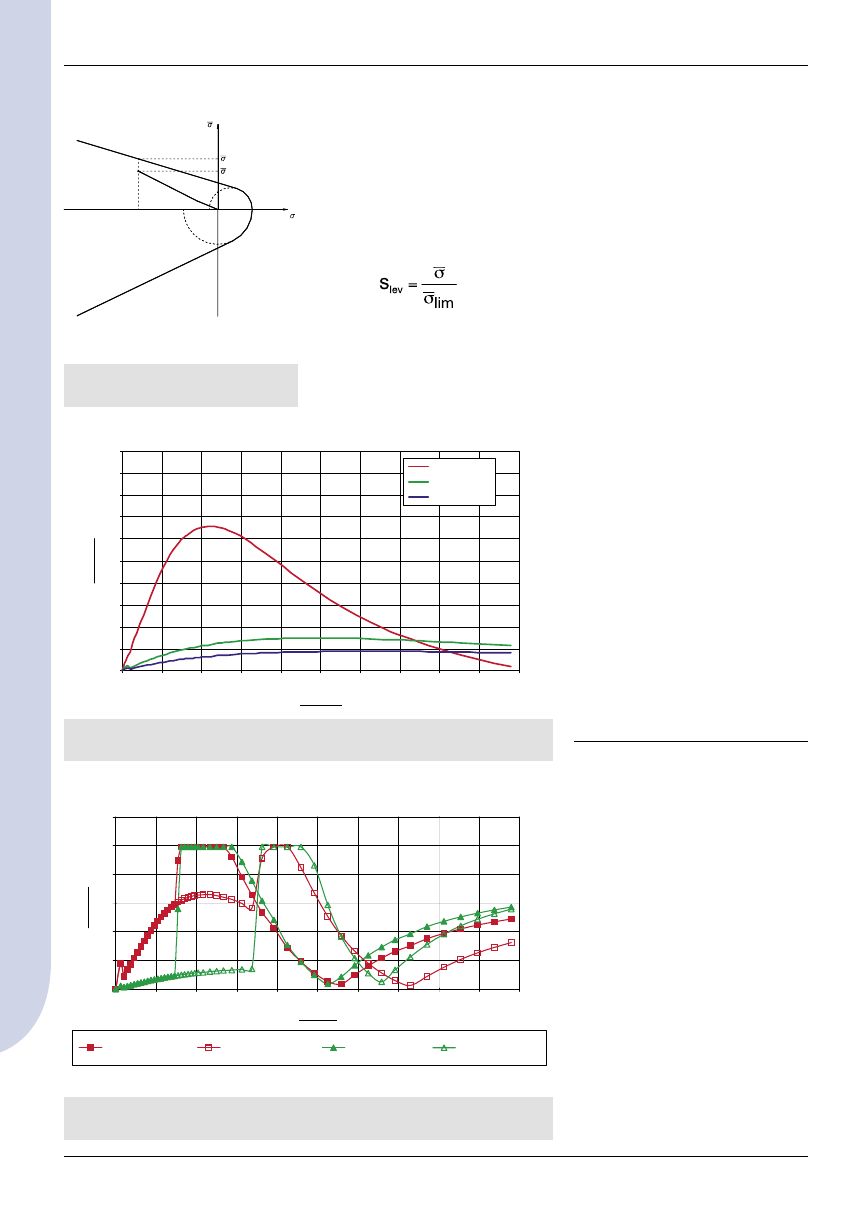
Rys. 4. Wpływ czasu rozdeskowania bloku 4 x 4 x 4 m na maksymalną różnicę

temperatur wnętrze–powierzchnia

24

24,5

25

25,5

26

26,5

27

27,5

28

2

3

4

5

6

7

8

Czas rozdeskowania (usunięcia izolacji), dni

,

ar

ut

ar

ep

me

T

o

C

maks. różnica temperatur wnętrze–powierzchnia (deskowanie)
maks. różnica temperatur wnętrze–powierzchnia (styropian 5 cm)
maks. różnica temperatur wnętrze–powierzchnia (styropian 10 cm)

Rys. 5. Wpływ temperatury początkowej mieszanki betonowej i temperatury

otoczenia na maksymalną różnicę temperatur wnętrze–powierzchnia

T

z

=T

p

T

z

-T

p

=5

o

C

T

z

-T

p

=10

o

C

BLOK 4 x 4 x 4 m

T

z

-T

p

= -5

o

C

T

z

-T

p

= -10

o

C

8

10

12

14

16

18

20

22

24

26

28

0

5

10

15

20

25

30

35

40

Temperatura zewnętrzna,

o

C

rut

ar

ep

met

a

ci

nz

ór

anl

a

my

sk

a

M

n

w

ę

,i

nh

czr

ei

wo

p i

azr

t

o

C

Rys. 6. Rozkład temperatury [°C] w 6 dniu dojrzewania betonu w bloku 4 x 4 x 4 m

(przekrój w osi symetrii bloku)

PRZEGLĄD BUDOWLANY

9/2006

20

KONSTRUKCJE–ELEMENTY–MATERIAŁY

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

σ

m

(naprężenie średnie), σ (pier-

wiastek z drugiego niezmienni-

ka dewiatora stanu naprężenia),
Θ

(kąt Lode’go). Poziom wytęże-

nia, który w jednoosiowym sta-

nie naprężenia można zdefinio-

wać jako stosunek naprężenia

do wytrzymałości, jest definiowa-

ny jako:

gdzie σ

lim

jest wartością na po-

wierzchni granicznej (rys. 7).

Przykładowe wykresy obrazują-

ce zmiany wytężenia powierzchni

analizowanego bloku w zależno-

ści od zastosowanej izolacji ter-

micznej oraz czasu usunięcia tej

izolacji pokazano na rysunkach

8 i 9. Rysunek 10 przedstawia

porównanie wytężenia powierzch-

ni bloku bez zbrojenia oraz

ze zbrojeniem w postaci siatki

powierzchniowej

∅

8 mm lub

∅

16 mm (stal A-II, rozstaw prętów

30 cm).

Przyjęty w modelu materiało-

wym rozmyty obraz zarysowa-

nia nie pozwala na ścisłą lokali-

zację rys i obserwację procesu

ich propagacji. Umożliwia nato-

miast wskazanie obszarów kon-

strukcji, w których zarysowanie

może wystąpić oraz czasu wystą-

pienia zarysowania. Przybliżony

kierunek rysy można określić

na podstawie kierunku naprężeń

głównych, przyjmując, że rysa

powstaje prostopadle do kierun-

ku naprężeń głównych rozcią-

gających. Przykładowy rozkład

naprężeń głównych rozciągają-

cych oraz ich kierunki przedsta-

wiono na rysunku 11, a wytęże-

nie powierzchni bloku na rysunku

12. Kolorem czarnym zaznaczono

obszary o wytężeniu równym 1,

które oznacza zarysowane obszary.

4. Podsumowanie

Proces wznoszenia konstruk-

cji masywnych wiąże się z ryzy-

kiem powstawania rys w okresie

twardnienia betonu. Powodem

powstawania rys i spękań tych

konstrukcji są przede wszystkim

oddziaływania pośrednie, związa-

ne ze zmianami temperatury i wil-

gotności twardniejącego betonu.

Przedstawiany problem nabiera

szczególnego znaczenia wobec

wzrastających w ostatnich latach

wymagań dotyczących trwało-

ści i jakości konstrukcji, a także

wymagań inwestorów, niejedno-

krotnie narzucających koniecz-

ność betonowania dużych ele-

mentów w krótkim terminie i przy

niekorzystnych warunkach pogo-

dowych [10].

Ocena ryzyka wystąpienia rys ter-

Rys. 7. Graficzna ilustracja poziomu

wytężenia

POŁUDNIKI ROZCIĄGANIA

ccc

f

POŁUDNIKI ŚCISKANIA

lim

ścieżka

napręż

enia

m

ttt

f

Rys. 8. Wytężenie powierzchni bloku 4 x 4 x 4 m w zależności od zastosowanej

izolacji termicznej

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

0

2

4

6

8

10

12

14

16

18

20

Czas, dni

ty

W

żę

ei

ne

deskowanie
styropian 5 cm
styropian 10 cm

0

0,2

0,4

0,6

0,8

1

1,2

0

2

4

6

8

10

12

14

16

18

20

Czas, dni

ty

W

żę

ei

ne

deskowanie – 3 dni

deskowanie – 7 dni

styropian – 3 dni

styropian – 7 dni

Rys. 9. Wytężenie powierzchni bloku 4 x 4 x 4 m w zależności od czasu rozde-

skowania (lub usunięcia izolacji termicznej)

PRZEGLĄD BUDOWLANY

9/2006

KONSTRUKCJE–ELEMENTY–MATERIAŁY

21

A

R

T

Y

K

U

Ł

Y

P

R

O

B

L

E

M

O

W

E

miczno-skurczowych w konstruk-

cjach masywnych jest zadaniem

trudnym. Istotne znaczenie mają

doświadczenia zebrane w trak-

cie realizacji konstrukcji masyw-

nych [1, 7, 8, 10], które pozwoliły

na wypracowanie praktycznych

środków zaradczych zmniej-

szających ryzyko zarysowania.

Przedstawiony w artykule model

numeryczny może być również

pomocny. Umożliwia on komplek-

sową analizę konstrukcji masyw-

nych, obejmującą wyznaczenie pól

termiczno-wilgotnościowych oraz

naprężeń i wytężenia konstrukcji

z uwzględnieniem uwarunkowań

technologiczno-materiałowych.

BIBLIOGRAFIA

[1] Kiernożycki W., Betonowe konstrukcje

masywne. Polski Cement, Kraków 2003

[2] Klemczak B., Lepko-sprężysto-

plastyczny model materiałowy

do numerycznej symulacji zjawisk

zachodzących we wczesnym okresie

dojrzewania betonu. Praca doktorska,

Gliwice 1999

[3] Klemczak B., Krause P., Badania

i symulacje komputerowe procesu

twardnienia betonu w niskich

temperaturach. Inżynieria i Budownictwo,

Nr 2, 2005, s. 65–68

[4] S. Majewski, Mechanika betonu

konstrukcyjnego w ujęciu sprężysto-

plastycznym, Wydawnictwo Politechniki

Śląskiej, Gliwice 2003

[5] Majewski S., Matuszkiewicz T., Wanecki

P., Klemczak B., Analiza numeryczna

naprężeń termicznych w betonowym

przekroju skrzynkowym. XLII Konferencja

Naukowa KILiW PAN i KN PZITB, Kraków-

Krynica, t.5, 1996, s. 117–124

[6] Majewski S., Klemczak B., Analiza

numeryczna poziomu wytężenia żelbetowej

ściany kondygnacji piwnicznej. Zeszyty

Naukowe Politechniki Śląskiej. Seria:

Budownictwo z.81/95, s. 495–505.

[7] Witakowski P., Termodynamiczna teoria

dojrzewania. Zastosowanie do konstrukcji

masywnych z betonu. Politechnika

Krakowska, Inżynieria Lądowa z. 70,

Kraków 1998

[8] Andreasik M., Naprężenia termiczno-

skurczowe w masywach betonowych. Praca

doktorska, Kraków 1982

[9] CEB-FIP, CEB-FIP Model Code 1990,

Thomas Telford, 1991

[10] Ajdukiewicz A., Kliszczewicz

A., Węglorz M., Wielkowymiarowe

konstrukcje żelbetowe wznoszone w zimie

– doświadczenia realizacyjne.

XLVIII Konferencja Naukowa KILiW PAN i KN

PZITB Krynica 2002, t. 2, s. 281–288

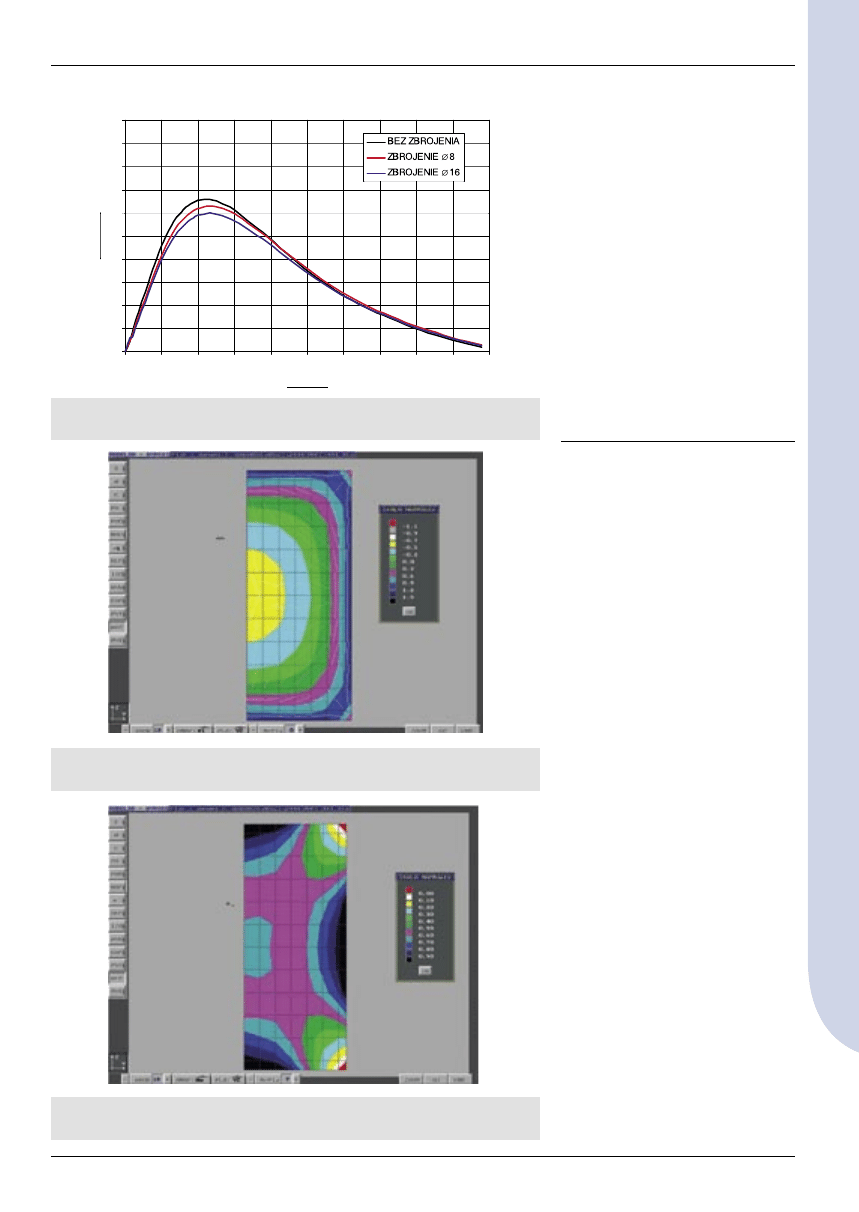
Rys. 10. Wytężenie powierzchni bloku 4 x 4 x 4 m, w zależności od zastosowa-

nego zbrojenia powierzchniowego

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

0

2

4

6

8

10

12

14

16

18

20

Czas, dni

Wytężenie

Rys. 11. Rozkład i kierunki naprężeń głównych rozciągających po 3 dniach

od zabetonowania bloku 4 x 4 x 4 m (powierzchnia bloku)

Rys. 12. Obszar zarysowanej powierzchni bloku 4 x 4 x 4 m (kolor czarny)