Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

42

22

Relacje

Niech X i Y oznaczaj dowolne niepuste zbiory. Zbiór

{

}

Y

X

Y

X

∈

∧

∈

=

×

y

x

y

x

:

)

,

(

nazywamy

produktem

kartezja skim zbiorów

X i Y. Je li Y = X, to produkt

X

X

× oznaczamy symbolem

2

X

i nazywamy drug pot g

kartezja sk zbioru X.

Dowolny podzbiór

ℜ produktu

Y

X

× nazywamy

relacj dwuczłonow

zachodz c mi dzy elementami zbio-

ru X i elementami zbioru Y. Je li

ℜ⊂

X

X

× , to mówimy, e relacja ℜ zachodzi mi dzy elementami zbioru X.

Niech

Y

X

×

⊂

ℜ

. Rzut relacji na o odci tych (poziom ) nazywamy

dziedzin

tej

relacji

, rzut relacji na o

rz dnych (pionow ) nazywamy jej

zbiorem warto ci

.

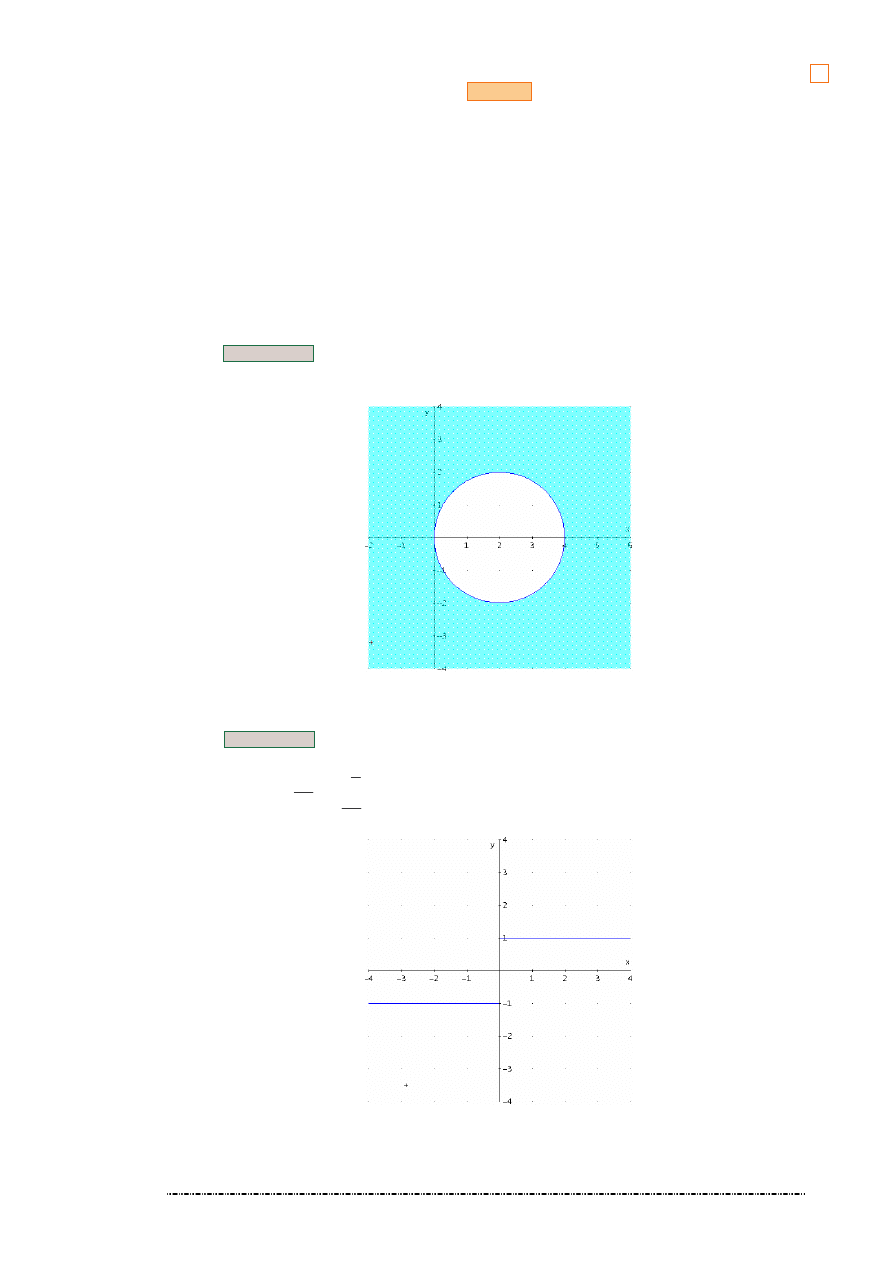
1. Przykład

}

4

:

)

,

{(

2

2

2

x

y

x

R

y

x

≥

+

∈

=

ℜ

}

4

)

2

(

:

)

,

{(

2

2

2

≥

+

−

∈

=

y

x

R

y

x

R

D

=

ℜ

,

R

V

=

ℜ

2. Przykład

}

|

|

:

)

,

{(

2

x

x

y

R

y

x

=

∈

=

ℜ

<

−

=

−

>

=

=

,

0

1

,

0

1

x

x

x

x

x

x

dla

dla

}

0

{

\

R

D

=

ℜ

,

}

1

,

1

{

−

=

ℜ

V

.

Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

43

Relacja

ℜ⊂X×Y jest

prawostronnie jednoznaczna

, je li spełnia warunek

[

]

2

1

2

1

,

)

,

(

)

,

(

2

1

y

y

y

x

y

x

y

y

x

=

ℜ

∈

∧

ℜ

∈

∀

∀

∈

∈

Y

X

(proste pionowe (równoległe do osi rz dnych) przecinaj

ℜ w co najwy ej jednym punkcie).

23

Funkcje (odwzorowania)

Niech X

i Y b d dowolnymi niepustymi zbiorami. Relacj

Y

X ×

⊂

f

nazywamy funkcj

Y

X

f

→

:

, gdy ma

ona nast puj ce własno ci:

1)

jej dziedzin jest zbiór X, tzn.

f

y

x

Y

y

X

x

∈

∃

∀

∈

∈

)

,

(

;

2)

jest ona prawostronnie jednoznaczna, tzn.

[

]

2

1

2

1

,

)

,

(

)

,

(

2

1

y

y

f

y

x

f

y

x

y

y

x

=

∈

∧

∈

∀

∀

∈

∈

Y

X

.

Poniewa dla danego

X

x

∈ istnieje dokładnie jedno y takie, e

f

y

x

∈

)

,

(

, przeto to jedyne y oznaczamy

przez

)

(x

f

i nazywamy warto ci funkcji f w punkcie x.

Je li

Y

X

f

→

:

, to czytamy: f

jest funkcj ze zbioru

X

w zbiór

Y. Zbiór X nazywamy przy tym

dziedzin

(zbiorem argumentów) odwzorowania f, zbiór

{

}

X

V

∈

=

x

x

f

f

:

)

(

nazywamy

zbiorem warto ci

funkcji f.

Funkcje

)

(x

f

x

,

)

(x

g

x

s

równe

wtedy i tylko wtedy, gdy:

1

° s okre lone na tej samej dziedzinie D,

2

°

)

(

)

(

x

g

x

f

x

=

∀

∈D

.

3. Przykład

Zbadaj równo funkcji:

1

1

)

(

,

:

;

1

1

)

(

,

:

2

−

−

=

→

⊃

+

=

→

⊃

x

x

x

g

D

g

x

x

f

D

f

g

f

R

R

R

R

.

Poniewa

},

1

{

\

−

= R

f

D

},

1

,

1

{

\

−

= R

g

D

wi c nie jest spełniony pierwszy warunek definicji.

4. Przykład

Zbadaj równo funkcji:

2

)

(

,

:

;

)

(

,

:

x

x

g

g

x

x

f

f

=

→

=

→

R

R

R

R

.

W tym przypadku

g

f

D

D

=

= R

, lecz

1

)

1

(

−

=

−

f

,

1

)

1

(

=

−

g

. Funkcje nie s równe.

24

Funkcje monotoniczne

Funkcja rosn ca

)]

(

)

(

[

2

1

2

1

,

2

1

x

f

x

f

x

x

f

x

x

<

<

∀

∈D

Funkcja nierosn ca

)]

(

)

(

[

2

1

2

1

,

2

1

x

f

x

f

x

x

f

x

x

≥

<

∀

∈D

Funkcja malej ca

)]

(

)

(

[

2

1

2

1

,

2

1

x

f

x

f

x

x

f

x

x

>

<

∀

∈D

Funkcja niemalej ca

)]

(

)

(

[

2

1

2

1

,

2

1

x

f

x

f

x

x

f

x

x

≤

<

∀

∈D

Funkcja stała

)]

(

)

(

[

2

1

,

2

1

x

f

x

f

f

x

x

=

∀

∈D

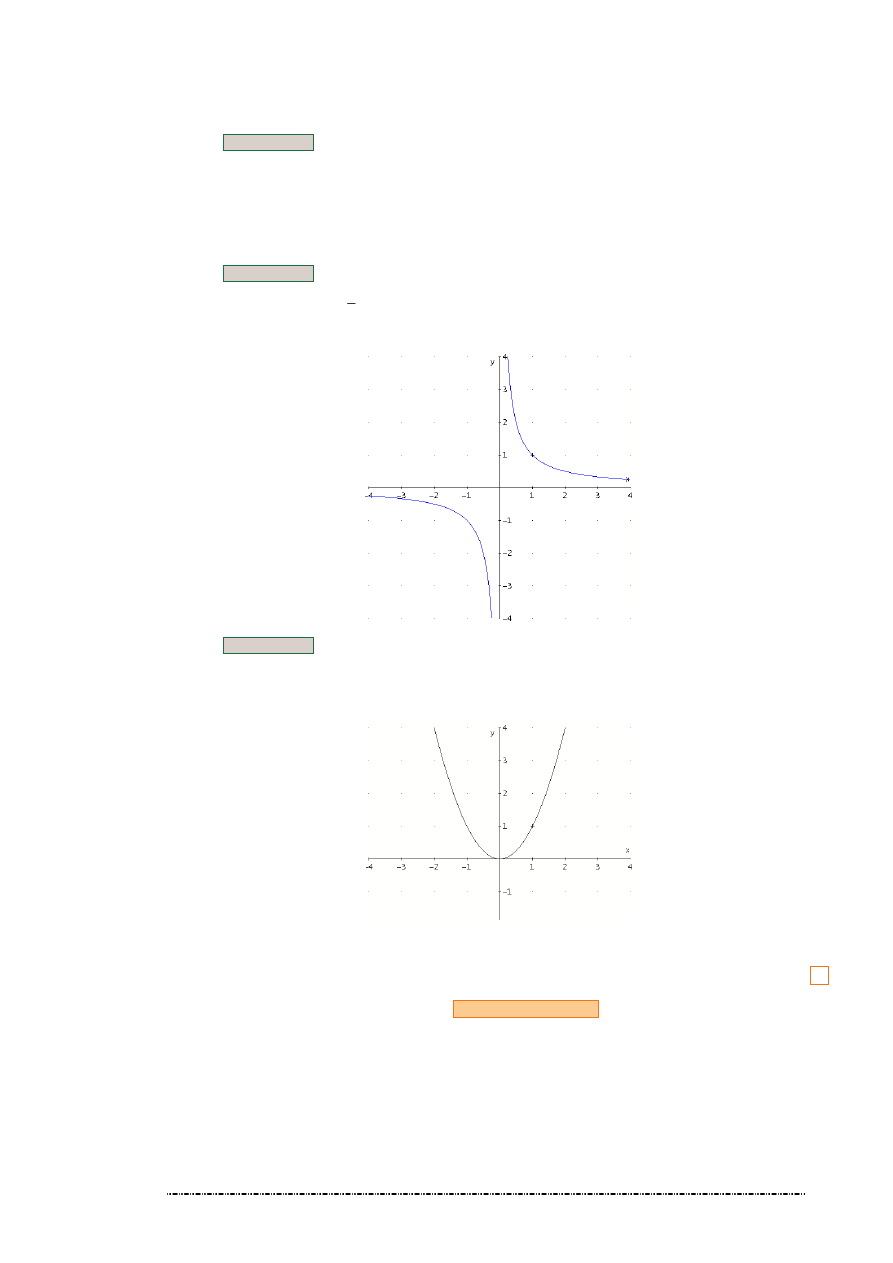
Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

44

Funkcj nazywamy

przedziałami monotoniczn

, je li jej dziedzin mo na przedstawi w postaci sumy prze-

działów takich, e na ka dym z tych przedziałów funkcja jest monotoniczna.

5. Przykład

Funkcja

R

R

x

x

f

→

−

→

=

:

)

4

2

(

jest rosn ca. Jest to przykład funkcji liniowej. Funkcja liniowa okre lona jest wzo-

rem

R

R

b

ax

x

f

→

+

→

=

:

)

(

, gdzie a, b s ustalonymi liczbami rzeczywistymi. Funkcja ta jest rosn ca wtedy i tylko

wtedy, gdy

0

>

a

; jest malej ca wtedy i tylko wtedy, gdy

0

<

a

; dla

0

=

a

funkcja liniowa jest stała.

6. Przykład

Funkcja

x

x

f

f

1

)

(

,

:

=

→ R

R {0}

\

jest przedziałami monotoniczna: jest malej ca w przedziale

)

0

,

(

−∞

oraz malej ca w

przedziale

)

,

0

(

∞ .

7. Przykład

Funkcja

2

)

(

,

:

x

x

f

f

=

→ R

R

jest przedziałami monotoniczna: jest malej ca w przedziale

]

0

,

(

−∞

oraz rosn ca w

przedziale

)

,

0

[

∞ .

25

Funkcja odwrotna

Je li w funkcji zdaniowej definiuj cej relacj

ℜ zamienimy miejscami zmienne x i y, to otrzymujemy funkcj

zdaniow definiuj c

relacj odwrotn

1

−

ℜ . Wykres relacji

1

−

ℜ mo na otrzyma z wykresu relacji ℜ w tym samym

układzie współrz dnych Oxy przez symetryczne odbicie wzgl dem prostej o równaniu

x

y

= .

Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

45

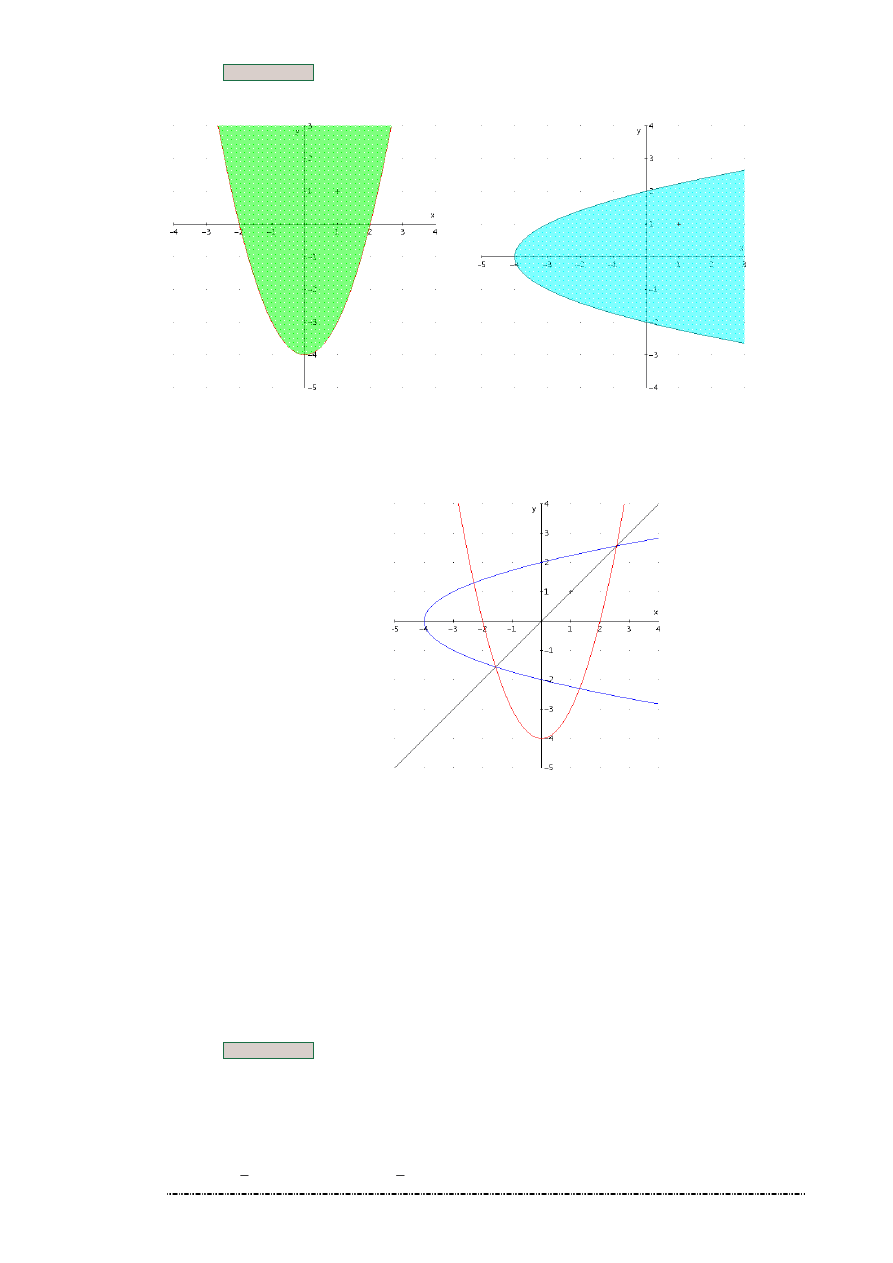
8. Przykład

}

4

:

)

,

{(

2

2

−

>

=

ℜ

x

y

y

x

}

4

:

)

,

{(

2

1

2

−

>

=

ℜ

−

y

x

y

x

Funkcja jako relacja jest odwracalna, lecz relacja do niej odwrotna nie musi by te funkcj , np.

}

4

:

)

,

{(

2

−

=

=

ℜ

x

y

y

x

jest funkcj ,

}

4

:

)

,

{(

2

1

−

=

=

ℜ

−

y

x

y

x

nie jest funkcj .

W sytuacji, gdy obie relacje

ℜ i

1

−

ℜ s funkcjami mówimy, e relacja ℜ jest

funkcj odwracaln

.

Funkcja f jest funkcj odwracaln , je li jest relacj lewostronnie jednoznaczn .

Relacja

ℜ⊂X×Y jest

lewostronnie jednoznaczna

, je li spełnia warunek

[

]

2

1

2

1

,

)

,

(

)

,

(

2

1

x

x

y

x

y

x

y

x

x

=

ℜ

∈

∧

ℜ

∈

∀

∀

∈

∈

Y

X

(proste poziome (równoległe do osi odci tych) przecinaj

ℜ w co najwy ej jednym punkcie).

Wykres funkcji

1

−

f

mo na otrzyma z wykresu funkcji f w tym samym układzie współrz dnych Oxy przez symetryczne

odbicie wzgl dem prostej o równaniu

x

y

= .

9. Przykład

Zbuduj funkcj odwrotn funkcji

(

)

[ ]

R

→

−

−

=

3

;

1

:

6

2x

x

f

.

Znajdujemy

[ ]

0

;

8

1

−

=

=

−

f

f

D

V

.

Funkcja

1

−

f

okre lona jest przez wzór

6

2

−

= y

x

(w napisie

6

2

−

= x

y

zamienili my rolami zmienne). Po wyliczeniu

y mamy

3

2

1

+

= x

y

. Zatem

[ ]

R

→

−

+

=

−

0

;

8

:

)

3

(

2

1

1

x

x

f

.

Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

46

10. Przykład

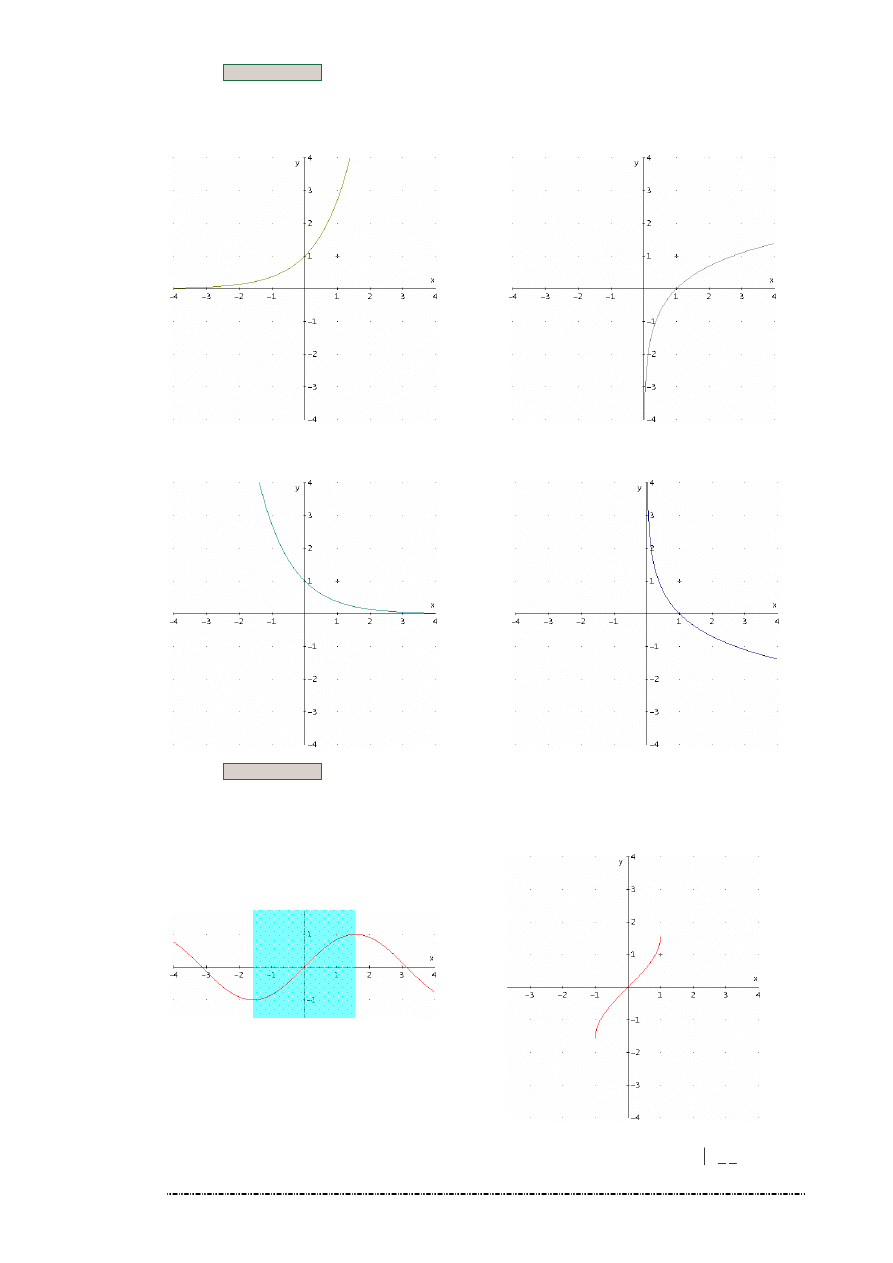
Funkcjami wzajemnie odwrotnymi s funkcja wykładnicza i funkcja logarytmiczna.

1

),

(

>

=

a

a

x

f

x

1

),

log

(

1

>

=

−

a

x

x

f

a

1

0

),

(

<

<

=

a

a

x

f

x

1

0

),

log

(

1

<

<

=

−

a

x

x

f

a

11. Przykład

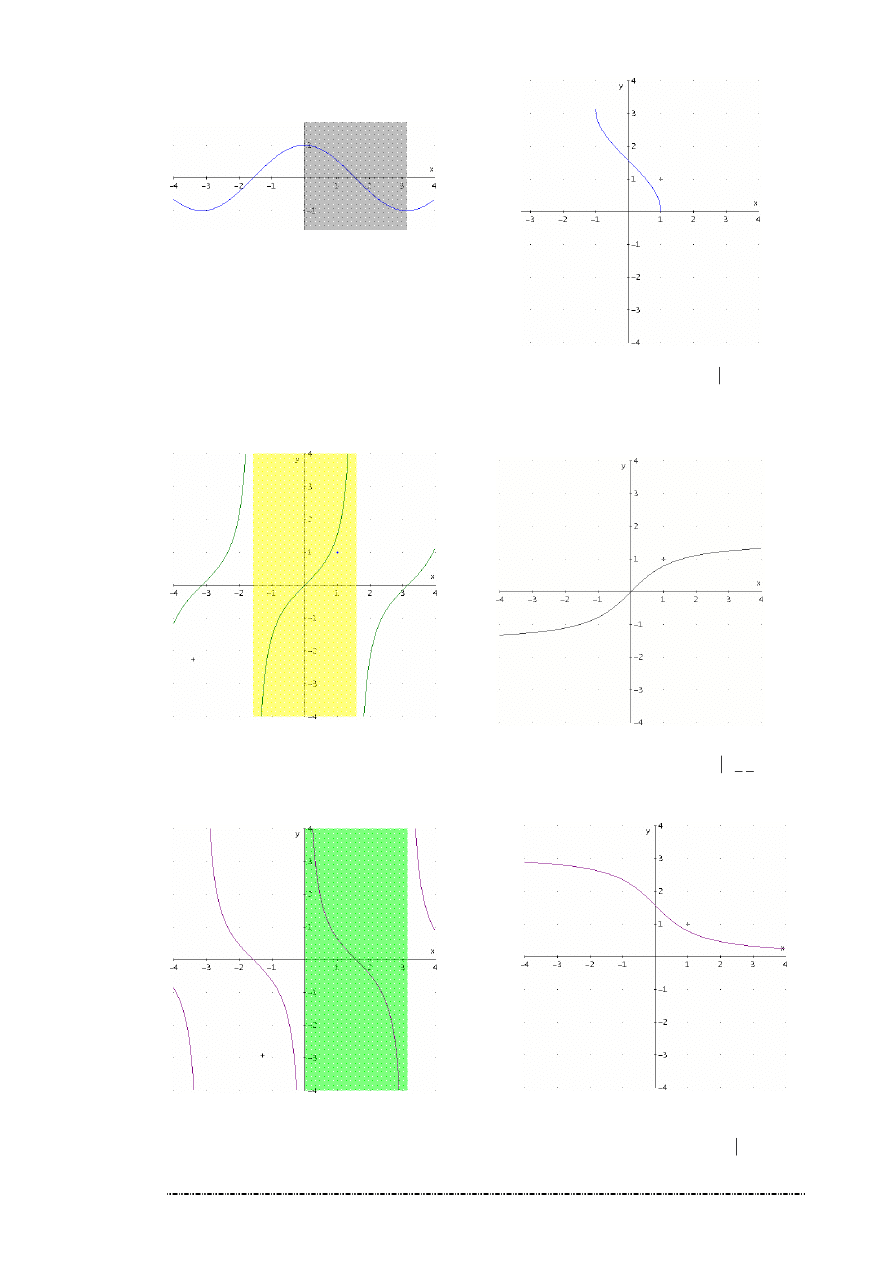
Funkcje trygonometryczne nie s odwracalne w całych swoich dziedzinach. Ka da z nich ma jednak przedziały, w któ-
rych jest ró nowarto ciowa, czyli odwracalna. W zwi zku z tym przyjmujemy nast puj ce okre lenia:

x

x

f

sin

)

(

=

Funkcja odwrotna:

[ ]

R

→

−

=

−

π

π

−

1

,

1

:

sin

1

2

,

2

arcsin

Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

47

x

x

f

cos

)

(

=

Funkcja odwrotna

[ ]

[ ]

R

→

−

=

−

π

1

,

1

:

cos

1

,

0

arccos

x

x

f

tg

=

)

(

Funkcja odwrotna

R

R →

=

−

π

π

−

:

1

2

,

2

tg

arctg

x

x

f

ctg

=

)

(

( )

R

R →

=

−

π

:

1

,

0

ctg

arcctg

Funkcje te nazywamy

funkcjami cyklometrycznymi (kołowymi)

.

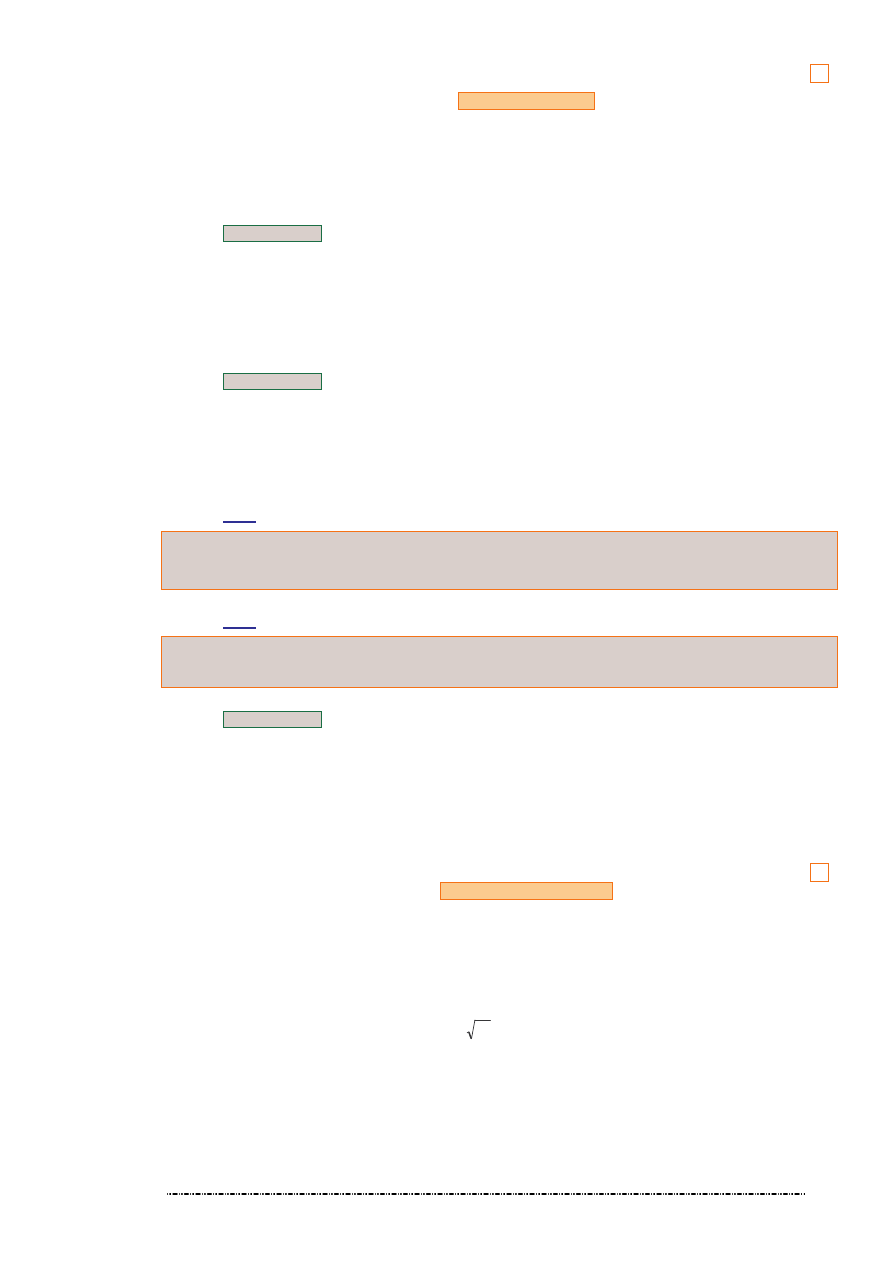
Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

48

26

Funkcja zło ona

Niech b d dane funkcje

1

f i

2

f . Je li

∅

≠

∩

2

1

f

f

D

V

, to funkcj

(

)

)

(

1

2

x

f

f

x

nazywamy funkcj zło on

z funkcji

1

f

i

2

f

i oznaczamy symbolem

1

2

f

f

.

12. Przykład

Zbuduj funkcje zło one

1

2

f

f

,

2

1

f

f

, je li:

1

)

(

,

:

;

)

(

,

:

2

2

3

1

1

−

=

→

=

→

x

x

f

f

x

x

f

f

R

R

R

R

.

R

R

x

x

f

f

→

−

=

:

)

1

(

3

1

2

,

R

R

x

x

f

f

→

−

=

:

)

)

1

(

(

3

2

1

.

13. Przykład

Zbuduj funkcje zło one

1

2

f

f

,

2

1

f

f

, je li:

1

2

)

(

,

:

;

sin

)

(

,

:

2

2

1

1

−

=

→

=

→

x

x

f

f

x

x

f

f

R

R

R

R

.

R

R

x

x

f

f

→

−

=

:

)

1

sin

2

(

1

2

,

R

R

x

x

f

f

→

−

=

:

))

1

2

sin(

(

2

1

.

Fakt.

Funkcja rosn ca oraz funkcja malej ca s odwracalne i przy tym obie funkcje f i

1

−

f

s tego samego rodzaju monoto-

niczno ci.

Fakt.

Funkcja zło ona z dwu funkcji tej samej monotoniczno ci (tzn. rosn cych albo malej cych) jest funkcj rosn c . Funkcja
zło ona z dwu funkcji ró nej monotoniczno ci (tzn. rosn cej z malej c albo malej cej z rosn c ) jest funkcj malej c .

14. Przykład

Zbadamy monotoniczno funkcji okre lonej wzorem

)

arcsin(log

)

(

2

x

x

f

=

.

Poniewa

1

2

f

f

f

=

, gdzie

)

log

(

2

1

x

x

f

=

,

)

arcsin

(

2

x

x

f

=

s funkcjami rosn cymi, wi c dana funkcja jest

funkcj rosn c (jako zło enie dwu funkcji rosn cych).

27

Funkcje elementarne

Podstawowymi funkcjami elementarnymi

nazywamy funkcje: stałe, pot gowe, wykładnicze, logarytmiczne, trygono-

metryczne oraz cyklometryczne. Funkcje, które mo na otrzyma z podstawowych funkcji elementarnych za pomoc
sko czonej liczby działa arytmetycznych oraz operacji zło enia funkcji, nazywamy

funkcjami elementarnymi

.

•

Moduł jest funkcj elementarn , gdy

2

|

|

x

x

=

dla ka dego

R

x

∈ .

• Wielomianem

nazywamy funkcj

R

R

W

→

:

okre lon wzorem

0

1

1

1

...

)

(

a

x

a

x

a

x

a

x

W

n

n

n

n

+

+

+

+

=

−

−

gdzie

}

0

{

∪

∈ N

n

, oraz

R

a

i

∈ dla

n

i

≤

≤

0

, przy czym

0

≠

n

a

. Liczb n nazywamy stopniem wielomianu W.

•

Funkcj , któr mo na zapisa w postaci ilorazu dwu wielomianów, nazywamy

funkcj wymiern

.

Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

49

Funkcj

0

;

0

;

)

(

,

:

≠

≠

+

+

=

→

⊃

d

c

b

a

c

d

cx

b

ax

x

f

D

f

R

R

nazywamy

homografi

. Wykresem homografii jest hiper-

bola.

Je li stopie wielomianu L(x) jest mniejszy ni stopie wielomianu M(x), to funkcj nazywamy

funkcj wymiern

wła ciw

. Ka da funkcja wymierna jest sum wielomianu i funkcji wymiernej wła ciwej.

1

1

1

1

)

1

(

)

1

(

)

1

(

1

)

(

)

(

1

2

2

2

2

2

2

2

2

2

2

4

2

2

4

+

−

+

+

=

+

−

+

+

+

+

=

+

+

+

+

=

+

+

+

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

Ułamkiem prostym pierwszego rodzaju

nazywamy funkcj wymiern postaci

n

a

x

A

)

(

−

Ułamkiem prostym drugiego rodzaju

jest funkcja

0

4

;

)

(

2

2

<

−

=

∆

+

+

+

ac

b

q

px

x

B

Ax

n

Fakt.

Ka d funkcj wymiern wła ciw mo emy zapisa w postaci sumy ułamków prostych wła ciwych.

15. Przykład

Funkcj wymiern

x

x

x

−

+

2

1

przedstawi w postaci sumy rzeczywistych ułamków prostych.

Rozwi zanie.

Mianownik jest rozkładalny na iloczyn czynników, wi c dokonujemy rozkładu funkcji podcałkowej na sum ułamków
prostych:

)

1

(

)

(

)

1

(

)

1

(

1

)

1

(

1

1

2

−

−

+

=

−

+

−

=

−

+

=

−

+

=

−

+

x

x

A

x

B

A

x

x

Bx

x

A

x

B

x

A

x

x

x

x

x

x

Współczynniki A, B wyznaczamy z to samo ci

A

x

B

A

x

−

+

=

+

)

(

1

(przyrównuj c współczynniki przy jednakowych pot gach):

=

−

=

+

.

1

,

1

A

B

A

Dlatego

1

2

1

1

2

−

+

−

=

−

+

x

x

x

x

x

.

16. Przykład

Funkcj wymiern

1

1

2

2

−

+

x

x

przedstawi w postaci sumy rzeczywistych ułamków prostych.

Rozwi zanie.

Nie jest to funkcja wymierna wła ciwa (stopie licznika nie jest mniejszy od stopnia mianownika), wykonujemy dziele-
nie wielomianów.

1

2

1

1

2

)

1

(

1

1

2

2

2

2

2

−

+

=

−

+

−

=

−

+

x

x

x

x

x

.

Do drugiego składnika stosujemy rozkład funkcji wymiernej wła ciwej na sum ułamków prostych.

)

1

)(

1

(

)

(

)

(

)

1

)(

1

(

)

1

(

)

1

(

1

1

)

1

)(

1

(

2

1

2

2

−

+

+

−

+

+

=

−

+

+

+

−

=

−

+

+

=

−

+

=

−

x

x

B

A

x

B

A

x

x

x

B

x

A

x

B

x

A

x

x

x

Współczynniki A, B wyznaczamy z to samo ci

Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

50

)

(

)

(

2

B

A

x

B

A

+

−

+

+

=

(przyrównuj c współczynniki przy jednakowych pot gach):

=

+

−

=

+

.

2

,

0

B

A

B

A

Dlatego

1

1

1

1

1

2

2

−

+

+

−

=

−

x

x

x

. Ostatecznie mamy

1

1

1

1

1

1

1

2

2

−

+

+

−

=

−

+

x

x

x

x

.

17. Przykład

Funkcj wymiern

x

x

x

x

x

2

2

5

4

2

3

2

+

+

−

−

przedstawi w postaci sumy rzeczywistych ułamków prostych.

Rozwi zanie.

=

+

+

+

+

+

+

=

+

+

+

+

=

+

+

−

−

=

+

+

−

−

)

2

2

(

)

(

)

2

2

(

2

2

)

2

2

(

4

4

2

2

4

4

2

2

2

2

2

2

3

2

x

x

x

x

C

Bx

x

x

A

x

x

C

Bx

x

A

x

x

x

x

x

x

x

x

x

x

)

2

2

(

2

)

2

(

)

(

)

2

2

(

)

(

)

2

2

(

2

2

2

2

+

+

+

+

+

+

=

+

+

+

+

+

+

=

x

x

x

A

x

C

A

x

B

A

x

x

x

x

C

Bx

x

x

A

−

=

−

=

+

=

+

4

2

4

2

1

A

C

A

B

A

→

=

=

−

=

0

3

2

C

B

A

→

2

2

3

2

2

2

4

4

2

2

3

2

+

+

+

−

=

+

+

−

−

x

x

x

x

x

x

x

x

x

18. Przykład

Funkcj wymiern

2

3

2

2

1

x

x

x

+

−

przedstawi w postaci sumy rzeczywistych ułamków prostych.

Rozwi zanie.

)

2

(

2

)

2

(

)

(

)

2

(

)

2

(

)

2

(

2

)

2

(

1

2

1

2

2

2

2

2

2

2

2

3

2

+

+

+

+

+

=

+

+

+

+

+

=

+

+

+

=

+

−

=

+

−

x

x

B

x

B

A

x

C

A

x

x

Cx

x

B

x

Ax

x

C

x

B

x

A

x

x

x

x

x

x

−

=

=

+

=

+

1

2

0

2

1

B

B

A

C

A

→

=

−

=

=

4

3

2

1

4

1

C

B

A

→

)

2

(

4

3

2

1

4

1

2

1

2

2

3

2

+

+

−

=

+

−

x

x

x

x

x

x

19. Przykład

Funkcj wymiern

x

x

x

x

x

+

+

+

−

3

2

3

4

1

przedstawi w postaci sumy rzeczywistych ułamków prostych.

Rozwi zanie.

Poniewa wielomian wyst puj cy w mianowniku ma stopie mniejszy ni wielomian wyst puj cy w liczniku, wi c w
wyniku dzielenia otrzymamy

x

x

x

x

x

x

x

x

x

+

+

+

−

=

+

+

+

−

3

3

2

3

4

1

1

1

.

Z kolei

1

)

1

(

1

1

2

2

3

+

+

+

=

+

+

=

+

+

x

C

Bx

x

A

x

x

x

x

x

x

.

Współczynniki A, B i C wyznaczamy z to samo ci

A

Cx

x

B

A

x

C

Bx

x

A

x

+

+

+

=

+

+

+

=

+

2

2

)

(

)

(

)

1

(

1

(przyrównuj c współczynniki przy jednakowych pot gach):

Stanisław Kowalski,

Wykłady z matematyki –

Funkcja jako relacja

–

wykład 4.

51

=

=

=

+

1

,

1

,

0

A

C

B

A

Dlatego

1

1

1

1

2

3

+

−

−

=

+

+

x

x

x

x

x

x

. Ostatecznie mamy

1

1

1

1

1

1

1

2

3

3

2

3

4

+

−

−

+

−

=

+

+

+

−

=

+

+

+

−

x

x

x

x

x

x

x

x

x

x

x

x

x

.