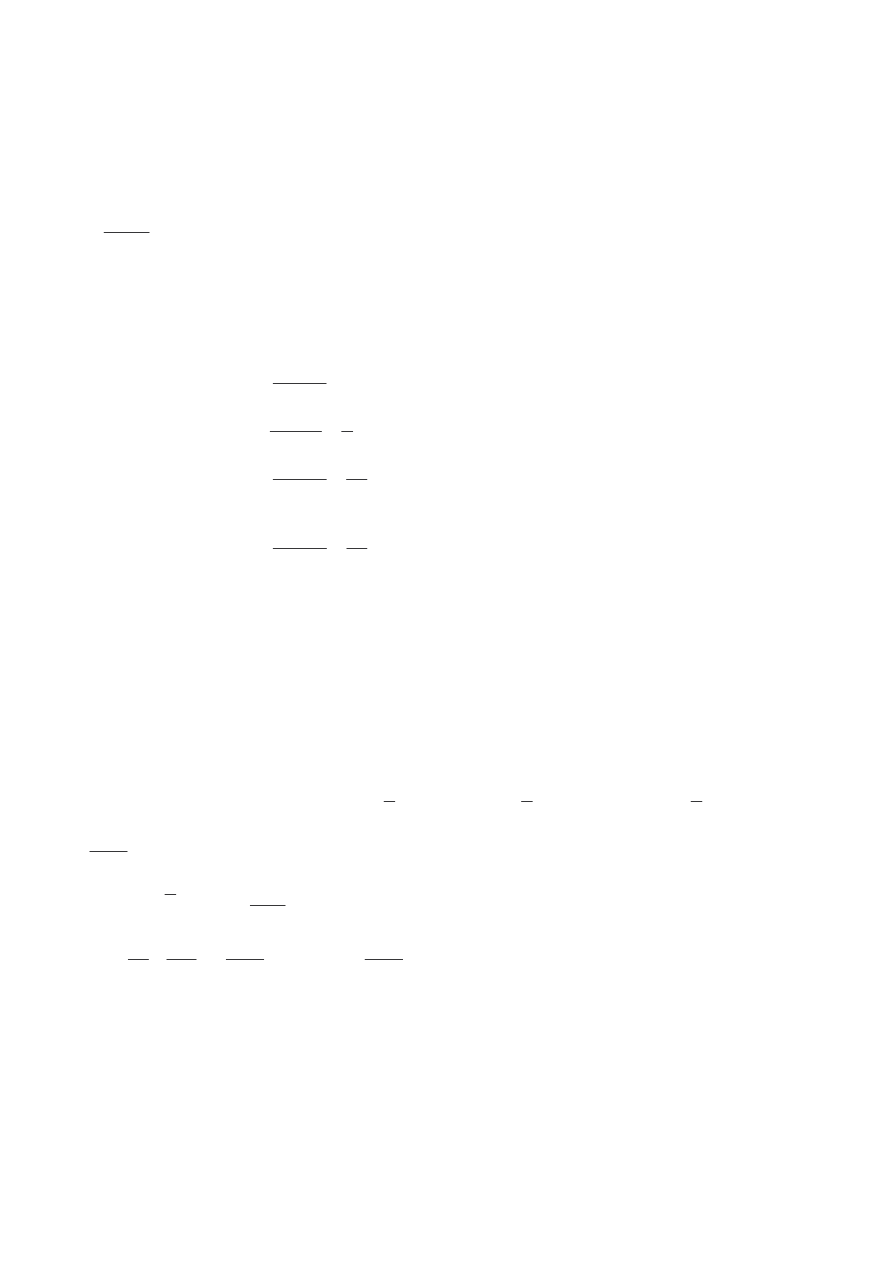
Uwaga. Je eli wprowadzimy oznaczenie
)
(
0
ih
x
f
y
i
+
=
, dla
n
i
...,
,
2
,
1
=
, to
.
)
1
(
0
j
k
i
k
j
j
i
k
y
j
k
y
−
+
=
⋅
⋅
−
=
∆
Wzory interpolacyjne Newtona – pierwszy wzór interpolacyjny.
Załó my, e
.
0
1
h
x
x
N
n
h
i
i
=
−
∈
∀
>
∃
−
Wówczas
.
0
h
i
x
x
N
i
i
⋅
+
=
∈
∀
Przyjmijmy oznaczenie
.
0
h
x
x
q
−
=
We my pod uwag nast puj cy układ funkcji bazowych
).
1
)....(
2
)(
1
(
)
(
...,
),
1
(
)
(
,
)
(
,
1
)
(
2
1
0
+
−
−
−
=
Φ
−
=
Φ
=
Φ
=
Φ
n
q
q
q
q
x
q
q
x
q
x
x
n
Wówczas wielomian interpolacyjny w mo na zapisa w postaci:
=
+
−
−
+
+
−
+
+
=
Φ
⋅
=
∈
∀
n
i
n
i
i
n
q
q
q
b
q
q
b
q
b
b
x
b
x
w
R
x
0
).
1
(
...
)
1
(
...
)
1
(
)
(
)
(
2
1
0
Poniewa dla
0
x
x
=
,
0
0
0
=
−
=
h
x
x
q
1
x
x
=
,
1
0
1
=
=
−
=
h
h
h
x
x
q
2
x
x
=
,
2
2
0
2
=
=
−
=
h
h
h
x
x
q
……………………………….
n
x
x
=
,
0
n
h
nh
h
x
x
q
n
=
=
−
=
wi c współczynniki wielomianu interpolacyjnego w mo na wyznaczy rozwi zuj c układ równa :
=
+
+
−
−
+
−
+
+
=
=
+
+
=
=
+
=
=
=
n
n
n
y
b
n
b
n
n
n
b
n
n
na
b
x
w
y
b
b
b
x
w
y
b
b
x
w
y
b
x
w
!
....
)
2
)(
1
(
)
1
(
)
(
...
..........
..........
..........
..........
..........
..........
..........
..........
..........
..........
2
2
)
(
)
(
)
(
3
2
1
0
2
2
1
0
2
1
1
0
1
0
0
0
Z układu tego wynika, e
=
∆
−
∆
=
−
−
−
=
−
−
=
∆
=
−
=
−
=
=
]
[
2
1
]
)
[(
2
1
)
2
(
2
1
,
,
0
1
1
0
1
2
0
1
2
2
0
0
1
0
1
1
0
0
y
y
b
b
b
y
b
b
y
b
y
y
y
b
y
b
y
b
,
!
2
0
2
y
∆
=
itd.
Zatem
.
!
)
(
0
n
y
b
n
P
i
i
n
∆
=
∈
∀
St d wynika, e pierwszy wzór interpolacyjny Newtona ma posta :
).
1
(
...
)
1
(
!
...
)
1
(
!
2
!
1
!
0
)
(
0
0
2
0
0
+
−
−
∆
+
+
−
∆
+
∆
+
=
n
q
q
q
n
y
q
q
y
q
y
y
x
w
n
Algorytm obliczania warto ci funkcji za pomoc wielomianu interpolacyjnego Newtona
Dane: n - całkowite, h, x
0
, q – rzeczywiste, y[n] – wektor
Podaj warto ci n, x
0
, h, x
od i = 0 do n podaj warto ci
0
i
y
od i = 1 do n
od j = 0 do n-i wykonuj
1
,
1
,
1
−
−
+
−
=
i
j
i
j
ji
y
y
y
tablica ró nic sko czonych

h
x
x
q
0
−
=
od i = 0 do n wykonuj
i
i
y
b
0
=
od j = 0 do n wykonuj
)
(
1
j
q
j
b
b
i
i
−
+
=
w = 0
od i = 0 do n wykonuj
i
b
w
w
+
=
Drukuj w.
Numeryczne całkowanie funkcji.
Numeryczne obliczanie warto ci całki
b
a
dx
x
f )
(
polega na poszukiwaniu jej warto ci w postaci
kombinacji liniowej warto ci funkcji podcałkowej f(x) i jej pochodnych do pewnego ustalonego rz du
wł cznie w ustalonych punktach w złowych.
Niech
,
,
N
m
n
∈
R
R
b
a
f
→
⊂
]
,
[
:
b dzie funkcj klasy
])
,
([ b
a
C
m
, za
)
(
)
(
n
P
k
m
P
i
∈
∀
∈
∀
]
,
[ b
a
x
ik
∈
ustalonymi punktami. Szukamy takich liczb
ik
A dla i =1,2,…,m;
k =0,1,…,n, aby
=
=
−
⋅
=
≈
b
a
n
m
ik
i
ik
k
i
x
f
A
f
Q
dx
x
f
.)
(
)
(
)
(
0
1
)
1
(
Def. Powy sze przedstawienie warto ci całki nazywamy kwadratur liniow , liczby
ik
A nazywamy
współczynnikami kwadratury za punkty
ik
x nazywamy w złami kwadratury.
Rozwa amy zadanie polegaj ce na takim doborze warto ci współczynników i w złów, aby
kwadratura była dokładna w przypadku, gdy funkcj f jest wielomian okre lonego stopnia.
Rozwa ymy obecnie przypadek, gdy znane s jedynie warto ci funkcji f w w złach
.
,
...
,
,
1
0
n
x
x
x
Załó my, e w zły s uporz dkowane rosn co i s parami ró ne, tzn.
.
...
1
0
n
x
x
x
<
<
<
Rozwa ana kwadratura ma zatem posta :
=
⋅
=
n
k
k
k
x
f
A
f
Q
0
).
(
)
(
Def. Mówimy, e kwadratura Q jest rz du
N
r
∈ , je li dla dowolnego wielomianu w stopnia
mniejszego od
r
:
=
b
a
dx
x
w
w
Q
)
(
)
(
oraz istnieje wielomian w stopnia
r
taki, e
≠
b
a
dx
x
w
w
Q
.
)
(
)
(
Kwadratury Newtona – Cotesa.
Def. Kwadraturami Newtona – Cotesa przybli aj cymi warto całki
b
a
dx
x
f )
(
nazywamy kwadratury
otrzymane poprzez zast pienie funkcji podcałkowej jej wielomianem interpolacyjnym Lagrange’a
opartym na równoodległych w złach
.
,
)
(
n
a
b
h
h
i
a
x
n
P
i
i
−
=
⋅
+
=
∈
∀
W tym przypadku
=
b
a
n
dx
x
L
f
Q
.
)
(
)
(
Przypomnijmy, e po wprowadzeniu oznaczenia
h
t
a
x
⋅
+
=
wielomian L
n
mo na zapisa w postaci:
,
)
(
)
(
0
0
∏
=
≠
=
−
−
⋅
=
+
n
i
n
i
i
j
j
j
i
j
t
x
f
th
a
L
gdzie
.
,
)
(
n
a
b
h
h
i
a
x
n
P
i
i
−
=
⋅
+
=
∈
∀

Zatem w tym przypadku
,)
(
)
(
)
(
)
(
)
(
)
(
0
0
0
0
0
0
0
0
∏
∏
∏
=
=
≠
=
=
≠
=
=
≠
=
⋅
=
⋅
⋅
−
−
⋅
=
+
−
−
⋅
=
−
−
⋅
=
n
i
i
n
n n
i
n
b
a
n
i
b
a
n
n
j
i
j
i
i
i
i
j
j
i
i
j
j
i
i
j
j
x
f
A
dt
h
j
i
j
t
x
f
th
a
d
j
i
j
t
x
f
dx
x
x
x
x
x
f
f
Q
gdzie (*)
∏
≠
=
−
−
⋅
=
n
n
i
dt
j
i
j
t
h
A
i
j
j
0
.
0
Lemat.
.
)
(
i
n
i
A
A
n
P
i
−
=
∈
∀
Przykłady najprostszych kwadratur Newtona – Cotesa.
1.
Dla
0
=
n
⋅
=
≈
b
a
a
f
h
f
Q
dx
x
f
)
(
)
(
)
(
. Ten sposób obliczania całki nosi nazw metody
prostok tów.
Twierdzenie. Je eli f jest funkcj klasy
])
,
([
1
b
a
C
, to bł d metody prostok tów wynosi
).
,
(
,
)
(
2
)
(
)
(
2
b
a
gdzie
f
a
b
f
R
∈
′
⋅
−
=
ξ
ξ
Wzór ten mo emy zastosowa w ka dym z przedziałów
]
,
[
1
+
i
i
x
x
dla i = 0,1,…,n-1.
Otrzymamy wówczas, e
.
)
(
)
(
1
0
−
=
⋅
=
n
i
i
h
x
f
f
Q
2.
Dla n = 1 w złami kwadratury s kra ce przedziału całkowania. Ze wzoru (*) obliczamy
współczynniki kwadratury
−
=
+
−
⋅
−
=
−
−
⋅
−
=
1
0
1
0
2
0
,
2
]
2
[
)
(
1
0
1
)
(
a
b
t
t
a
b
dt
t
a
b
A
.
2
]
2
[
)
(
0
1
0
)
(
1
0
2
1
0
1
a
b
t
a
b
dt
t
a
b
A
−
=
⋅
−
=
−
−
⋅
−
=
Kwadratura N – C dla n = 1 ma wi c posta :
=
+
⋅
−
=
⋅
=
1
0
)).
(
)
(
(
2
)
(
)
(
i
i
i
b
f
a
f
a
b
x
f
A
f
Q
Ten sposób obliczania całki nosi nazw metody
trapezów.
Twierdzenie. Je eli
]),
,
([
2
b
a
C
f
∈
to bł d metody trapezów wyra a si wzorem
).
,
(
,
)
(
12
)
(
)
(
3
b
a
gdzie
f
a
b
f
R
∈
′′
⋅
−
=
ξ
ξ
Wzór ten mo emy zastosowa w ka dym z przedziałów
]
,
[
1
+
i
i
x
x
dla i = 0,1,…,n
−1.
Otrzymamy wówczas, e
(
)
.
...
2
)
(
)
(
2
)
(
1
1
0
1
1
1
0
+
+
+
+
⋅
=
+
⋅
−
=
−
−
−
+
=
n
n
n
i
i
i
i
y
y
y
y
h
x
f
x
f
x
x
f
Q
i
3.
Dla n = 2 w złami kwadratury s
.
,
2
,
2
1
0
b
x
b
a
x
a
x
=
+
=
=
Ze wzoru (*) wynika, e
współczynniki kwadratury w tym przypadku s równe odpowiednio
,
6
4
2
12
3
8
4
2
2
3
3
4
)
2
0
)(
1
0
(
)
2
)(
1
(
2
2
0
2
3
2
0
0
a
b
a
b
t
t
t
a
b
dt
t
t
a
b
A
−
=
+
−
⋅
−
=
+
−
⋅
−
=
−
−
−
−
⋅
−
=
,
6
)
(
4
)
2
1
)(
0
1
(
)
2
)(
0
(
2
2
0
1
a
b
dt
t
t
a
b
A
−
=
−
−
−
−
⋅
−
=
.
0
2
A
A
=
Otrzymana w tym przypadku kwadratura ma posta
)
4
(
6
)
(
)
2
(
4
)
(
6
)
(
2
1
0
y
y
y
a
b
b
f
b
a
f
a
f
a
b
f
Q
+
+
⋅
−
=
+
+
+
−
=
i nazywana jest wzorem
parabol lub wzorem Simpsona.
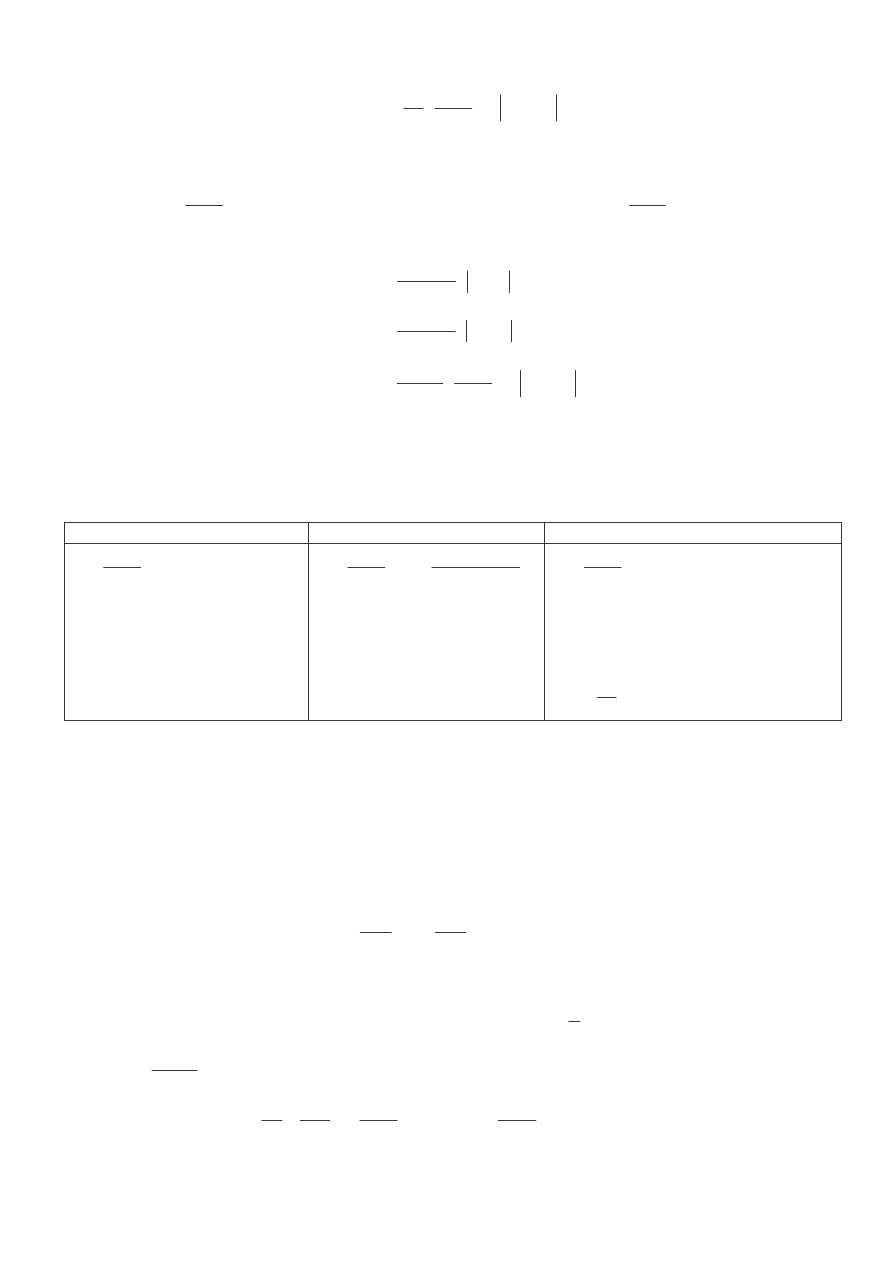
Twierdzenie. Rz d metody Simpsona wynosi 4. Ponadto, je eli
]),
,
([
4
b
a
C
f
∈
to bł d metody
Simpsona wyra a si wzorem
).
,
(
,
)
(
2
90
1
)
(
)
4
(
5
b
a
gdzie
f
a
b
f
R
∈
⋅
−
=
ξ
ξ
Wzór ten mo emy zastosowa w ka dym z przedziałów
]
,
[
2
+
i
i
x
x
dla i = 0,1,…,2k.
(oczywi cie, gdy n = 2k ). Otrzymamy wówczas, e
(
)
.
4
2
...
4
2
4
3
)
(
1
2
3
2
1
0
n
n
n
y
y
y
y
y
y
y
n
a
b
f
Q
+
+
+
+
+
+
+
⋅
−
=
−
−
( bo,
h
n
a
b
=
−
2
)
Bł dy poszczególnych metod dla w złów
n
x
x
x
,
...
,
,
1
0
wyra aj si wzorami:
− dla metody prostok tów
).
,
(
,
)
(
2
)
(
)
(
2
b
a
gdzie
f
n
a
b
f
R
∈
′
⋅
−
=
ξ
ξ
− dla metody trapezów
).
,
(
,
)
(
12
)
(
)
(
2
3
b
a
gdzie
f
n
a
b
f
R
∈
′′
⋅
−
=
ξ
ξ
− dla metody Simpsona
).
,
(
,
)
(
2
180
1
)
(
)
4
(
5
4
b
a
gdzie
f
a
b
n
f
R
∈
⋅
−
=
ξ
ξ
Twierdzenie. Kwadratury Newtona – Cotesa oparte na n+1 w złach s rz du n+2 dla n – parzystych,
za rz du n+1 dla n – nieparzystych.
Algorytmy dla poszczególnych metod:
Metoda prostok tów
Metoda trapezów
Metoda Simpsona
0
,
=
−
=
c
n
a
b
h
Dla i = 0, 1, … , n-1 wykonuj
x=a+ih
c=c+f(x)
Q(f)=hc
2
)
(
)
(
,
b
f
a
f
c
n
a
b
h
+
=
−
=
Dla i = 1, 2, … , n-1 wykonuj
x=a+ih
c=c+f(x)
Q(f)=hc
1
),
(
)
(
,
=
+
=
−
=
p
b
f
a
f
c
n
a
b
h
Dla i = 1, 2, … , n-1 wykonuj
x=a+ih
je eli p = 1 to p:=0, c:=c+4f(x)
else
p:=1, c:=c+2f(x)
Q(f)=
3
hc
Numeryczne ró niczkowanie funkcji
Niech f:[a,b]
→R b dzie funkcj ró niczkowaln na przedziale (a,b),
],
,
[
,
...
,
,
1
0
b
a
x
x
x
n
∈
gdzie
,
...
1
0
n
x
x
x
<
<
<
za
)
(
...,
),
(
),
(
1
1
0
0
n
n
x
f
y
x
f
y
x
f
y
=
=
=
b d znanymi warto ciami funkcji f.
Szukamy warto ci i − tej pochodnej funkcji f w punkcie
].
,
[
0
n
x
x
x
∈
Rozwi zanie tego problemu
polega na interpolacji funkcji f na przedziale [a,b] wielomianem interpolacyjnym w, a nast pnie
przyj ciu, e warto i – tej pochodnej funkcji f w punkcie x równa jest w przybli eniu warto ci i – tej
pochodnej wielomianu w tym punkcie
)
(
)
(
x
dx
w
d
x
dx
f
d
i
i
i
i
≈
dla
].
,
[
0
n
x
x
x
∈
Ró niczkowanie funkcji w oparciu o wielomian interpolacyjny Newtona
Załó my, e w zły
n
x
x
x
,
...
,
,
1
0
s równoodległe tzn.
.
)
(
0
0
h
k
x
x
n
P
k
h
k
⋅
+
=
∈
∀
>
∃
Oznaczmy
przez
h
x
x
q
0
−
=
i rozwa my pierwszy wzór interpolacyjny Newtona
).
1
(
...
)
1
(
!
...
)
1
(
!
2
!
1
!
0
)
(
0
0
2
0
0
+
−
−
∆
+
+
−
∆
+
∆
+
=
n
q
q
q
n
y
q
q
y
q
y
y
x
w
n
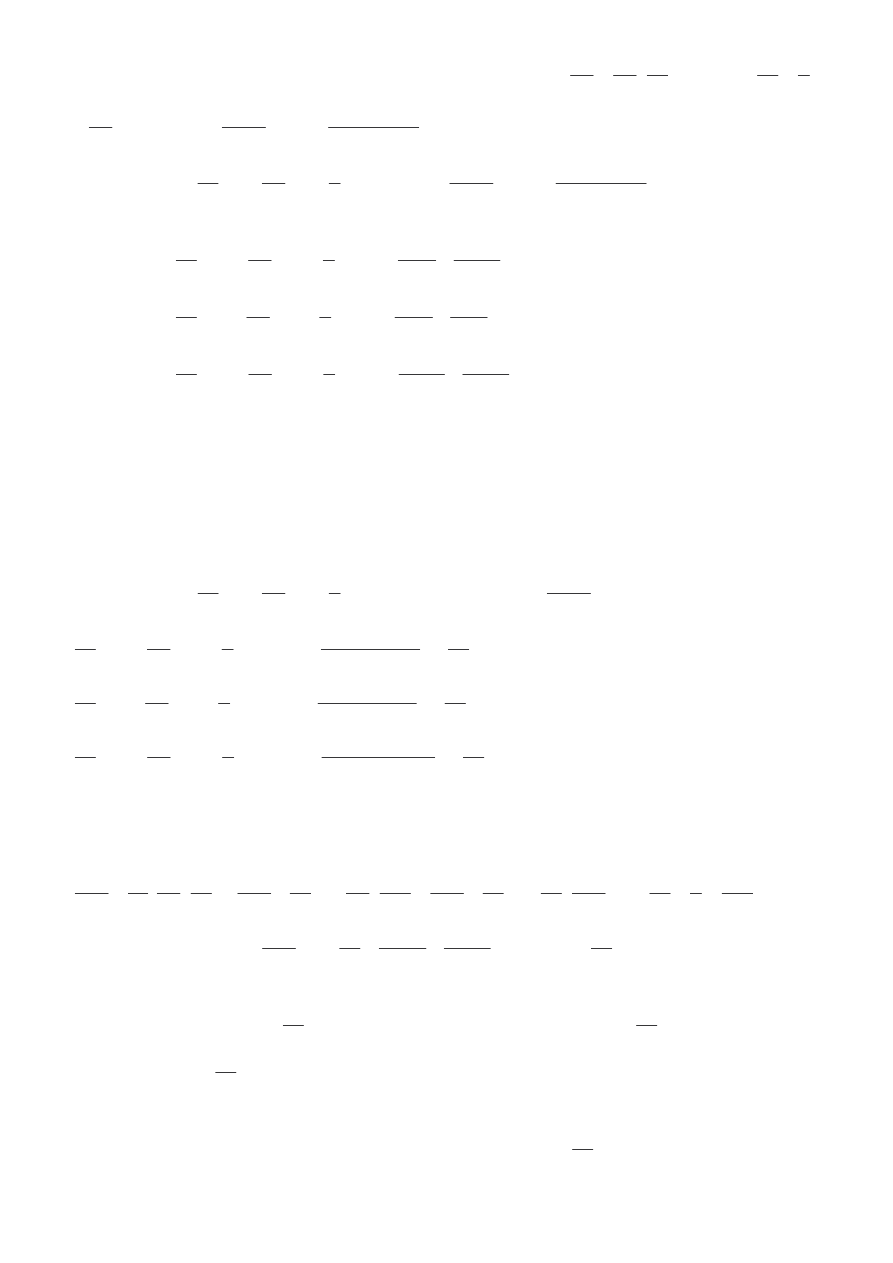
Korzystaj c z reguł ró niczkowania funkcji zło onej otrzymamy, e
.
dx
dq
dq
dw
dx
dw
⋅
=
Poniewa
h
dx
dq
1
=
i
...
!
3
2
6
3
!
2
1
2
2
0
3
0
2
0
+
+
−
⋅
∆
+
−
⋅
∆
+
∆
=
q
q
y
q
y
y
dq
dw
, wi c
.
...
!
3
2
6
3
!
2
1
2
1
)
(
)
(
]
,
[
2
0
3
0
2
0
0
+
+
−
⋅
∆
+
−
⋅
∆
+
∆
⋅
=
≈
∈
∀
q
q
y
q
y
y
h
x
dx
dw
x
dx
df
x
x
x
n
St d w szczególno ci otrzymamy, e
- dla q = 0
,
...
!
3
2
!
2
1
)
(
)
(
0
3
0
2
0
0
0
+
∆
+
∆
−
∆
⋅
=
≈
y
y
y
h
x
dx
dw
x
dx
df
- dla q = 1
,
...
!
3
!
2
1
)
(
)
(
0
3
0
2
0
1
1
+
∆
−
∆
+
∆
⋅
=
≈
y
y
y
h
x
dx
dw
x
dx
df
- dla q = 2
.
...
!
3
2
!
2
3
1
)
(
)
(
0
3
0
2
0
2
2
+
∆
+
∆
+
∆
⋅
=
≈
y
y
y
h
x
dx
dw
x
dx
df
Powy sze wzory okre laj warto ci pochodnych funkcji f w punktach w złowych.
Rozwa my przypadek, gdy znane s warto ci funkcji jedynie w trzech w złach równoodległych
).
2
(
),
(
),
(
0
2
0
1
0
0
h
x
f
y
h
x
f
y
x
f
y
+
=
+
=
=
Stosuj c oznaczenie
h
x
x
h
x
x
2
,
0
2
0
1
+
=
+
=
stwierdzamy, e mo emy obliczy jedynie dwie ró nice
,
0
1
0
y
y
y
−
=
∆
oraz
.
2
)
(
)
(
0
1
2
0
1
1
2
0
2
y
y
y
y
y
y
y
y
+
−
=
−
−
−
=
∆
W tym przypadku naturalnym jest pomini cie wyrazów
zawieraj cych ró nice rz du wy szego ni 2. Otrzymamy zatem, e
,
!
2
1
2
)
2
(
1
)
(
)
(
]
,
[
0
1
2
0
1
0
−
⋅
+
−
+
−
⋅
=
≈
∈
∀
q
y
y
y
y
y
h
x
dx
dw
x
dx
df
x
x
x
n
),
4
3
(
2
1
2
2
1
)
(
)
(
2
1
0
0
1
2
0
1
0
0
y
y
y
h
y
y
y
y
y
h
x
dx
dw
x
dx
df
−
+
−
⋅
=
+
−
−
−
⋅
=
≈
),
(
2
1
2
2
1
)
(
)
(
0
2
0
1
2
0
1
1
1
y
y
h
y
y
y
y
y
h
x
dx
dw
x
dx
df
−
⋅
=
+
−
+
−
⋅
=
≈
).
3
4
(
2
1
2
2
(
3
1
)
(
)
(
2
1
0
0
1
2
0
1
2
2
y
y
y
h
y
y
y
y
y
h
x
dx
dw
x
dx
df
+
−
⋅
=
+
−
+
−
⋅
=
≈
Wyznaczanie pochodnej rz du drugiego
Drugiego rz du pochodna wielomianu interpolacyjnego Newtona ma posta :
,
1
)
(
2
2
2
2
2
2
2
2
2
2
2
2
2
dq
w
d
h
dx
dq
dq
w
d
dx
q
d
dq
dw
dx
dq
dq
w
d
dx
dq
dq
dw
dx
d
dx
w
d
⋅
=
⋅
=
⋅
+
⋅
=
⋅
=
bo
h
dx
dq
1
=
i
.
0
2
2
=
dx
q
d
St d
otrzymamy, e
(
)
.
...
)
1
(
1
...
!
3
6
6
!
2
2
1
)
(
)
(
0
3
0
2
2
0
3
0
2
2
2
2
+
∆
⋅
−
+
∆
⋅
=
+
∆
⋅
−
+
∆
⋅
=
≈
′′
y
q
y
h
y
q
y
h
x
dx
w
d
x
f
Wstawiaj c kolejno warto ci
,
2
,
1
,
0
=
=
=
q
q
q
otrzymamy warto ci pochodnej rz du drugiego w
w złach
),
...
(
1
)
(
)
(
0
3
0
2
2
0
0
+
∆
−
∆
⋅
=
′′
≈
′′
y
y
h
x
w
x
f
),
...
(
1
)
(
)
(
0
2
2
1
1
+
∆
⋅
=
′′
≈
′′
y
h
x
w
x
f
).
...
(
1
)
(
)
(
0
3
0
2
2
2
2
+
∆
+
∆
⋅
=
′′
≈
′′
y
y
h
x
w
x
f
Przy znajomo ci warto ci funkcji tylko w trzech w złach, istnieje mo liwo obliczenia
pochodnej rz du drugiego funkcji f jedynie w w le
1
x :
(
)
.
2
1
)
(
0
1
2
2
1
y
y
y
h
x
f
+
−
⋅
≈
′′

W pozostałych w złach otrzymaliby my ten sam wynik, który niewiele ma wspólnego z
rzeczywisto ci .
Znaj c warto ci funkcji w czterech w złach, mo emy sensownie oblicza warto ci pochodnej
we wszystkich w złach. I tak np:
(
)
,
4
5
2
1
)
(
3
2
1
0
2
0
y
y
y
y
h
x
f
−
+
−
⋅
≈
′′
(
)
,
2
2
1
)
(
2
1
2
1
y
y
h
x
f
+
−
⋅
≈
′′
(
)
.
2
1
)
(
3
0
1
2
2
y
y
y
h
x
f
+
−
⋅
≈
′′
Uwaga: Mo na pokaza , e bł dy metod interpolacyjnych s proporcjonalne do warto ci kroku h,
natomiast bł dy zaokr gle s odwrotnie proporcjonalne do warto ci ,
k
h gdzie k jest maksymalnym
wykładnikiem we wzorze interpolacyjnym. Zatem zmniejszanie kroku h powoduje z jednej strony
zmniejszanie bł du interpolacji, a z drugiej strony bł dy zaokr glenia powi kszaj si . Zatem w
przypadku, gdy mamy mo liwo liczy warto ci funkcji w dowolnym punkcie, nie nale y przesadza
ze zmniejszaniem warto ci kroku h.
Wyszukiwarka
Podobne podstrony:
Calkowanie numeryczne, WIP AIR, SEM 1, TEINF, TEINF, Teinf projekty
całkowanie numeryczne
Calkowanie numeryczne
Wykład 8-Całkowanie numeryczne. Kwadratury Newtona-Cotesa
1 Metody całkowania numerycznego 1 1
Całkowanie numeryczne
Calkowanie numeryczne pdf
calkowanie numeryczne
sciaga malek 24-25, Algorytmy wielokrotnego całkowania numeryczne
Całkowanie numeryczne, Studia, ZiIP, SEMESTR III, Metody numeryczne
Całkowanie numeryczne metoda trapezów mini, Studia, ZiIP, SEMESTR III, Metody numeryczne
Całkowanie numeryczne
Wykład 9- Całkowanie numeryczne.Kwadratury Gaussa
całkowanie numeryczne
1 Metody całkowania numerycznego 2id 8579
Calkowanie numeryczne 2009
Całkowanie numeryczne
Calkowanie numeryczne, WIP AIR, SEM 1, TEINF, TEINF, Teinf projekty
więcej podobnych podstron