plik

5 2

Układy cyfrowe

LEKTRONIKA DLA WSZYSTKICH 2/97

P i e r w s z e k r o k i

w cyfrówce

część 2

W poprzednim odcinku

przedstawiłem ci szerokie tło

zagadnienia. Dowiedziałeś się, że

cała technika cyfrowa

w rzeczywistości opiera się na kilku

podstawowych cegiełkach, zwanych

bramkami. Co ważne, mogłeś sobie

uświadomić, że technika cyfrowa

nie jest nierozłącznie związana

z układami scalonymi − układy

logiczne i cyfrowe mogą być

realizowane z użyciem na przykład

elementów hydraulicznych

i pneumatycznych.

W dzisiejszym odcinku nie

zaspokoję jeszcze twoich gorących

oczekiwań − nie podam ci jeszcze

opisu poszczególnych układów

scalonych.

Przedstawię ci za to bardzo ważne

zagadnienia dotyczące bramek. Jeśli

nawet znasz już trochę technikę

cyfrową, nie lekceważ podanych

wskazówek.

Jeśli zaczynasz od początku,

przeanalizuj podany materiał

kilkakrotnie, aby dobrze ci się

utrwalił.

Dlatego zachęcam cię do używania

sformułowania typu: “na wyjściu bramki
U1A występuje stan wysoki” (lub krótko
stan H), zamiast: “na wyjściu bramki
U1A występuje jedynka”. Naprawdę za−
oszczędzi to pomyłek i nieporozumień.

Mamy trzy podstawowe bramki: NOT,

AND i OR. Są to powszechnie używane
określenia angielskie oznaczające po pol−
sku: NIE, I, LUB. W ramach niniejszego
cyklu będziemy używać terminów angiel−
skich zrozumiałych na całym świecie. Ca−
ła  źródłowa  literatura  elektroniczna  uka−
zuje  się  po  angielsku  i chyba  nie  ma
większego  sensu  trzymać  się  lokalnych
nazw i określeń.

Zapewnie

w mądrych

książkach

o technice cyfrowej spotkałeś tak zwane
tabele prawdy. Nie próbuj uczyć się tych
tablic na pamięć, tylko spróbuj zrozumieć
zasady.  Wprawdzie  tabele  te  rzetelnie
opisują zachowanie układów logicznych,
ale  ja  na  początek  zalecałbym  ci  raczej
podejście  intuicyjne.  Poczuj  więc  cyfro−
wego bluesa.

A jeśli chcesz, to w przyszłości ko−

rzystając z książek, zajmiesz się tablica−
mi prawdy i algebrą Boole’a. Niekiedy
bywa to pomocne przy realizacji bardziej
skomplikowanych układów.

NOT, AND, OR

W naszych rozważaniach przyjmuje−

my, że stan wysoki to napięcie równe lub
bliskie  dodatniemu  napięciu  zasilające−
mu,  natomiast  stan  niski  to  napięcie
równe lub bliskie potencjałowi masy. Nie
rozpatrujemy  żadnych  stanów  pośred−
nich − interesuje nas tylko czy jest napię−
cie, czy go nie ma.

Najprostsza bramka NOT, zwana też

negatorem lub inwerterem, realizuje ne−
gację − stan na wyjściu jest przeciwny niż
stan na wejściu. Jeśli na wejście poda−
my stan wysoki, na wyjściu pojawi się
stan niski, i na odwrót.

Rysunek 1

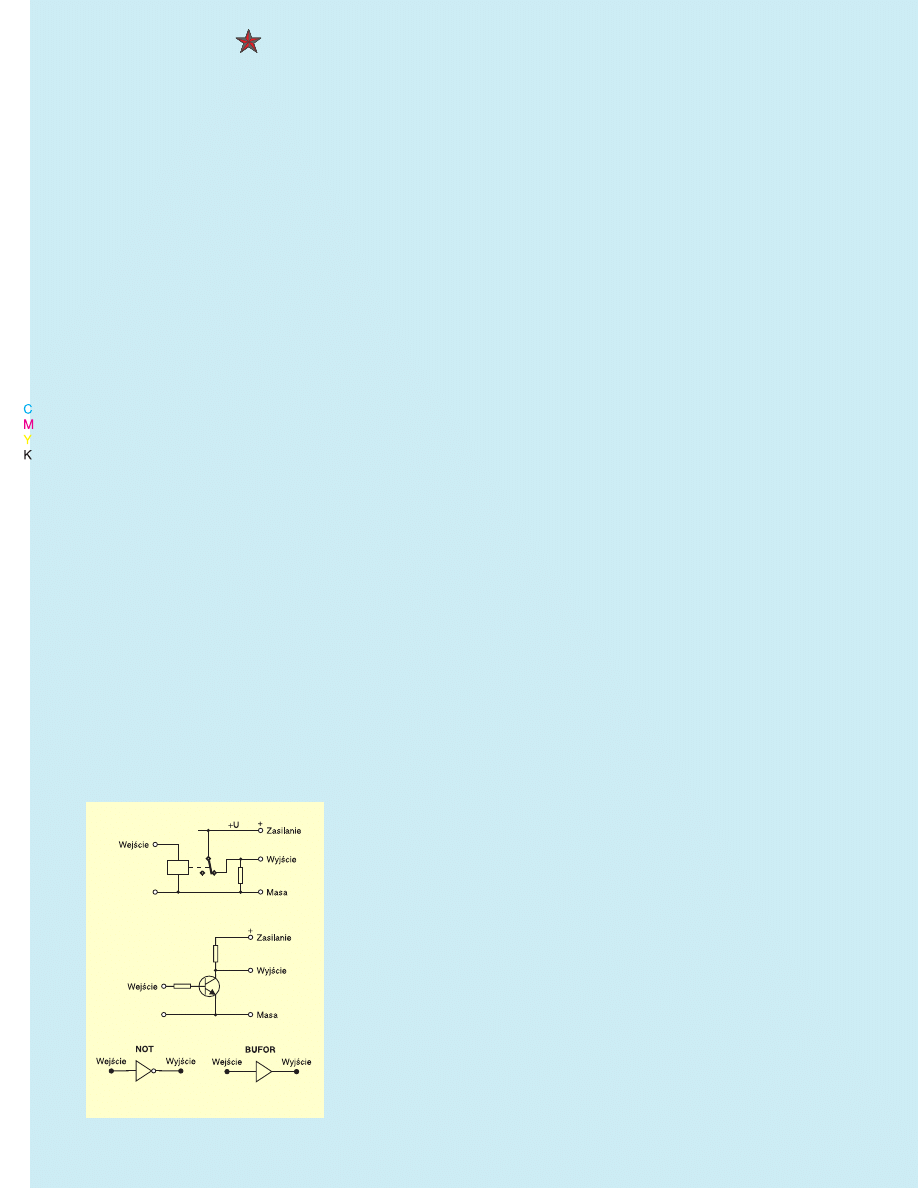
Rysunek 1 pokazuje przykładowe spo−

soby realizacji bramki NOT oraz po−
wszechnie używany symbol tej bramki.

Przy okazji, na rysunku 1 podałem

symbol bufora − jest to element, który po
prostu powtarza na wyjściu stan z we−

Może w pierwszej chwili podane in−

formacje  wydadzą  ci  się  niezgodne
z tym, czego nauczyłeś się z książek. Tak
jednak  nie  jest  − żadnej  sprzeczności  tu
nie ma, ja chcę ci tylko pokazać i zapro−
ponować  intuicyjne  podejście  do  ukła−
dów logicznych. Takie podejście pozwoli
ci  bez  trudu  projektować  prostsze  ukła−
dy. Zaryzykuję twierdzenie, że “szkolne”
podejście,  oparte  na  algebrze  Boole’a
i licznych  wzorach,  jest  coraz  mniej  po−
trzebne  w praktyce  − skomplikowane
układy  logiczne  realizuje  się  obecnie
z użyciem  mikroprocesorów  i układów
programowalnych  PLD,  i czarną  robotę
wykonuje  wtedy  komputer,  a nie  czło−
wiek.

Natomiast prostszych układów scalo−

nych, zawierających bramki, nie wolno
lekceważyć, bowiem długo jeszcze będą
stosowane w urządzeniach elektronicz−
nych.

Przypomnij sobie...

W układach logicznych i cyfrowych

mamy do czynienia z dwoma podstawo−
wymi stanami: jest/nie ma, prawda/fałsz,
lub inaczej wysoki/niski. Stany te ozna−
czane są często 1, 0 albo T, F (True −
prawda, False − fałsz).

Nas interesować będą urządzenia

elektryczne, w szczególności układy sca−
lone. Układy takie zasilane są napięciem
w granicach 2...20V. Ujemny biegun za−
silania  jest  masą  i względem  tej  masy
mierzymy  napięcia.  Umawiamy  się,  że
obecność  napięcia  na  wejściu  lub  wy−
jściu  będziemy  nazywać  stanem  wyso−
kim  − będziemy  go  oznaczać  literą
H (ang. High − wysoki). Brak napięcia to
stan niski − oznaczymy go zgodnie z po−
daną  konwencją,  literą  L  (Low  − niski).
Przyzwyczaj  się  do  oznaczania  stanów
logicznych  literami  L i H.  Jest  to  prak−
tyczne,  ponieważ  w przyszłości  unik−
niesz  wielu  pomyłek.  Nie  przyzwyczajaj
się do oznaczeń 1, 0, bowiem jedynka lo−
giczna może  ci się potem  mylić  z liczbą
1 lub dużą literą I, a zero logiczne co jakiś
czas pomyli się z dużą literą O (a pamię−
taj, że litery I, O są używane do opisywa−
nia wejść i wyjść układów cyfrowych).

Rys. 1. Bramka NOT − inwerter.

Układy cyfrowe

LEKTRONIKA DLA WSZYSTKICH 2/97

jścia. Może się zdziwisz i zapytasz: po
co? Przekonasz się, że wbrew pozorom
jest to bardzo przydatny element.

Bramka AND realizuje tzw. iloczyn lo−

giczny − stan na wyjściu bramki AND
zmienia się na wysoki dopiero wtedy,
gdy na wszystkie wejścia bramki podany
jest stan wysoki.....

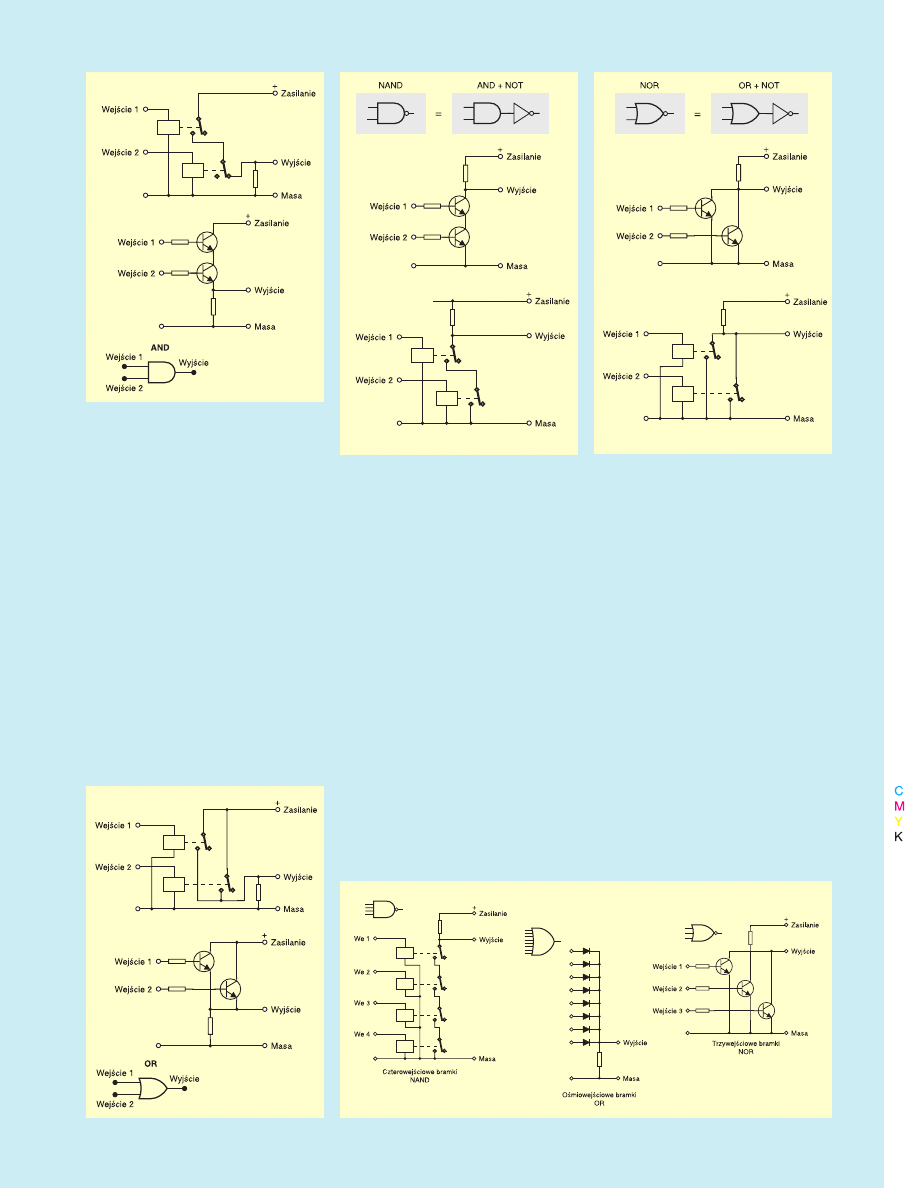
Na rysunku 2

rysunku 2

rysunku 2 możesz zobaczyć kilka

przykładów realizacji bramki AND oraz
najczęściej używany symbol tej bramki.

Bramka OR realizuje funkcję tak zwa−

nej  sumy  logicznej  − wystarczy  podać
stan  wysoki  na  przynajmniej  jedno  we−
jście  bramki  OR,  a stan  na  jej  wyjściu
zmieni się na wysoki.

Rysunek 3

Rysunek 3 pokazuje kilka realizacji

bramek OR.

W praktyce pojedynczych bramek

AND i OR używa się rzadko, można na−
wet powiedzieć bardzo rzadko. W więk−
szości układów budowanych z bramek
stosuje się bramki NAND i NOR.

Rys. 2.
Bramka AND.

Rys. 3.
Bramka OR.

Rys. 4. Bramka NAND

Rys. 6. Bramki wielowejściowe.

Rys. 5. Bramka NOR

Najpopularniejsze
cegiełki: NAND i NOR

Bramka NAND to jakby połączenie

bramek AND i NOT (rys. 4

rys. 4

rys. 4). Kółeczko na

wyjściu świadczy, że mamy do czynienia
z negacją. W praktyce bramkę NAND
można zrealizować równie prosto lub na−
wet prościej, niż bramkę AND − porównaj
rysunki 2 i 4. To samo dotyczy bramki
NOR (rysunek 5

rysunek 5

rysunek 5).

Z rysunku 4 możesz się dowiedzieć,

jak pracuje bramka NAND: stan wyjścia
zmienia  się  z wysokiego  na  niski  tylko
wtedy, gdy na wszystkich wejściach jest
stan  wysoki.  W bramce  NOR  stan  wy−
jścia  zmienia  się  z wysokiego  na  niski,
gdy na co najmniej jednym wejściu wy−
stępuje stan wysoki.

Zauważ, że mówiliśmy tu jakby o sta−

nie  spoczynku  na  wyjściu.  Możemy  to
tak rozumieć. W bramkach AND i OR ta−
kim  stanem  spoczynku  na  wyjściu  jest
stan logiczny niski, a w bramkach NAND
i NOR  − stan  wysoki.  Milcząco  zakłada−
my  też,  że  stanem  spoczynku  na  we−

jściach jest stan niski.

Stan wyjścia zmienia się po spełnie−

niu warunku:
− dla bramek AND i NAND na wszyst−

kich wejściach musi być stan wysoki,

− dla bramek OR i NOR przynajmniej na

jednym wejściu musi być stan wysoki.

Do tej pory rysowałem ci bramki dwu−

wejściowe. W praktyce takich bramek
używa się najczęściej. Ale istnieją też (w
postaci układów scalonych) bramki wie−
lowejściowe − kilka z nich zobaczysz na
rysunku 6

rysunku 6

rysunku 6.

A do czego potrzebne będą ci bramki?

Przejrzyj  kilka  numerów  EdW,  a zoba−
czysz,  jak  wykorzystuje  się  bramki
w praktyce. W jednym z następnych od−
cinków  podam  ci  garść  wskazówek  na
temat  praktycznego  wykorzystania  bra−
mek.

Na razie widzisz, że za pomocą bramek

OR,  NOR  możesz  sprawdzać,  czy  na
wszystkich  wejściach  występuje  stan
niski.  Natomiast  bramki  AND  i NAND
poinformują  cię,  czy  na  wszystkich  we−
jściach występuje stan wysoki.

5 4

Układy cyfrowe

LEKTRONIKA DLA WSZYSTKICH 2/97

Ale to za mało. Proponuję ci wyrobie−

nie sobie nawyków myślowych opartych
na wyobrażeniu bramki jako elementu,
który coś przepuszcza lub nie przepusz−
cza.

Bramka jako... bramka

Nazwa “bramka” kojarzy się z bramą,

drzwiami, wrotami, czyli w sumie z za−
mykaniem i otwieraniem.

I rzeczywiście, klasyczna bramka ma

wiele  wspólnego  z otwieraniem  i zamy−
kaniem.  Prawdziwa  bramka  to  urządze−
nie, które albo przepuszcza sygnał, albo
go nie przepuszcza. Niejako samorzutnie
nasuwałby  się  tu  wniosek,  że  bramka
powinna  mieć  wejście  sygnału,  wyjście
sygnału

i jakieś

wejście

sterujące.

Rzeczywiście,  w przypadku  elementów
OR,  NOR,  AND  i NAND,  wyobrażenie
o bramce  jako  elemencie  zamykającym
i otwierającym  drogę  sygnału  jest  jak
najbardziej słuszne.

Jeśli jedno z wejść wspomnianych

bramek potraktujemy jako wejście syg−
nału (oczywiście logicznego), to pozosta−
łe wejścia możemy traktować jako we−
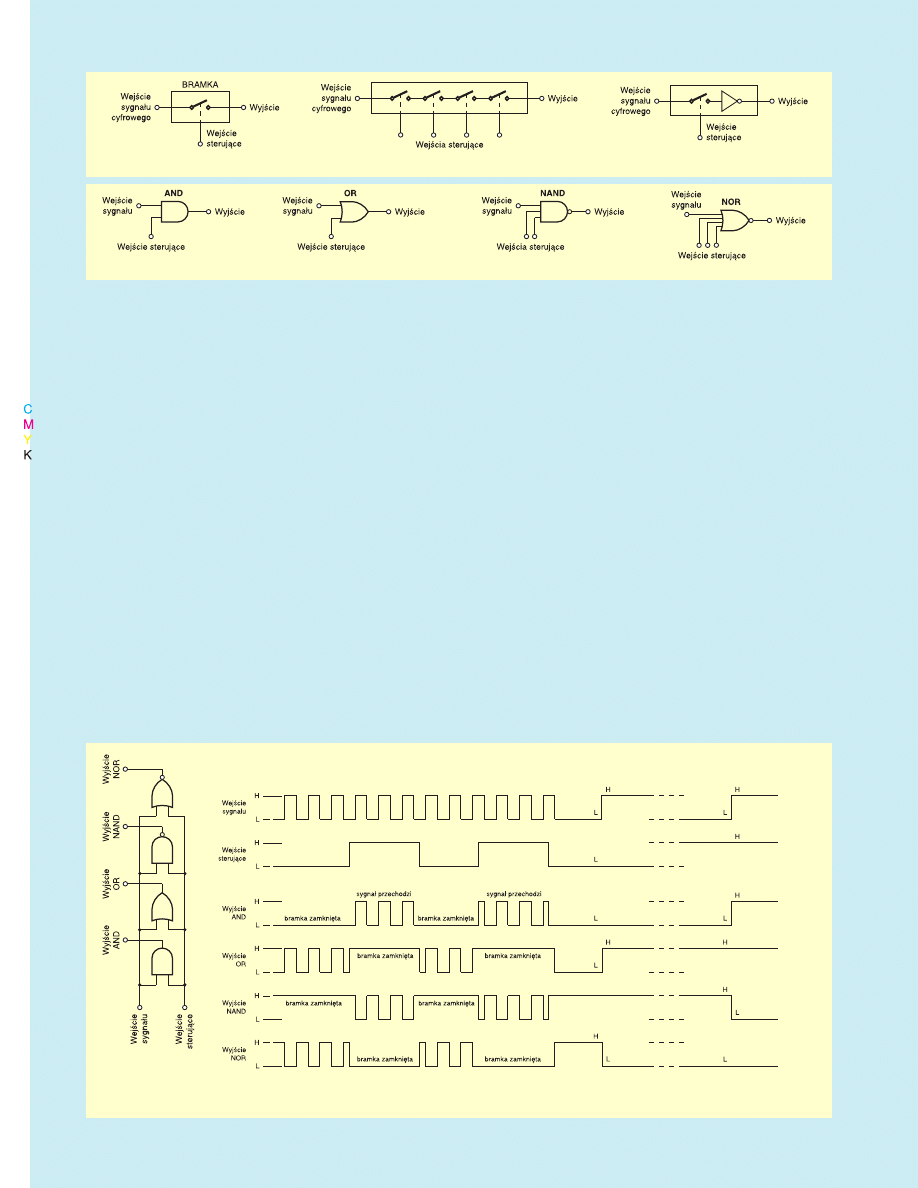
jścia sterujące. Ideę zobaczysz na rys. 7

rys. 7

rys. 7.

Bramka AND czy NAND zostanie ot−

warta tylko wtedy, jeśli na wszystkich
wejściach sterujących będzie stan wyso−
ki. Analogicznie, bramka OR czy NOR bę−
dzie otwarta, gdy na wszystkich we−
jściach sterujących jest stan niski.

Korzystając z rysunku 8

rysunku 8

rysunku 8 i podanych

wcześniej  informacji  zastanów  się,  czy
rzeczywiście  tak  jest.  Takie  rozumienie
bramki  będzie  ci  wręcz  niezbędne,  jeśli
będziesz projektował układy, kierując się
intuicją.

Doszliśmy tu do ważnego punktu na−

szych rozważań. Może zapytasz, po co
aż cztery różne bramki? Czy nie wystar−
czyłaby jedna?

To jest dobre pytanie. Przypuszczam,

że w pełni docenisz sprawę dopiero wte−
dy, gdy natkniesz się na kłopot: w jakimś
układzie  liczącym  licznik  będzie  zliczał
o jeden  impuls  za  dużo  lub  za  mało.  Na
razie  dokładnie  przeanalizuj  rysunek  9

rysunek 9

i zauważ czym w poszczególnych bram−
kach  różni  się  sygnał  na  wyjściu,  gdy
bramka  jest  zamknięta,  i gdy  przepusz−
cza sygnał. Zwróć szczególną uwagę, co
się  dzieje  na  wyjściach  w momentach
zmiany stanu na wejściu sterującym.

W takiej roli bramki stosowane są na

przykład  w częstościomierzach,  gdzie
wzorcowy  impuls  otwiera  bramkę  na
ściśle  określony  czas  i umożliwia  zlicza−
nie  impulsów  podanych  na  wejście.
W zależności  od  zastosowanego  liczni−
ka, trzeba wykorzystać właściwą bramkę
− do  tej  sprawy  wrócimy  jeszcze  przy
omawianiu liczników.

Oczywiście

powyższe

informacje

o bramkowaniu nie dotyczą bramki NOT:
mówimy  o bramce  NOT,  a przecież  nie
ma  tu  mowy  o żadnym  bramkowaniu,
tylko  o zmianie  sygnału  logicznego  na
przeciwny.  Ściśle  biorąc,  nie  powinniś−
my więc mówić “bramka NOT”, obecnie
jednak często używa się pojęcia bramki
w szerszym  znaczeniu,  i nie  zdziw  się,
jeśli w literaturze spotkasz takie określe−
nie. Zauważ, że w podręcznikach stosuje
się  zazwyczaj  określenie  “element
NOT” lub “funktor NOT”. My, praktycy,
zazwyczaj zamiast “bramka NOT” mówi−
my krótko “negator” lub “inwerter”.

Piotr Górecki

Rys. 7. Bramka jako sterowany zawór.

Rys. 8. Wykorzystanie bramek w roli zaworu.

Rys. 9. Różnice
w działaniu bramek.

Układy cyfrowe

LEKTRONIKA DLA WSZYSTKICH 2/97

Rys. 10. Bramki EX−OR i EX−NOR.

Rys. 11. Wykonanie bramki EX−OR z bramek NAND.

Inne bramki

Istnieją też elementy logiczne, realizu−

jące jeszcze inne funkcje. Zapewne spo−
tkałeś  już  określenie  EX−OR  i EX−NOR.
Elementy  takie  również  nazywamy
bramkami.  W literaturze  niekiedy  są
oznaczane  jako  bramki  XOR  lub  XNOR.
Elementów  tych  z pewnością  będziesz
używał w swoich układach.

Na pewno chciałbyś intuicyjnie zrozu−

mieć ich działanie, a jest ono bardzo
proste.

Spróbuj zapamiętać: na wyjściu dwu−

wejściowej bramki EX−OR pojawia się
stan wysoki, gdy na wejściach występu−
ją różne stany logiczne. Natomiast gdy
oba wejścia mają ten sam stan logiczny
(obojętnie czy wysoki, czy niski), na wy−
jściu występuje stan niski.

Bramka EX−NOR działa tylko trochę

inaczej − gdy stan wejść jest jednakowy,
na wyjściu pojawia się stan wysoki, gdy
stany są różne − stan niski.

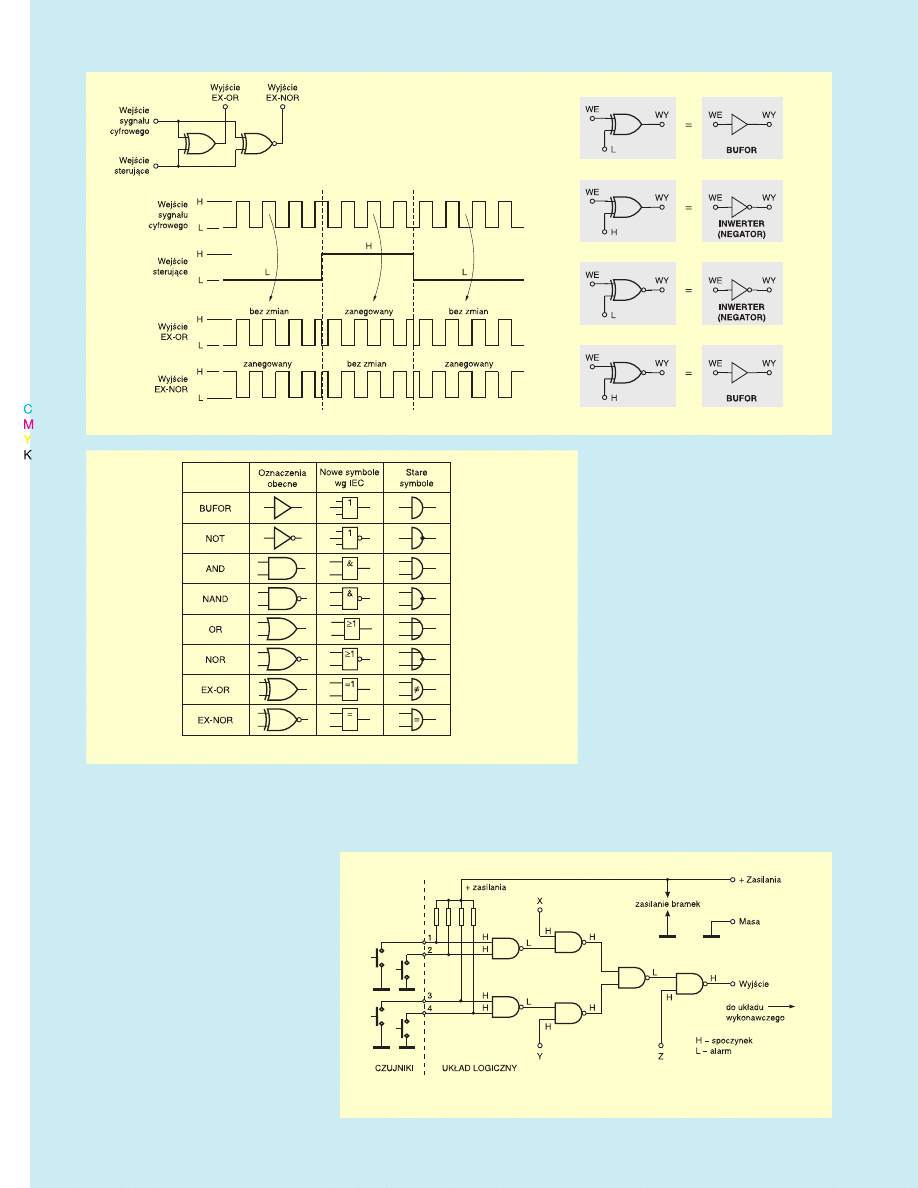
Jest to rzeczywiście proste. Na rysun−

rysun−

ku 10

ku 10 znajdziesz symbole i opis działania
bramek EX−OR i EX−NOR.

Na rysunku 11

rysunku 11

rysunku 11 zobaczysz, jak wyko−

nać  bramkę  EX−OR  z bramek  NAND.
W praktyce  nigdy  się  tak  nie  robi,  bo−
wiem  produkowane  są  układy  scalone
zawierające po cztery bramki EX−OR albo
EX−NOR w jednym układzie scalonym.

Do czego wykorzystasz w praktyce

bramki EX−OR i EX−NOR?

Najczęściej do sprawdzenia, czy dane

sygnały mają takie same poziomy logicz−
ne. Ale nie tylko.

Na rysunku 12

rysunku 12

rysunku 12 zobaczysz inną możli−

wość,  przydatną  w praktyce:  w zależ−
ności od stanu na jednym z wejść, bram−
ka  EX−OR  (lub  EX−NOR)  neguje  sygnał
wejściowy,  albo  przepuszcza  go  bez
zmian. Zapamiętaj właściwość pokazaną
na rysunku 12 − przyda ci się, gdy w trak−
cie

projektowania

zagospodarujesz

bramki EX−OR i EX−NOR nie wykorzysta−
ne w swej klasycznej roli.

Może zapytasz jeszcze, czy istnieją

wielowejściowe  bramki  EX−OR  i EX−
NOR?  W praktyce  spotkasz  się  tylko
z bramkami  dwuwejściwymi.  Bramki  te
można w prosty sposób łączyć, by uzys−
kać coś podobnego do bramki wielowe−
jściowej,  ale  stosuje  się  to  bardzo  rza−
dko. Istnieją też wielowejściowe układy
zwane  generatorami  i kontrolerami  pa−

rzystości,  przeznaczone  do  systemów
przesyłania  danych  − ich  działanie  nieco
przypomina  działanie  opisywanych  bra−
mek.

Uważaj teraz! W starej krajowej litera−

turze lub w publikacjach obcojęzycznych
spotyka  się  odmienne  symbole  bramek
(oraz  innych  układów  logicznych).  Żeby
nie  robić  ci  wody  z mózgu,  na  poprzed−
nich  rysunkach  podałem  ci  najczęściej
spotykane

oznaczenia,

występujące

w większości dostępnych dziś źródeł.

Na rysunku 13

rysunku 13

rysunku 13, w pierwszej kolumnie

znajdziesz  oznaczenia  według  dotych−
czas  obowiązujących  norm  krajowych,
w drugiej  kolumnie  nowe  oznaczenia,
zgodne  z zaleceniami  międzynarodowej
organizacji  ISO,  które  są  obecnie  wpro−
wadzane  w wielu  krajach,  także  u nas.
Przyzwyczajaj  się  powoli  do  tych  no−
wych symboli. W trzeciej kolumnie zna−
jdziesz  dawne  oznaczenia,  spotykane
w starszej literaturze.

Logika ujemna

Popatrz teraz na układ pokazany na ry−

ry−

sunku 14

sunku 14. Układ taki może być zastoso−
wany  w małej  centralce  alarmowej.  Do
czterech  wejść  oznaczonych  1...4  dołą−
czone są czujniki. Wejście Z służy do cał−
kowitego  wyłączania  centralki.  Nato−
miast  wejścia  X,  Y umożliwiają  włącza−
nie i wyłączanie pewnych stref (na przy−
kład garaż powinien być chroniony w no−
cy  także  podczas  obecności  domowni−
ków).  Naruszenie  (zwarcie)  któregokol−
wiek  czujnika  wywoła  alarm,  o ile  tylko
na  wejściach  zezwalających,  oznaczo−
nych  X,  Y,  Z,  będzie  występował  stan
wysoki. W stanie gotowości (czuwania),
w poszczególnych  punktach  układu  wy−
stąpią  stany  logiczne,  takie  jak  podano
na rysunku.

Zauważ, że jeśli naruszony zostanie

przynajmniej  jeden  czujnik,  zmieni  się
stan  na  wyjściu  którejś  z bramek  ozna−
czonych A, B. Coś tu jakby nie gra: choć
są  to  niewątpliwie  bramki  NAND,
w rzeczywistości  realizują  funkcję  OR
lub  NOR!  Następne  bramki,  oznaczone
C i D rzeczywiście

realizują

funkcję

NAND − stan wyjścia zmienia się, gdy na
wszystkich  wejściach  pojawi  się  stan
wysoki.  Ale  bramka  oznaczona  E znów
pełni  jakby  funkcję  OR  czy  NOR  − poja−
wienie  się  stanu  niskiego  na  przynaj−
mniej  jednym  jej  wejściu  zmienia  stan

5 6

Układy cyfrowe

LEKTRONIKA DLA WSZYSTKICH 2/97

Rys. 12. Nietypowe wykorzystanie bramek EX−OR i EX−NOR.

Rys. 14. Przykładowy układ logiczny.

Rys. 13. Spotykane sybmole bramek.

wyjścia.  Ostatnia  bramka,  oznaczona  F,
realizuje  funkcję  NAND  − zmienia  stan
wyjścia,  gdy  na  wszystkich  wejściach
wystąpi stan wysoki. Dokładnie to przea−
nalizuj. Coś nam tu przypomina opis dzia−
łania bramki OR i NOR. Jak to rozumieć?

Do tej pory zakładaliśmy, zresztą cał−

kowicie słusznie, że brak napięcia to stan
niski − L, a obecność napięcia (dodatnie−
go) to stan wysoki − H.

Ale przecież jest to kwestia umowy:

równie  dobrze  moglibyśmy  ustalić,  że
brak  napięcia  to  stan  wysoki,  a obec−
ność  napięcia  −  stan  niski.  Tym  sposo−
bem  doszliśmy  do  tak  zwanej  logiki
ujemnej.

Jeśli zaglądałeś do podręczników

omawiających  technikę  cyfrową,  to  ist−
nieje  duże  prawdopodobieństwo,  że  ja−
kiś  niepoprawny  teoretyk  próbował  ci
namieszać  w głowie,  omawiając  szcze−
gółowo  zarówno  logikę  dodatnią,  jak

i ujemną. Wydaje się to bardzo skompli−
kowane. Ta cała logika ujemna to praw−
da, ale praktykującemu elektronikowi
może narobić w głowie sporo zamiesza−

nia i wtedy więcej z niej szkody niż po−
żytku.

Wyjaśniam więc raz na zawsze: we

wszystkich praktycznych opisach i publi−
kacjach  z jakimi  się  spotkasz,  a przede
wszystkim w firmowych katalogach cyf−
rowych  układów  scalonych,  stosuje  się
oznaczenia  i pojęcia  związane  z logiką
dodatnią,  gdzie  stan  niski  to  napięcie
bliskie  zera,  a stan  wysoki  to  napięcie
bliskie  dodatniego  napięcia  zasilania.
W zasadzie  możesz  więc  nie  zawracać
sobie głowy logiką ujemną, ale koniecz−
nie musisz zrozumieć pewne istotne za−
gadnienie,  które  dało  o sobie  znać  przy
analizie rysunku 14. Oto ono:

Zgodnie z tym, co pokazałem na ry−

sunku 14 musisz zapamiętać, że dowol−
na bramka AND, NAND, OR, NOR może
pełnić zarówno swą “przepisową” funk−
cję, jak też funkcję niejako przeciwną.

Może jesteś zaskoczony: jak to jest,

że ta sama bramka pełni funkcję AND
i jednocześnie (tak!) funkcję OR? Teore−
tyk odpowie: tu właśnie wchodzi w grę

Układy cyfrowe

LEKTRONIKA DLA WSZYSTKICH 2/97

Jeśli zajmujesz się techniką

cyfrową, powinieneś o każdej

porze dnia i nocy pamiętać, jak

działają bramki NOT, OR, NOR,

AND, NAND, EX−OR i EX−NOR.

Musisz dokładne rozumieć

działanie bramki jako

sterowanego zaworu.

Powinieneś rozumieć dlaczego
każda bramka NAND czy AND

umożliwia zrealizowanie

funkcji NOR i OR, i jakie to ma

znaczenie praktyczne.

Nie bój się logiki ujemnej − to

nic trudnego; pamiętaj, że

o rzeczywistej funkcji bramki

decydują stany na jej wejściach

podczas “spoczynku”.

Nie ucz się żadnych tabelek −
staraj się zrozumieć zasady.

W razie potrzeby przygotuj

sobie ściągawkę zawierającą

podstawowe informacje.

Dowolna bramka może

w praktycznym układzie pełnić

zarówno swą “przepisową”

funkcję, jak też funkcję niejako

przeciwną. W praktyce

używając bramek jednego typu

(ale muszą to być bramki

z negacją) NOR, bądź NAND,

możesz zrealizować wszystkie

funkcje podstawowe: NOT, OR,

NOR, AND, NAND, a także

wszelkie funkcje złożone.

logika ujemna. Nie przestrasz się tej
logiki ujemnej, jest to bardzo proste −
spróbuj wyczuć zagadnienie intuicyj−
nie.

Zauważ,

że

w układzie z rysun−
ku 14 “prawdziwą”
funkcję

pełnioną

przez bramki wy−
znaczają stany spo−
czynkowe na we−
jściach danej bram−
ki.

Nieprzypadko−

wo wcześniej do
znudzenia wkłada−
łem ci do głowy, że
bramka

AND

NAND

“zmienia

stan wyjścia, gdy
wszystkie

we−

jścia...”,  natomiast
bramka OR i NOR −
”gdy  przynajmniej  jedno  wejście...”.
Przemyśl to i spróbuj zrozumieć. Nie ra−
dzę  ci  natomiast  zapamiętywać  jakich−
kolwiek  tabelek,  bo  zaplączesz  się  bez−
nadziejnie.

Teraz już chyba w pełni rozumiesz, że

używając bramek jednego typu (ale mu−
szą to być bramki z negacją, a więc NOR
bądź NAND), możesz zrealizować wszys−
tkie funkcje NOT, OR, NOR, AND,
NAND.

Ma to bardzo ważne konsekwencje

praktyczne.

Niech do ciebie dotrze, że w układzie

z rysunku  14  nie  musieliśmy  stosować
bramek NOR czy OR − odpowiednio wy−
korzystaliśmy  bramki  NAND.  Przeanali−
zuj  rysunek  14  i upewnij  się  jeszcze
raz, że w rzeczywistości bramki A, B i E
pełnią w urządzeniu funkcje odpowiada−
jące bramce NOR.

To, co ci teraz usiłuję wbić do głowy,

jest ogromnie ważne w praktyce − jeśli
uchwycisz ideę, będziesz potrafił zbudo−
wać dowolny układ, korzystając wyłącz−
nie z bramek NAND lub NOR. Oczywiś−
cie musisz pomału nabrać wprawy.

Nie znaczy to jednak, że masz wyko−

nywać  układy  zawierające  tylko  bramki
NAND albo NOR. Bez przesady! Zacho−
waj rozsądek. Przejrzyj dokładnie wcześ−
niejsze  numery  Elektroniki  dla  Wszyst−
kich  czy  Elektroniki  Praktycznej  i zwróć
uwagę, jak wykorzystuje się i jakie bram−
ki w przezentowanych tam układach.

W każdym razie zrozumienie, a właś−

ciwie  wyczucie  i przyswojenie  omówio−
nych  właśnie  zasad,  jest  bardzo  cenne
przy  projektowaniu  urządzeń  cyfrowych
zawierających bramki. Szybko się o tym
przekonasz, jeśli będziesz sam projekto−
wał  układy.  Może  pomyślisz,  że  nama−
wiam cię do czegoś wręcz przeciwnego,
niż zalecają szkolne podręczniki. W wielu
szkolnych  ćwiczeniach  masz  za  zadanie

zrealizować daną wzorem funkcję logicz−
ną  przy  użyciu  dowolnych  bramek.
W praktyce  najczęściej  bywa  zupełnie
inaczej.  Przy  prostszych  układach  nikt

nie zastanawia się
nad  wzorami,  tyl−
ko od razu próbuje
narysować  sche−
mat  układu  i na
bieżąco  zastana−
wia  się,  czy  układ
spełni postawione
zadanie

i jakich

dostępnych kos−
tek trzeba użyć.

Jeśli masz cier−

pliwość,  weź  te−
raz  kartkę  i nary−
suj  jakiś  niezbyt
s k o m p l i k o w a n y
układ  logiczny  za−
wierający  bramki

NOT, OR, NOR, AND i NAND. Potem spró−
buj zrealizować układ pełniący takie sa−
me funkcje przy użyciu jednego typu bra−
mek: NOR albo NAND.

Zakoduj sobie w głowie raz na za−

wsze,  że  każdą  funkcję  logiczną  można
zrealizować z pomocą bramek NAND czy
też  NOR.  Używając  odpowiednio  dużej
ilości takich bramek, teoretycznie mógł−
byś  wykonać  do−
wolny  przerzutnik,
licznik,

dekoder,

a nawet mikropro−
cesor.

Nie

bę−

dziesz tego robił,
bo wcześniej zro−
bili to za ciebie inni
i masz do dyspozy−
cji

wiele

cyfro−

wych

układów

scalonych  pełnią−
cych  najróżniejsze
funkcje.  Układy  te
zacznę ci przedsta−
wiać  w jednym  z
następnych  odcin−
ków.  Wykaż  cierp−
liwość: zanim prze−
jdziemy  do  prze−
rzutników

liczni−

ków,

rejestrów

i d e k o d e r ó w ,
wcześniej musisz
przyswoić

sobie

sporo

rzetelnej

wiedzy.

Dlatego

w następnym od−
cinku zajmiemy się
budową wewnętr−
zną

współczes−

nych  bramek  i in−
nych  układów  cyfrowych  oraz  praktycz−
nymi  konsekwencjami  różnic  w ich  bu−
dowie.

Piotr Górecki