MODEL ODPOWIEDZI I SCHEMAT PUNKTOWANIA ARKUSZA
EGZAMINACYJNEGO I
Odpowiedzi do zadań zamkniętych
Nr
zadania
Propozycje rozwiązań
Punkty
1
Ruch samochodu jest ruchem jednostajnie przyspieszonym. Droga przebyta
przez samochód jest iloczynem średniej prędkości i czasu. Ponieważ
początkowa prędkość jest równa zeru, to średnia prędkość jest równa
połowie końcowej prędkości. Przebyta droga wynosi więc:
m
140
s
10
2
s
/
m
28
t
2
v
s
=
⋅
=
⋅
=
.
Odpowiedź C.
1
2
Piłka porusza się ruchem jednostajnie zmiennym pod wpływem siły
ciężkości. Na wysokości 3,2 m jej prędkość wynosiła zero. Z zasady
zachowania energii dostajemy końcową prędkość v = [2gh]
1/2
=
[2·10m/s·3,2m]
1/2
= 8 m/s.
Odpowiedź B.
Możliwe jest też inne rozwiązanie prowadzące do tego samego wyniku.
1
3
Z wykresu odczytujemy, że podniesienie nieznanej masy m o każde 10
metrów wymaga pracy W = 30 000 J. Wiemy, że podniesienie ruchem
jednostajnym masy m na wysokość h w jednorodnym polu grawitacyjnym
ziemskim wymaga pracy: W = mgh, a więc m = W/gh = 300 kg.
Odpowiedź C.
1
4
Z trzeciego prawa Keplera wiemy, że stosunek trzeciej potęgi promienia
orbity do kwadratu okresu obiegu planety wokół Słońca jest stały, taki sam
dla każdej planety.
A więc (R
Jowisz
/R
Ziemia
)
3
= (T
Jowisz
/T
Ziemia
)
2
. Stosunek kwadratów okresów
wynosi (12/1)
2
= 144. Stosunek promieni orbit Jowisza i Ziemi jest więc
równy pierwiastkowi trzeciego stopnia z 144, a zatem 5,2.
Odpowiedź A.
Ten sam wynik otrzymamy z równania dynamicznego mówiącego, że rolę
siły dośrodkowej spełnia siła grawitacji.
1
5
Dwa połączone szeregowo kondensatory mają pojemność 5 pF. Dołączenie
do nich równolegle pojemności 10 pF daje całkowitą pojemność 15 pF.
Odpowiedź C.
1
6
Przy emisji elektronu w rozpadzie
β liczba masowa jądra nie ulega zmianie,
natomiast liczba porządkowa, zgodnie z prawem zachowania ładunku,
rośnie o jeden. Warunki te spełnia jądro niklu
, z punktu a.
Ni
60
28
Odpowiedź A.
1
1
7
Przez kondensator nie płynie prąd stały z ogniwa. A więc pierwsza żarówka
nie może świecić po naładowaniu się kondensatora, bo nie płynie przez nią
prąd.
Odpowiedź D.
1
8
W danym procesie nie zmieniło się ciśnienie gazu (przemiana izobaryczna),
a więc temperatura bezwzględna musiała wzrosnąć proporcjonalnie do
wzrostu objętości. Objętość wzrosła dwukrotnie, temperatura wzrosła
dwukrotnie.
Odpowiedź B.
1
9
Siła działająca pomiędzy równoległymi przewodami z prądem zależy od
wartości obu prądów oraz wzajemnego zwrotu przepływu prądu. Zmiana
zwrotów obu prądów bez zmiany ich wartości nie wpływa na kierunek ani
wartość siły.
Odpowiedź D.
1
10
Energia całkowita drgań E
całk
= 1/2
.
kA
2
=
2
2
2
A
T
4
m
2
1
⋅
⋅
⋅
π
.Dwukrotne
zmniejszenie okresu drgań przy stałej amplitudzie oznacza , że energia
całkowita drgań zwiększa się 4 razy.
Odpowiedź B.
1
11
Soczewka skupiająca ogniskuje równoległą wiązkę światła słonecznego w
ognisku, a więc w odległości ogniskowej od soczewki.
Odpowiedź C.
1
Razem punktów
11
Odpowiedzi do zadań otwartych
Numer
zadania
Propozycje rozwiązań Liczba
punktów
Czas na pokonanie pierwszych 4 km wynosi 4/60 godz = 4 min. Czas na
pokonanie pozostałych 6 km wynosi 6/10 godz = 36/60 godz = 36 min.
Całkowity czas jazdy wynosi 36+4 = 40 min.
2
12
Średnia prędkość, to całkowita droga podzielona przez całkowity czas, a
więc 10km/40 min = (10·60/40) km/h = 15 km/h 4,17m/s
≈
1
3
Wykres pokazuje jednostajny przyrost prędkości w czasie. Przyczepa
porusza się więc ruchem jednostajnie przyspieszonym. Z wykresu
odczytujemy, że przyrost prędkości w czasie 40 sekund wyniósł 10m/s.
Przyspieszenie wynosi więc 10/40 = 0,25 m/s
2
.
1
13
Skoro masa przyczepy wynosi 300 kg, to siła konieczna do nadania jej
przyspieszenia 0,25 m/s
2
wynosi F=0,25·300 = 75 N.
1
2
2
W zderzeniu niesprężystym zachowany zostaje pęd. Pęd lżejszego
samochodu wynosi 8 000 kg m/s, pęd drugiego samochodu wynosi - 18 000
kg m/s. Znak minus oznacza, że zwrot prędkości drugiego samochodu
będzie przeciwny niż pierwszego. Całkowity pęd wynosił - 10 000 kg m/s.
1
Po zderzeniu oba samochody poruszały się razem. Całkowita masa obu
pojazdów wynosiła 2 000 kg, a ich prędkość musiała być taka, żeby pęd
wynosił - 10 000 kg m/s. Prędkość wynosiła więc -10 000/2000 = -5 m/s.
1
14
Oba pojazdy tuż po zderzeniu poruszały się z prędkością 5 m/s o takim
zwrocie, jak zwrot prędkości cięższego samochodu przed zderzeniem.
1
3
Prędkość kątowa koła wynosi
ω = v/r
Czas pełnego obrotu koła wynosi T = 2
π/ω = 2 π r/v ,
T=
s
s
m
m
45
,
0
/
5
36
,
0
14
,
3
2
=
⋅
⋅
1
15
Ilość obrotów n = s/2πr =
20
36
,
0
14
,
3
2
45
≈
⋅
⋅
m
m
1
2
Natężenie pola, przy warunku jednorodności, to iloraz napięcia U i
odległości między głowicą a papierem l, a więc E = U/l
1
16
Siła F = qE = qU/l = 3·10
-13
C
.
8V /(10
-4
m ) = 24·10
-9
N.
1
2
Natężenie prądu płynącego przez opornik R
1
wynosi 5 A. Natężenia prądu
płynącego przez oporniki R
2
i R
3
są jednakowe, bo opory te połączone są
równolegle i mają taką samą wartość. Z pierwszego prawa Kirchhoffa
wnioskujemy, że natężenie prądu płynącego przez opornik R
3
wynosi 2,5 A.
1
Woltomierz mierzy spadek napięcia na oporniku, czyli iloczyn natężenia
prądu i wartości oporu. W tym przypadku jest to 2,5A·1
Ω = 2,5 V.
1
Napięcie między biegunami baterii jest sumą napięć na oporze R1 i
woltomierzu.
1
17
Wartość napięcia jest więc równa: 10V+2,5V = 12,5V
1
4
Obwód wtórny transformatora powinien mieć więcej zwojów, niż obwód
pierwotny, aby napięcie na wyjściu transformatora było większe niż na
wejściu.
1
18
Pożądany stosunek napięć ma wynosić 2, a więc w obwodzie wtórnym
powinno być dwukrotnie więcej zwojów, niż w pierwotnym. Liczba zwojów
powinna wynosić 1000.
1
2
3
Siła nacisku samochodu na powierzchnię jest równa iloczynowi ciśnienia
powietrza w oponach i powierzchni styku.
F = 4·2·10
5
Pa
.
0,1m·0,1m= 8·10
3
N.
1
19
Masa samochodu, to siła ciążenia (równa tutaj sile nacisku) podzielona
przez przyspieszenie ziemskie, czyli m =
kg
s
m
N
800
/
10
10
8
2
3
=
⋅
1
2
Ciśnienie na głębokości h = 3 m pod wodą jest sumą ciśnienia
atmosferycznego i ciśnienia słupa wody. Wynosi ono :
p
1
= 3m·10m/s
2
·10
3
kg/m
3
+ 10
5
Pa = 1,3·10
5
Pa.
1
Ciśnienie metanu w pęcherzyku jest takie samo, jak ciśnienie na zewnątrz
pęcherzyka. Ponieważ temperatura metanu nie zmieniła się, to
zmniejszaniu się ciśnienia towarzyszyło zwiększanie się objętości gazu
1
20
Z prawa gazu doskonałego p
1
/p
2
= V
2
/V
1
. Ponieważ p
1
/p
2
= 1,3 , to
V
2
/V
1
= 1,3. Objętość metanu zwiększyła się 1,3 raza.
1
3
Silnik wykonał pracę mechaniczną W = 10
8
J. Ponieważ sprawność wynosi
25%, musiał uzyskać ze spalenia benzyny ciepło Q=10
8
J/0,25 = 4·10
8
J.
1
21
Ciepło spalania wynosi 4·10
7
J/kg, a więc silnik musiał spalić masę
m=
=
⋅
⋅
kg
J
J
/
10
4
10
4
7
8
10 kg benzyny.
1
2
Dźwięk musiał przebyć drogę l do skały i jeszcze raz tę samą drogę
powrotną z prędkością v= 330 m/s. A więc 2l =vt= 330m/s·0,5s = 165 m.
Odległość od skał l = 165m/2 = 82,5 m.
1
22
Długość fali, to stosunek jej prędkości do częstotliwości :
f
v
=
λ
=
=
⋅ s
s
m
/
1
220
/
330
1,5m.
1
2
Ogniskowa opisanej soczewki związana jest z promieniem soczewki
wzorem soczewkowym 1/f = (n
wz
-1)(1/r).
1
23
Stąd r= (n-1)f = (1,5-1)·0,5m = 0,25m. Promień soczewki wynosi 0,25 m.
1
2
Razem punktów
29
4
MODEL ODPOWIEDZI I SCHEMAT OCENIANIA ARKUSZA
EGZAMINACYJNEGO II
Nr
zad.
Propozycje rozwiązań
Liczba
punktów
24.1
Opór kuchenki R= U
s
/I
s
=22
Ω.
Opór przewodnika R' =
ρ l/s = 1,7 Ω.
Całkowity opór jest równy R+R’
A więc natężenie prądu I = U
s
/(R+R') 9,3 A.
≈
1
1
1
1
24.2 U = I
.
R= 204,6 V
1
24.3 P = RI
2
=U
.
I 1902,8 W
≈
1
24.4 P' = R' I
2
147 W
≈
1
24.5
E = P·t
≈ 190280Wh
E
≈ 190,3 kWh
1
1
24.6
E
0
= (P+P')t
E
0
≈ 205 kWh
1
1
24.7 0,3(zł/kWh)
.
P' t = 4,41zł
1
24.8
Przewód powinien być grubszy, będzie miał mniejszy opór i straty energii
będą mniejsze
2
14
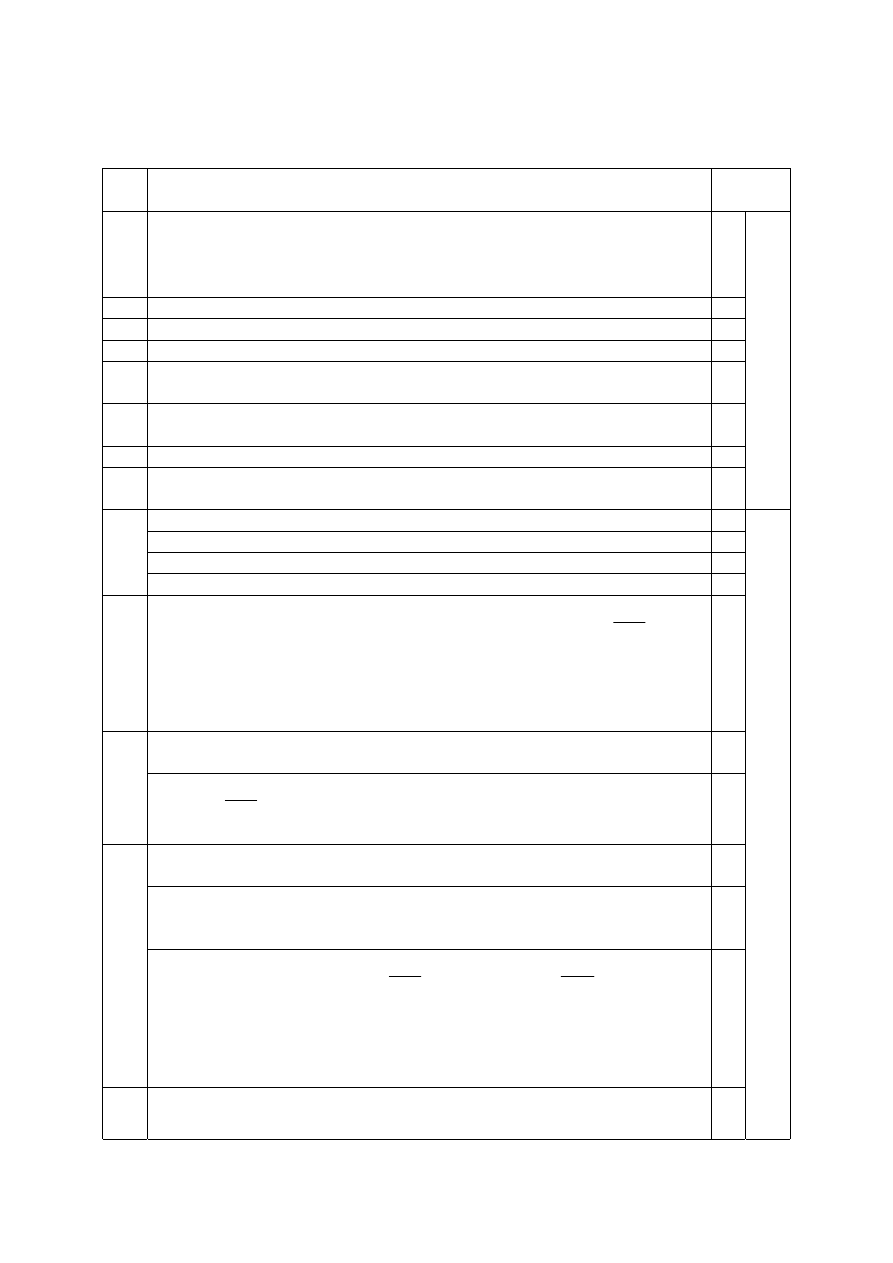
Wyskalowanie wykresu.
1
Naniesienie punktów pomiarowych.
1
Naniesienie niepewności pomiarowych.
1
25.1
Wykreślenie prostej „najlepszego dopasowania”
1
25.2
Z praw ruchu, dla małych drgań wahadła matematycznego T
2
=
l
g
⋅
2
4
π
,
gdzie g jest przyspieszeniem ziemskim. Wykres T
2
( l ) dla takiego wahadła
jest półprostą o początku w punkcie (0,0). Okres nie zależy od masy.
Przedłużenie narysowanego wykresu przechodzi przez punkt (0,0). Zatem
badane wahadło może być traktowane jak matematyczne.
3
Z wykresu obliczamy współczynnik kierunkowy narysowanej prostej,
a=4s
2
/m.( patrz wykres 1 )
2
25.3
Zatem g=
a
2
4
π
=9,86m/ s
2
Uwaga. Wynik może być nieco inny, gdy inaczej poprowadzono prostą.
1
Narysowanie prostych o najmniejszym i największym nachyleniu (wykres
2)
1
Obliczenie na podstawie wykresu współczynników kierunkowych:
a
min
3,56s
2
/m
≈
a
max
4,2 s
2
/m
≈
2
2
25.4 Obliczenie przyspieszeń: g
max
=
min
2
4
a
π
≈ 11,08m/s
2
, g
min
=
39
,
9
a
4
max
2
≈
π
m/s
2
g
∈ [ 9,39m/s
2
; 11,08m/s
2
]
Uwaga. Wartości liczbowe mogą wyjść nieco inne, bo zależą od tego jak
poprowadzono proste. Liczy się metoda.
1
1
25.5
Z wykresu odczytujemy, że długość wahadła powinna wynosić 1,0 m z
niepewnością 0,04m
(
)
m
02
,
0
m
1
±
1
1
19
Rozłożenie prędkości v
0
na składowe: v
0x
= v
0
cos 45
0
= 4,95 m/s ,
v
0y
= v
0
sin 45
0
=4,95m/s.
Obliczenie wartości prędkości na tym etapie nie jest konieczne.
1
Składowa ruchu wzdłuż poziomu: x (t) = v
0
cos 45
0
t.
1
Składowa ruchu wzdłuż pionu: y(t) = 2,45+v
0
sin45
0
t – gt
2
/2.
1
26.1
Eliminuję t, dostaję równanie toru:
y(x) = 2,45+x tg 45
0
– gx
2
/(2v
0
2
cos
2
45
0
)
.
Uwaga. Można to zrobić w innym układzie odniesienia.
1
Wstawiając x = 4,2 m znajdujemy y = 3,05 m, a zatem tor środka piłki
przechodzi przez środek kosza.
1
Kąt, pod jakim wpada piłka do kosza, określony jest wzorem: tg
β = -v
x
/v
y
.
1
v
y
=v
0
sin45
0
-gt= -3,55m/s
1
t=x /(v
0
cos45
0
)=4,2m / (4,95m/s)=0,85s. Jest to czas, po którym piłka
wpadnie do kosza.
1
tg
β = 4,95/3,55 = 1,39.
1
26.2
Kąty, pod którymi możliwe jest wejście piłki do kosza mają tangensy
zawarte pomiędzy 0 a tg 60
0
≅ 1,73. Obliczony tangens kąta wpadania
mieści się w danym zakresie. A zatem piłka wpadnie do kosza.
2
Najwygodniej skorzystać z zasady zachowania energii, np.
mgh
1
+
=
2
2
0
mv
2
45
cos
0
2
2
0
mv
+mg
max
h
2
Wyznaczenie h
= h
1
+v
0
2
(1-cos
2
45
0
)/2g
max
1
26.3
Obliczenie wartości h
max
=3,68m
1
Całkowita energia wypromieniowana przez Słońce w ciągu jednej sekundy
wynosi: E
c
= 4
π R
2
·1340J
1
Za poprawną selekcję danych
1
27.1
Po obliczeniach E
c
= 3,79 ·10
26
J.
1
Niedobór masy m
1
= 4·1,0073 - 4,0015 – 2
.
0,0005 = 0,0267 atomowej
jednostki masy.
∆
1
W kilogramach niedobór masy wynosi:
∆ m = 0,0267·1,66·10
-27
kg =
4,43·10
-29
kg.
1
Za poprawną selekcję danych
1
Wydzielona energia w wyniku reakcji syntezy: ∆E = ∆mc
2
= 3,99 ·10
-12
J
1
27.2
W megaelektronowoltach: E = m
1
.
931,5
∆
∆
2
2
c
c
MeV ⋅ ≈ 24,9MeV
1
Aby uzyskać obliczoną poprzednio ilość energii emitowaną przez Słońce,
liczba reakcji na sekundę wyniesie: n = E
c
/ E
∆
1
27.3
n = 3
/
=
J
10
79
,
26
⋅
J
10
99
,
3
12
−
⋅
38
10
95
,
0
⋅
1
Masa zamieniana na Słońcu w energię podczas każdej sekundy jest równa:
M
x
=
⋅
∆m n
1
27.4
M
x
= 4,43
.
10
-29
kg
.
0,95
.
10
38
= 4,21
.
10
9
kg
1
12
UWAGA!
W zadaniach 24, 25, 26, 27 wartości liczbowe wyników mogą się nieznacznie
różnić od zamieszczonych powyżej, bo zależą od przyjętych przybliżeń. Liczy się metoda
rozwiązania.
6
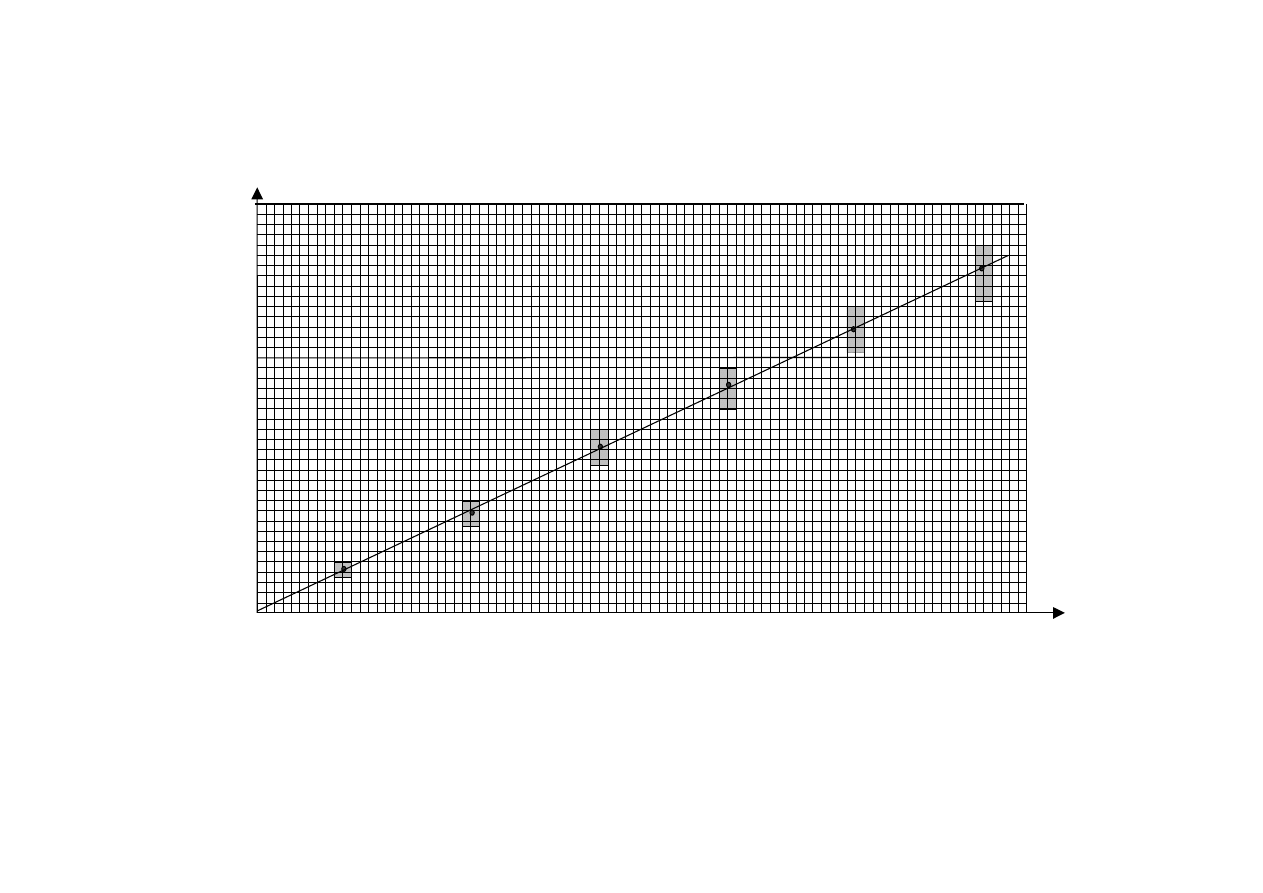
WYKRES 1
3
l[m]
5
6
7
4
2
1
0
0
1.5
1.0
0.5
T
2
[s
2
]
7
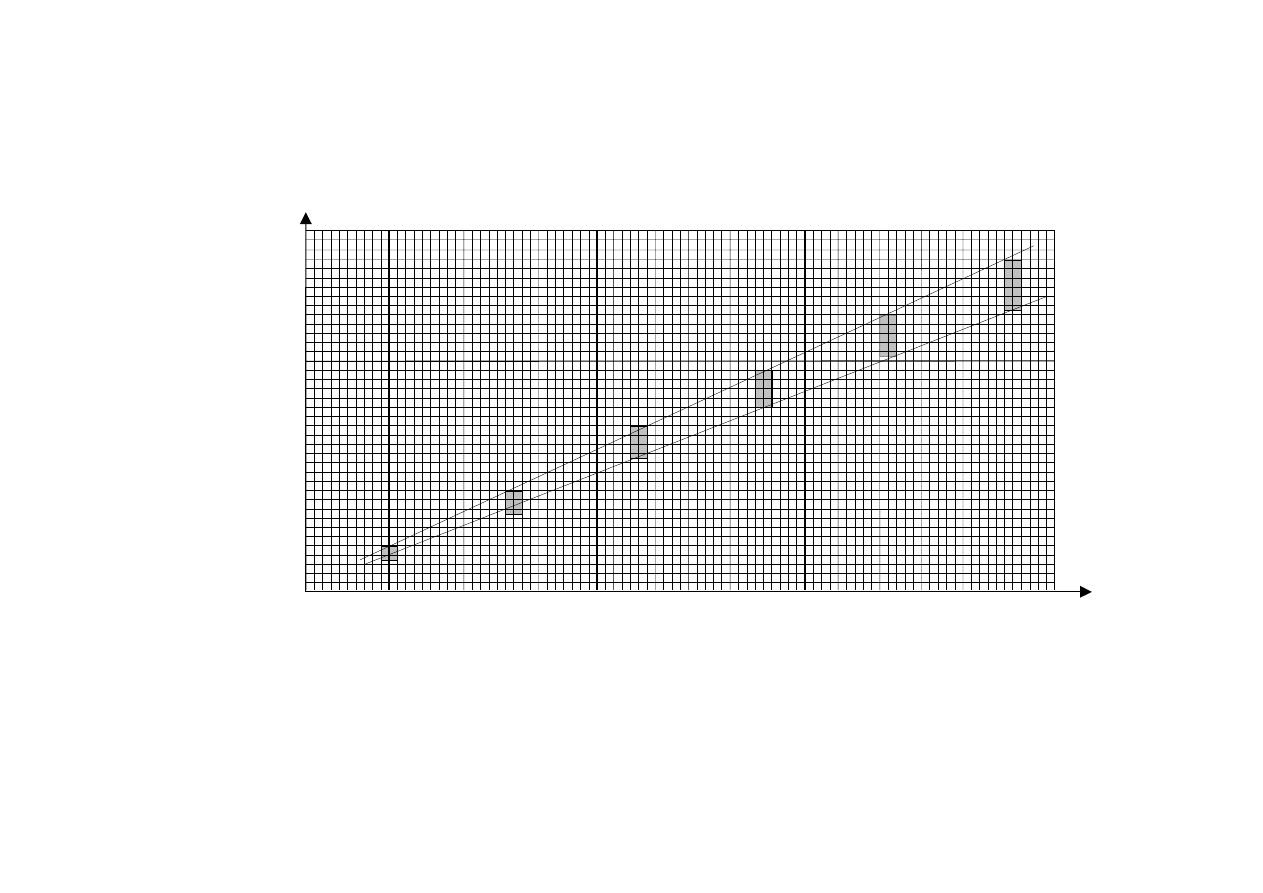
WYKRES 2
3
l[m]
5
6
7
4
2
1
0
1.5
1.0
0.5
T
2
[s
2
]
8