
Akademia Górniczo-Hutnicza
Katedra Robotyki i Mechatroniki
Identyfikacja i analiza sygnałów
Laboratorium 4
Wprowadzenie do przetwarzania sygnałów w dziedzinie
częstotliwości
Analiza sygnałów w dziedzinie częstotliwości
Analiza sygnałów w dziedzinie częstotliwości oparta jest na twierdzeniu Fouriera o rozkładzie
sygnału okresowego na sumę składników sinusoidalnych. Do przetworzenia sygnałów
nieokresowych w dziedzinę częstotliwości stosowane jest całkowe przekształcenie Fouriera.
Sygnał nieokresowy traktowany jest tutaj jako okresowy o nieskończonym okresie. Całkowe
przekształcenie Fouriera dla przebiegu dyskretnego ma postać:
( )
( )
df
e
f
X
f
1
t
n
x
t
f
2
j
2
f
2
f
s
s
s
∆
π
−
⋅
=
∆
∫
( 1 )
( )
( )
∑
+ ∞
− ∞
=
∆
π
−
∆
=
n
t
f
2
j
e
t
n
x
f
X
gdzie:
f
s
– częstotliwość próbkowania sygnału
∆
t – okres próbkowanie dla sygnału,
n – całkowity indeks próbki w sygnale.
W procesie przetwarzania sygnałów rzeczywistych nigdy jednak nie ma możliwości pomiaru
nieskończonej długości próbki sygnału. Zakłada się więc iż zmierzony sygnał jest wycinkiem
sygnału okresowego o okresie T. W wyniku poczynienia powyższych założeń definicja
dyskretnej transformacji Fouriera ma postać:
( )
(
)
s
s
N
nk
2
j
1
N
0
k
e
f
k
X
t
n
x
π
−
=
⋅
∆
=
∆
∑
( 2 )
(
)
( )
∑
−
=
π
−
∆
=
∆
1
N
0
n
N
nk
2
j
s
s
s
e
t
n
x
N
1
f
k
X
( 3 )
gdzie:
N
s
– liczba próbek,
T – N
s
∆
t,
f
s
– N
s
∆
f,
k – kolejny numer prążka w widmie,
n
−
kolejny numer próbki w przebiegu czasowym.
Zastosowanie dyskretnej transformaty Fouriera w Matlabie
Dyskretna transformata Fouriera (DFT) jest podstawowym narzędziem w cyfrowym
przetwarzaniu sygnałów. Podstawą realizacji DFT jest szybka transformata Fouriera (ang.
FFT). Wiele funkcji przybornika SPT (np. związanych z tworzeniem charakterystyk
częstotliwościowych w dziedzinie Z, analizą widma i cepstrum oraz z projektowaniem
niektórych filtrów) wykorzystuje funkcję FFT wewnętrznie.
Podstawowy zbiór poleceń Matlaba zawiera polecenia
fft
i
ifft
, pozwalające na obliczenie
dyskretnej transformaty Fouriera i jej odwrotności. Dla ciągu wejściowego x i jego
transformaty X (dyskretna transformata Fouriera dla równomiernie rozmieszczonych
częstotliwości wzdłuż jednostkowego okręgu) wprowadzono dwie funkcje, wiążące obydwa
ciągi:
1
N
,...,
2
,
1
,
0
n
,
W
)
1
k
(
X
N
1
)
1
n
(
x
1
N
,...,
2
,
1
,
0
k
,
W
)
1
n
(
x
)
1
k
(
X
1
N
0
k
kn
N
1
N
0
n
kn
N
−
=
+
=
+
−
=
+
=
+
∑
∑
−
=
−
−
=
( 4 )
gdzie
π
−
=
N
2
j
N
e
W
.
W równaniach tych pierwszy indeks ciągu ma wartość 1 zamiast 0. Jest to związane z
konwencją indeksowania wektorów, przyjętą w pakiecie Matlab.
Uwaga: W Matlabie zastosowano ujemną wartość j dla obliczeń funkcji
fft
. Jest to
konwencja inżynierska. W dziedzinie fizyki i matematyki typowe jest użycie dodatniej
wartość j.
W wywołaniu podstawowym funkcja
fft
oblicza DFT z wejściowego wektora lub macierzy
(dla sygnałów w postaci macierzy DFT jest obliczana dla każdej kolumny).
Przykładowo utworzono sekwencję x, składającą się z dwóch sinusoid o częstotliwościach 15
i 40 Hz, próbkowanych z częstotliwością 100 Hz.
t=(0:1/99:1);
x=sin(2*pi*15*t)+sin(2*pi*40*t);
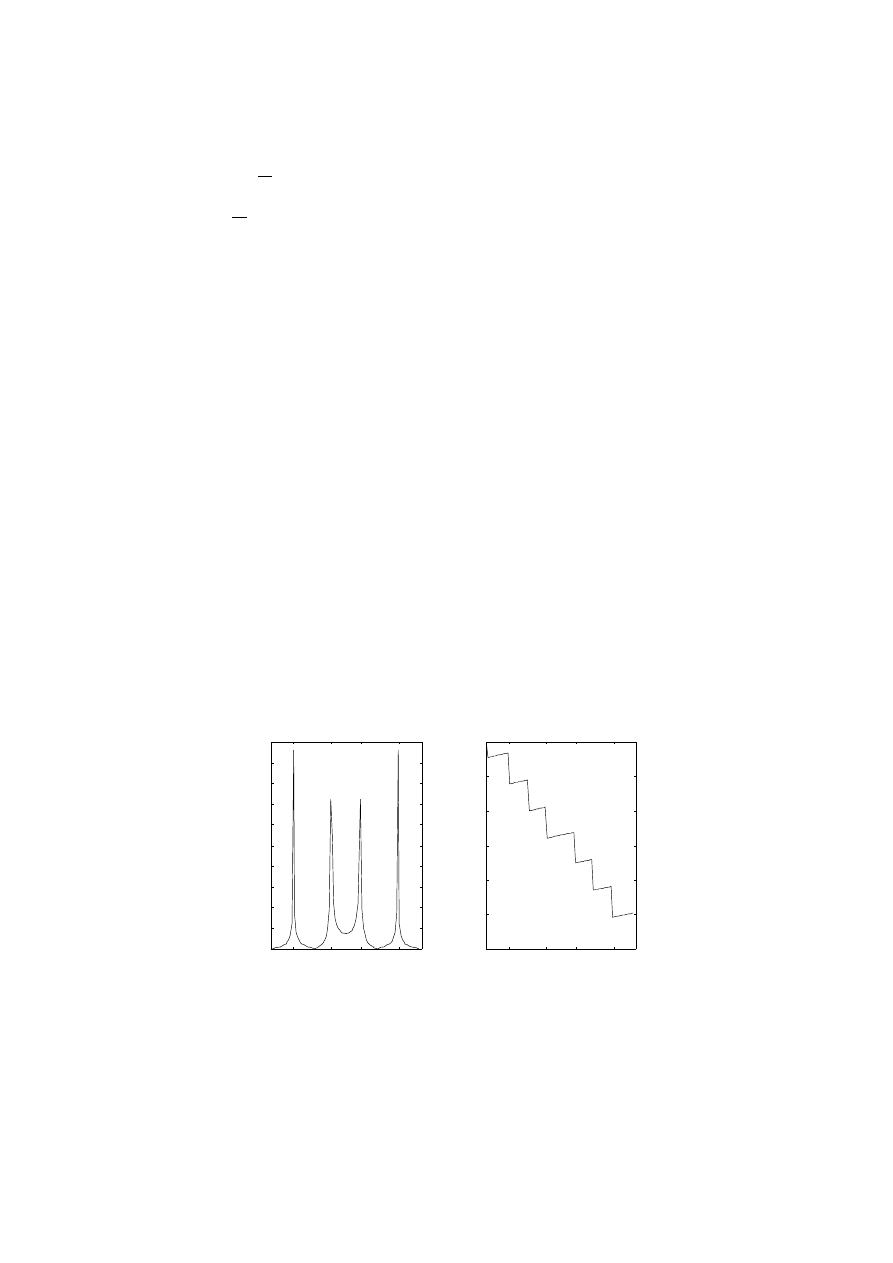
Następnie obliczono DFT z tej sekwencji oraz charakterystyki częstotliwościowe:
amplitudową i fazową.
y=fft(x);
m=abs(y);
p=unwrap(angle(y));
f=(0:length(y)-1)'*99/length(y);
subplot(1,2,1), plot(f,m,'black')
set(gca,'XTick',[15 40 60 85]);
subplot(1,2,2), plot(f,p*180/pi,'black')
set(gca,'XTick',[15 40 60 85]);
1 5
4 0
6 0
8 5
0
5
1 0
1 5
2 0
2 5
3 0
3 5
4 0
4 5
5 0
1 5
4 0
6 0
8 5
- 1 2 0 0
- 1 0 0 0
- 8 0 0
- 6 0 0
- 4 0 0
- 2 0 0
0
Rys. 1 Charakterystyki częstotliwościowe: amplitudowa i fazowa uzyskane po transfomacji przykładowej
sekwencji funkcją
fft
Drugi argument wejściowy w funkcji
fft
zadaje liczbę punktów
n
, dla których obliczana jest
transformata.
y=fft(x,n);

W przypadku gdy ciąg
x
jest krótszy od
n
,
fft
uzupełnia długość próbki zerami lub obcina
jej część, jeśli jest ona dłuższa od
n
. Jeśli
n
nie jest podane, domyślnie jest wykorzystywana
cała sekwencja danych.
Czas wykonania funkcji zależy od długości
n
ciągu poddanego działaniu DFT.
•
Dla
n
będących potęgą dwójki,
fft
używa realizowanych z dużą szybkością algorytmów
radix-2 i dlatego rezultat jest otrzymany w stosunkowo krótkim czasie. Dodatkowo
algorytm ten jest optymalizowany dla rzeczywistych wartości x. Może to spowodować
wzrostu szybkości obliczeń do 40% w porównaniu z obliczeniami dokonywanymi na
wartościach zespolonych.
•
Dla każdego
n
, które nie jest potęgą liczby dwa,
fft
używa algorytmu czynników
pierwszych. Prędkość dokonywania tych obliczeń w dużym stopniu zależy od rozmiaru
n
oraz od liczby czynników pierwszych, na które można rozłożyć liczbę
n
. Przykładowo
funkcja
fft
transformuje sekwencję o długości 1000 dużo szybciej niż sekwencję o
długości 1013, pomimo że ich moduły są zbliżone.
•
Dla
n
będącego liczbą pierwszą nie można użyć algorytmów FFT i dlatego DFT oblicza
się bezpośrednio z definicji przekształcenia.
Do obliczenia odwrotnej transformacji Fouriera (funkcja
ifft
) również podaje się jako
argument wejściowy ciąg próbek oraz opcjonalnie liczbę
n
punktów. Poniżej przedstawiono
przykładową sekwencję oryginalną
x
i jej wersję zrekonstruowaną (po uprzedniej
transformacie).
t=(0:1/7:1);
x=sin(2*pi*20*t);
f=real(ifft(fft(x)));
format long
w=[x' f']
•
w =
•
0 0
•
-0.78183148246803 -0.78183148246803
•
-0.97492791218182 -0.97492791218182
•
-0.43388373911756 -0.43388373911756
•
0.43388373911756 0.43388373911756
•
0.97492791218183 0.97492791218183
•
0.78183148246803 0.78183148246803
•
0.00000000000000 0.00000000000000
Jak widać wyniki są identyczne (w granicach błędu zaokrąglenia).
Przybornik zawiera także funkcje
fft2
i
ifft2
, służące do obliczania dwuwymiarowego
przekształcenia Fouriera oraz jego odwrotności. Funkcje te wykorzystuje się dla
przetwarzania sygnałów płaskich lub w przetwarzaniu obrazów.
Czasami jest dogodnie przegrupować wyniki obliczeń funkcji
fft
i
fft2
w ten sposób, by
składnik o zerowej częstotliwości znalazł się w środku sekwencji. Matlabowska funkcja
fftshift
wykonuje tą operację automatycznie.
Przykład transformacji Fouriera dla wybranych sygnałów
fs = 64; % Częstotliwość próbkowania sygnału
t=0:(1/fs):1; % Wektor czasu
% Utworzenie okresowego przebiegu prostokątnego

ind = round(fs/4);
x = zeros(size(t));
x(1:ind) = 1;
% Pobranie od analizy czterech okresów przebiegu
t=[t,t(end)+t,2*t(end)+t,3*t(end)+t];
x=[x,x,x,x];
% Wyplotowanie przebiegu
plot(t,x)
pause;
% Dokonanie transformaty Fouriera dla przebiegu
y = fft(x);
% Wyznaczenie wektora częstotliwości
f = (0:length(y)-1)'*fs/length(y);
% Narysowanie postaci częstotliwościowej sygnału dla dodatnich
% częstotliwości
ind=find(f<=fs/2);
plot(f(ind),abs(y(ind)))
pause;
% Transformacja Fouriera impulsu jednostkowego
fs = 128; % Częstotliwość próbkowania sygnału
t=0:(1/fs):1; % Wektor czasu
x=zeros(size(t));
x(3)=2;
% Wyplotowanie przebiegu
plot(t,x)
pause;
% Dokonanie transformaty Fouriera dla przebiegu
y = fft(x);
% Wyznaczenie wektora częstotliwości
f = (0:length(y)-1)'*fs/length(y);
% Narysowanie postaci częstotliwościowej sygnału dla dodatnich
% częstotliwości
ind=find(f<=fs/2);
plot(f(ind),abs(y(ind)))
set(gca,
'ylim'
,[0,1.2])
Zależności związane z transformacją Fouriera
W czasie stosowania przekształcenia Fouriera do analizy sygnałów w identyfikacji modeli
modalnych korzysta się z pewnych własności tego przekształcenia, do najważniejszych
należą:
-
skalowanie w dziedzinie czasu - jeżeli X(f) jest transformatą Fouriera sygnału x(t), to
X
f
a
a
jest transformatą Fouriera sygnału x(at).

-
przesuwanie osi czasu - jeżeli X(f) jest transformatą Fouriera sygnału x(t), to X f e
j ft
( )
−
2
0
π
jest transformatą Fouriera sygnału x t t
(
)
−
0
.
-
przesuwanie osi częstości - jeżeli X(f) jest transformatą Fouriera sygnału x(t), to
X f f
(
)
−
0
jest transformatą Fouriera sygnału x t e
j
f t
( )
2
0
π
.
-
różniczkowanie i całkowanie - jeżeli X(f) jest transformatą Fouriera sygnału x(t), to
)
f
(
fX
2
j
π
jest transformatą Fouriera sygnału
dt
)
t
(
dx
oraz
f
2
j
)
f
(
X
π
jest transformatą Fouriera
sygnału
( )
τ
τ
∫
∞
−
d
)
(
x
t
.
-
splot – całka splotu dwóch funkcji f(t) i h(t) jest zdefiniowana jako:
( )
(
)
)
t
(
h
)
t
(
f
d
t
h
)
(
f
t
x
∗
=
τ
τ
−
⋅
τ
=
∫
+ ∞
∞
−
jeżeli x(t) jest splotem dwu funkcji
( )
)
t
(
h
)
t
(
f
t
x
∗
=
w dziedzinie czasu to w dziedzinie
częstotliwości
( )
)
f
(
H
)
f
(
F
f
X
⋅
=
. Splot w dziedzinie czasu odpowiada mnożeniu w
dziedzinie częstotliwości.
Błędy związane z przetwarzaniem sygnału do dziedziny częstotliwości
-
aliazing – wystąpi jeśli najwyższa częstotliwość zawarta w sygnale jest wyższa od połowy
częstotliwości próbkowania sygnału.
-
przecieki widma – związane są z wyborem długości próbki sygnału branego do analizy.
Od sposobu tego wyboru zależy stopień przecieków widma w analizie sygnałów w
dziedzinie częstości. Do analizy brana jest próbka o skończonym czasie trwania T w
związku z tym w realizacji transformacji Fouriera zakłada się, że sygnał jest okresowy o
okresie T. Jeżeli rzeczywisty sygnał nie jest okresowy, występuje błąd przecieków widma.
fs = 100; % Częstotliwość próbkowania sygnału
t=0:(1/fs):1; % Wektor czasu
% Utworzenie przebiegu sinusoidalnego
f1 = 5;
x = sin(2*pi*f1*t);
% Wyplotowanie przebiegu
plot(t,x)
pause;
% Dokonanie transformaty Fouriera sygnału
y = fft(x);
% Wyznaczenie wektora częstotliwości
f = (0:length(y)-1)'*fs/length(y);
% Narysowanie częstotliwościowej postaci sygnału dla dodatnich
% częstotliwości
ind=find(f<=fs/2);
fs1=f(ind);
am1 = abs(y(ind));
plot(fs1,am1)
pause;

% Utworzenie przebiegu sinusoidalnego
f2 = 5.5;
x = sin(2*pi*f2*t);
% Wyplotowanie przebiegu
plot(t,x)
pause;
% Dokonanie transformaty Fouriera sygnału
y = fft(x);
% Wyznaczenie wektora częstotliwości
f = (0:length(y)-1)'*fs/length(y);
% Narysowanie częstotliwościowej postaci sygnału dla dodatnich
% częstotliwości
ind=find(f<=fs/2);
fs2=f(ind);
am2 = abs(y(ind));
plot(fs1,am1,fs2,am2)
Funkcje okien czasowych
Metodą zmniejszania przecieków jest zastosowanie okien czasowych o odpowiednio
dobranym przebiegu do wybierania analizowanego odcinka (próbki) ze zmierzonego sygnału.
Ogólną ideą zastosowania okien czasowych do wybierania próbki o długości T z danej
realizacji jest zmniejszenie wpływu wycięcia próbki na wyniki analizy, prążków znajdujących
się na końcach analizowanej próbki. Wybór odpowiedniego okna jest kompromisem między
dobrą estymacją amplitudy sygnału a dobrą rozdzielczością widma. Działanie okna
czasowego polega na pomnożeniu kolejnych próbek sygnału przez funkcję opisującą okno
)
t
(
w
)
t
(
x
)
t
(
x
=
gdzie:
x(t)
−
zmierzony sygnał,
w(t)
−
funkcja okna czasowego,
(t)
x
−
sygnał pomnożony przez funkcję okna.
W dziedzinie częstości odpowiada to splotowi widm.
Podstawowe funkcje okien
Podstawowym oknem jest okno prostokątne, będące wektorem jedynek.
n=50;
w=boxcar(n);
plot(w)
Powyższe instrukcje umożliwiają wygenerowanie okna prostokątnego o długości 50.
Trójkątne okno
bartlett
jest wynikiem splotu dwóch okien prostokątnych. Tworzy się je
przy pomocy funkcji odpowiednio
bartlett
i
triang
.
plot(bartlett(w))
plot(triang(w))

Uogólnione okno cosinusowe
Okna Blackmana, Hamminga i Hanninga są specjalnymi przypadkami uogólnionego okna
cosinusowego. Są one sumą funkcji harmonicznych o częstotliwościach (pulsacjach) 0, 2
π
/(N
- 1) oraz 4
π
/(N - 1), gdzie N jest długością okna.
Poniżej przedstawiono jedną z metod tworzenia tych okien.
ind=(0:n-1)’*2*pi/(n-1);
w=A-B*cos(ind)+C*cos(2*ind);
Współczynniki
A
,
B
i
C
są stałymi definiowanymi dla konkretnego okna. Idea doboru
A
,
B
,
C
jest taka, by poprzez sumowanie w dziedzinie częstotliwości pojedynczych składników
tworzących okno, doprowadzić do obniżenia wysokości listków bocznych występujących dla
niskich częstotliwości. Szkodliwym efektem ubocznym tej operacji jest jednak powiększenie
szerokości listka głównego.
Okna Hamminga i Hanninga są dwuczłonowymi, uogólnionymi oknami cosinusowymi,
powstałymi przy współczynnikach:
A=0.54
,
B=0.46
dla Hamminga, oraz
A=0.5
,
B=0.5
dla
Hanninga (C w obu przypadkach jest równe zero). W Matlabie są one obliczane przez funkcje
hamming
i
hanning
.
Należy zauważyć, że definicja okna Hanninga daje zera dla 1-szej i n-tej próbki
(współczynniki
A=0.5
i
B=0.5
). By wyeliminować zera na krawędzi okna, funkcja
hanning
stosuje cosinusoidy o częstotliwości 2
π
/(N+1) zamiast 2
π
/(N - 1).
Okno Blackmana jest popularnym trzyczłonowym oknem, zadanym przez parametry
A=0.42
,
B=0.5
i
C=0.08
. Obliczane jest za pomocą funkcji
blackman
.
plot(hanning(w))
plot(hamming(w))
plot(bartlett(w))
Okno Kaisera
Okno Kaisera jest oknem, dla którego stosunek energii listka głównego do energii listków
bocznych jest maksymalny. Dla okna Kaisera o określonej długości parametr
β
decyduje o
wysokości listków bocznych. Przy zadanym
β
wysokość listków bocznych nie zależy od
długości okna.
Funkcja
kaiser(n,beta)
oblicza okno Kaisera o długości
n
, z parametrem
β
.
Poniżej przedstawiono częstotliwościowe widma kilku okien Kaisera o długości 50 dla
różnych wartościach
β:
n=50;
w1=kaiser(n,1); w2=kaiser(n,4); w3=kaiser(n,9);
plot(w1);
[W1,f]=freqz(w1/sum(w1),1,512,2);
[W2,f]=freqz(w2/sum(w2),1,512,2);
[W3,f]=freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs(W1)),...
f,20*log10(abs(W2)),...
f,20*log10(abs(W3)))

Gdy
β
wzrasta, wysokość listków bocznych maleje, a szerokość listka głównego rośnie.
Poniższy program ilustruje fakt, że wysokość listków bocznych widma okna Kaisera jest
stała, kiedy zmienia się tylko długość okna (
β
=const).
w1=kaiser(50,4);
w2=kaiser(20,4);
w3=kaiser(101,4);
[W1,f]=freqz(w1/sum(w1),1,512,2);
[W2,f]=freqz(w2/sum(w2),1,512,2);
[W3,f]=freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs(W1)),...
f,20*log10(abs(W2)),...
f,20*log10(abs(W3)))
Okno Chebyshewa
Okno Chebyshewa minimalizuje szerokość listka głównego dla zadanej wysokości listków
bocznych. Charakteryzuje się stałymi oscylacjami, to znaczy wszystkie listki boczne mają tą
samą wysokość. Funkcja
chebwin
z parametrami w
n
(długość filtru) i
Rs
(wysokość listków
bocznych) wyznacza przebieg okna Chebyshewa.
n=51;
Rs=40;
w=chebwin(n,Rs);
plot(w)
Okno Chebyshewa posiada dwa wysokie impulsy na obu swoich końcach. Okna Chebyshewa
są zdefiniowane jedynie dla nieparzystych długości. Jeśli
n
jest parzyste, to funkcja
chebwin
projektuje okno Cheyshewa o długości
n+1
.
Przebieg charakterystyki częstotliwościowej ma stałe oscylacje na poziomie -40 dB.
[W,f]=freqz(w,1,512,2);
plot(f,20*log10(abs(W)/sum(w)))
Stosując funkcje dostępne w pakiecie Matlab, można zaprojektować dowolne okno czasowe.
Porównanie zastosowania różnego rodzaju okien czasowych
% Zastosowanie okien czasowych
fs = 128; % Częstotliwość próbkowania sygnału
t=0:(1/fs):1; % Wektor czasu
% Utworzenie przebiegu sinusoidalnego
f1 = 10.5;
f2 = 15;
x = 10*sin(2*pi*f1*t) + 0.1*sin(2*pi*f2*t);
% Zastosowanie okna prostokątnego
y = fft(x);
f = (0:length(y)-1)'*fs/length(y);
ind=find(f<=fs/2);
f1=f(ind); am1 = 20*log10(abs(y(ind)));

plot
(f1,am1)
pause;
% Zastosowanie okna Hanninga
w = hanning(length(x));
y = fft(x'.*w);
ind=find(f<=fs/2);
f2=f(ind); am2 = 20*log10(abs(y(ind)/norm(w)));
plot(f2,am2)
pause;
% Zastosowanie okna Hamminga
w = hamming(length(x));
y = fft(x'.* w);
ind=find(f<=fs/2);
f3=f(ind); am3 = 20*log10(abs(y(ind)/norm(w)));
plot(f3,am3)
pause;
% Zastosowanie okna Kaisera
w = kaiser(length(x),6);
y = fft(x'.* w);
ind=find(f<=fs/2);
f4=f(ind); am4 = 20*log10(abs(y(ind)/norm(w)));
plot(f4,am4)
pause;
% Zastosowanie okna Chebyshewa
w = chebwin(length(x),40);
y = fft(x'.* w);
ind=find(f<=fs/2);
f5=f(ind); am5 = 20*log10(abs(y(ind)/norm(w)));
plot(f5,am5)
W przypadku testu impulsowego sygnał wymuszający ma postać krótkotrwałego impulsu,
natomiast odpowiedź ma charakter zanikającej sinusoidy. Dla tego typu sygnału odpowiedzi
stosuje się okno wykładnicze
αt
e
w(t)
−
=
Powodem stosowania tego typu okna w przypadku układów z małym tłumieniem i
stosunkowo krótką próbką sygnału jest fakt, że mierzona odpowiedź nie zanika całkowicie na
końcu próbki, co powoduje przecieki widma i nieciągłości. Mnożąc taki sygnał przez okno
wykładnicze otrzymuje się próbkę, której wartości amplitudy na końcu próbki są bliskie zeru,
co zmniejsza błędy spowodowane przeciekami widma. Dla odpowiedzi układów ze
stosunkowo dużym tłumieniem lub gdy próbka jest długa sygnał zanika wcześniej niż kończy
się okno i do analizy brane są szumy pomiarowe. Pomnożenie takiego sygnału przez okno
wykładnicze zmniejsza wpływ tych szumów na wyniki analizy. Podobnie w przypadku
wymuszenia, które ma przebieg krótkotrwałego impulsu, poza impulsem występują tylko
szumy pomiarowe. W tym przypadku stosuje się okno prostokątne o czasie trwania impulsu,
pozostałe próbki przyjmuje się równe zeru.

Zadania do wykonania
1. Wygenerować kilkusekundowy sygnał będący złożeniem trzech przebiegów
sinusoidalnych o częstotliwościach: 10, 80 i 120 Hz. Amplitudy sygnałów powinny
znajdować się w proporcjach 1:3:1 oraz fazy powinny być przesunięte o ok. 20
o
.
2. Utworzyć transformatę Fouriera sygnału i pokazać ją graficznie w postaci wykresów
amplitudowo-częstotliwościowych oraz fazowo-częstotliwościowych. Należy zwrócić
uwagę na dobór odpowiedniej częstotliwości próbkowania oraz poprawne
wyskalowanie osi częstotliwości. Na wykresie zaznaczyć pionową linią częstotliwość
Nyqiusta. Skomentować uzyskane wyniki. (Uwaga: Do zestawiania wyników
transformacji można wykorzystać funkcję „subplot”)
3. Zmienić częstotliwość próbkowania sygnału z zadania 2 tak aby częstotliwość
Nyquista była równa 100 Hz oraz wykonać zadanie 2 dla tak przygotowanego
sygnału. Skomentować różnice.
4. Dokonać odwrotnej transformacji Fouriera sygnału z zadania 2 oraz porównać wyniki
ze sygnałem oryginalnym. Porównanie wykonać poprzez wykonanie obu wykresów w
jednym oknie.
5. Wykonać transformacje Fouriera sygnałów:
•
dwóch impulsów występujących w bliskiej odległości
•
przebiegu szumu losowego
•
przebiegu kroku jednostkowego
•
przebiegu trójkątnego
6. Wygenerować sygnał sinusoidalny o częstotliwości 11 Hz próbkowany z
częstotliwością 200Hz. Przygotować dwie realizacje tego sygnału jedną o długości 1s
oraz drugą o długości 0.95s. Wykonać przekształcenie Fouriera dla obu próbek
przygotowanego sygnału. Moduły obu transformat narysować na jednym wykresie.
Skomentować uzyskane wyniki.
7. Powtórzyć eksperyment z punktu 6 nakładając wcześniej na sygnały okno Hanninga.
Skomentować uzyskane wyniki.
8. Zmodyfikować sygnał testowy tworzony w ramach zadania 2 poprzez dodanie do
niego sinusoid o częstotliwościach 12 i 81 Hz. Wykonać porównanie działania
różnych okien czasowych nakładanych na testowy sygnał. Sprawdzić jaki wpływ na
długość zastosowanego okna na wynikowe widmo.
Wyszukiwarka
Podobne podstrony:
przetworniki indukcyjne
Prop aut W9 Ses cyfr Przetworniki fotoelektryczne
Lab4
Przetworstwo produktow rolniczych
MLEKO I PRZETWORY MLECZNE (2)
Ceny detaliczne i spożycie warzyw i ich przetworów
W10 Przetw A Cmin
W9 Przetw C A
przetworniki II opracowane
Lab4
Przetwarzanie mleka koziego
dupont przetworstwo tworzyw4
Przetwornica buck id 406722 Nieznany
Materiały nieżelazne Tworzywa sztuczne Przetwórstwo Auto Expert
więcej podobnych podstron