1
Data wykonania ćwiczenia: 16.01.2015r.
Prowadzący: dr inż. Tomasz Kapłon
LOGIKA UKŁADÓW CYFROWYCH
Temat: Zastosowanie języka wyrażeń regularnych do syntezy i analizy automatów skończonych
I.
Cel ćwiczenia
Nabycie umiejętności syntezy automatu skończonego na podstawie charakteryzującego
go wyrażenia regularnego.
II.
Program ćwiczenia
L.p.
Zadanie
Wykonanie
1.
Dokonać syntezy strukturalnej
automatu w oparciu o poniższe
wyrażenia regularne:
S
1
= (z
1
z
2
+ z
1
z
1
z
2
)* z
1
z
2
| y
1
S
2
= /S
1
| y
2
Dokonano syntezy, połączono – układ nie
działał prawidłowo, chociaż w projekcie nie
było żadnego błędu – w symulatorze działa
Tabela 1
III.
Wstęp teoretyczny
a) Automat skończony akceptuje słowa należące do języka regularnego reprezentowanego
przez wyrażenia regularne, których używamy w celu oznaczenia zbiorów słów powstałych
w wyniku konkatenacji, sumy i iteracji. Wyrażenie regularne składa się z określonych słów
połączonych znakami symbolizującymi dane operacje.
b) Synteza abstrakcyjna automatu polega na znalezieniu takiego opisu formalnego
automatu, na podstawie którego można zbudować tablice przejść i wyjść automatu.
Etapy syntezy abstrakcyjnej:
algorytm słowny
przedstawienie algorytmu słownego w postaci wyrażeń regularnych
określenie grafu przejść
IV.
Realizacja ćwiczenia
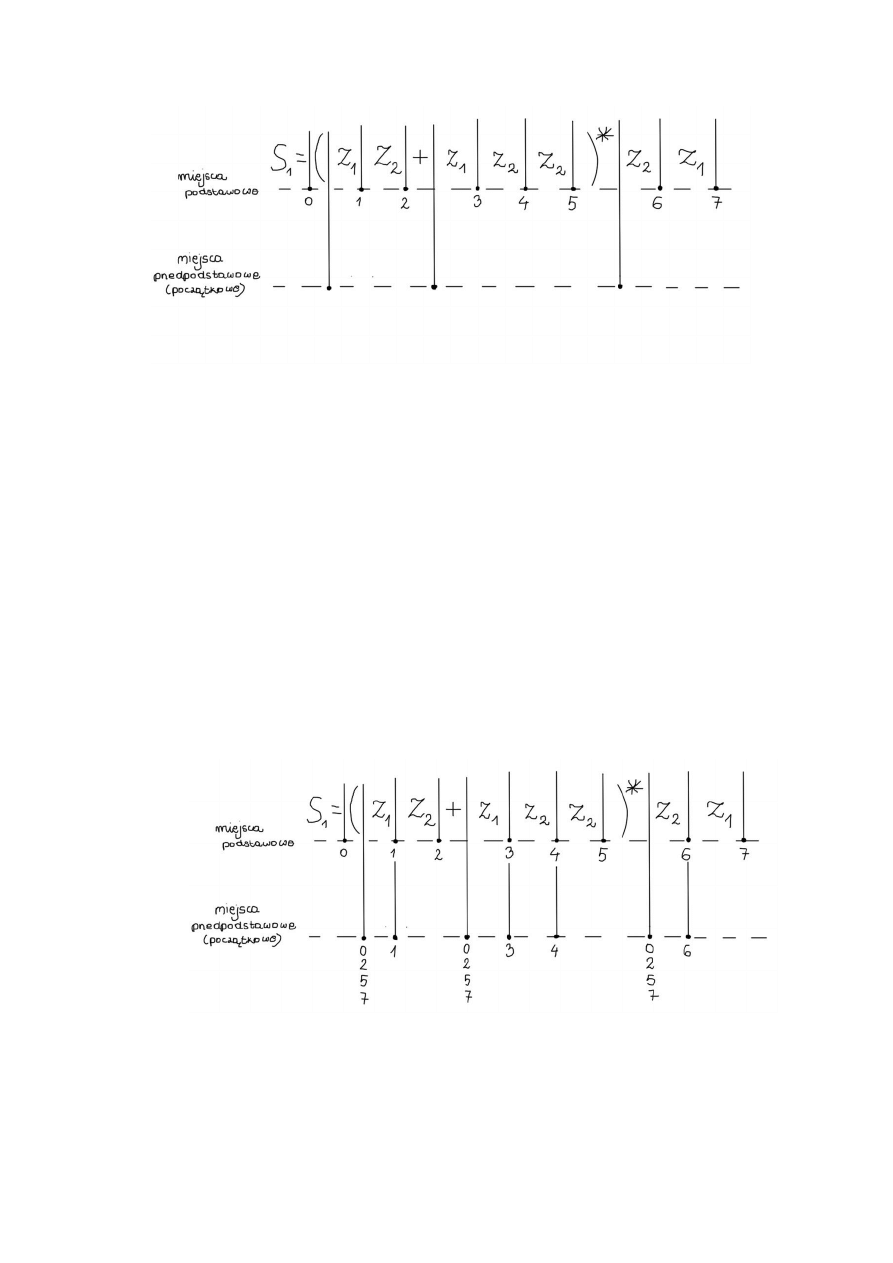
1. W celu określenia stanów automatu, należy w wyrażeniu regularnym oznaczyć miejsca
podstawowe i przedpodstawowe:
miejsce przedpodstawowe (początkowe) to miejsce, na prawo od którego stoi litera
miejsce podstawowe to miejsce, na lewo od którego stoi litera, a na prawo miejsce
przedpodstawowe
a) Na początku zaznaczamy poszczególne miejsca i oznaczamy miejsca podstawowe
kolejnymi cyframi (rys. 1).
2
Rysunek 1
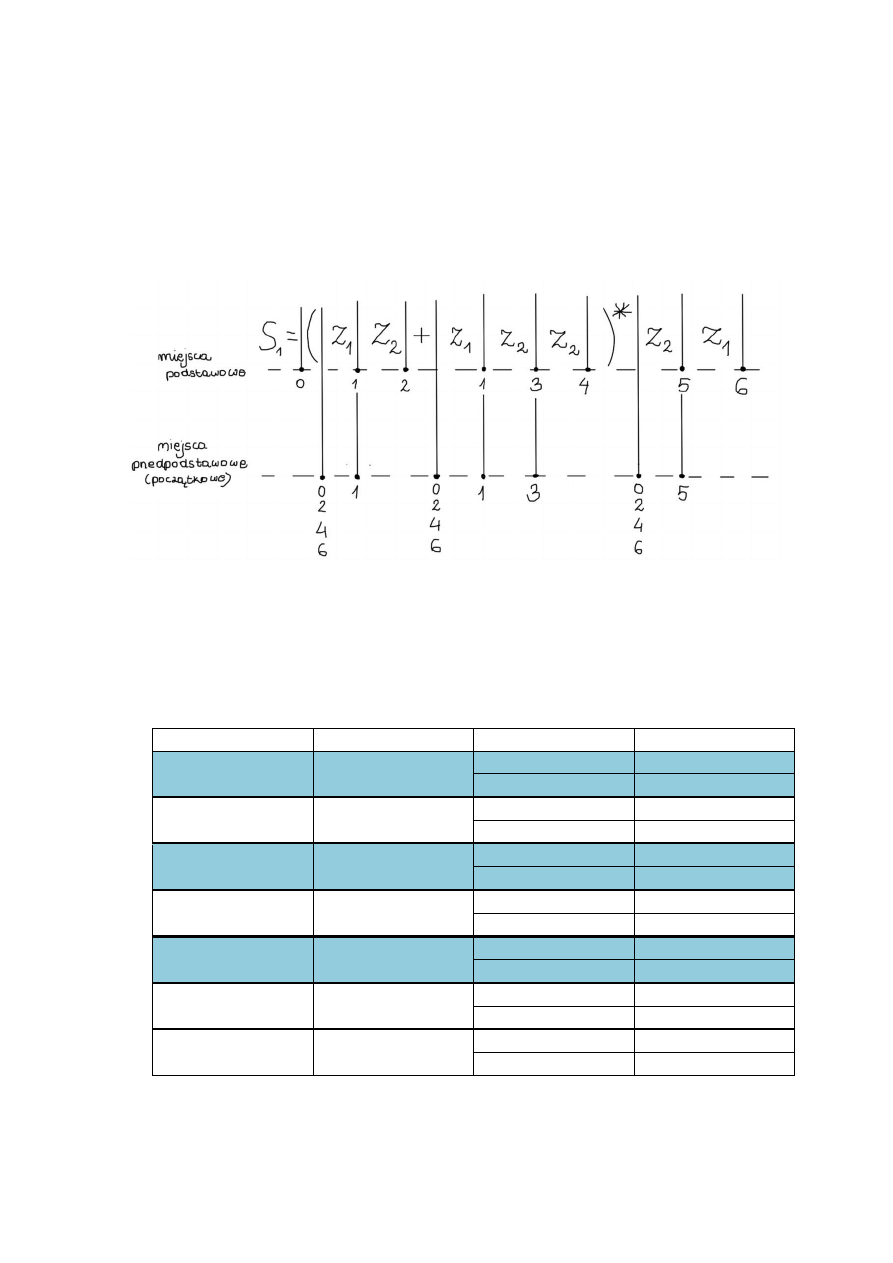
b) Następnie miejsca przedpodstawowe oznacza się odpowiednimi symbolami miejsc
podstawowych według poniższych reguł:
Symbol miejsca podstawowego znajdującego się przed nawiasem iteracyjnym (0)
rozmieszcza się w miejscach początkowych członów dysjunktywnych w danym
nawiasie (człony dysjunktywne – czyli połączone znakiem sumy) oraz w miejscu
przedpodstawowym za danym nawiasem
Symbol miejsca końcowego dowolnego członu dysjunktywnego zamkniętego w
nawiasy iteracyjne (2, 5) rozmieszczamy w miejscach początkowych wszystkich
członów dysjunktywnych w danym nawiasie oraz w miejscu przedpodstawowym
bezpośrednio za danym nawiasem
Symboli miejsc podstawowych, na lewo i prawo od których stoją litery (1, 3, 4, 6) nie
rozmieszcza się niegdzie więcej i przepisuje poziom niżej
Symbol miejsca końcowego wyrażenia (7) rozmieszcza się we wszystkich tych
miejscach przedpodstawowych, gdzie umieściliśmy symbol miejsca początkowego
wyrażenia (0)
Rysunek 2
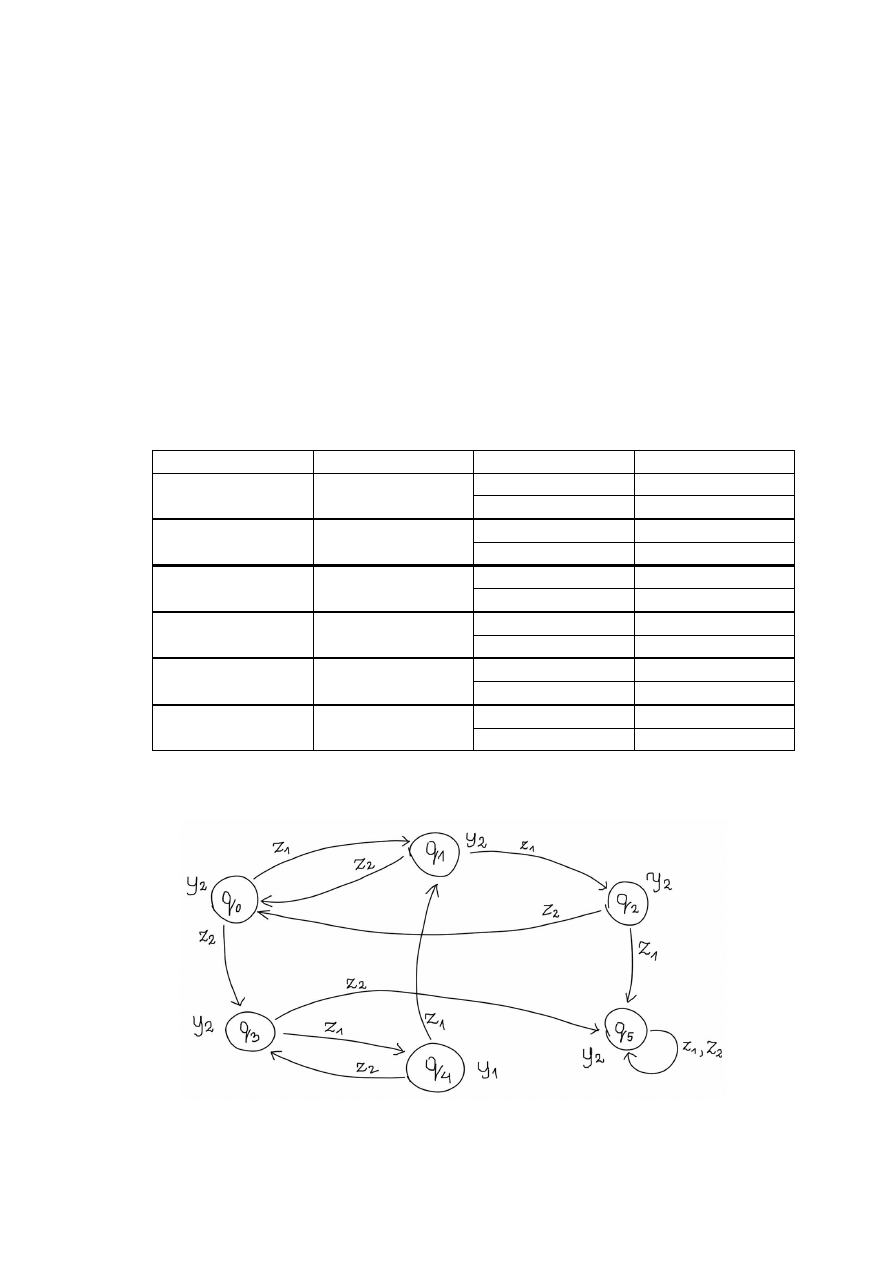
2. W drugim kroku przeprowadzamy minimalizację stanów. Jeżeli kilka miejsc
przedpodstawowych oznakowane jest jednakowym zbiorem symboli i na prawo od tych
3
miejsc zapisane są takie same litery, to miejsca „podstawowe” położone na prawo od tych
liter są sobie równoważne.
1 ≡ 3 (rys. 2)
3 -> 1
4 -> 3
5 -> 4
6 -> 5
7 -> 6
Rysunek 3
3. Następnie określamy tabelę przejść automatu (tab. 2), patrząc na miejsca przedpodstawowe i
podawane na nie litery. Jeżeli przejście za pomocą danej litery nie istnieje, oznaczamy je na
razie gwiazdką. Sygnał wyjściowy, którego wystąpienie warunkowane jest przez wyrażenie S
1
przypisujemy jedynie stanowi końcowemu (6). Korzystając z wyrażenia S
2
, pozostałym
stanom przypisujemy wyjście y
2.
Wyjście
Stan
Słowo wejściowe
Następny stan
y
2
0
z
1
1
z
2
5
y
2
1
z
1
3
z
2
2
y
2
2
z
1
1
z
2
5
y
2
3
z
1
*
z
2
4
y
2
4
z
1
1
z
2
5
y
2
5
z
1
6
z
2
*
y
1
6
z
1
1
z
2
5
Tabela 2 – tabela przejść - wyjść
4
4. Minimalizujemy tabelę – równoważne są stany, które mają takie same przejścia i wyjścia,
czyli 0≡2≡4 (tab. 2).
2 -> 0
4 -> 0
3 -> 2
5 -> 3
6 -> 4
Wprowadzamy dodatkowy stan (5), do którego przechodzi automat, jeśli dane przejście
oznaczyliśmy gwiazdką. Oznaczamy stany automatu:
0 -> q
0
1 -> q
1
2 -> q
2
3 -> q
3
4 -> q
4
5 -> q
5
Y
Q(t)
Z
Q(t+1)
y
2
q
0
z
1
q
1
z
2
q
3
y
2
q
1
z
1
q
2
z
2
q
0
y
2
q
2
z
1
q
5
z
2
q
0
y
2
q
3
z
1
q
4
z
2
q
5
y
1
q
4
z
1
q
1
z
2
q
3
y
2
q
5
z
1
q
5
z
2
q
5
Tabela 3 – zminimalizowana tabela przejść - wyjść
5. Na podstawie tabeli przejść utworzyliśmy graf automatu Moore’a (rys. 4).
Rysunek 4 – graf automatu Moore’a reprezentowanego przez wyrażenie S
1
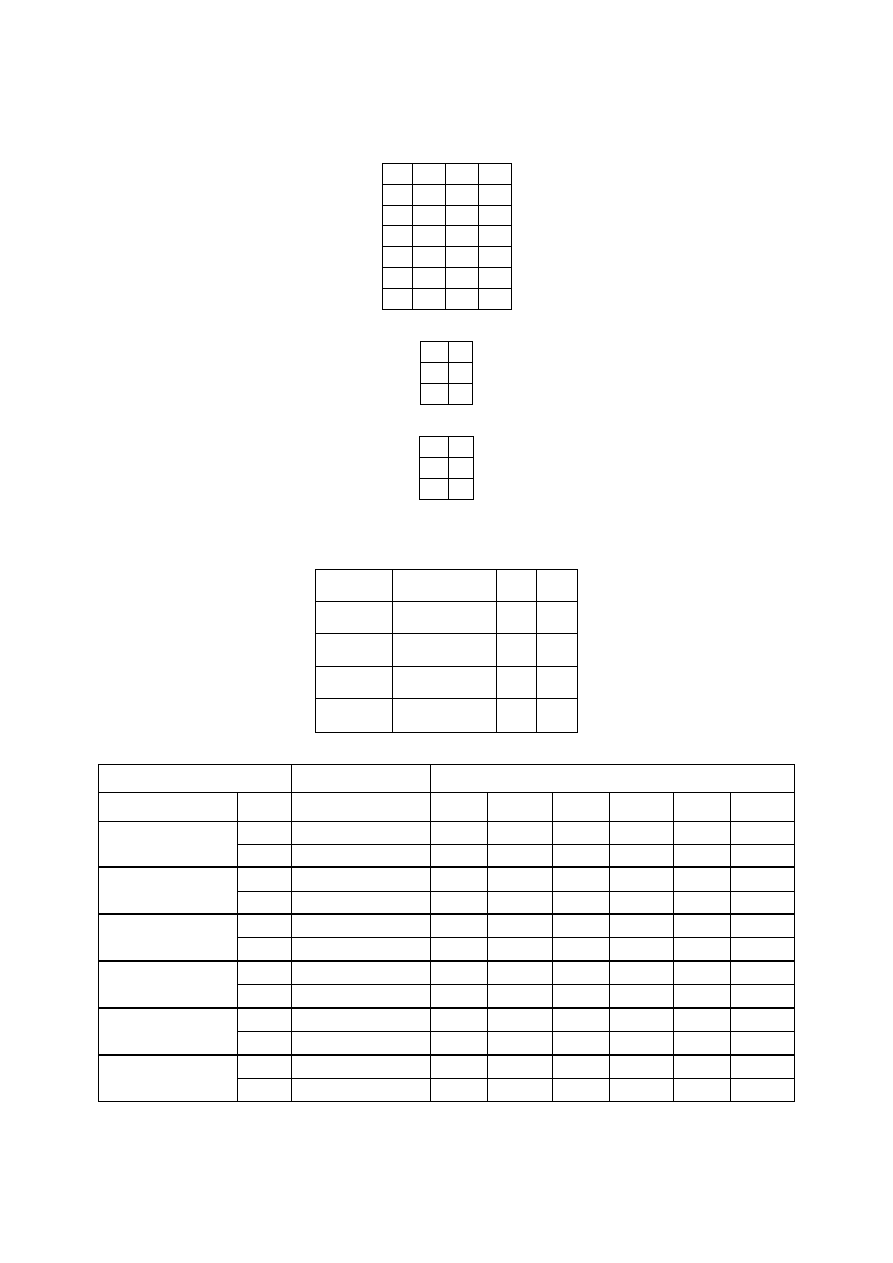
5
6. Synteza strukturalna automatu
kodowanie stanów, wejść i wyjść
q
i
Q
2
Q
1
Q
0
q
0
0
0
0
q
1
0
0
1
q
2
0
1
0
q
3
0
1
1
q
4
1
0
0
q
5
1
0
1
Tabela 4 – kodowanie stanów
z
i
Z
z
1
0
z
2
1
Tabela 5 – kodowanie sygnałów wejściowych
y
i
Y
y
1
0
y
2
1
Tabela 6 – kodowanie sygnałów wyjściowych
kodowanie tabeli przejść
Q (t)
Q (t+1)
J
K
0
0
0
*
0
1
1
*
1
0
*
1
1
1
*
0
Tabela 7 – tabela wzbudzeń przerzutnika JK
t
t+1
t
Q
2
Q
1
Q
0
Z
Q
2
Q
1
Q
0
J
2
K
2
J
1
K
1
J
0
K
0
000
0
001
0
*
0
*
1
*
1
011
0
*
1
*
1
*
001
0
010
0
*
1
*
*
1
1
000
0
*
0
*
*
1
010
0
101
1
*
*
1
1
*
1
000
0
*
*
1
0
*
011
0
100
1
*
*
1
*
1
1
101
1
*
*
1
*
0
100
0
001
*
1
0
*
1
*
1
011
*
1
1
*
1
*
101
0
101
*
0
0
*
*
0
1
101
*
0
0
*
*
0
Tabela 8 – kodowanie tabeli przejść
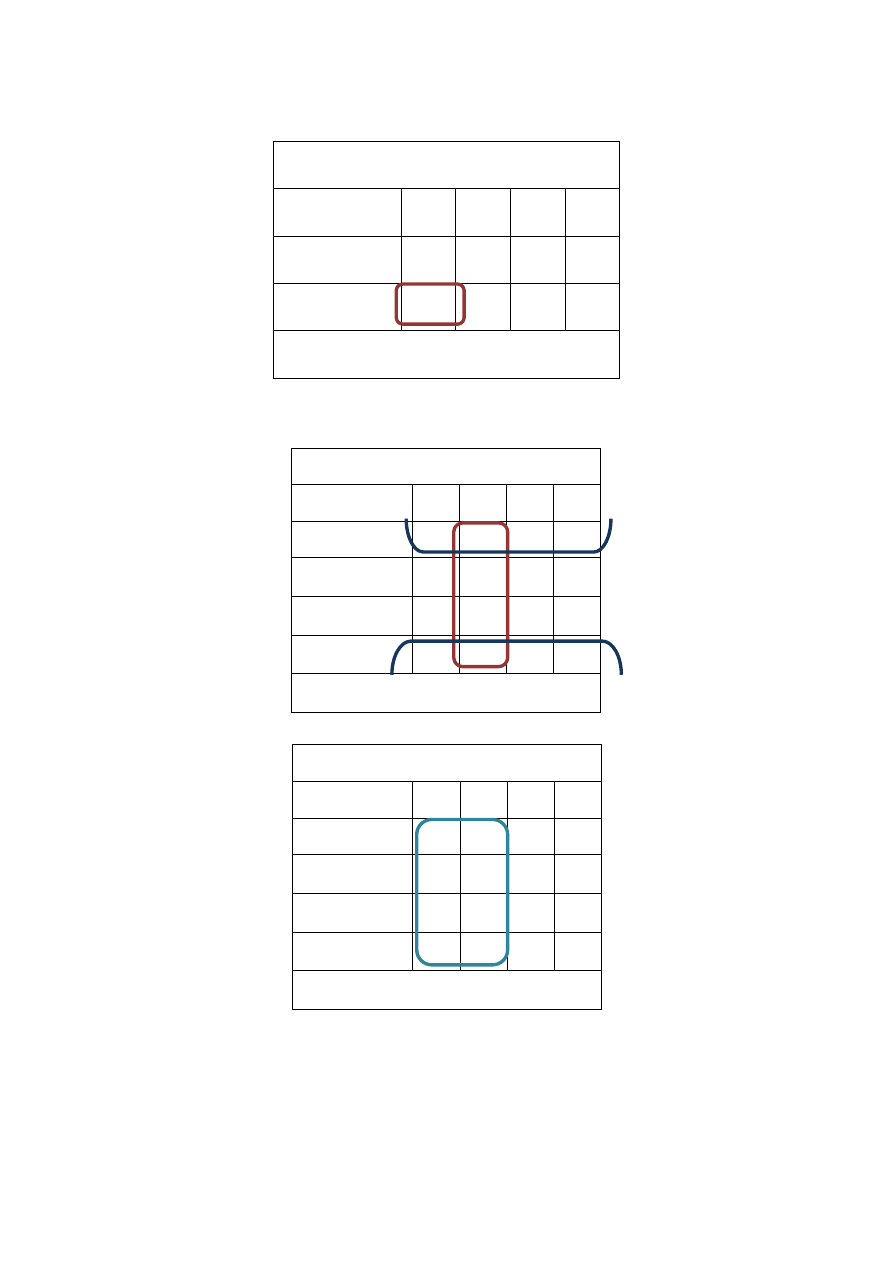
6
synteza wyjść
Y
Q
2
/ Q
1
Q
0
00
01
11
10
0
1
1
1
1
1
0
1
1
1
Y = /Q
2
+ Q
1
+ Q
0
Tabela 9 – minimalizacja funkcji wyjściowej
synteza wejść
Tabela 10 – synteza wejścia J przerzutnika Q
2
K
2
Q
2
Q
1
/ Q
0
Z
00
01
11
10
00
*
*
*
*
01
*
*
*
*
11
*
*
*
*
10
1
1
0
0
K
2
= /Q
0
Tabela 11 - synteza wejścia K przerzutnika Q
2
J
2
Q
2
Q
1
/ Q
0
Z
00
01
11
10
00
0
0
0
0
01
1
0
1
1
11
*
*
*
*
10
*
*
*
*
J
2
= Q
1
(Q
0
+ /Z)
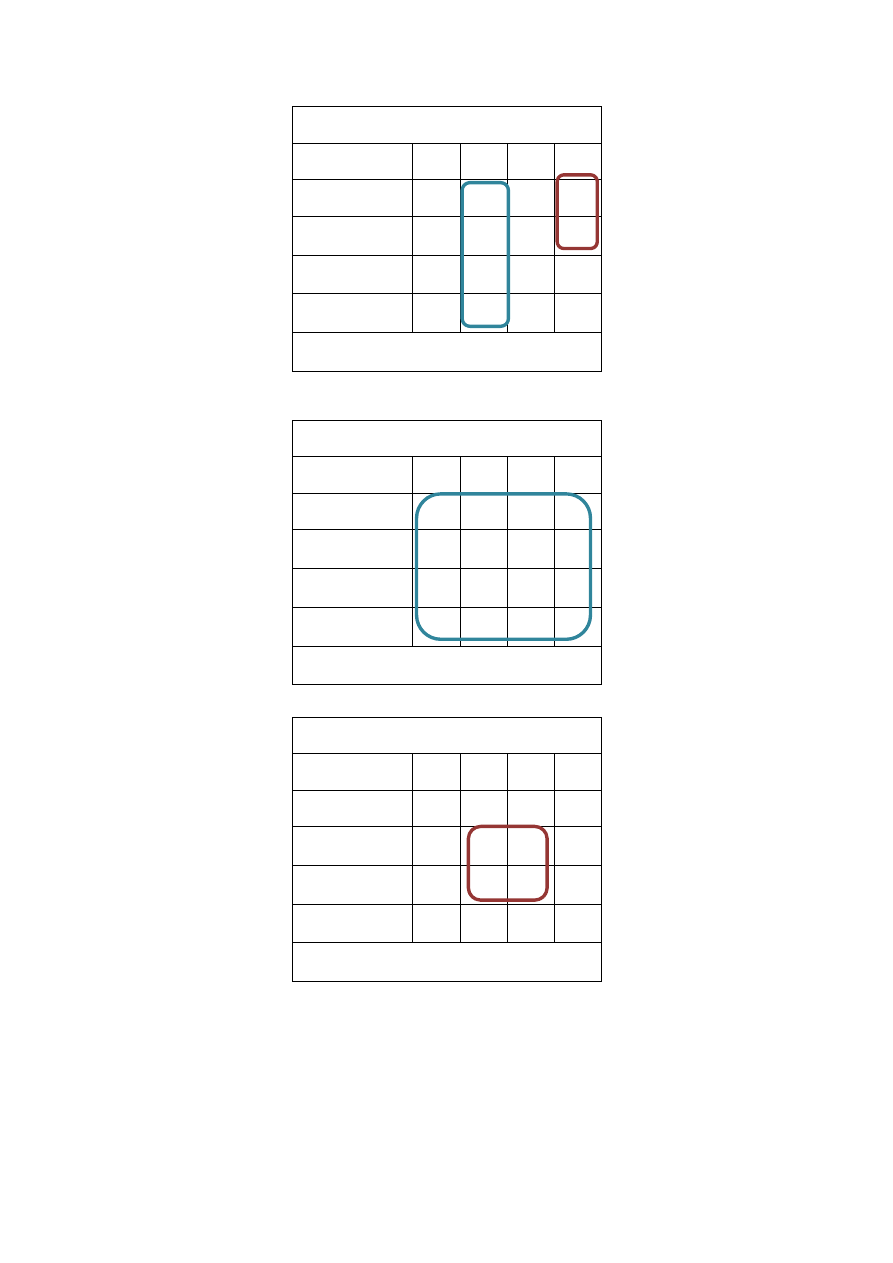
7
J
1
Q
2
Q
1
/ Q
0
Z
00
01
11
10
00
0
1
0
1
01
*
*
*
*
11
*
*
*
*
10
0
1
0
0
J
1
= /Q
0
Z + /Q
2
Q
0
/Z
Tabela 12 - synteza wejścia J przerzutnika Q
1
K
1
Q
2
Q
1
/ Q
0
Z
00
01
11
10
00
*
*
*
*
01
1
1
1
1
11
*
*
*
*
10
*
*
*
*
K
1
= 1
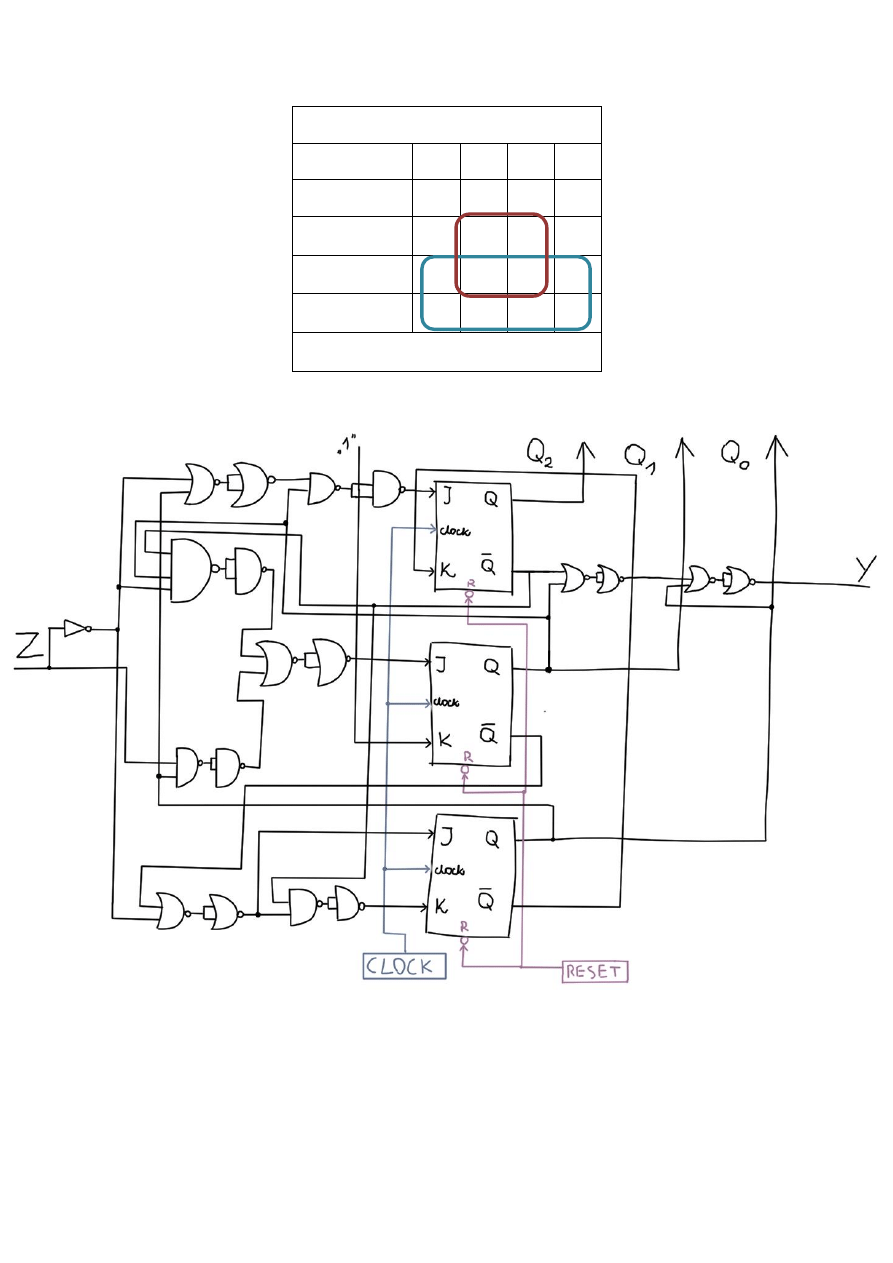
Tabela 13 - synteza wejścia K przerzutnika Q
1
J
0
Q
2
Q
1
/ Q
0
Z
00
01
11
10
00
1
1
*
*
01
1
0
*
*
11
*
*
*
*
10
1
1
*
*
J
0
= /Q
1
+ /Z
Tabela 14 - synteza wejścia J przerzutnika Q
0
8
K
0
Q
2
Q
1
/ Q
0
Z
00
01
11
10
00
*
*
1
1
01
*
*
0
1
11
*
*
*
*
10
*
*
0
0
K
0
= /Q
2
(/Q
1
+ /Z)
Tabela 15 - synteza wejścia K przerzutnika Q
0
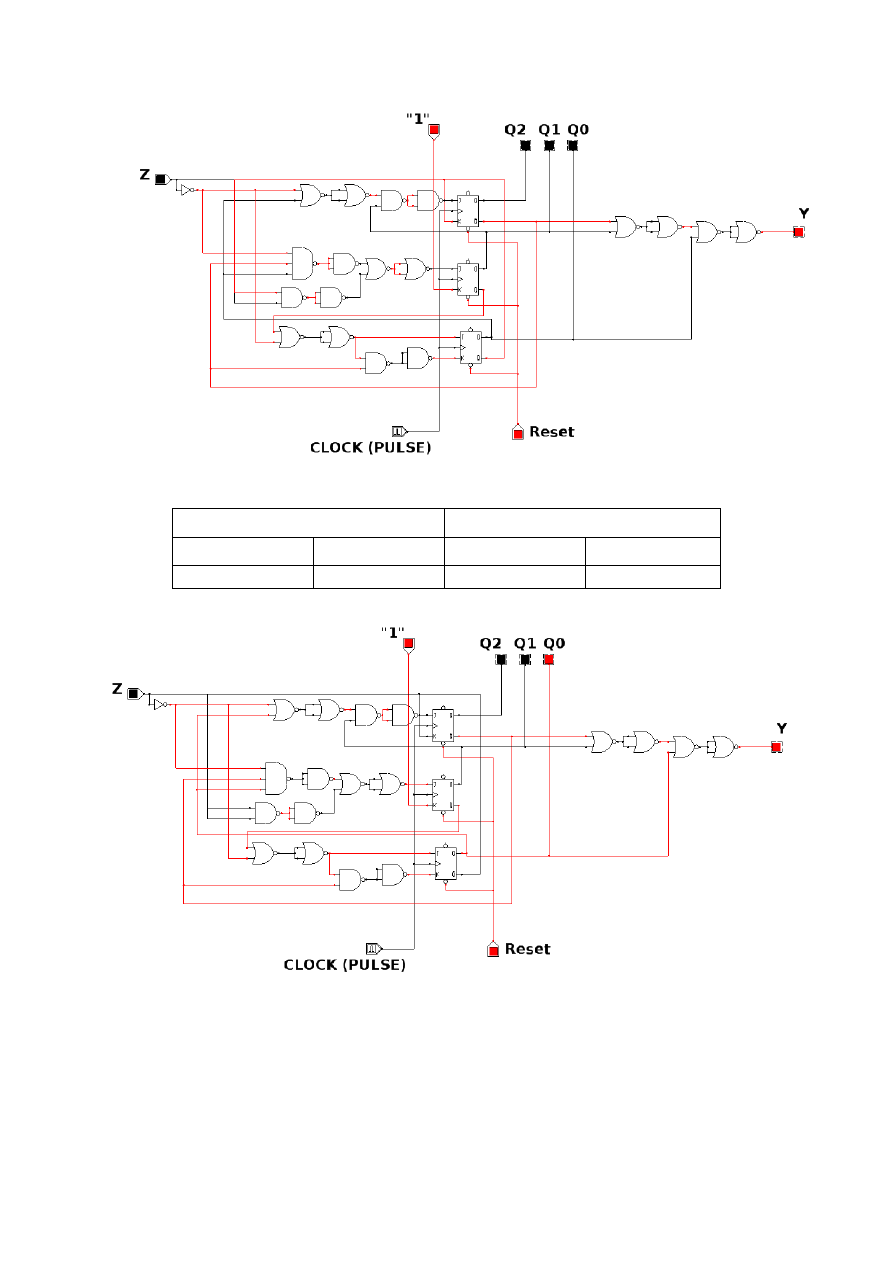
schemat układu
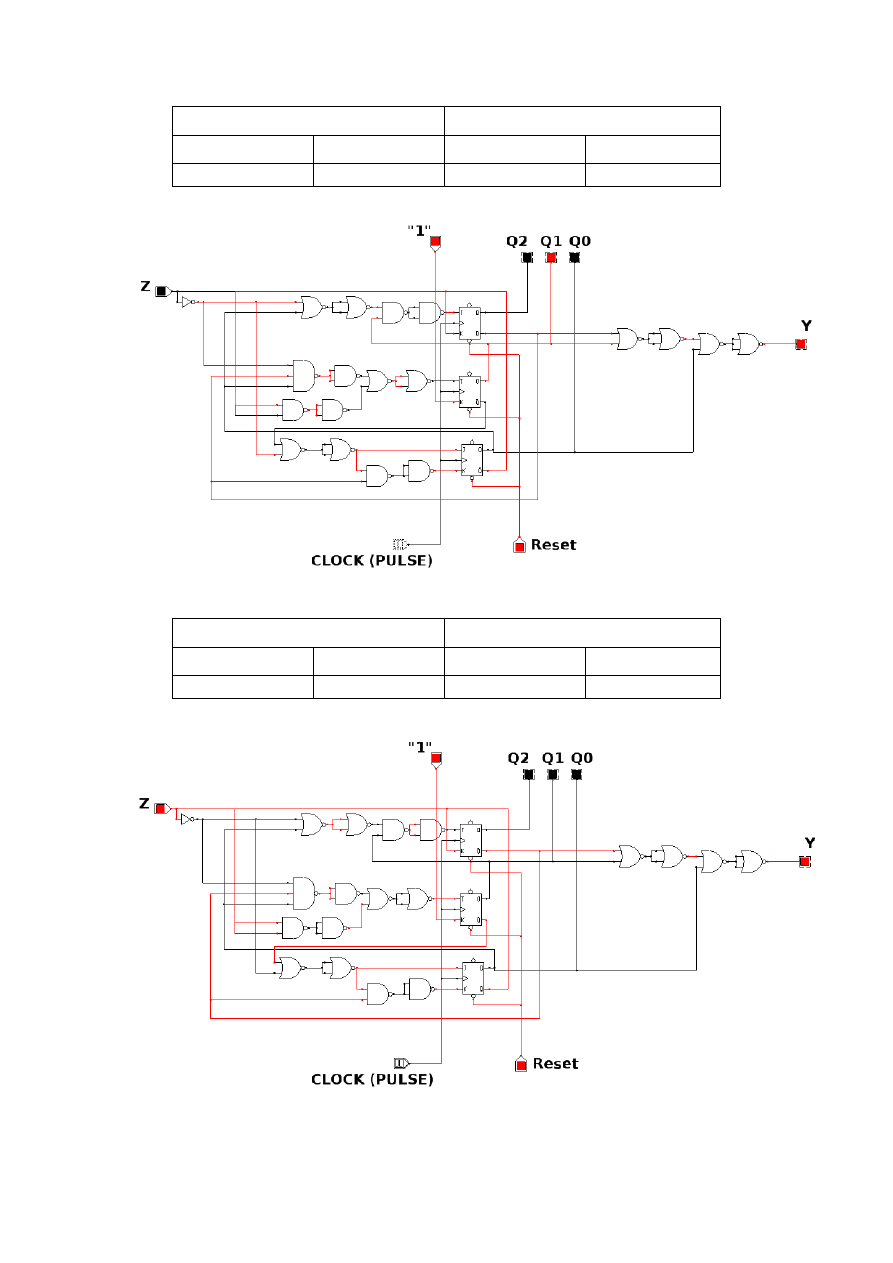
7. Symulacja działania
Symulacja działania układu w programie Cedar Logic Simulator. Tabele nad każdym etapem
symulacji przedstawiają dane przejście. Przetestowano tylko niektóre kombinacje sygnałów
wejściowych.
9
Rysunek 5 – stan q
0
automatu
t
t+1
Q
Z
Q
Y
q
0
z
1
q
1
y
2
Tabela 16
Rysunek 6
10
t
t+1
Q
Z
Q
Y
q
1
z
1
q
2
y
2
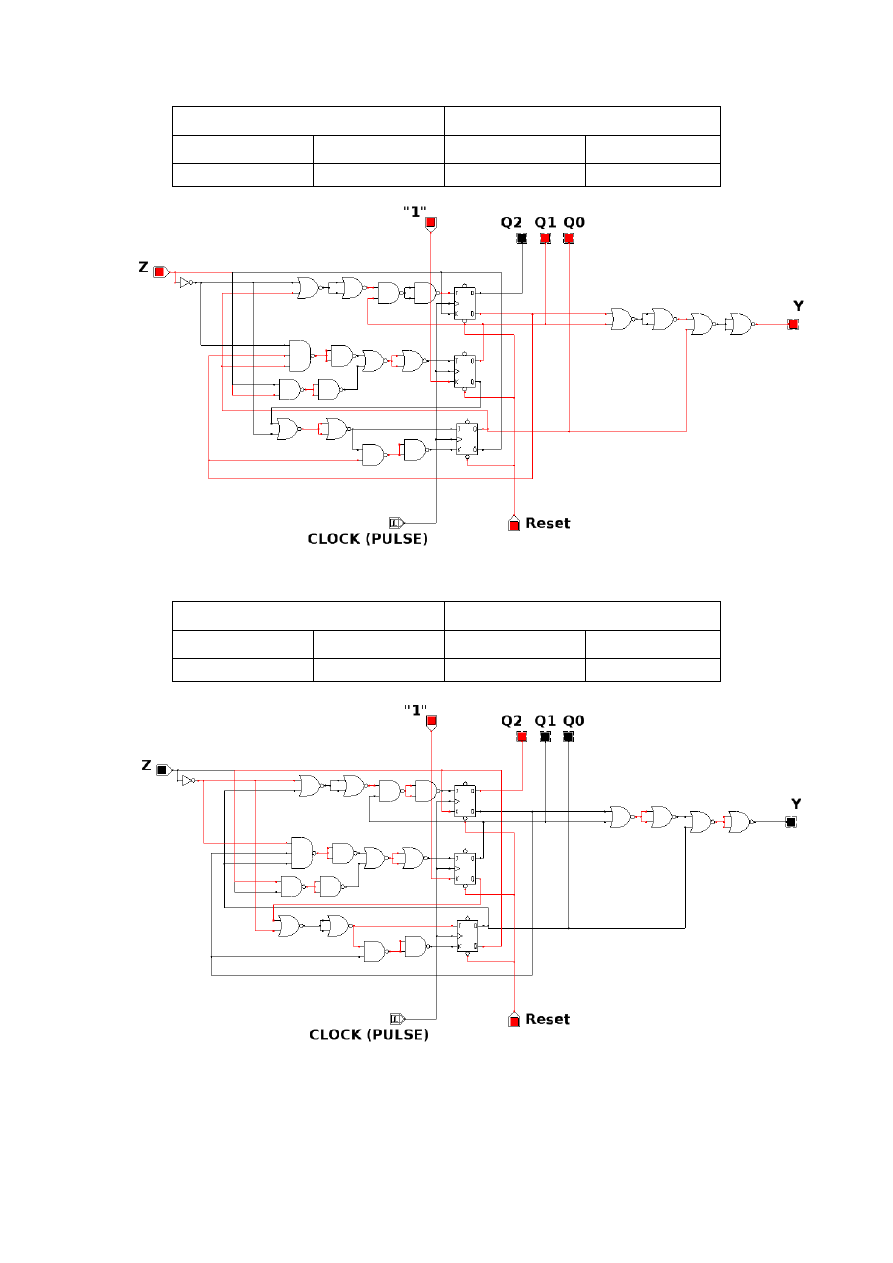
Tabela 17
Rysunek 7
t
t+1
Q
Z
Q
Y
q
2
z
2
q
0
y
2
Tabela 18
Rysunek 8
11
t
t+1
Q
Z
Q
Y
q
0
z
2
q
3
y
2
Tabela 19
Rysunek 9
t
t+1
Q
Z
Q
Y
q
3
z
1
q
4
y
1
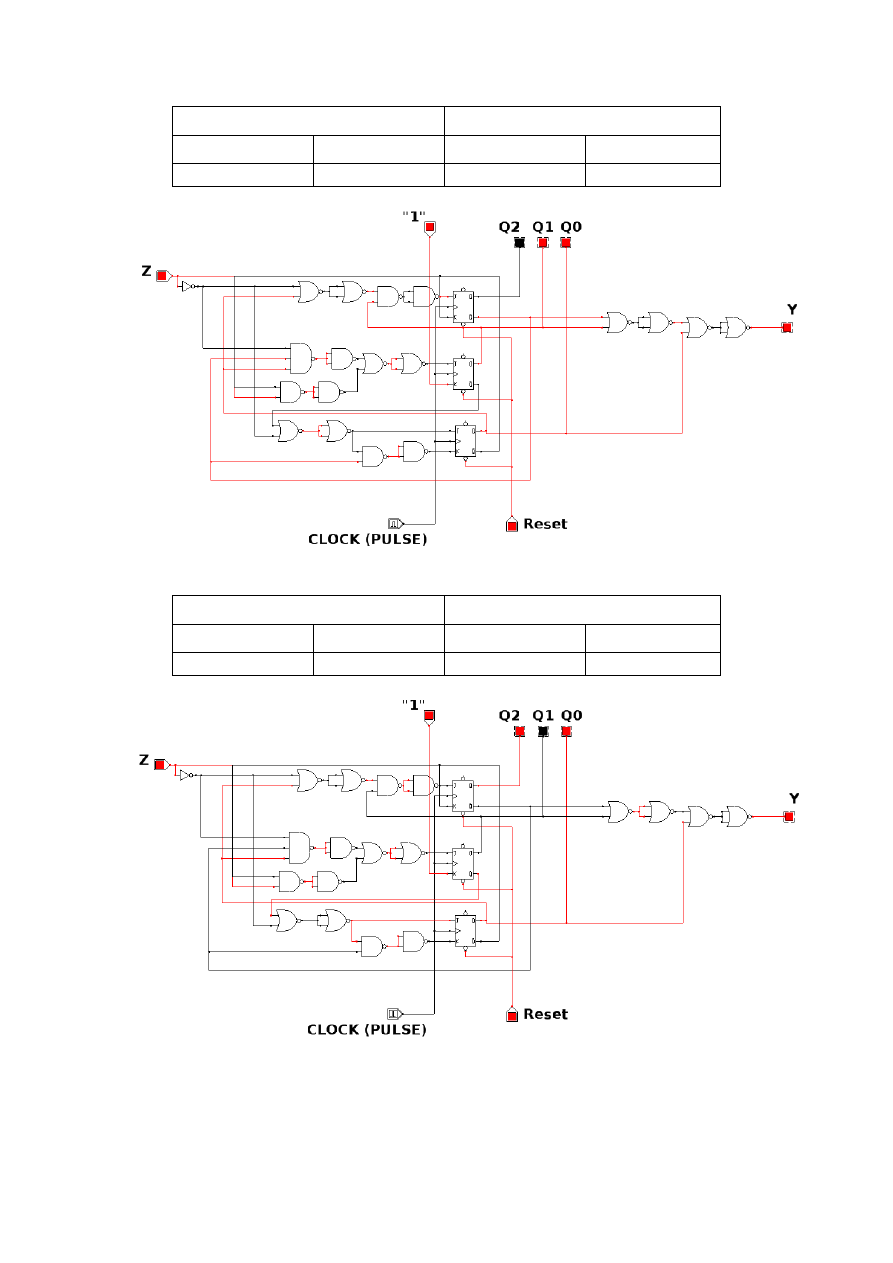
Tabela 20
Rysunek 10
Na tym etapie automat zaakceptował podane przez nas wyrażenie regularne w postaci z
1
z
1
z
2
z
2
z
1
– na wyjściu pojawiło się y
1
(rys. 10).
12
t
t+1
Q
Z
Q
Y
q
4
z
2
q
3
y
2
Tabela 21
Rysunek 11
t
t+1
Q
Z
Q
Y
q
3
z
2
q
5
y
2
Tabela 22
Rysunek 12
13
W tym kroku podaliśmy na stan q
3
słowo z
2
– takie przejście nie było określone w wyrażeniu
regularnym, więc automat przeszedł w dodatkowy stan q
5
(rys. 12), który wprowadziliśmy do
tego celu.