Politechnika 
Wrocławska 
Wydział Elektryczny

Wojciech Calów

Rok studiów : III
Semestr : VI
Rok akad. :2012/13

Laboratorium Metod Numerycznych

Data
23.05.2013

Temat :

Metoda Newtona-Raphsona

Ocena:

1. Cel ćwiczenia

Równania:

x1.^2   +   x2.^2  =  10
x1.^2   -  2*x2.^2 = 1

2. Program.

% ================== parabola 

t=-10:0.0001:10;
X1=-10:0.0001:10;
X2=-10:0.0001:10;
f21=sqrt(1+2*(X1.^2));
f22=-sqrt(1+2*(X1.^2));
 

% ================== koło

T= 0:0.0001:2*pi;
C1=sqrt(10)*cos(T);
S1=sqrt(10)*sin(T);
 

% ================== rysunek

figure(1);
plot(f21,t,

'r'

,C1,S1,

'k'

,f22,t,

'b'

);

xlabel(

'X2'

); 

ylabel(

'X1'

);

a=4;
axis([-a a -a a]);
grid 

on

;

y=[5 -0.8];

% ============================================================

eps=10^(-8); 

% dokladnosc

x1=-2.64;
x2=-1.73;
k=0;
X=[x1,x2];

while

 max(abs(X))>eps && (k<100)

    k=k+1;
    f1 = x1.^2 + x2.^2 - 10;
    f2 = x1.^2 - 2* x2.^2 - 1;
    f = [f1;f2];

    J=[(2*x1) (2*x2); (2*x1) (-4*x2)];
    J1=inv(J);
    q= J1*f;
    x1=x1-q(1);
    x2=x2-q(2);
    X=[x1,x2];

end

;

x1
x2
blad_x1 = ( x1.^2 - 2* x2.^2 - 1)
blad_x2 = (x1.^2 + x2.^2 - 10) 

 

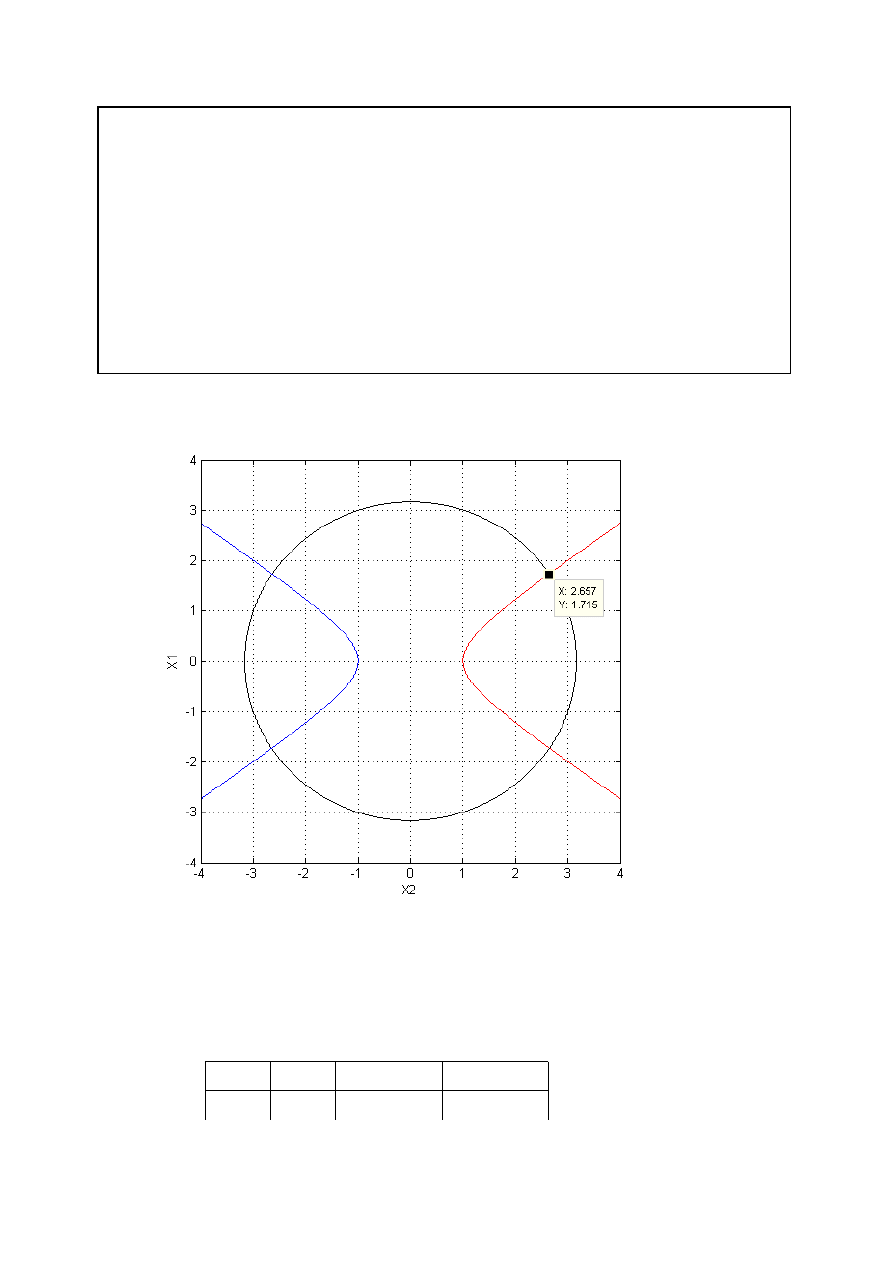
3. Wykres

4. Wnioski
Program działa i oblicza jeden z czterech symetrycznych wartości rozwiązań układu 
równań.
Wyniki:

x1

x2

blad_x1

blad_x2

-2.6458 -1.7321 -8.8818e-016 -1.7764e-015

Widzimy, że uzyskaliśmy dokładność większą niż zadaną (10^(-8)).