1
OBLICZENIA RÓWNOLEGLE
Temat 1:
Algorytm, zlozonosc - przypomnienie
Prowadz acy:
dr inz. Zbigniew TARAPATA
pok.225A, tel.: 83-94-13
e-mail:
Zbigniew.Tarapata@wat.edu.pl
Zbigniew.Tarapata@wat.edu.pl
http://
tarapata.
tarapata.
strefa
strefa
.pl
.pl
/
/
p_obliczenia_rownolegle
p_obliczenia_rownolegle
/
/
2
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
PLAN REFERATU
n
n
Z
Z
l
l
o
o
z
z
ono
ono
sc
sc
algorytmu
algorytmu
a zlozonosc
problemu
problemu
(zadania);
n
n
Optymalno
Optymalno
sc
sc
algorytmu ze wzgledu na
dok
dok
l
l
adno
adno
sc
sc
,
a optymalnosc ze wzgledu na
z
z
l
l
o
o
z
z
ono
ono
sc
sc
;
n
Zlozonosc
pesymistyczna
pesymistyczna
, zlozonosc
oczekiwana
oczekiwana
,
wra
wra
z
z
liwo
liwo
sc
sc
algorytmów;
n
n
Problem decyzyjny
Problem decyzyjny
a
optymalizacyjny;
optymalizacyjny;
n
n
Klasy z
Klasy z
l
l
o
o
z
z
ono
ono
s
s
ci
ci
obliczeniowej problemów;
n
n
Dowodzenie przynale
Dowodzenie przynale
z
z
no
no
s
s
ci
ci
problemu
do klasy z
do klasy z
l
l
o
o
z
z
ono
ono
s
s
ci
ci
;
n
n
Metody badania
Metody badania
zlozonosci, dokladno sci algorytmów;
2
3
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
ALGORYTM - przypomnienie podstawowych pojec
n
n
Algorytmika
Algorytmika jest dziedzina wiedzy zajmujaca sie badaniem
algorytm
algorytm
ó
ó
w
w
;
n
W informatyce jest ona nieodlacznie zwiazana z algorytmami
przetwarzania
struktur
danych
danych
;
n
Potocznie
algorytm
algorytm jest rozumiany jako pewien przepis na
wykonanie jakiegos zestawu czynno sci, prowadzacych do
osi agniecia oczekiwanego i z góry okreslonego celu;
n
Mówi si e równiez, ze:
n
-
algorytm
jest pewna scisle okreslona procedura obliczeniowa,
która dla zestawu wlasciwych danych wejsciowych wytwarza
zadane dane wyjsciowe;
n
-
algorytm
jest to zbiór regul postepowania umozliwiajacych
rozwiazanie okreslonego zadania w skonczonej liczbie kroków
i w skonczonym czasie.
Termin algorytm wywodzi si
Termin algorytm wywodzi si
e
e
od zlatynizowanej formy
od zlatynizowanej formy
(
(
Algorismus
Algorismus
,
,
Algorithmus
Algorithmus
) nazwiska matematyka arabskiego
) nazwiska matematyka arabskiego
z
z
IX w.,
IX w.,
Al
Al
-
-
Chuwarizmiego
Chuwarizmiego
.
.
4
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
ZLOZONOSC ALGORYTMU
A ZLOZONOSC PROBLEMU (ZADANIA)
n
n
Z
Z
l
l
o
o
z
z
ono
ono
sc
sc
algorytmu
algorytmu
– liczba kroków algorytmu
(czas) potrzebna na rozwiazanie danego
problemu dla najgorszego przypadku danych
ustalonego rozmiaru;
n
Zlozonosc
problemu (zadania)
problemu (zadania)
- zlozonosc
najlepszego algorytmu rozwiazujacego ten
problem;
3
5
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
OPTYMALNOSC W SENSIE ZLOZONOSCI,
OPTYMALNOSC W SENSIE DOKLADNOSCI
n
Algorytm nazywamy
optymalnym ze wzgl
optymalnym ze wzgl
e
e
du na z
du na z
l
l
o
o
z
z
ono
ono
sc
sc
jezeli nie istnieje inny algorytm (dla tego samego problemu)
o zlozonosci lepszej;
n
Algorytm nazywamy
optymalnym ze wzgl
optymalnym ze wzgl
e
e
du na dok
du na dok
l
l
adno
adno
sc
sc
(dla danego problemu, przy posiadanej informacji) jezeli blad
tego algorytmu jest najmniejszy sposród bledów wszystkich
algorytmów rozwiazujacych dany problem;
n
Algorytm A nazywamy
ε
ε
-
-
aproksymacyjnym
aproksymacyjnym
(
ε
ε-
przybli
przybli
z
z
onym
onym
)
(
ε
ε
>1
>1
) jezeli zachodzi nastepujaca zaleznosc:
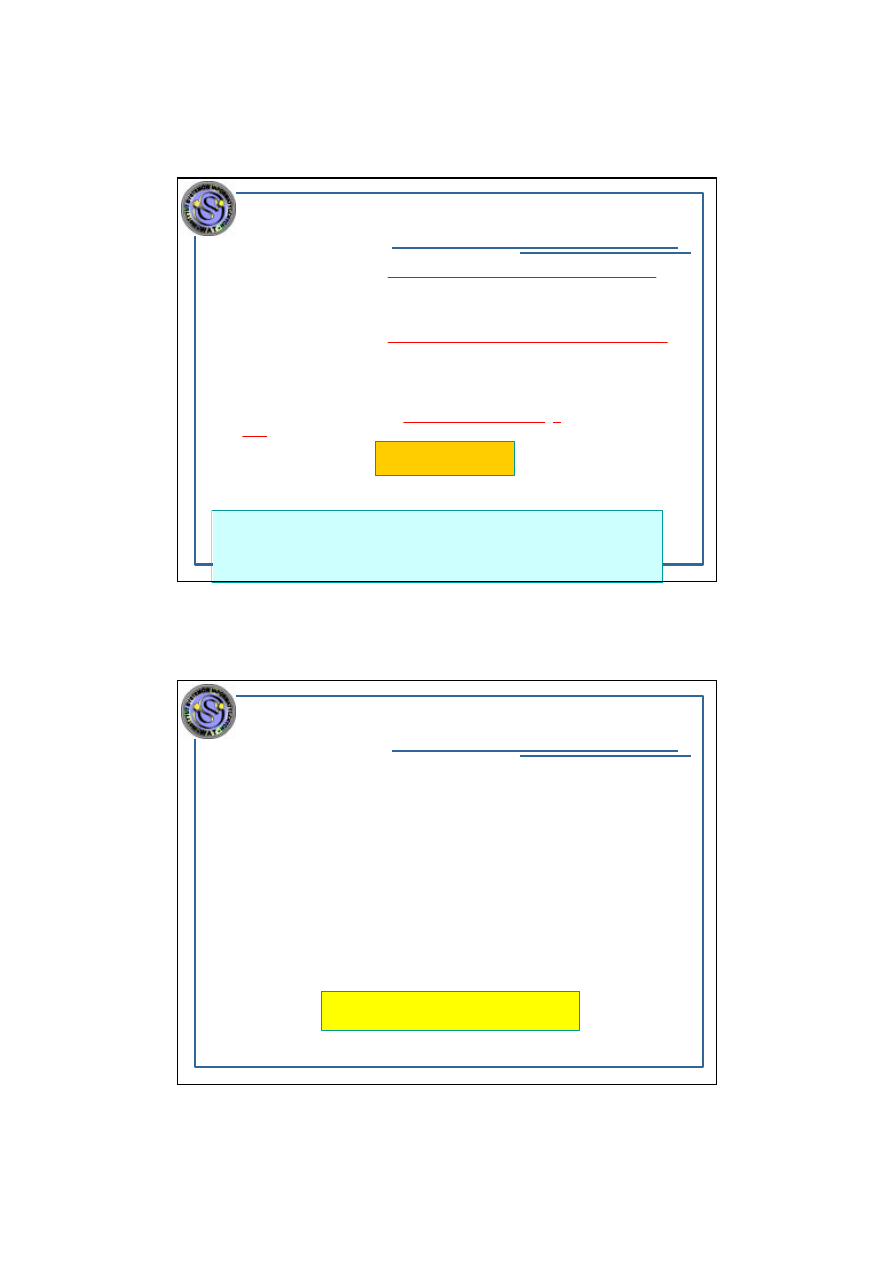
gdzie S(A(Z)) – wartosc rozwiazania problemu Z przez algorytm
A, S(Z) – wartosc optymalnego rozwiazania problemu Z;
UWAGA!
Optymalnosc algorytmu ze wzgledu na dokladnosc oraz zlozonosc
nie musi sie pokrywac !!!
( ( ))
( )
S A Z
S Z
ε
≤ ⋅
6
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
PESYMISTYCZNA ZLOZONOSC
OBLICZENIOWA
Niech:
D
n
- zbiór danych rozmiaru n dla rozwazanego
problemu;
- liczba operacji podstawowych wykonanych
przez algorytm na danych I
∈D
n
;
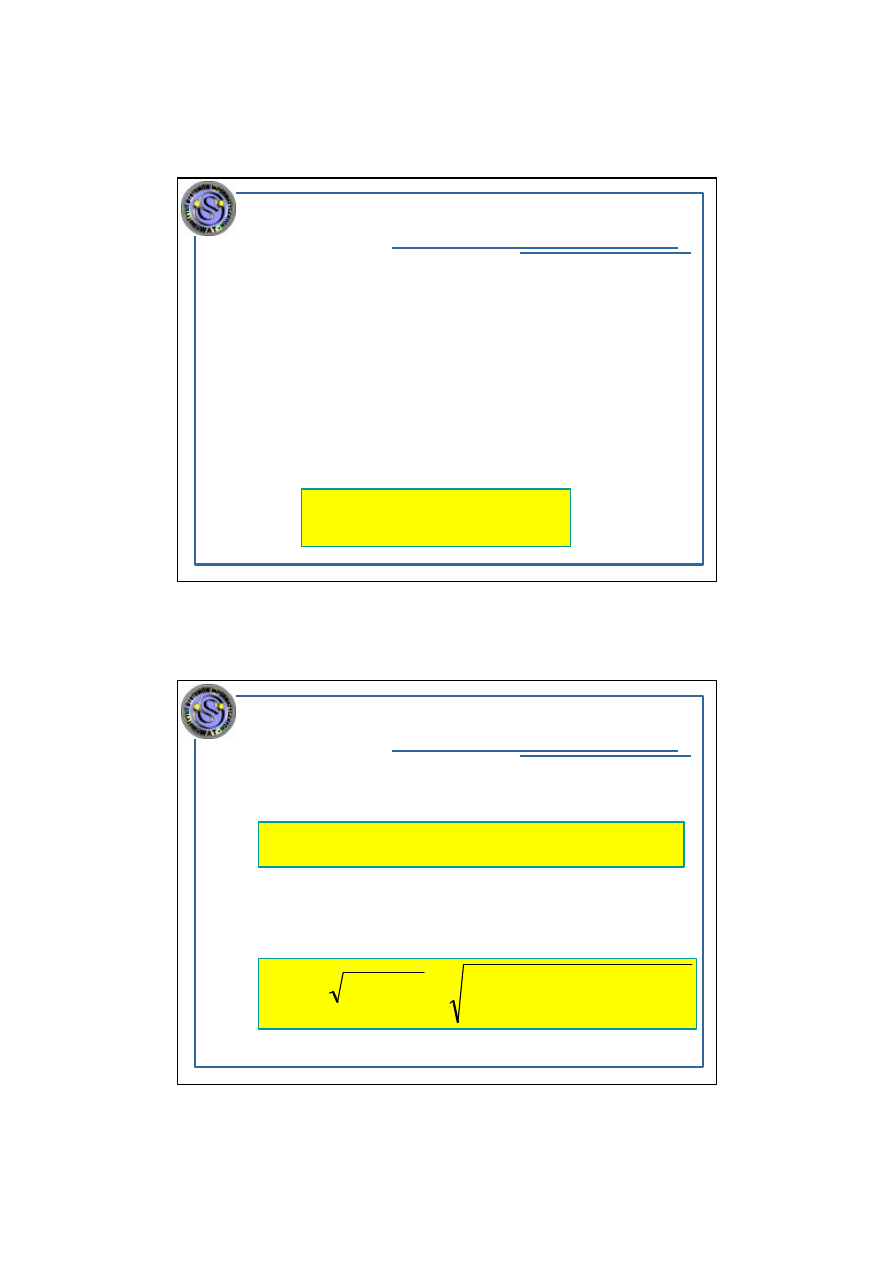
Pesymistyczna
zlozonosc
obliczeniowa
W(n)
definiowana jest jako :
( )
I
t
( )
( )
{
}
n
D
I
I
t
n
W
∈
=
:
max
4
7
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
OCZEKIWANA ZLOZONOSC
OBLICZENIOWA
Niech:
-prawdopodobienstwo wystepowania danych I
∈D
n
;
- zmienna losowa o wartosciach
i rozkladzie ;
Oczekiwana zlozonosc obliczeniowa
A(n) definiowana
jest jako :
( )
I
p
n
X
( )
I
t
( )
I
p
( )
( ) ( )
)
(
n
D
I
X
E
I
t
I
p
n
A
n
=
=
∑
∈
8
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
WRAZLIWOSC PESYMISTYCZNA
I OCZEKIWANA ALGORYTMÓW
Wrazliwosc pesymistyczna
:
( )
( ) ( )
{
}
n
D
I
I
I
t
I
t
n
∈
−
=
∆
2
1
2
1
,
:
max
Wrazliwosc oczekiwana
:
( )
( )
( ) ( ) ( )
(
)
2
E
∑
∈
−
⋅
=
=
n
D
I
n
n
X
I
t
I
p
X
Var
n
δ
5
9
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
DEFINICJE RZEDÓW ZLOZONOSCI
OBLICZENIOWEJ
Niech R* =R
+
∪{0}.
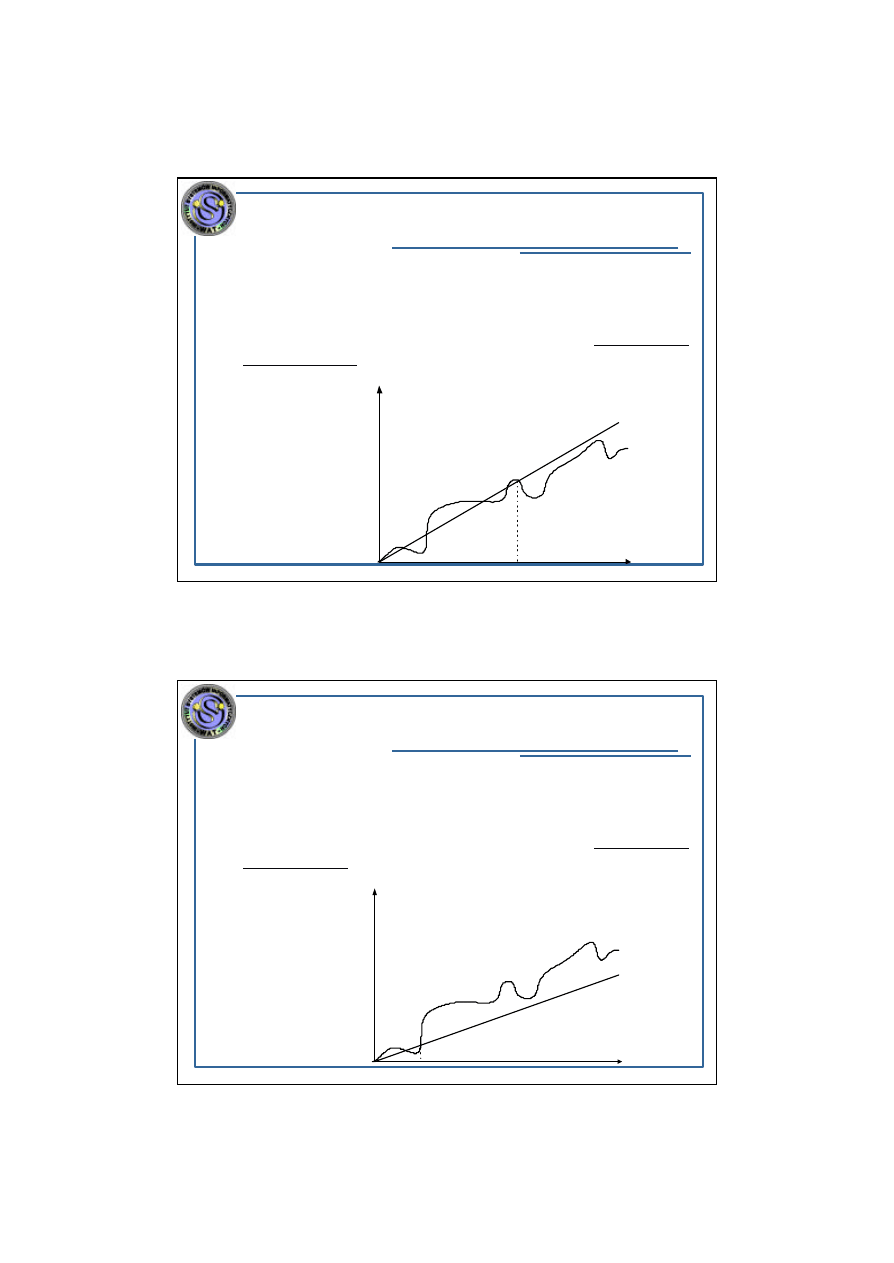
Mówimy, ze funkcja
f(x):R*
→R* jest rzedu
O
O
(
(
g(x)
g(x)
)
)
(g(x):R*
→R*), jesli istnieje taka stala c>0 oraz x
0
∈R*,
ze dla kazdego x
≥x
0
zachodzi f(x)
≤c⋅g(x) (f nie rosnie
szybciej niz g).
x
y
x
0
f(x)
cg(x)
f(x)=O(g(x))
10
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
DEFINICJE RZEDÓW ZLOZONOSCI
OBLICZENIOWEJ, c.d.
Niech R* =R
+
∪{0}.
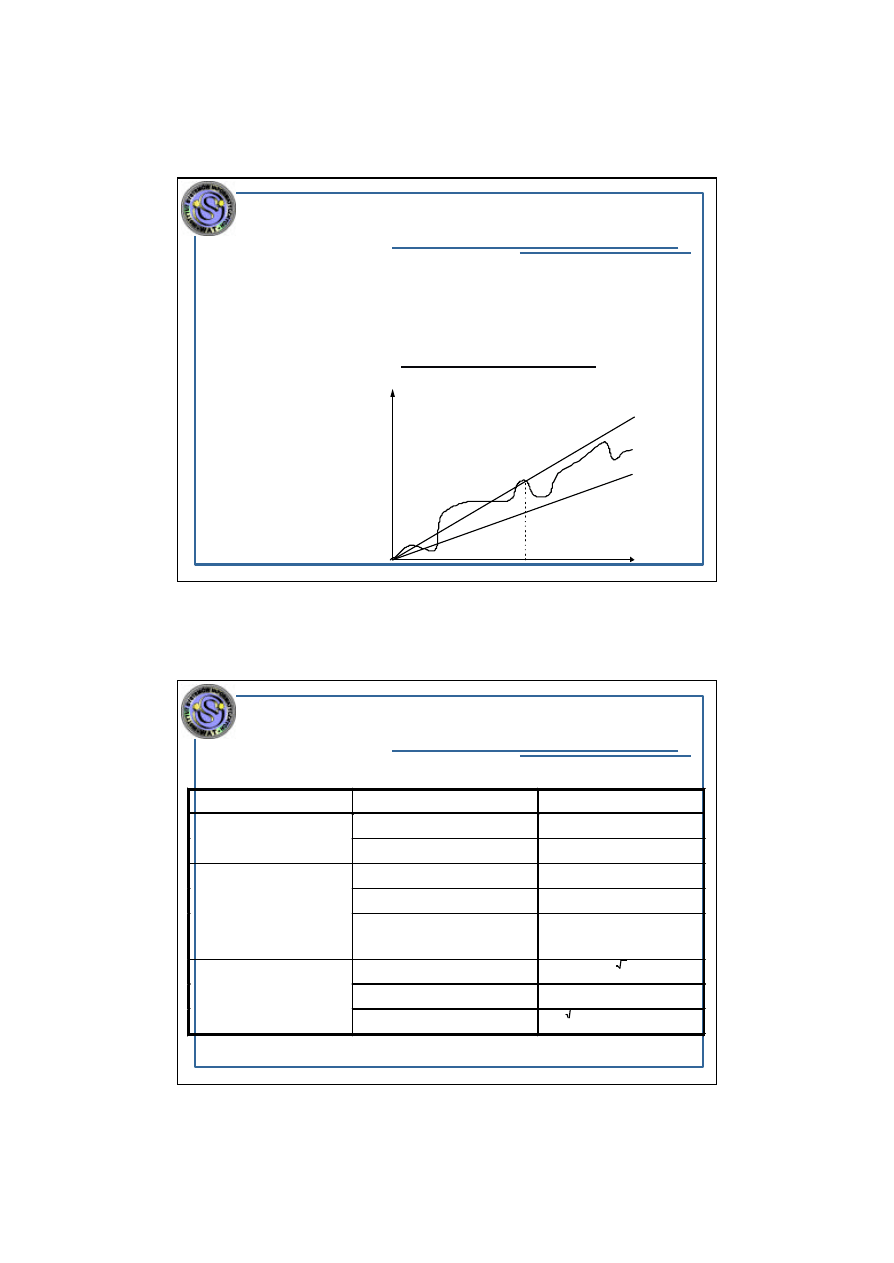
Mówimy, ze
funkcja f(x):R*
→R* jest rzedu
Ω
Ω
(
(
g(x)
g(x)
)
)
(g(x):R*
→R*), jesli istnieje taka stala c>0 oraz x
0
∈R*,
ze dla kazdego x
≥x
0
zachodzi g(x)
≤c⋅f(x) (f nie rosnie
wolniej niz g).
x
y
x
0
cf(x)
g(x)
f
f
(x)=
(x)=
Ω
Ω
(
(
g(x)
g(x)
)
)
6
11
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
Niech R* =R
+
∪{0}.
Mówimy, ze
funkcja f(x):R*
→R* jest rzedu
Θ
Θ
(
(
g(x)
g(x)
)
)
(g(x):R*
→R*), jesli istnieja takie stale c
1
, c
2
>0 oraz
x
0
∈R*,
ze dla kazdego
x
≥x
0
zachodzi
c
1
g(x)
≤f(x)≤c
2
g(x) (f rosnie tak samo jak g).
x
y
x
0
f(x)
c
1
g(x)
c
2
g(x)
f
f
(x)=
(x)=
Θ
Θ
(
(
g(x)
g(x)
)
)
DEFINICJE RZEDÓW ZLOZONOSCI
OBLICZENIOWEJ, c.d.
12
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
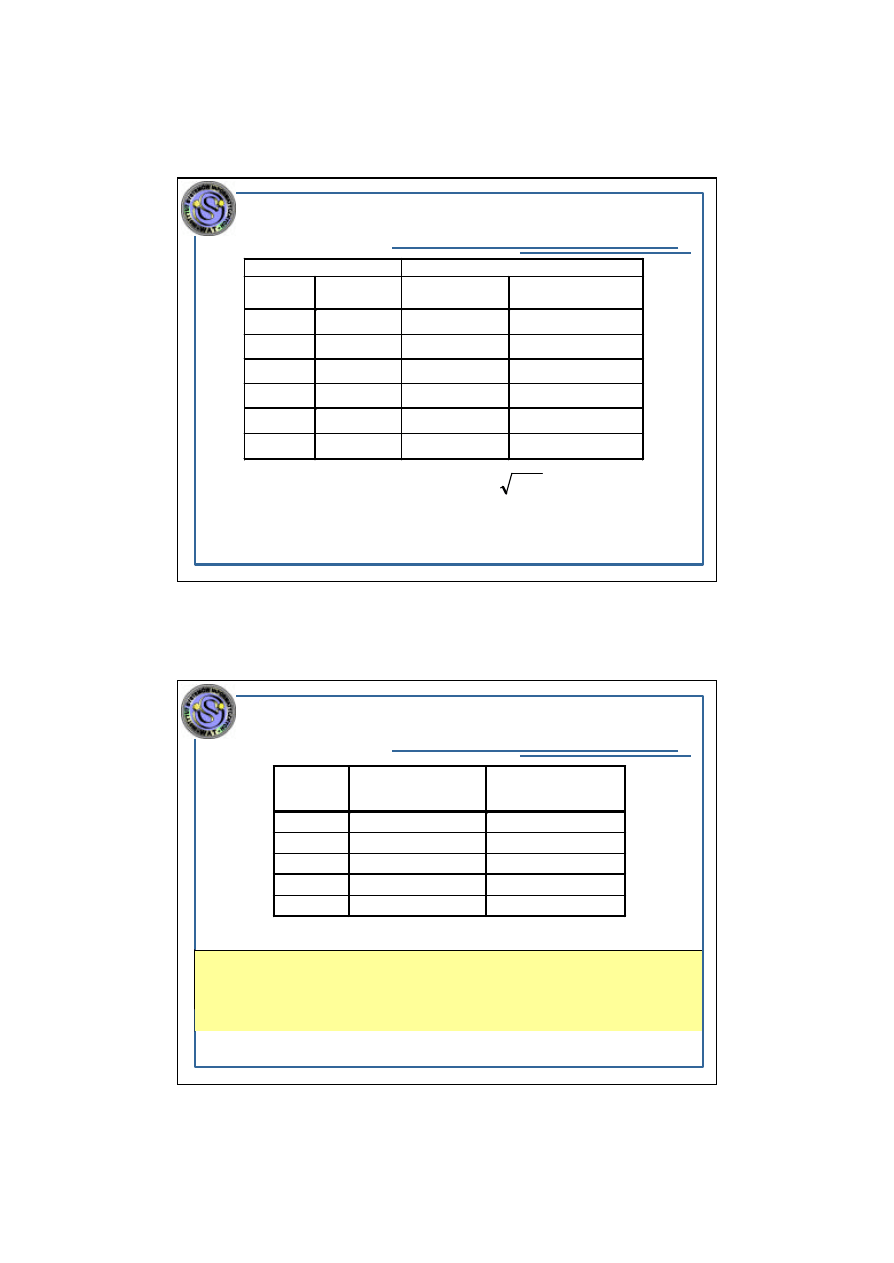
KLASY I TYPY FUNKCJI ZLOZONOSCI
OBLICZENIOWEJ
Klasa funkcji
Typ funkcji
Przyklady
stala
(
)
n
e
n
2
sin
−
Θ
,
( )
n
/
1
Θ
subliniowa
polilogarytmiczna
(
)
n
log
log
Θ
,
(
)
n
2
log
Θ
liniowa
( )
n
Θ
,
(
)
(
)
n
n
n
/
1
1
+
Θ
quasi-liniowa
(
)
n
nlog
Θ
,
(
)
n
n
log
log
Θ
wielomianowa
kwadratowa
( )
2
n
Θ
,
Θ
2
n
superwielomianowa
( )
n
n
lg
Θ
,
( )
n
e
Θ
wykladnicza
( )
n
2
Θ
,
( )
n
n 3
2
Θ
niewielomianowa
superwykladnicza
( )
n
n
2
Θ
,
( )
n
n
Θ
7
13
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
Wplyw wzrostu predkosci komputera na
maksymalny rozmiar zagadnienia, które
mozna rozwiazac w jednostce czasu
Algorytm
Maksymalny rozmiar zagadnienia
Symbol
Zlozonosc
przed wzrostem
predkosci
po 100-krotnym
wzroscie predkosci
5
A
( )
n
Θ
N
5
5
100N
4
A
( )
2
n
Θ
N
4
10 N
4
3
A
( )
3
n
Θ
N
3
4.64 N
3
2
A
( )
5
n
Θ
N
2
3.5 N
2
1
A
( )
n
2
Θ
N
1
6.64+N
1
0
A
(
)
n
n log
Θ
N
0
0
100N dla
1
0
>>
N
h
N
1
2
4
=
,
( )
100
1
2
4
4
⋅
=
h
N
c
⇒
10
100
4
=
=
c
h
N
1
2
1
=
,
100
1
2
1
1
⋅
=
+
h
c
N
⇒
100
2
1
=
c
⇒
c
1
=log
2
100=6.64
14
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
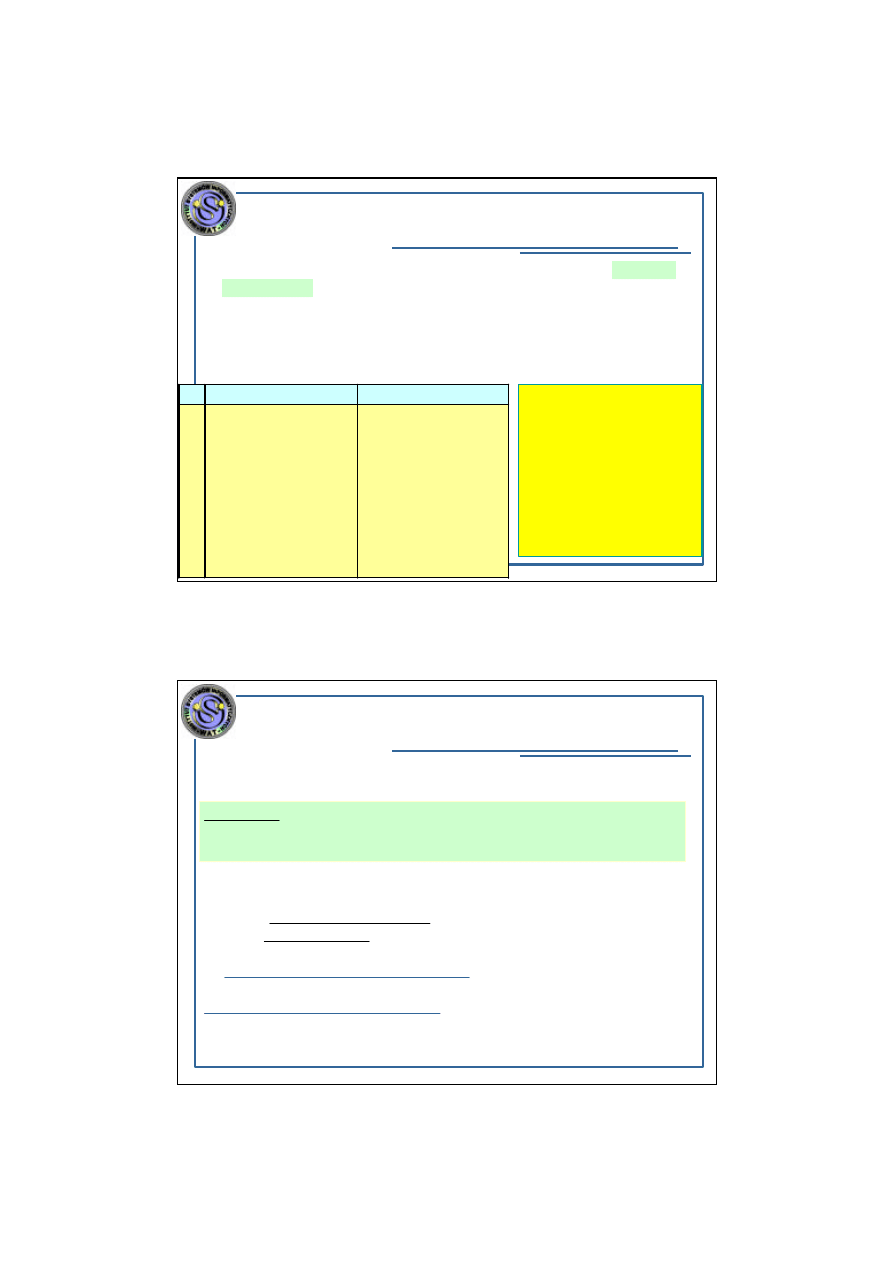
Zwiazek pomiedzy rz edem zlozonosci, stala
proporcjonalnosci, rozmiarem danych i
rzeczywistym czasem obliczen na minikomputerze
i superkomputerze
n
Cray-1
3
3n
[ns]
PENTIUM IV 1.6 GHz
195000n [ns]
10
3 µs
300 µs
100
3 ms
3 ms
1 000
3 s
30 ms
10 000
49 min.
300 ms
1000 000
95 lat
3 s
Mimo ze algorytm szescienny „wystartowal” z wiekszym impetem,
drugi algorytm (liniowy), majacy zlozonosc o 2 rzedy nizsza
(O(n) w stosunku do O(n
3
)),
„dogonil go” i okazal sie szybszy dla
100
>
n
.
8
15
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI
OBLICZENIOWEJ
Metody szacowania zlozonosci algorytmów
Aby oszacowac zlozonosc algorytmu zlicza sie tzw. operacje
podstawowe dla badanego problemu lub klasy rozwazanych
algorytmów, tj. takie, które sa najczesciej wykonywane
(ignorujac pozostale operacje pomocnicze, takie jak
instrukcje inicjalizacji, instrukcje organizacji petli itp.).
Tabela 1 Przyklady operacji podstawowych dla typowych
problemów obliczeniowych
Lp.
Problem
Operacja
1.
2.
3.
4.
Znalezienie x na liscie
nazwisk.
Mnozenie dwóch macierzy
liczb rzeczywistych.
Porzadkowanie liczb.
Wyznaczanie drogi
najkrótszej w grafie zadanym
w postaci listy sasiadów.
Porównanie x z pozycja na
liscie.
Mnozenie dwóch macierzy
liczb typu real (lub mnozenie
i dodawanie).
Porównanie dwóch liczb
(lub porównanie i zamiana).
Operacja na wskazniku listy.
Zalety zliczania operacji
Zalety zliczania operacji
podstawowych:
podstawowych:
-
Uniezale znienie sie od
rodzaju i liczby
procesorów ;
-
Mozliwosc przewidywania
zachowania sie algorytmu
dla róznych danych;
-
Swoboda wyboru operacji
podstawowej;
16
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI OBLICZENIOWEJ
Przyk
Przyk
l
l
ady praktyczne mierzenia z
ady praktyczne mierzenia z
l
l
o
o
z
z
ono
ono
s
s
ci obliczeniowej
ci obliczeniowej
–
–
Przyk
Przyk
l
l
ad 4
ad 4
Przyklad 4: Prosta petla
for (i=sum=0; i<n; i++) sum+=a[i];
Powyzsza petla powtarza sie n razy, podczas kaz dego jej przebiegu
realizuje dwa przypisania: aktualizujace zmienna „sum” i zmiane wartosci
zmiennej „i”. Mamy zatem 2 n przypisan podczas calego wykonania petli;
jej
asymptotyczna z
asymptotyczna z
l
l
o
o
z
z
ono
ono
sc
sc
wynosi O(
wynosi O(
n
n
).
).
Czy mo
Czy mo
z
z
emy zapisa
emy zapisa
c
c
, r
, r
ó
ó
wnie
wnie
z
z
Ω
Ω
(
(
n
n
) ?
) ?
TAK
Zatem mozemy zapisac
Θ(n).
9
17
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI OBLICZENIOWEJ
Przyk
Przyk
l
l
ady praktyczne mierzenia z
ady praktyczne mierzenia z
l
l
o
o
z
z
ono
ono
s
s
ci obliczeniowej
ci obliczeniowej
–
–
Przyk
Przyk
l
l
ad 5
ad 5
Przyklad 5: Petla zagniez dzona
for (i=0; i<n; i++) {
for (j=1, sum=a[0]; j<=i; j++)
sum+=a[j]; }
Na samym poczatku zmiennej „i” nadawana jest wartosc poczatkowa. Petla
zewnetrzna powtarza sie n razy, a w kazdej jej iteracji wykonuje sie wewnetrzna
petla oraz instrukcja przypisania wartosci zmiennym „i”, „ j”, „ sum”. Petla
wewnetrzna wykonuje sie „i” razy dla kazdego i e {1,...,n-1}, a na kazda iteracje
przypadaja dwa przypisania:jedno dla „sum”, jedno dla „j”. Mamy zatem
1 + 3n + 2(1+2+...+n-1) = 1 + 3n + n (n-1) = O(n) + O(n
2
) = O(n
2
)
przypisan wykonywanych w calym programie. Jej
asymptotyczna z
asymptotyczna z
l
l
o
o
z
z
ono
ono
sc
sc
wynosi
wynosi
O(n
O(n
2
2
).
).
Czy mo
Czy mo
z
z
emy zapisa
emy zapisa
c
c
r
r
ó
ó
wnie
wnie
z
z
Ω
Ω
(
(
n
n
2
2
),
),
Θ
Θ
(
(
n
n
2
2
)
)
?
?
P
P
e
e
tle zagnie
tle zagnie
z
z
d
d
z
z
one maj
one maj
a
a
zwykle wi
zwykle wi
e
e
ksz
ksz
a
a
z
z
l
l
o
o
z
z
ono
ono
sc
sc
ni
ni
z
z
pojedyncze, jednak nie musi
pojedyncze, jednak nie musi
tak by
tak by
c
c
zawsze.
zawsze.
TAK
18
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI OBLICZENIOWEJ
Przyk
Przyk
l
l
ady praktyczne mierzenia z
ady praktyczne mierzenia z
l
l
o
o
z
z
ono
ono
s
s
ci obliczeniowej
ci obliczeniowej
–
–
Przyk
Przyk
l
l
ad 6
ad 6
Analiza tych dwóch przypadk ów byla stosunkowo prosta poniewaz liczba
iteracji nie zalezala od wartosci elementów tablicy.
Wyznaczenie zloz onosci asymptotycznej jest trudniejsze jezeli liczba iteracji
nie jest zawsze jednakowa.
Przyklad 6: Znajdz najdluzsza podtablice zawierajac a
liczby uporzadkowane rosnaco.
for (i=0; len=1; i<n-1; i++) {
for (i1=i2=k=i; k<n-1 && a[k]<a[k+1]; k++,i2++);
if(len < i2-i1+1) len=i2-i1+1; }
=> Jesli liczby w tablicy sa uporzadkowane malejaco, to pe tla zewne trzna
wykonuje sie n-1 razy, a w kaz dym jej przebiegu petla wewne trzna
wykona sie tylko raz. Zlozonosc algorytmu wynosi wi ec wtedy
O(n).
O(n).
10
19
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI OBLICZENIOWEJ
Przyk
Przyk
l
l
ady praktyczne mierzenia z
ady praktyczne mierzenia z
l
l
o
o
z
z
ono
ono
s
s
ci obliczeniowej
ci obliczeniowej
–
–
Przyk
Przyk
l
l
ad 6, c.d.
ad 6, c.d.
Analiza tych dwóch przypadk ów byla stosunkowo prosta poniewaz liczba
iteracji nie zalezala od wartosci elementów tablicy.
Wyznaczenie zloz onosci asymptotycznej jest trudniejsze jezeli liczba iteracji
nie jest zawsze jednakowa.
Przyklad 6: Znajdz najdluzsza podtablice zawierajac a
liczby uporzadkowane rosnaco.
for (i=0; len=1; i<n-1; i++) {
for (i1=i2=k=i; k<n-1 && a[k]<a[k+1]; k++,i2++);
if(len < i2-i1+1) len=i2-i1+1; }
=> Jesli liczby w tablicy sa uporzadkowane rosnaco, to petla zewnetrzna
wykonuje sie n-1 razy, a w kaz dym jej przebiegu petla wewne trzna
wykona sie i razy dla i
∈{1,...,n-1}.
Zl ozonosc algorytmu wynosi wi ec wtedy
O(n
O(n
2
2
).
).
Poniewa
Poniewa
z
z
z
z
l
l
o
o
z
z
ono
ono
sc
sc
algorytmu jest mierzona dla przypadku
algorytmu jest mierzona dla przypadku
„
„
najgorszych danych
najgorszych danych
”
”
zatem z
zatem z
l
l
o
o
z
z
ono
ono
sc
sc
algorytmu wynosi
algorytmu wynosi
O(n
O(n
2
2
).
).
20
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI OBLICZENIOWEJ
Przyk
Przyk
l
l
ady praktyczne mierzenia z
ady praktyczne mierzenia z
l
l
o
o
z
z
ono
ono
s
s
ci obliczeniowej
ci obliczeniowej
–
–
Przyk
Przyk
l
l
ad 6, c.d.
ad 6, c.d.
Analiza tych dwóch przypadk ów byla stosunkowo prosta poniewaz liczba
iteracji nie zalezala od wartosci elementów tablicy.
Wyznaczenie zloz onosci asymptotycznej jest trudniejsze jezeli liczba iteracji
nie jest zawsze jednakowa.
Przyklad 6: Znajdz najdluzsza podtablice zawierajac a
liczby uporzadkowane rosnaco.
for (i=0; len=1; i<n-1; i++) {
for (i1=i2=k=i; k<n-1 && a[k]<a[k+1]; k++,i2++);
if(len < i2-i1+1) len=i2-i1+1; }
=> Z reguly dane nie sa uporzadkowane i ocena zloz onosci algorytmu jest
rzecz a nielatwa, ale bardzo istotna. Staramy sie wyznaczy zloz onosc
w „ przypadku optymistycznym”, „ przypadku pesymistycznym” oraz
„ przypadku srednim”. Czesto poslugujemy sie wtedy przyblizeniami
opartymi o notacje „ duze O,
Ω i Θ”.
11
21
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI OBLICZENIOWEJ
Przyk
Przyk
l
l
ady praktyczne mierzenia z
ady praktyczne mierzenia z
l
l
o
o
z
z
ono
ono
s
s
ci obliczeniowej
ci obliczeniowej
–
–
Przyk
Przyk
l
l
ad 7
ad 7
Przyklad 7:
Algorytm sortowania
Insertion-Sort(A)
1. for j:=2 to length[A]
2.
do key:=A[j]
/* Wstaw A [i] w posortowany
ciag A[1..j-1].*/
3.
i:= j-1
4.
while i>0 i A[i] > key
5.
do A[i+1] := A[i]
6.
i:= i-1
7.
A[i+1] := key
Przyklad dzialania algorytmu
5 2 4 6 1 3
2 5 4 6 1 3
2 4 5 6 1 3
2 4 5 6 1 3
1 2 4 5 6 3
1 2 3 4 5 6
22
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI OBLICZENIOWEJ
Przyk
Przyk
l
l
ady praktyczne mierzenia z
ady praktyczne mierzenia z
l
l
o
o
z
z
ono
ono
s
s
ci obliczeniowej
ci obliczeniowej
–
–
Przyk
Przyk
l
l
ad 7, c.d.
ad 7, c.d.
Insertion-Sort(A)
koszt
koszt
liczba wykona
liczba wykona
n
n
1.
for j:=2 to length[A]
c
1
n
2.
do key:=A[i]
c
2
n-1
3.
i:= j-1
c
3
n-1
4.
while i>0 i A[i] > key
c
4
5.
do A[i+1] := A[i]
c
5
6.
i:= i-1
c
6
7.
A[i+1] := key
c
7
n-1
∑
=
n
j
j
t
2
∑
=
−
n
j
j
t
2
)
1
(
∑
=
−
n
j
j
t
2
)
1
(
12
23
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SZACOWANIE ZLOZONOSCI OBLICZENIOWEJ
Przyk
Przyk
l
l
ady praktyczne mierzenia z
ady praktyczne mierzenia z
l
l
o
o
z
z
ono
ono
s
s
ci obliczeniowej
ci obliczeniowej
–
–
Przyk
Przyk
l
l
ad 7, c.d.
ad 7, c.d.
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
(
7
2
6
2
5
2
4
3
2
1
−
+
−
+
−
+
+
−
+
−
+
=
∑
∑
∑
=
=
=
n
c
t
c
t
c
t
c
n
c
n
c
n
c
n
T
n
j
j
n
j
j
n
j
j
1
2
)
1
(
2
−
+
=
∑
=
n
n
j
n
j
2
)
1
(
)
1
(
2
−
=
−
∑
=
n
n
j
n
j
=
−
+
−
+
−
+
−
+
+
−
+
−
+
=
)
1
(
2
)
1
(
2
)
1
(
1
2
)
1
(
)
1
(
)
1
(
)
(
7
6
5
4
3
2
1
n
c
n
n
c
n
n
c
n
n
c
n
c
n
c
n
c
n
T
)
(
2
2
2
2
2
2
7
4
3
2
7
6
5
4
3
2
1
2
6
5
4
c
c
c
c
n
c
c
c
c
c
c
c
n
c
c
c
+
+
+
−
+
−
−
+
+
+
+
+
+
=
2
2
( )
(
)
T n
an
bn
c
O n
=
+ + =
24
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
SPOSOBY BADANIA OPTYMALNOSCI
ALGORYTMÓW
n
Istnieje pewna granica
zwana
wewnetrzna
zlozonoscia
problemu
(ang. inherent problem
complexity), tzn. minimalna ilosc pracy niezbednej
do wykonania w celu rozwiazania zadania, której
nie mozna przekroczyc, poprawiajac zlozonosc
algorytmu;
n
Aby pokazac, ze
algorytm jest optymalny
algorytm jest optymalny
ze
ze
wzgl
wzgl
e
e
du na z
du na z
l
l
o
o
z
z
ono
ono
sc
sc
najczesciej dowodzi sie, ze
istnieje pewne dolne oszacowanie liczby operacji
podstawowych potrzebnych do rozwiazania
problemu.
13
25
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
Aby zbadac, czy algorytm jest optymalny nalezy:
1. Zaprojektowac
mozliwie najlepszy algorytm,
powiedzmy A. Nastepnie przeanalizowac algorytm
A, otrzymujac zlozonosc najgorszego przypadku
W
.
2. Dla pewnej funkcji
F
udowodnic twierdzenie
mówiace, ze
dla dowolnego algorytmu w rozwa
dla dowolnego algorytmu w rozwa
z
z
anej
anej
klasie istniej
klasie istniej
a
a
dane rozmiaru
dane rozmiaru
n
n
takie,
takie,
z
z
e algorytm
e algorytm
musi wykona
musi wykona
c
c
przynajmniej
przynajmniej
F(n
F(n
)
)
krok
krok
ó
ó
w.
w.
3. Jesli funkcje
W
i
F
sa równe, to algorytm A jest
optymalny (dla najgorszego przypadku).
SPOSOBY BADANIA OPTYMALNOSCI
ALGORYTMÓW
26
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
Przyklad
Problem
: Znajdowanie najwiekszej wsród n liczb.
Klasa algorytmów
: Algorytmy, które porównuja
liczby i przepisuja je.
Operacja podstawowa
: Porównanie dwóch
wielkosci.
SPOSOBY BADANIA OPTYMALNOSCI
ALGORYTMÓW
14
27
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
Algorytm_2
Dane
: L, n, gdzie L jest tablica
n-elementowa .
Wyniki
: max, najwiekszy element
w L.
begin
1.
max:= L[1];
2.
for index:= 2 to n do
3.
if max < L[index] then
max:= L[index]
end;
Oszacowanie g
Oszacowanie g
ó
ó
rne
rne
:
Przypuscmy, ze
liczby zapisane s a w tablicy L. Poró wnania s a
realizowane w linii 3, która jest wykonywana n-1
razy. Zatem n-1 jest g órna granica liczby
porównan koniecznych do znalezienia
maksimum w najgorszym przypadku danych.
Oszacowanie dolne
Oszacowanie dolne
:
:
Przypuscmy, ze nie
ma dwóch jednakowych liczb w L.
Zalo zenie takie jest dopuszczalne,
poniewaz dolne oszacowanie w tym
szczególnym przypadku jest równiez
dolnym oszacowaniem w przypadku
ogólnym. Gdy mamy n róznych liczb, to
n-1 z nich nie sa najwiekszymi. Ale zeby
stwierdzi c, ze jakis element nie jest
maksymalny, trzeba go porównac z
przynajmniej jednym z pozostalych.
Zatem
n-1
elementów musi byc
wyeliminowanych droga porównania z
pozostalymi. Poniewaz
w kazdym
porównaniu biora
udzial
tylko 2
elementy, wiec trzeba wykonac
przynajmniej n-1
porównan. Zatem
F(n)=n-1
jest poszukiwanym dolnym
oszacowaniem i na tej podstawie
wnioskujemy,
ze algorytm_2 jest
optymalny.
SPOSOBY BADANIA OPTYMALNOSCI
ALGORYTMÓW, PRZYKLAD C.D.
28
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
Przyklad
Problem
: Dane sa dwie macierze
rozmiaru
. Obliczyc macierz
.
Klasa algorytmów
: Algorytmy wykonujace
dodawania, odejmowania, mnozenia i dzielenia na
elementach macierzy.
Operacja podstawowa
: Mnozenie.
Oszacowanie górne
: Jak wiadomo, zwykly algorytm
wykonuje n
3
mnozen, zatem n
3
jest oszacowaniem
z góry.
Oszacowanie dolne
: Jak wiadomo, zlozonosc
pamieciowa wynosi 2n
2
, wiec
mnozen jest
niezbednych.
SPOSOBY BADANIA OPTYMALNOSCI
ALGORYTMÓW, PRZYKLAD
ij
A
a
=
ij
B
b
=
n
n
×
B
A
C
×
=
( )
2
n
Ω
15
29
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
n
Wniosek
: Nie ma mozliwosci stwierdzenia na tej
podstawie, czy algorytm klasyczny jest
optymalny, czy nie. Dlatego wlozono wiele
wysilku w poprawienie oszacowania dolnego, jak
dotad bezskutecznie. Z drugiej strony szuka sie
nowych, lepszych algorytmów.
n
Obecnie
najlepszy znany algorytm mno
najlepszy znany algorytm mno
z
z
enia
enia
dw
dw
ó
ó
ch macierzy kwadratowych wykonuje oko
ch macierzy kwadratowych wykonuje oko
l
l
o
o
n
n
2,376
2,376
mno
mno
z
z
e
e
n
n
.
.
n
Czy jest to algorytm optymalny? Nie wiadomo,
ciagle bowiem oszacowanie górne przewyzsza
oszacowanie dolne.
SPOSOBY BADANIA OPTYMALNOSCI
ALGORYTMÓW, PRZYKLAD C.D.
30
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
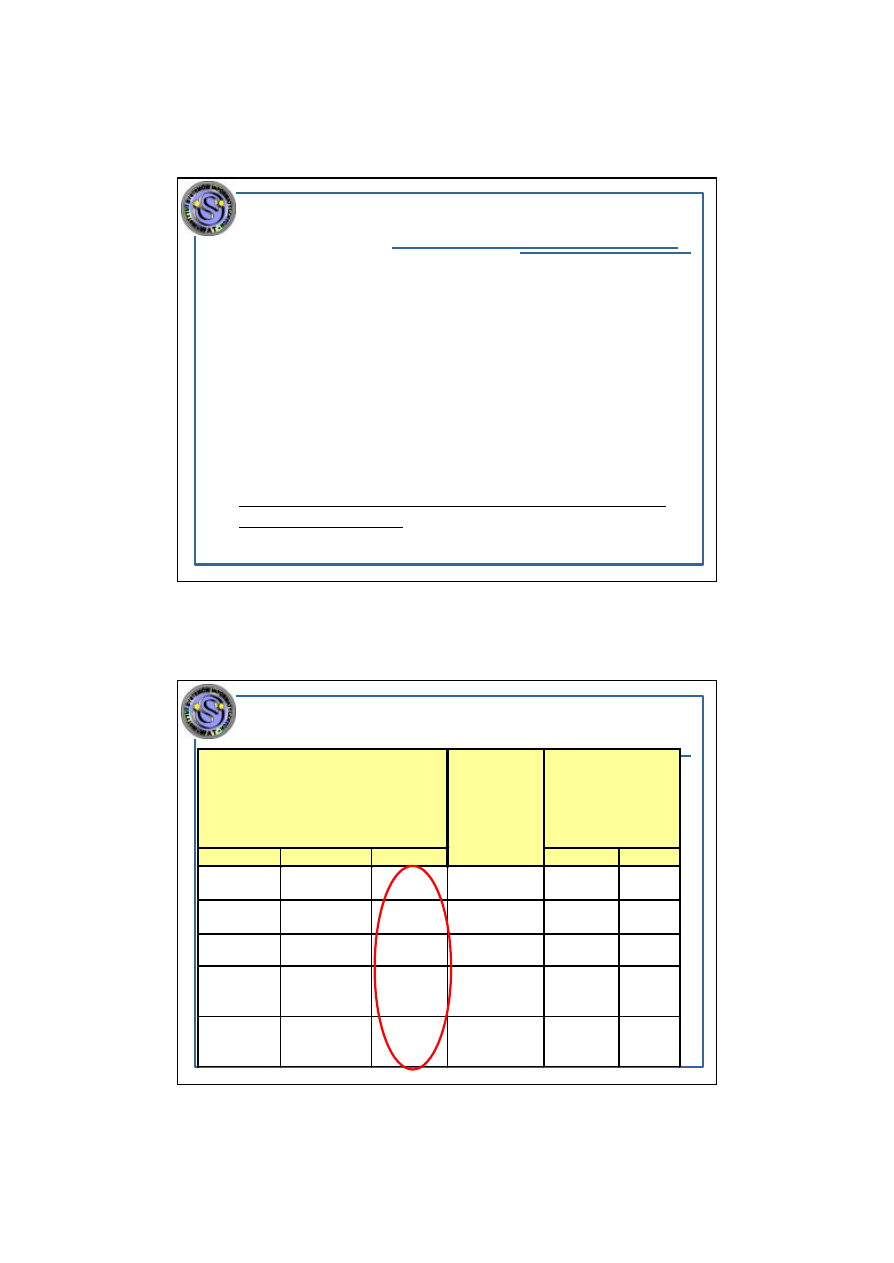
PRZYKLAD POSTEPU, JAKI DOKONAL SIE
W DZIEDZINIE PROJEKTOWANIA ALGORYTM ÓW
BADAJACYCH PLANARNOSC GRAFU
Algorytm
Rozmiar
analizowanego
grafu
w przypadku
udostepniania
komputera na okres
Symbol
Autor [rok]
Zlozonosc
Czas obliczen
dla
ms
c
10
=
100
=
n
minuty
godziny
1
A
Kuratowski
[1930]
6
cn
325 lat
4
8
2
A
Goldstein
[1963]
3
cn
2.8 godzin
18
71
3
A
Lempel et al.
[1967]
2
cn
100 sekund
77
6 000
4
A
Hopcroft-
Tarjan
[1971]
n
cn
2
log
7 sekund
643
24 673
5
A
Hopcroft-
Tarjan
[1974]
cn
1 sekunda
6 000
4
10
36
⋅
16
31
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
PROBLEM DECYZYJNY
A PROBLEM OPTYMALIZACYJNY
Problem decyzyjny – taki, dla którego odpowiedz brzmi „tak” albo „nie”.
Problem optymalizacyjny – polega na wyznaczaniu takiego elementu
zbioru rozwiazan dopuszczalnych, dla którego funkcja celu osiaga
ekstremum na tym zbiorze.
Przyklad
Optymalizacyjny
problem zaladunku mozna
sformulowac nastepujaco:
wyznaczyc
{ }
{
}
n
1,
j
,
0,1
x
:
E
x
B
S
x
j
n
n
*
=
∈
∈
=
⊂
∈
taki, ze
( )
( )
∑
=
∈
∈
=
=
n
j
j
j
x
c
1
S
x
S
x
*
m
x
c,
m
x
c,
ax
ax
gdzie
≤
∈
=
∑
=
n
1
j
j
j
n
d
x
a
:
B
x
S
oraz
j
c - wartosc towaru typu
n
1
j
j
,
,
=
,
j
a - objetosc towaru typu
n
1
j
j
,
,
=
,
d - pojemnosc srodka transportu.
Zwiazany z tym problemem
problem decyzyjny
sformulujemy w postaci
b) czy istnieje
n
B
x
∈
spelniajacy ograniczenia
( )
S
x
y,
x
c,
∈
≥
32
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
WIELOMIANOWA
TRANSFORMOWALNOSC
(SPROWADZALNOSC) PROBLEMÓW
Definicja
Problem decyzyjny
Π
1
jest
wielomianowo transformowalny
(sprowadzalny, redukowalny)
do problemu decyzyjnego
Π
2
(co zapisujemy
Π
1
α Π
2
) jesli dla dowolnego lancucha danych x
problemu
Π
1
mozna w wielomianowym czasie (wielomian zalezy
od
x
) zbudowac lancuch y danych problemu
Π
2
taki, ze x jest
lancuchem danych konkretnego problemu
Π
1
z odpowiedzia „tak”
wtedy i tylko wtedy, gdy y jest lancuchem danych konkretnego
problemu
Π
2
z odpowiedzia „tak”.
17
33
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
KLASY ZLOZONOSCI OBLICZENIOWEJ
PROBLEMÓW
Definicja
Klasa P
nazywamy klase wszystkich problemów decyzyjnych, których zlozonosc
obliczeniowa jest wielomianowa tzn. takich, które DTM rozwiazuje w czasie
ograniczonym od góry przez wielomian.
Definicja
Klasa NP
nazywamy klase wszystkich problemów de cyzyjnych, które sa
rozwiazywalne w czasie wielomianowym przez NDTM.
lub równowaznie
Definicja
Mówimy, ze
problem decyzyjny
Π nalezy do NP
jesli istnieje wielomian p(n) od
rozmiaru tego problemu oraz algorytm
α (algorytm weryfikacji potwierdzenia)
takie, ze dla kazdego konkretnego problemu
?
D
z
∈
z odpowiedzia „tak”
i lancuchem danych x(z) istnieje lancuch (potwierdzenie) c(x) symboli alfabetu
wejsciowego
Σ taki, ze:
-
( )
(
)
( )
(
)
z
x
p
z
x
c
≤
,
- algorytm
α po otrzymaniu na wejsciu sekwencji
( )
( )
( )
z
x
c
#
z
x
(# oznacza koniec
danych i poczatek potwierdzenia) dochodzi do odpowiedzi „tak” po nie wiecej
niz
( )
( )
z
x
p
krokach.
NP
P
⊂
34
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
KLASY ZLOZONOSCI OBLICZENIOWEJ
PROBLEMÓW, PRZYKLAD 1
Przyklad
Klika k-elementowa
: dla danego grafu G o zbiorze wierzcholków
V zbadac czy istnieje podgraf pelny o licznosci zbioru
wierzcholków równej k.
Dla rozwiazania tego zadania nalezaloby przejrzec
k
V
podzbiorów zbioru V.
Nie jest znany algorytm wielomianowy dla tego zadania.
Istnieje natomiast dla konkretnego zadania z odpowiedzia „tak”
„potwierdzenie” w postaci kodu zbioru C elementów kliki o
licznosci k, które mozna zweryfikowac w czasie wielomianowym
przy pomocy pewnego algorytmu
α sprawdzajacego:
- czy zbiór C ma licznosc k,
- czy podgraf zawierajacy wierzcholki ze zbioru C jest pelny.
18
35
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
KLASY ZLOZONOSCI OBLICZENIOWEJ
PROBLEMÓW, PRZYKLAD 2
Przyklad
Zadanie komiwojazera
: dla sieci o
V
n
=
wierzcholkach
i odleglosciach miedzy wierzcholkami zadanymi
calkowitoliczbowa macierza
( )
n x n
ij
d
d
=
zbadac czy istnieje cykl
Hamiltona o dlugosci mniejszej lub równej zadanej liczbie L
(calkowitej).
Dla konkretnego zadania z odpowiedzia „tak” wystarczajacym
potwierdzeniem bedzie kod cyklu Hamiltona spelniajacy
wymagana dlugosc.
Przy pomocy algorytmu wielomianowego
α mozna sprawdzic czy:
-
( )
ij
d
d
L,
n,
=
poprawne dane,
- kod przedstawia cykl Hamiltona,
- dlugosc cyklu Hamiltona jest mniejsza lub równa L.
36
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
KLASY ZLOZONOSCI OBLICZENIOWEJ
PROBLEMÓW, PRZYKLAD 3
Przyklad
Problem SPELNIALNOSCI
: czy istnieje wektor
n
B
x
∈
, dla
którego formula alternatywno – koniunkcyjna jest równa 1.
Dla konkretnego zadania z odpowiedzia „tak” dobrym
potwierdzeniem jest wlasnie kod wektora x, dla którego ta
formula przyjmuje wartosc 1.
Algorytm
α w czasie wielomianowym sprawdza czy:
- formula zawiera n zmiennych,
- wyrazenie jest w poprawnej formie,
- formula przyjmuje wartosc 1.
19
37
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
KLASY ZLOZONOSCI OBLICZENIOWEJ
PROBLEMÓW, PROBLEMY NP-ZUPELNE
Wazna podklasa problemów w NP jest klasa problemów
NP – zupelnych
, które maja miedzy innymi taka wlasnosc, ze
j
j
j
e
e
e
s
s
s
l
l
l
i
i
i
k
k
k
t
t
t
ó
ó
ó
r
r
r
y
y
y
k
k
k
o
o
o
l
l
l
w
w
w
i
i
i
e
e
e
k
k
k
z
z
z
n
n
n
i
i
i
c
c
c
h
h
h
m
m
m
i
i
i
a
a
a
l
l
l
b
b
b
y
y
y
w
w
w
i
i
i
e
e
e
l
l
l
o
o
o
m
m
m
i
i
i
a
a
a
n
n
n
o
o
o
w
w
w
y
y
y
(
(
(
n
n
n
a
a
a
D
D
D
T
T
T
M
M
M
)
)
)
a
a
a
l
l
l
g
g
g
o
o
o
r
r
r
y
y
y
t
t
t
m
m
m
r
r
r
o
o
o
z
z
z
w
w
w
i
i
i
a
a
a
z
z
z
a
a
a
n
n
n
i
i
i
a
a
a
,
,
,
t
t
t
o
o
o
i
i
i
s
s
s
t
t
t
n
n
n
i
i
i
a
a
a
l
l
l
b
b
b
y
y
y
w
w
w
i
i
i
e
e
e
l
l
l
o
o
o
m
m
m
i
i
i
a
a
a
n
n
n
o
o
o
w
w
w
y
y
y
a
a
a
l
l
l
g
g
g
o
o
o
r
r
r
y
y
y
t
t
t
m
m
m
d
d
d
l
l
l
a
a
a
k
k
k
a
a
a
z
z
z
d
d
d
e
e
e
g
g
g
o
o
o
p
p
p
r
r
r
o
o
o
b
b
b
l
l
l
e
e
e
m
m
m
u
u
u
n
n
n
a
a
a
l
l
l
e
e
e
z
z
z
a
a
a
c
c
c
e
e
e
g
g
g
o
o
o
d
d
d
o
o
o
N
N
N
P
P
P
.
.
.
Definicja
Problem
NP
?
∈
nazywamy NP – zupelnym jesli dla kazdego
NP
?
∈
′
zachodzi
?
?
∝
′
.
38
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
KLASY ZLOZONOSCI OBLICZENIOWEJ
PROBLEMÓW, PROBLEMY NP-ZUPELNE
Twierdzenie (Cook, 1971)
Problem
SPELNIALNOSCI
jest NP – zupelny.
Dysponujac takim jednym problemem NP – zupelnym mozna
latwiej wykazac NP – zupelnosc innych problemów.
Przyklady problemów NP – zupelnych :
♦
klika k-elementowa,
♦
cykl (droga) Hamiltona,
♦
zadanie komiwojazera.
Znanych jest okolo kilku tysiecy problemów NP – zupelnych.
20
39
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
DOWODZENIE NP-ZUPELNOSCI
PROBLEMÓW
Glówna technika dowodzenia NP-zupelnosci problemów jest technika
ograniczania.
W celu wykazania, ze rozpatrywany problem
NP
?
1
∈
jest
NP-zupelny nalezy zgodnie z ta technika udowodnic, ze zawiera on w
sobie znany NP-zupelny problem
Π
2
jako przypadek szczególny
problemu
Π
1
.
Przyklad (
najdluzsza droga w grafie
)
Dany jest graf
(
)
E
V,
G
=
i liczba naturalna
.
V
k
<
Problem
Π
1
: czy graf G zawiera droge prosta (kazdy wierzcholek
tylko raz moze wystapic) zawierajaca nie mniej niz k galezi.
Przyjmujac
1
−
=
V
k
otrzymujemy jako przypadek szczególny
problem
Π
2
w postaci drogi Hamiltona, który jest NP-zupelny.
Zauwazmy ponadto, ze
NP
?
1
∈
gdyz sprawdzalnym wielomianowo
potwierdzeniem moze byc kod takiej drogi.
Zachodzi równiez
1
2
?
?
∝
co uzyskujemy ograniczajac problem
Π
1
do
tych
1
?
D
z
∈
dla których
1
−
=
V
k
.
40
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
DOWODZENIE NP-ZUPELNOSCI
PROBLEMÓW, c.d.
Przyklad (
konstrukcja niezawodnej sieci
)
Dane sa dwie symetryczne macierze
( )
nxn
ij
d
d
=
- macierz odleglosci miedzy wierzcholkami,
( )
nxn
ij
r
r
=
- macierz wielokrotnosci polaczen miedzy
wierzcholkami .
Problem
Π
1
: czy istnieje siec zawi erajaca n-wierzcholków, w
której suma odleglosci jest nie wieksza od L, taka ze miedzy i-tym
oraz j-tym wierzcholkiem istnieje nie mniej niz r
ij
rozlacznych
wierzcholkowo dróg.
Przyjmujac
2
r
1,
d
n,
L
ij
ij
=
=
=
dla wszystkich
j
r
≠
, jedynym grafem z n
wierzcholkami, w którym miedzy dwoma dowolnymi wierzcholkami
istnieja dwie nie majace wspólnych wierzcholków drogi, jest cykl z n
wierzcholkami. Zatem szczególny przypadek problemu
Π
1
jest problemem
Π
2
sprowadzajacym sie do pytania o istnienie cyklu Hamiltona w sieci
n-wierzcholkowej z
2
r
1,
d
ij
ij
=
=
. Problem
Π
2
jest NP-zupelny. Ponadto
NP
?
1
∈
oraz
1
2
?
?
∝
.
21
41
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
Wsród problemów NP-zupelnych mozemy zaobserwowac takie,
których szczególne przypadki staja sie problemami
„latwymi”
i takie, które pozostaja
„trudne”
równiez dla szczególnych
przypadków.
1
0
. Przypadki „latwe”
Przyklad
Maksymalna klika w grafie planarnym moze miec nie wiecej niz 4
wierzcholki. W takim szczególnym grafie mozna podac algorytm
wyznaczania kliki maksymalnej o zlozonosci
( )
4
V
O
czyli
„planarna klika” nalezy do P.
Do klasy P nalezy równiez zadanie tzw.”2-SPELNIALNOSCI”
tzn. zadanie, w którym kazdy czynnik zawiera tylko 2 literaly
(
)
i
i
x
x
lub
.
WNIOSEK: problem
WNIOSEK: problem
ó
ó
w nie nale
w nie nale
z
z
y formu
y formu
l
l
owa
owa
c
c
zbyt og
zbyt og
ó
ó
lnie, gdy
lnie, gdy
z
z
wtedy jest
wtedy jest
szansa,
szansa,
z
z
e zadanie mo
e zadanie mo
z
z
e mie
e mie
c
c
wielomianowy algorytm rozwi
wielomianowy algorytm rozwi
a
a
zania, mimo
zania, mimo
z
z
e jego uog
e jego uog
ó
ó
lnienie nale
lnienie nale
z
z
y do klasy NP
y do klasy NP
-
-
zupe
zupe
l
l
nych.
nych.
DOWODZENIE NP-ZUPELNOSCI
PROBLEMÓW, c.d.
42
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
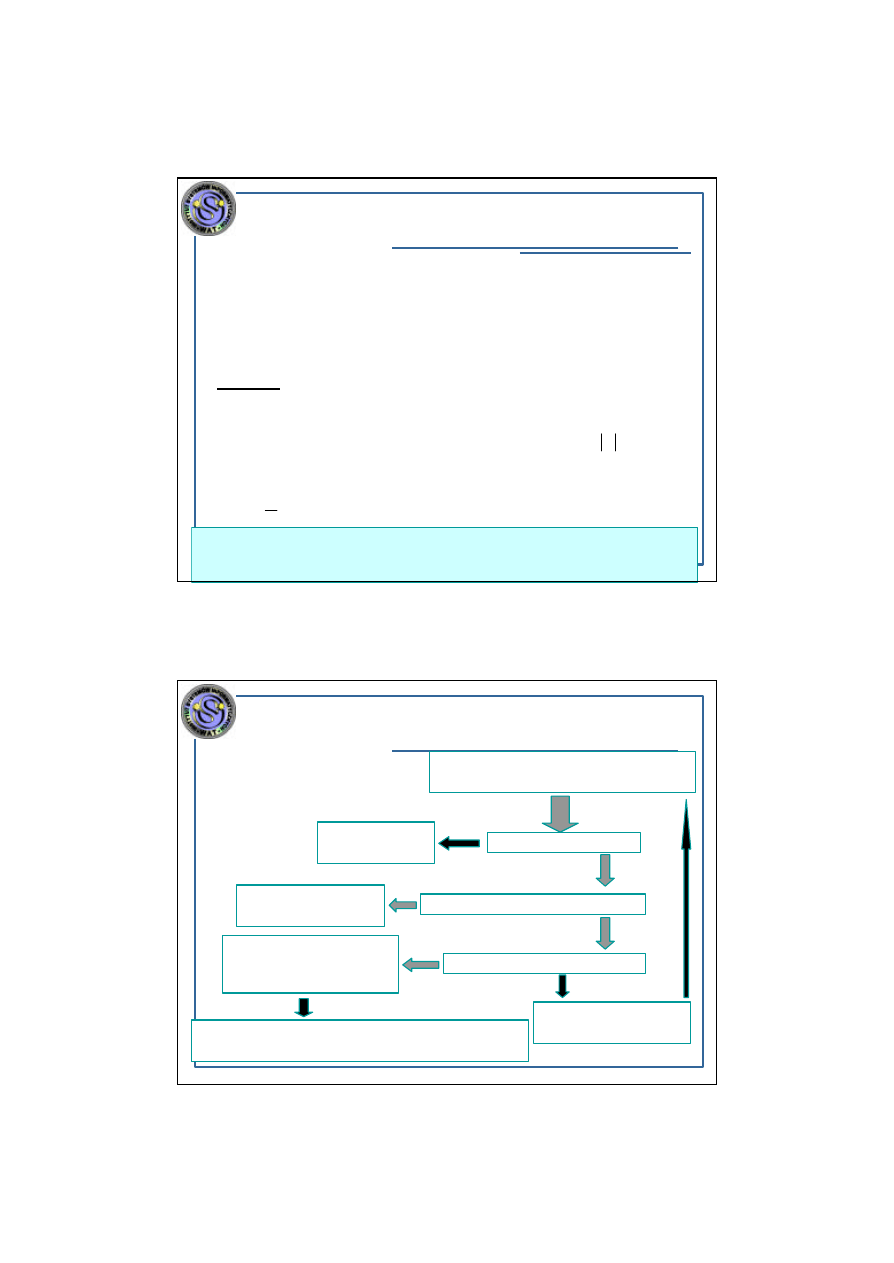
OGÓLNY SCHEMAT ROZWIAZYWANIA
PROBLEM ÓW OPTYMALIZACYJNYCH
Problem optymalizacyjny
Problem optymalizacyjny
X
X
wersja decyzyjna
wersja decyzyjna
X
X
d
d
X
X
d
d
∈
∈
P
P
?
?
↔
↔
X
X
d
d
∈
∈
NPC
NPC
?
?
Zbuduj efektywny
Zbuduj efektywny
algorytm dla
algorytm dla
X
X
X
X
d
d
∈
∈
PseudoP
PseudoP
?
?
↔
↔
X
X
d
d
∈
∈
NPC!
NPC!
?
?
Zbuduj dla
Zbuduj dla
X
X
algorytm
algorytm
pseudowielomianowy
pseudowielomianowy
Zadowalaj
Zadowalaj
a
a
nas przybli
nas przybli
z
z
enia?
enia?
Tak
Wielomianowe algorytmy:
Wielomianowe algorytmy:
•
•
przybli
przybli
z
z
one
one
•
•
schematy aproksymacyjne
schematy aproksymacyjne
Nie
Okre
Okre
s
s
l satysfakcjonuj
l satysfakcjonuj
a
a
c
c
a
a
restrykcj
restrykcj
e
e
zagadnienia
zagadnienia
X
X
•
Ma
Ma
l
l
e dane: szukanie wyczerpuj
e dane: szukanie wyczerpuj
a
a
ce (
ce (
branch
branch
&
&
bound
bound
)
)
•
•
Heurystyki: tabu
Heurystyki: tabu
search
search
, algorytmy genetyczne, ...
, algorytmy genetyczne, ...
Brak
22
43
Z.Tarapata, Obliczenia równolegle, wyklad nr 1
Dziekuje za uwage