RÓWNANIA RÓŻNICZKOWE

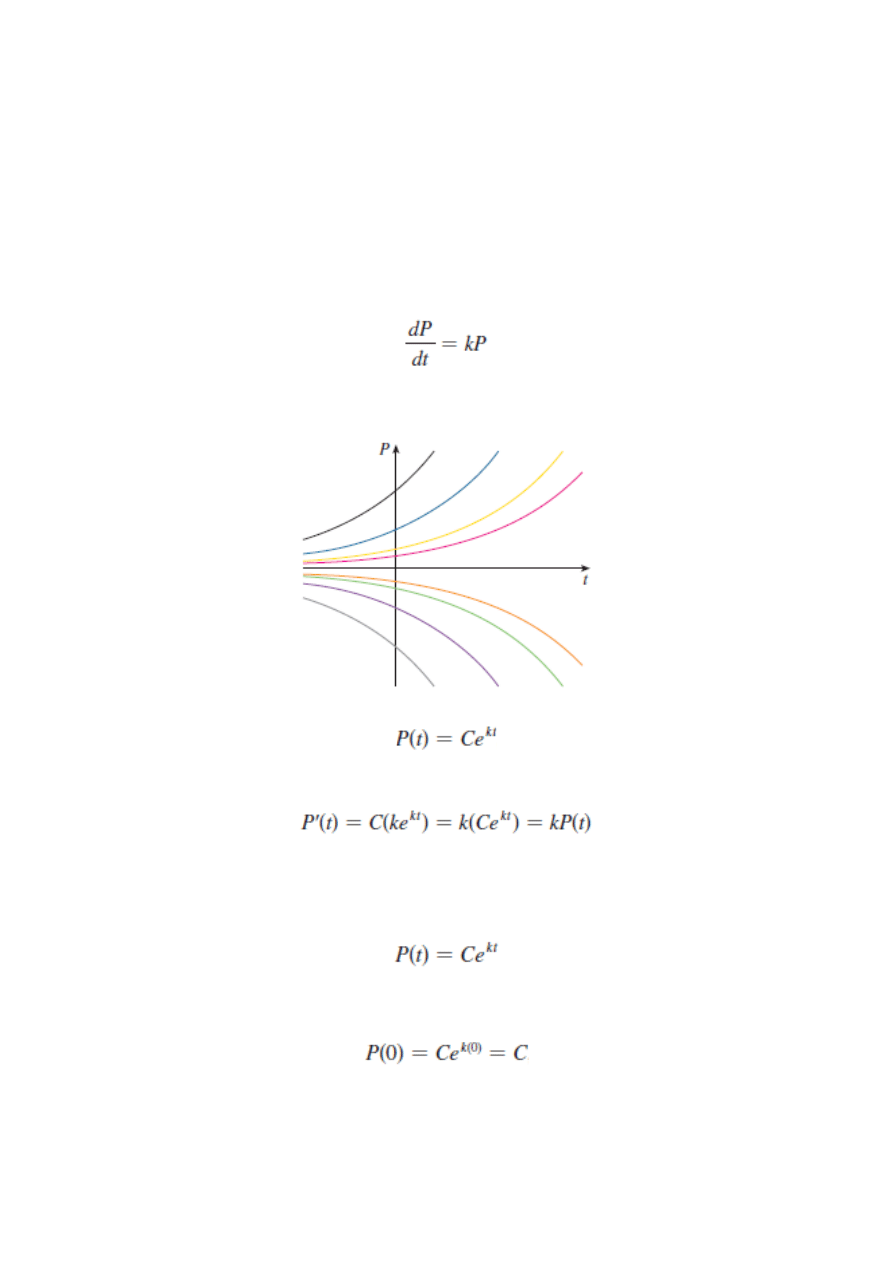
Modele wzrostu populacji

P – populacja  t- czas  k – stała proporcjonalności

Zatem dowolna funkcja postaci

jest rozwiązaniem równania. 

Jest to dobry model wzrostu populacji w idealnych warunkach. 

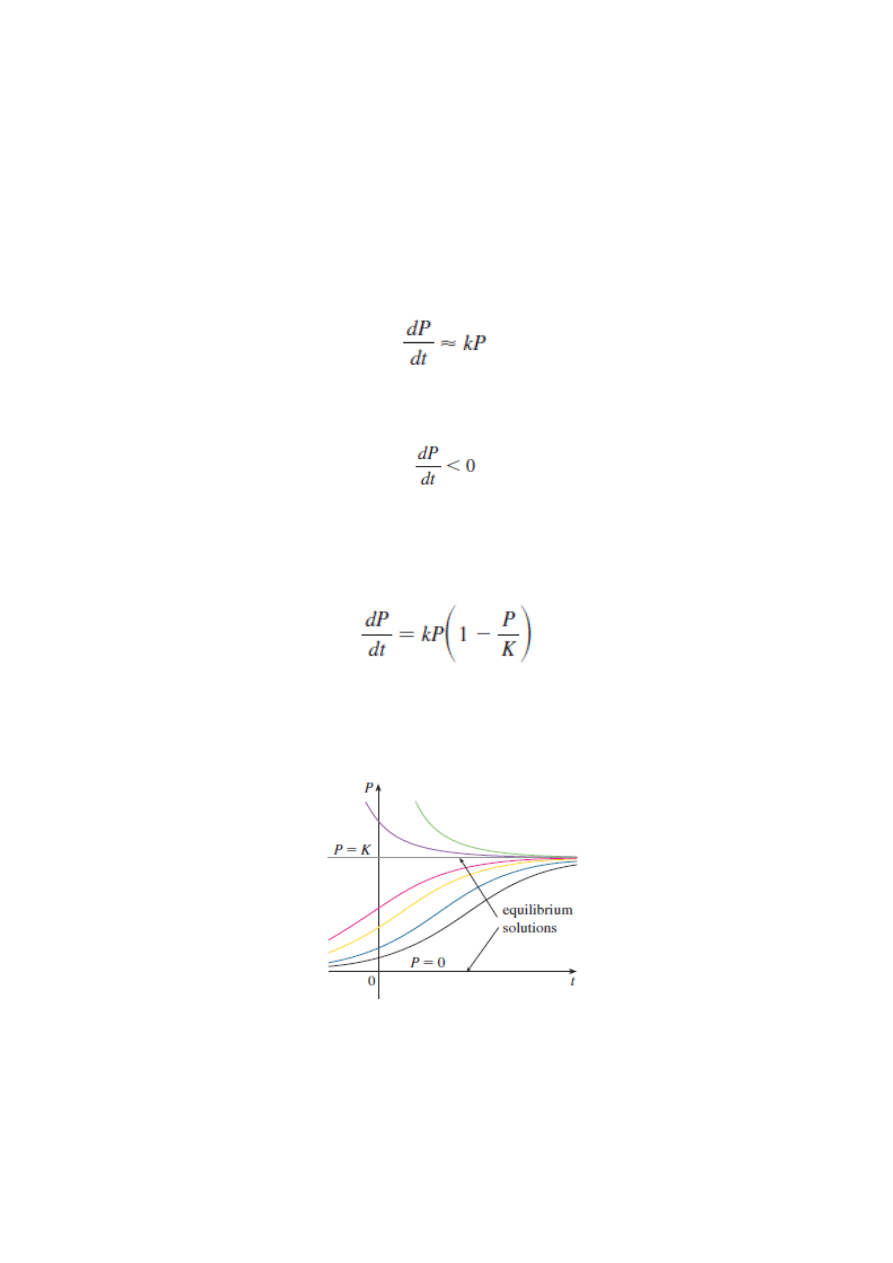
Wzrost populacji w środowisku z ograniczeniami 

−

pojemność danego środowiska

K -  pojemność danego środowiska

populacja wzrasta bez ograniczeń aż do czasu gdy przekroczy liczbę K

dla P < K; 

gdy P > K, czyli populacja maleje gdy przekroczy liczbę K.

Najprostsze równanie spełniające te założenia to 

Jest to tzw. równanie logistyczne (Verhulst, ok. 1840 r).

Równanie to posiada dwa stałe rozwiązania, tzw. rozwiązania równowagi

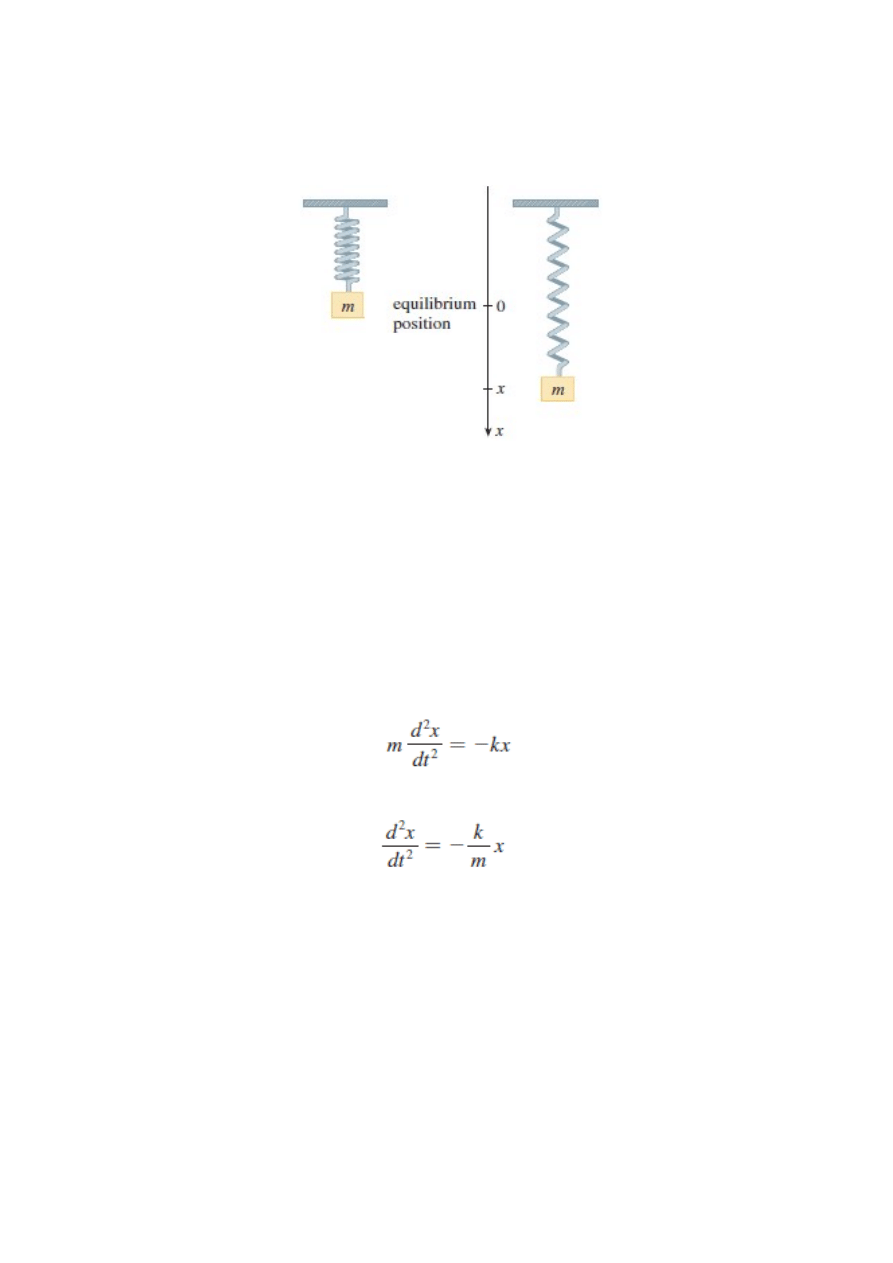
Model ruchu sprężyny

Sprężyna   działa   zgodnie   z   prawem   Hooke'a,   które   mówi,   że   jeśli     jest 
rozciągnięta   lub   zduszona   o   x   w   stosunku   do   swojej   naturalnej   długości   to 
reaguje z siłą proporcjonalną do x, tj. 

F = - kx

gdzie k jest stałą zależną od sprężyny.  

Z drugiego prawa Newton'a  (siła = masa razy przyspieszenie)

Znamy funkcje o podobnej własności (druga pochodna jest proporcjonalna 
samej funkcji), 

np. sinx oraz cosx. 

Oznacza to że sprężyna powinna oscylować wokół stanu równowagi. 

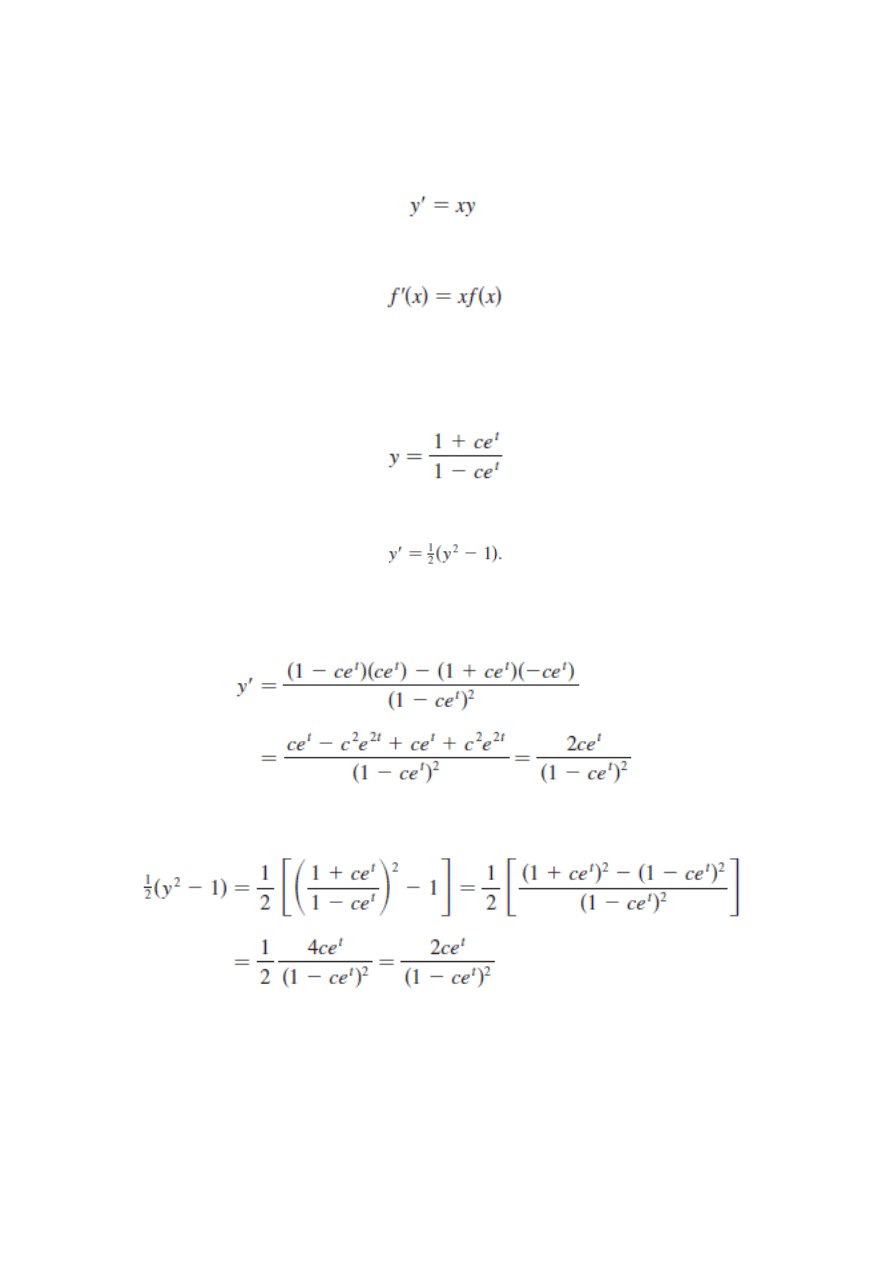
OGÓŁNE  RÓWNANIA RÓŻNICZKOWEGO

Rozwiązania tego równania są postaci y=f(x) i muszą spełniać równanie

Przykład 

Funkcje postaci 

są rozwiązaniami równania 

Obliczamy pochodną  

i podstawiamy 

W rozwiązywaniu równań różniczkowych jest bardzo ważne spełnienie warunku 
y(x

0

) = C, tzw. warunku początkowego. 

Przykład cd. Jakie rozwiązanie spełnia warunek początkowy y(0) = 2?

Podstawiając do ogólnej postaci rozwiązania wartości t=0 oraz y=2 

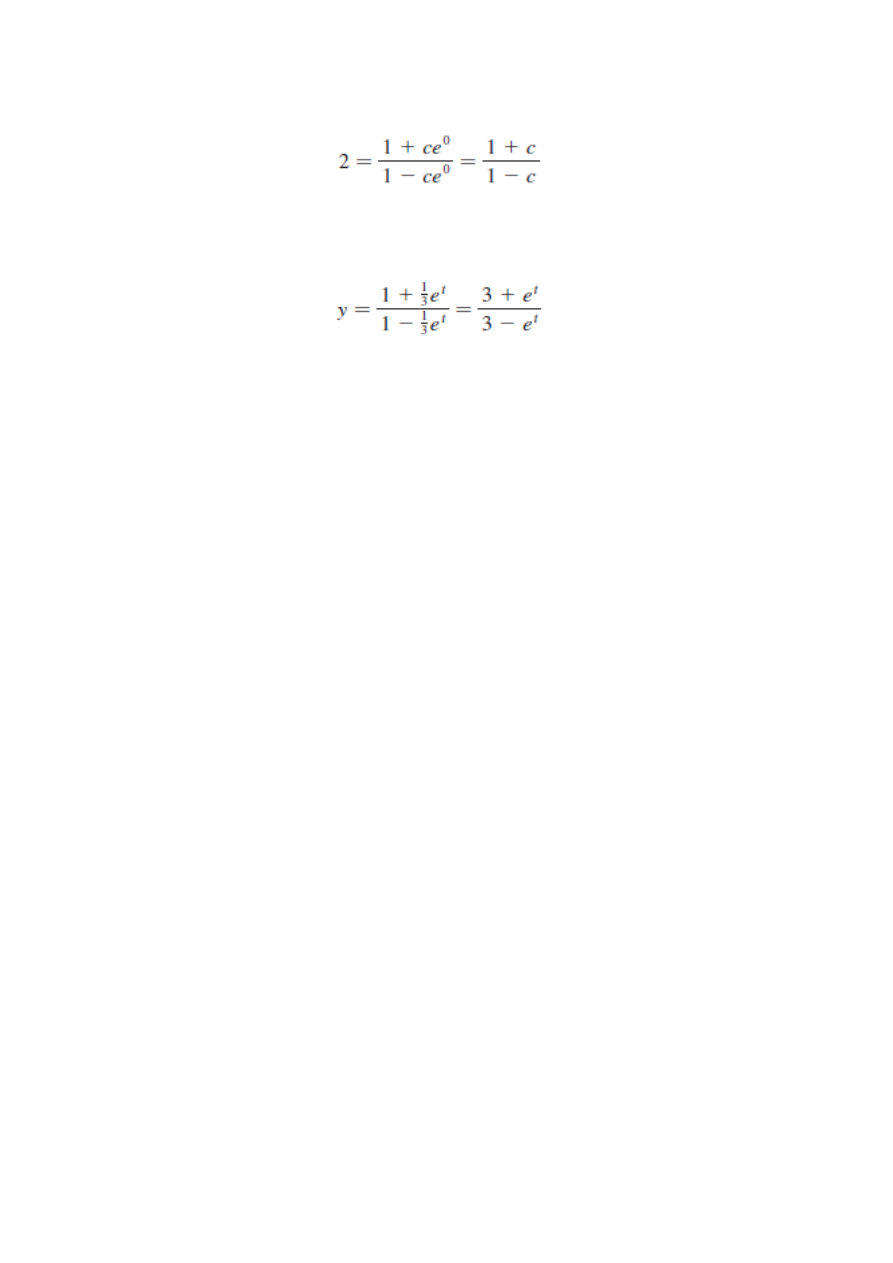
otrzymujemy

skąd c = 1/3.  Zatem rozwiązaniem równania różniczkowego z warunkiem 
początkowym y(0)= 2 jest 

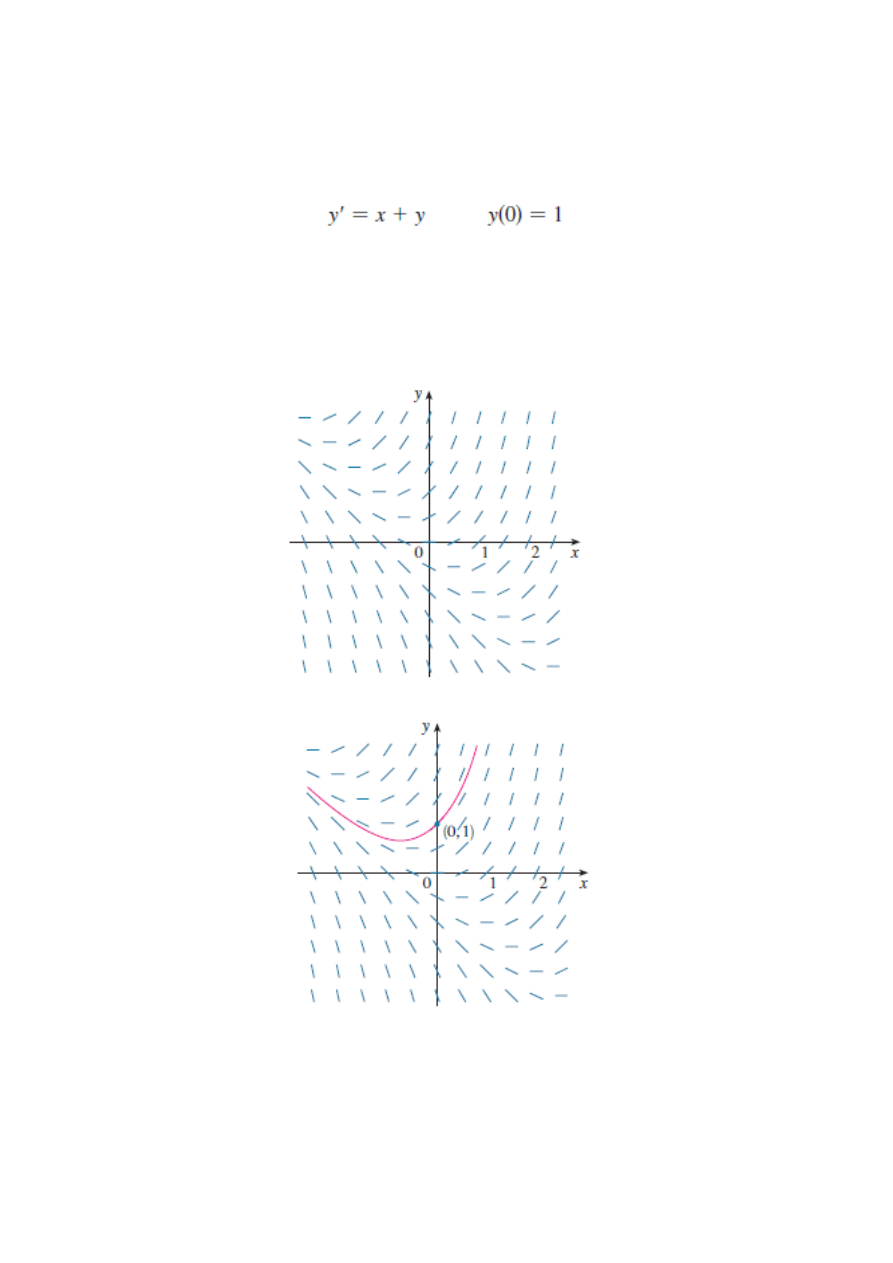
Metoda pól kierunków

Przykład

Trudno zgadnąć rozwiązanie ale metoda pól kierunkowych pozwoli naszkicować 
rozwiązanie.

  y' -  współczynnik kierunkowy stycznej do funkcji y(x)

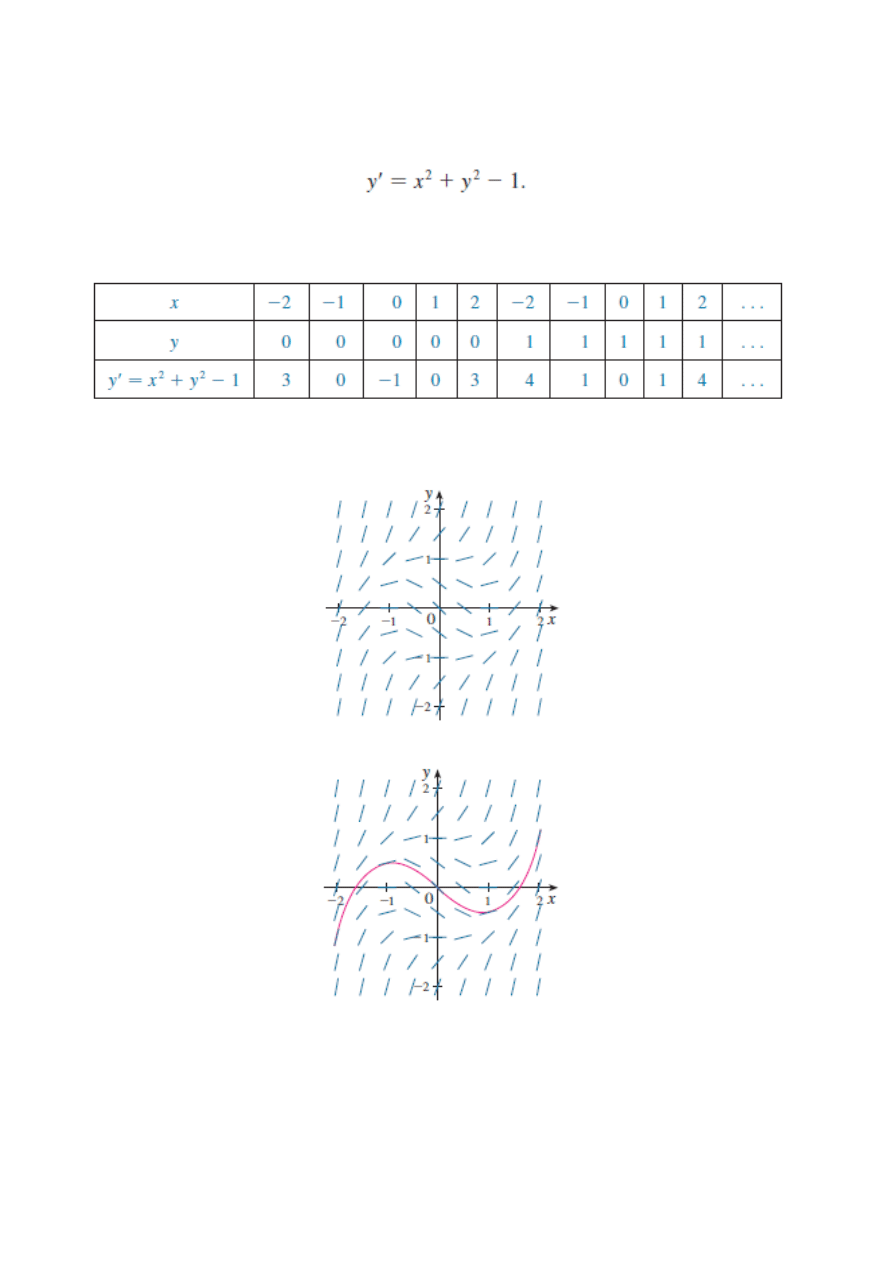
Przykład 

Naszkicuj rozwiązanie równania 

Rozwiązanie

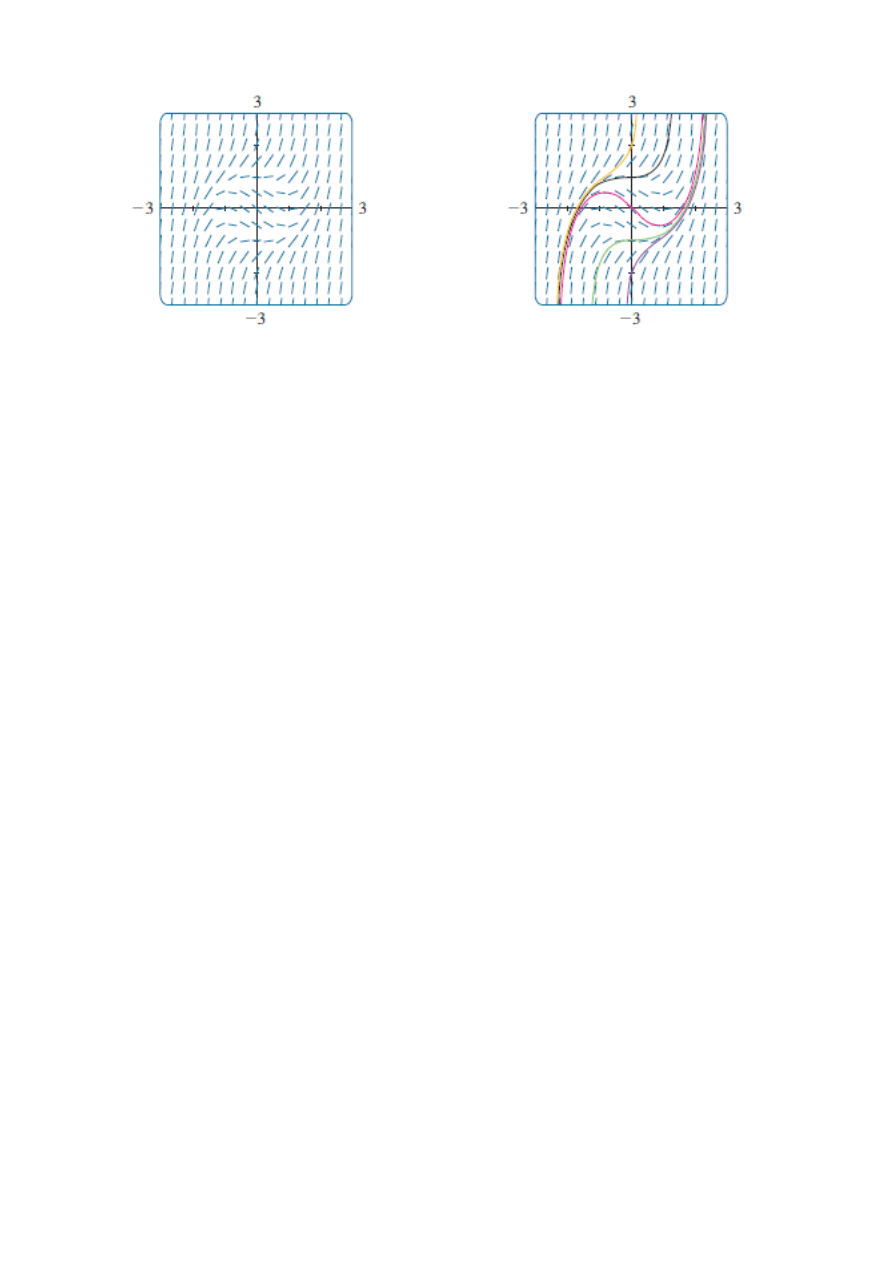
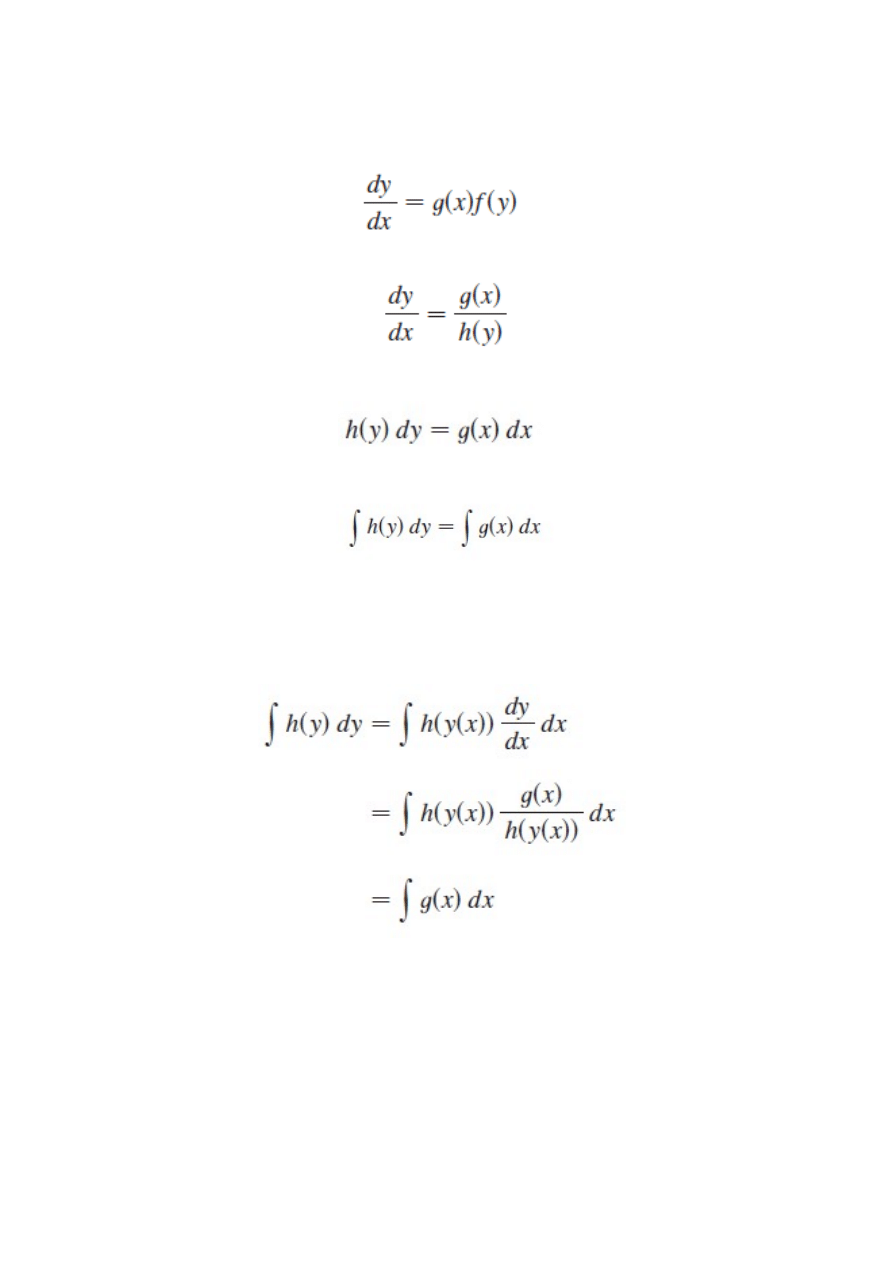
Równanie o rozdzielonych zmiennych

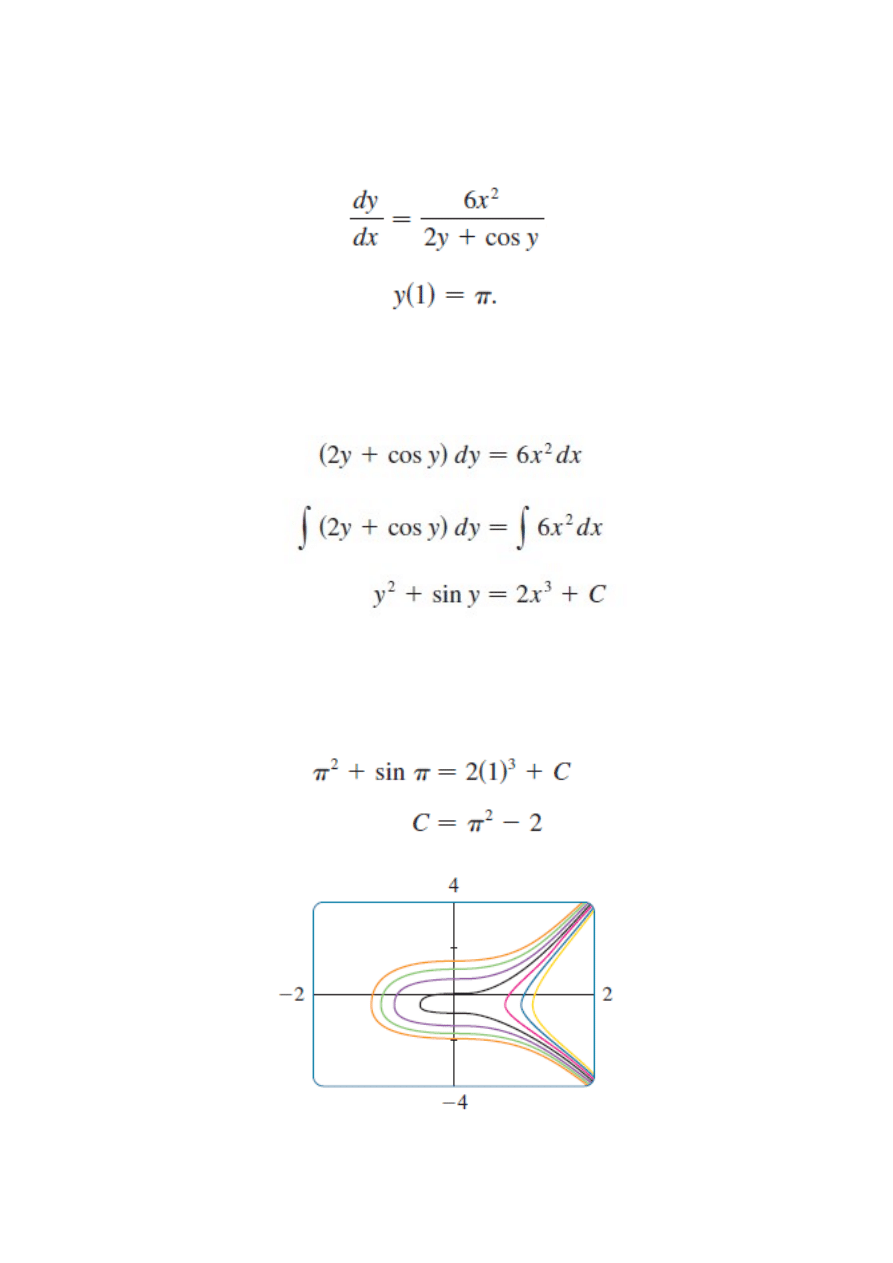
Przykład

Rozwiąż równanie  

z warunkiem początkowym 

Rozwiązanie. 

Znajdujemy C dla warunku początkowego

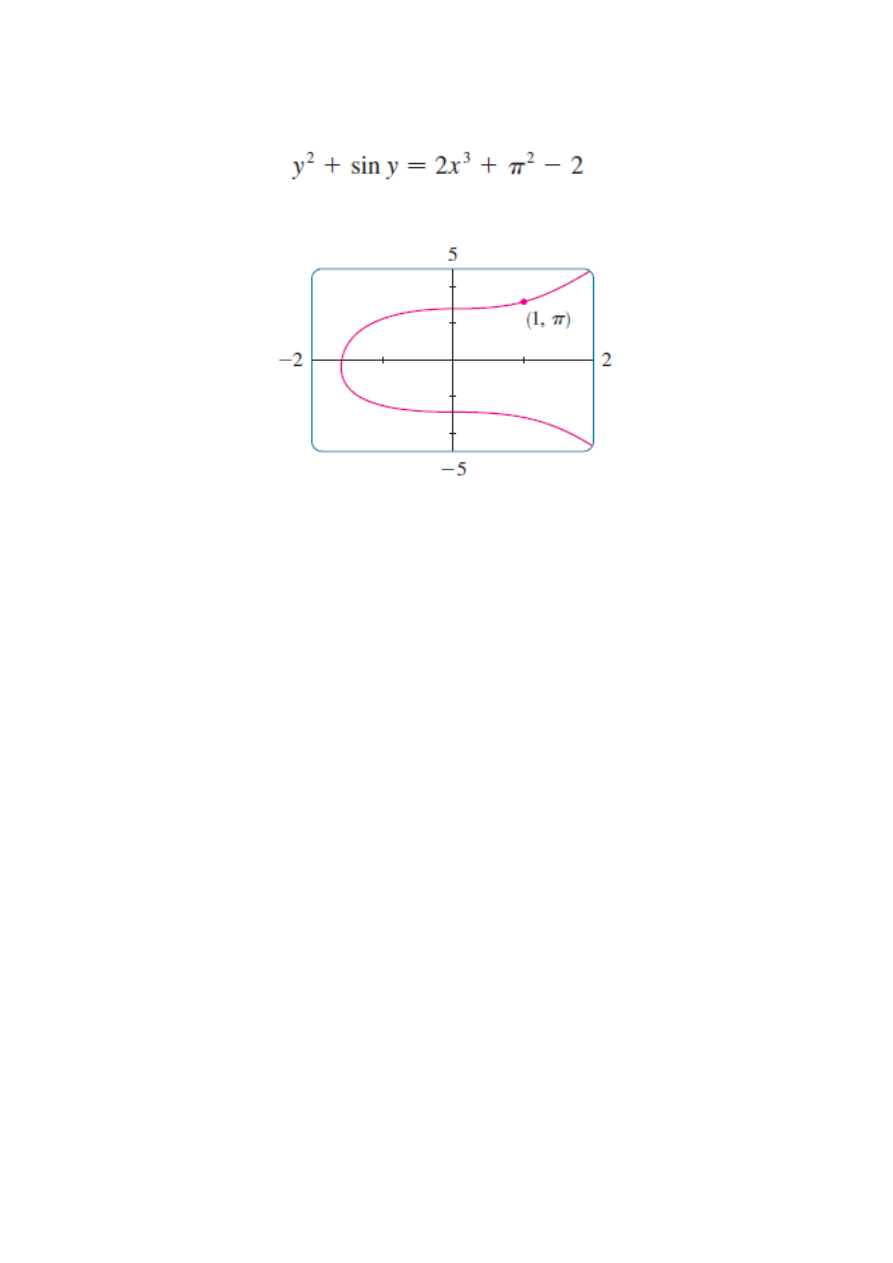
Postać uwikłana rozwiązania 

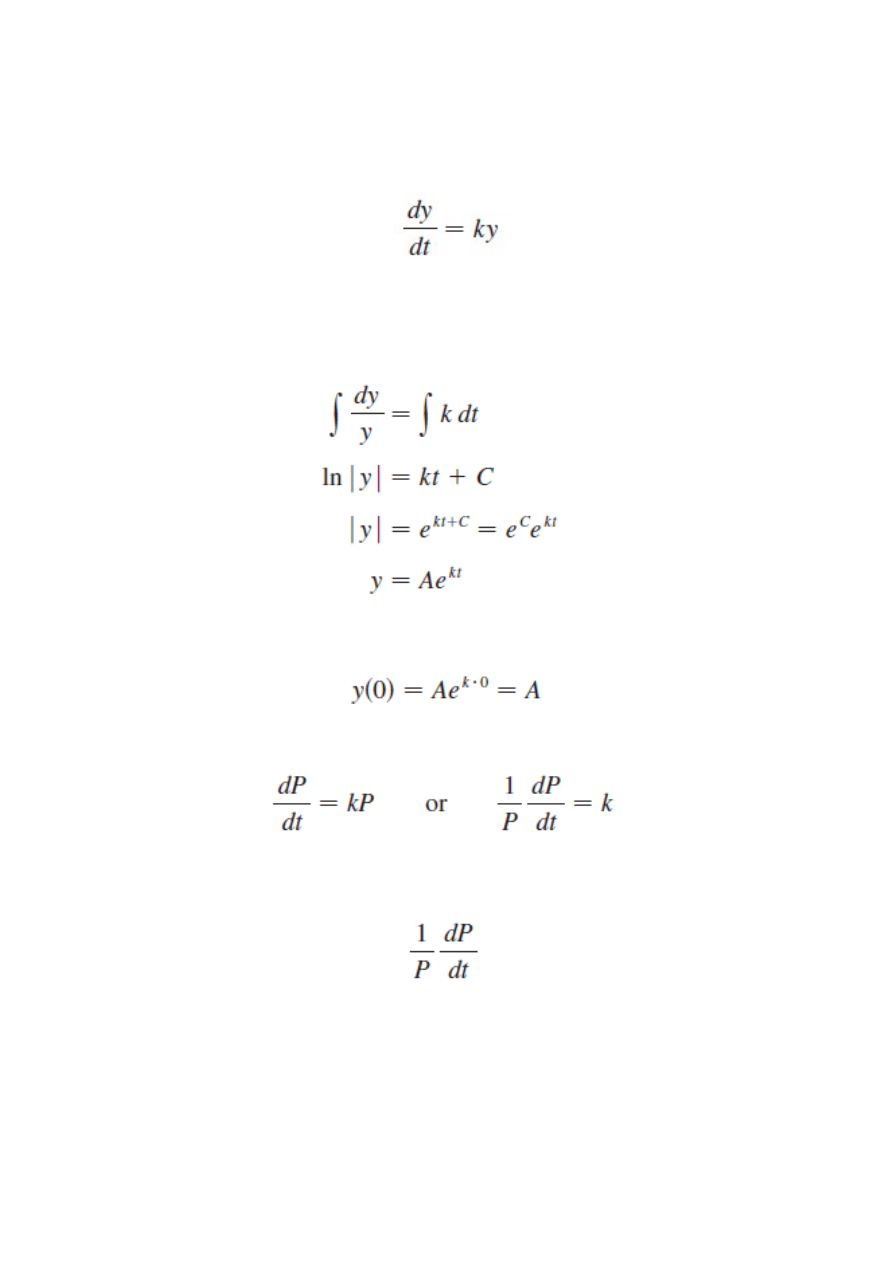
Model rozwoju populacji

 k > 0  prawo naturalnego wzrostu

 k < 0  prawo naturalnego rozpadu

warunek początkowy

Wzrost populacji

Wartość nazywamy relatywnym wzrostem

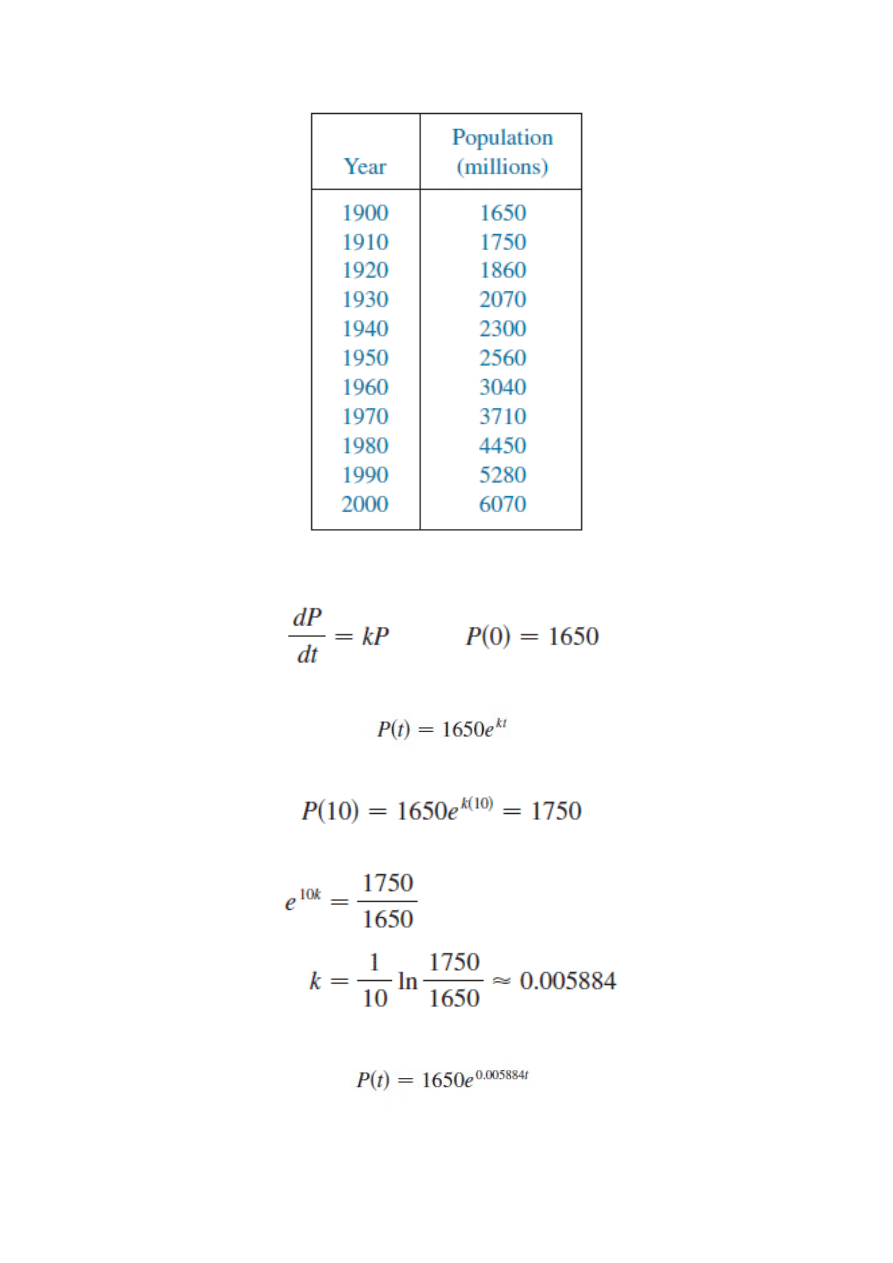
Przykład   

Wtedy otrzymujemy funkcję wzrostu postaci:

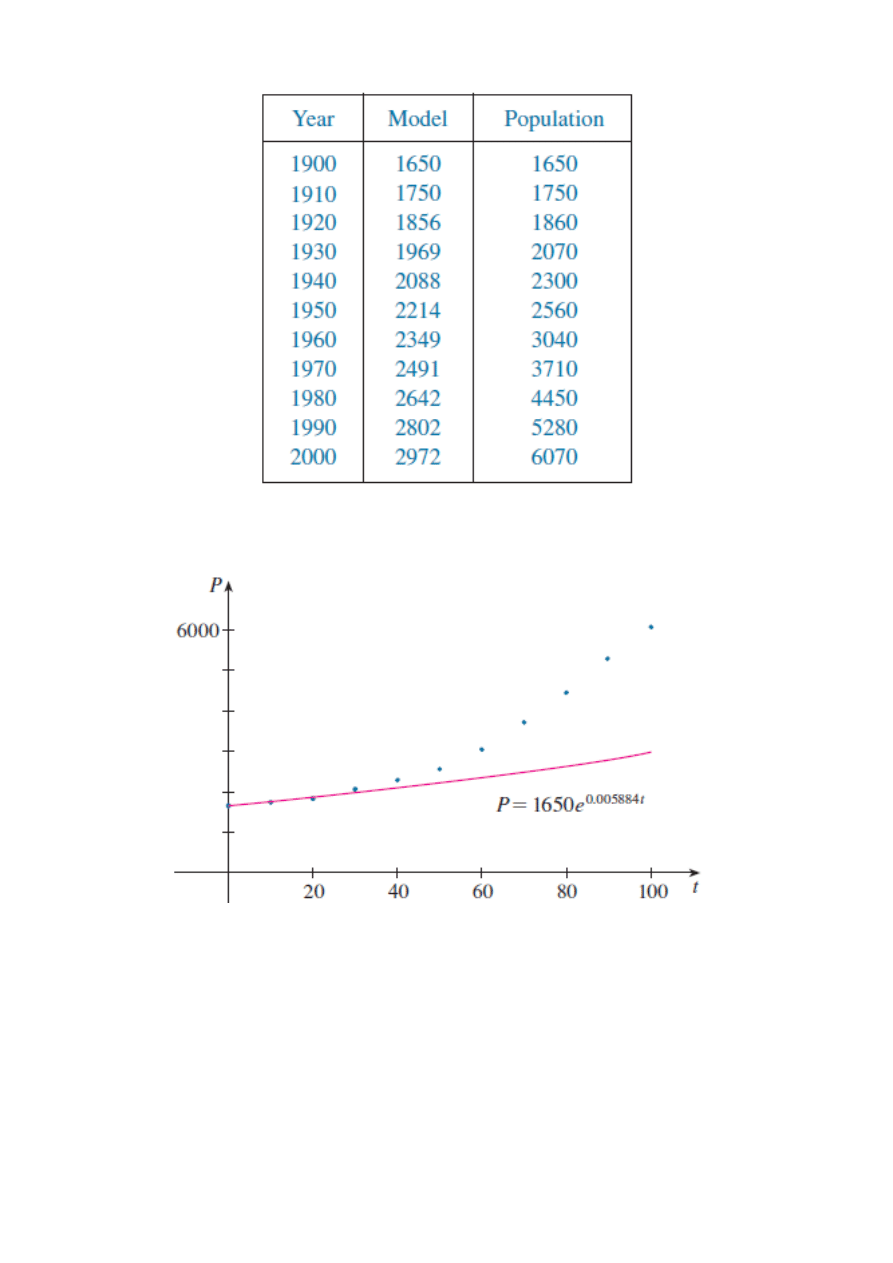
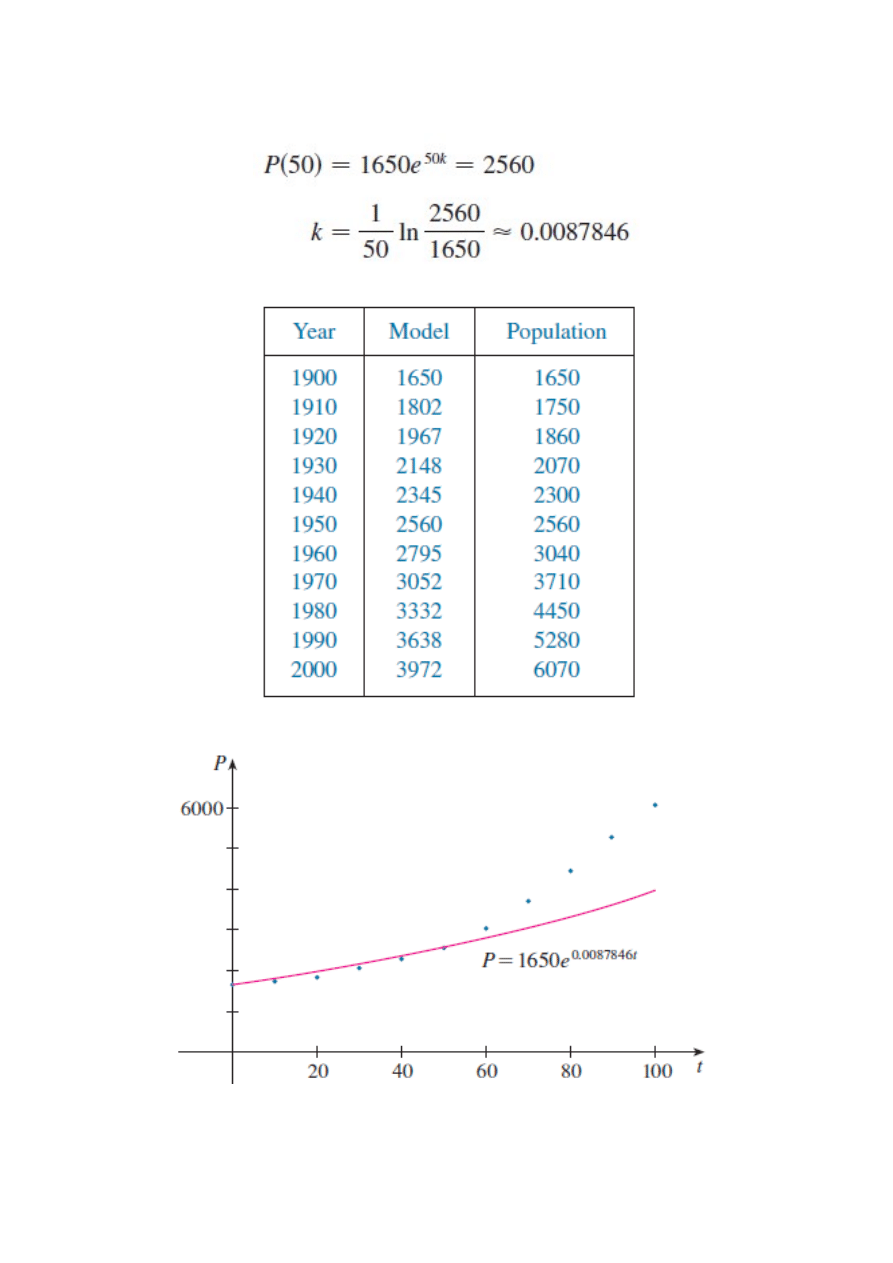
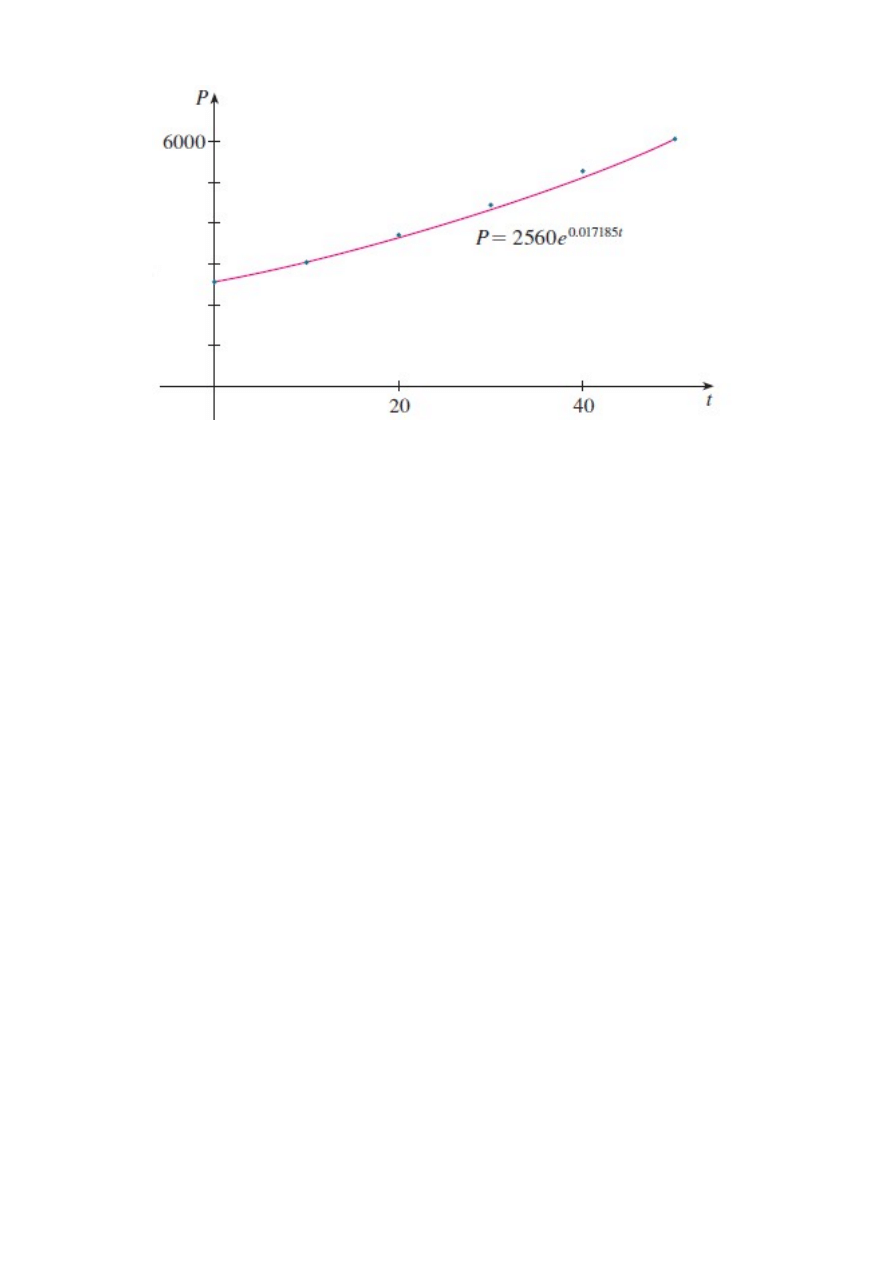
Inne możliwe k:  

Przykład  

Użyj tabeli i modelu do estymacji populacji w roku 1993 i 2010.  

Niech t=0=1950

Obliczmy k przy pomocy roku 1960. 

Wtedy 

Stan 2010:  

6,887,600,000 

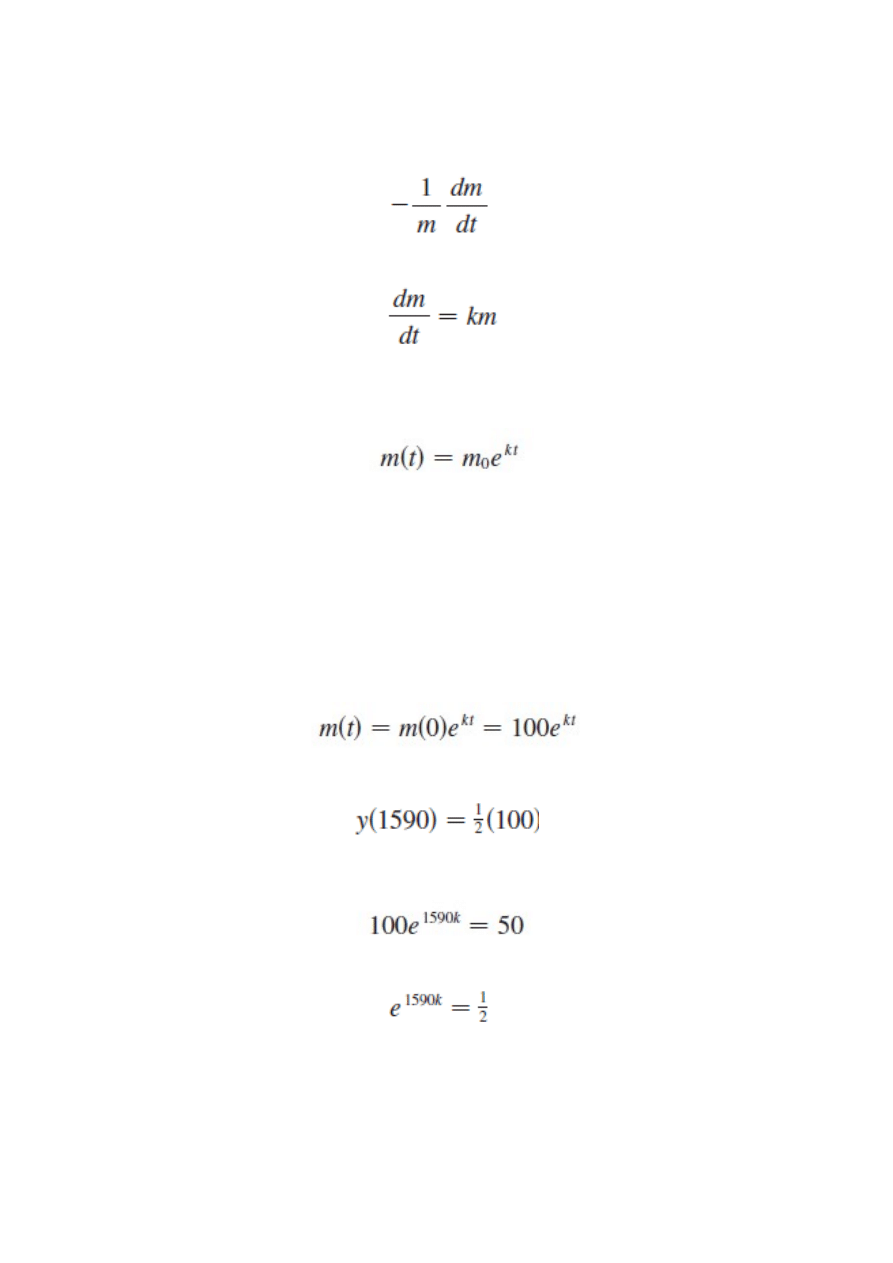
Rozpad radioaktywny

 k < 0

czas połowicznego rozpadu

Przykład Rad 226 – czas połowicznego rozpadu 1590 lat

Próbka ma 100 mg.  Znajdź wzór na masę próbki z zależności od czasu. Jaką 
będzie miała masę po 1000 lat?  Kiedy będzie miała masę mniejszą niż 30mg?

Wiemy, że 

Zatem 

oraz 

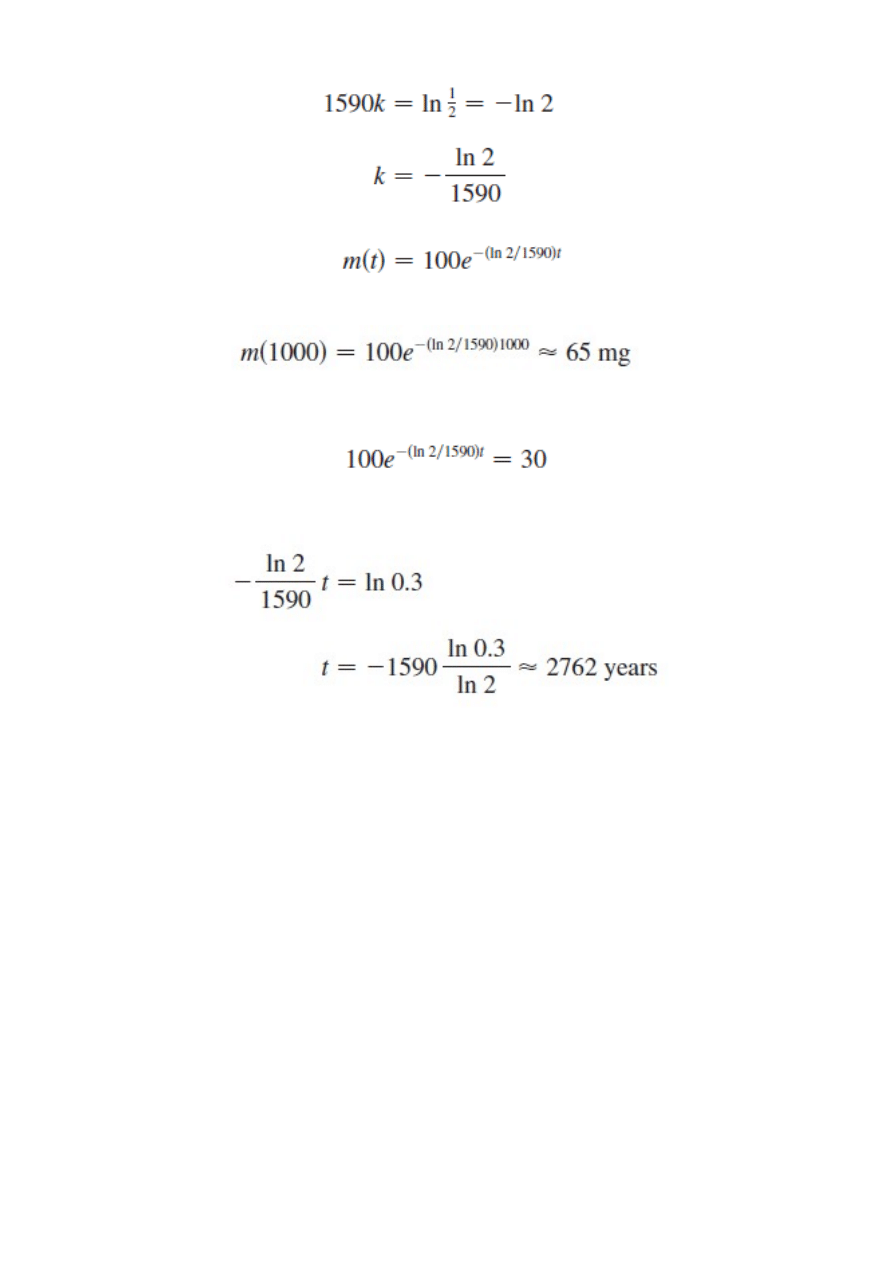
Zatem

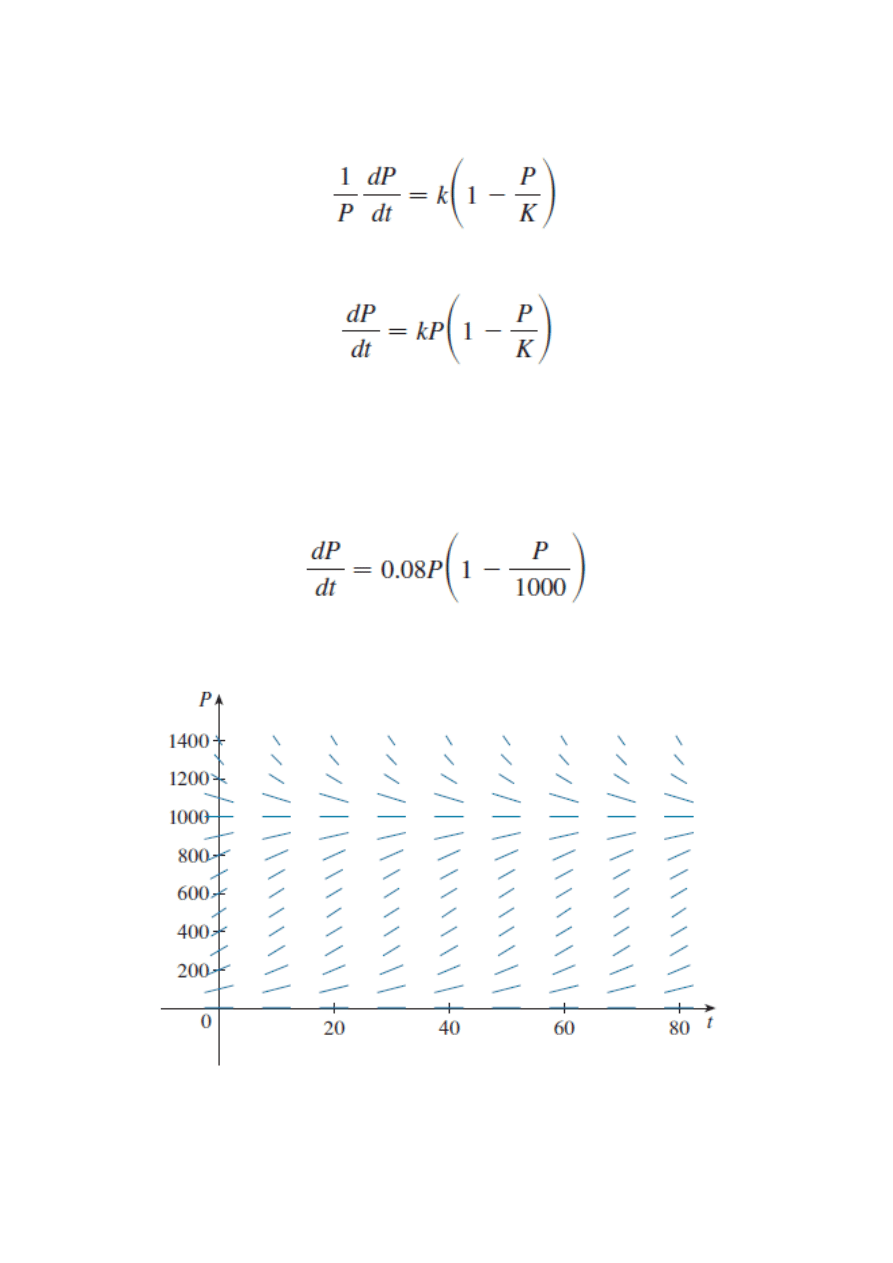
Model  logistyczny

Pole kierunków

Przykład  k= 0,08 K= 1000

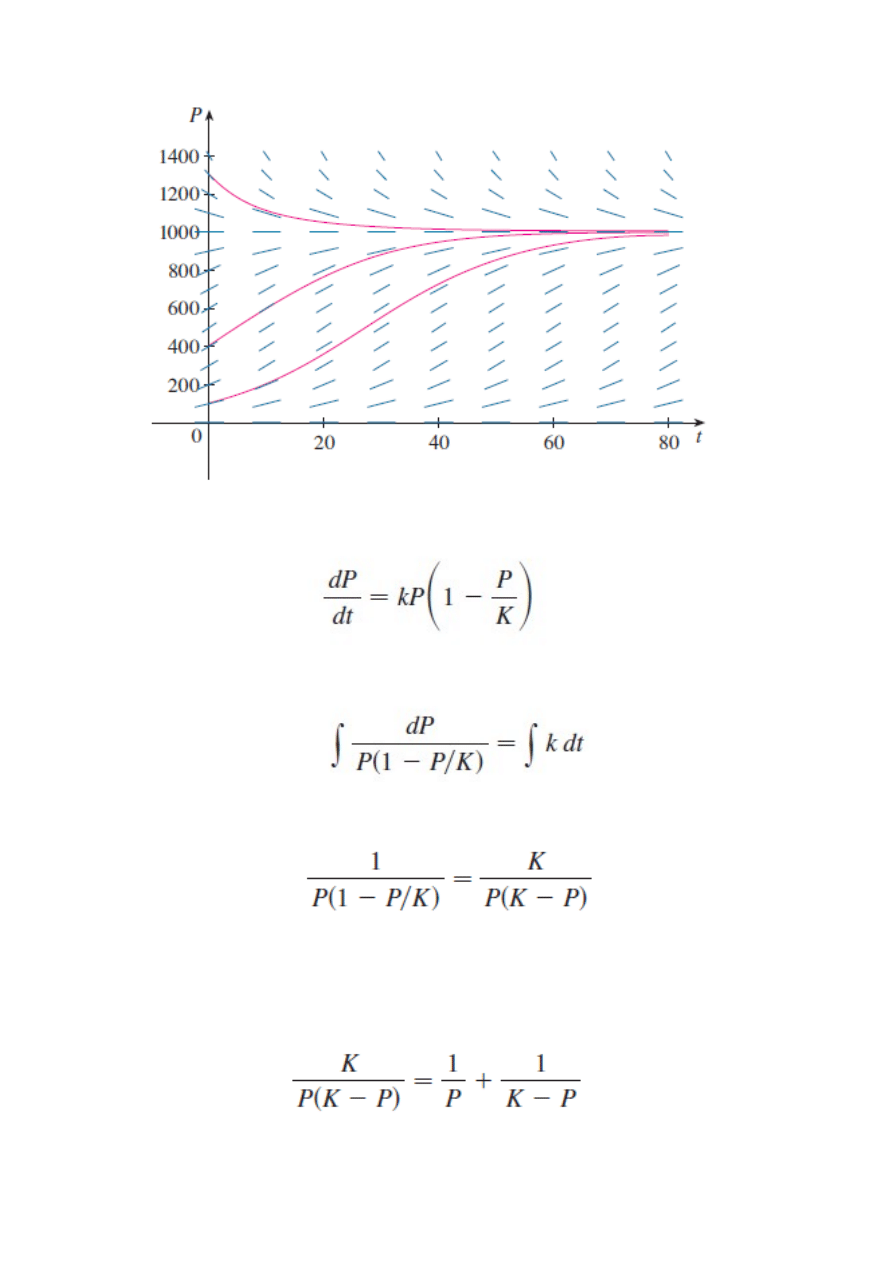
Rozwiązanie

Lewa strona 

Po rozkładzie

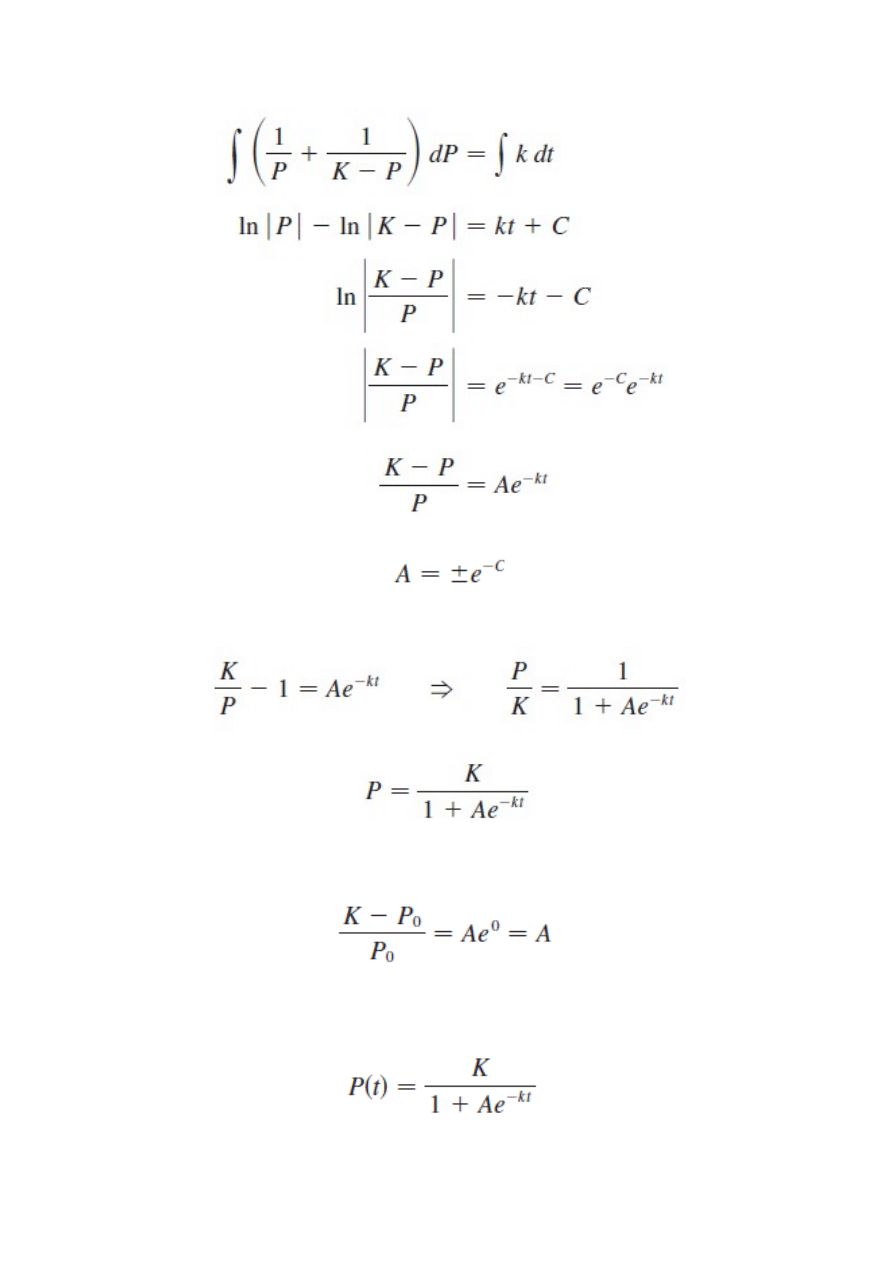
Biorąc t=0 

Ogólna postać rozwiązania 

z