Zadania  z  oryginalną  numeracją  pochodzą  z   Informatora  o  egzaminie  maturalnym  od  2010  roku 
z matematyki (zdawanej jako przedmiot obowiązkowy) – Arkusz P2. 

Potrzebne wzory oraz inne informacje znajdziesz w 

tablicach

. 

 
Tydzień 15. 
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. B 

 

 

 
Możemy, zgodnie z własnościami wartości bezwzględnej, zapisać warunki równoważne 

 

Po ich rozwiązaniu otrzymujemy 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. A 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. C 

 

 

 
Możemy np. rozwiązać warunek 

. Jego rozwiązaniem jest liczba 100. 

 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. D 

 

 
Suma  miar  dwóch  sąsiednich  kątów  równoległoboku  jest  równa  180

o

.  Zatem  kąty  spełniające  warunek 

zadania to kąty o miarach 75

o

 i 105

o

. 

 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. A 

 

 

 
Możemy rozwiązać dwa warunki wynikające z definicji miejsca zerowego funkcji. 

 

 

 

Funkcja nie posiada miejsc zerowych. 
 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. A 

 

 

 
Wystarczy sprawdzić w tablicy wartości funkcji trygonometrycznych, aby stwierdzić, że 

 dla 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. D 

 

 

 
Przy przekształcaniu danego wyrażenia będziemy korzystali z definicji potęgi o wykładniku wymiernym 
i z własności potęg. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. B 

 

 
Zbiór wartości możemy odczytać z wykresu. 
 

 

 

 

 

 

 

 

 

 

 

 

Odp. C 

 

 

 
Skorzystamy ze wzoru na n-ty wyraz ciągu geometrycznego (a

n

), o pierwszym wyrazie a

1

 i ilorazie q. 

  i  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Odp. C 

 

 

 
Obliczymy długości boków tego trójkąta. 

 

 

 

 

 

 

Boki AB i AC okazały się tej samej długości, a zatem są one ramionami trójkąta równoramiennego. 
Ramię tego trójkąta ma długość 

. 

c 

2 

4 

α

 

 

 
Na początek pogrupujemy wyrazy i wyłączymy wspólny czynnik przed nawias. 

 

 

 

Drugi z czynników rozkładamy na iloczyn czynników liniowych. 

 

  lub 

  lub  

 

 

Rozwiązaniem tego równania jest 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

      

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
Przedstawmy w tabeli wyniki takiego doświadczenia. 

 
 
 
 
 
 
 

Na podstawie tabeli możemy ustalić, że 

 

Na  żółto  zaznaczono  te  wyniki.  Które  sprzyjają  zdarzeniu  A  –  liczby  oczek  otrzymane  w  obu  rzutach 
różnią się o 1. Stąd |A| = 16. 

 

 

 

 

1 

2 

2 

3 

3 

3 

1  (1,1)  (1,2)  (1,2)  (1,3)  (1,3)  (1,3) 
2  (2,1)  (2,2)  (2,2)  (2,3)  (2,3)  (2,3) 
2  (2,1)  (2,2)  (2,2)  (2,3)  (2,3)  (2,3) 
3  (3,1)  (3,2)  (3,2)  (3,3)  (3,3)  (3,3) 
3  (3,1)  (3,2)  (3,2)  (3,3)  (3,3)  (3,3) 
3  (3,1)  (3,2)  (3,2)  (3,3)  (3,3)  (3,3) 

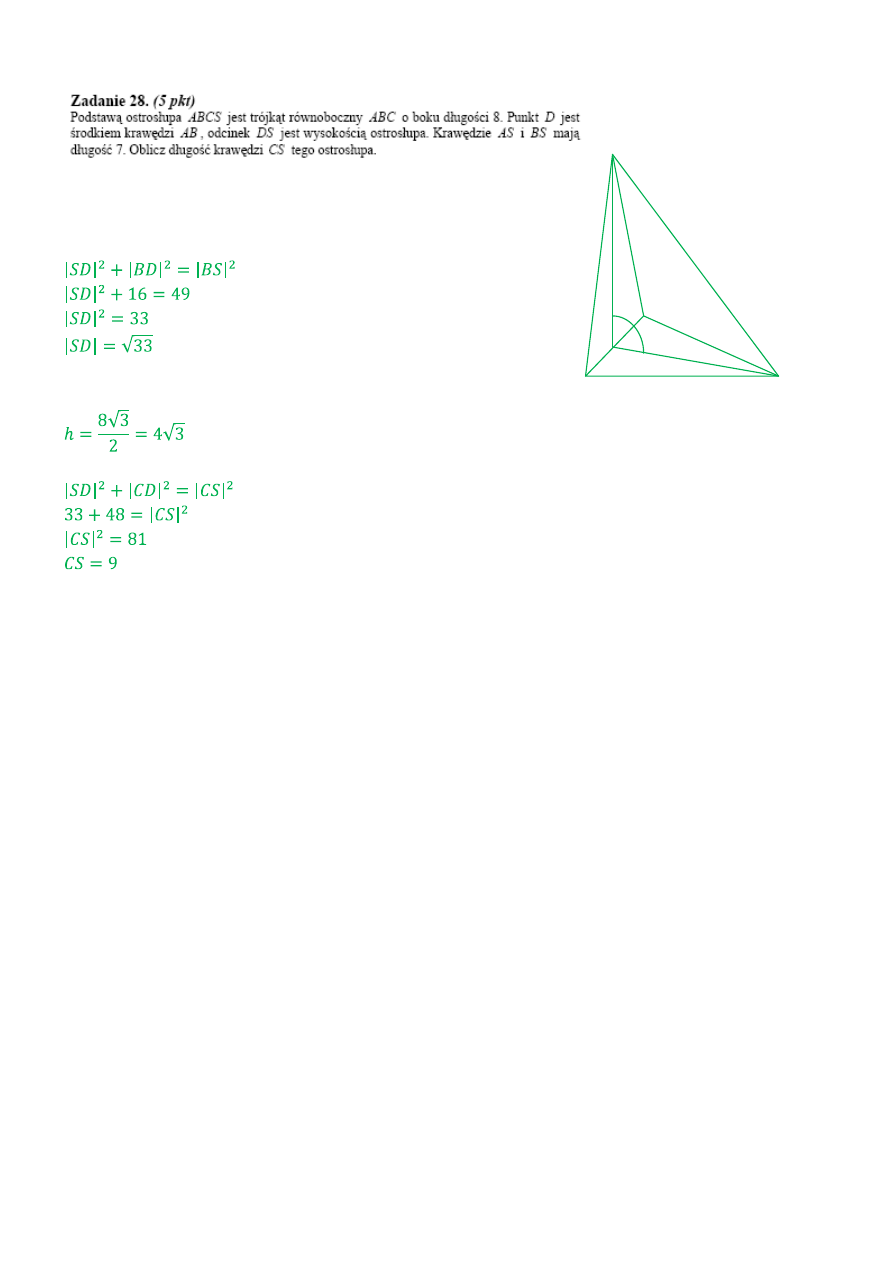
A 

B 

C 

7 

D 

H 

h 

•

 

S 

 

 

 
 
W trójkącie równoramiennym ABS, H jest jego wysokością. Korzystając 
z twierdzenia Pitagorasa obliczymy długość SD. 

 

 

 

 

Do obliczenia długości CS potrzebujemy jeszcze długości odcinka 
DC , czyli wysokości trójkąta równobocznego.  

 

Teraz obliczymy długość CS znów korzystając z twierdzenia Pitagorasa.