AUTORKA: EL

Ż

BIETA SZUMI

Ń

SKA

NAUCZYCIELKA ZESPOŁU SZKÓŁ
OGÓLNOKSZTAŁC

Ą

CYCH

„SCHOLASTICUS” W ŁODZI

ZNANE RÓWNANIA PROSTEJ

NA PŁASZCZY

Ź

NIE I W PRZESTRZENI

2

SPIS TRE

Ś

CI:

PROSTA NA PŁASZCZY

Ż

NIE

Str

1

.

Równanie

kierunkowe

prostej

3

2.

Równanie

ogólne

prostej.

5

3.

Równanie

odcinkowe

prostej.

7

4. Równanie prostej przechodz

ą

cej przez dwa punkty na płaszczy

ź

nie.

7

5. Przedstawienie parametryczne prostej na płaszczy

ź

nie.

10

6.Posta

ć

normalna równania prostej.

11

PROSTA W PRZESTRZENI

7. Prosta okre

ś

lona

przez

jej

rzuty.

14

8. Prosta jako cz

ęść

wspólna płaszczyzn, podanych w postaci ogólnej.

15

9. Równanie prostej przechodz

ą

cej przez dwa punkty w przestrzeni.

15

10.Przedstawienie parametryczne prostej w przestrzeni.

16

3

PROSTA NA PŁASZCZY

Ź

NIE

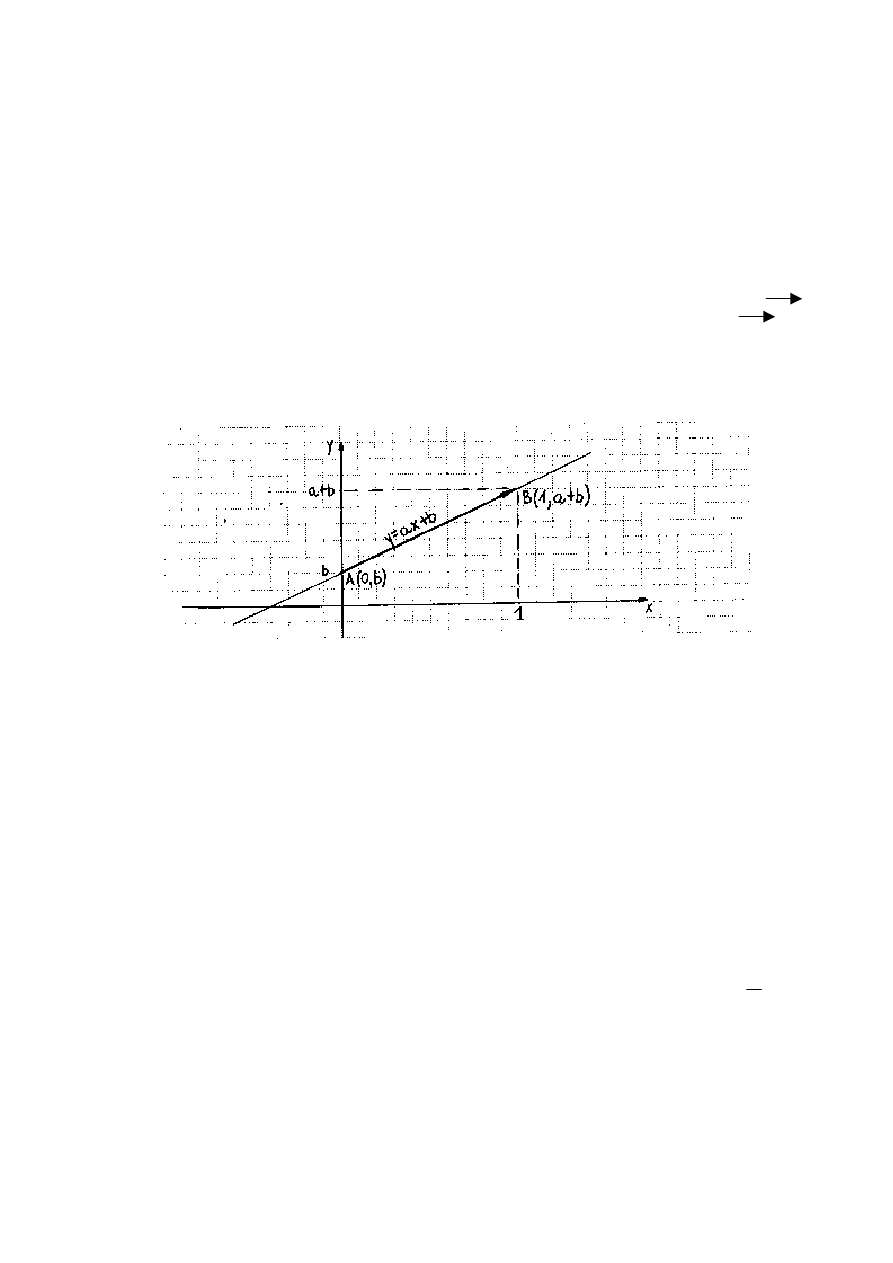
1. Równanie kierunkowe prostej

Niech

b

ę

dzie dany na płaszczy

ź

nie układ prostok

ą

tny współrz

ę

dnych 0xy oraz dowolna

prosta l. Opisuj

ą

c prost

ą

mo

ż

na posłu

ż

y

ć

si

ę

wzorem y=ax+b, który okre

ś

la funkcj

ę

liniow

ą

, ale

jednocze

ś

nie jest równaniem stopnia pierwszego o dwóch niewiadomych x i y. Równanie to

spełniaj

ą

współrz

ę

dne punktów (x, y) prostej l wyznaczonej przez punkty (0, b) oraz (1, a+b) i

dlatego wzór y=ax+b nazywamy równaniem prostej l.
Ka

ż

dy wektor równoległy do prostej l to wektor kierunkowy tej prostej. Na przykład wektor

AB,

gdzie A(0, b) za

ś

B(1, a+b) jest wektorem równoległym do prostej. Ma on współrz

ę

dne AB=[1, a].

Ka

ż

dy z wektorów kierunkowych tej prostej jest postaci k [1, a], gdy k

≠

0.

Liczb

ę

a nazywamy współczynnikiem kierunkowym prostej l,

liczb

ę

b nazywamy rz

ę

dn

ą

punktu przeci

ę

cia prostej l z osi

ą

0y

równanie y = ax + b (1.1.) RÓWNANIEM KIERUNKOWYM PROSTEJ.

Równanie (1.1.). ma szerokie zastosowanie:

proste dane równaniami: y=ax+b

y= a

1

x+b s

ą

równoległe wtedy i tylko wtedy gdy a = a

1

proste dane równaniami: y=ax+b

y= a

1

x+ b s

ą

prostopadłe wtedy i tylko wtedy gdy

a

a

= −

1

1

4

Interpretacja współczynnika kierunkowego

Niech dowolna prosta l b

ę

dzie nachylona do osi 0x pod k

ą

tem

α

, gdzie:

π

≤

α

≤

0 a = tg

α

α

≠

0,5

π

α

- k

ą

t o jaki nale

ż

y obróci

ć

o

ś

0x w kierunku dodatnim, aby stała si

ę

równolegla do

prostej l, nazywamy go k

ą

tem nachylenia prostej l do osi 0x,

a - współczynnik kierunkowy (k

ą

towy) prostej l.

Warto

ś

ci współczynnika kierunkowego

a > 0 gdy k

ą

t

α

jest ostry

a = 0 gdy prosta jest równoległa do osi 0x (y=b)

a < 0 gdy k

ą

t

α

jest rozwarty

a nie jest okre

ś

lony gdy

α

= 0,5

π

Gdy mamy prost

ą

równoległ

ą

do osi 0y - prosta ta nie jest wykresem funkcji, nie ma

wektora kierunkowego postaci [1, a], ani nie jest okre

ś

lony współczynnik a.

Je

ś

li prosta przecina o

ś

odci

ę

tych w punkcie x

o

,jej równanie to: x= x

o

, gdzie x

o

jest dowoln

ą

liczb

ą

rzeczywist

ą

.

5

WNIOSEK

Ka

ż

d

ą

prost

ą

zawart

ą

w płaszczy

ź

nie układu współrz

ę

dnych mo

ż

na przedstawi

ć

-równaniem kierunkowym y=ax+b lub

-równaniem x= x

o

(1.2.), gdzie x

o

jest dowoln

ą

liczb

ą

rzeczywist

ą

ZADANIE 1
Rozstrzygnij, czy punkty K(-1, -2), L(1, 3), M(2, 5) s

ą

współliniowe.

Rozwi

ą

zanie: KL=[1-(-1); 3-(-2)]=[2; 5]=2[1; 2,5]

LM=[2-1;

5-3]=[1,

2]

współrz

ę

dne wektorów kierunkowych nie s

ą

proporcjonalne, zatem punkty K, L, M nie s

ą

współliniowe.

ZADANIE 2
Wyznacz równanie prostej przechodz

ą

cej przez punkt P(2, -1) i równoległej do prostej AB, gdzie A

(0, 1); B (1, 3).

Rozwi

ą

zanie: AB = [1, 2], zatem a = 2, prosta jest postaci y=2x+b

-1=2x2+b

b=-5

szukana prosta ma wi

ę

c posta

ć

y = 2x - 5.

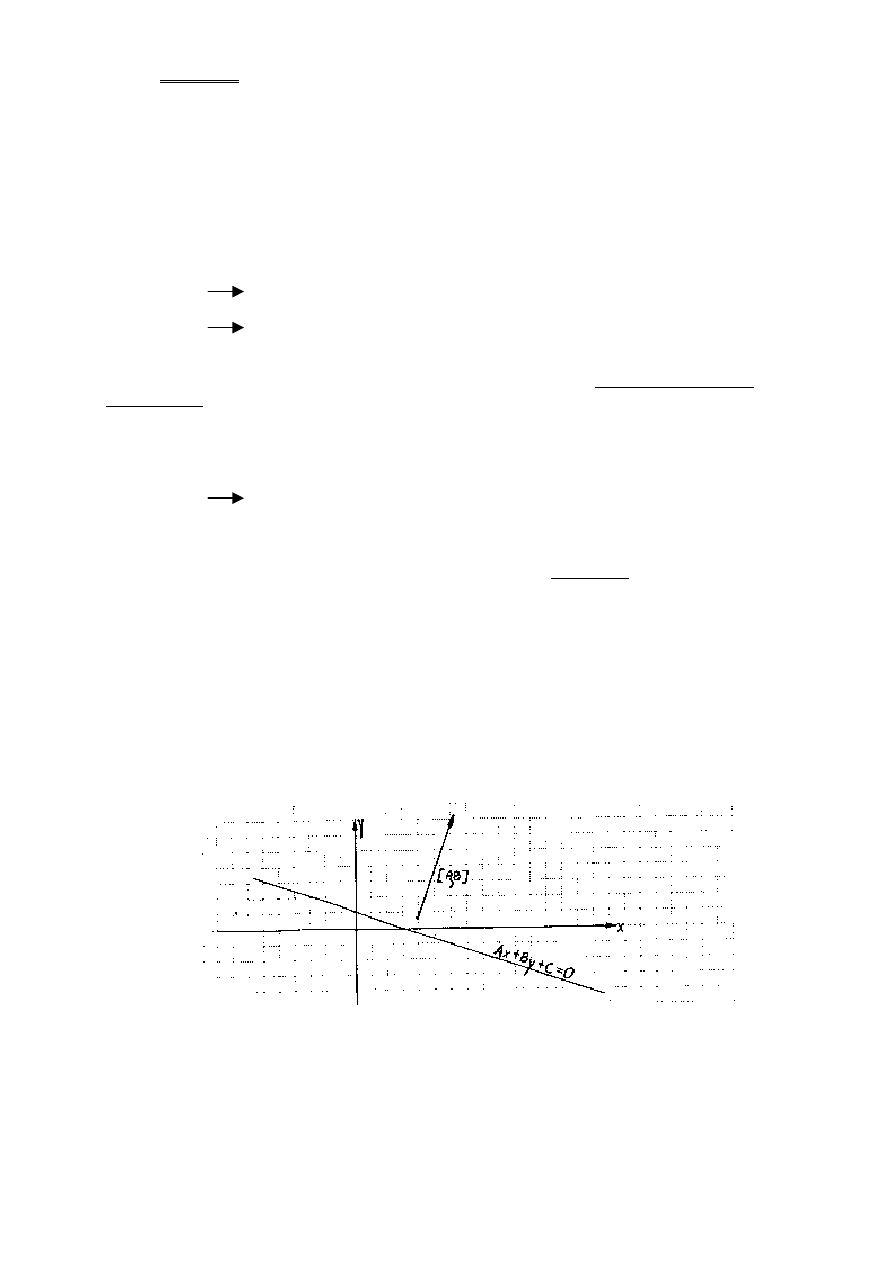
2. Równanie ogólne prostej.

Ka

ż

d

ą

prost

ą

na płaszczy

ź

nie mo

ż

na przedstawi

ć

równaniem postaci Ax+By+C=0,

gdzie [A, B] s

ą

współrz

ę

dnymi dowolnego niezerowego wektora prostopadłego do naszej prostej

oraz A

2

+ B

2

> 0 (A i B nie s

ą

jednocze

ś

nie zerami).

6

We

ź

my punkt (x, y).Ten punkt nale

ż

y do prostej wtedy i tylko wtedy, gdy wektor o współrz

ę

dnych

[x - x

o

, y - y

o

] jest prostopadły do wektora [A, B]. Wówczas mamy:

A(x - x

o

) + B(y - y

o

) = 0

Ax + By + (-A x

o

- B y

o

) = 0

podstawiaj

ą

c -A x

o

- B y

o

= C otrzymujemy równanie, w którym A

2

+ B

2

> 0

Ax + By + C = 0 (2.1.) nazywane OGÓLNYM RÓWNANIEM PROSTEJ

Przekształ

ć

my równanie Ax+By+C=0 i tak:

gdy

B

≠

0

By = - Ax - C / :B

y

A

B

x

C

B

= −

−

równanie ma posta

ć

równania y=ax+b (1.1.)

gdy B = 0

Ax = - C

x

C

A

= −

równanie ma posta

ć

równania x = x

o

(1.2.)

co jest zgodne z wnioskiem z poprzedniego rozdziału.

We

ź

my równanie Ax + By + C = 0:

gdy A = B = C = 0 równanie (2.1.) jest spełnione przez współrz

ę

dne dowolnego

punktu płaszczyzny. Zbiór okre

ś

lony tym równaniem stanowi cał

ą

płaszczyzn

ę

.

gdy A = B = 0 lecz C

≠

0 równanie (2.1.) nie jest spełnione przez współrz

ę

dne

ż

adnego punktu na płaszczy

ź

nie. Równanie przedstawia wi

ę

c zbiór pusty.

gdy A = 0 równanie (2.1.) jest spełnione przez punkty prostej

y

C

B

= −

b

ę

d

ą

cej

prost

ą

równoległ

ą

do osi 0x, gdy

ż

współczynnik kierunkowy równania 1. 1.

a

A

B

= −

= 0.

gdy B = 0 równanie (2.1.) jest spełnione przez punkty prostej x = -

C

A

b

ę

d

ą

cej

prost

ą

równoległ

ą

do 0si 0y.

gdy C = 0 równanie (2.1.) jest spełnione przez punkty prostej y =

−

A

B

x

przechodz

ą

cej przez punkt (0, 0)

7

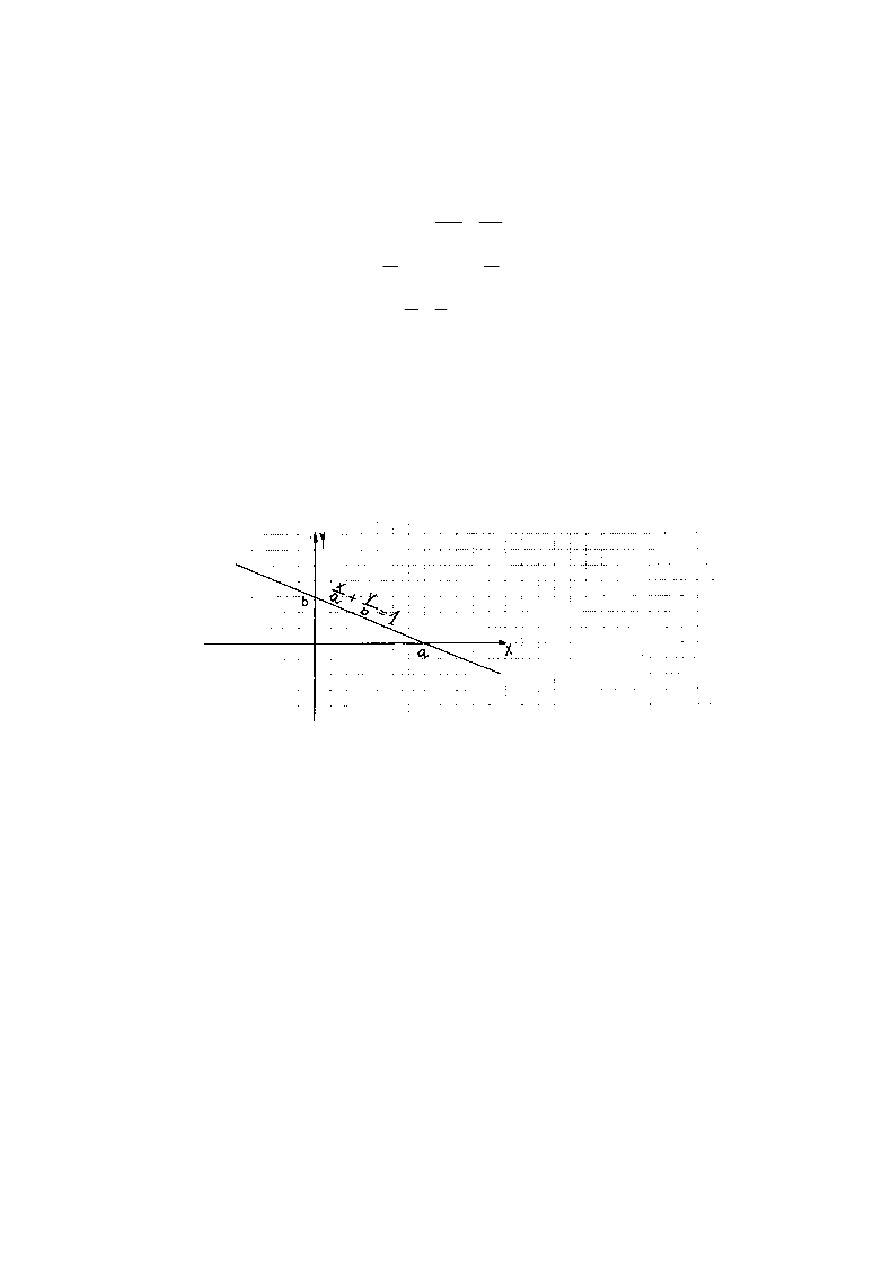
3. Równanie odcinkowe prostej

Je

ż

eli wszystkie współczynniki A, B, C równania (2.1.) s

ą

liczbami ró

ż

nymi od zera to

przekształcaj

ą

c je otrzymujemy kolejno:

Ax + By = - C / :(-C)

−

−

=

Ax

C

By

C

1

oznaczaj

ą

c a = -

C

A

oraz b = -

C

B

otrzymujemy równanie:

x

a

y

b

+ =

1

(3.1.)

Równanie to nazywamy RÓWNANIEM ODCINKOWYM PROSTEJ

Równanie (3.1.) ma praktyczne zastosowanie, gdy

ż

przedstawia prost

ą

przecinaj

ą

c

ą

:

-o

ś

odci

ę

tych w punkcie x = a

-o

ś

rz

ę

dnych w punkcie y = b

4. Równanie prostej przechodz

ą

cej przez dwa punkty na płaszczy

ź

nie.

Niech prosta y=ax+b przechodzi przez punkt A(x

1

, y

1

).

wówczas

y

1

= a x

1

+ b

odejmuj

ą

c stronami otrzymujemy równanie y - y

1

= a (x - x

1

) (4.1.)

Równanie (4.1.) przedstawia dowoln

ą

prost

ą

, która nie jest prostopadła do osi 0x i przechodz

ą

c

ą

przez punkt A (x

1

, y

1

).

Zauwa

ż

my,

ż

e jest niesko

ń

czenie wiele prostych przechodz

ą

cych przez punkt A.

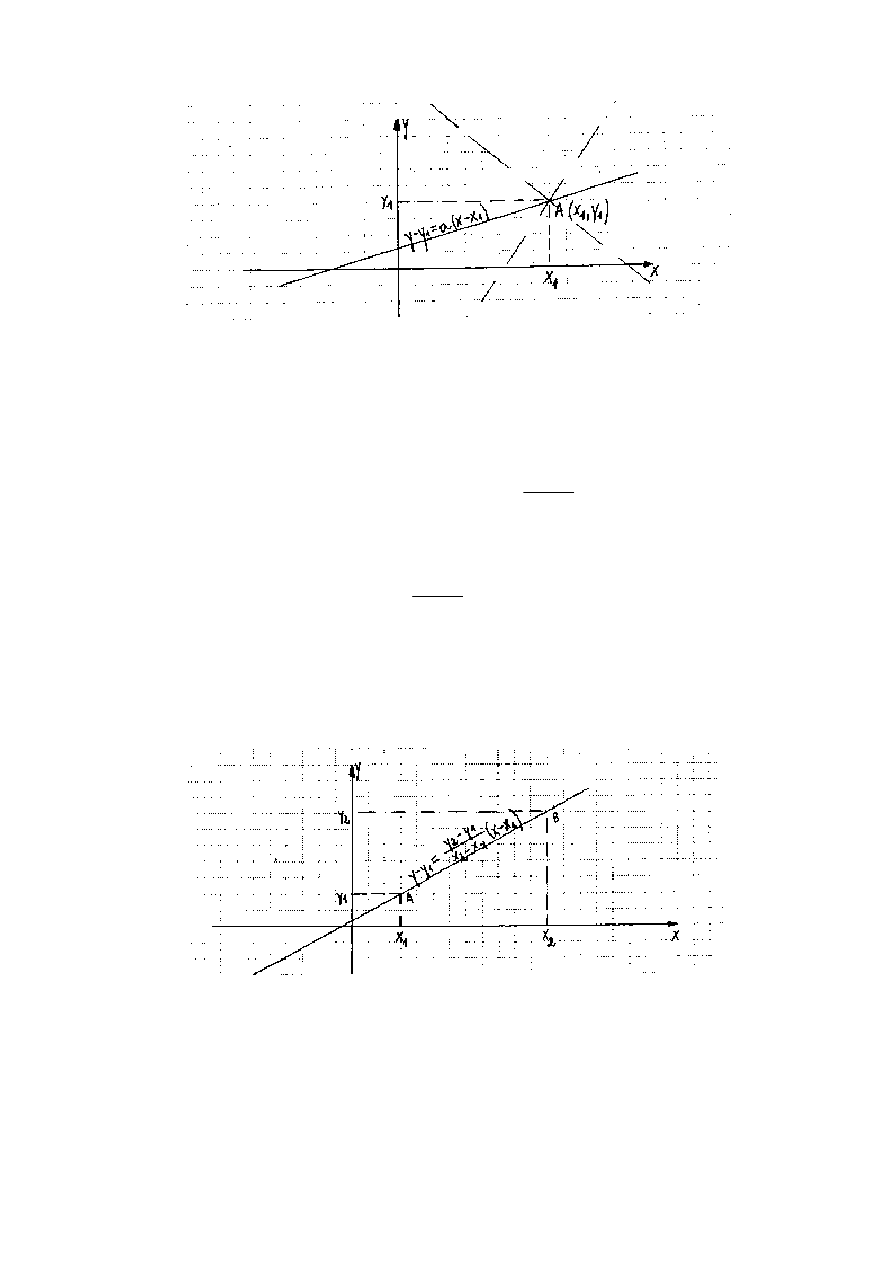
8

Niech prosta (4.1.) przechodz

ą

ca przez punkt A ( x

1

, y

1

), przechodzi przez drugi punkt

B (x

2

, y

2

), gdzie x

2

≠

x

1

.Współrz

ę

dne x

2

, y

2

spełniaj

ą

wówczas równanie (4.1.):

y

2

- y

1

= a (x

2

- x

1

)

sk

ą

d mamy

a

y

y

x

x

=

−
−

2

1

2

1

co podstawiaj

ą

c do (4.1.) daje

y

y

y

y

x

x

x

x

− =

−
−

−

1

2

1

2

1

1

(

)

(4.2.)

Równanie (4.2.) przedstawia PROST

Ą

PRZECHODZ

Ą

C

Ą

PRZEZ DWA PUNKTY.

Prosta ta przechodzi przez punkty A (x

1

, y

1

) oraz B (x

2

, y

2

).

Prosta AB jest nieprostopadła do osi 0x, bo zało

ż

yli

ś

my x

1

≠

x

2

.

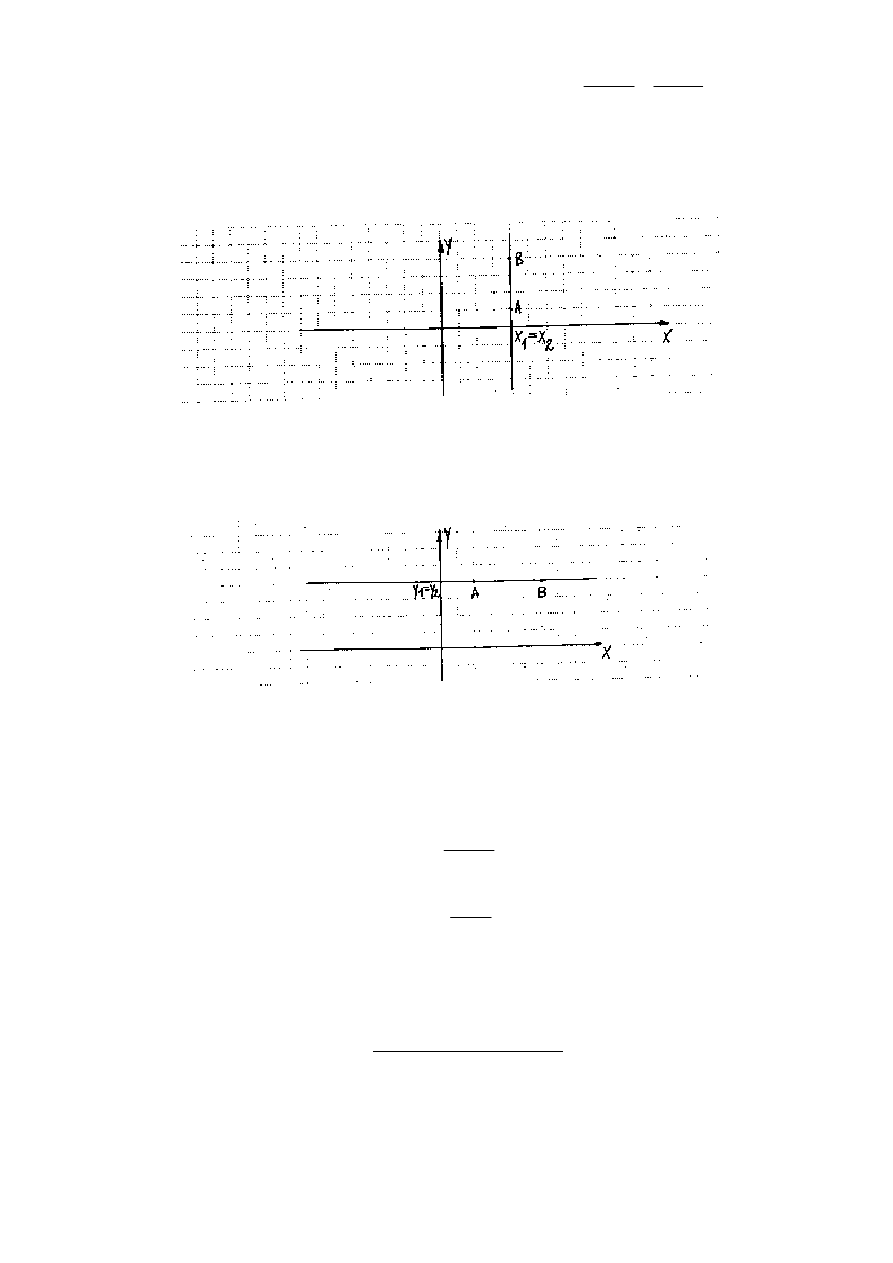
9

Przekształcaj

ą

c równanie (4.2.) mo

ż

na przedstawi

ć

je w postaci

x

x

x

x

y

y

y

y

−

−

= −

−

1

2

1

1

2

1

(4.3.)

kiedy prosta AB jest nierównoległa do osi układu współrz

ę

dnych.

Je

ś

li x

1

= x

2

, ale y

1

≠

y

2

prosta AB jest prostopadła do osi 0x i przecina o

ś

odci

ę

tych

w punkcie x = x

1

, a jej równanie ma wówczas posta

ć

równania (1.2.) x = x

o

.

Je

ś

li y

1

= y

2

, ale x

1

≠

x

2

prosta AB jest równoległa do osi 0x i przecina o

ś

rz

ę

dnych

w punkcie y = y

1

, a jej równanie ma wówczas posta

ć

y = b (współczynnik kierunkowy

równania (1.1.) a=0)

ZADANIE 3.
Podaj równanie prostej przechodz

ą

cej przez punkty P(1, 4) i R(-1, 0)

Rozwi

ą

zanie: podstawiaj

ą

c współrz

ę

dne punktów P i R do równania (4.2.) otrzymujemy

y

y

y

y

x

x

x

x

− =

−
−

−

1

2

1

2

1

1

(

)

y

x

− = −

− −

−

4

0 4

1 1

1

(

)

y-4 = 2 (x-1)

y = 2x -2 +4

równanie prostej: y=2x+2.

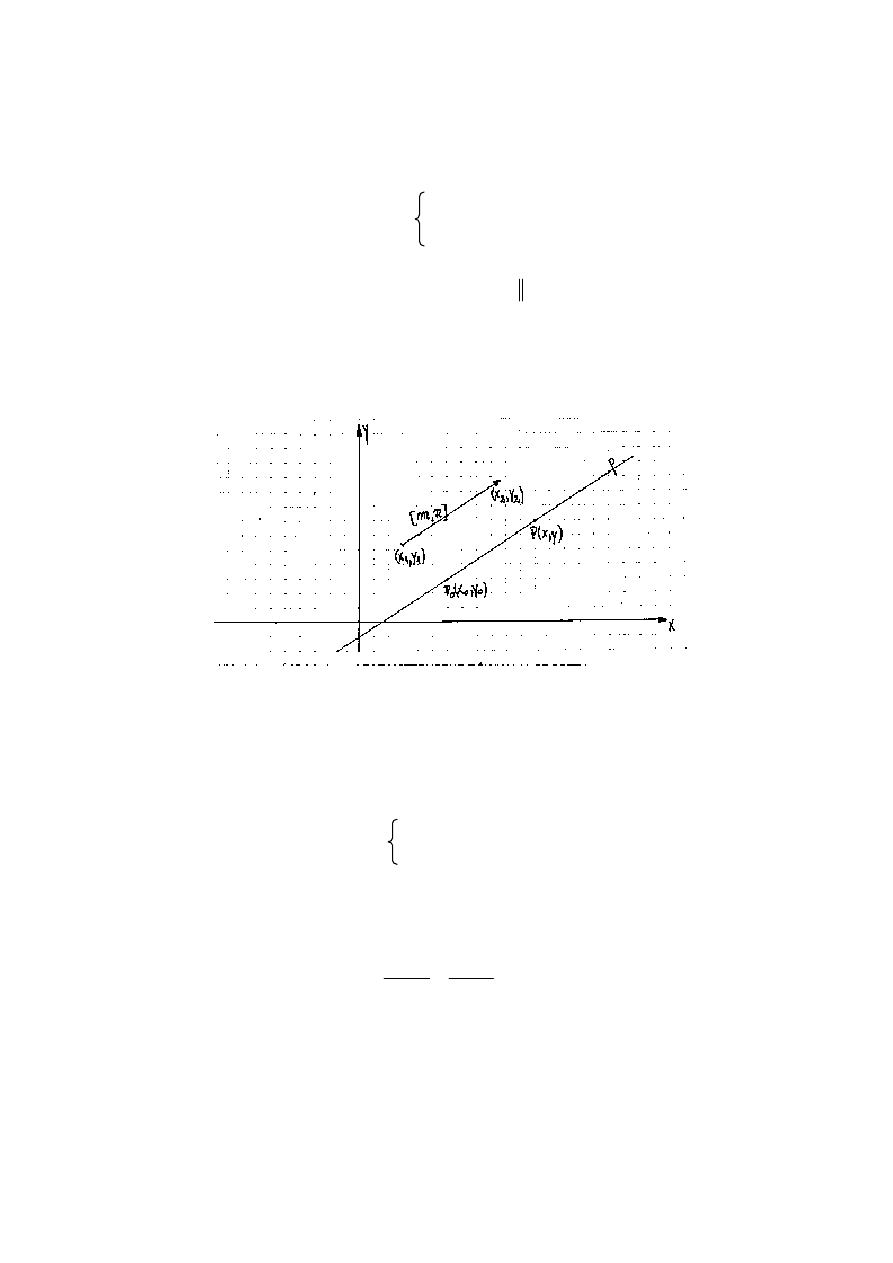
10

5. Przedstawienie parametryczne prostej na płaszczy

ź

nie.

Na to by punkt P (x, y) le

ż

ał na prostej p przechodz

ą

cej przez punkt P

o

(x

o

, y

o

) i równoległej

do niezerowego wektora [m, n] ( punkty P i P

o

maj

ą

ró

ż

n

ą

co najmniej jedn

ą

współrz

ę

dn

ą

)

potrzeba i wystarcza,

ż

eby jego współrz

ę

dne dały si

ę

napisa

ć

w postaci równa

ń

:

x= x

o

+ms

y= y

o

+ns

(5.1.)

gdzie m i n s

ą

współczynnikami kierunkowymi prostej p, s

ą

tak

ż

e współrz

ę

dnymi dowolnego

wektora równoległego do prostej p, co zapisujemy

[ , ]

m n p

, s

∈

R

.

([m, n]=[ x

2

- x

1

, y

2

- y

1

]), liczby m i n nie s

ą

jednocze

ś

nie zerami.

s jest parametrem, czyli liczb

ą

ró

ż

n

ą

od zera, której istnienie umo

ż

liwia warunki (5.1.)

je

ż

eli s = 0 otrzymujemy punkt P

o

(x

o

, y

o

)

Układ równa

ń

(5.1.) stanowi PARAMETRYCZNE RÓWNANIA PROSTEJ.

Równania te spełnione s

ą

przez wszystkie punkty prostej p i tylko przez jej punkty.

Za pomoc

ą

tej postaci dadz

ą

si

ę

przedstawi

ć

wszystkie proste płaszczyzny, podobnie jak za

pomoc

ą

równania ogólnego prostej (2.1.)

Równania parametryczne prostej p mo

ż

na przedstawi

ć

w postaci

x= x

o

+( x

2

- x

1

) s

y= y

o

+( y

2

- y

1

) s (5.2.)

Prosta p spełniaj

ą

ca warunki (5.2.) przechodzi przez dwa punkty o współrz

ę

dnych (x

1

, y

1

) oraz

(x

2

, y

2

).

Gdy m

≠

0 oraz n

≠

0 ruguj

ą

c s z równa

ń

(5.1.) otrzymujemy równanie

x

x

m

y

y

n

o

o

−

= −

(5.3.)

wówczas prosta p nie jest równoległa ani do osi 0x ani do osi 0y.

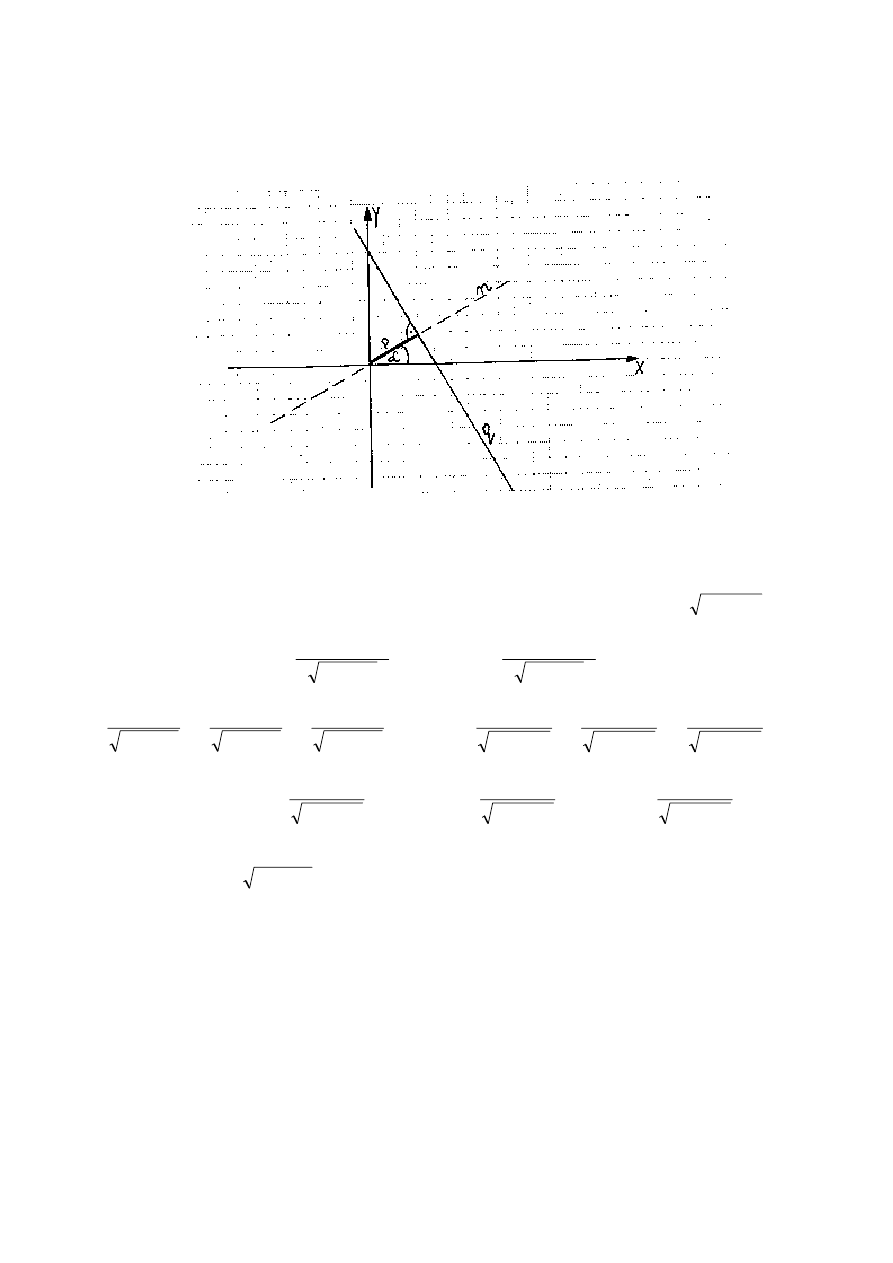
11

6. Posta

ć

normalna równania prostej

Niech prosta q le

ż

y w płaszczy

ź

nie prostok

ą

tnego układu współrz

ę

dnych. Wykre

ś

lmy do

niej, z pocz

ą

tku układu współrz

ę

dnych, o

ś

normaln

ą

(prostopadł

ą

) n.

Oznaczmy: p - odległo

ść

prostej q od pocz

ą

tku układu współrz

ę

dnych

α

- k

ą

t jaki tworzy dodatni kierunek osi 0x z osi

ą

n (0

≤

α

< 2

π

)

Przekształ

ć

my równanie (2.1.) Ax + By + C = 0 (A

2

+ B

2

> 0) dziel

ą

c je przez

2

2

B

A

+

±

Wówczas otrzymujemy

Ax

By

C

A

B

+

+

+

=

2

2

0

lub -

Ax

By

C

A

B

+

+

+

=

2

2

0

, czyli

A

A

B

x

B

A

B

y

C

A

B

2

2

2

2

2

2

0

+

+

+

+

+

=

lub

0

2

2

2

2

2

2

=

+

−

+

+

−

+

+

−

B

A

C

y

B

A

B

x

B

A

A

przyjmujemy: cos

α

=

B

A

A

+

±

2

(*)

sin

α

=

B

A

B

+

±

2

(**) p =

B

A

C

+

2

Uwaga: znak przy

A

B

2

2

+

w (*) i (**) nale

ż

y przyj

ąć

przeciwny ni

ż

znak wyrazu C.

otrzymujemy równanie xcos

α

+ ysin

α

- p = 0 (6.1.)

Równanie (6.1.) nosi nazw

ę

RÓWNANIA NORMALNEGO PROSTEJ

Ka

ż

d

ą

prost

ą

na płaszczy

ź

nie mo

ż

na przedstawi

ć

za pomoc

ą

równania (6.1.)

Rozpatrzmy kilka skrajnych przypadków:

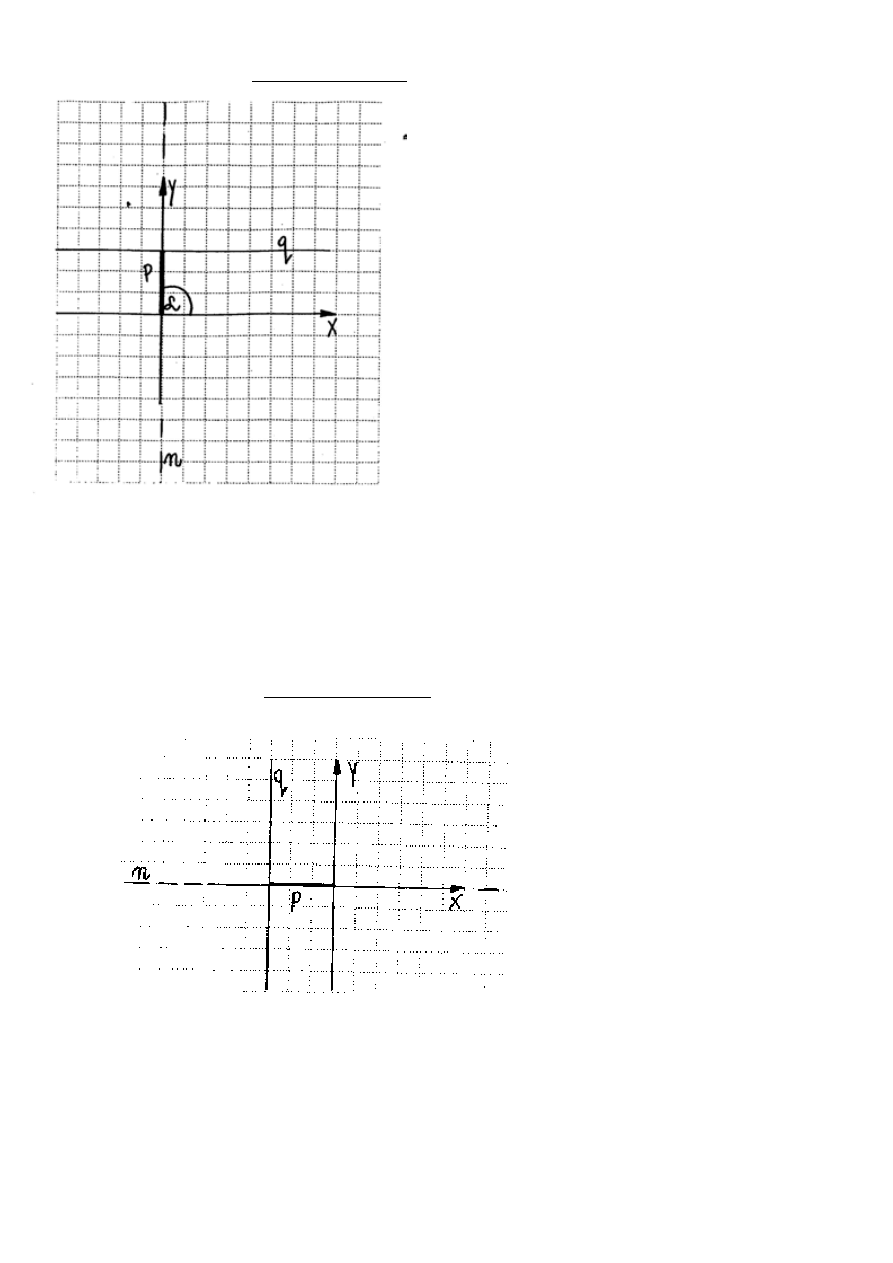
12

i ) gdy prosta q jest równoległa do osi 0x:

α

=

π

/ 2 sin

π

/ 2=1

p>0 cos

π

/ 2=0

x cos

π

/ 2 + y sin

π

/ 2 - p=0

x 0 + y 1 - p = 0

y = p

( ii ) gdy prosta q pokrywa si

ę

z osi

ą

0x (szczególny przypadek równoległo

ś

ci do 0x)

p =0 y =0



( iii ) gdy prosta q jest prostopadła do osi 0x:

α

= 0 sin0 = 0

p>0 cos 0 = 1
x cos 0 +y sin 0 - p = 0
x 1 + y 0 - p = 0
x = p

( iiii ) gdy prosta q pokrywa si

ę

z osi

ą

0y (szczególny przypadek prostopadło

ś

ci do 0x)

p = 0 x = 0

13

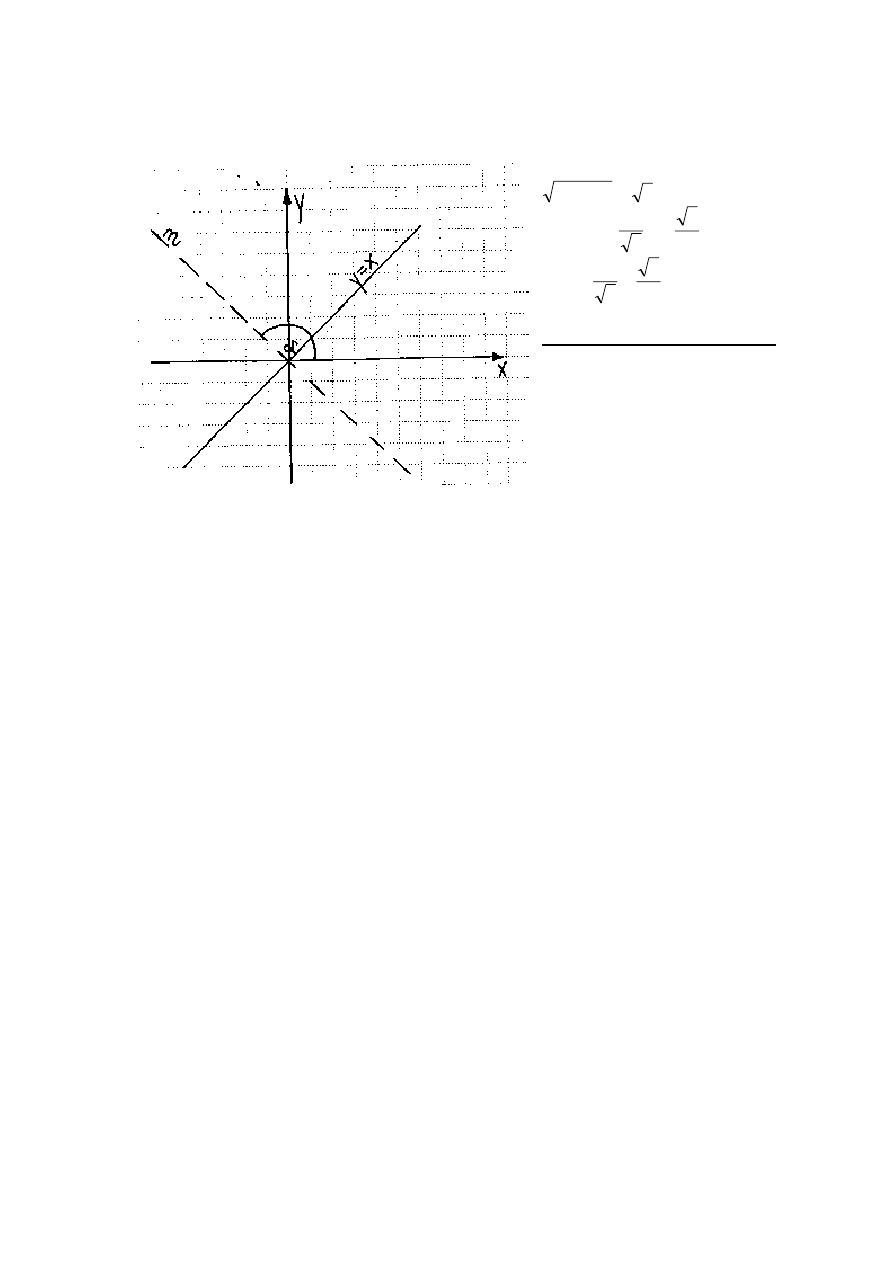
ZADANIE 4.
Zapisz równanie kierunkowe prostej y=x w postaci normalnej. Przedstaw pomocniczy rysunek.

Rozwi

ą

zanie: zapiszmy równanie y=x w postaci ogólnej Ax+By+C=0

-x+y=0 A = -1, B = 1, C = 0

A

B

2

2

+

=

2

cos

α

=

−

= −

1

2

2

2

sin

α

=

1

2

2

2

=

zatem

α

= 0, 75

π

p = 0

x cos 0, 75

π

+ y sin 0, 75

π

= 0

14

PROSTA W PRZESTRZENI

Prost

ą

w przestrzeni okre

ś

la si

ę

jako lini

ę

przeci

ę

cia dwóch płaszczyzn i wyznacza

si

ę

j

ą

analitycznie za pomoc

ą

układu równa

ń

liniowych. Zakładamy tu nierównoległo

ść

tych

płaszczyzn. Jest oczywiste,

ż

e ka

ż

da prosta da si

ę

przedstawi

ć

niesko

ń

czenie wieloma

sposobami, poniewa

ż

istnieje niesko

ń

czenie wiele par płaszczyzn przechodz

ą

cych

przez nasz

ą

prost

ą

.

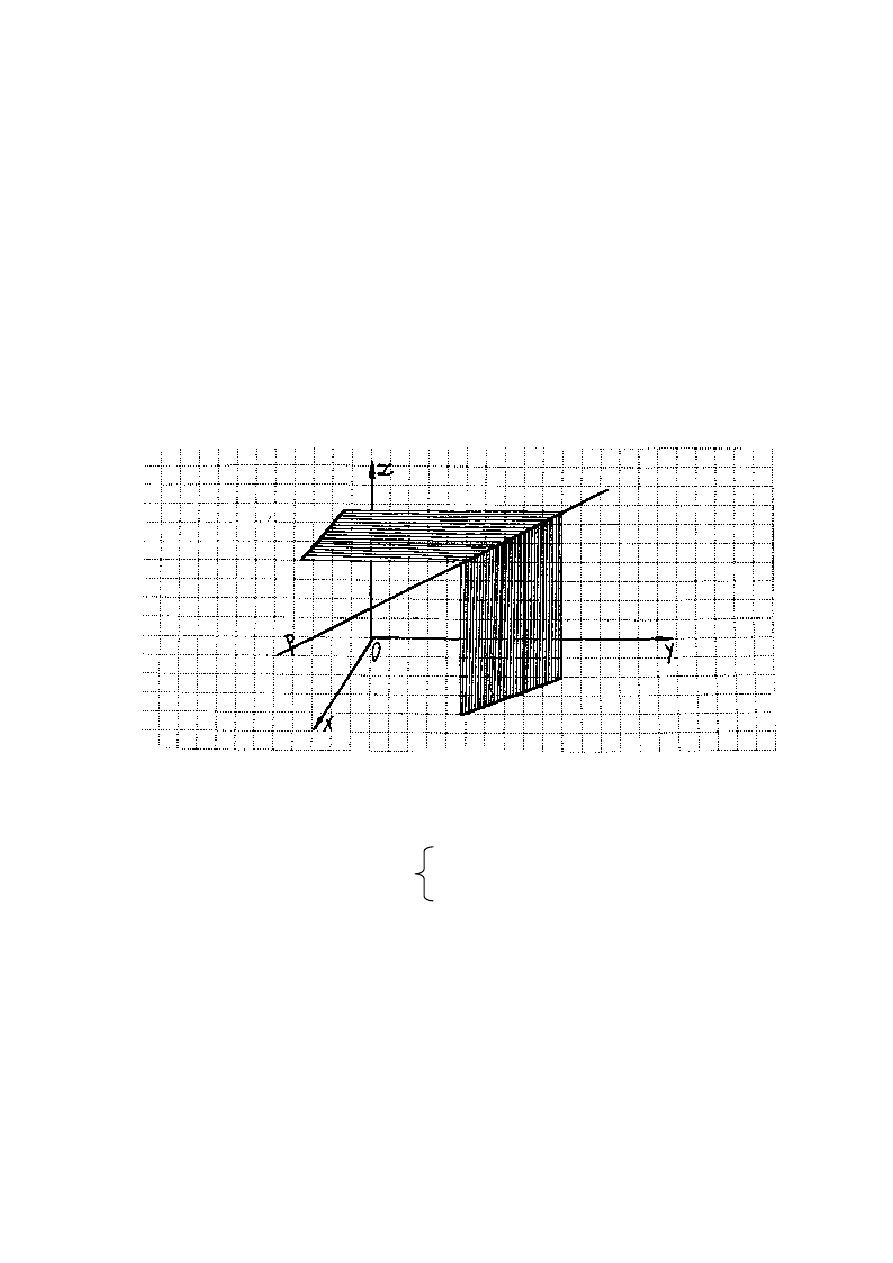
7. Prosta okre

ś

lona przez jej rzuty.

Przedstawienie prostej w przestrzeni mo

ż

e nast

ą

pi

ć

przez okre

ś

lenie jej rzutów

równoległych do osi układu współrz

ę

dnych, przy czym wybieramy dwie spo

ś

ród płaszczyzn

tego układu np. 0xy i 0xz.

Je

ś

li rzuty prostej (nazwijmy j

ą

p) na płaszczyzny 0xy i 0xz maj

ą

w tych płaszczyznach równania:

y = ax + b

z = cx + d (7.1.)

to równania te wyznaczaj

ą

jednoznacznie prost

ą

p.

Równania (7.1.) traktujemy jako równania dwóch płaszczyzn przechodz

ą

cych przez prost

ą

p,

z których pierwsza płaszczyzna jest równoległa do osi 0z, za

ś

druga jest równoległa do osi 0y.

15

8. Prosta jako cz

ęść

wspólna płaszczyzn, podanych w postaci ogólnej.

Je

ż

eli dwie nierównoległe płaszczyzny przestrzeni zapiszemy w postaci ogólnej:

A

1

x + B

1

y + C

1

z + D

1

= 0

A

2

x + B

2

y + C

2

z + D

2

= 0 (8.1.)

to układ równa

ń

(8.1.) b

ę

dzie spełniony przez punkty dokładnie jednej prostej.

Na to, by punkt le

ż

ał na tej prostej, potrzeba i wystarcza,

ż

eby jego współrz

ę

dne spełniały

jednocze

ś

nie obydwa równania (8.1.)

Układ równa

ń

(8.1.) wyznacza kraw

ę

d

ź

przeci

ę

cia dwóch płaszczyzn, przy czym:

A

1

, B

1

, C

1

nie s

ą

jednocze

ś

nie zerami

podobnie A

2

, B

2

, C

2

nie s

ą

jednocze

ś

nie zerami

oraz wektory [A

1

, B

1

, C

1

] i [A

2

, B

2

, C

2

] nie s

ą

równoległe

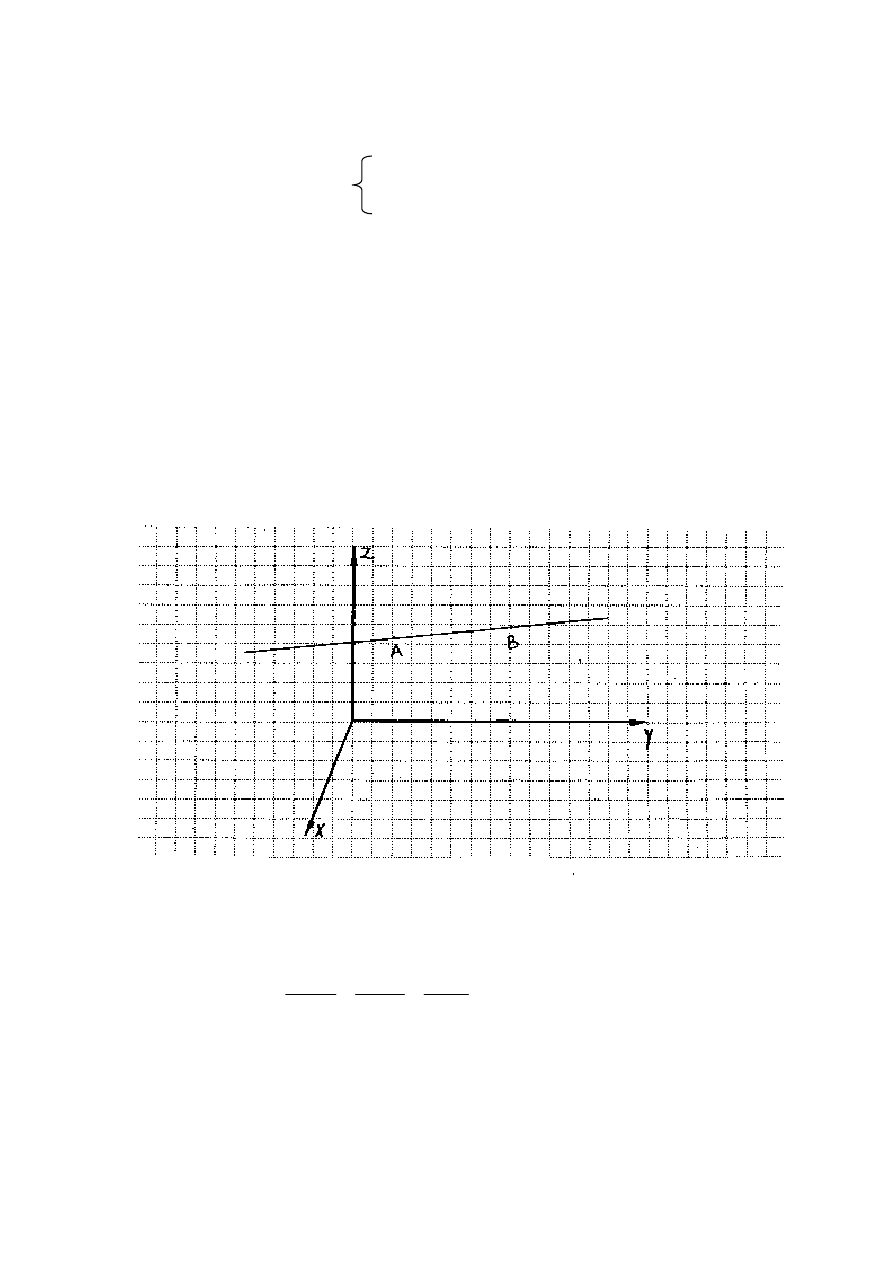
9. Równanie prostej przechodz

ą

cej przez dwa punkty w przestrzeni.

Niech prosta przechodzi przez punkty A (x

1

, y

1

, z

1

) i B (x

2

, y

2

, z

2

).

,

Analogicznie do równania (4.3.) zapiszemy równania prostej przechodz

ą

cej przez dwa ró

ż

ne

punkty przestrzeni:

x

x

x

x

y

y

y

y

z

z

z

z

−

−

= −

−

= −

−

1

2

1

1

2

1

1

2

1

(9.1.)

Równania (9.1.) s

ą

w rzeczywisto

ś

ci układem trzech równa

ń

, które zostan

ą

spełnione przez takie

punkty A i B,

ż

e prosta AB nie jest równoległa do

ż

adnej z płaszczyzn prostok

ą

tnego układu

współrz

ę

dnych.

16

10. Przedstawienie parametryczne prostej w przestrzeni.

Prosta w przestrzeni mo

ż

e by

ć

przedstawiona równie

ż

w postaci parametrycznej.

Analogicznie jak na płaszczy

ź

nie we

ź

my dowolny niezerowy wektor równoległy do prostej p.

Niech współrz

ę

dne tego wektora b

ę

d

ą

oznaczone [m, n, l ]. We

ź

my dwa ró

ż

ne punkty prostej:

P

o

( x

o

, y

o

, z

o

) i P (x, y, z).

Wówczas, je

ś

li prosta p nie jest równoległa do

ż

adnej z płaszczyzn układu współrz

ę

dnych

( m

≠

0, n

≠

0, l

≠

0 ), mo

ż

na j

ą

przedstawi

ć

nast

ę

puj

ą

co:

x

x

m

y

y

n

z

z

l

o

o

o

−

= −

= −

(10.1.)

za

ś

ogólnie, analogicznie jak dla prostej na płaszczy

ź

nie (równanie (5.1.) ), równanie prostej

przechodz

ą

cej przez dwa ró

ż

ne punkty P i P

o

daje si

ę

przedstawi

ć

układem równa

ń

:

x = x

o

+ ms

y = y

o

+ ns

z = z

o

+ ls (10.2.)

Z układu równa

ń

(10.1.) wynika,

ż

e gdy parametr s = 0, punkt P pokrywa si

ę

z punktem P

o

.

17

LITERATURA

1. Stanisław Ziele

ń

- Matematyka dla klasy I szkoły

ś

redniej

2. Stanisław Ziele

ń

- Matematyka dla klasy III szkoły

ś

redniej

3. Franciszek Leja - Geometria analityczna


4. Marceli Stark - Geometria analityczna


5. Jerzy Królikowski, Celestyn Steckiewicz - Matematyka - geometria

analityczna