WEAIiE
Imię i Nazwisko:
1. Michał Idzik
2. Bartosz Niemczura
Imię i Nazwisko:
1. Michał Idzik
2. Bartosz Niemczura
ROK I
GRUPA 1
ZESPÓŁ 9
Pracownia
fizyczna I i II
TEMAT:
Interferencja fal akustycznych
TEMAT:
Interferencja fal akustycznych
TEMAT:
Interferencja fal akustycznych
TEMAT:
Interferencja fal akustycznych
Nr ćwiczenia
25
Data wykonania:
09.04.10
Data oddania:
16.04.10
Zwrot do
poprawy:
Data oddania:
Data
zaliczenia:
OCENA
I. Cel ćwiczenia
Celem doświadczenia jest wyznaczenie prędkości dźwięku w powietrzu i wykładnika w równaniu
adiabaty κ oraz zapoznanie się z zasadą działania rury Quinckego.
II. Wstęp teoretyczny
Zjawisko rozprzestrzeniania się zaburzeń ośrodka nazywamy falą. Źródłem każdej fali jest drgający
ośrodek sprężysty. W wyniku jego właściwości sprężystych, w ruch drgający wprawiane są kolejne
warstwy, znajdujące się wokół ośrodka. Taki rodzaj ruchu nazywamy ruchem falowym i opisujemy za
pomocą równania:
gdzie A – amplituda (maksymalne wychylenie) drgań,
- faza. Do opisu
ruchu falowego często używamy również trzech innych wielkości: okresu, częstotliwości i długości fali.
Okresem drgań (ozn. T [s]) nazywamy czas, w którym każdy punkt fali wykonuje pełne drganie.
Częstotliwość (ozn. f [Hz]) to ilość drgań wykonywanych w ciągu 1s. Z kolei długość fali (ozn. λ [m])
to najmniejsza odległość dwóch punktów o tej samej fazie drgań (np. odległość między dwoma
minimami). Wielkości te możemy powiązać ze sobą, używając w tym celu pojęcia prędkości fali
(prędkości, z jaką rozchodzą się miejsca o tej samej fazie, ozn. v [m/s]):
oraz
.
Niezwykle istotną cechą fali jest fakt, że przenosi ona jedynie energię (nie występuje tu jakikolwiek
transport masy!). Ze względu na sposób przenoszenia energii i kierunek rozchodzenia się drgań, fale
możemy podzielić na podłużne i poprzeczne. W przypadku fal poprzecznych kierunek drgań jest
prostopadły do kierunku ich rozchodzenia się, w przypadku fal podłużnych- równoległy.
Z pojęciem fali wiążą się także zjawiska falowe, między innymi odbicie, dyfrakcja (ugięcie) oraz -
szczególnie istotna w naszym doświadczeniu- interferencja, czyli nakładanie się kilku fal, prowadzące do
zmiany ich amplitudy wypadkowej. Np. dla dwóch interferujących fal możemy wyznaczyć warunek na
minimum:
gdzie x
1
,x
2
- drogi przebyte przez fale, n- liczba naturalna (n>0).
Przykładem fal podłużnych i jednocześnie szczególnym przypadkiem ruchu falowego są fale
akustyczne. Wywołują one wrażenia słuchowe (w określonym zakresie częstotliwości), postrzegane
przez nas jako dźwięki. Oprócz słyszalnych przez ludzkie ucho dźwięków, możemy także wyróżnić tzw.
infradźwięki (o częstotliwościach mniejszych niż 16Hz) i ultradźwięki (o częstotliwościach większych
niż 16kHz), niewykrywalne przez nasz narząd słuchu. Dźwięki, które słyszymy różnią się od siebie dość
znacznie, ponieważ na ich parametry wpływa wiele różnych czynników. Aby móc interpretować cechy
I
Michał Idzik, Bartosz Niemczura - Interferencja fal akustycznych
charakterystyczne dźwięku, wprowadzono kilka pojęć, opisujących jego właściwości. Wyróżniamy
wśród nich barwę, wysokość oraz natężenie dźwięku. Barwa określa brzmienie charakterystyczne dla
danego źródła dźwięku (jest zależna od wielu czynników pośrednich, tzw. składu widmowego fali),
wysokość jest ściśle związana z częstotliwością dźwięku i wzrasta bądź maleje wraz z nią, natomiast
natężenie określa głośność i wyrażone jest ogólnym wzorem:
(gdzie P- moc fali akustycznej, S-
pole powierzchni, na którą pada fala). Z uwagi na wygodę zazwyczaj stosuje się jednak wielkość,
nazywaną poziomem natężenia dźwięku (lub po prostu głośnością) i zapisuje (w skali logarytmicznej)
wzorem:
. Jednostką natężenia dźwięku jest decybel (dB).
Prędkość rozchodzenia się fali dźwiękowej, podobnie jak mechanicznej, można wyrazić zależnością
, jednakże należy pamiętać iż jest ona zależna przede wszystkim od temperatury otoczenia. Aby
to uwzględnić, stosujemy wzór na prędkość rozchodzenia się fali w gazie (doskonałym):
gdzie: R=8,32
J
mol
⋅ K
- stała gazowa, T- temperatura bezwzględna, κ- wykładnik równania adiabaty, μ
– masa molowa użytego gazu.
III. Wyniki pomiarów
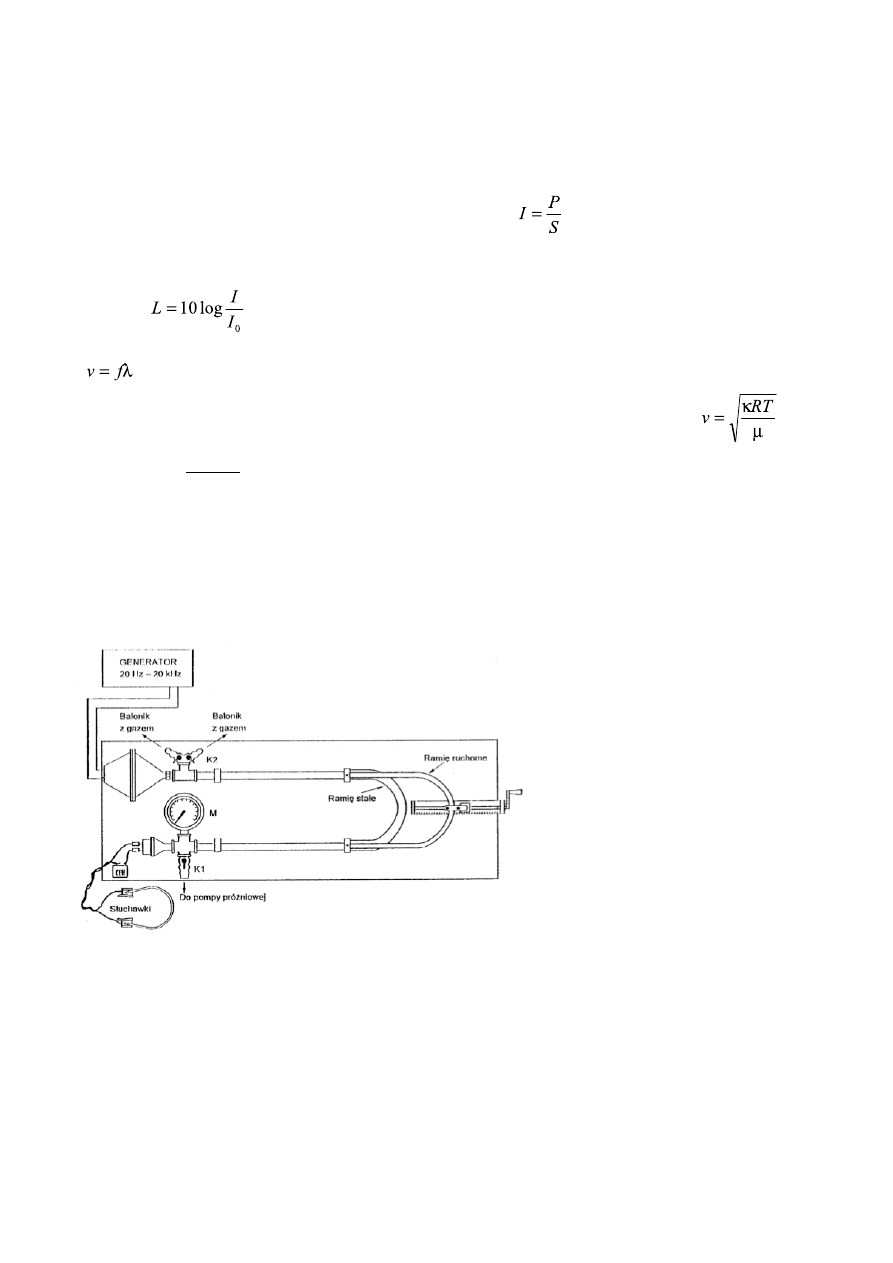
Doświadczenie rozpoczęliśmy od zapoznania się z układem pomiarowym. Znaleźliśmy na korpusie
generatora gałkę potencjometru
regulacji amplitudy drgań i
skręciliśmy ją do pozycji
początkowej. Następnie włączyliśmy
zasilanie generatora ustawionego na
220V. Odczytaliśmy temperaturę
panującą w laboratorium t
= 23°C .
Zgodnie z zaleceniami
prowadzących badaliśmy długości fal
dla częstotliwości z zakresów
600
÷ 1000Hz oraz
2000
÷ 3300Hz . Wykonaliśmy 5
pomiarów z pierwszego zakresu
oraz 12 dla zakresu drugiego. Dla
każdej z częstotliwości
przeszukaliśmy dokładnie raz cały
dostępny przesuw rury. Przesuwając ruchome ramię kontrolowaliśmy wskazania oscyloskopu aby
wykryć położenia minimów fali dźwiękowej. Odpowiednie położenia notowaliśmy w tabeli
(zamieszczonej w kolejnym paragrafie razem z obliczonymi wartościami).
II
Michał Idzik, Bartosz Niemczura - Interferencja fal akustycznych
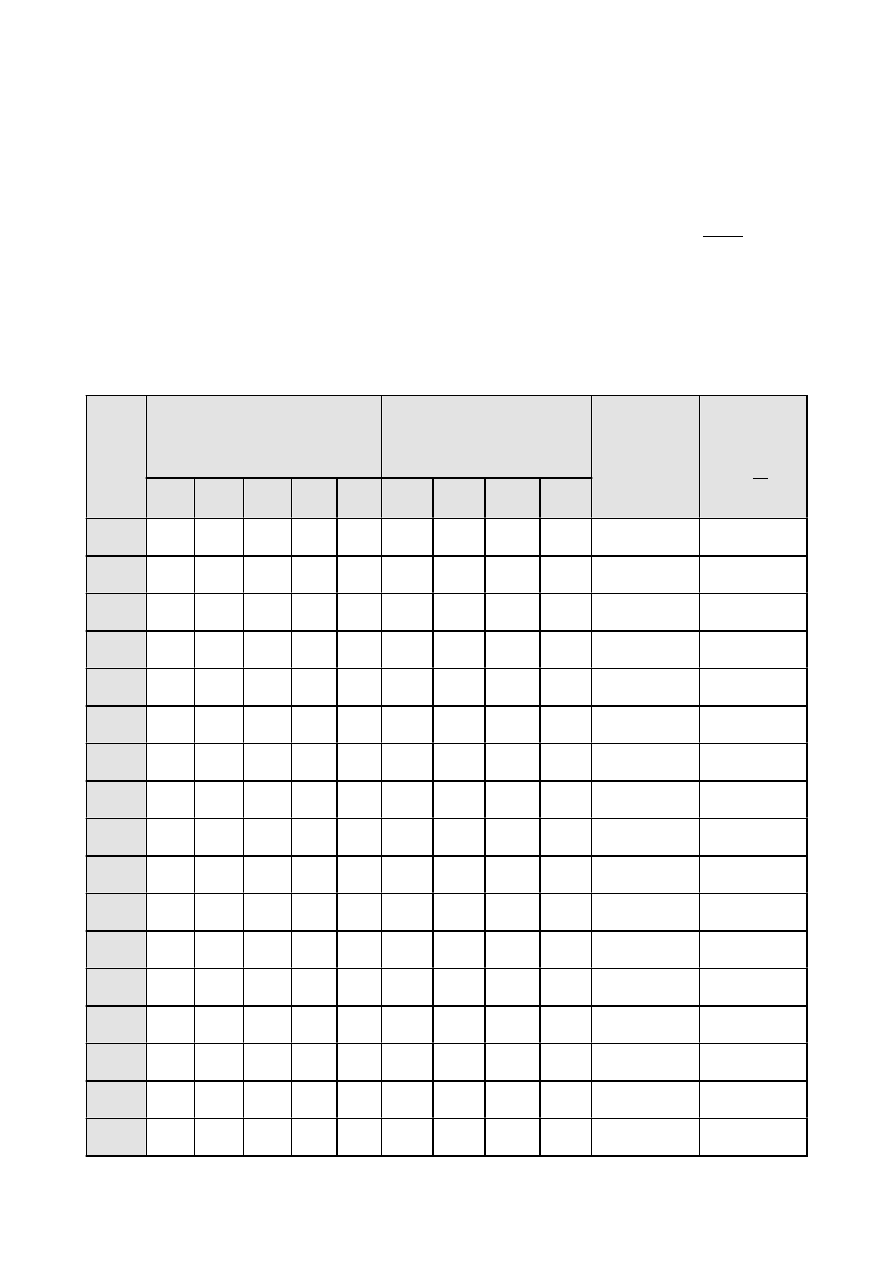
IV.Opracowanie wyników pomiarów
Dla każdej częstotliwości i wykrytych minimów policzyliśmy różnice ich kolejnych położeń ze wzoru:
Δ
i
= a
i
+1
− a
i
. Następnie obliczyliśmy średnie długości fali korzystając ze wzoru:
λ
sr
= 2
Δ
i
i
=1
n
−1
∑
n
− 1
, gdzie n
to liczba znalezionych minimów natomiast liczba „2” oznacza, że różnica dróg przebytych przez fale
biegnące w jednej i w drugiej rurze jest dwukrotnie większa niż przesunięcie ruchomej części rury
wzdłuż skali. Dla tak obliczonych wartości
λ
sr
i zadanych częstotliwości policzyliśmy prędkość dźwięku
w każdym z przypadków: v
k
=
λ
sr
k
⋅ f
k
. Przykładowe obliczenia tych wartości znajdują się w załczniku
(odnośnik 4.1), natomiast ich wyniki w poniższej tabeli.
f [Hz]
Położenie kolejnych minimów
[mm]
Położenie kolejnych minimów
[mm]
Położenie kolejnych minimów
[mm]
Położenie kolejnych minimów
[mm]
Położenie kolejnych minimów
[mm]
Różnica położeń kolejnych
minimów
Δ
i
= a
i
+1
− a
i
[mm]
Różnica położeń kolejnych
minimów
Δ
i
= a
i
+1
− a
i
[mm]
Różnica położeń kolejnych
minimów
Δ
i
= a
i
+1
− a
i
[mm]
Różnica położeń kolejnych
minimów
Δ
i
= a
i
+1
− a
i
[mm]
Długość fali
λ
sr
[mm]
Prędkość
dźwięku
v
k
[
m
s
]
f [Hz]
a
1
a
2
a
3
a
4
a
5
Δ
1
Δ
2
Δ
3
Δ
4
Długość fali
λ
sr
[mm]
Prędkość
dźwięku
v
k
[
m
s
]
602
111
399
288
576
346,75
703
86
337
251
502
352,91
804
75
286
211
422
339,29
899
75
268
193
386
347,01
1003
61
235
405
174
170
344
345,03
2008
60
145
235 317 405
85
90
82
88
172,5
346,38
2104
60
140
223 310 391
80
83
87
81
165,5
348,21
2201
54
130
200 287 365
76
70
87
78
155,5
342,26
2301
40
111
187 264 335
71
76
77
71
147,5
339,40
2400
43
109
183 264 335
66
74
81
71
146
354
2502
36
107
174 243 303
71
67
69
60
133,5
334,02
2599
36
102
169 235 301
66
67
66
66
132,5
344,37
2700
35
100
164 228 290
65
64
64
62
127,5
344,25
2803
33
94
156 218 279
61
62
62
61
123
344,77
2900
30
90
150 210 270
60
60
60
60
120
348
3005
30
87
144 202 260
57
57
58
58
115
345,58
3298
22
75
126 179 221
53
51
53
42
99,5
328,15
III
Michał Idzik, Bartosz Niemczura - Interferencja fal akustycznych
Średnią prędkość dźwięku w powietrzu dla zmierzonej temperatury t
= 23°C wyznaczyliśmy ze
wzoru (4.2):
Wynik ostatniego (siedemnastego) pomiaru dla częstotliwości 3298Hz odrzuciliśmy traktując go jako
błąd gruby.
Aby określić dokładność tego pomiaru zastosowaliśmy wzór na niepewość standardową typu A (4.3):
W następnej kolejności przystąpiliśmy do obliczania wartości dźwięku w temperaturze t
= 0°C .
Wykorzystaliśmy zależność (4.4) v
0
= v
k
T
0
T
sr
= 331,25
m
s
(wynikającą z równości:
), gdzie
T
0
= 273,15K , T
sr
= t + 273,15K = 296,15K . Aby porównać nasz wynik z wartością tablicową
policzyliśmy również jego niepewność złożoną (4.5):
u(v
0
)
=
δv
0
δv
sr
⎛
⎝⎜
⎞
⎠⎟
2
[u(v
sr
)]
2
+
δv
0
δT
sr
⎛
⎝⎜
⎞
⎠⎟
2
[u(T
sr
)]
2
2
= 1,14
m
s
, przyjmując u(T )
=
1K
3
= 0,58K
Następnie przystąpiliśmy do wyznaczenia wykładnika adiabaty
κ =
c
p
c
v
. W tym celu wyznaczyliśmy
najpierw masę molową powietrza jako mieszaniny gazów (4.6):
µ = ω
N
µ
N
+
ω
O
µ
O
+
ω
Ar
µ
Ar
= 28,95
g
mol
, gdzie
ω
i
to wagi wynikające ze składu procentowego
powietrza, natomiast
µ
i
to masy molowe głównych składników powietrza.
Ostatecznie wartość
κ obliczyliśmy przekształcając wzór na prędkość dźwięku w gazie
doskonałym(4.7):
u(v
sr
)
=
(v
i
− v
sr
)
2
i
=1
10
∑
16
⋅15
= 1,14
m
s
IV
Michał Idzik, Bartosz Niemczura - Interferencja fal akustycznych
κ =
v
sr
2
⋅
µ
RT
sr
= 1,39
V
sr
=
v
i
i
=1
16
∑
16
= 344,19
m
s
Podsumowanie wszystkich wyników przedstawiliśmy w poniższej tabeli:
Średnia prędkość v
sr
w temperaturze
pomiaru i jej niepewność
v
sr
= 344,19
m
s
u(v
sr
)
= 1,14
m
s
Obliczona prędkość dźwięku w temp 0
° C i
jej niepewność
v
0
= 331,25
m
s
u(v
0
)
= 1,14
m
s
Tablicowa wartość prędkości dźwięku w
temp 0
° C
v
0
= 331,3
m
s
Obliczony wykładnik
κ w równaniu adiabaty
(wartość teoretyczna dla powietrza 1,4)
κ = 1,39
V. Wnioski
• Nasze doświadczenie pokazuje, że prędkość dźwięku zależy głównie od temepratury
otoczenia. Nie zależy natomiast od częstotliwości drgań, ponieważ wraz z nią zmienia się długość
fali. Znikome znaczenie mają również czynniki zewnętrzne takie jak np. wilgotność otoczenia, poziom
hałasu w otoczeniu.
• Wyznaczona prędkość dźwięku dla temperatury 0° C: zgadza się z wartością
tablicową w granicach wyznaczonej niepewności u(v
sr
)
= 1,14
m
s
. Oznacza to, że nasze wyniki są
prawidłowe, a wykonane pomiary dokładne.
• Obliczony wartość κ = 1, 39 również jest bliska wartości tablicowej dla powietrza κ = 1, 4 .
VI. Uwagi
Konspekt nie wymaga liczenia niepewności wartości wykładnika adiabaty
κ , dlatego
porównanie go z wartością tablicową traktujemy jako przybliżenie.
Obliczenia zostały wykonane przy pomocy programów komputerowych Numbers oraz Pages.
Zgodnie z zaleceniem prowadzących, wszystkie obliczenia zostały spisane ręcznie i umieszczone w
załączniku (przykładowy odnośnik do danego obliczenia wygląda następująco:
(4.3)
). W załączniku
umieszczamy również wyniki pomiarów przeprowadzonych w trakcie zajęć oraz pisemnie
opracowanie zagadnień związanych z interferencją fal akustycznych.
VII. Bibliografia
D. Halliday, R. Resnick, Fizyka, PWN, Warszawa 1996
S. Szczeniowski, Fizyka doświadczalna, T. III, PWN, Warszawa 1980
Wikipedia -
Encyklopedia powszechna, pisana i redagowana przez internautów
V
Michał Idzik, Bartosz Niemczura - Interferencja fal akustycznych
v
0
= 331,25
m
s