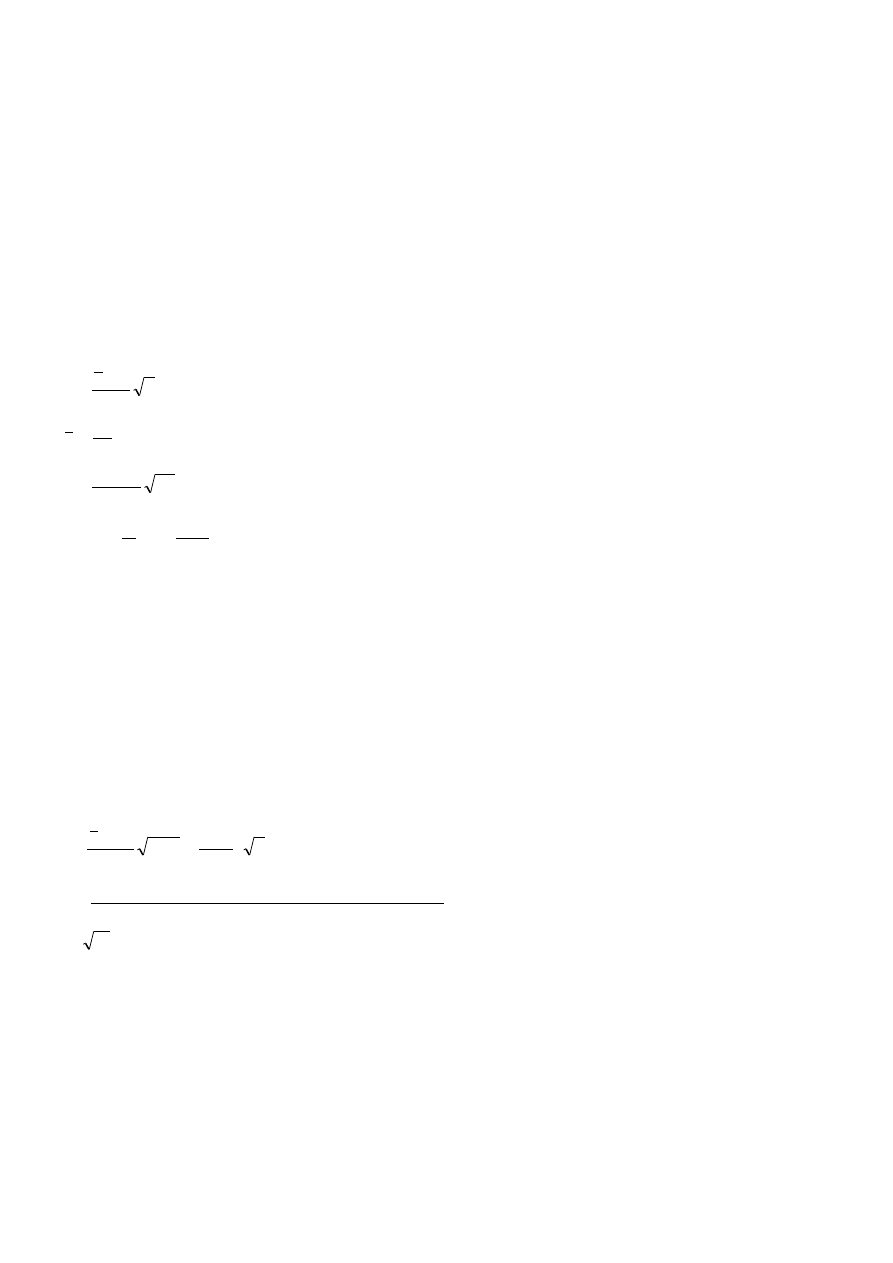
LISTA 11

Zadanie1
Z wieloletnich obserwacji liczby kontuzji, jakim ulegli zawodnicy sekcji judo Warszawskiego Klubu Sportowego
„Gwardia” wynika, że średnia liczba kontuzji wynosi 2 z odchyleniem standardowym równym 1,3. W grupie 25
losowo wybranych zawodników tej sekcji w 1994 r. zanotowano łącznie 55 kontuzji, a odchylenie standardowe liczby
kontuzji było równe 1,5: Czy na podstawie powyższych wyników można uznać, że:
1. Średnia liczba kontuzji w 1994r. nie różniła się w porównaniu ze średnią w poprzednich latach?
2. Wariancja liczby kontuzji w 1994r. była wyższa w porównaniu z wariancją w poprzednich latach? Przyjąć poziom
istotności 0.02.

0

1

H

odrzucenia

do

podstaw

brak

)

,

99

,

0

(

)

99

,

0

,

(

:

99

,

0

2

02

,

0

1

2

1

77

,

0

25

3

,

1

2

2

,

2

2

,

2

25

55

m

-

x

u

sie

roznily

H

sie

roznily

nie

K

u

K

u

u

x

n

srednie

srednie

H

o











































Zadanie 2
W teście badającym pamięć uczniów, dla 8 wylosowanych uczniów otrzymano następujące liczby zapamiętanych
przez nich elementów: 16, 13, 14, 21, 19, 18, 26, 17. Natomiast po specjalnym treningu pamięci grupa ta wykazała
następujące wyniki: 21, 17, 20, 26, 23, 22, 21, 18. Przyjmując poziom istotności alfa = 0.05 zweryfikować hipotezę, że
trening zwiększa liczbę zapamiętanych przez uczniów elementów.

0

2

2

2

2

2

2

0

1

0

H

odrzucamy

)

,

995

,

0

1

,

0

2

2

)

|

(|

)

(

32

,

3

11

11

8

)

3

1

(

...

)

3

5

(

)

3

6

(

)

3

4

(

)

3

5

(

39

,

2

7

32

,

3

0

3

1

0

:

0

:

K

t

K

t

t

P

t

t

P

s

s

n

s

x

t

m

H

m

H

o











































































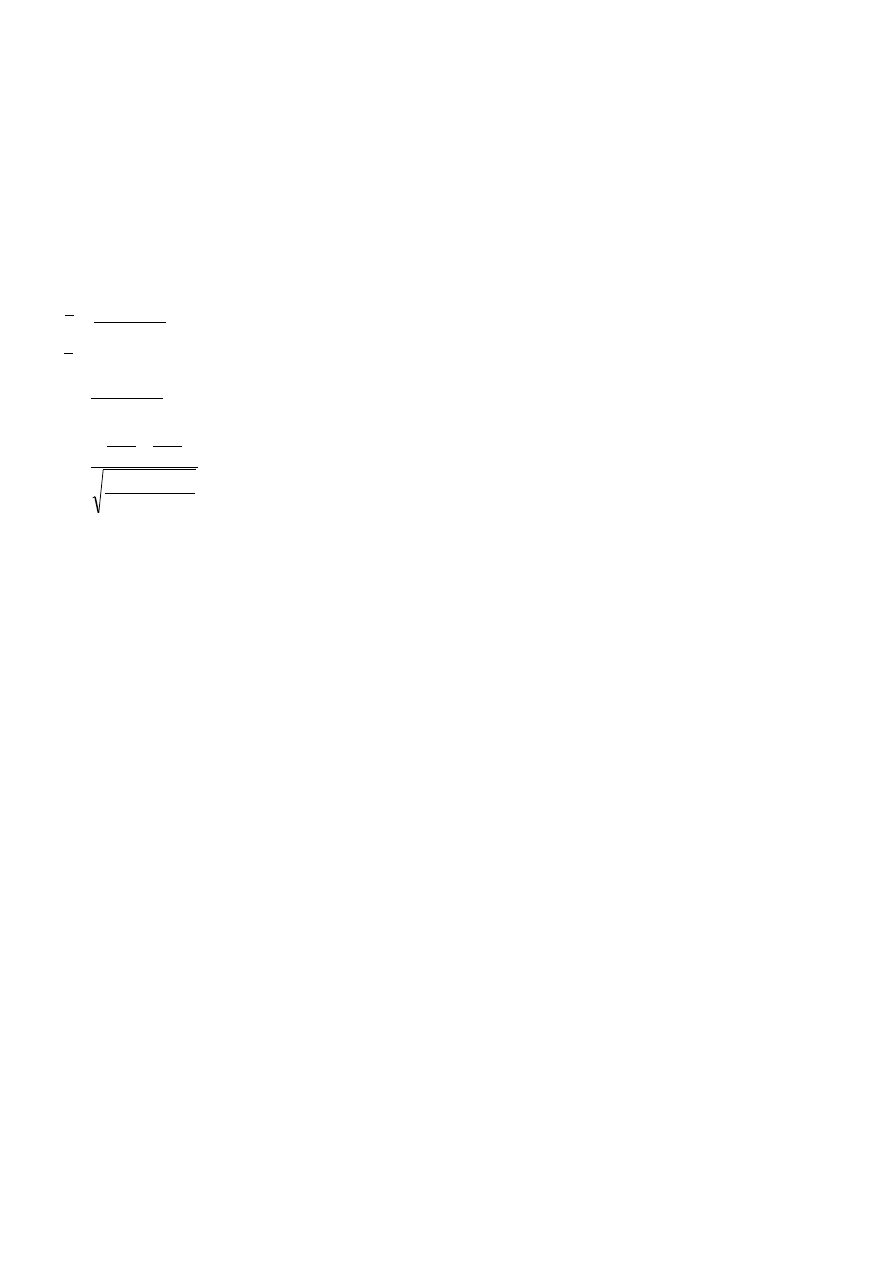
Zadanie 3
Wysunięto hipotezę, że studenci AM palą rzadziej papierosy niż studenci Politechniki. W celu jej sprawdzenia
wylosowano po 250 studentów z każdej uczelni i zapytano ich czy palą. W grupie studentów AM paliło 68 osób, a w
grupie studentów Politechniki - 86 osób.
1. Na poziomie istotności równym 0.05 zweryfikować prawdziwość postawionej hipotezy.
2. Przy jakim poziomie istotności podjęta decyzja weryfikacyjna może ulec zmianie?

)

64

,

1

;

(

64

,

1

95

,

0

1

05

,

0

)

(

76

,

1

125

692

,

0

308

,

0

250

86

250

68

125

250

250

250

250

692

,

0

308

,

0

1

308

,

0

250

250

68

86

05

,

0

:

:

2

1

1

2

1

0



























































K

u

u

u

P

u

n

q

p

p

p

H

p

p

H











Zadanie 4
Analiza rozkładu ocen z matematyki uzyskanych w dwóch 100-osobowych, losowo wybranych grupach kandydatów
zdających do liceów ogólnokształcących na kierunek matematyczno-fizyczny i biologiczno-chemiczny dostarczyła
m.in. informacji, że wartość drugiego momentu centralnego w rozkładzie ocen na kierunek matematyczno-fizyczny
wynosiła 0.7424, a na kierunek biologiczno-chemiczny – 1.6016.
1. Czy na tej podstawie można uznać, że wariancje ocen z matematyki na oba kierunki są różne?
2. Określić graniczny poziom istotności, przy którym następuje zmiana w podejmowaniu decyzji weryfikacyjnej.

Zadanie 5
W grupie 100 losowo wybranych pracowników Banku PKO S.A. 36 osób otrzymało w lutym 1995r. premię w
wysokości 15-20%. W lutym 1994r. w podobnej próbie 100 pracowników premię w takiej wysokości otrzymały 24
osoby.
1. Czy można twierdzić, że odsetek ogółu pracowników Banku PKO S.A. otrzymujących premię w wysokości 15-20%
był w 1994r. niższy w porównaniu z rokiem 1995? Przy weryfikacji przyjąć poziom istotności równy 0.05.
2. Do jakiego przedziału liczbowego powinna należeć wartość odpowiedniej statystyki z próby, aby nie było podstaw
do odrzucenia hipotezy zerowej?

Zadanie 6
Rozkład tygodniowego czasu poświęconego na naukę poza uczelnią studentów I roku studiów dziennych SGH jest
rozkładem N(m,5), natomiast w rozkładzie normalnym tygodniowego czasu studentów II roku odchylenie
standardowe wynosi 6 godzin. Pobrano niezależnie 10 elementową próbę studentów I roku oraz 24 elementową
studentów II roku; średnie w tych próbach wynosiły odpowiednio: 20 godzin oraz 15 godzin.
1. Czy na poziomie istotności 0,1 można przyjąć iż średni czas nauki poza uczelnią ogółu studentów I roku jest wyższy
niż na roku II.
2. Do jakiego przedziału liczbowego powinny należeć wartości odpowiedniej statystyki, aby nie było podstaw do
odrzucenia weryfikowanej hipotezy?