ATOM WODORU

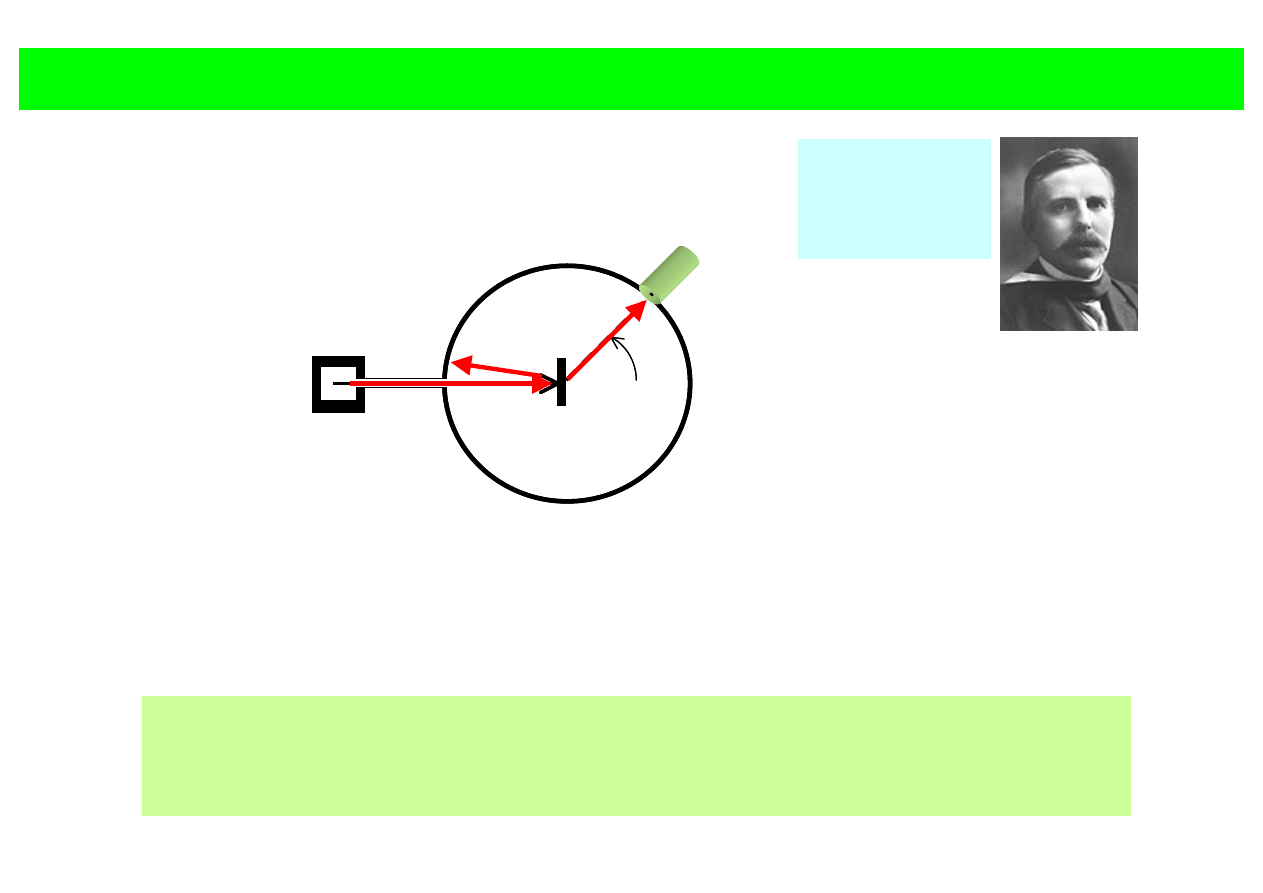
dośw. Ernsta Rutherforda (~1910)

1871-1937

Nobel 1908

(Chemia)

1871-1937

Nobel 1908

(Chemia)

źródło cząstek α

(jądra He)

źródło cząstek α

(jądra He)

θ

detektor cząstek α

θ

detektor cząstek α

Folia metal.

Folia metal.

• rozproszenie:

cząstka naładowana → odpychające oddziaływanie kulombowskie

• silne wsteczne rozprosz. → silne oddz.→ silne pola→ ładunek ~ punktowy
• brak odrzutu atomów folii → ładunki rozpraszające w ciężkich „obiektach”

)

)

~ cała materia folii skupiona w ciężkim jądrze

atomy = ciężkie jądra naładowane dodatnio o b. małych rozmiarach

(~ 10

-14

m << rozmiar atomu ~ 10

-10

m )

)

)

~ cała materia folii skupiona w ciężkim jądrze

atomy = ciężkie jądra naładowane dodatnio o b. małych rozmiarach

(~ 10

-14

m << rozmiar atomu ~ 10

-10

m )

E. Rutheford (1911 r.) rozpraszanie cząstek

α na folii złota:

• dodatnio

naładowane jądr rzędu

≈10

–14

m,

• rozmiary atomu – rzędu 10

–10

m

• masa protonu = 1836 m

e

Postulaty Bohra

Niels Bohr (1885–1967)

Nobel 1922

I.

Elektrony poruszają się w atomach nie promieniując energii, po takich orbitach kołowych, że
moment pędu elektronu jest równy całkowitej wartości stałej h

h

n

mvr

=

n = 1, 2, 3, ...

(12.1)

II.

Przejścia elektronu z orbity o energii En na orbitę, gdzie energia wynosi Em, towarzyszy

emisja lub absorpcja fotonu o częstości

ν

ν

h

E

E

m

n

=

−

(12.2)

Energia kinetyczna

Z przyrównania siły elektrostatycznej z siłą odśrodkową.

r

e

mr

n

m

mv

K

o

πε

8

2

1

2

2

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛

=

=

h

(12.3)

Z wyrażenia (12.3) wyliczymy dozwolone orbity

2

2

2

2

4

n

r

n

me

n

r

o

o

=

=

h

πε

(12.4)

gdzie

2

2

4

me

r

o

o

h

πε

=

=

5.29

×10

–11

m

jest promieniem Bohra.

Promienie orbit są skwantowane i wynoszą: r

o

, 4r

o

, 9r

o

,..., itd.

Dopuszczalne

wartości energii wynoszą

r

e

r

e

r

e

U

K

E

o

o

o

πε

πε

πε

8

4

8

2

2

2

−

=

−

=

+

=

stąd

2

2

2

2

2

4

1

59

13

1

32

n

.

n

me

n

E

o

−

=

−

=

h

ε

π

eV (12.5)

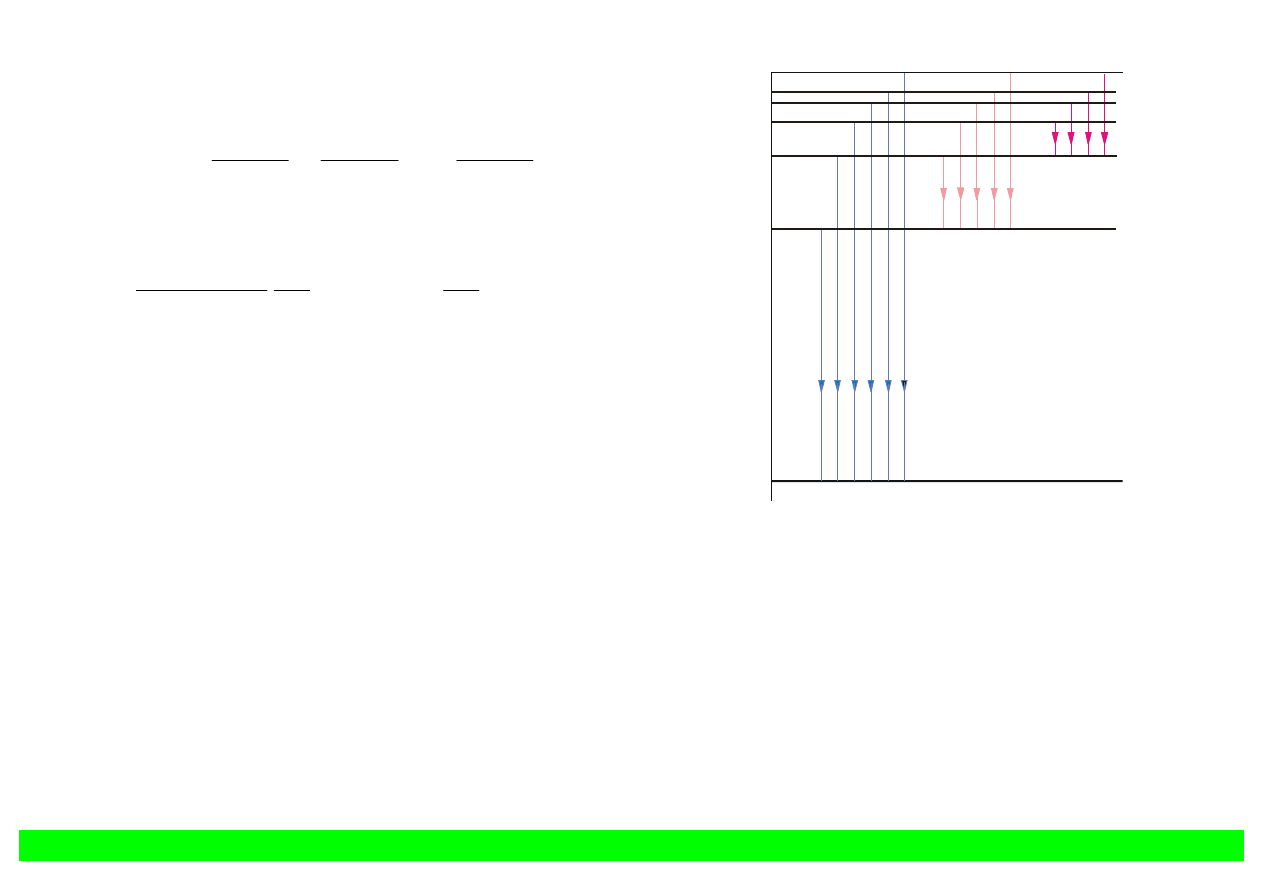
Gdy n rośnie, poziomy leżą coraz bliżej siebie.

0

-0,54

-0,85

-1,51

-3,39

-13,59

Seria

Pashena

Seria

Balmera

Seria Lymana

1

2

3

4

5

n

E

(e

V

)

Rys. 12.1. Schemat poziomów

energetycznych atomu wodoru

Energia jonizacji atomu

wynosi 13,59 eV (przejście ze stanu n = 1 do nieskończoności).

Chociaż teoria Bohra jest przestarzała, jednak jest bardzo prosta. Jej znaczenie historyczne jest duże.
Symbole teorii bohrowskiej stosowane są do chwili obecnej.

Współczesny model atomu był zaproponowany w 1926 r., wkrótce po sformułowaniu równania
Schrödingera

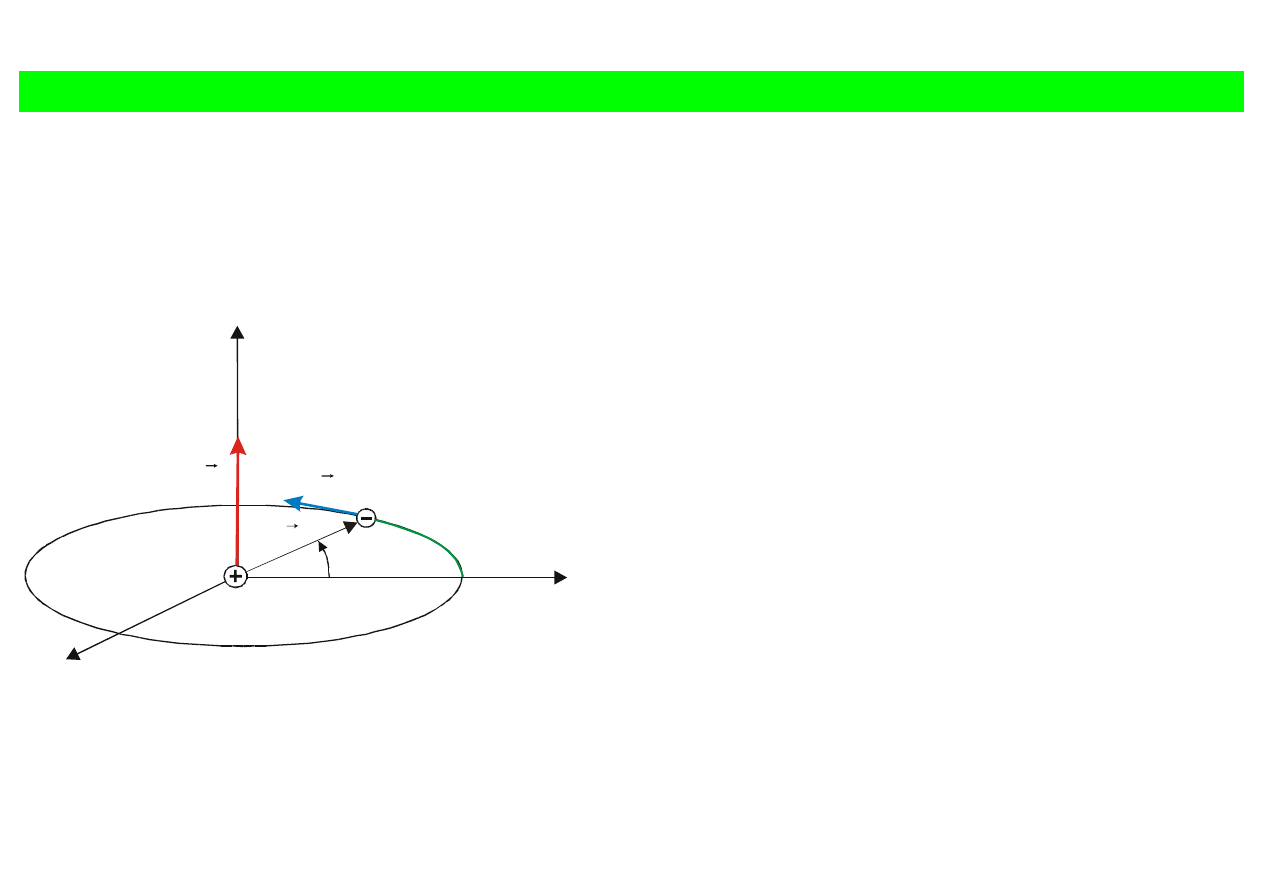
Orbitalny moment pędu

Wątpliwości odnośnie teorii Bohra:

• dlaczego moment pędu elektronu jest skwantowany?

• dlaczego elektron nie emituje promieniowania i nie spada na jądro?

x

y

z

s=r

ϕ

ϕ

r

p

z

L

Rys. 12.2. Paczka falowa poruszająca się po

okręgu o promieniu r.

Moment pędu elektronu (paczki falowej)

k

r

L

z

h

=

Ponieważ droga elektronu na orbicie

ϕ

d

r

s

=

, to

funkcja falowa elektronu

( )

ϕ

Ψ

Ψ

Ψ

ikr

o

iks

o

e

e

r

=

=

Musi być spełniony warunek

( )

(

)

π

ϕ

Ψ

ϕ

Ψ

2

+

=

lub

)

(

ikr

o

ikr

o

e

e

π

ϕ

ϕ

Ψ

Ψ

2

+

=

Równanie to będzie spełnione jeżeli

1

2

=

π

ikr

e

(12.6)

Ponieważ

(

)

(

)

(

)

kr

sin

i

kr

cos

ikr

exp

π

π

π

2

2

2

+

=

,

z równania (12.6) wynika, że

l

m

kr

=

m

l

= 0,

±1, ±2,....

Stąd

h

h

l

m

kr

=

czyli

h

l

z

m

L

=

(12.7)

Wykazaliśmy, że

orbitalny moment pędu względem osi z (lub innego ustalonego kierunku) jest skwantowany i
może przyjmować wartości 0,

±h, ±2h, ±3h,....itd.

Ścisły dowód tego twierdzenia wychodzi poza ramy wykładu.

Składowa momentu pędu nie może być większa od całkowitego momentu pędu.

Przy ustalonej wartości całkowitego momentu pędu istnieje pewna maksymalna wartość m

l

.

Oznaczmy ją przez l. Między l i m

l

zachodzi warunek

l

m

l

≤

Z powyższego wynika, że liczba m

l

może przybierać 2l+1 wartości:

l

,

1

l

,...,

1

,

0

.......,

,

1

l

,

l

−

+

−

−

.

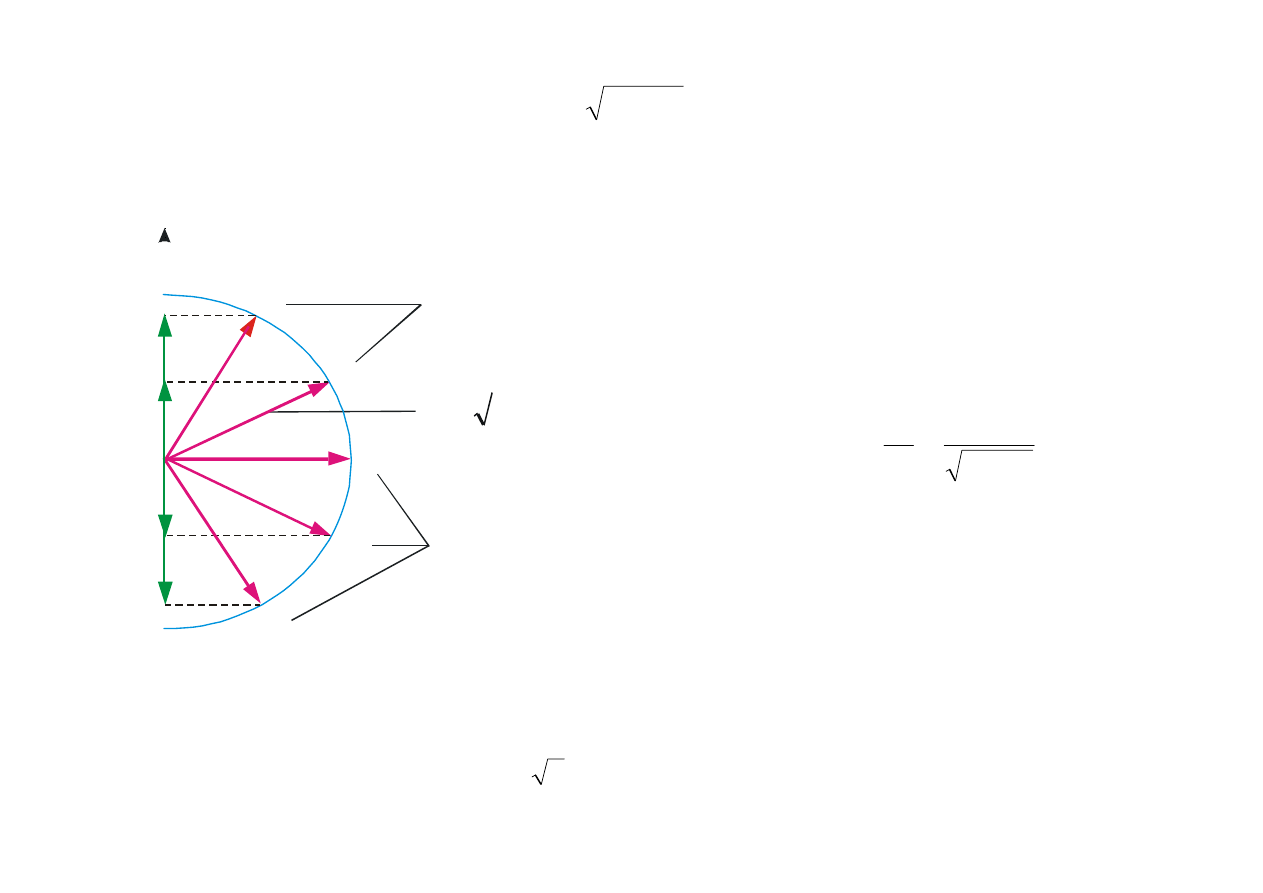
Orbitalny moment pędu L

(

)

h

1

+

=

l

l

L

(12.8)

ma różne wartości L

z

, gdzie l = 0, 1, 2, ... itd.

h

2

h

2

−

h

−

h

2

1

-1

-2

0

h

6

L

=

z

m

l

m

l

Rys. 12.3. Przestrzenne kwantowanie
orbitalnego momentu pędu. W przypadku
przedstawionym na rysunku l = 2 i L =

6

h .

Rzuty wektora L na wyróżniony kierunek
wynoszą: 2h, h, 0, –h, –2h.

Orbitalny moment pędu i jego rzut na
ustalony kierunek są skwantowane.

Ilość możliwych ustaleń wektora L wynosi 2l +
1, przy czym kąty między L

z

i L spełniają

warunek

(

)

1

+

=

=

l

l

m

L

L

cos

l

z

θ

(12.9)

Wektor orbitalnego momentu pędu jest
skwantowany w przestrzeni.

Wyróżniony kierunek – kierunek

B

r

(zewnętrznego lub własnego, wytworzonego
przez atom). Przyjmiemy dalej, że ten
wyróżniony kierunek pokrywa się z osią z.

• liczba l – orbitalna (azymutalna) liczba kwantową – określa wartość orbitalnego momentu

pędu,

• liczba m

l

– magnetyczna liczba kwantowa

Funkcja falowa związana z magnetyczną liczbą falową ma postać

ϕ

Ψ

Ψ

l

im

o

e

=

Stałą

Ψ

ο

wyznaczymy z warunku normalizacji

π

Ψ

ϕ

Ψ

ψ

ΨΨ

π

ϕ

ϕ

π

2

2

2

0

2

2

0

o

im

im

o

*

d

e

e

d

l

l

=

=

∫

∫

−

Zatem

(

)

1

2

−

=

π

Ψ

o

. Ostatecznie więc

ϕ

π

Ψ

l

im

e

2

1

=

(12.10)

Równanie Schrödingera dla atomu wodoru

Erwin Schrödinger

(1887–1961)

Nobel 1933

Energia potencjalna oddziaływania elektron-jądro

( )

r

e

r

U

o

πε

4

2

−

=

Układ sferyczny

Położenie określone jest przez promień wodzący r, kąt biegunowy

ϑ

i kąt azymutalny

ϕ

.

x

y

z

ϕ

ϑ

r

P

Rys. 12.4. Kartezjańskie (x,y,z) i sferyczne (r,

ϑ

,

ϕ

) współrzędne punktu P.

ϑ

ϕ

ϑ

ϕ

ϑ

cos

r

z

sin

sin

r

y

cos

sin

r

x

=

=

=

Jądro znajduje się w początku układu
współrzędnych i jest nieruchome (jego masa
jest 1836 razy większa od masy elektronu).

Równanie Schrödingera we współrzędnych kartezjańskich

(

)

Ψ

∂

Ψ

∂

∂

Ψ

∂

∂

Ψ

∂

U

E

m

z

y

x

−

−

=

+

+

2

2

2

2

2

2

2

2

h

(12.11)

W układzie sferycznym

(

)

Ψ

∂ϕ

Ψ

∂

ϑ

∂ϑ

Ψ

∂

ϑ

∂ϑ

∂

ϑ

∂

Ψ

∂

∂

∂

U

E

m

sin

r

sin

sin

r

r

r

r

r

−

−

=

+

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

2

2

2

2

2

2

2

2

2

1

1

1

h

(12.12)

Równanie Schrödingera dla atomu wodoru

Ψ

πε

∂ϕ

Ψ

∂

ϑ

∂ϑ

Ψ

∂

ϑ

∂ϑ

∂

ϑ

∂

Ψ

∂

∂

∂

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

−

=

⎥

⎦

⎤

⎢

⎣

⎡

+

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

r

e

E

m

sin

sin

sin

r

r

r

r

r

o

4

2

1

1

1

1

2

2

2

2

2

2

2

2

h

(12.13)

W ogólnym przypadku funkcja falowa

Ψ(

r,

ϑ

,

ϕ

).

Istnieją pewne sytuacje fizyczne, że

Ψ

jest tylko funkcją r:

• mamy

stan

s,

•

żaden kierunek w przestrzeni nie jest wyróżniony (

0

=

L

r

),

Dla stanu s równanie Schrödingera

0

4

2

1

2

2

2

2

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

+

⎟

⎠

⎞

⎜

⎝

⎛

Ψ

πε

Ψ

r

e

E

m

dr

d

r

dr

d

r

o

h

(12.14)

Funkcja

Ψ

musi spełniać następujące warunki:

•

0

→

∞

→

Ψ

,

r

,

• p musi osiągnąć max. w pewnej odległości od jądra i jednocześnie p = 0 dla r = 0

Warunki te spełnia

( )

o

r

/

r

o

e

r

−

=

Ψ

Ψ

(12.15)

gdzie

r

o

= const.

Prawdopodobieństwo radialne

znalezienia elektronu w elemencie objętości

dr

r

dV

2

4

π

=

:

( )

dr

e

r

dr

r

r

p

o

r

r

o

2

2

2

2

2

4

4

Ψ

π

π

Ψ

−

=

=

• funkcja ta spełnia warunki: p(0) = 0 i

( )

0

=

∞

p

,

• różniczka funkcji r

2

exp(–2r/r

o

) osiąga max. dla r = r

o

.

Podstawiając (12.15) do (12.14) i wykonując różniczkowanie

0

1

2

2

2

1

2

2

2

2

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

+

−

−

o

r

/

r

o

o

o

o

e

r

me

E

m

r

r

r

Ψ

πε

h

h

Ponieważ

Ψ

o

exp(–r/r

o

)

≠

0, więc

0

1

2

2

2

1

2

2

2

2

=

+

+

−

r

me

E

m

r

r

r

o

o

o

h

h

πε

Równanie to jest spełnione tylko wówczas gdy:

0

2

2

2

2

=

+

−

h

o

o

me

r

πε

0

2

1

2

2

=

+

h

mE

r

o

Z tych równań

m

.

me

r

o

o

11

2

2

10

29

5

4

−

×

=

=

h

πε

(12.16)

eV

.

me

mr

E

o

o

59

13

32

2

2

2

4

2

2

−

=

−

=

=

h

h

ε

π

(12.17)

Przyjęta funkcja jest rozwiązaniem równania Schrödingera, jeżeli r

o

i E są określone (12.16) i (12.17).

• takimi wzorami wyrażają się promień orbity i najniższy poziom energetyczny elektronu w wg

modelu Bohra,

• rozwiązując równanie Schrödingera otrzymaliśmy wzory na r i E bez żadnych założeń,

• r

o

będziemy interpretować jako odległość od jądra, przy której prawdopodobieństwo

znalezienia elektronu osiągnie wartość maksymalną,

• postulat (12.1) różni się od powyższych wniosków z dwu powodów: przyjęcie klasycznej

orbity traci sens, moment pędu równy jest nie n

h

lecz l

h

(jak się dalej przekonamy l < n)

Fakt, że teoria Bohra prawidłowo opisuje widmo poziomów energetycznych atomu wodoru,
jest szczęśliwym zbiegiem okoliczności.

Postępując w sposób analogiczny można wykazać, że funkcja

o

r

/

r

o

o

e

r

r

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

2

1

Ψ

Ψ

jest rozwiązaniem równania Schrödingera, jeżeli

2

2

2

4

32

4

1

h

o

me

E

ε

π

−

=

(12.18)

Poziomy energetyczne elektronu w atomie wodoru

2

2

2

2

4

1

32

n

me

E

o

n

h

ε

π

−

=

gdzie n = 1, 2, 3,.... (całkowita liczba dodatnia) zwana główną liczbą kwantową.

Dokładna analiza funkcji falowych wykazuje, że część radialna funkcji zależy od n i l, a część kątowa
– od l i m

l

. Tak więc możemy zapisać, że

( )

( )

( )

ϕ

Φ

ϑ

Θ

Ψ

ml

lm

nl

nlm

l

l

r

R

=

Podstawiając taką funkcję do równania Schrödingera otrzymujemy:

•

trzy równania zwane odpowiednio radialne, biegunowe, azymutalne,

•

każde z nich opisuje zachowanie się funkcji falowej w zależności od

ϕ

ϑ

,

,

r

,

•

z równań tych wyznacza się możliwe wartości energii, momentu pędu i jednej jego
składowej; wielkości te są określone przez podanie trzech liczb kwantowych n, l, m

l

.

Okazuje się przy tym, że dla danego n, orbitalna liczba kwantowa może przyjmować wartości:

l = 0, 1, 2, ..., n–1.

Trzy liczby kwantowe są związane ze sobą w następujący sposób:

główna liczba kwantowa

n = 1, 2, 3,....

orbitalna liczba kwantowa l = 0, 1, 2, ..., n–1
magnetyczna liczba kwantowam

l

= –l, –l+1, ..., 0, ..., l–1, l

Przy określonej n (określonej wartości energii), liczba możliwych wartości l i m

l

, czyli liczba

niezależnych rozwiązań równania Schrödingera będzie wynosiła

(

)

2

1

0

1

2

n

l

n

l

=

+

∑

−

=

(12.26)

Jeżeli elektron jest w takim stanie, że jednej wartości energii odpowiada kilka niezależnych
rozwiązań równania Schrödingera, to mówimy, że stan taki jest n

2

-krotnie zwyrodniały.

Dla zadanych wartości liczb kwantowych n, l, m

l

; funkcja falowa ma określoną postać którą

oznaczamy symbolem

l

m

,

l,

n

Ψ

i nazywamy orbitalem atomowym.

Każdy orbital oznaczony jest tym samym symbolem co odpowiadający mu stan elektronowy.
Istnieją ogólnie przyjęte symbole liczb kwantowych n i l. Tworzy się je z cyfry oznaczającej
główną liczbę kwantową i litery przyporządkowanej liczbie l w następujący sposób

l

=

0, 1, 2, 3, 4

s, p, d, f, g

Dla stanu podstawowego atomu wodoru n = 1, a zatem l = m

l

= 0. Stan ten oznaczamy symbolem 1s.

Dla najniższego stanu wzbudzonego n = 2, a zatem l = 0 lub l = 1:

• dla

l = 0 (stan 2s), m

l

= 0,

• dla

l = 1 (stany 2p), m

l

= –1, 0 lub 1 – celem rozróżnienia stanów 2p o różnej wartości liczby m

l

stosuje się niekiedy dodatkowy indeks podający wartości tej liczby.

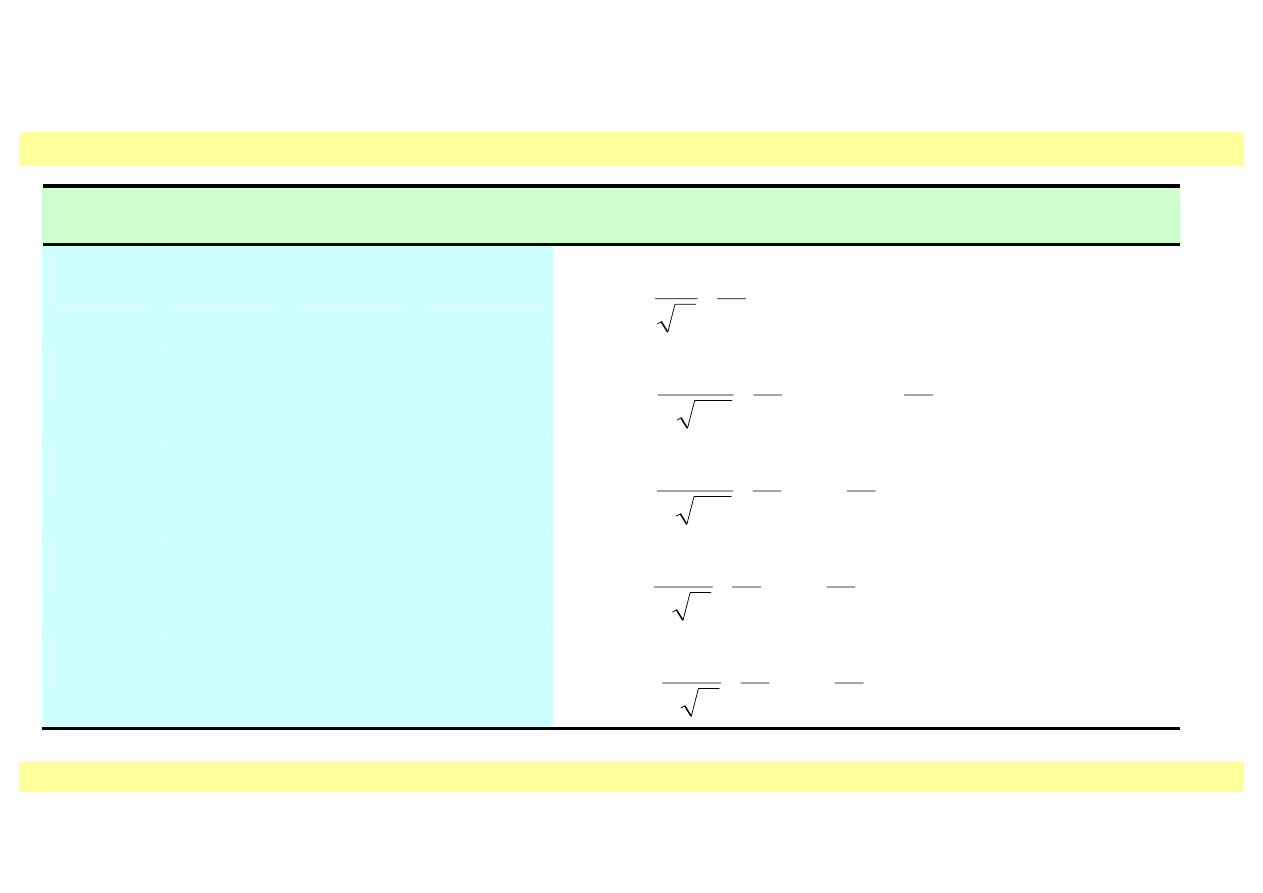
Tabela 12.1. Funkcje falowe atomu wodoru

Stan

n

l

m

l

Funkcje falowe

1s

1

0

0

o

r

/

r

/

o

e

r

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

2

3

100

1

1

π

Ψ

2s

2

0

0

o

r

/

r

o

/

o

e

r

r

r

2

2

3

200

2

1

2

4

1

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

π

Ψ

2p

0

2

1

0

ϑ

π

Ψ

cos

e

r

r

r

o

r

/

r

o

/

o

2

2

3

210

1

2

4

1

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

2p

1

2

1

1

ϕ

ϑ

π

Ψ

i

r

/

r

o

/

o

e

sin

e

r

r

r

o

2

2

3

211

1

8

1

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

2p

–1

2

1

–1

ϕ

ϑ

π

Ψ

i

r

/

r

o

/

o

e

sin

e

r

r

r

o

−

−

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

2

2

3

1

21

1

8

1

Warunek unormowania funkcji

Przykład

– rozpatrzymy funkcję

o

r

r

Ae

−

=

100

Ψ

. Musi być spełniony warunek

1

2

2

100

=

=

∫

∫

−

dV

e

A

dV

o

r

/

r

Ψ

Ponieważ

ϕ

ϑ

ϑ

d

d

dr

sin

r

dV

2

=

więc

1

2

0

0

0

2

2

2

=

∫

∫

∫

∞

−

π

π

ϕ

ϑ

ϑ

d

d

sin

dr

e

r

A

o

r

/

r

Uwzględniając, że

( )

3

0

2

2

2

2

o

r

/

r

r

dr

e

r

o

=

∫

∞

−

mamy

(

)

1

4

2

2

3

2

=

π

o

r

A

Stąd

2

3

1

1

/

o

r

A

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

π

Znając funkcje falowe można obliczyć prawdopodobieństwo znalezienia elektronu w określonym
elemencie objętości.

Prawdopodobieństwo radialne (zależne od r) i prawdopodobieństwo kątowe (zależne

od

ϑ

i

ϕ

).

Prawdopodobieństwo radialne

( )

dr

r

R

dr

r

p

nl

2

2

=

Gęstością prawdopodobieństwa

( )

2

2

r

R

r

p

nl

=

.

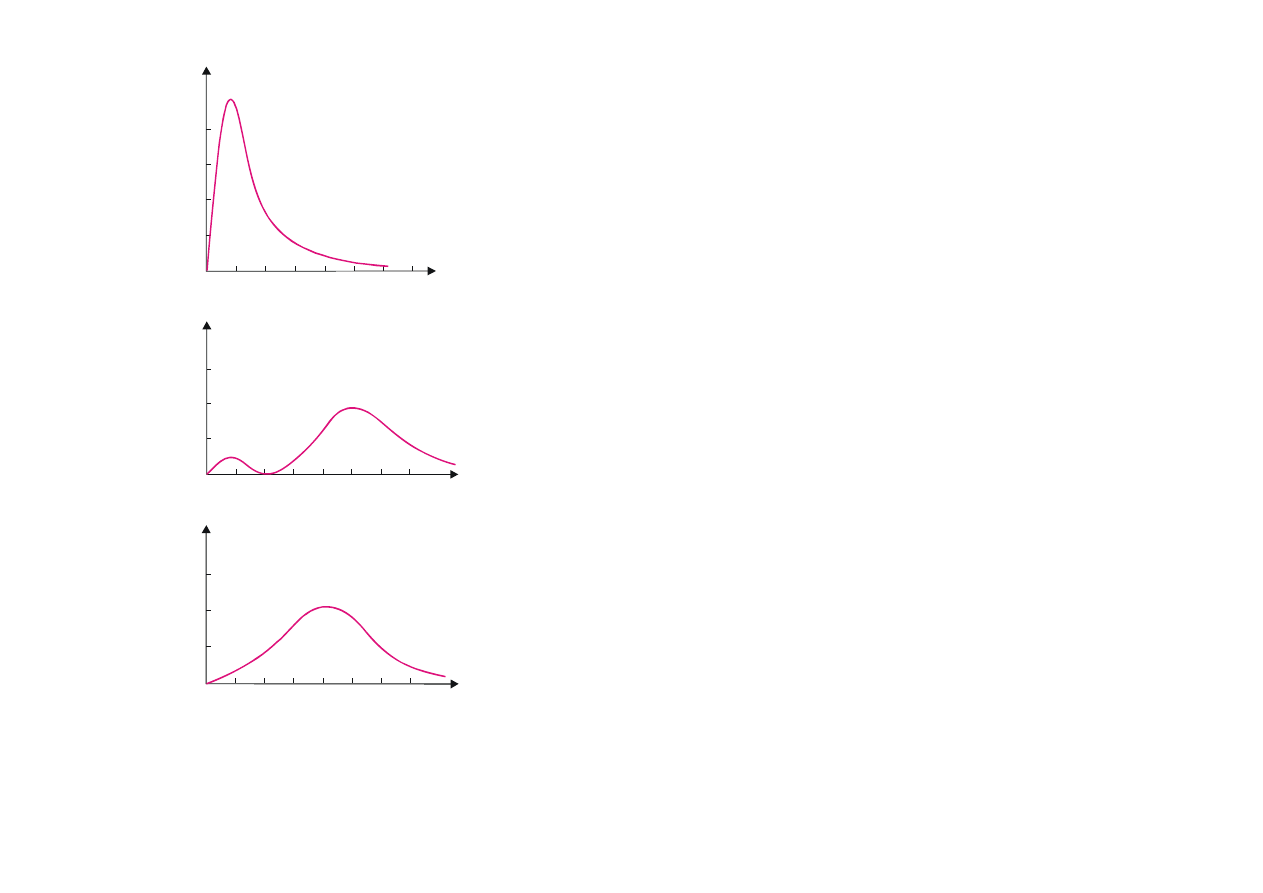
2

nl

2

R

r

2

nl

2

R

r

2

nl

2

R

r

1 2 3 4 5 6 7

1 2 3 4 5 6 7

1 2 3 4 5 6 7

n=1

l=0

n=2
l=0

n=2
l=1

0.4

0.3

0.2

0.1

0

0.3

0.2

0.1

0

0.3

0.2

0.1

0

r/r

o

r/r

o

r/r

o

Rys. 12.5. Radialne gęstości prawdo-

podobieństwa dla atomu wodoru gdy n = 1 i 2.

W stanie 1s – p(r) osiąga maksimum dla r = r

o

.

W stanie 2s – istnieją dwa maksima: dla r = r

o

i

r

≈ 5r

o.

W stanie 2p – p(r) osiąga maksimum w pobliżu
r = 4r

o

.

Dla wszystkich stanów zależność

Ψ

∝

exp(im

ϕ

). Zatem gęstość prawdopodobieństwa

nie będzie zależała od

ϕ

, gdyż

(

)

(

)

1

=

−

ϕ

ϕ

im

exp

im

exp

Całkowita gęstość prawdopodobieństwa

( ) ( )

ϑ

p

r

p

.

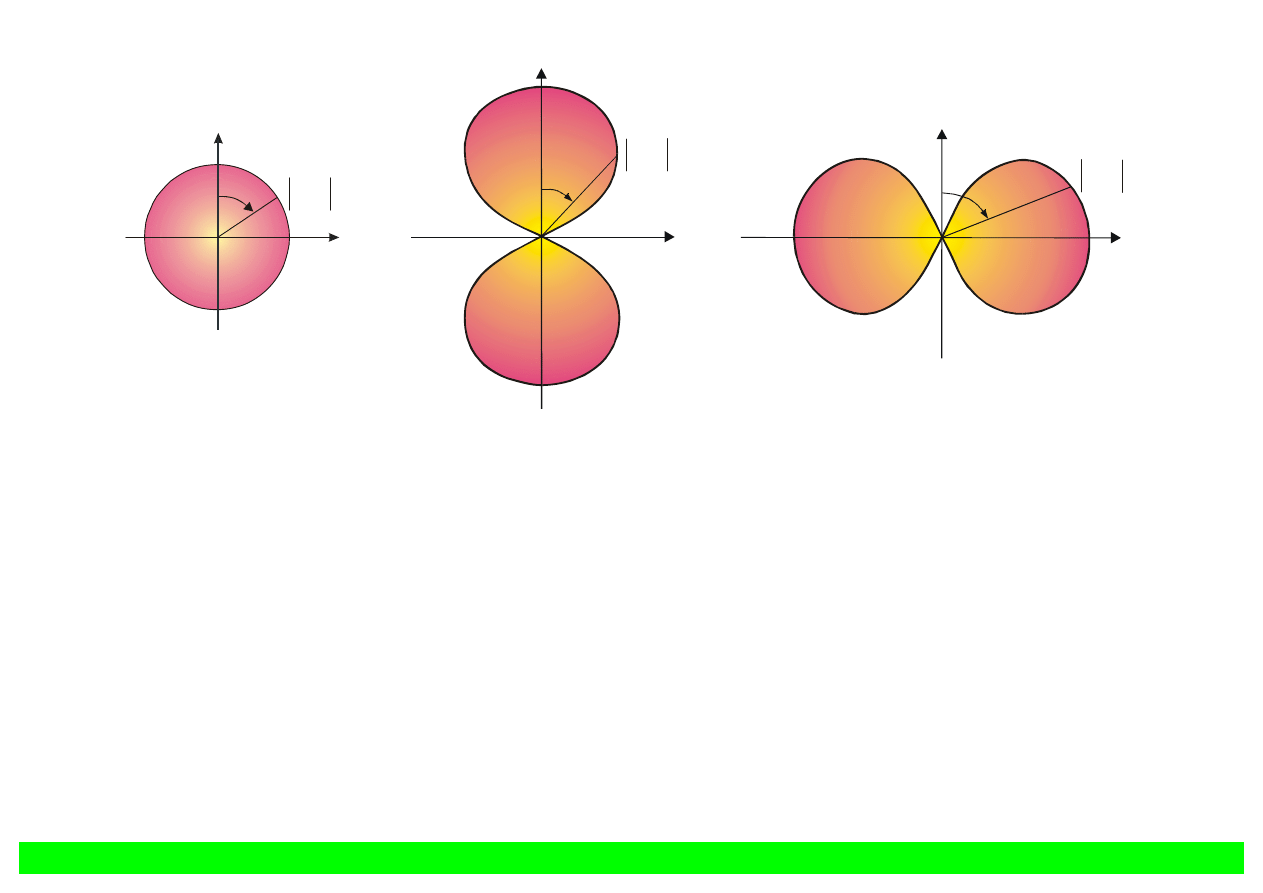
l=0

m =0

l

y

z

ϑ

2

lm

l

Θ

y

z

ϑ

2

lm

l

Θ

1

m

l

±

=

l=1

l=1

m =0

l

y

z

ϑ

2

lm

l

Θ

Rys. 12.6. Wykresy biegunowe kierunkowej zależności gęstości prawdopodobieństwa dla

atomu wodoru w przypadku l = 0 i l = 1.

Miarą prawdopodobieństwa znalezienia elektronu w danym kierunku jest odległość między
początkiem układu współrzędnych i punktem przecięcia prostej poprowadzonej pod danym kątem, z
wykresem funkcji

2

l

lm

Θ

.

W stanie s (l = 0) p(r) = const.

(chmura elektronowa wykazuje symetrię kulistą)

W stanie l = 1 i m = 0,

( )

ϑ

ϑ

2

cos

~

p

Dla l = 1 i

1

±

=

m

,

( )

ϑ

ϑ

2

sin

~

p

.

W każdym przypadku gęstość prawdopodobieństwa wykazuje symetrię obrotową względem osi z.

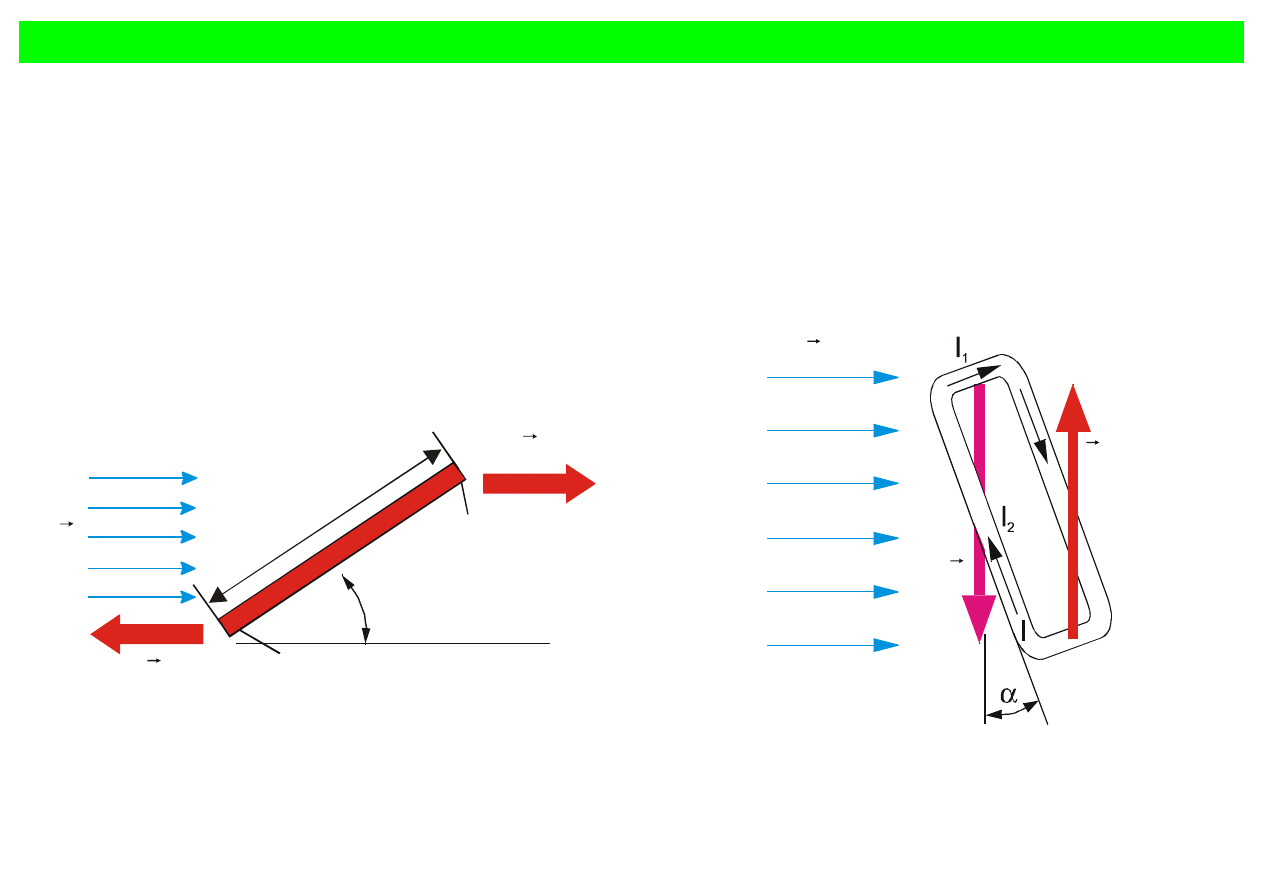
Orbitalny moment magnetyczny

Przypomnienie

Gdyby istniał ładunek magnetyczny, to w polu magnetycznym działałaby na niego siła

B

q

F

m

r

r

⋅

=

analogiczna do siły działającej na ładunek elektryczny w polu elektrycznym.

l

α

B

F

F

+q

m

-q

m

Rys. 6.10. Magnes o długości l położony pod

kątem

α

do linii sił pola magnetycznego

B

r

.

F

F

B

Rys. 6.11 Prostokątna ramka o powierzchni l

1

l

2

w jednorodnym polu magnetycznym.

Moment sił działających na magnes wynosi

α

sin

Fl

T

=

czyli

α

sin

Bl

q

T

m

=

Iloczyn q

m

l =

μ

określa się jako moment magnetyczny. Wobec tego

α

μ

sin

B

T

=

a w zapisie wektorowym

B

T

r

r

r

×

=

μ

W analogiczny sposób zachowuje się pętla z prądem (rys. 6.11).

Siły magnetyczne przyłożone do dwóch przeciwległych boków o długości l

1

tworzą moment obrotowy

α

sin

Fl

T

2

=

Ponieważ

B

Il

F

1

=

, stąd

(

)(

)

α

α

α

sin

ISB

sin

B

l

Il

sin

l

B

Il

T

=

=

=

2

1

2

1

Wynika z tego, że

pętla z prądem wytwarza pole magnetyczne identycznie jak magnes

IS

=

μ

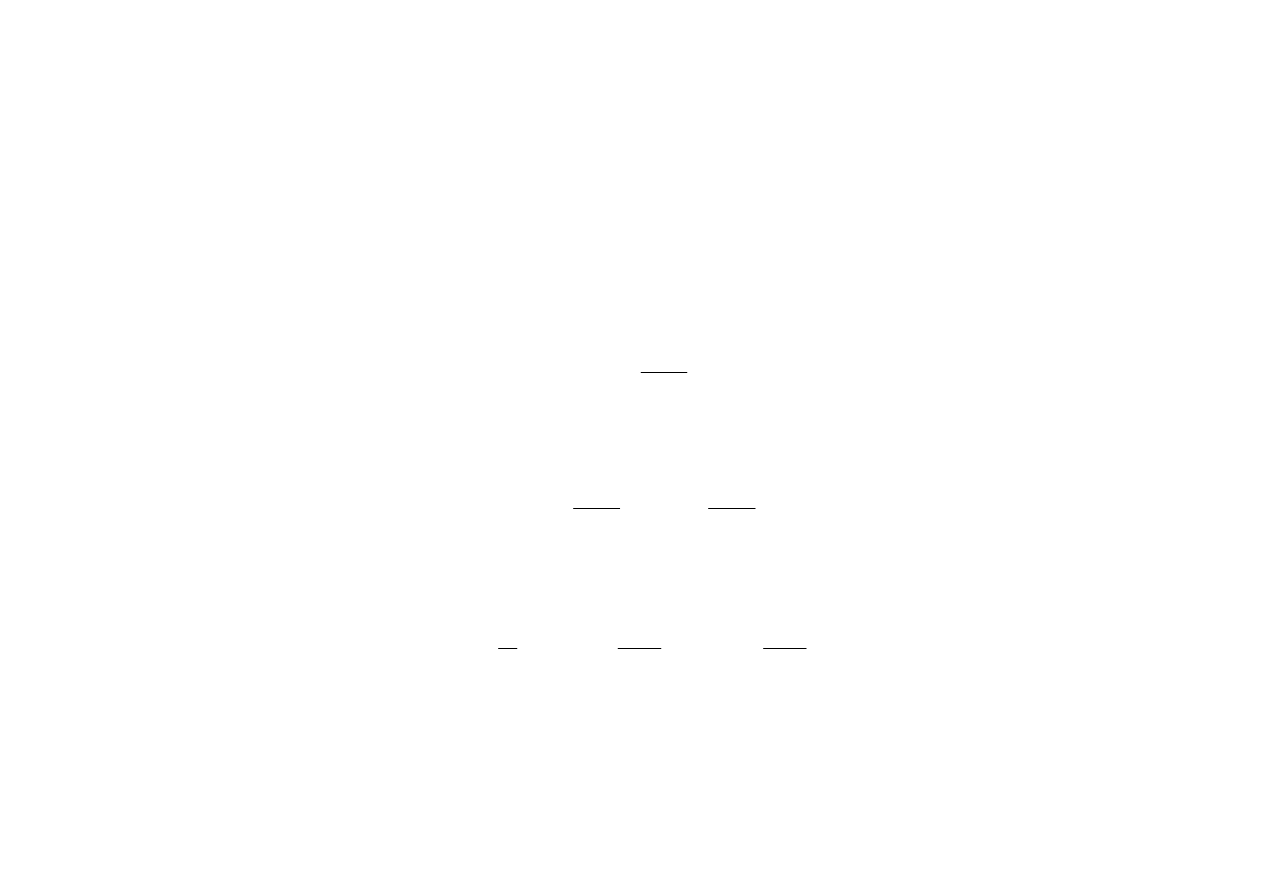
Z ruchem orbitalnym elektronu związany jest moment magnetyczny elektronu.

Moment magnetyczny zamkniętego, płaskiego obwodu z prądem wynosi

S

I

r

r

⋅

=

μ

Cząstka o ładunku q poruszająca się po orbicie kołowej z prędkością v, wytwarza prąd o natężeniu

r

v

q

I

π

2

=

Orbitalny moment magnetyczny

2

2

2

qvr

r

r

qv

l

=

=

π

π

μ

a w zapisie wektorowym

L

m

q

p

r

m

q

v

r

q

l

r

r

r

r

r

2

2

2

=

×

=

×

=

μ

gdzie

p

r

L

r

r

r

×

=

jest orbitalnym momentem pędu.

Stosunek

μ

/L nazywamy stosunkiem giromagnetycznym.

Dla elektronu

(

)

(

)

1

1

2

2

+

−

=

+

−

=

−

=

l

l

l

l

m

e

L

m

e

B

l

μ

μ

h

(12.28)

Znak minus oznacza, że

μ

l

jest skierowany przeciwnie niż

L

r

, co spowodowane jest ujemnym

ładunkiem elektronu.

μ

B

nazywany

magnetonem Bohra

jest jednostką atomowego momentu magnetycznego

2

24

10

27

9

2

Am

.

m

e

B

−

×

=

=

h

μ

(12.29)

Na cząstkę o momencie magnetycznym l

μ

r

w zewnętrznym polu magnetycznym

B

r

działa moment sił

B

T

l

r

r

r

×

=

μ

(12.30)

który dąży do ustawienia wektora momentu magnetycznego wzdłuż kierunku pola.

Energia potencjalna momentu

w zewnętrznym polu magnetycznym wynosi natomiast

θ

μ

μ

cos

B

B

U

l

l

−

=

⋅

=

r

r

(12.31)

gdzie

θ

jest kątem między

l

μ

r

i

B

r

.

• orbitalny moment pędu (

L

r

) i jego rzut na ustalony kierunek (

z

L

), są skwantowane,

• kąt między L i L

z

jest zawsze różny od zera, więc

• wektor

L

r

i wektor

l

μ

r

nie mogą ustawić się równolegle czy też antyrównolegle do pola

B

r

.

Składowa orbitalnego momentu magnetycznego w kierunku zewnętrznego pola

(

)

l

l

lz

m

m

e

cos

l

l

m

e

cos

2

1

2

h

−

=

+

−

=

=

θ

θ

μ

μ

(12.32)

Widzimy teraz, dlaczego m

l

nazywa się magnetyczną liczbą kwantową – określa bowiem rzut

momentu magnetycznego na kierunek zewnętrznego pola magnetycznego.

Kąt

θ

między wektorami

l

μ

r

i

B

r

jest zawsze różny od zera, więc w zewnętrznym polu magnetycznym

na moment magnetyczny zawsze będzie działać moment siły

B

L

m

e

T

r

r

r

×

⎟

⎠

⎞

⎜

⎝

⎛

−

=

2

Moment ten powoduje zmianę momentu pędu

L

d

r

zgodnie z prawem Newtona

T

dt

L

d

r

r

=

.

Zmiana

L

d

r

powoduje precesję

L

r

o kąt

ω

L

dt

, gdzie

ω

L

dt

jest prędkością kątową precesji zwanej

prędkością Larmona.

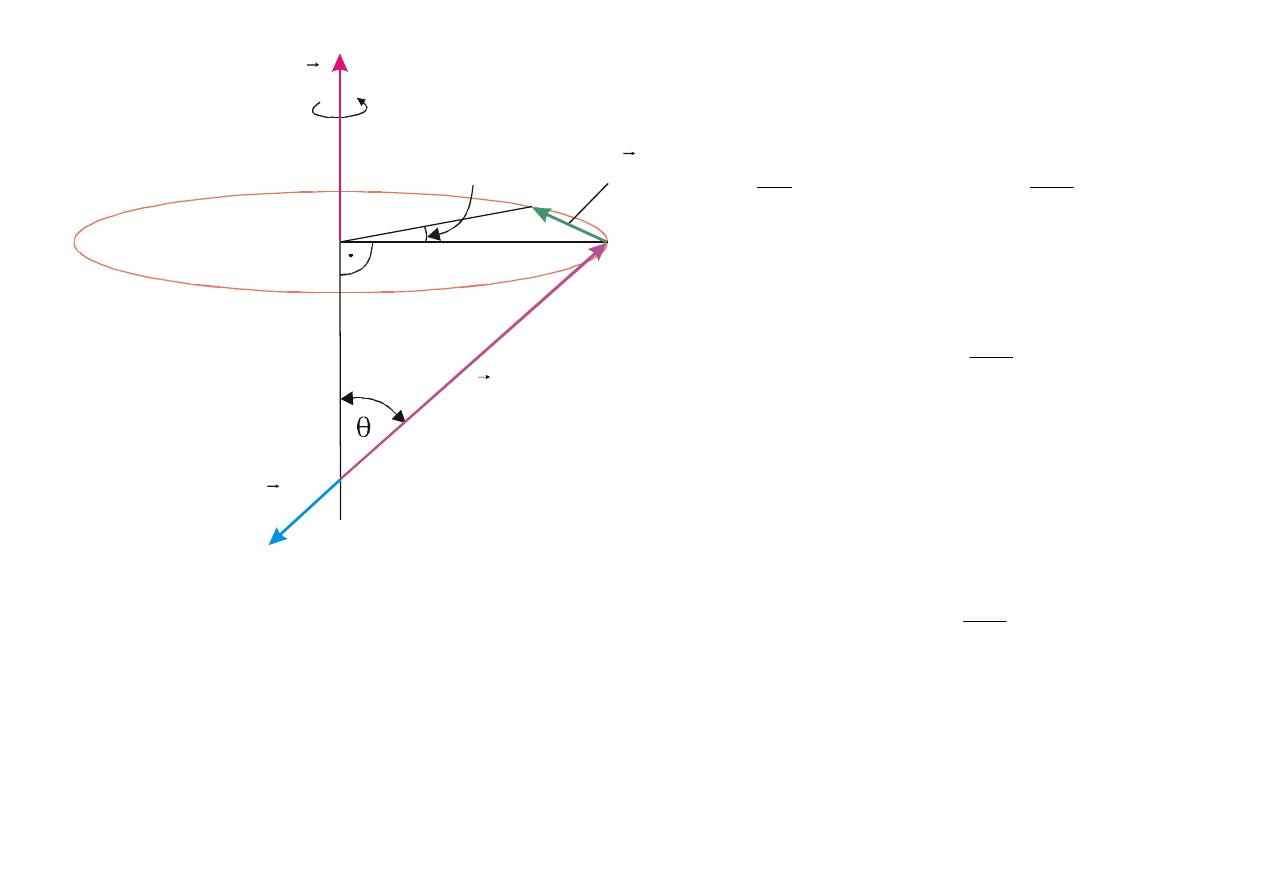
B

μ

L

L

dL

d

ϕ

Rys. 12.7. Oddziaływanie momentu magnetycznego

z zewnętrznym polem magnetycznym.

Z rys. 12.7 widać, że

dt

sin

L

dL

L

θω

=

czyli

θ

θ

ω

sin

LB

m

e

T

sin

L

dt

dL

L

2

=

=

=

Tak więc

m

eB

L

2

=

ω

(12.33)

i nazywana jest

częstością Larmona

.

Energia potencjalna momentu
magnetycznego w polu
magnetycznym [wyrażenie (12.31)]

B

m

Bm

m

e

cos

B

U

l

B

l

l

μ

θ

μ

=

=

−

=

2

h

(12.34)

Oznacza to, że pole magnetyczne będzie zmieniało poziomy energetyczne elektronu.

Ponieważ dla ustalonego n i l istnieje 2l+1 możliwych wartości m

l

, więc pierwotny poziom

energetyczny zostanie rozszczepiony na 2l+1 podpoziomów.

Dla elektronu w atomie wodoru w stanie 2p (l = 1) w polu indukcji B = 1T

⎪

⎪
⎩

⎪⎪

⎨

⎧

−

=

×

−

=

=

×

=

−

−

1

10

27

9

0

0

1

10

27

9

24

24

l

l

l

m

J

,

m

m

J

,

U

Rozszczepienie poziomów energetycznych nie jest duże, ale może być z powodzeniem mierzone
eksperymentalnie. Pojedyncza linia widmowa ulega rozszczepieniu na trzy blisko siebie położone
linie, przy czym odstęp energetyczny między dwoma kolejnymi liniami wynosi

μ

B

B

.

Zjawisko rozszczepienia linii widmowych w zewnętrznym polu magnetycznym nosi nazwę

zjawiska

Zeemana

. Zjawisko to potwierdza skwantowanie orbitalnego momentu pędu w atomie.

Spin elektronu

Spinowy moment pędu i spinowy moment magnetyczny

Linie widmowe składają się z blisko siebie położonych linii nawet bez obecności zewnętrznego

B

r

.

Takie rozszczepienie pojedynczej linii widmowej nazywane jest strukturą subtelną linii widmowych.
Pewnym przypadkiem struktury subtelnej jest zjawisko Zeemana.

Elektron poza orbitalnym momentem pędu ma

własny moment pędu zwany spinowym lub krótko

spinem

:

•

jego istnienie jest jego naturalną (wewnętrzną) właściwością,

• jego istnienie zaproponowali w 1925 roku Goudsmit i Uhlenbeck w celu wyjaśnienia struktury

subtelnej linii widmowych.

Spinowy moment pędu

elektronu

(

)

h

1

+

=

s

s

L

s

(12.35)

gdzie s jest spinową liczbą kwantową równą 1/2.

Spin elektronu

2

3h

=

s

L

jest podstawową właściwością elektronu (podobnie jak masa i ładunek).

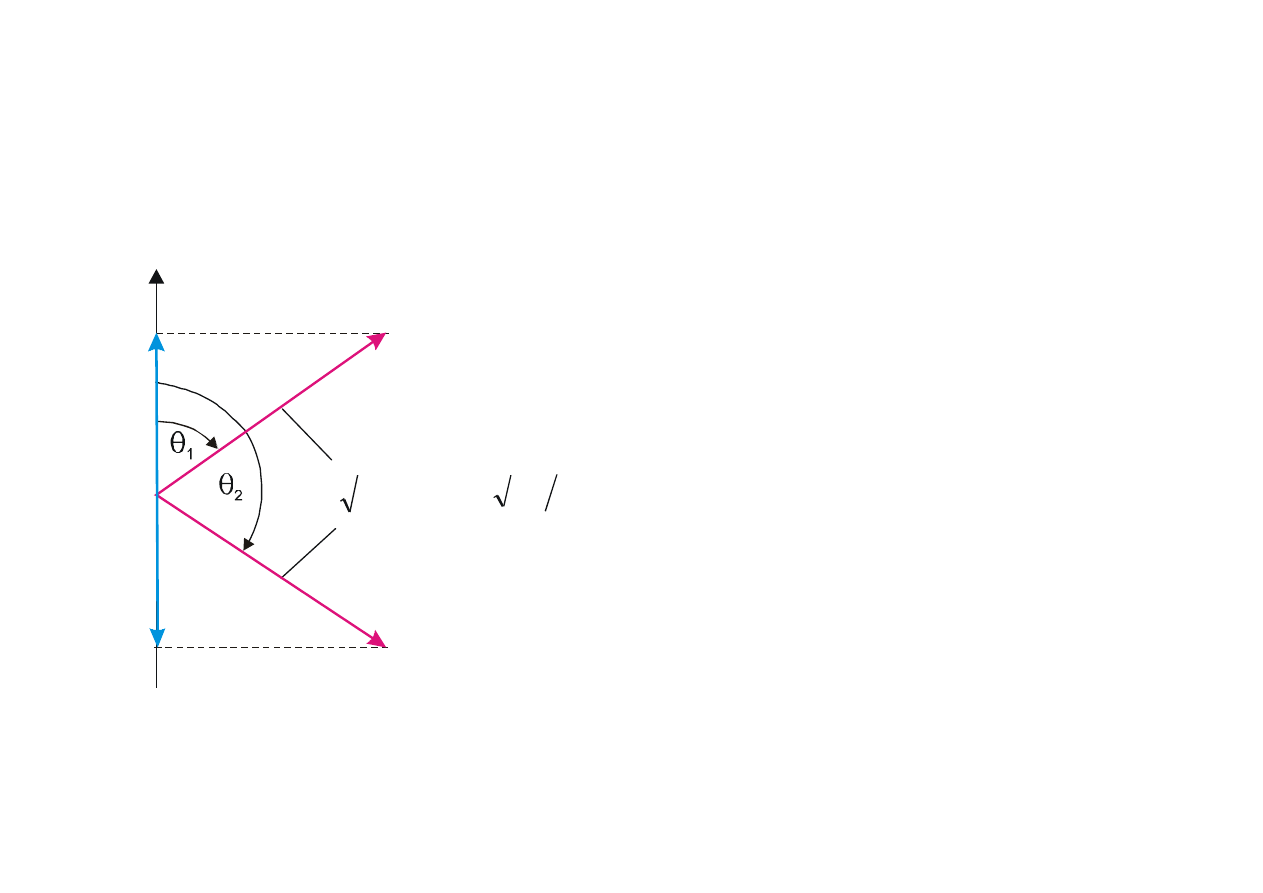
Rzut spinowego momentu pędu na wyróżniony kierunek jest skwantowany

h

s

sz

m

L

=

(12.36)

gdzie m

s

przyjmuje dwie wartości, 1/2 lub –1/2; i nosi nazwę magnetycznej spinowej liczby kwantowej.

(rys. 12.8).

h/2

h/2

−

(

)

2

3

1

s

s

L

s

h

h =

+

=

z

Rys. 12.8. Spinowy moment pędu elektronu

i jego rzut na określony kierunek w przestrzeni.

Liczba kwantowa:
m

s

=

½ spin skierowany w górę, a

m

s

= –1/2 spin skierowany w dół

Możliwe kąty między wektorem L

s

a

wyróżnionym kierunkiem w przestrzeni
wynoszą 54,7

° i 125,3°.

Stan elektronu w atomie będziemy więc
opisywać za pomocą czterech liczb
kwantowych: n, l, m

l

i m

s

.

Liczba niezależnych stanów związanych z główną liczbą kwantową – n

2

.

Po uwzględnieniu spinu całkowita liczba stanów – 2n

2

.

Ze spinowym momentem pędu L

s

związany jest

spinowy moment magnetyczny

μ

s

(

)

1

+

−

=

−

=

s

s

m

e

L

m

e

s

s

h

r

r

μ

(12.37)

Rzut spinowego momentu magnetycznego na wyróżniony kierunek

(

)

B

sz

m

e

cos

s

s

m

e

μ

θ

μ

±

=

±

=

+

−

=

2

1

h

h

(12.38)

może przyjmować dwie, różniące się znakiem wartości, co do modułu równe magnetonowi Bohra.

Anomalią magnetomechaniczna

:

stosunek giromagnetyczny dla momentu spinowego jest

dwukrotnie większy niż dla momentu orbitalnego

.

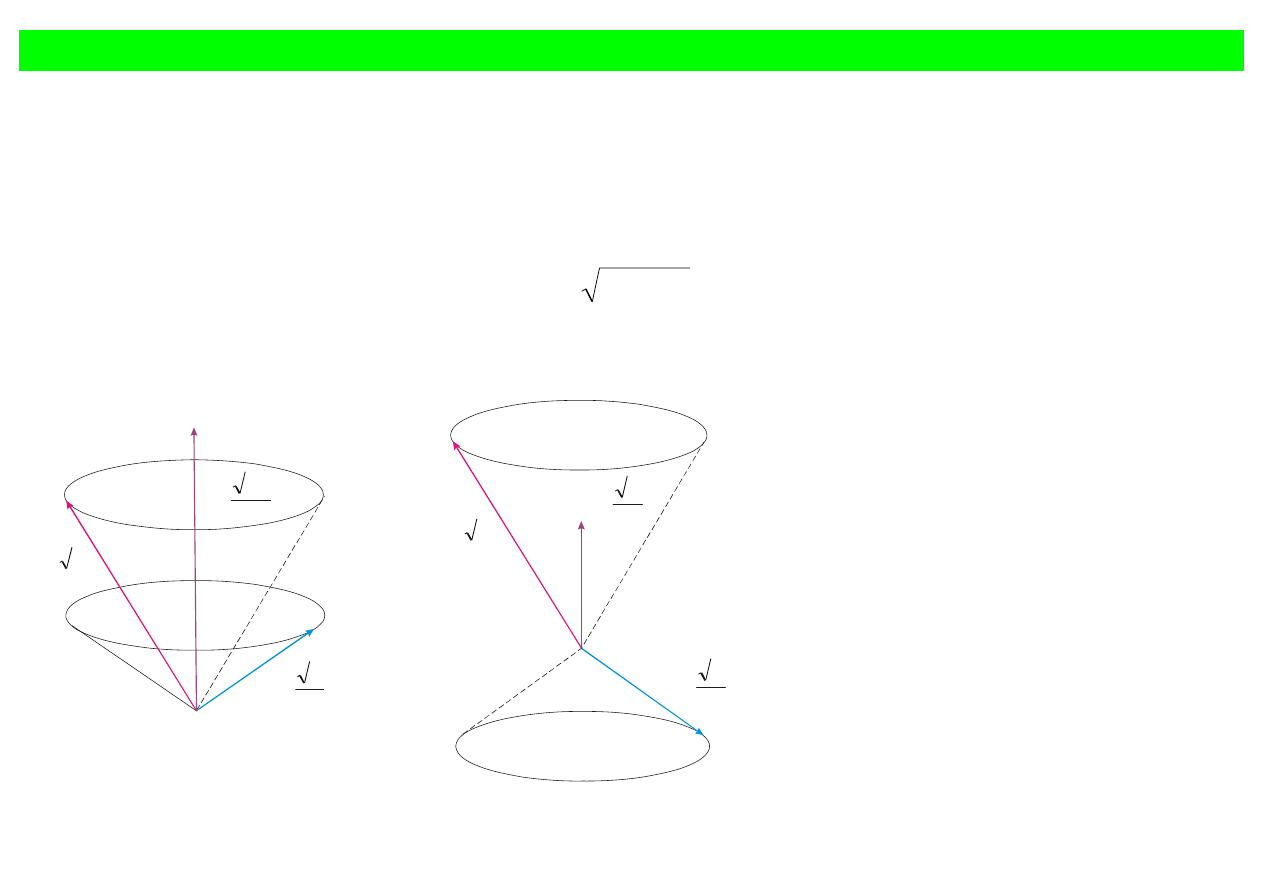
Całkowity moment pędu i całkowity moment magnetyczny

Całkowity moment pędu J

r

równy jest sumie wektorów L

r

i

s

L

r

s

L

L

J

r

r

r

+

=

(12.39)

Okazuje się, że całkowity moment pędu, podobnie jak

L

r

i

s

L

r

, jest skwantowany i wynosi

(

)

h

1

+

=

j

j

J

(12.40)

gdzie j jest liczbą kwantową całkowitego momentu pędu wynoszącą j = l + s lub j = l – s.
Ponieważ s = 1/2, więc j = l – 1/2 lub j = l + 1/2.

h

2

15

J

=

h

2

3

L

s

=

h

2

3

L

s

=

h

2

3

J

=

h

2

L

=

h

2

L

=

Ponieważ wektory L

r

,

s

L

r

i J

r

są

skwantowane, więc istnieją tylko
pewne dozwolone orientacje tych
wektorów względem siebie.

Rys. 12.9. Możliwe rezultaty dodawania orbitalnego i spinowego momentu pędu elektronu

dla l = 1 i s = 1/2.