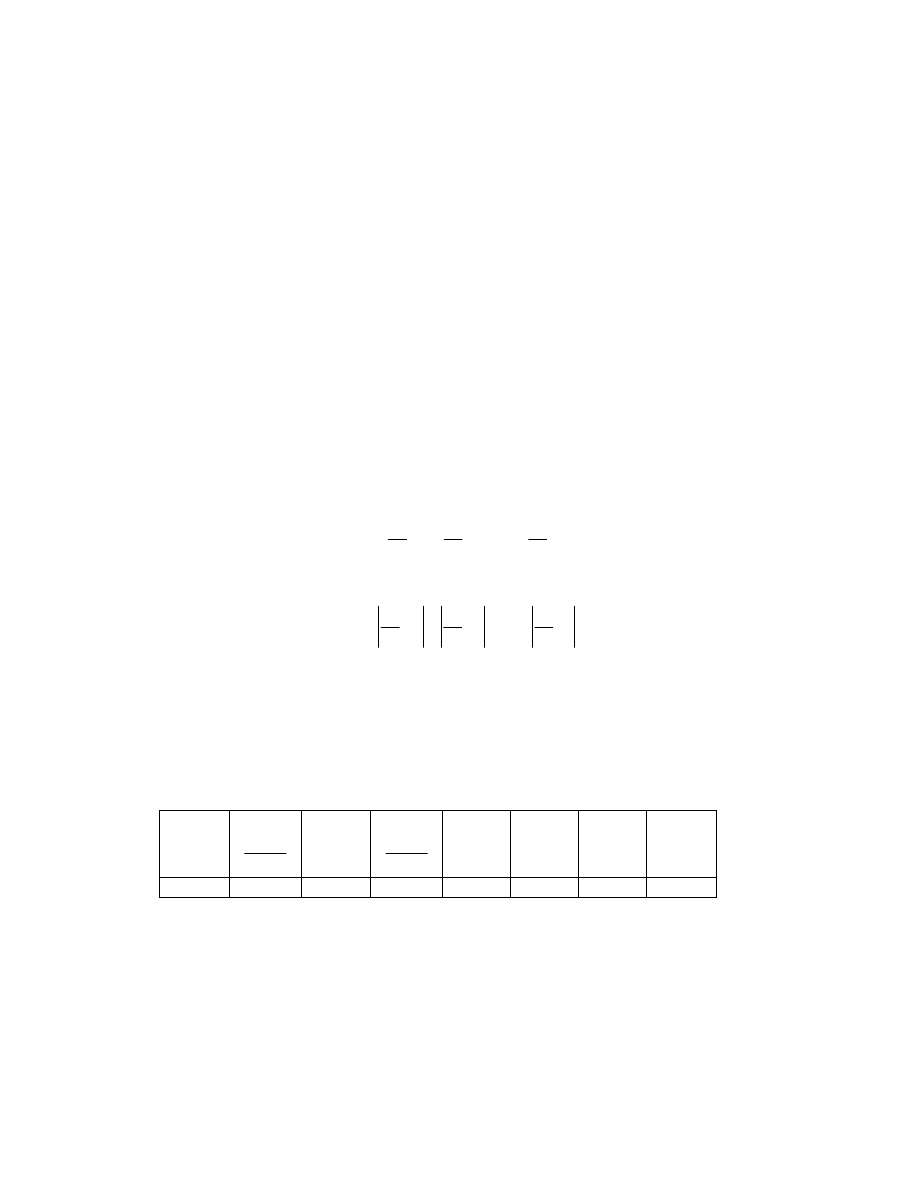
Określenie niepewności maksymalnych wielkości mierzonych pośrednio
Uwaga:
W przykładach zamieszczonych poniżej wszystkie dane są zaczerpnięte ze sprawozdań
studentów, którzy wykonywali dane ćwiczenia we wcześniejszych latach. Nie należy się
sugerować ani wynikami pomiarów, ani uzyskanymi w przykładach wynikami obliczeń.
Przykłady te służą wyłącznie zademonstrowaniu użycia rzeczywistych wyników
eksperymentalnych do opracowania wyników doświadczenia.
W większości pomiarów mamy do czynienia z pomiarem pośrednim, tzn. poszukiwana
wielkość fizyczna jest funkcja jednej lub kilku wielkości mierzonych bezpośrednio
y=f(u,v,...,z). W tym przypadku niepewności wielkości mierzonych bezpośrednio u
∆ , v
∆ , ...,
z
∆ określa się według reguł dla pomiarów bezpośrednich a następnie przy pomocy tych
niepewności oraz zależności funkcyjnej y=f(u,v,...,z) określa się niepewność maksymalną
y
∆ .
Metoda różniczki zupełnej
Metoda ta opiera się na tym, że zmianę wartości funkcji spowodowanej niewielką
zmianą jej zmiennych można przedstawić za pomocą różniczki zupełnej:
dz
z
f
dv
v
f
du
u
f
dy
∂
∂
+
+
∂
∂
+
∂
∂
=
K
Jeżeli różniczki du, dv, ..., dz zastąpimy niepewnościami pomiarowymi u
∆ , v
∆ , ..., z
∆ to tak
obliczona wielkość wyrazi maksymalną niepewność y
∆ wielkości y:
z
z
f
v
v
f
u
u
f
y
∆
∂
∂
+
+
∆
∂
∂
+
∆
∂
∂
=
∆
K
Wzięto wartości bezwzględne po to, by otrzymana w ten sposób niepewność była
rzeczywiście niepewnością maksymalną.
PRZYKŁAD 1:
Wyznaczanie ciepła topnienia lodu przy pomocy kalorymetru (ćwiczenie C1):
Przypuśćmy, że wykonując ćwiczenie C1 student otrzymał następujące wyniki:
m
k
[kg]
c
k
[
K
kg
J
⋅
]
m
w
[kg]
c
w
[
K
kg
J
⋅
]
T
0
[K]
T
1
[K]
T
2
[K]
m
l
[kg]
0.0927
896
0.141
4190
273
291
288
0.0045
Czcionką wytłuszczoną zaznaczono wielkości mierzone bezpośrednio.
Niepewności pomiarowe:
∆m
k
=10
-4
kg
∆m
w
=
∆m
l
=2
⋅10
-4
kg
∆T
1
=
∆T
2
=1 K
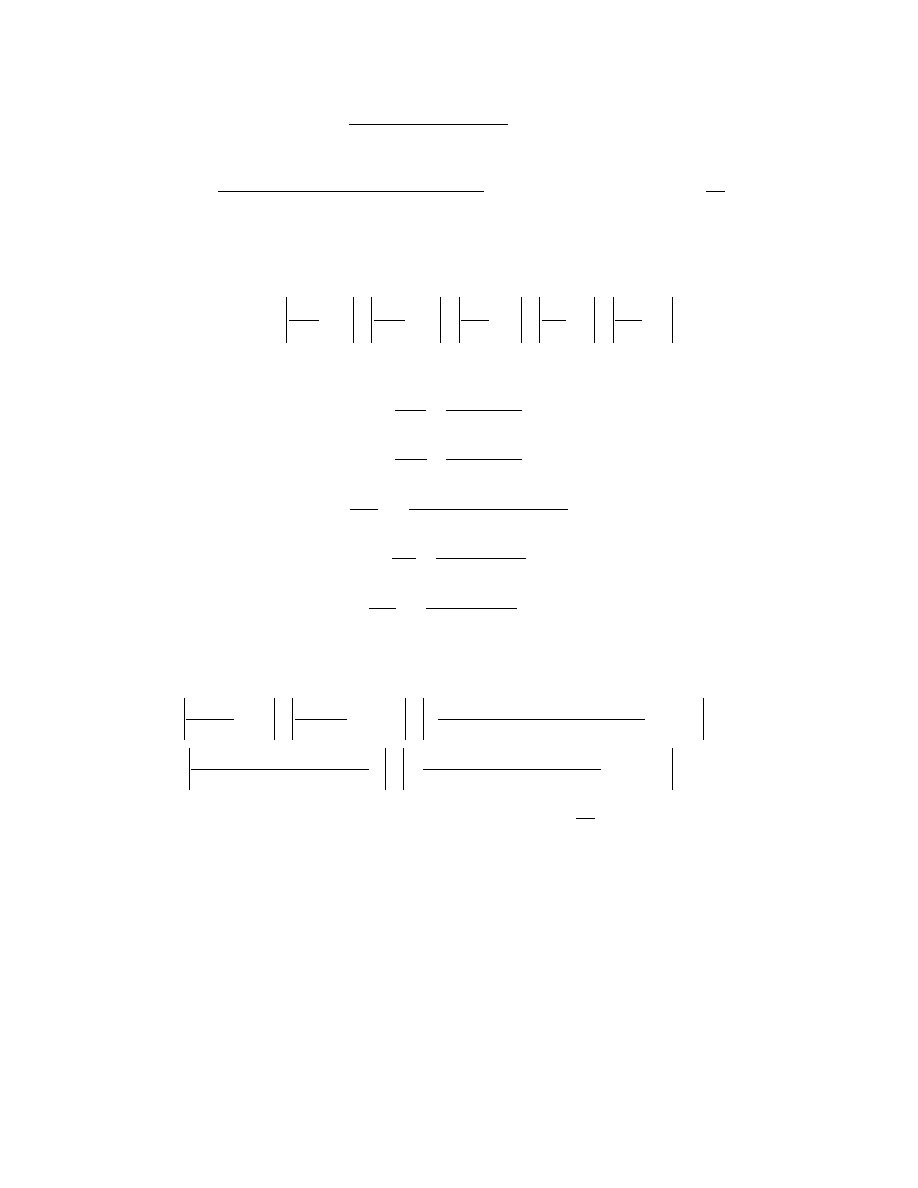
Ciepło topnienia lodu obliczamy korzystając ze wzoru:
)
(
)
)(
(
0
2
2
1
T
T
c
m
T
T
c
m
c
m
c
w
l
w
w
k
k
l
−
−
−
+
=
Podstawiając dane z tabeli otrzymujemy:
]
[
386383
)
273
288
(
4190
0045
.
0
)
288
291
)(
4190
141
.
0
896
0927
.
0
(
kg
J
c
l
=
−
⋅
−
−
⋅
+
⋅
=
Określamy niepewność pomiaru metodą różniczki zupełnej:
2
2
1
1
T
T
c
T
T
c
m
m
c
m
m
c
m
m
c
c
l
l
l
l
l
w
w
l
k
k
l
l
∆
∂
∂
+
∆
∂
∂
+
∆
∂
∂
+
∆
∂
∂
+
∆
∂
∂
=
∆
Obliczamy różniczki cząstkowe:
l
k
k
l
m
T
T
c
m
c
)
(
2
1
−
=
∂
∂
l
w
w
l
m
T
T
c
m
c
)
(
2
1
−
=
∂
∂
2
2
1
)
)(
(
l
k
k
w
w
l
l
m
T
T
c
m
c
m
m
c
−
+
−
=
∂
∂
l
w
w
k
k
l
m
c
m
c
m
T
c
+
=
∂
∂
1
w
l
w
w
k
k
l
c
m
c
m
c
m
T
c
−
+
−
=
∂
∂
2
Biorąc pod uwagę powyższe zależności oraz wartości niepewności pomiarowych
∆m
k
,
∆m
w
,
∆m
l
,
∆T
1
,
∆T
2
obliczamy
∆c
l
.
kg
J
c
l
324263
3
.
153934
3
.
149744
9
.
19965
7
.
558
7
.
59
1
)
4190
0045
.
0
4190
141
.
0
896
0927
.
0
(
1
0045
.
0
4190
141
.
0
896
0927
.
0
10
2
0045
.
0
3
)
896
0927
.
0
141
.
0
4190
(
10
2
0045
.
0
3
4190
10
0045
.
0
3
896
4
2
4
4
=
+
+
+
+
=
=
⋅
−
⋅
+
⋅
−
+
⋅
⋅
+
⋅
+
+
⋅
⋅
⋅
⋅
+
⋅
−
+
⋅
⋅
⋅
+
⋅
⋅
=
∆
−
−
−
UWAGA!
Jest to przykład, w którym oszacowana niepewność pomiaru jest prównywalna z uzyskaną w
doświadczeniu wartością c
l
. W sprawozdaniu należałoby więc przeprowadzić wnikliwą
dyskusję otrzymanych wyników ze wskazaniem źródeł popełnionych błędów.
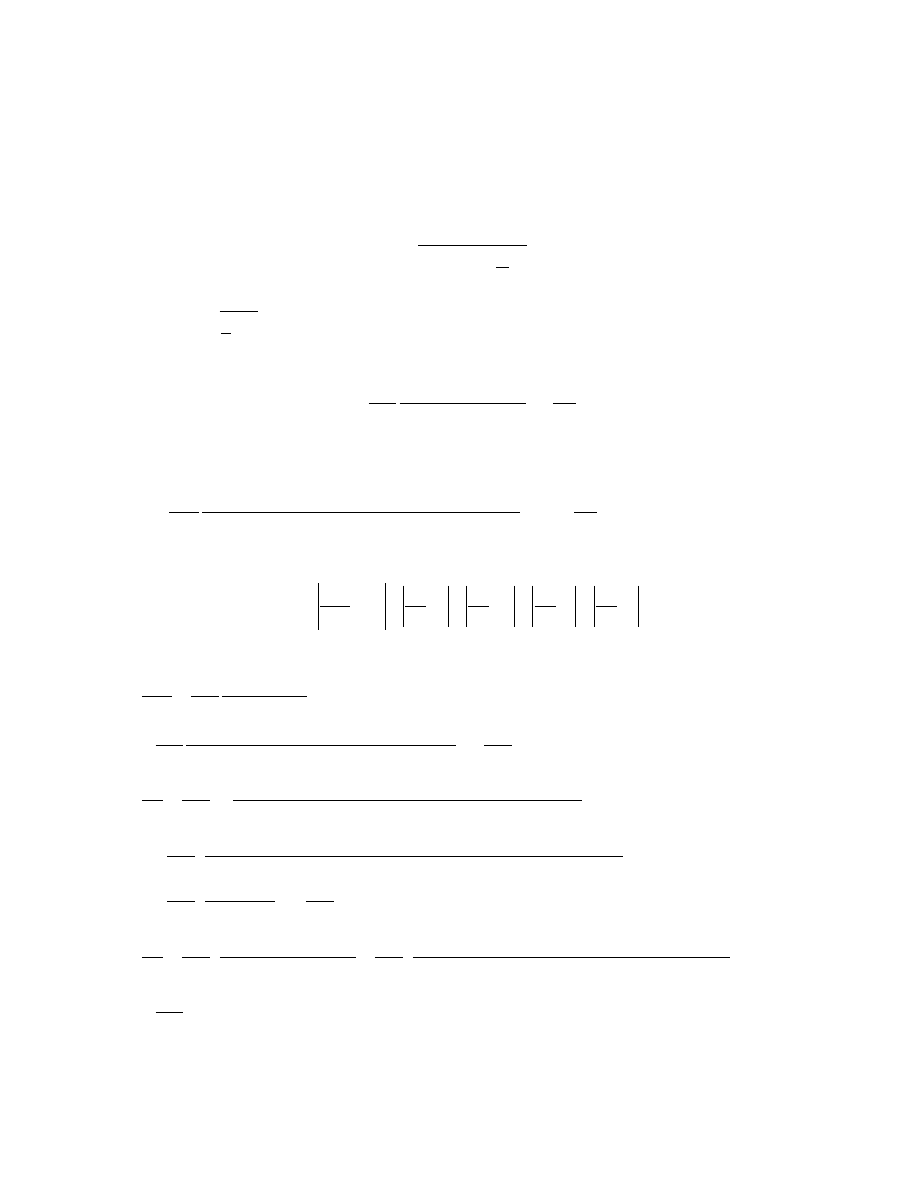
PRZYKŁAD 2:
Wyznaczanie współczynnika lepkości metodą Stokesa (ćwiczenie M6).
Wielkościami mierzonymi bezpośrednio w ćwiczeniu M6 są: r, s, t i m (masa kulki).
Współczynnik lepkości obliczamy ze wzoru:
)
4
.
2
1
(
9
)
(
2
2
R
r
s
t
g
r
p
k
+
−
=
ρ
ρ
η
gdzie
3
3
4
r
m
k
k
π
ρ =
Po podstawieniu i przekształceniach otrzymamy:
)
4
.
2
(
)
4
3
(
18
3
r
R
sr
t
r
m
R
g
p
k
+
−
=
ρ
π
π
η
2
m
Ns
Zakładając, że otrzymano następujące wyniki (średnie wartości z kilku pomiarów):
m
k
=0.341 g, R=0.042 m, s=28 cm, r=4.11
⋅10
-3
m, t=5.43 s otrzymamy wartość współczynnika
lepkości dla parafiny (zakładamy, że gęstość parafiny wynosi 800 kg/m
3
):
2
3
3
3
3
3
20
.
1
)
10
11
.
4
4
.
2
042
.
0
(
10
11
.
4
28
.
0
43
.
5
)
800
)
10
11
.
4
(
4
10
341
.
0
3
(
042
.
0
18
81
.
9
m
Ns
=
⋅
⋅
+
⋅
⋅
⋅
−
⋅
⋅
=
−
−
−
−
π
π
η
Obliczamy niepewność
η
∆
:
s
s
t
t
R
R
r
r
m
m
k
k
∆
∂
∂
+
∆
∂
∂
+
∆
∂
∂
+
∆
∂
∂
+
∆
∂
∂
=
∆
η
η
η
η
η
η
Obliczamy kolejne różniczki cząstkowe:
kg
10
21
.
11455
18
)
10
11
.
4
4
.
2
042
.
0
(
10
11
.
4
28
.
0
43
.
5
042
.
0
3
18
)
4
.
2
(
3
18
6
3
3
−
−
−
=
∆
⋅
==
⋅
⋅
+
⋅
⋅
⋅
⋅
=
=
+
=
∂
∂
k
k
m
g
g
r
R
sr
Rt
g
m
π
π
π
η
m
10
07
.
132804
18
10
57
.
4
060
.
0
18
052
.
0
10
69
.
1
)
062
.
0
10
7206
.
1
052
.
0
800
10
69
.
1
12
(
43
.
5
042
.
0
18
)
4
.
2
(
))
8
.
4
)(
4
3
(
)
4
.
2
(
12
(
18
5
8
2
5
3
5
2
2
3
2
−
−
−
−
−
=
∆
⋅
−
=
⋅
⋅
−
=
=
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
⋅
−
=
=
+
+
−
+
+
−
=
∂
∂
r
g
g
g
r
R
r
r
R
r
m
r
R
r
Rt
g
r
p
k
p
π
π
π
π
ρ
π
ρ
π
π
η
m
10
576
.
5
18
)
10
11
.
4
4
.
2
042
.
0
(
28
.
0
43
.
5
4
.
2
)
800
)
10
11
.
4
(
4
10
341
.
0
3
(
18
)
4
.
2
(
4
.
2
)
4
3
(
18
3
2
3
3
3
3
2
3
−
−
−
−
=
∆
⋅
=
=
⋅
⋅
+
⋅
⋅
⋅
−
⋅
⋅
⋅
=
+
−
⋅
=
∂
∂
R
g
g
r
R
s
t
r
m
g
R
p
k
π
π
π
ρ
π
π
η

s
2
.
0
231
.
0
18
)
10
11
.
4
4
.
2
042
.
0
(
10
11
.
4
28
.
0
)
800
)
10
11
.
4
(
4
10
341
.
0
3
(
042
.
0
18
)
4
.
2
(
)
4
3
(
18
3
3
3
3
3
3
=
∆
⋅
=
=
⋅
⋅
+
⋅
⋅
⋅
−
⋅
⋅
=
+
−
=
∂
∂
−
−
−
−
t
g
g
r
R
sr
r
m
R
g
t
p
k
π
π
π
ρ
π
π
η
m
10
10
355
.
3
18
)
10
11
.
4
4
.
2
042
.
0
(
28
.
0
43
.
5
)
800
)
10
11
.
4
(
4
10
341
.
0
3
(
042
.
0
18
)
4
.
2
(
)
4
3
(
18
3
3
3
2
3
3
3
2
3
−
−
−
−
−
=
∆
⋅
⋅
−
=
=
⋅
⋅
+
⋅
⋅
−
⋅
⋅
−
=
+
−
⋅
−
=
∂
∂
s
g
g
r
R
s
t
r
m
R
g
s
p
k
π
π
π
ρ
π
π
η
Ostatecznie:
(
)
2
3
3
5
6
24
.
0
10
018
.
0
2
.
0
231
.
0
10
576
.
5
10
07
.
132804
10
21
.
11455
18
81
.
9
m
Ns
=
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
∆
−
−
−
−
π
η
Zatem:
2
)
24
.
0
20
.
1
(
m
Ns
±
=
η
Wyszukiwarka
Podobne podstrony:
Ćwiczenie C1 doc
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
cwiczenia 9 kryzys
Ćwiczenia 1, cz 1
Ćwiczenie 8
9 ćwiczenie 2014
więcej podobnych podstron