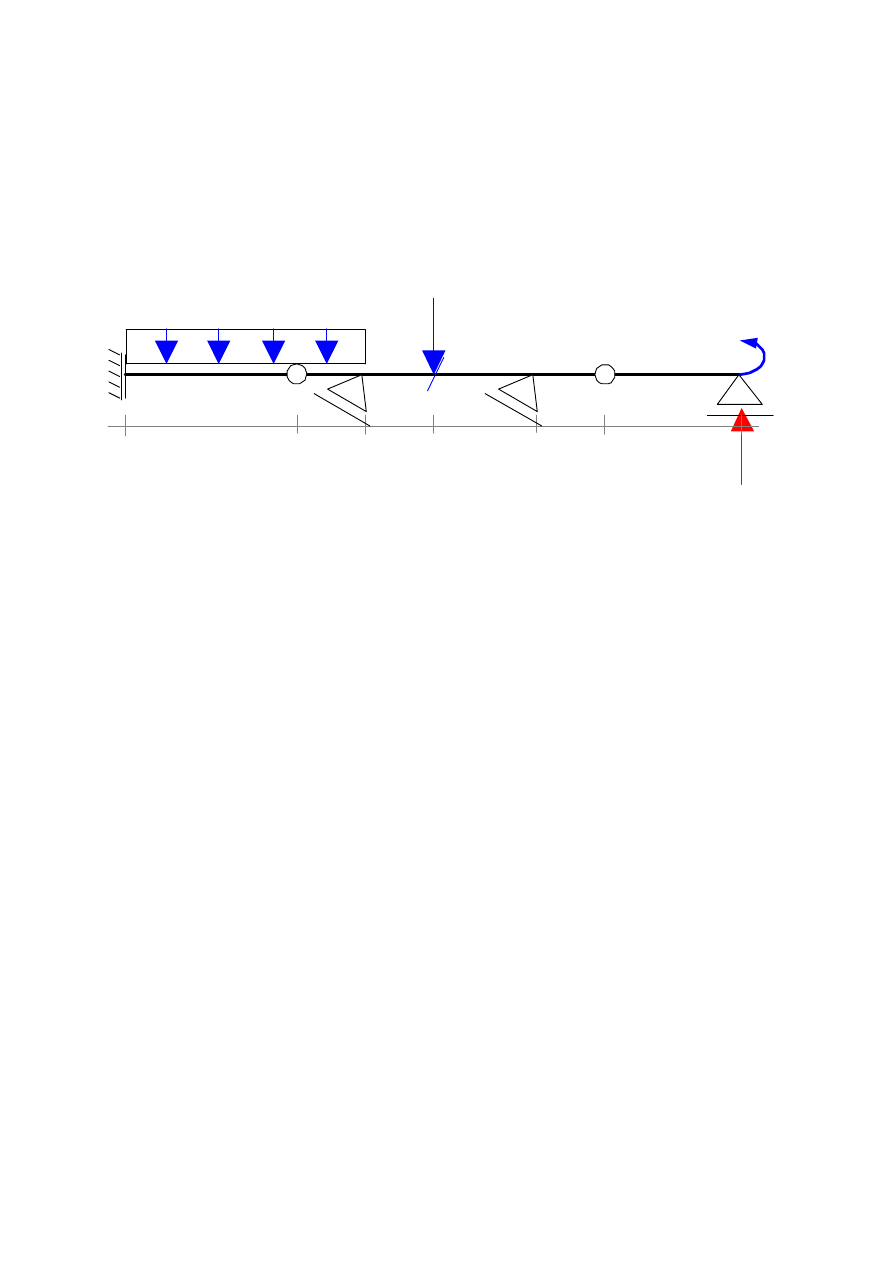
1
TEMAT ZADANIA:
Belke wieloprzeslowa przegubowa rozwiazac analitycznie.
Wyznaczyc reakcje i sporzadzic wykresy sil przekrojowych.
Metoda kinematyczna wyznaczyc wielkosci R, M
∝
, T
∝
.
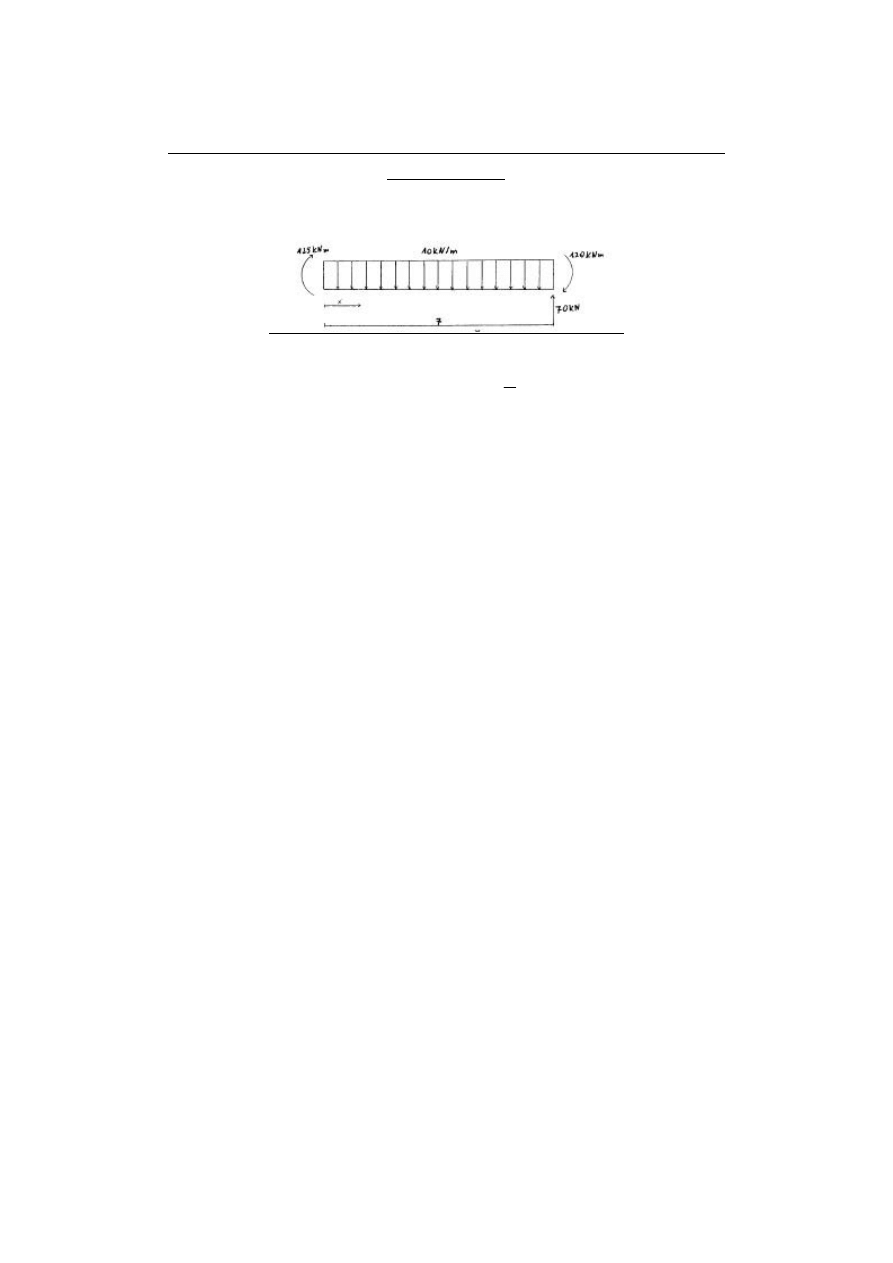
4m
5m
3m
2m
2m
2m
R
10kN/m
60kNm
α−α
45
o
45
o
30kN
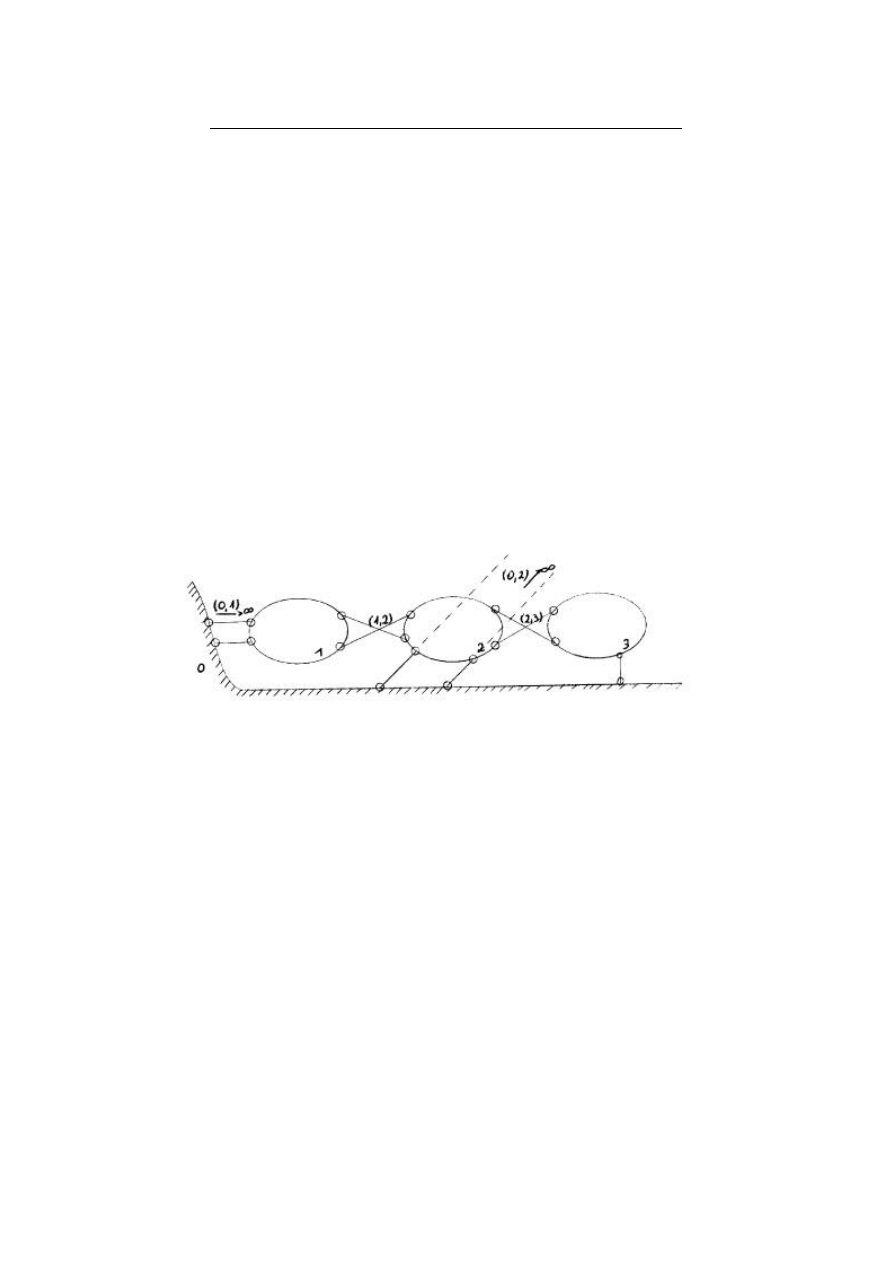
2
Statyczna wyznaczalnosc i niezmiennosc ukladu
Warunek ilosciowy geometrycznej niezmiennosci:
t
e
3
=
gdzie:
e
-liczba wiezi elementarnych
t -liczba tarcz
3
3
9
⋅
=
Wniosek:
Warunek ilosciowy spelniony
Warunek jakosciowy niezmiennosc ukladu:
Najpierw rozpatrze tarcze 0, 1 i 2. Skorzystam z twierdzenia o trzech tarczach. Jak
widac srodki obrotu tarcz (0,1), (2,1) oraz (0,2) nie leza na jednej prostej wiec ta
czesc ukladu jest geometrycznie niezmienna. Teraz tarcze 0,1,2 traktuje jako
ostoje polaczona z tarcza nr 3. Teraz wykorzystam twierdzenie o dwóch tarczach.
Tarcza 3 jest polaczona z ostoja za pomoca 1 wiezi i przegubu (kierunek wiezi nie
przechodzi przez przegub), a wiec ta czesc ukladu takze jest geometrycznie
niezmienna.
Wniosek:
Warunek jakosciowy jest spelniony
UKLAD JEST STATYCZNIE WYZNACZALNY!!!
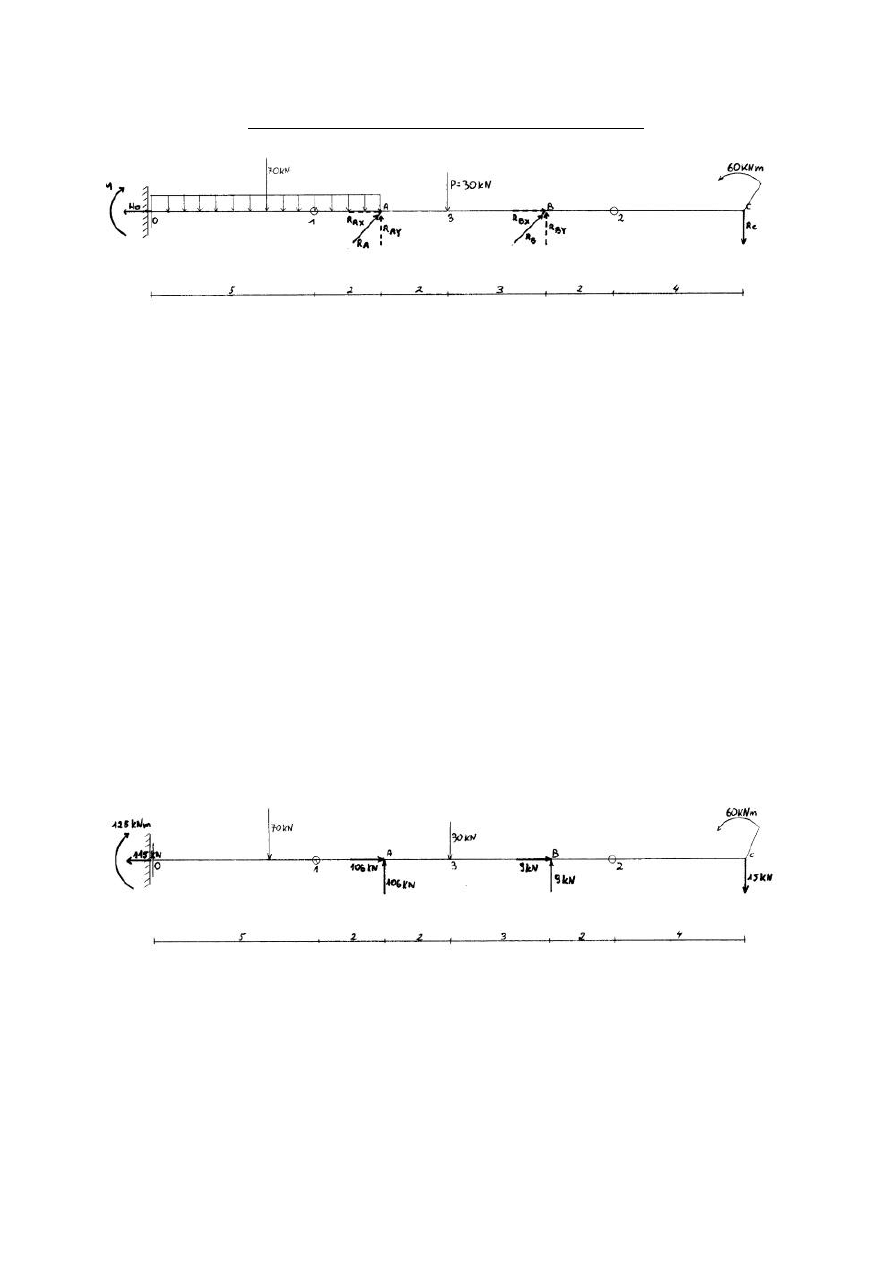
3
Rozwiazanie belki metoda bezposrednia:
Obliczenia pomocnicze:
BY
BX
AY
AX
R
R
tg
R
R
tg
=
⇒
=
=
⇒
=
1
1
β
α
Wyznaczenie reakcji:
∑
∑
∑
∑
∑
=
=
=
=
=
0
0
0
0
)
(
0
)
(
1
1
2
M
Y
X
lewy
M
prawy
M
=
=
=
=
=
=
=
⇒
⋅
+
−
⋅
−
⋅
+
⋅
−
⋅
+
⋅
⋅
−
=
−
−
+
+
=
+
+
−
=
+
⋅
⋅
−
=
+
−
kN
R
R
kN
R
R
kN
H
kNm
M
kN
R
R
R
R
M
R
R
R
R
R
H
M
R
BY
BX
AY
AX
O
C
C
BY
AY
BY
AY
C
BX
AX
O
C
9
106
115
125
15
13
60
7
4
30
2
2
10
5
,
2
5
10
0
30
70
0
0
5
,
2
5
10
0
4
60
Sprawdzenie:
0
125
5
,
5
70
2
106
3
9
9
15
60
?
0
3
=
+
⋅
−
⋅
+
⋅
−
⋅
+
−
=
∑
M
Wniosek:
Obliczenia sa dobre!!!

4
WYZNACZENIE SIL PRZEKROJOWYCH
Momenty:
kNm
M
kNm
M
x
x
x
M
x
kNm
M
kNm
M
x
x
x
x
M
x
kNm
M
kNm
M
x
x
x
M
x
kNm
M
kNm
M
x
x
M
x
120
)
7
(
;
125
)
0
(
2
10
125
)
(
)
7
,
0
(
120
)
11
(
;
48
)
9
(
)
9
(
30
)
6
(
9
15
60
)
(
)
11
,
9
(
48
)
9
(
;
30
)
6
(
)
6
(
9
15
60
)
(
)
9
,
6
(
30
)
6
(
;
60
)
0
(
15
60
)
(
)
6
,
0
(
4
4
3
4
3
3
3
3
3
2
2
2
2
1
1
1
−
=
=
−
=
∈
−
=
−
=
−
−
−
+
−
=
∈
−
=
−
=
−
+
−
=
∈
−
=
=
−
=
∈
Sily tnace:
kN
T
T
x
x
T
x
kN
x
T
x
kN
x
T
x
kN
x
T
x
70
)
7
(
;
0
)
0
(
10
)
(
)
7
,
0
(
36
30
9
15
)
(
)
11
,
9
(
6
9
15
)
(
)
9
,
6
(
15
)
(
)
6
,
0
(
4
4
3
3
2
2
1
1
−
=
=
−
=
∈
=
+
−
=
∈
=
−
=
∈
=
∈
Sily osiowe:
kN
x
N
x
kN
x
N
x
x
N
x
115
106
9
)
(
)
18
,
11
(
9
)
(
)
11
,
6
(
0
)
(
)
6
,
0
(
3
3
2
2
1
1
=
+
=
∈
=
∈
=
∈
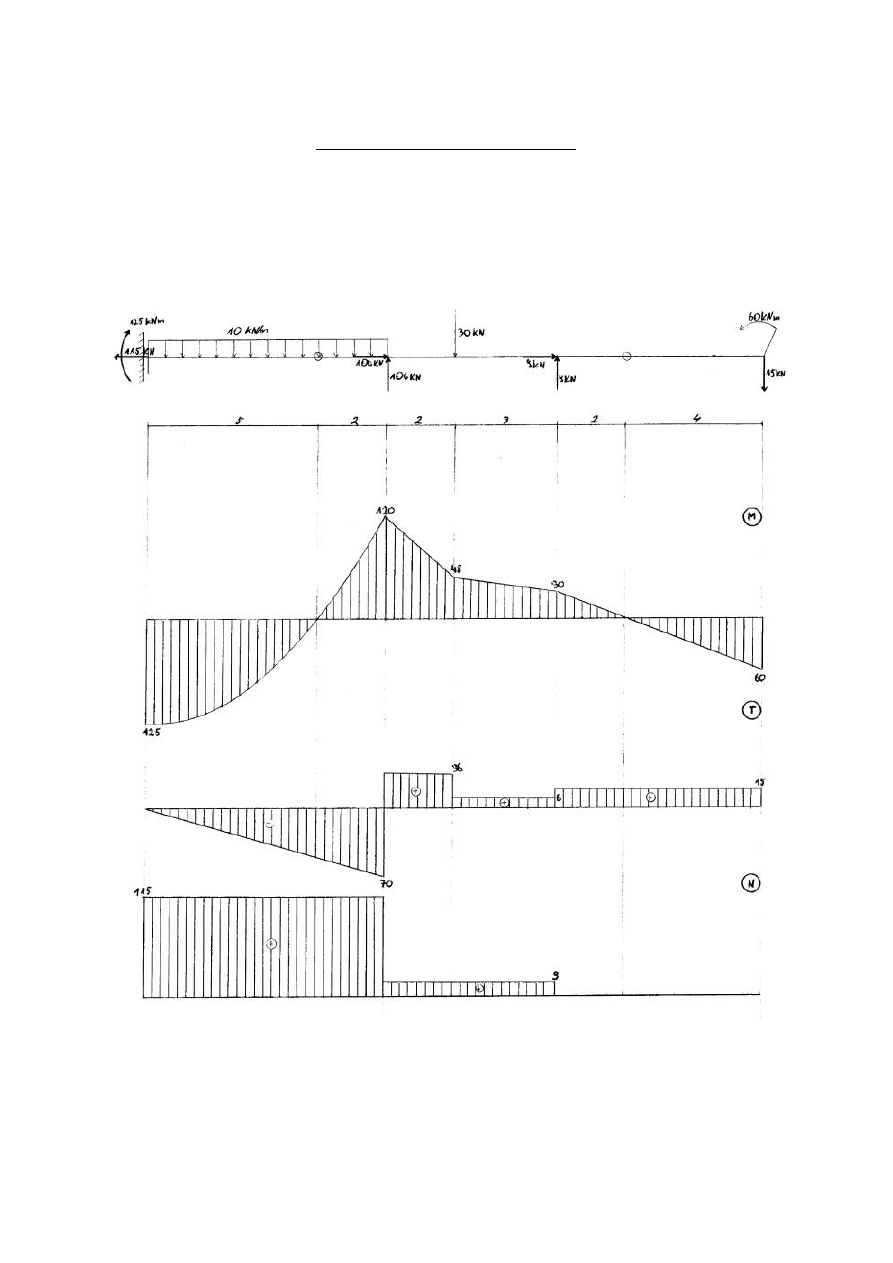
5
Wykresy sil przekrojowych
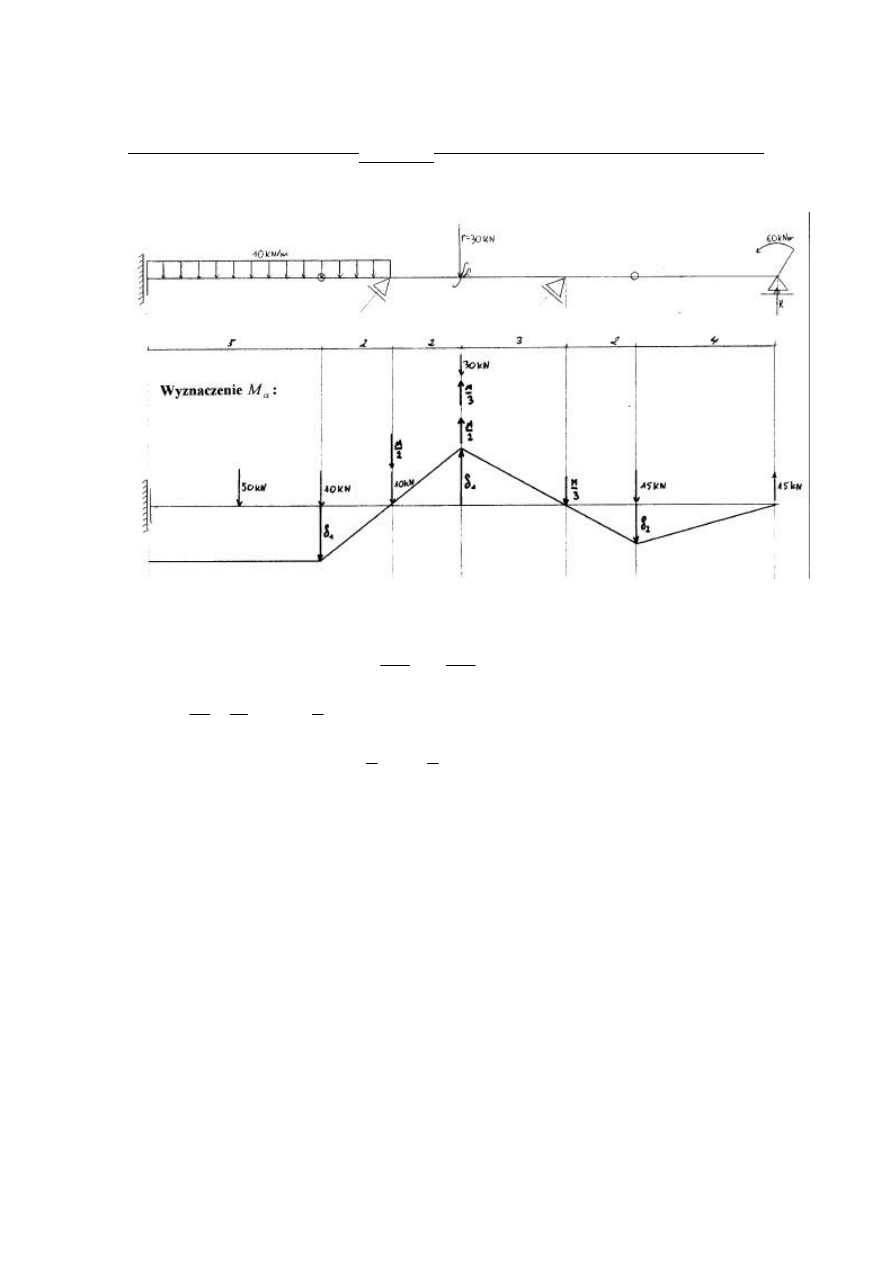
Schemat obliczeniowy
6
Analiza momentu w przedziale O-A za pomoca przedzialu
funkcyjnego
5
125
5
2
10
125
)
(
2
/
1
2
±
=
=
−
=
x
x
x
x
x
M
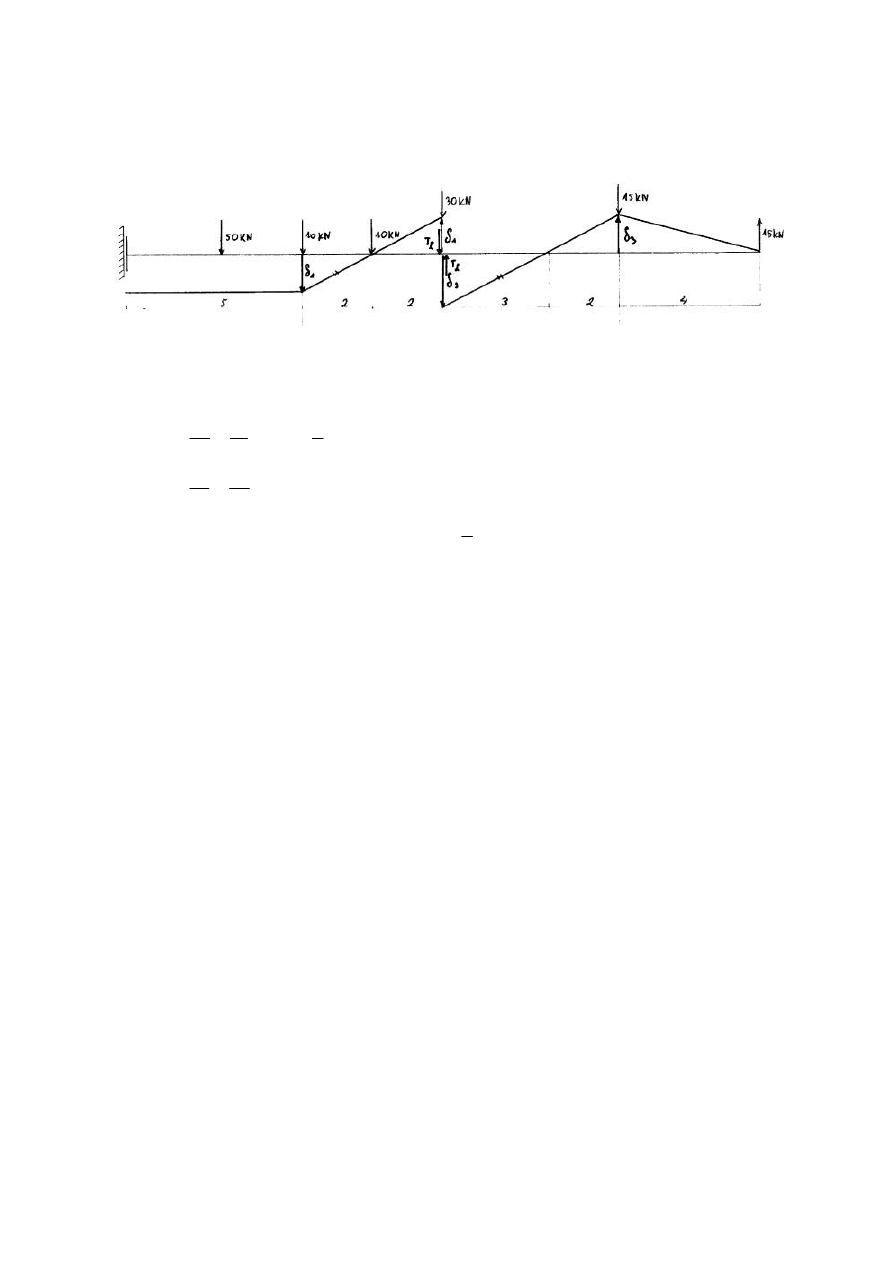
7
Wyznaczenie wielkosci
α
α
T
M
R
,
,
za pomoca metody kinematycznej
kNm
M
M
M
M
dw
48
6
5
3
2
15
30
10
50
3
2
3
2
0
15
3
2
30
10
50
1
1
1
1
1
2
1
2
2
1
1
1
1
1
−
=
⇒
−
=
⋅
+
−
+
=
⇒
=
=
+
+
+
−
+
=
α
α
α
α
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
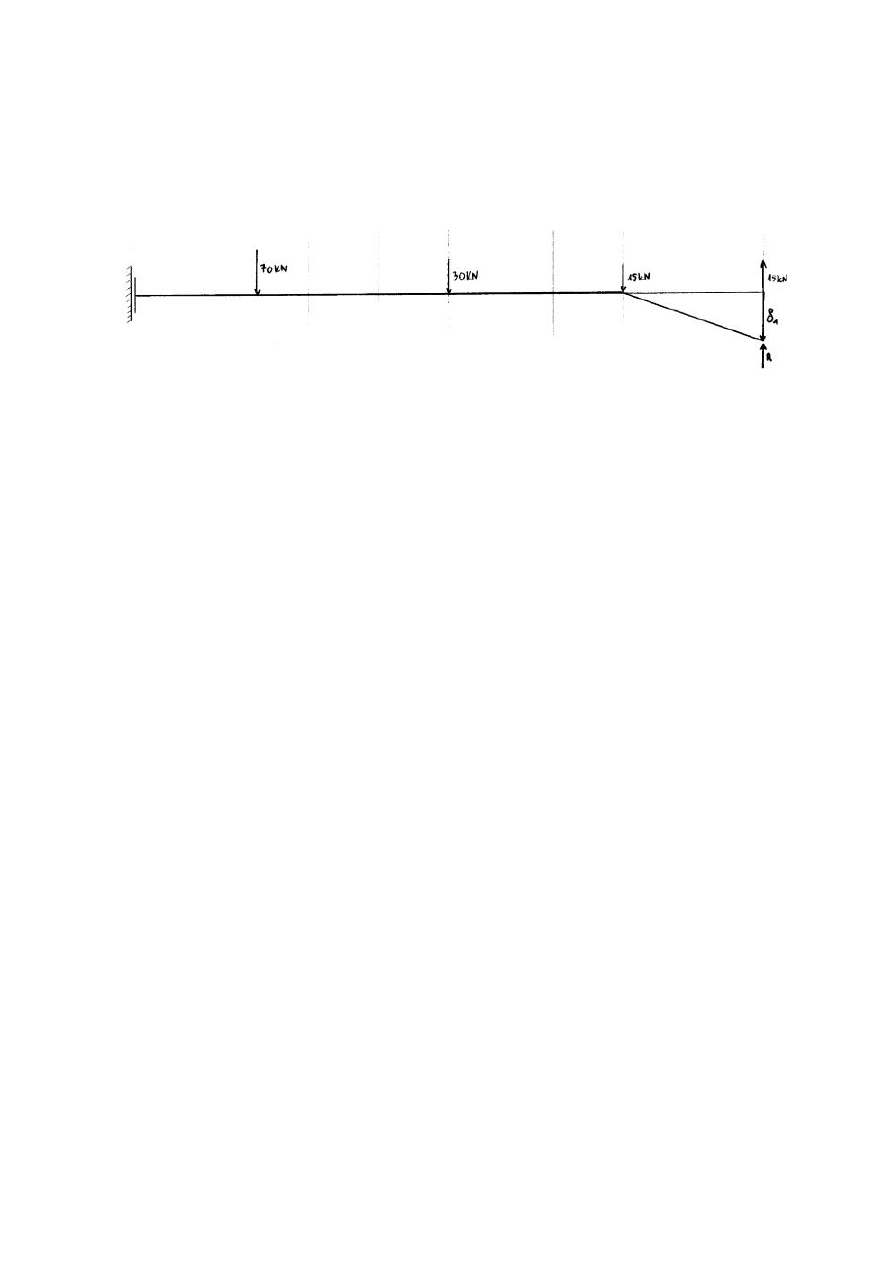
8
Wyznaczenie
α
T :
kN
T
T
T
T
T
dw
6
2
3
15
30
10
50
3
2
2
3
2
3
0
15
30
10
50
1
1
1
1
1
1
2
3
2
3
1
2
1
2
3
2
1
1
1
1
=
⇒
+
=
−
−
+
=
⇒
=
=
⇒
=
=
−
−
−
−
+
=
α
α
α
α
α
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
9
Wyznaczenie
R :
kN
R
R
dw
15
0
15
1
1
−
=
⇒
=
−
−
=
δ
δ
Wyszukiwarka
Podobne podstrony:
Belka wieloprzęsłowa II
Belka wieloprzęsłowa
belka stropowa wieloprzesłowa
belka stropowa wieloprzesłowa
Hala CECHOWANIE BELKA SPRĘŻONA ok
belka spr podl
kratownica belka 57
W08s-Slabe kwasy i zasady wieloprotonowe, chemia, szkolka
Wyrazy mieszkają w wielopiętrowym domu
Belka MS id 82485 Nieznany (2)
K zesp belka cz 2
więcej podobnych podstron