Politechnika Wrocławska

Wydział Elektryczny

Wojciech Calów

Rok studiów : III
Semestr : VI
Rok akad. : 2012/13

 Laboratorium Metod Numerycznych

Data: 

Temat : 

Metoda eliminacji Gaussa 

rozwiązywania układów równań 

liniowych.

Ocena: 

1. Program

% 1 Program do rozwiązywania układów liniowych wykorzystujący 
procedurę

clc; clear 

all

; close 

all

;

A=[5 -2 1 -1;1 6 -2 3;1 -3 4 -2;2 1 -5 4];

% podanie macierzy równan

b=[4; 3; 12; 10];       

% podanie wektora prawej strony

x=gauss(A,b)            

% obliczanie równań

blad=A*x-b              

% blad obliczen 

% 2 Obliczanie wyznacznika macierzy korzystaj¹c z macierzy 

trójkatnej otrzymanej po pierwszym etapie procedury eliminacji 
Gaussa.

%% Wyznaczanie wyznacznika 

clc; clear 

all

; close 

all

;

A=[5 -2 1 -1;1 6 -2 3;1 -3 4 -2;2 1 -5 4]; 

% wspolczynniki

n=size(A,1);        

% rozmiar

%% Macierz trojkatna 

for

 i=2:n,                      

 

for

 k=i:n,                                     

  p=A(k,i-1)/A(i-1,i-1);        

  

for

 l=1:n,                    

   

if

 l<i,

     A(k,l)=0;
   

else

     A(k,l)=A(k,l)-A(i-1,l)*p;
   

end

;

  

end

;    

 

end

;

end

;

disp(

'Macierz trojkatna'

); disp(A);

%% Wyznacznik

wyznA=1;

for

 i=1:n

    wyznA=A(i,i)*wyznA; 

%obliczanie wyznacznika

end

;                 

disp(

'Nasz obliczony wyznacznik'

);

disp(wyznA);        

% wyœwietlenie wartoœci wyznacznika

blad=det(A)-wyznA;  

% sprawdzenie poprawnoœci wyniku

disp(

'Blad wyznacznika'

);

disp(blad);

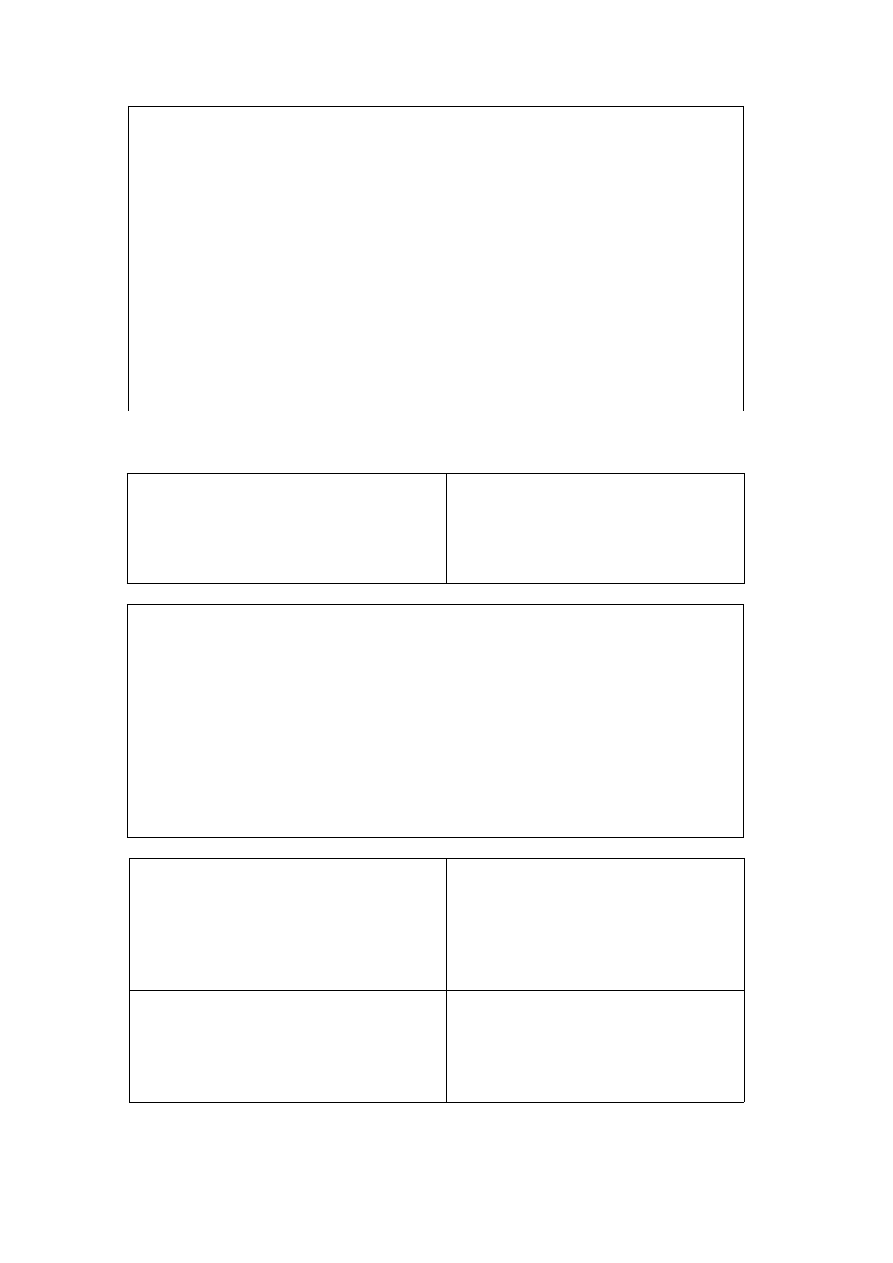
% 3 Macierz odwrotna

% niezbędny plik gauss.m w tym folderze

clc; clear 

all; 

close 

all

A=[5 -2 1 -1; 1 6 -2 3 ; 1 -3 4 -2 ; 2 1 -5 4 ];
b=[4; 3; 12; 10];

% liczenie odwrotna

n=size(A);

% Rozmiar macierzy

j=eye(n); 

%macierz jedynkowa

 

for

 i=1:1:n,

    odwrotnaA(:,i)= gauss(A,j(:,i));

% obliczanie macierzy odwrotnej 

end

;

z=inv(A)                  

% odwrotna policzona przez matlaba

odwrotnaA                 

% nasza macierz obliczona

blad_invA=z-odwrotnaA     

% sprawdzenie wyniku - blad

2. Wyniki

Ad1 

x =
    0.5663

   -2.7831
    5.9398

   10.3373

bl = 1.0e-014 *
         0

    0.3553
   -0.3553

   -0.3553

Ad 2 

Macierz trojkatna
    5.0000   -2.0000    1.0000   -1.0000
         0    6.4000   -2.2000    3.2000
         0         0    2.9063   -0.5000
         0         0         0    2.6774

Nasz obliczony wyznacznik
  249.0000

Blad wyznacznika
     0

Ad 3

z =
    0.1968    0.0522   -0.0281   -0.0040
    0.0683    0.1406   -0.1526   -0.1647
   -0.1486    0.1647    0.4498    0.0643
   -0.3012    0.1446    0.6145    0.3735

blad_invA =
  1.0e-015 *
         0         0    0.0208    0.0061
         0    0.0278    0.0555         0
         0   -0.0278   -0.1110         0
         0   -0.0555   -0.1110         0

odwrotnaA =
    0.1968    0.0522   -0.0281   -0.0040
    0.0683    0.1406   -0.1526   -0.1647
   -0.1486    0.1647    0.4498    0.0643
   -0.3012    0.1446    0.6145    0.3735