Wstęp

2

1. Algebra zbiorów

3

1.1. Działania algebry zbiorów

3

1.2. Inkluzja (zawieranie) i równość zbiorów

4

1.3. Metody dowodzenia własności zbiorów

5

1.4. Uniwersum i zbiór pusty

6

2. Zbiór potęgowy i inne rodziny zbiorów

11

Bibliografia

15

Algebra zbiorów

2

Wstęp

Zbiory i działania na zbiorach pełnią istotną rolę w informatyce. Przykładem zbioru
informacji gromadzonej w systemie informatycznym jest baza danych. Również
w programistyce spotykamy się ze zbiorem jako jednym z podstawowych typów
danych. Dobry programista musi umiejętnie korzystać ze struktur mających charakter
zbioru, a dobry bazodanowiec musi znać podstawowe własności działań na zbiorach,
aby umieć odpowiednio ekstrahować informacje ze swojej bazy.

Moduł trzeci przedstawia podstawowe pojęcia algebry zbiorów i ich — użyteczne
również z punktu widzenia informatyki — własności.

Omówimy pojęcia pierwotne teorii mnogości: zbiór i relację przynależności. Zostaną
zdefiniowanerelacjerówności i inkluzji zbiorów, a także działania teoriomnogościowe.
Przedstawione zostaną również (w większości wraz z dowodami) własności tych
działań oraz zależności między tymi własnościami.

Zdefiniujemy też pojęcie zbioru potęgowego oraz ciała zbiorów i omówimy ich
własności.

3

1. Algebra zbiorów

Pojęcia

zbioru

i

relacji należenia

są w matematyce traktowane jako pojęcia pierwotne,

czyli pozostawiane bez definicji. Gdyby przyjrzeć się bliżej problemowi definicji
zbioru, można zauważyć, że gdyby nawet udało się zdefiniować zbiór jako na przykład
„grupę pewnych elementów”, zrodzi się wtedy automatycznie pytanie o definicję
takiej „grupy”. Gdyby i to zdefiniować, trzeba byłoby użyć jakichś innych pojęć,
o definicję których znowu trzeba byłoby zadbać itp. Problem ten wiódłby oczywiście
do podobnych rozważań i sporów o definiowanie w nieskończoność. Ustalono
zatem, że dwa wyżej wspomniane pojęcia przyjmuje się za

pierwotne

. Pojęcia te są

odpowiednio charakteryzowane przez aksjomaty tzw.

teorii mnogości

(np.

Zermelo-

Fraenkla

).

W dalszych rozważaniach dużymi literami A, B oznaczać będziemy zbiory, małymi
zaś x, y — elementy zbiorów. Przez zapis x ∈ A rozumiemy zwyczajowo intuicję:
element x należy do zbioru

A

.

Przykład 1

Rozważmy następujące przykłady zbiorów:
 A = {a, b, 1, 0} — jak można łatwo zauważyć, zbiór ten ma cztery elementy. Są

to: a, b, 1, 0. Możemy zatem zapisać: a ∈ A, b ∈ A, 1

∈ A, 0

∈ A;

 B = {{a}, b, {1, 0}} — zbiór ten ma trzy elementy. Są to: {a}, b, {1, 0}. Mimo

że {a} sam w sobie jest zbiorem (jednoelementowym), to jest on elementem
rozważanego zbioru

B. Podobnie {1, 0} jest zbiorem dwuelementowym, ale

jako całość jest elementem zbioru B. Prawdą jest zatem, że {a} ∈ B, b ∈ B oraz
{1, 0} ∈ B. Ale nie jest prawdą, że a ∈ B (choć oczywiście a ∈ {a}). Mamy też
0

∉ B

(choć 0

∈ {1, 0});

 C = {{a, {b}}} — zbiór C ma tylko jeden element. Jest nim (dwuelementowy)

zbiór {a, {b}}. Mamy zatem {a, {b}} ∈ C. Ale nie jest prawdą, że a ∈ C czy też
nie jest prawdą, że b ∈ C;

 D = {a, {a, {b}}} — zbiór D ma dwa elementy. Są to: a oraz zbiór {a, {b}}.

Mamy oczywiście a ∈ D, ale też b ∉ D;

 N

= {0, 1, 2, 3, 4, ...}

— zbiór liczb naturalnych jest zbiorem nieskończonym;

 Z

= {... , –4, –3, –2, –1, 0, 1, 2, 3, 4, ...}

— zbiór liczb całkowitych (zbiór

nieskończony).

1.1. Działania algebry zbiorów

Jeżeli A oraz B są zbiorami, to:

 przez zapis A ∪ B rozumieć będziemy zbiór spełniający warunek
x ∈ A ∪ B ⇔ (x ∈ A ∨ x ∈ B) (element należy do zbioru A ∪ B wtedy

i tylko wtedy, gdy należy do jednego z nich lub do drugiego). Zbiór A ∪ B
nazywamy

sumą

zbiorów A oraz B. Interpretacja graficzna sumy zbiorów

przedstawiona jest na rysunku 1;

A B

A B

Rysunek 1

4

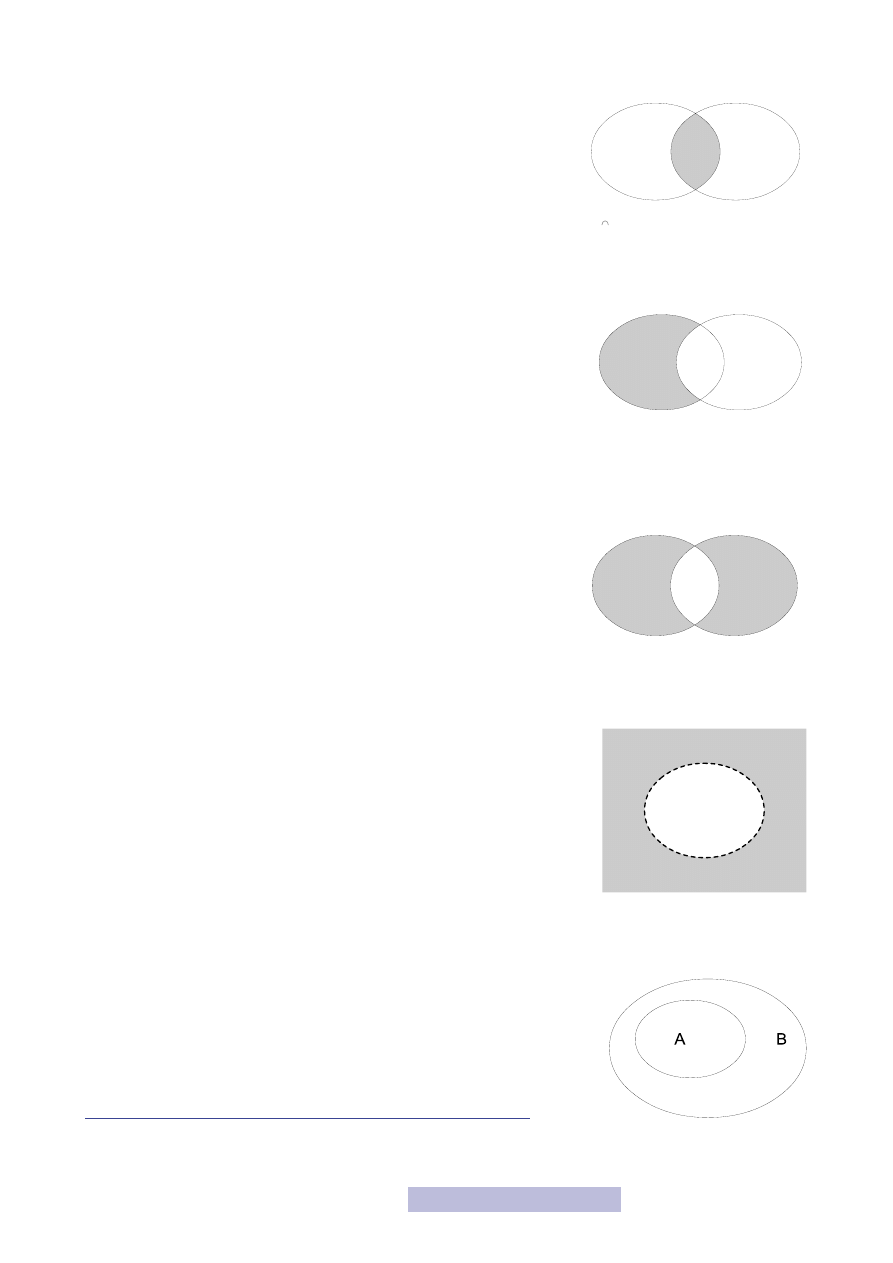
 przez zapis A ∩ B rozumiemy zbiór spełniający warunek

x ∈ A ∩ B ⇔ (x ∈ A ∧ x ∈ B) (element należy do zbioru
A ∩ B wtedy i tylko wtedy, gdy należy do jednego z nich
i jednocześnie do drugiego). Zbiór A ∩ B nazywamy

iloczynem

lub

częścią wspólną

zbiorów A oraz B. Interpretacja graficzna

iloczynu zbiorów przedstawiona jest na rysunku 2;

 przez zapis A – B rozumiemy zbiór spełniający warunek

x ∈ A – B ⇔ (x ∈ A ∧ x ∉ B) (element należy do zbioru A
– B wtedy i tylko wtedy, gdy należy do pierwszego z nich i nie należy do
drugiego). Zbiór A – B nazywamy

różnicą

zbiorów A oraz B. Interpretacja

graficzna różnicy zbiorów przedstawiona jest na rysunku 3;

 przez zapis A ÷ B rozumiemy zbiór spełniający warunek

x ∈ A ÷ B ⇔ [(x ∈ A ∧ x ∉ B) ∨ (x ∈ B ∧ x ∉ A)]. Zbiór A ÷ B
nazywamy

różnicą symetryczną

zbiorów A oraz B. Interpretacja graficzna

różnicy symetrycznej zbiorów przedstawiona jest na rysunku 4;

 przez zapis A’ rozumiemy zbiór spełniający warunek

x ∈ A’ ⇔ x ∉ A ⇔ ¬x ∈ A (element należy do zbioru A’
wtedy i tylko wtedy, gdy nie należy do zbioru A). Zbiór
A’ nazywamy

dopełnieniem

zbioru A. Interpretacja graficzna

dopełnienia zbioru przedstawiona jest na rysunku 5.

1.2. Inkluzja (zawieranie) i równość zbiorów

Między zbiorami rozważa się dwie podstawowe zależności: zawierania
i równości zbiorów. Powiemy, że zbiór

A zawiera się w zbiorze B, co

zapisujemy A ⊆ B (rysunek 6), jeżeli każdy element zbioru A należy również
do zbioru B.

Formalnie możemy ten fakt zapisać następująco:

A ⊆ B ⇔ ∀

x

(x ∈ A ⇒ x ∈ B).

Powiemy, że zbiór A jest równy zbiorowi B wtedy i tylko wtedy, gdy zbiór
A zawiera się w zbiorze B oraz zbiór B zawiera się w zbiorze A (każdy element
zbioru A należy do zbioru B oraz każdy element zbioru B należy do zbioru A).

Formalnie:

A = B ⇔ [(A ⊆ B) ∧ (B ⊆ A)].

Po odpowiednich przekształceniach możemy otrzymać:

A = B ⇔ [(A ⊆ B) ∧ (B ⊆ A)] ⇔ [∀

x

(x ∈ A ⇒ x ∈ B) ∧ ∀

x

(x ∈ B ⇒ x ∈ A)] ⇔

1

⇔ ∀

x

[(x ∈ A ⇒ x ∈ B) ∧ (x ∈ B ⇒ x ∈ A)] ⇔

2

∀

x

(x ∈ A ⇔ x ∈ B).

Finalnie mamy:

A = B ⇔ ∀

x

(x ∈ A ⇔ x ∈ B).

Dla zdefiniowanych wyżej działań i zależności między zbiorami możemy
udowodnić wiele własności zbiorów i działań na zbiorach.

1

Zgodnie z prawem rachunku kwantyfikatorów [

∀

x

A(x )

∧ ∀

x

B(x)]

⇔

∀

x

[A(x)

∧

B(x)].

2

Z prawa rachunku zdań [(α ⇒ β) ∧ (β ⇒ α)] ⇔ (α ⇔ β).

A B

A B

A B

A – B

A

A,

A B

Rysunek 2

Rysunek 3

Rysunek 4

Rysunek 5

Rysunek 6

A B

A B

A B

A-B

5

Twierdzenie 1

Dla dowolnych zbiorów A, B, C zachodzą następujące własności:

(a)

A ∩ A = A — i d e m p o t e n t n o ś ć iloczynu,

(b)

A ∪ A = A — i d e m p o t e n t n o ś ć sumy,

(c)

A ∩ B = B ∩ A — p r z e m i e n n o ś ć iloczynu,

(d)

A ∪ B = B ∪ A — p r z e m i e n n o ś ć sumy,

(e)

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) — r o z d z i e l n o ś ć i l o c z y n u w z g l ę d e m

s u m y,

(f)

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) — r o z d z i e l n o ś ć s u m y w z g l ę d e m

i l o c z y n u ,

(g)

A ∩ (A ∪ B) = A — p o c h ł a n i a n i e ,

(h)

A ∪ (A ∩ B) = A — p o c h ł a n i a n i e ,

(i)

(A ∪ B)’ = A’ ∩ B’ — p r a w o d e M o r g a n a algebry zbiorów,

(j)

(A ∩ B)’ = A’ ∪ B’ — p r a w o d e M o r g a n a algebry zbiorów,

(k)

A ∩ B ⊆ A,

(l)

A ⊆ A ∪ B.

1.3. Metody dowodzenia własności zbiorów

Udowodnimy dla przykładu własność (a) z

twierdzenia 1

(idempotentności iloczynu

zbiorów):

A ∩ A = A.

Aby udowodnić tę własność, zgodnie z definicją równości zbiorów, należy pokazać, że:

∀

x

(x ∈ A ∩ A ⇔ x ∈ A),

czyli dla dowolnego elementu x należy wykazać prawdziwość równoważności
x ∈ A ∩ A ⇔ x ∈ A.

Weźmy zatem dowolny element x.

Rozpisując lewą stronę równoważności, otrzymujemy:

L : x ∈ A ∩ A ⇔ x ∈ A ∧ x ∈ A ⇔

3

x ∈ A : P

Następnie

—

wykorzystując

prawo

przechodniości

równoważności

[(α ⇔ β) ∧ (β ⇔ γ)] ⇒ (α ⇔ γ) — otrzymujemy finalnie:

x ∈ A ∩ A ⇔ x ∈ A.

Dowód (e)

Należy pokazać, że ∀

x

[x ∈ A ∩ (B ∪ C) ⇔ x ∈ (A ∩ B) ∪ (A ∩ C)].

Weźmy dowolny element x. Mamy:

L : x ∈ A ∩ (B ∪ C) ⇔

4

x ∈ A ∧ x ∈ (B ∪ C) ⇔

5

x ∈ A ∧ (x ∈ B ∨ x ∈ C) ⇔

6

⇔ (x ∈ A ∧ x ∈ B) ∨ (x ∈ A ∧ x ∈

C) ⇔ (x ∈ (A ∩ B)) ∨

(x ∈ (A ∩ C)) ⇔ x ∈ (A ∩ B) ∪ (A ∩ C) : P

3

Wykorzystujemy tu prawo idempotentności koniunkcji: α ∧ α ⇔ α.

4

Korzystamy z definicji iloczynu zbiorów: x ∈ A ∩ B ⇔ (x ∈ A ∧ x ∈ B).

5

Definicja sumy x ∈ A ∪ B ⇔ (x ∈ A ∨ x ∈ B).

6

Prawo rozdzielności koniunkcji względem alternatywy α ∧ (β ∨ γ) ⇔ (α ∧ β) ∨ (α ∧ γ).

6

I ponownie wykorzystując przechodniość równoważności, otrzymujemy:

x ∈ A ∩ (B ∪ C) ⇔ x ∈ (A ∩ B) ∪ (A ∩ C).

Dowód (g)

Należy pokazać, że ∀

x

[x ∈ A ∩ (A ∪ B) ⇔ x ∈ A].

Weźmy dowolny element x. Mamy:

L : x ∈ A ∩ (A ∪ B) ⇔ x ∈ A ∧ x ∈ (A ∪ B) ⇔ x ∈ A ∧ (x ∈ A ∨ x ∈ B) ⇔

7

x ∈ A : P

Korzystając z przechodniości równoważności, mamy:

x ∈ A ∩ (A ∪ B) ⇔ x ∈ A.

Dowód (i)

Należy pokazać, że ∀

x

[x ∈ (A ∪ B)’ ⇔ x ∈ A’ ∩ B’].

Weźmy dowolny element x. Mamy:

L : x ∈ (A ∪ B)’ ⇔

8

¬x ∈ (A ∪ B) ⇔ ¬(x ∈ A ∨ x ∈ B) ⇔

9

(¬x ∈ A ∧ ¬x ∈ B) ⇔

⇔ x ∈ A’ ∧ x ∈ B’ ⇔ x ∈ A’ ∩ B’ : P

I wreszcie:

x ∈ (A ∪ B)’ ⇔ x ∈ A’ ∩ B’.

1.4. Uniwersum i zbiór pusty

Łatwo dowodzi się faktu, że nie ma (uniwersalnego) zbioru wszystkich elementów.
Założenie takie dałoby natychmiastową sprzeczność, zakłada się bowiem, że żaden
zbiór nie może należeć do siebie samego. Dlatego jeżeli rozważamy jakieś zbiory,
bardzo często przydaje się pojęcie uniwersum — przestrzeni. Przestrzeń to, mówiąc
krótko, świat — rzeczywistość, którą w danym momencie się rozważa (czyli tak
naprawdę jakaś część całego świata — pełnej rzeczywistości). Jeżeli zastanawiamy
się nad własnościami przedziałów na osi rzeczywistej, jako uniwersum możemy
przyjąć zbiór wszystkich liczb rzeczywistych. Jeżeli mówimy o własnościach zbiorów
punktów na płaszczyźnie (w układzie współrzędnych), to jako uniwersum można
przyjąć zbiór wszystkich punktów płaszczyzny. Uniwersum będzie tutaj oznaczane
jako X. Jeżeli rozważamy pewne zbiory nad pewnym uniwersum, możemy ograniczyć
pojęcie dopełnienia zbioru do dopełnienia względem uniwersum, tzn. przez zapis A’
rozumieć będziemy różnicę X – A. W dowodach własności związanych z uniwersum
X będziemy przyjmować, że wyrażenie x

∈

X jest prawdziwe.

Istotną rolę w teorii mnogości spełnia także

zbiór pusty

. Jest to zbiór, o którym

zakłada się, że nie ma żadnych elementów. Zakładamy również, że zbiór pusty jest
tylko jeden. Zbiór pusty oznaczamy zwyczajowo jako ∅.

7

Prawo pochłaniania α ∧ (β ∨ α) ⇔ α.

8

Definicja dopełnienia zbioru.

9

Prawo de Morgana rachunku zdań ¬(α ∨ β) ⇔ (¬α ∧ ¬β).

7

Twierdzenie 2

Rozważmy jako uniwersum zbiór X. Dla dowolnego zbioru A zawartego w zbiorze X
zachodzą następujące własności:
(a) A ∩ X = A,
(b) A ∪ X = X,
(c) A ∪ A’ = X.

Dowód (a)

Należy pokazać, że ∀

x

[x ∈ A ∩ X ⇔ x ∈ A].

Weźmy dowolny element x. Mamy:

L : x ∈ A ∩ X ⇔ x ∈ A ∧ x ∈ X.

Zauważmy, że prawy czynnik powyższej koniunkcji jest prawdziwy. Przypomnijmy
także, że jeżeli jeden z czynników koniunkcji jest prawdziwy, to cała koniunkcja
zależy tylko od drugiego z czynników i jest jemu równoważna. Uzasadniona jest
zatem następująca równoważność:

x ∈ A ∧ x ∈ X ⇔ x ∈ A : P,

I finalnie:

x ∈ A ∩ X ⇔ x ∈ A.

Dowód (c)

Należy pokazać, że ∀

x

[x ∈ A ∪ A’ ⇔ x ∈ X].

Weźmy dowolny element x. Mamy:

L : x ∈ A ∪ A’ ⇔ x ∈ A ∨ x ∈ A’ ⇔ x ∈ A ∨ ¬x ∈ A.

Zauważmy, że powyższa alternatywa jest prawdziwa

10

. Zatem uzasadniona jest

następująca równoważność:

x ∈ A ∨ ¬x ∈ A ⇔ x ∈ X : P.

I finalnie:

x ∈ A ∪ A’ ⇔ x ∈ X.

Twierdzenie 3

Dla dowolnego zbioru A zachodzą następujące własności:
(a) ∅ ⊆ A,
(b) A ∩ ∅ = ∅,
(c) A ∪ ∅ = A,
(d) A ∩ A’ = ∅.

Dowód (a)

Zgodnie z definicją inkluzji (zawierania) zbiorów należy pokazać, że

∀

x

[x ∈ ∅ ⇒ x ∈ A].

10

Jest to pewne podstawienie tautologii α ∨ ¬α.

8

Weźmy zatem dowolny element x. Jeżeli rozważymy poprzednik powyższej
implikacji, łatwo można zauważyć, że wyrażenie x ∈ ∅ jest fałszywe (do zbioru
pustego nie należy żaden element). Przypomnijmy z rachunku zdań, że implikacja
o fałszywym poprzedniku jest prawdziwa niezależnie od następnika. Prawdziwe jest
zatem wyrażenie:

x ∈ ∅ ⇒ x

∈ A, co kończy dowód

11

.

Dowód (b)

Należy pokazać, że ∀

x

[x ∈ A ∩ ∅ ⇔ x ∈ ∅].

Weźmy dowolny element x. Mamy:

L : x ∈ A ∩ ∅ ⇔ x ∈ A ∧ x ∈ ∅.

Zauważmy, że prawy czynnik powyższej koniunkcji jest fałszywy. Przypomnijmy także,
że jeżeli jeden z czynników koniunkcji jest fałszywy, to cała koniunkcja jest fałszywa.
Oczywiście, dwa dowolne fałszywe wyrażenia są sobie logicznie równoważne, zatem
uzasadniona jest następująca równoważność:

x ∈ A ∧ x ∈ ∅ ⇔ x ∈ ∅ : P,

I finalnie:

x ∈ A ∩ ∅ ⇔ x ∈ ∅.

Dowód (d)

Należy pokazać, że ∀

x

[x ∈ A ∩ A’ ⇔ x ∈ ∅].

Weźmy dowolny element x. Mamy:

L : x ∈ A ∩ A’ ⇔ x ∈ A ∧ x ∈ A’ ⇔ x ∈ A ∧ ¬x ∈ A.

Zauważmy, że powyższa koniunkcja jest fałszywa

12

. Zatem uzasadniona jest

następująca równoważność:

x ∈ A ∧ ¬x ∈ A ⇔ x ∈ ∅ : P.

I finalnie:

x ∈ A

∩ A’ ⇔ x ∈ ∅.

Opisywane wyżej własności dotyczą przede wszystkim działań na zbiorach. Poniżej
przedstawionych jest kilka własności zależności między zbiorami.

Twierdzenie 4

Dla dowolnych zbiorów A, B, C, D zachodzą następujące własności:
(a) A ⊆ B ∧ B ⊆ C ⇒ A ⊆ C,
(b) A ⊆ B ∧ C ⊆ B ⇒ A ∪ C ⊆ B,
(c) A ⊆ B ∧ C ⊆ D ⇒ A – D ⊆ B – C,
(d) A ⊆ B ⇔ A ∪ B = B,
(e) A ⊆ B ⇔ A ∩ B = A,
(f) A ⊆ B ⇔ A – B = ∅,
(g) A ⊆ B ⇒ B

’

⊆ A

’

,

11

Zauważmy, że z tej własności wynika na mocy dowolności zbioru A własność ∅ ⊆ ∅.

12

Jest to pewne podstawienie kontrtautologii α ∧ ¬α.

9

(h) C ⊆ D ⇒ A – D ⊆ A – C,
(i) A ⊆ B ⇒ A ∪ (B – A) = B.

Dowód (a)

Załóżmy, że A ⊆ B oraz B ⊆ C. Z obu założeń otrzymujemy zgodnie z definicją
inkluzji zbiorów ∀

x

[x ∈ A ⇒ x ∈ B] oraz ∀

x

[x ∈ B ⇒ x ∈ C]. Aby udowodnić tezę

A ⊆ C, należy pokazać, że ∀

x

[x ∈ A ⇒ x ∈ C].

Weźmy więc dowolny element x i załóżmy, że x ∈ A. Na mocy założeń mamy kolejno
x

∈ B oraz x ∈ C, co kończy dowód.

Dowód (b)

Załóżmy, że A ⊆ B oraz C

⊆

B. Otrzymujemy ∀

x

[x ∈ A ⇒ x ∈ B] oraz

∀

x

[x ∈ C ⇒ x ∈ B]. Aby udowodnić tezę A ∪ C ⊆ B, należy pokazać, że

∀

x

[x ∈ A ∪ C ⇒ x ∈ B].

Weźmy więc dowolny element x i załóżmy, że x ∈ A ∪ C. Mamy:

x ∈ A ∨ x ∈ C.

Stosując kolejno oba założenia, otrzymujemy:

x ∈ B ∨ x ∈ B,

czyli:

x ∈ B,

co kończy dowód.

Dowód (d)

Aby pokazać, że A ⊆ B ⇔ A ∪ B = B, musimy udowodnić dwie implikacje:
(*)

A ⊆ B ⇒ A ∪ B = B oraz

(**) A ∪ B = B

⇒ A ⊆ B.

(*)

Załóżmy, że A ⊆ B,

czyli ∀

x

[x ∈ A ⇒ x ∈ B]. Aby udowodnić równość zbiorów

A ∪ B = B, wykażemy dwie inkluzje: A ∪ B ⊆ B oraz B

⊆ A ∪ B. Druga z nich jest

oczywista na podstawie jednej z własności z

twierdzenia 1

13

.

Aby udowodnić pierwszą inkluzję, załóżmy, że

x ∈ A ∪ B.

Mamy:

x ∈ A ∨ x ∈ B.

Teraz, korzystając z założenia dowodu (*), mamy:

x ∈ B ∨ x ∈ B

i oczywiście x ∈ B,

co kończy dowód pierwszej z inkluzji potrzebnych do

udowodnienia implikacji (*).

(**)

Załóżmy, że A ∪ B = B,

czyli ∀

x

[x ∈ A ∪ B ⇔ x ∈ B]. Aby udowodnić inkluzję

A ⊆ B, załóżmy, że x ∈ A.

13

Cytowana własność jest postaci A

⊆

A

∪

B, ale oczywiście — zważywszy na przemienność

sumy zbiorów — oznacza to samo.

10

Wiemy, że w ogólnym przypadku A ⊆ A ∪ B, czyli ∀

x

[x ∈ A ⇒ x ∈ A ∪ B].

Otrzymujemy zatem:

x ∈ A ∨ x ∈ B.

Teraz, korzystając z założenia dowodu (**), mamy:

x ∈ B,

co kończy dowód implikacji (**).

Oczywiście zważywszy na odpowiednie prawo rachunku zdań

14

, równoważność

A ⊆ B ⇔ A ∪ B = B została udowodniona.

Dowód (h)

Załóżmy, że A ⊆ B,

czyli ∀

x

[x ∈ A ⇒ x ∈ B]. Rozważmy dowolny element x.

Przypomnijmy, że — zgodnie z odpowiednim prawem rachunku zdań — implikacja
x ∈ A ⇒ x ∈ B jest równoważna implikacji ¬x ∈ B ⇒ ¬x ∈ A, która inaczej zapisana
przybiera postać: x ∈ B

‘

⇒ x ∈ A

‘

. Mamy zatem:

∀

x

[x ∈ B

‘

⇒ x ∈ A

‘

],

czyli:

B

‘

⊆ A

‘

.

14

Prawo [(α ⇒ β) ∧ (β ⇒ α)] ⇔ (α ⇔ β).

11

2. Zbiór potęgowy

i inne rodziny zbiorów

Czasem — z pewnych powodów — istnieje potrzeba rozpatrywania zbiorów, których
elementami są również zbiory. Zbiory zbiorów nazywamy rodzinami. Typowym
przykładem rodziny zbiorów jest zbiór potęgowy danego zbioru.

Zbiorem potęgowym zbioru X nazywamy zbiór P(X) wszystkich podzbiorów tego
zbioru, symbolicznie:

P(X) = {A: A ⊆ X}.

Możemy też zapisać:

A ∈ P(X) ⇔ A ⊆ X.

Dla dowolnego zbioru X jego zbiór potęgowy P(X) nie jest zbiorem pustym, bo

∅ ∈ P(X) oraz X ∈ P(X).

Przykład 1

Jeśli X

1

= ∅, to P(X

1

) = {∅}. Nie ma bowiem innego podzbioru zbioru pustego poza

nim samym.

Przykład 2

Niech X

2

= {a, b, c}, wtedy P(X

2

)={∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.

Przykład 3

Niech X

3

= {{a}, {{b}, c}}. Zauważmy, że zbiór ma tylko dwa elementy.

Są to {a} oraz {{b}, c}. Zbiór potęgowy wygląda zatem następująco:
P(X

3

) = {∅, {{a}}, {{{b}, c}}, {{a}, {{b}, c}}}.

Twierdzenie 5

Dla dowolnych zbiorów A i B zachodzą poniższe własności:

(a) A, B ∈ P(X) ⇒ A ∩ B, A ∪ B, A – B ∈ P(X),

(b) X ⊆ Y ⇒ P(X) ⊆ P(Y).

Dowód (a)

Niech A, B ∈ P(X), wtedy A ⊆ X oraz B ⊆ X, ale oczywiście również zbiory A ∩ B,
A ∪ B, A – B są podzbiorami zbioru X, więc A ∩ B, A ∪ B, A – B ∈ P(X).

12

Dowód (b)

Załóżmy, że X ⊆ Y. Mamy pokazać, iż P(X) ⊆ P(Y).

Weźmy zatem dowolny element A zbioru potęgowego P(X). Mamy:

A ∈ P(X) ⇔

15

A ⊆ X ⇒

16

A ⊆ Y ⇔

17

A ∈ P(Y).

Ostatecznie, korzystając z praw przechodniości równoważności i implikacji, mamy:

A

∈ P(X) ⇒ A ∈ P(Y).

Przykład 4

Rozważmy zbiór X

4

= {a, b, c, d}. Zauważmy, że mamy wtedy X

4

= X

2

∪ {d}.

Można zauważyć, że elementami zbioru potęgowego P(X

4

) będą wszystkie elementy

zbioru potęgowego P(X

2

) oraz wszystkie sumy elementów zbioru P(X

2

) ze zbiorem

jednoelementowym {d}. Symbolicznie mamy w naszym przypadku:

P(X

4

) = P(X

2

) ∪ {A

∪ {d} : A ∈ P(X

2

)}.

W rozważanym przypadku mamy:

P(X

4

) = P(X

2

) ∪ {A

∪ {d} : A ∈ P(X

2

)} =

= {∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}} ∪

∪ {∅ ∪ {d}, {a} ∪ {d}, {b} ∪ {d}, {c} ∪ {d}, {a, b} ∪

{d}, {a, c} ∪ {d}, {b, c} ∪ {d}, {a, b, c} ∪ {d}} =

= {∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}} ∪

∪ {{d}, {a, d}, {b, d}, {c, d}, {a, b, d}, {a, c, d}, {b, c, d}, {a, b, c, d}} =

= {∅, {a}, {b}, {c}, {d}, {a, b}, {a, c}, {b, c}, {a, d}, {b, d},

{c, d}, {a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}, {a, b, c, d}}.

Twierdzenie 6

Jeżeli zbiór A ma n elementów, to jego zbiór potęgowy P(A) ma 2

n

elementów.

Dowód

Dowód przeprowadzony zostanie przez indukcję ze względu na ilość elementów
zbioru A.

B a z a i n d u k c j i — rozważmy zbiór niemający elementów (n = 0). Jedynym takim
zbiorem jest oczywiście zbiór pusty ∅. Zauważmy również, że P(∅) = {∅}. Zatem
w tym przypadku zbiór potęgowy faktycznie ma 2

0

= 1 elementów.

Z a ł o ż e n i e k r o k u i n d u k c y j n e g o — załóżmy, że zbiór potęgowy zbioru
mającego k elementów ma 2

k

elementów.

K r o k i n d u k c y j n y — rozważmy zbiór k + 1-elementowy. Możemy zapisać ten
zbiór następująco:

{a

1

, a

2

, a

3

, ..., a

k

, a

k+1

} (zbiór ten oznaczamy dalej jako A

k+1

).

15

Z definicji zbioru potęgowego.

16

Z założenia, że X

⊆

Y.

17

Z definicji zbioru potęgowego.

13

Zauważmy, że zbiór ten można potraktować również jako poniższą sumę:

{a

1

, a

2

, a

3

, ..., a

k

} ∪ {a

k+1

} (inaczej możemy zapisać A

k

∪ {a

k+1

}).

Oczywiście, zbiór A

k

= {a

1

, a

2

, a

3

, ..., a

k

} jest zbiorem k-elementowym, a zatem jego

zbiór potęgowy P(A

k

) ma zgodnie z założeniem indukcyjnym 2

k

elementów. Łatwo

można zauważyć (patrz

przykład 5

), że zbiór potęgowy P(A

k+1

) można przedstawić

następująco: P(A

k+1

) = P(A

k

) ∪ {X ∪ {a

k+1

} : X ∈ P(A

k

)}. Zbiory P(A

k

) oraz {X ∪

{a

k+1

} : X ∈ P(A

k

)} są rozłączne oraz każdy z nich ma 2

k

elementów. Zatem zbiór

P(A

k+1

) ma 2

k

+ 2

k

= 2 ⋅ 2

k

= 2

k+1

elementów, co kończy dowód.

Innym dobrym przykładem rodziny zbiorów jest

ciało zbiorów

. Rozważmy zbiór X

oraz jego zbiór potęgowy P(X).

Rodzinę ℑ podzbiorów zbioru X nazwiemy ciałem zbiorów, jeżeli spełnione są
następujące warunki:
1. ℑ ≠ ∅.
2. Jeżeli A ∈ ℑ, to X – A ∈ ℑ (dopełnienia zbiorów należących do ℑ należą również

do ℑ).

3. Jeżeli A ∈ ℑ oraz B ∈ ℑ, to A ∪ B ∈ ℑ (sumy zbiorów należących do ℑ należą

również do ℑ).

Przykład 5

Rozważmy następujący zbiór X = {a, b, c} oraz rodzinę ℑ

1

= {{a}, {b}}.

Zauważmy, że X

– {a} = {b, c} ∉ ℑ

1

, a także X

– {b} = {a, c} ∉ ℑ

1

. Każde z tych

spostrzeżeń wystarcza, aby orzec, że ℑ

1

nie jest ciałem zbiorów. Warunek sumy

również nie jest spełniony, bowiem {a} ∪ {b} = {a, b} ∉ ℑ

1

.

Przykład 6

Wzbogaćmy zatem rozważaną wyżej rodzinę ℑ

1

o wskazane wyżej zbiory.

Niech ℑ

2

= {{a}, {b}, {b, c}, {a, c}, {a, b}}.

Zauważmy następujące fakty: {a} ∪ {b, c} =

{a, b, c} = X ∉ ℑ

2

oraz

X

– {a, b} = {c} ∉ ℑ

2

. Jeżeli wzbogacimy rodzinę ℑ

2

o powyższe zbiory, to rodzina

ta jeszcze nie spełnia aksjomatów ciała zbiorów, gdyż X

–

X

= ∅ ∉ ℑ

2

. Okazuje się, że

dopiero pełny zbiór potęgowy P(X) jest ciałem zbiorów zawierającym rodzinę ℑ

1

.

Przykład 7

Nie tylko zbiory potęgowe są ciałami zbiorów. Jeżeli rozważymy zbiór
X = {a, b, c, d} oraz rodzinę ℑ

3

= {∅, {a, c}, {b, d}, X}, to łatwo zauważyć, że

spełnia ona aksjomaty ciała zbiorów.

Zachodzą następujące własności ciał zbiorów:

Twierdzenie 7

Dla dowolnego zbioru X

i dowolnego ciała zbiorów ℑ takiego, że ℑ ⊆

P(X) jest:

(a) jeżeli A ∈ ℑ oraz B ∈ ℑ, to A ∩ B ∈ ℑ (iloczyny zbiorów należących do ℑ należą

również do ℑ),

14

(b) ∅ ∈ ℑ,
(c) X ∈ ℑ.

Dowód (a)

Rozważmy zbiory A oraz B należące do rodziny ℑ. Oczywiście ich dopełnienia
X – A

oraz X – B również należą do ℑ.

Także suma tych zbiorów oraz dopełnienie tej sumy musi należeć do ℑ. Zauważmy,
że zgodnie z prawami de Morgana algebry zbiorów mamy: A ∩ B =

(A

’

∪ B

’

)

’

.

I ostatecznie — uwzględniając zbiór X jako uniwersum rozważań — mamy:
A ∩ B =

X – (X – A

∪ X – B), a zatem iloczyn A ∩ B również należy do rodziny ℑ.

15

Bibliografia

1.

Gubareni N., 2001: Logika dla studentów, Wydawnictwo Politechniki
Częstochowskiej.

2.

Kuratowski K., 2004: Wstęp do teorii mnogości i topologii, PWN, Warszawa.

3.

Kuratowski K., Mostowski A., 1978: Teoria mnogości, PWN, Warszawa.

4.

Marek W., Onyszkiewicz J., 2003: Elementy logiki i teorii mnogości w zadaniach,
PWN, Warszawa.

5.

Rasiowa H., 2004: Wstęp do matematyki współczesnej, PWN, Warszawa.

6.

Słupecki J., Hałkowska K., Piróg-Rzepecka K., 1994: Logika i teoria mnogości,
Warszawa.

Bibliografia stron WWW

7. Wydział Matematyki, Informatyki i Mechaniki Uniwersytetu Warszawskiego.

Witryna internetowa. h�p://www.mimuw.edu.pl/~tiuryn/skrypt-98.ps.gz, stan

z 21.09.2005 (J. Tiuryn, Wstęp do teorii mnogości i logiki).