Dane ogólne.

strefa wiatrowa

I A

wysoko

ść

trzonu nad terenem

H

40 m

⋅

:=

ś

rednica wewn

ę

trzna

D

d

1.4 m

⋅

(

)

:=

nominalna temperatura gazów spalinowych

T

n

433 K

⋅

:=

pr

ę

dko

ść

gazów spalinowych

v

11

m

s

⋅

:=

liczba czopuchów

n

c

1

:=

poziomy czopuchów

h

c1

4.5 m

⋅

:=

stal płaszcza

10HA

wyposa

ż

enie

wg obowi

ą

zuj

ą

cych przepisów

warunki gruntowe

piasek drobny

okres eksploatacji komina

T

e

10 lat

⋅

:=

liczba segmentów

n

s

6

:=

wysko

ść

najni

ż

szego segmentu (cokołu)

h

c

10 m

⋅

:=

wysoko

ś

ci pzostałych segmentów

h

s

6 m

⋅

:=

grubo

ś

ci

ś

cianek i pozimy ko

ń

ców poszczególnych segmentów ( od podstawy komina )

segment najni

ż

szy

i

1

:=

t

i

16 mm

⋅

:=

z

i

h

c

:=

z

i

10 m

=

segment

i

2

:=

t

i

10 mm

⋅

:=

z

i

z

1

i

1

−

(

) h

s

⋅

+

:=

z

i

16 m

=

segment

i

3

:=

t

i

9 mm

⋅

:=

z

i

z

2

i

2

−

(

) h

s

⋅

+

:=

z

i

22 m

=

segment

i

4

:=

t

i

8 mm

⋅

:=

z

i

z

2

i

2

−

(

) h

s

⋅

+

:=

z

i

28 m

=

segment

i

5

:=

t

i

7 mm

⋅

:=

z

i

z

2

i

2

−

(

) h

s

⋅

+

:=

z

i

34 m

=

segment

i

6

:=

t

i

6 mm

⋅

:=

z

i

z

2

i

2

−

(

) h

s

⋅

+

:=

z

i

40 m

=

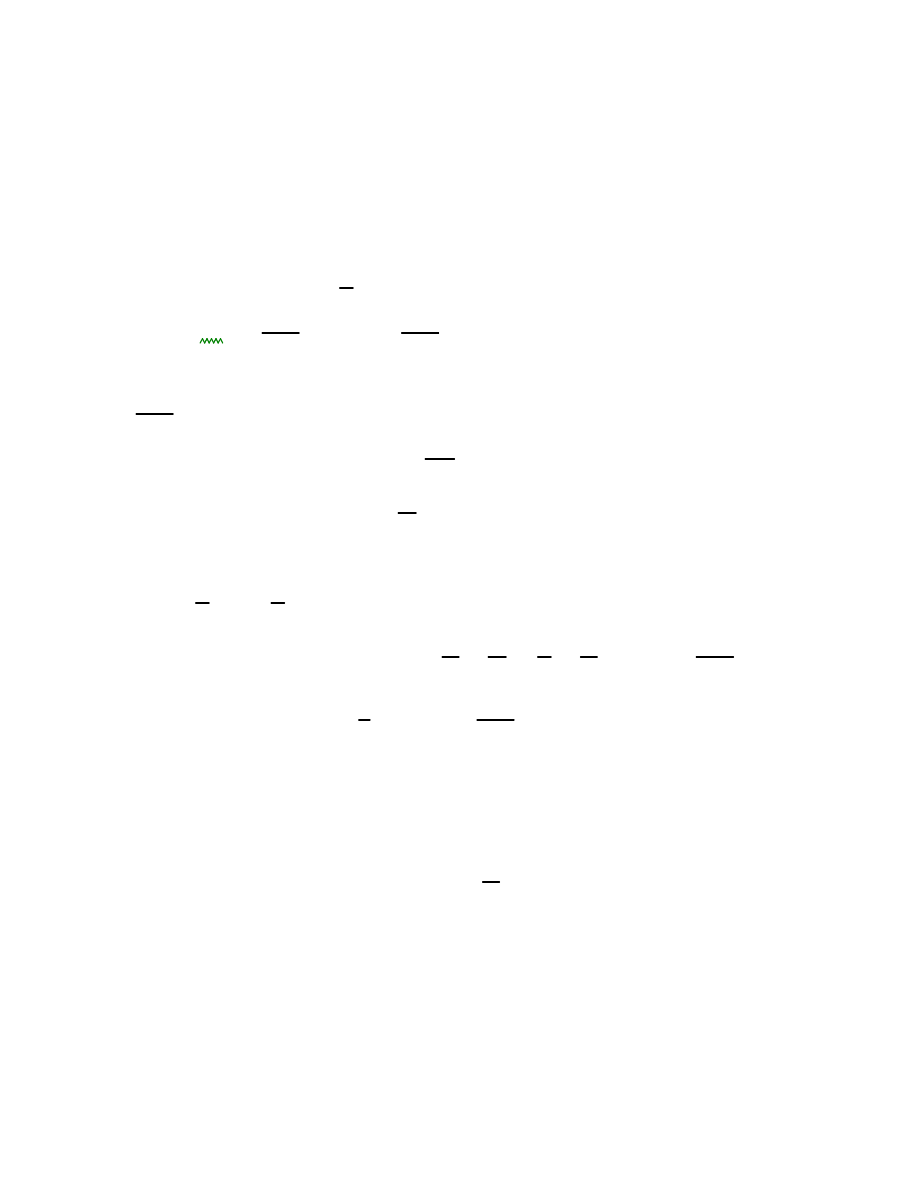
1. Wpływy termiczne na wła

ś

ciwo

ś

ci mechaniczne stali.

Trzon komina jest jednowarstwowy i nie posiada izolacji termicznej.

temperatura awaryjna

T

w

1.2 T

n

⋅

:=

T

w

519.6 K

=

Wyznacznie współczynnika przenikania ciepła.

współczynnik napływu ciepła

v

11

m

s

⋅

=

<

16 m/s

α

n

2 v

⋅

8

+

:=

α

n

α

n

W

m

2

K

⋅

⋅

:=

α

n

30

W

m

2

K

⋅

⋅

=

współczynnik odpływu ciepła

H

40 m

=

<

40 m

α

o

26

W

m

2

K

⋅

⋅

:=

współczynnik przenikania ciepła dla stali

λ

1

58

W

m K

⋅

⋅

:=

promie

ń

wewn

ę

trzny

r

d

D

d

2

:=

r

d

700 mm

⋅

=

r

1

r

d

:=

współczynnik uwzgl

ę

dniaj

ą

cy wpływ krzywizny

ś

cianki

χ

1

0.49

0.57

r

d

r

1

⋅

+

0.06

r

d

r

1













2

⋅

−

:=

χ

1

1

=

odwrotno

ść

współczynnika przenikania ciepła

k'

1

α

n

t

1

λ

1

χ

1

⋅

r

d

r

1

⋅













+

1

α

o

+

:=

k'

0.07

m

2

K

⋅

W

⋅

=

współczynnik przenikania ciepła

k

1

k'

:=

k

13.88

W

m

2

K

⋅

⋅

=

Temperatura płaszcza w okresie letnim.

przyj

ę

ta temperatura zewn

ę

trzna letnia

T

zl

308 K

⋅

:=

ró

ż

nica temperatur po obu stronach przeszkody

∆

T

T

w

T

zl

−

:=

∆

T

211.6 K

=

spadek temperatury przy napływie ciepła

∆

T

n

k

1

α

n

⋅

∆

T

⋅

:=

∆

T

n

97.87 K

=

temperatura na wewn

ę

trznej powierzchni płaszcza

T

pl

T

w

∆

T

n

−

:=

T

pl

421.73 K

=

Temperatura płaszcza w okresie zimowym.

przyj

ę

ta temperatura zewn

ę

trzna zimowa

T

zz

241 K

⋅

:=

ró

ż

nica temperatur po obu stronach przeszkody

∆

T

T

w

T

zz

−

:=

∆

T

278.6 K

=

spadek temperatury przy napływie ciepła

∆

T

n

k

1

α

n

⋅

∆

T

⋅

:=

∆

T

n

128.85 K

=

temperatura na wewn

ę

trznej powierzchni płaszcza

T

pz

T

w

∆

T

n

−

:=

T

pz

390.75 K

=

Wpływ temperatury na wytrzymało

ść

obliczeniow

ą

stali.

normowa wytrzymało

ść

obliczeniowa stali

f

d

290 MPa

⋅

:=

maksymalna temperatura na wewn

ę

trznej powierzchni płaszcza

T

pl

421.73 K

=

>

343 K

Nale

ż

y uwzgl

ę

dni

ć

zmniejszenie si

ę

wytrzymało

ś

ci obliczeniowej stali.

T

T

pl

K

273

−

148.73

=

:=

f

dT

f

d

1.022

0.197 10

3

−

⋅

T

⋅

−

1.590 10

6

−

⋅

T

2

⋅

−

(

)

⋅

:=

f

dT

277.68 MPa

⋅

=

Wpływ temperatury na moduł spr

ęż

ysto

ś

ci podłu

ż

nej stali.

warto

ść

normowa

E

205000 MPa

⋅

:=

E

T

E 0.987

0.300 10

3

−

⋅

T

⋅

+

1.857 10

6

−

⋅

T

2

⋅

−

(

)

⋅

:=

E

T

203060.74 MPa

⋅

=

2. Wpływ korozji na wytrzymało

ść

stali.

planowany czas u

ż

ytkowania komina

T

e

10 lat

⋅

=

stopie

ń

zagro

ż

enia korozyjnego wg tablicy 2 normy

ze wzgl

ę

du na silnie agresywn

ą

atmosfer

ę

zewn

ę

trzn

ą

s

1

1

:=

ze wzgl

ę

du na zasiarczenie w

ę

gla

s

2

3

:=

ze wzgl

ę

du na mo

ż

liwo

ść

wykroplenia kondensatu

s

3

4

:=

∆

t

0.1

1

3

i

s

i

∑

=

⋅

:=

∆

t

0.8

=

współczynnik korozyjny

α

kor

1

1

0.04 T

e.

⋅

∆

t

⋅

+

:=

α

kor

0.76

=

3. Obci

ąż

enie wiatrem w I sytuacji projektowej.

strefa wiatrowa I

teren A

charakterystyczne ci

ś

nienie pr

ę

dko

ś

ci wiatru

q

k

250 Pa

⋅

:=

współczynnik dla czasu eksploatacji 3 lata

D

T

0.65

:=

Współczynnik ekspozycji.

współczynnik przeliczeniowy zale

ż

ny od rodzaju terenu

k

1

:=

wysoko

ść

nad poziomem terenu

z

H

m

:=

z

40

=

wykładnik zale

ż

ny od rodzaju terenu

α

0.14

:=

współczynnik ekspozycji

C

e

k

z

10













2

α

⋅

⋅

:=

C

e

1.47

=

Współczynnik aerodynamiczny dla komina stalowego z drabin

ą

włazow

ą

.

H

D

d

28.57

=

> 25

D

d

H

0.04

=

< 0.04

⇒

C

xo

0.7

:=

( tablica Z2-3 )

pole rzutu bocznego drabiny na płaszczyzn

ę

symetrii

A

d

0.1

m

2

m

⋅

:=

liczba przewodów kominowych

n

1

:=

ś

rednica wewn

ę

trzna komina

D

d

1.4 m

=

współczynnik aerodynamiczny

C

x

C

xo

2.4

A

d

n D

d

⋅

⋅

+

:=

C

x

0.87

=

3.1. Współczynnik działania porywów wiatru.

podstawowy okres drga

ń

własnych

T

1

0.001

H

2

D

⋅

:=

T

1

1.14

=

cz

ę

stotliwo

ść

drga

ń

własnych

n

1

T

1

:=

n

0.87

=

Współczynnik szczytowej warto

ś

ci obci

ąż

enia.

Ψ

2 ln 600 n

⋅

(

)

⋅

0.577

2 ln 600 n

⋅

(

)

⋅

+

:=

Ψ

3.7

=

Wyznacznie współczynnika

δδδδ

s

.

współczynnik chropowato

ś

ci dla terenu A

r

0.08

:=

współczynnik pozarezonansowego oddziaływania turbulentnego

k

b

2.25

0.227 1

3.24

D

H

⋅

+













⋅

ln H

( )

⋅

−

:=

k

b

1.32

=

logarytmiczny dekrement tłumienia drga

ń

wg tablicy Z3-2

dla komina spawanego jednoprzewodowego bez wykładziny

δ

s

1

0.015

:=

dodatek na poł

ą

czenia kołnierzowe

δ

s

2

0.015

:=

δ

s

1

2

i

δ

s

i

∑

=

:=

δ

s

0.03

=

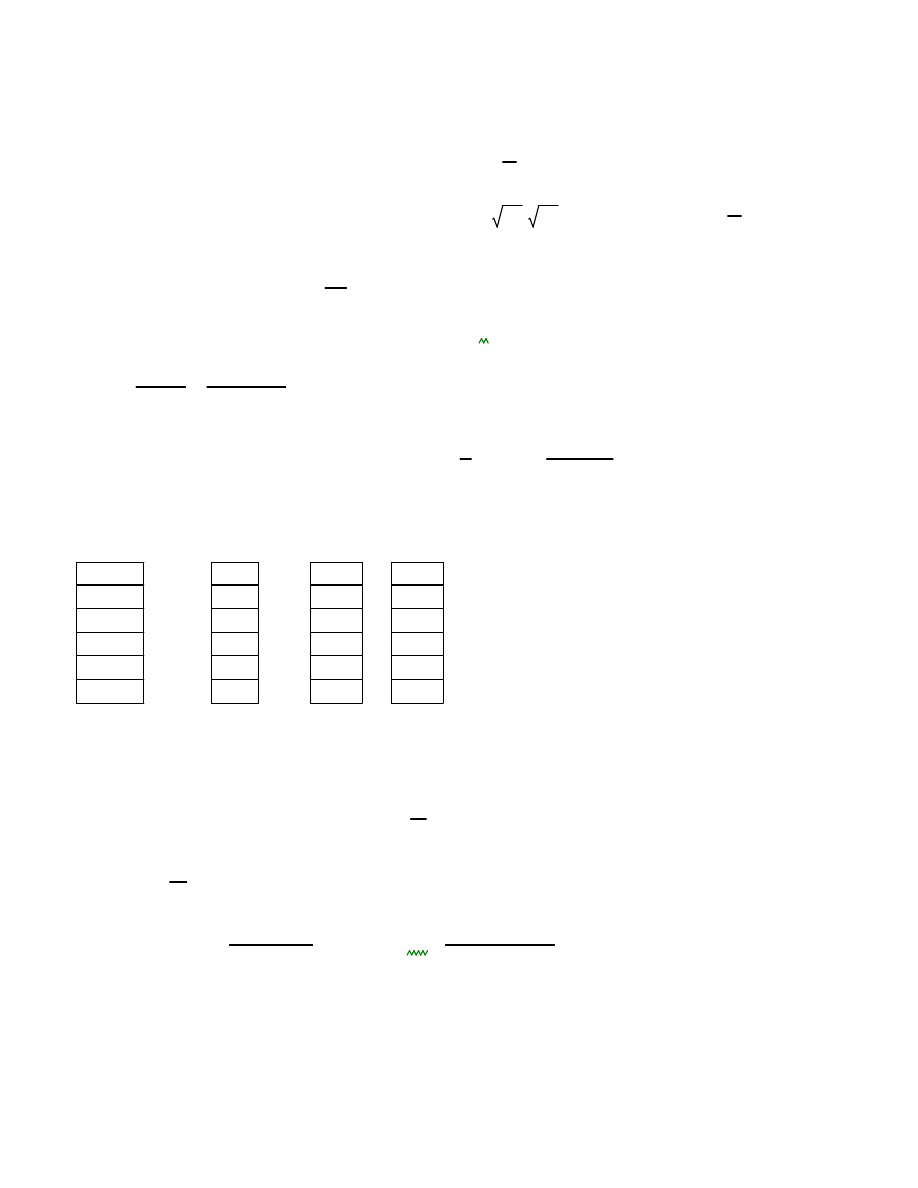
pr

ę

dko

ść

charakterystyczna dla I strefy wiatrowej

v

k

20

m

s

⋅

:=

pr

ę

dko

ść

wiatru na wysoko

ś

ci wierzchołka komina

v

H

v

k

D

T

⋅

C

e

⋅

:=

v

H

19.58

m

s

⋅

=

Masa równowa

ż

na komina.

g

ę

sto

ść

masy stali

ρ

7850

kg

m

3

⋅

:=

masy poszczególnych segmentów na jednostk

ę

długo

ś

ci

i

1 n

s

..

:=

j

1 n

s

..

:=

m

I

i

ρ

π

−

D

d

2

⋅

4

π

D

d

t

i

+

(

)

2

⋅

4

+









⋅

:=

bezwymiarowe współrz

ę

dne komina

ζ

i

z

i

H

:=

ζ

1

j

z

j

1.5 m

⋅

−

H

:=

masa skupiona jest tylko na najwy

ż

szym elemencie

M

ns

300 kg

⋅

:=

m

I

i

277.79

173.25

155.87

138.5

121.14

103.8

m

1

−

kg

⋅

=

M

j

0

0

0

0

0

300

kg

=

ζ

1

j

0.21

0.36

0.51

0.66

0.81

0.96

=

ζ

i

0.25

0.4

0.55

0.7

0.85

1

=

masa równowa

ż

na komina

m

e1

1

n

s

i

m

I

i

ζ

i

( )

4.2

ζ

i 1

−

( )

4.2

+









⋅









∑

=

4.2

1

n

s

j

M

j

H

ζ

1

j

( )

3.2

⋅













∑

=

⋅

+

:=

m

e1

335.64

kg

m

⋅

=

współczynnik

δ

a

T

1

v

H

⋅

C

x

⋅

D

d

⋅

2 m

e1

⋅

:=

δ

a

δ

a

kg

1

−

m

3

⋅

sec

1

−

⋅

:=

δ

a

0.04

=

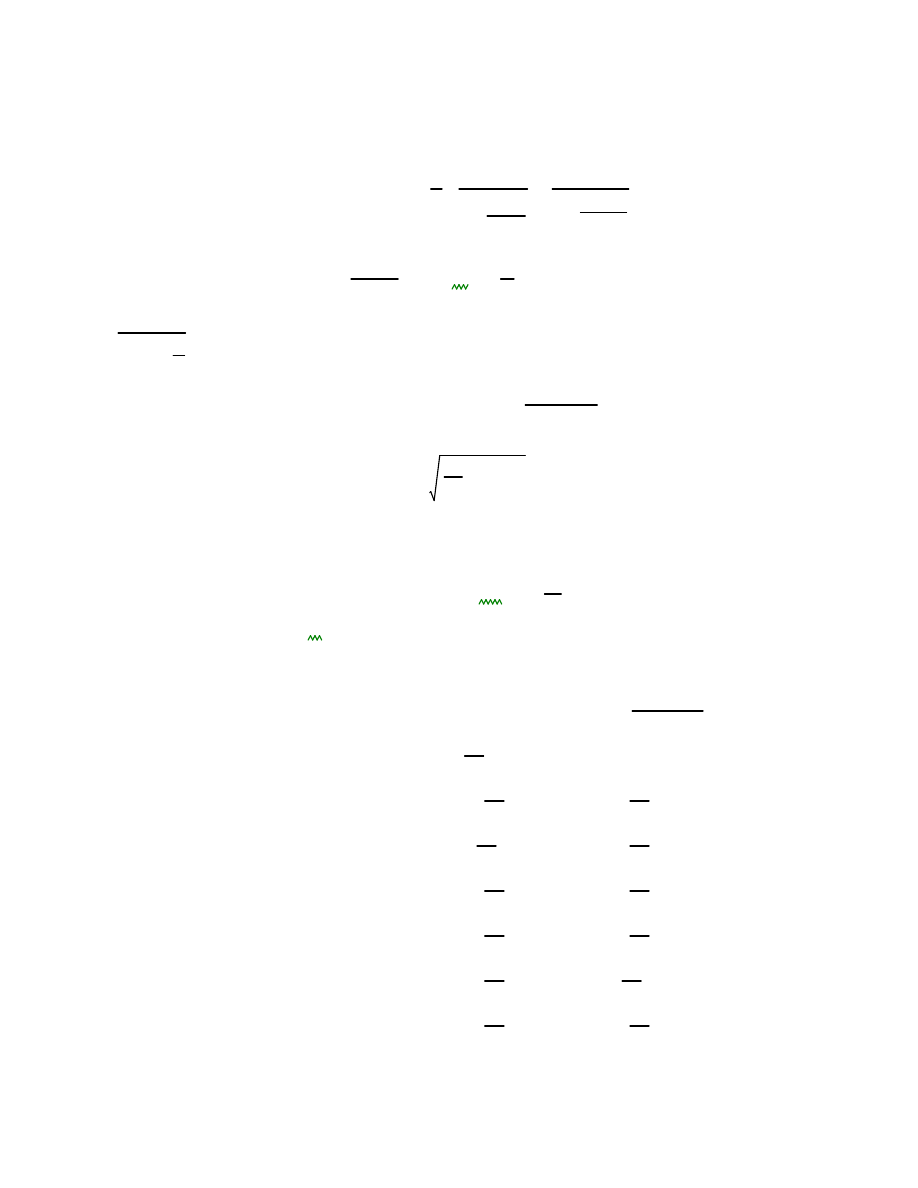
Wyznacznie współczynnika

δδδδ

b

.

współczynnik oddziaływania rezonansowego

K

L

π

3

1

1

8 n

⋅

H

⋅

3 v

H.

⋅

+

















⋅

1

1

10 n

⋅

D

⋅

v

H.

+

















⋅

:=

K

L

0.11

=

współczynnik energii porywów

χ

1200 n

⋅

v

H

:=

χ

χ

m

s

⋅

:=

χ

53.63

=

K

O

χ

2

1

χ

2

+

(

)

4

3

:=

K

O

0.07

=

współczynnik rezonansowego oddziływania turbulentnego

k

r

2

π

⋅

K

L

⋅

K

O

⋅

δ

s

δ

a

+

:=

k

r

0.7

=

współczynnik działania porywów wiatru

β

1

Ψ

r

C

e

k

b

k

r

+

(

)

⋅

⋅

+

:=

β

2.22

=

> 1.8

3.2. Obci

ąż

enie wiatrem poszczególnych segmentów w I sytuacji projektowej.

współczynnik ekspozycji dla poszczególnych segmentów

C

e

i

k

z

i

10













2

α

⋅

⋅

:=

liczba przewodów kominowych

n

1

:=

obci

ąż

enie charakterystyczne wiatrem na górnej kraw

ę

dzi segmentów

p

Ik

i

q

k

D

T

⋅

C

e

i

⋅

C

x

⋅

n

⋅

D

d

⋅

β

⋅

:=

ś

rednie obci

ąż

enie charakterystyczne poszczególnych segmentów

p

Iksr

i

p

Ik

i 1

−

p

Ik

i

+

2

:=

z

0

0 m

=

C

e

0

0

=

p

Ik

0

0

kN

m

⋅

=

segment 1

z

1

10 m

=

C

e

1

1

=

p

Ik

1

0.44

kN

m

⋅

=

p

Iksr

1

0.22

kN

m

⋅

=

segment 2

z

2

16 m

=

C

e

1

1

=

p

Ik

2

0.5

kN

m

⋅

=

p

Iksr

2

0.47

kN

m

⋅

=

segment 3

z

3

22 m

=

C

e

1

1

=

p

Ik

3

0.55

kN

m

⋅

=

p

Iksr

3

0.53

kN

m

⋅

=

segment 4

z

4

28 m

=

C

e

1

1

=

p

Ik

4

0.59

kN

m

⋅

=

p

Iksr

4

0.57

kN

m

⋅

=

segment 5

z

5

34 m

=

C

e

1

1

=

p

Ik

5

0.62

kN

m

⋅

=

p

Iksr

5

0.6

kN

m

⋅

=

segment 6

z

6

40 m

=

C

e

1

1

=

p

Ik

6

0.65

kN

m

⋅

=

p

Iksr

6

0.64

kN

m

⋅

=

Warto

ś

ci obci

ąż

enia wiatrem poszczególnych segmentów.

1

2

3

4

5

6

200

300

400

500

600

700

p

Ik

i

p

Iksr

i

i

.

4. Siły wewn

ę

trzne w podstawach segmentów komina od obc. wiatrem.

4.1. Siły poprzeczne.

segment 6

n

1

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

3.81 kN

⋅

=

segment 5

n

2

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

7.44 kN

⋅

=

segment 4

n

3

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

10.86 kN

⋅

=

segment 3

n

4

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

14.02 kN

⋅

=

segment 2 n

5

:=

P

7 n

−

1

n

n

p

Iksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

16.85 kN

⋅

=

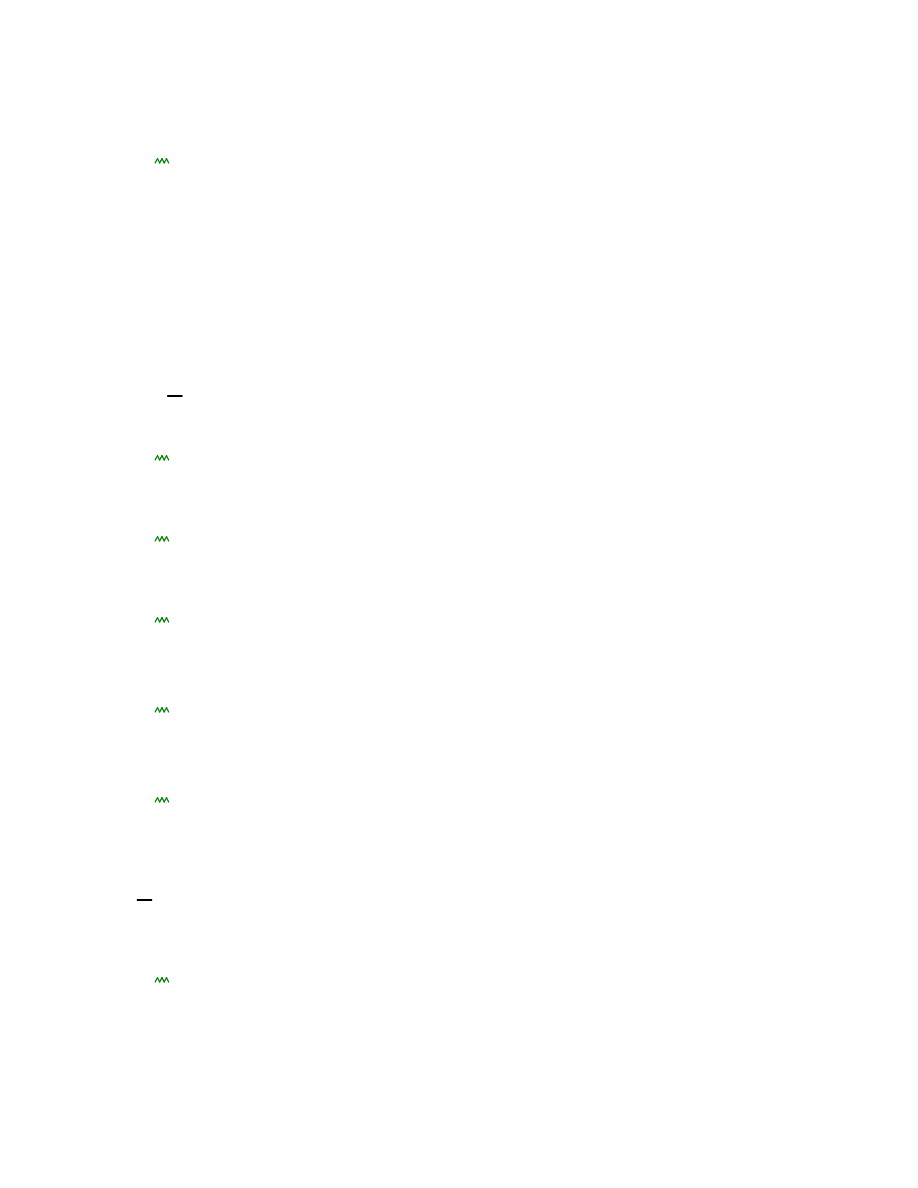
segment 1

n

6

:=

P

7 n

−

P

2

p

Iksr

7 n

−

h

c

⋅

+

:=

P

7 n

−

19.05 kN

⋅

=

4.2. Momenty zginaj

ą

ce.

i

1 n

s

..

:=

Siły poziome na poszczególnych segmentach.

p

i

p

Iksr

ns i

−

1

+

h

s

⋅

:=

p

n

s

p

Iksr

1

h

c

⋅

:=

Ś

rodki ci

ęż

ko

ś

ci segmentów.

x

i

H

h

c

−

h

s

2

−

n

s

1

−

i

−

(

)

h

s

⋅

−

:=

segment 6

n

1

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

11.44 kN m

⋅

⋅

=

segment 5

n

2

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

45.21 kN m

⋅

⋅

=

segment 4

n

3

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

100.12 kN m

⋅

⋅

=

segment 3

n

4

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

174.74 kN m

⋅

⋅

=

segment 2

n

5

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

267.34 kN m

⋅

⋅

=

Ś

rodki ci

ęż

ko

ś

ci segmentów.

x

i

H

h

s

2

−

n

s

i

−

(

)

h

s

⋅

−

:=

segment 1

n

6

:=

M

I

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

I

7 n

−

451.26 kN m

⋅

⋅

=

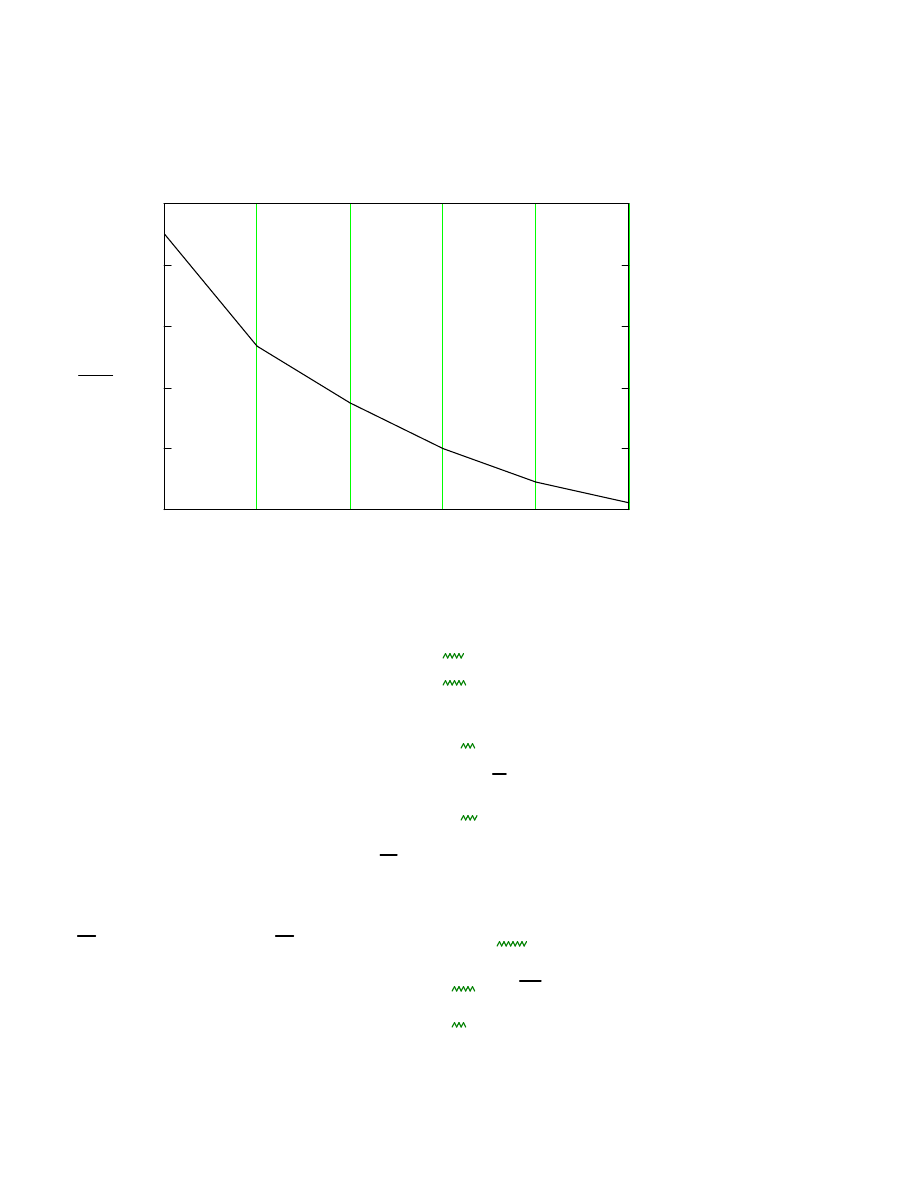
Momnty zginaj

ą

ce w kominie od obci

ąż

enia wiatrem.

1

2

3

4

5

6

0

1 10

5

×

2 10

5

×

3 10

5

×

4 10

5

×

5 10

5

×

M

I

i

i

.

5. Obci

ąż

enie wiatrem w II sytuacji projektowej.

strefa wiatrowa I

teren A

charakterystyczne ci

ś

nienie pr

ę

dko

ś

ci wiatru

q

k

250 Pa

⋅

:=

współczynnik dla czasu eksploatacji

T

e

10 lat

⋅

=

D

T

0.8

:=

Współczynnik ekspozycji.

współczynnik przeliczeniowy zale

ż

ny od rodzaju terenu

k

1

:=

wysko

ść

nad poziomem terenu

z

H

m

:=

z

40

=

wykładnik zale

ż

ny od rodzaju terenu

α

0.14

:=

współczynnik ekspozycji

C

e

k

z

10













2

α

⋅

⋅

:=

C

e

1.47

=

Współczynnik aerodynamiczny dla komina stalowego z drabin

ą

włazow

ą

.

H

D

d

28.57

=

> 25

D

d

H

0.04

=

< 0.04

⇒

C

xo

0.7

:=

( tablica Z2-3 )

pole rzutu bocznego drabiny na płaszczyzn

ę

symetrii

A

d

0.1

m

2

m

⋅

:=

liczba przewodów kominowych

n

1

:=

ś

rednica zewn

ę

trzna komina

D

d

1.4 m

=

współczynnik aerodynamiczny

C

x

C

xo

2.4

A

d

n D

d

⋅

⋅

+

:=

C

x

0.87

=

5.1. Współczynnik działania porywów wiatru.

podstawowy okres drga

ń

własnych

T

1

0.001

H

2

D

⋅

:=

T

1

1.14

=

cz

ę

stotliwo

ść

drga

ń

własnych

n

1

T

1

:=

n

0.87

=

Współczynnik szczytowej warto

ś

ci obci

ąż

enia.

Ψ

2 ln 600 n

⋅

(

)

⋅

0.577

2 ln 600 n

⋅

(

)

⋅

+

:=

Ψ

3.7

=

Wyznacznie współczynnika

δδδδ

s

.

współczynnik chropowato

ś

ci dla terenu A

r

0.08

:=

współczynnik pozarezonansowego oddziaływania turbulentnego

k

b

2.25

0.227 1

3.24

D

H

⋅

+













⋅

ln H

( )

⋅

−

:=

k

b

1.32

=

logarytmiczny dekrement tłumienia drga

ń

wg tablicy Z3-2

dla komina spawanego jednoprzewodowego bez wykładziny

δ

s

1

0.015

:=

dodatek na poł

ą

czenia kołnierzowe

δ

s

2

0.015

:=

δ

s

1

2

i

δ

s

i

∑

=

:=

δ

s

0.03

=

pr

ę

dko

ść

charakterystyczna dla I strefy wiatrowej

v

k

20

m

s

⋅

:=

pr

ę

dko

ść

wiatru na wysoko

ś

ci wierzchołka komina

v

H

v

k

D

T

⋅

C

e

⋅

:=

v

H

21.72

m

s

⋅

=

Masa równowa

ż

na komina.

g

ę

sto

ść

masy stali

ρ

7850

kg

m

3

⋅

:=

masy poszczególnych segmentów na jednostk

ę

długo

ś

ci z uwzgl

ę

dniniem dodatków na korozj

ę

i

1 n

s

..

:=

j

1 n

s

..

:=

t

k

T

e.

∆

t

⋅

mm

⋅

:=

t

k

8 mm

⋅

=

m

II

i

ρ

π

−

D

d

t

k

−

(

)

2

⋅

4

π

D

d

t

i

+

(

)

2

⋅

4

+









⋅

:=

bezwymiarowe współrz

ę

dne komina

ζ

i

z

i

H

:=

ζ

1

j

z

j

1.5 m

⋅

−

H

:=

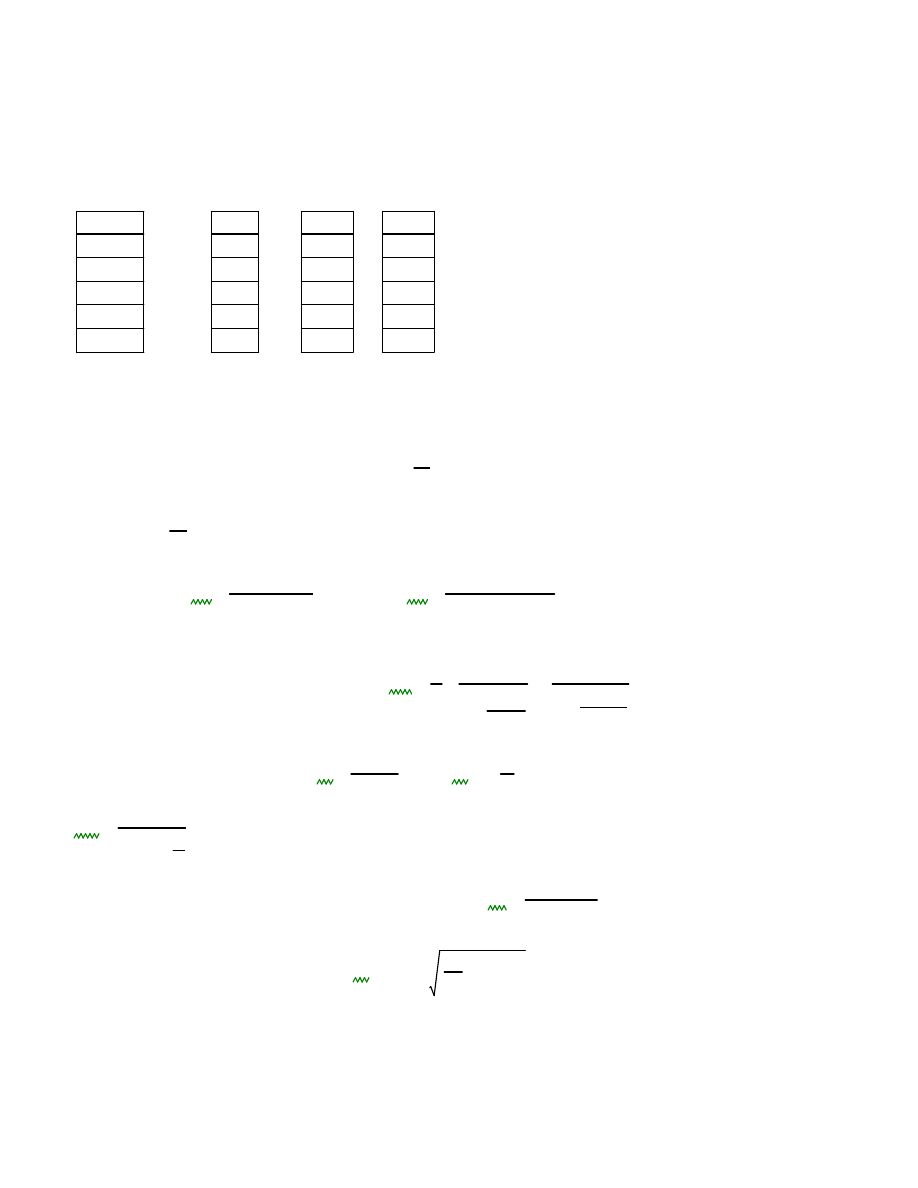
masa skupiona jest tylko na najwy

ż

szym elemencie

M

ns

300 kg

⋅

:=

m

II

i

415.5

310.96

293.58

276.21

258.85

241.51

m

1

−

kg

⋅

=

M

j

0

0

0

0

0

300

kg

=

ζ

1

j

0.21

0.36

0.51

0.66

0.81

0.96

=

ζ

i

0.25

0.4

0.55

0.7

0.85

1

=

masa równowa

ż

na komina

m

e2

1

n

s

i

m

II

i

ζ

i

( )

4.2

ζ

i 1

−

( )

4.2

+









⋅









∑

=

4.2

1

n

s

j

M

j

H

ζ

1

j

( )

3.2

⋅













∑

=

⋅

+

:=

m

e2

703.14

kg

m

⋅

=

współczynnik

δ

a

T

1

v

H

⋅

C

x

⋅

D

d

⋅

2 m

e1

⋅

:=

δ

a

δ

a

kg

1

−

m

3

⋅

sec

1

−

⋅

:=

δ

a

0.05

=

Wyznacznie współczynnika

δδδδ

b

.

współczynnik oddziaływania rezonansowego

K

L

π

3

1

1

8 n

⋅

H

⋅

3 v

H.

⋅

+

















⋅

1

1

10 n

⋅

D

⋅

v

H.

+

















⋅

:=

K

L

0.13

=

współczynnik energii porywów

χ

1200 n

⋅

v

H

:=

χ

χ

m

s

⋅

:=

χ

48.34

=

K

O

χ

2

1

χ

2

+

(

)

4

3

:=

K

O

0.08

=

współczynnik rezonansowego oddziływania turbulentnego

k

r

2

π

⋅

K

L

⋅

K

O

⋅

δ

s

δ

a

+

:=

k

r

0.8

=

współczynnik działania porywów wiatru

β

1

Ψ

r

C

e

k

b

k

r

+

(

)

⋅

⋅

+

:=

β

2.25

=

> 1.8

5.2. Obci

ąż

enie wiatrem poszczególnych segmentów w II sytuacji projektowej.

współczynnik ekspozycji dla poszczególnych segmentów

C

e

i

k

z

i

10













2

α

⋅

⋅

:=

liczba przewodów kominowych

n

1

:=

obci

ąż

enie charakterystyczne wiatrem na górnej kraw

ę

dzi segmentów

p

IIk

i

q

k

D

T

⋅

C

e

i

⋅

C

x

⋅

n

⋅

D

d

⋅

β

⋅

:=

ś

rednie obci

ąż

enie charakterystyczne poszczególnych segmentów

p

IIksr

i

p

IIk

i 1

−

p

IIk

i

+

2

:=

segment 1

z

1

10 m

=

C

e

1

1

=

p

IIk

1

0.55

kN

m

⋅

=

p

IIksr

1

0.27

kN

m

⋅

=

segment 2

z

2

16 m

=

C

e

1

1

=

p

IIk

2

0.63

kN

m

⋅

=

p

IIksr

2

0.59

kN

m

⋅

=

segment 3

z

3

22 m

=

C

e

1

1

=

p

IIk

3

0.69

kN

m

⋅

=

p

IIksr

3

0.66

kN

m

⋅

=

segment 4

z

4

28 m

=

C

e

1

1

=

p

IIk

4

0.73

kN

m

⋅

=

p

IIksr

4

0.71

kN

m

⋅

=

segment 5

z

5

34 m

=

C

e

1

1

=

p

IIk

5

0.77

kN

m

⋅

=

p

IIksr

5

0.75

kN

m

⋅

=

segment 6

z

6

40 m

=

C

e

1

1

=

p

IIk

6

0.81

kN

m

⋅

=

p

IIksr

6

0.79

kN

m

⋅

=

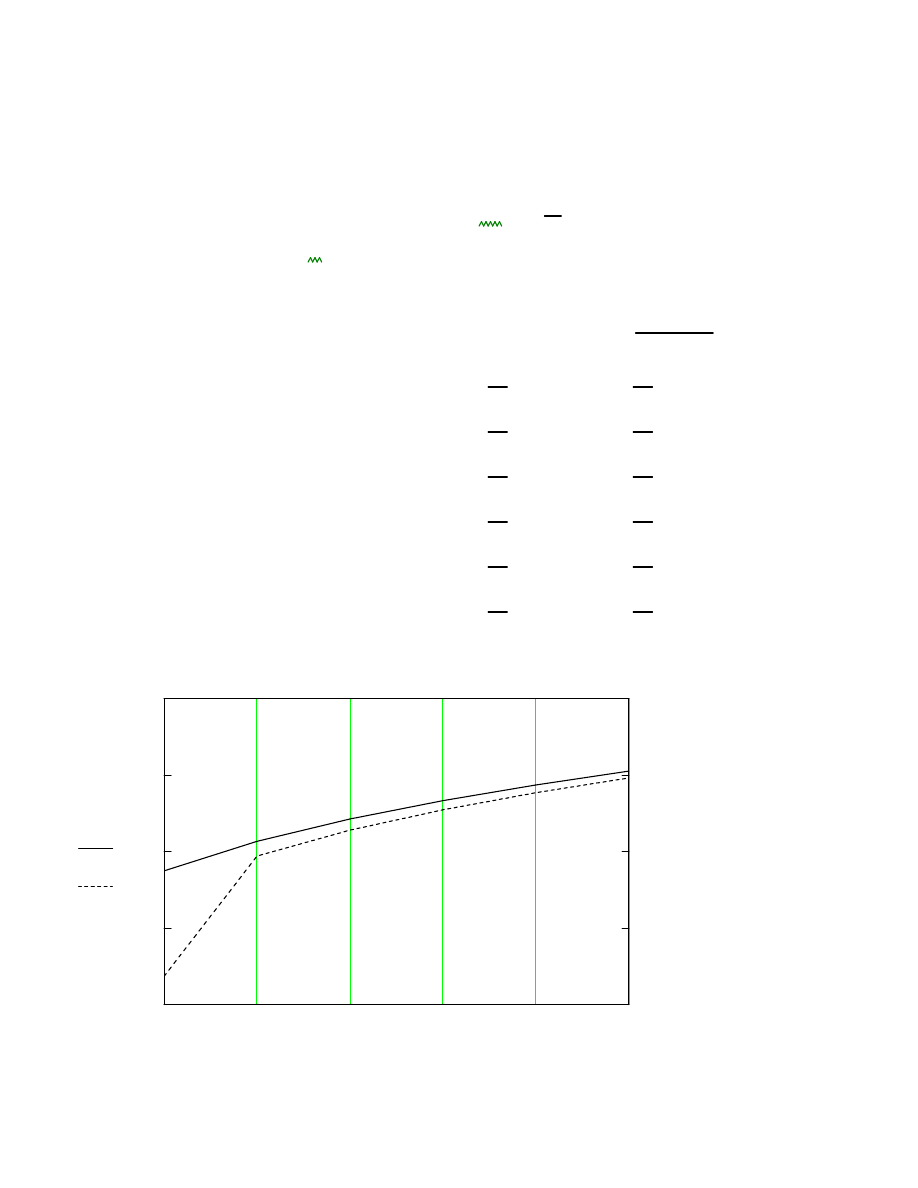
Warto

ś

ci obci

ąż

enia wiatrem poszczególnych segmentów.

1

2

3

4

5

6

200

400

600

800

1 10

3

×

p

IIk

i

p

IIksr

i

i

.

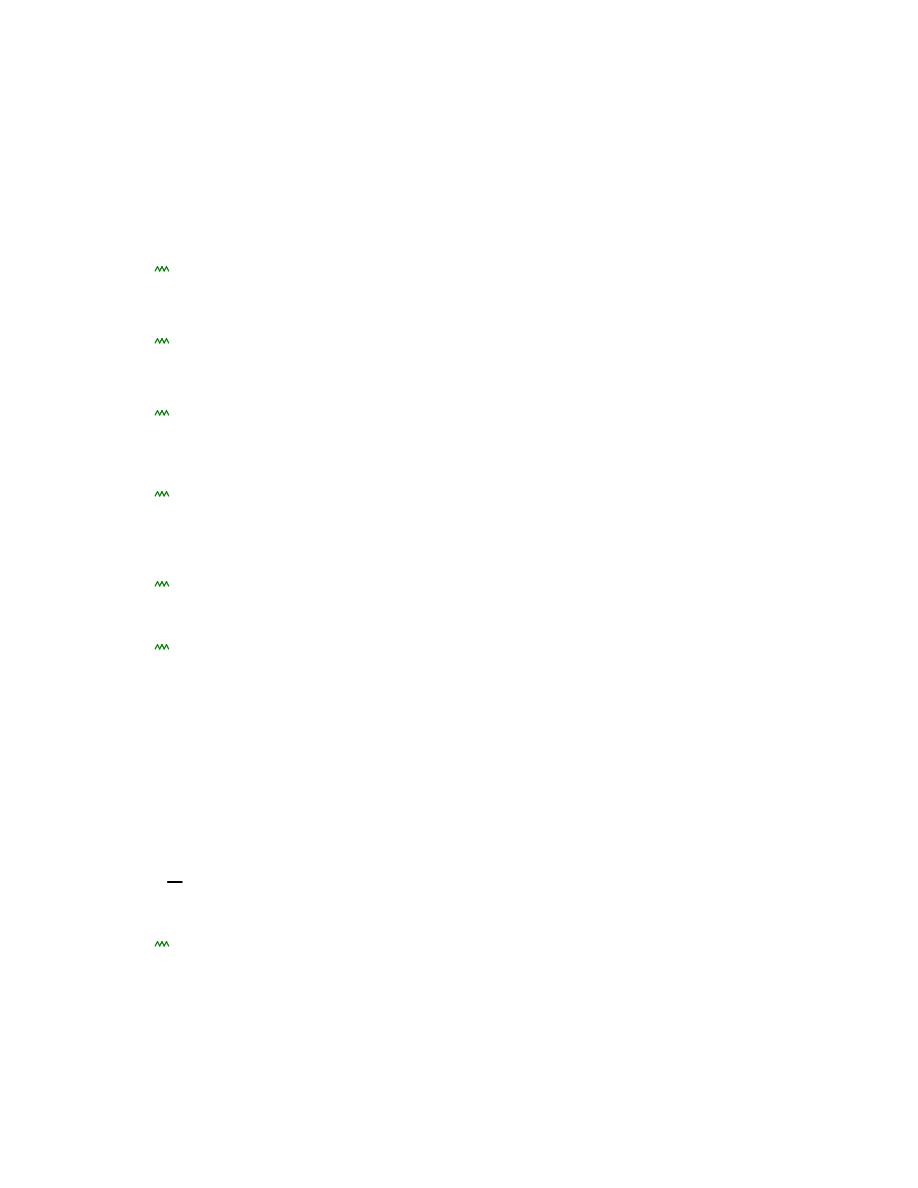
6. Siły wewn

ę

trzne w podstawach segmentów komina od obc. wiatrem.

6.1. Siły poprzeczne.

segment 6

n

1

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

4.76 kN

⋅

=

segment 5

n

2

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

9.28 kN

⋅

=

segment 4

n

3

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

13.54 kN

⋅

=

segment 3

n

4

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

17.48 kN

⋅

=

segment 2 n

5

:=

P

7 n

−

1

n

n

p

IIksr

7 n

−

h

s

⋅

(

)

∑

=

:=

P

7 n

−

21.01 kN

⋅

=

segment 1

n

6

:=

P

7 n

−

P

2

p

IIksr

7 n

−

h

c

⋅

+

:=

P

7 n

−

23.76 kN

⋅

=

6.2. Momenty zginaj

ą

ce.

i

1 n

s

..

:=

Siły poziome na poszczególnych segmentach.

p

i

p

IIksr

ns i

−

1

+

h

s

⋅

:=

p

n

s

p

IIksr

1

h

c

⋅

:=

Ś

rodki ci

ęż

ko

ś

ci segmentów.

x

i

H

h

c

−

h

s

2

−

n

s

1

−

i

−

(

)

h

s

⋅

−

:=

segment 6

n

1

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

14.27 kN m

⋅

⋅

=

segment 5

n

2

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

56.39 kN m

⋅

⋅

=

segment 4

n

3

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

124.85 kN m

⋅

⋅

=

segment 3

n

4

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

217.92 kN m

⋅

⋅

=

segment 2

n

5

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

333.39 kN m

⋅

⋅

=

Ś

rodki ci

ęż

ko

ś

ci segmentów.

x

i

H

h

s

2

−

n

s

i

−

(

)

h

s

⋅

−

:=

segment 1

n

6

:=

M

II

7 n

−

1

n

i

p

i

x

n 1

+

i

−

⋅

(

)

∑

=

:=

M

II

7 n

−

562.76 kN m

⋅

⋅

=

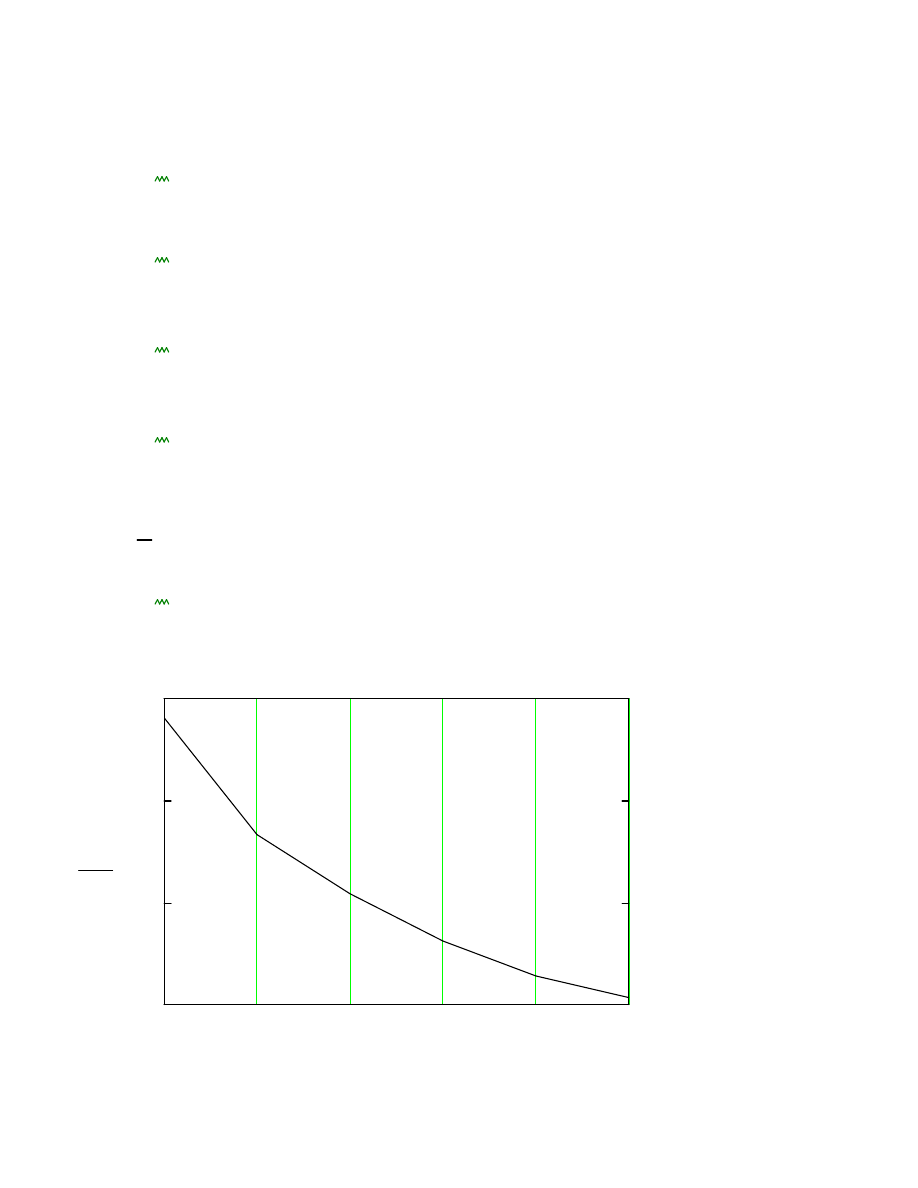
Momnty zginaj

ą

ce w kominie od obci

ąż

enia wiatrem.

1

2

3

4

5

6

0

2 10

5

×

4 10

5

×

6 10

5

×

M

II

i

i

.

7. Obci

ąż

enia prostopadłe do linii wiatru.

Obliczenia wykonano w I sytuacj projektowej.

Pr

ę

dko

ść

krytyczna przy której nast

ę

puje wzbudzenie wirowe.

liczba Strouhala

S

t

0.2

:=

odległo

ść

mi

ę

dzy osiami przewodów komina wieloprzewodowego

a

0

:=

okres dega

ń

własnych komina

T

1

1.14

=

pr

ę

dko

ść

krytyczna

v

cr

a

D

+

T

1

S

t

⋅

:=

v

cr

6.12

=

[ m/s ]

Liczba Scrutona.

masa równowa

ż

na

m

e1

335.64

kg

m

⋅

=

logarytmiczny dekrement tłumienia

δ

s

0.03

=

g

ę

sto

ść

powietrza

ρ

p

1.25

kg

m

3

⋅

:=

liczba Scrutona

S

c

2 m

e1

⋅

δ

s

⋅

ρ

p

D

d

2

⋅

:=

S

c

8.22

=

< 15

oraz

v

cr

6.12

=

Nale

ż

y uwzgl

ę

dni

ć

obci

ąż

enie wzbudzeniem wirowym.

7.1. Obci

ąż

enie wzbudzeniem wirowym wg procedury uproszczonej.

Obci

ąż

enie charakterystyczne w płaszczy

ź

nie prostopadłej do wiatru.

moduł współczynnika aerodynamicznej pulsacyjnej siły bocznej

c

lat

1

0.1 v

cr

⋅

D

⋅

−

:=

c

lat

0.14

=

warto

ść

obci

ąż

enia

p

y

0.05

ρ

p

⋅

T

1

( )

2

δ

s

⋅

c

lat

⋅

D

3

⋅

:=

p

y

p

y

kN

m

⋅

:=

p

y

0.62

kN

m

⋅

=

Obci

ąż

enie przyłozono na odcinku

l

o

0.25 H

⋅

:=

l

o

10 m

=

>

6 D

d

⋅

8.4 m

=

7.2. Momenty zginaj

ą

ce wywołane przyło

ż

onym obci

ąż

eniem.

segment 6

i

6

:=

M

y

i

p

y

h

s

2

⋅

2

:=

M

y

i

11.23 kN m

⋅

⋅

=

wypadkowa warto

ść

obci

ąż

enia

P

y

p

y

l

o

⋅

:=

P

y

6.24 kN

⋅

=

odległo

ść

od dołu komina

z

w

H

l

o

2

−

:=

z

w

35 m

=

Momenty w pozostałych segmentach.

i

1 n

s

1

−

..

:=

M

y

i

P

y

z

w

z

i

−

h

c

+

(

)

⋅

:=

i

1

2

3

4

5

=

z

i

10

16

22

28

34

m

=

M

y

1

218.29 kN m

⋅

⋅

=

M

y

2

180.87 kN m

⋅

⋅

=

i

1 n

s

..

:=

M

y

3

143.45 kN m

⋅

⋅

=

M

y

4

106.03 kN m

⋅

⋅

=

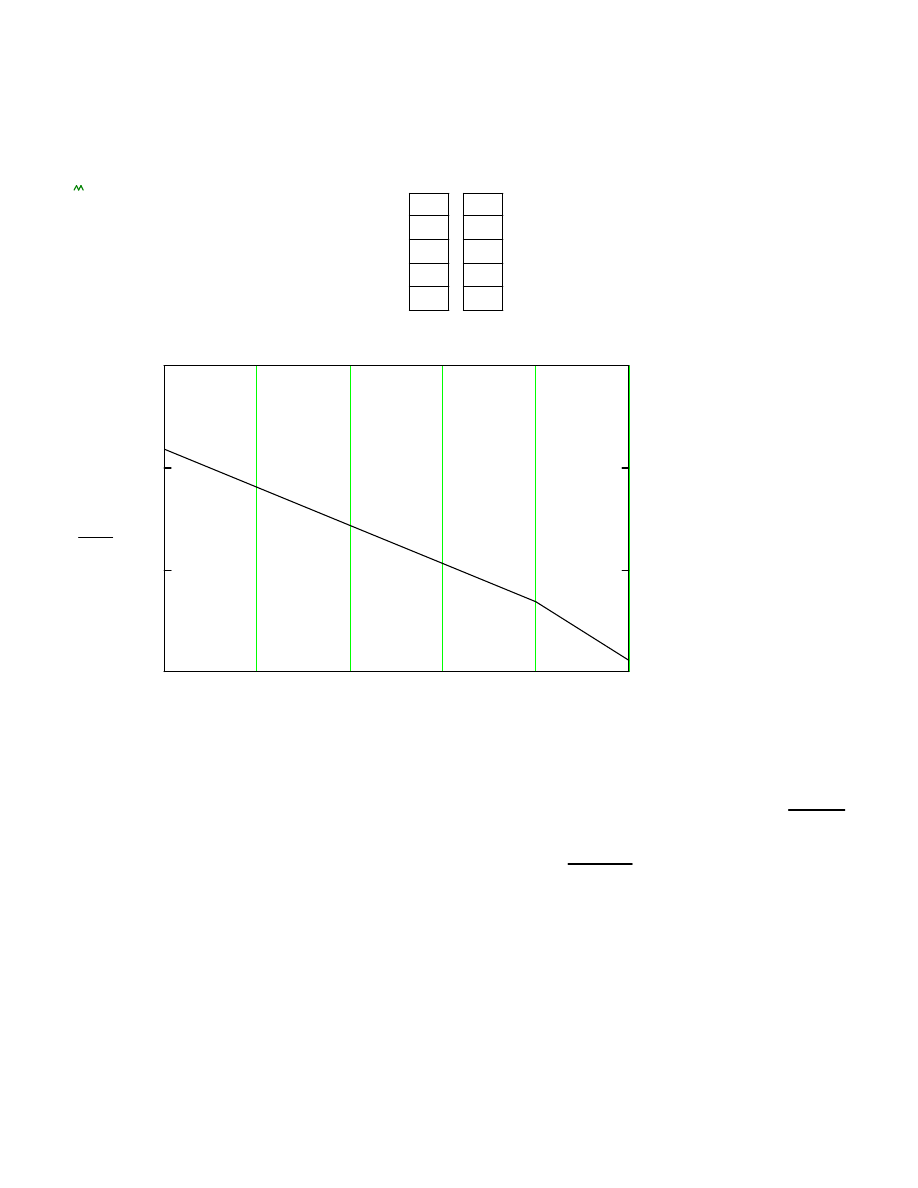
Momenty zginaj

ą

ce:

M

y

5

68.61 kN m

⋅

⋅

=

1

2

3

4

5

6

0

1 10

5

×

2 10

5

×

3 10

5

×

M

y

i

i

8. Obci

ąż

enia stałe.

wielko

ść

naddatku korozyjnego

t

k

8 mm

⋅

=

ci

ęż

ary poszczególnych segmentów

i

2 n

s

..

:=

G

I

i

m

I

i

h

s

⋅

:=

G

II

i

m

II

i

h

s

⋅

:=

G

III

i

G

I

i

G

II

i

+

2

:=

ci

ęż

ar cokoła

G

I

1

m

I

1

h

c

⋅

:=

G

II

1

m

II

1

h

c

⋅

:=

G

III

1

m

I

1

m

I

2

+

2

h

c

⋅

:=

ci

ęż

ar galeri

M

ns

300 kg

=

siły podłu

ż

ne w poszczególnych przekrojach

i

1 n

s

..

:=

N

I

i

i

n

s

n

G

III

n

M

ns

+









∑

=

:=

N

II

i

i

n

s

n

G

II

n

M

ns

+









∑

=

:=

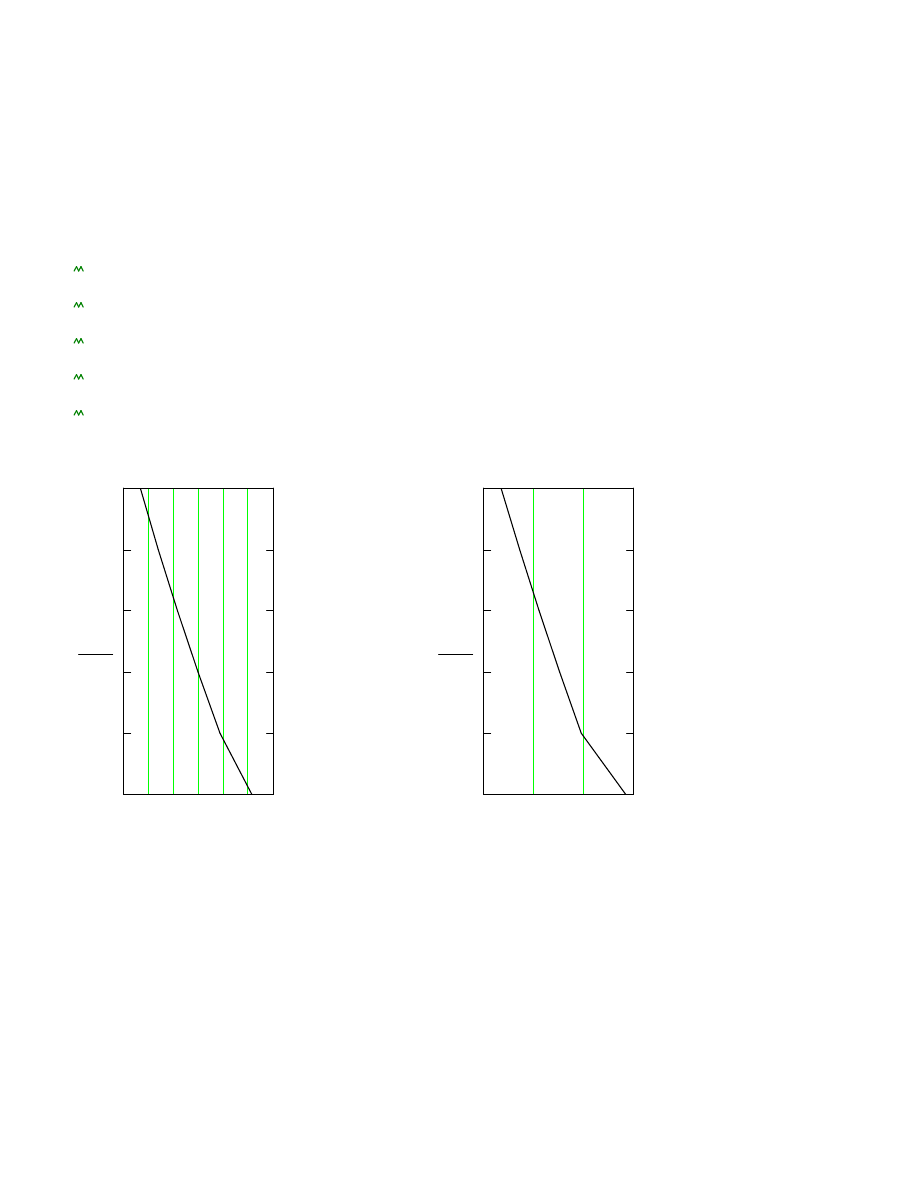
Siły podłu

ż

ne w podstawach poszczególnych segmentów.

segment

wysoko

ść

grubo

ść

wyj

ś

ciowa

ci

ęż

ar z połow

ą

naddatku

ci

ęż

ar z całym naddatkiem

i

1

:=

z

i

10 m

=

t

i

16 mm

⋅

=

N

I

i

10276.16 kg

=

N

II

i

14241.6 kg

⋅

=

i

2

:=

z

i

16 m

=

t

i

10 mm

⋅

=

N

I

i

7720.99 kg

=

N

II

i

9786.63 kg

⋅

=

i

3

:=

z

i

22 m

=

t

i

9 mm

⋅

=

N

I

i

5968.38 kg

=

N

II

i

7620.89 kg

⋅

=

i

4

:=

z

i

28 m

=

t

i

8 mm

⋅

=

N

I

i

4320.04 kg

=

N

II

i

5559.43 kg

⋅

=

i

5

:=

z

i

34 m

=

t

i

7 mm

⋅

=

N

I

i

2775.92 kg

=

N

II

i

3602.18 kg

⋅

=

i

6

:=

z

i

40 m

=

t

i

6 mm

⋅

=

N

I

i

1335.93 kg

=

N

II

i

1749.06 kg

⋅

=

Siły podłu

ż

ne w trzonie.

0

6 10

3

×

1.2 10

4

×

1

2

3

4

5

6

i

N

I

i

0

1 10

4

×

1

2

3

4

5

6

i

N

II

i

połowa naddatku na korozj

ę

cały naddatek na korozj

ę

9. Spr

ęż

yste wychylenie wierzchołka trzonu komina.

Ugi

ę

cie wierzchołka obliczono metod

ą

Maxwella-Mohra wyra

ż

on

ą

wzorem:

y

w

=

∑

∫

[(

M

r

*M

p

)]/EJ dx

gdzie M

r

-funkcja momentów zginaj

ą

cych rzeczywistych od obci

ąż

enia poziomego

M

p

-funkcja momentów zginaj

ą

cych od obci

ąż

enia wirtualnego

na poszczególnych segmentach komina

9.1. Ugi

ę

cie w I sytuacji projektowej.

Obci

ąż

enie jednostkowe jest przyło

ż

one w wierzchołku komina.

Segment 6.

i

6

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

:=

grubo

ść

ś

cianki trzonu

t

i

6 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

325353.99 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

11.44 m kN

⋅

=

M

pk

6 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

0.15 mm

⋅

=

Segment 5.

i

5

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

7 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

379986.25 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

45.21 m kN

⋅

=

M

pk

12 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

2.67 mm

⋅

=

Segment 4.

i

4

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

8 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

434735.12 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

100.12 m kN

⋅

=

M

pk

18 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

9.46 mm

⋅

=

Segment 3.

i

3

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

9 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

489600.77 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

174.74 m kN

⋅

=

M

pk

24 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

21.17 mm

⋅

=

Segment 2.

i

2

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

10 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

544583.35 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

267.34 m kN

⋅

=

M

pk

30 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

37.99 mm

⋅

=

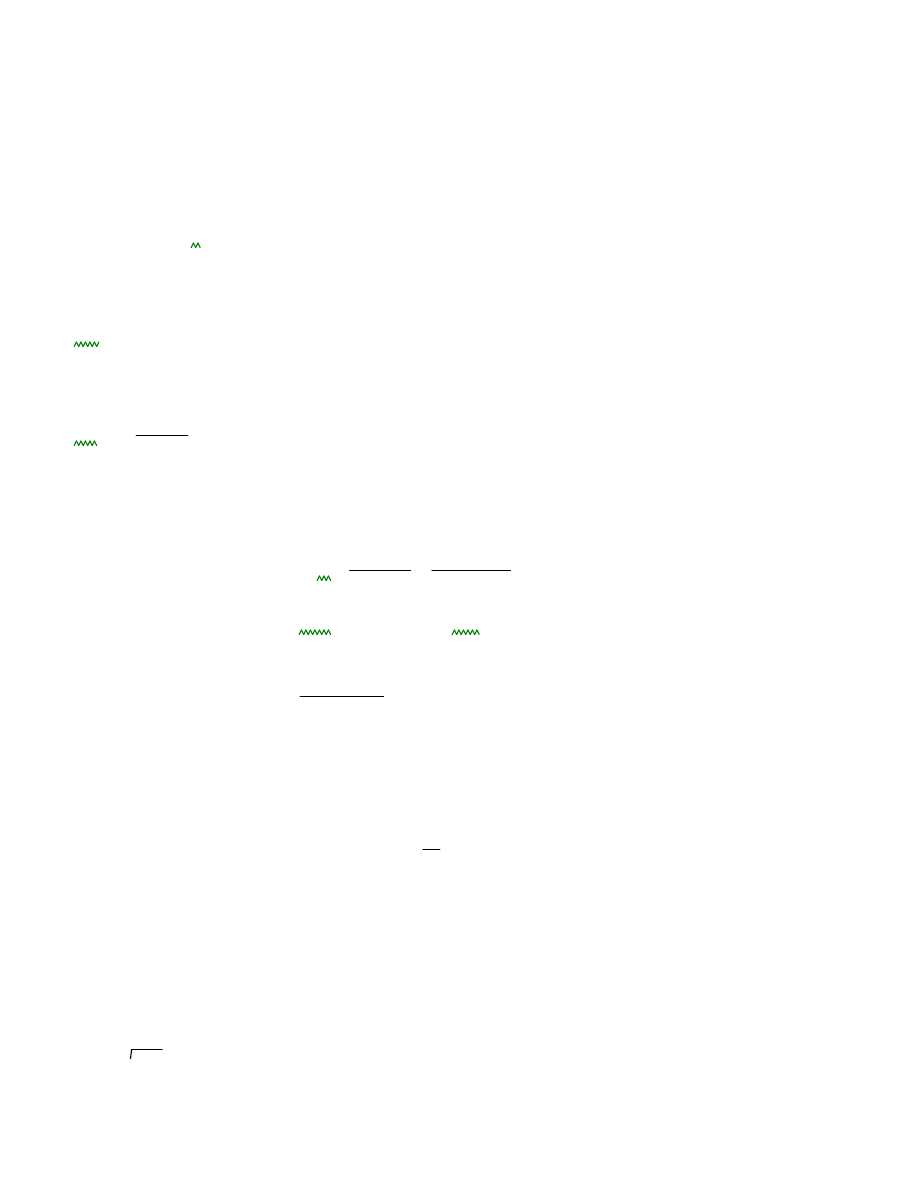
Segment 1.

i

1

:=

wysoko

ść

segmentu

x

0 m

⋅

h

c

..

:=

h

c

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

⋅

5 m

⋅

n

1

−

(

) h

s

⋅

+





⋅









∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

16 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

876943.99 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

c

( )

:=

M

rk

M

r

h

c

( )

:=

M

rk

413.15 m kN

⋅

=

M

pk

40 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

c

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

79.06 mm

⋅

=

Ugi

ę

cie wierzchołka komina

u

w

1

n

s

i

u

i

∑

=

:=

u

w

0.15 m

⋅

=

Dopusczalne ugi

ę

ci wierzchołka komina

u

dop

H

75

:=

u

dop

0.53 m

=

( jak dla komina jednopowłokowego )

u

w

0.15 m

=

<

u

dop

0.53 m

=

u

w

0.15 m

=

>

0.01 H

⋅

0.4 m

=

Nale

ż

y w I sytuacji projektowej uwzgl

ę

dni

ć

efekty II rz

ę

du.

obliczeniowa siła osiowa w przekroju zamocowania

N

o

N

I

1

1.1

⋅

g

⋅

:=

N

o

110.85 kN

⋅

=

sztywno

ść

komina w przekroju zamocowania

EJ

o

E J

⋅

:=

EJ

o

1797735.18 kN m

2

⋅

⋅

=

N

o

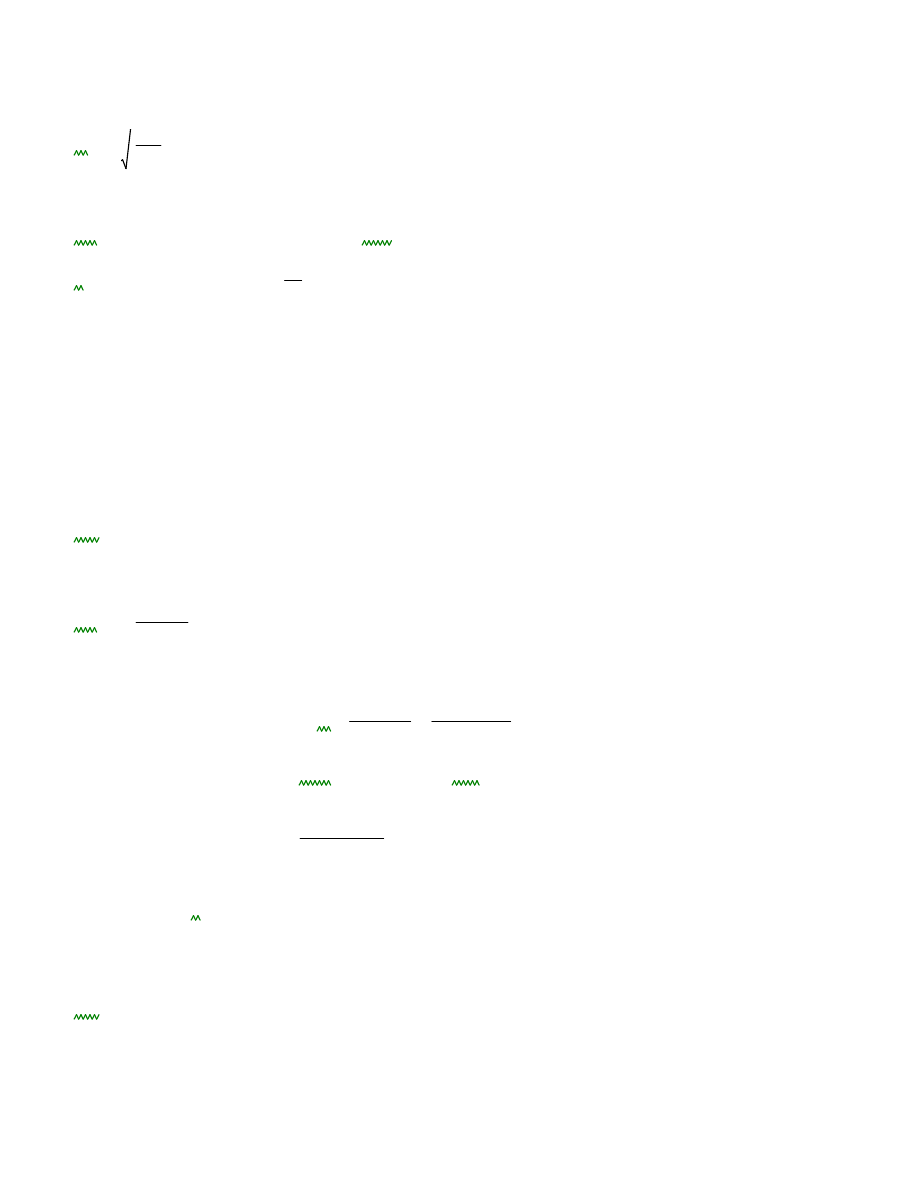
ε

H

N

o

EJ

o

⋅

:=

ε

0.31

=

< 0.8

zgodnie z norm

ą

oblicznia wg teorii II rz

ę

du przeprowadzono sposobem przybli

ż

onym

Zast

ę

pcze momenty wg teorii II rz

ę

du

N

o

N

o

kN

⋅

:=

N

o

110852.16 m s

2

−

kg

⋅

⋅

kN

⋅

=

EJ

o

E J

⋅

:=

EJ

o

1797735.18 kN m

2

⋅

⋅

=

i

1 n

s

..

:=

M'

I

i

M

I

i

1

ε

2

8

+













⋅

:=

9.1. Ugi

ę

cie w II sytuacji projektowej.

Obci

ąż

enie jednostkowe jest przyło

ż

one w wierzchołku komina.

Segment 6.

i

6

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

14 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

765686.46 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

11.44 m kN

⋅

=

M

pk

6 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

0.07 mm

⋅

=

Segment 5.

i

5

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

15 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

821256.26 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

45.21 m kN

⋅

=

M

pk

12 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

1.24 mm

⋅

=

Segment 4.

i

4

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

t

i

t

i

t

k

+

:=

t

i

16 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

grubo

ść

ś

cianki trzonu

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

876943.99 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

100.12 m kN

⋅

=

M

pk

18 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠




⌡

d

:=

u

i

4.69 mm

⋅

=

Segment 3.

i

3

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

17 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

932749.84 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

174.74 m kN

⋅

=

M

pk

24 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

11.11 mm

⋅

=

Segment 2.

i

2

:=

wysoko

ść

segmentu

x

0 m

⋅

h

s

..

:=

h

s

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

2

⋅

1

2

n

+

i

−













⋅













∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

18 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

988673.95 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

s

( )

:=

M

rk

M

r

h

s

( )

:=

M

rk

267.34 m kN

⋅

=

M

pk

30 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

s

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

20.93 mm

⋅

=

Segment 1.

i

1

:=

wysoko

ść

segmentu

x

0 m

⋅

h

c

..

:=

h

c

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia wirtualnego w postaci funkcji M

p

(x)

M

p

x

( )

1 x

⋅

M

pk

+

:=

przedstawienie momentów zginaj

ą

cych od obci

ąż

enia rzeczywistego w postaci funkcji M

r

(x)

M

r

x

( )

p

Iksr

i

x

2

⋅

2

i 1

+

n

s

n

p

Iksr

n

h

s

⋅

5 m

⋅

n

1

−

(

) h

s

⋅

+





⋅









∑

=

+

:=

grubo

ść

ś

cianki trzonu

t

i

t

i

t

k

+

:=

t

i

24 mm

⋅

=

ś

rednica wewn

ę

trzna

D

d

1400 mm

⋅

=

moment bezwładno

ś

ci przekroju

J

π

−

D

d

( )

4

⋅

64

π

D

d

t

i

+

(

)

4

⋅

64

+

:=

J

1326711.79 cm

4

⋅

=

Momenty na ko

ń

cu segmentu

M

pk

M

p

h

c

( )

:=

M

rk

M

r

h

c

( )

:=

M

rk

413.15 m kN

⋅

=

M

pk

40 m

=

Ugi

ę

cie segmentu.

u

i

0 m

⋅

h

c

x

M

p

x

( ) M

r

x

( )

⋅

E J

⋅

⌠





⌡

d

:=

u

i

52.26 mm

⋅

=

Ugi

ę

cie wierzchołka komina

u

w

1

n

s

i

u

i

∑

=

:=

u

w

0.09 m

⋅

=

Dopusczalne ugi

ę

ci wierzchołka komina

u

dop

H

75

:=

u

dop

0.53 m

=

( jak dla komina jednopowłokowego )

u

w

0.09 m

=

<

u

dop

0.53 m

=

u

w

0.09 m

=

<

0.01 H

⋅

0.4 m

=

Obliczenia dla II sytuacji projektowej mo

ż

na przeprowadzi

ć

wg teorii I rz

ę

du.

10. Sprawdzanie trzonu w I sytuacji projektowej.

10.1. Pierwsza kombinacja podstawowa obci

ąż

e

ń

.

Pierwsza kombinacja obejmuje:
- obci

ąż

enie stałe powi

ę

kszone o ci

ęż

ar połowy naddatku korozyjnego

- obci

ąż

enie wiatrem w linii wiatru dla 3-letniego czasu u

ż

ytkowania

- obci

ąż

enia technologiczne z pomini

ę

ciem obci

ąż

enia pomostu i drabin

No

ś

no

ść

w dolnym przekroju segmentu I (najni

ż

szego).

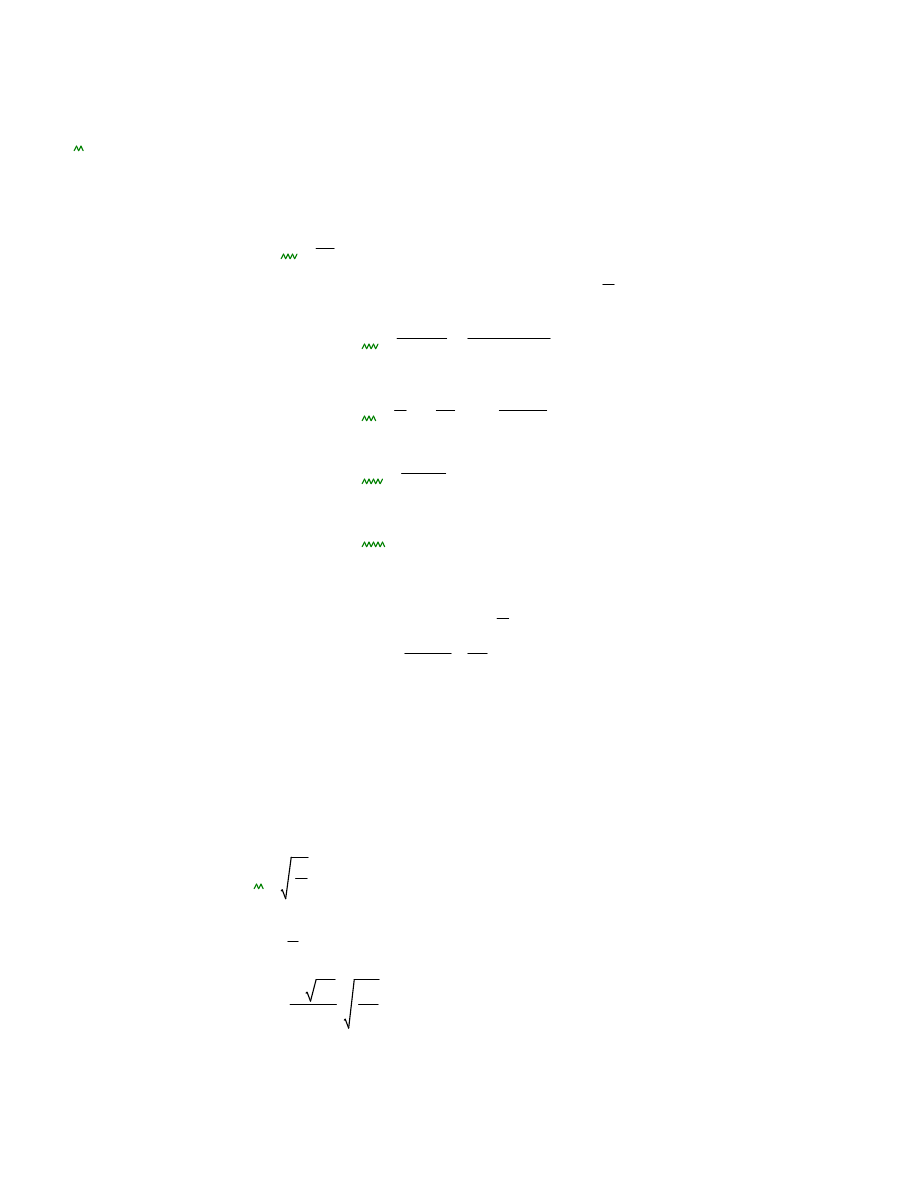
i

1

:=

długo

ść

oblczeniowa komina

l

c

1.12 H

⋅

:=

l

c

44.8 m

=

poziom

z

z

i

h

c

−

:=

z

0 m

=

promie

ń

zewn

ę

trzny trzonu

R

D

d

2

:=

R

700 mm

⋅

=

grubo

ść

segmentu z uwzgl

ę

dnieniem połowy naddatku korozyjnego

g

t

t

i

t

k

2

−

:=

g

t

20 mm

⋅

=

pole przekroju poprzecznego pier

ś

cienia

A

π

−

D

d

2

⋅

4

π

D

d

g

t

+

(

)

2

⋅

4

+

:=

A

442.96 cm

2

⋅

=

moment bezwładno

ś

ci przekroju

J

π

4

D

d

2













4

−

D

d

g

t

+

2













4

+









⋅

:=

J

1100877.68 cm

4

⋅

=

wska

ź

nik wytrzymało

ś

ci przekroju

W

J

0.5 D

d

⋅

:=

W

15726.82 cm

3

⋅

=

obliczeniowa siła

ś

ciskaj

ą

ca

N

o

1.1 N

I

i

⋅

g

⋅

:=

N

o

110.85 kN

⋅

=

obliczeniowy moment zginaj

ą

cy

M

o

1.3 M

I

i

⋅

:=

M

o

586.64 kN m

⋅

⋅

=

smukło

ść

wzgl

ę

dna przekroju

λ

'

p

R

g

t

1.59

⋅

f

dT

E

T













2

3

⋅

:=

λ

'

p

0.27

=

współczynnik niestateczno

ś

ci ogólnej

ϕ

p

1

λ

'

p

2.4

+









0.625

−

:=

ϕ

p

0.97

=

obliczeniowa no

ś

no

ść

przekroju na

ś

ciskanie

N

R

ϕ

p

α

kor

⋅

A

⋅

f

dT

⋅

:=

N

R

9072.97 kN

⋅

=

obliczeniowa no

ś

no

ść

przekroju na zginanie

M

R

1.2

ϕ

p

⋅

α

kor

⋅

W

⋅

f

dT

⋅

:=

M

R

3865.47 kN m

⋅

⋅

=

Współczynnik wyboczeniowy.

promie

ń

bezwładno

ś

ci

i

J

A

:=

i

498.52 mm

⋅

=

smukło

ść

λ

l

c

i

:=

smukło

ść

porównawcza

λ

'

λ

ϕ

p

⋅

2.73

f

dT

E

T

⋅

:=

λ

'

1.2

=

(

)

współczynnik niestateczno

ś

ci ogólnej

ϕ

1

λ

'

3.2

+

(

)

0.625

−

:=

ϕ

0.53

=

Oblczeniowa no

ś

no

ść

przekroju:

N

o

ϕ

N

R

⋅

M

o

M

R

+

0.18

=

10.1. Druga kombinacja podstawowa obci

ąż

e

ń

.

Druga kombinacja obejmuje warto

ś

ci charakterystyczne:

- obci

ąż

enie stałe powi

ę

kszone o połow

ę

naddatku korozyjnego

- obci

ąż

enie wiatrem w płaszczy

ź

nie prostopadłej do linii wiatru

- obci

ąż

enie technologiczne z pomini

ę

ciem obci

ąż

enia pomostów i drabin

No

ś

no

ść

w dolnym przekroju segmentu I (najni

ż

szym).

i

1

:=

poziom

z

z

i

h

c

−

:=

z

0 m

=

promie

ń

zewn

ę

trzny trzonu

R

D

d

2

:=

R

700 mm

⋅

=

grubo

ść

segmentu z uwzgl

ę

dnieniem połowy naddatku korozyjnego

g

t

t

i

t

k

2

−

:=

g

t

20 mm

⋅

=

liczba cykli obci

ąż

enia wzbudzeniem wirowym

okres eksploatacji

T

e

T

e

lat

:=

T

e

10

=

N

wz

5.1 10

6

⋅

T

e

T

1

⋅

e

0.16 v

cr

⋅

(

)

2

−

e

0.2 v

cr

⋅

(

)

2

−

−









⋅

:=

N

wz

7128799.66

=

pole przekroju poprzecznego pier

ś

cienia

A

π

−

D

d

2

⋅

4

π

D

d

g

t

+

(

)

2

⋅

4

+

:=

A

442.96 cm

2

⋅

=

moment bezwładno

ś

ci przekroju

J

π

4

D

d

2













4

−

D

d

g

t

+

2













4

+









⋅

:=

J

1100877.68 cm

4

⋅

=

wska

ź

nik wytrzymało

ś

ci przekroju

W

J

0.5 D

d

⋅

:=

W

15726.82 cm

3

⋅

=

charakterystyczna siła

ś

ciskaj

ą

ca

N

ch

N

I

i

g

⋅

:=

N

ch

100.77 kN

⋅

=

charakterystyczny moment zginaj

ą

cy

M

ch

M

y

i

:=

M

ch

218.29 kN m

⋅

⋅

=

maksymalne napr

ęż

enie w trzonie

σ

max

N

ch

A

M

ch

W

+

:=

σ

max

16.16 MPa

⋅

=

minimalne napr

ęż

enia w trzonie

σ

min

N

ch

A

M

ch

W

−

:=

σ

min

11.61

−

MPa

⋅

=

zakres zmiennoi

ś

ci napr

ęż

e

ń

∆σ

σ

min

σ

max

+

:=

∆σ

27.76 MPa

⋅

=

dla

N

wz

7128799.66

=

<

m

3

:=

kategoria zm

ę

czeniowa

∆σ

c

56 MPa

⋅

:=

wytrzymało

ść

zm

ę

czeniowa trzonu

∆σ

R

0.735

∆σ

c

⋅

5 10

6

⋅

N

wz









1

m

⋅

:=

∆σ

R

36.57 MPa

⋅

=

ś

rednia temperatura zewn

ę

trzna

T

z

T

zl

T

zz

+

2

:=

T

z

274.5 K

=

nie uwzgl

ę

dnia si

ę

wpływów temperatury gazów wewn

ą

trz komina na wytrzymało

ść

stali płaszcza

α

T

1

:=

∆σ

27.76 MPa

⋅

=

<

α

T

α

kor

⋅

∆σ

R

⋅

31.08 MPa

⋅

=

11. Sprawdzanie trzonu w II sytuacji projektowej.

11.1. Podstawowa kombinacja obci

ąż

e

ń

.

W II sytuacji projektowej uwzgl

ę

dnia si

ę

warto

ś

ci obliczeniowe:

- obci

ąż

enia stałego

- obci

ąż

enia wiatrem w linii wiatru (dla całego okresu eksploatacyjneg)

- obci

ąż

enia technologiczne z pomini

ę

ciem obci

ąż

enia pomstów i drabin

- obci

ąż

enie temperatur

ą

No

ś

no

ść

w dolnym przekroju segmentu I (najni

ż

szego).

i

1

:=

długo

ść

oblczeniowa komina

l

c

1.12 H

⋅

:=

l

c

44.8 m

=

poziom

z

z

i

h

c

−

:=

z

0 m

=

promie

ń

zewn

ę

trzny trzonu

R

D

d

2

:=

R

700 mm

⋅

=

grubo

ść

segmentu z uwzgl

ę

dnieniem połowy naddatku korozyjnego

g

t

t

i

:=

g

t

24 mm

⋅

=

pole przekroju poprzecznego pier

ś

cienia

A

π

−

D

d

2

⋅

4

π

D

d

g

t

+

(

)

2

⋅

4

+

:=

A

532.31 cm

2

⋅

=

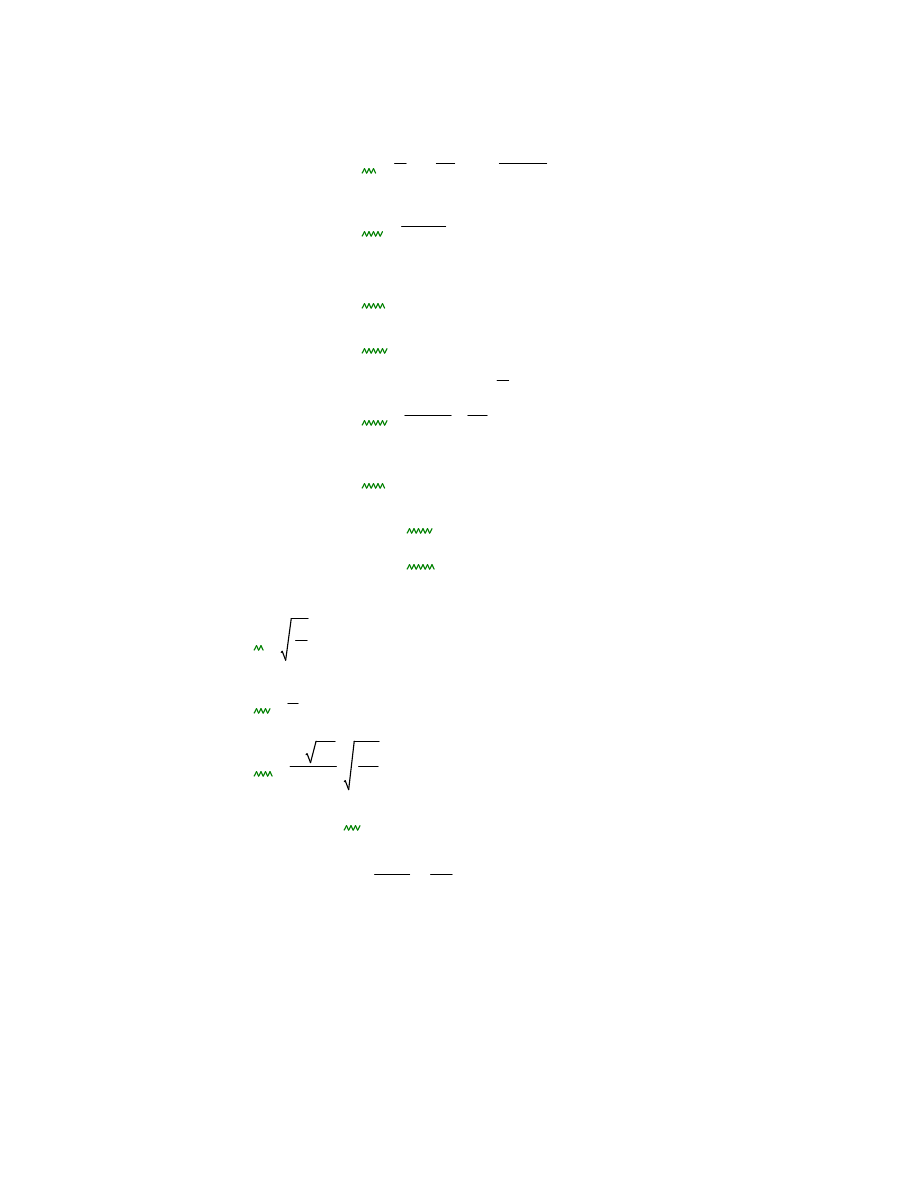
moment bezwładno

ś

ci przekroju

J

π

4

D

d

2













4

−

D

d

g

t

+

2













4

+









⋅

:=

J

1326711.79 cm

4

⋅

=

wska

ź

nik wytrzymało

ś

ci przekroju

W

J

0.5 D

d

⋅

:=

W

18953.03 cm

3

⋅

=

obliczeniowa siła

ś

ciskaj

ą

ca

N

o

1.1 N

II

i

⋅

g

⋅

:=

N

o

153.63 kN

⋅

=

obliczeniowy moment zginaj

ą

cy

M

o

1.3 M

II

i

⋅

:=

M

o

243.86 m kN m

⋅

⋅

=

smukło

ść

wzgl

ę

dna przekroju

λ

'

p

R

g

t

1.59

⋅

f

dT

E

T













2

3

⋅

:=

λ

'

p

0.23

=

współczynnik niestateczno

ś

ci ogólnej

ϕ

p

1

λ

'

p

2.4

+









0.625

−

:=

ϕ

p

0.98

=

obliczeniowa no

ś

no

ść

przekroju na

ś

ciskanie

N

R

ϕ

p

α

kor

⋅

A

⋅

f

dT

⋅

:=

N

R

12347.86 kN

⋅

=

obliczeniowa no

ś

no

ść

przekroju na zginanie

M

R

1.2

ϕ

p

⋅

α

kor

⋅

W

⋅

f

dT

⋅

:=

M

R

1758.59 m kN m

⋅

⋅

=

Współczynnik wyboczeniowy.

promie

ń

bezwładno

ś

ci

i

J

A

:=

i

499.24 mm

⋅

=

smukło

ść

λ

l

c

i

:=

smukło

ść

porównawcza

λ

'

λ

ϕ

p

⋅

2.73

f

dT

E

T

⋅

:=

λ

'

1.21

=

współczynnik niestateczno

ś

ci ogólnej

ϕ

1

λ

'

3.2

+

(

)

0.625

−

:=

ϕ

0.52

=

Oblczeniowa no

ś

no

ść

przekroju:

N

o

ϕ

N

R

⋅

M

o

M

R

+

0.16

=

12. Sprawdzanie no

ś

no

ś

ci poł

ą

cze

ń

kołnierzowych segmentów.

grubo

ś

ci blach kołnierzowych

g

b

16 mm

⋅

:=

szeroko

ść

kołnierza

r

k

230 mm

⋅

:=

liczba

ś

rub w poł

ą

czeniu

l

s

32

:=

rozmieszczonych na obwodzie co

α

360 deg

⋅

l

s

:=

α

11.25 deg

⋅

=

odległo

ść

mi

ę

dzy

ś

rubami

o

s

2

π

⋅

D

d

r

k

+

2

⋅

l

s

:=

o

s

160.02 mm

⋅

=

przyj

ę

te

ś

ruby M16

o czynnym polu przekroju

F

sr

157 mm

2

⋅

:=

d

16 mm

⋅

:=

promie

ń

okr

ę

gu na którym rozmieszczono

ś

ruby

r

s

D

d

2

r

k

2

+

:=

odległo

ś

ci

ś

rub od osi x-x

i

1 32

..

:=

ys

i

r

s

sin i

1

−

(

)

α

⋅

[

]

⋅

:=

Szukanie poło

ż

enia osi oboj

ę

tnej przekroju

odległo

ść

osi oboj

ę

tnej przekroju od osi x-x

y

o

456.5 mm

⋅

:=

odległo

ś

ci

ś

rub od osi oboj

ę

tnej

i

1 l

s

..

:=

ys

i

ys

i

y

o

+

:=

ys

i

if ys

i

0 m

⋅

>

ys

i

,

0 m

⋅

,

(

)

:=

moment statyczny

ś

rub wzgl

ę

dem osi oboj

ę

tnej

S

os

1

l

s

i

F

sr

ys

i

⋅

(

)

∑

=

:=

S

os

2657536.36 mm

3

⋅

=

obliczanie momentu statycznego

ś

ciskanej cz

ęś

ci kołnierza

promie

ń

zewn

ę

trzny kołnierza

y

z

D

d

2

r

k

+

:=

y

z

930 mm

⋅

=

promie

ń

wewn

ę

trzny kołnierza

y

w

D

d

2

:=

y

w

700 mm

⋅

=

y

0 mm

⋅

y

z

..

:=

y

z

S

ok

2

y

o

y

z

y

y

y

o

−

(

)

y

z

2

y

2

−

⋅

⌠




⌡

d

y

o

y

w

y

y

y

o

−

(

)

y

w

2

y

2

−

⋅

⌠




⌡

d

−

















⋅

:=

S

ok

88101237.14 mm

3

⋅

=

S

os

2657536.36 mm

3

⋅

=

<

S

ok

88101237.14 mm

3

⋅

=

Poło

ż

enie

ś

rodka ci

ęż

ko

ś

ci

ś

rub.

ł

ą

czne pole przekroju

ś

rub rozci

ą

ganych

A

c

n F

sr

⋅

:=

A

c

942 mm

2

⋅

=

odległo

ść

ś

rodka ci

ęż

ko

ś

ci

ś

rub od osi oboj

ę

tnej

y

sr

S

os

A

c

:=

y

sr

2821.16 mm

⋅

=

moment bezwładno

ś

ci

ś

rub wzgl

ę

dem osi oboj

ę

tnej

J

os

1

n

i

π

d

4

⋅

64

ys

i

( )

2

π

d

2

⋅

4

⋅

+













∑

=

:=

J

os

87612.81 cm

4

⋅

=

moment bezwładno

ś

ci kołnierza wzgl

ę

dem osi oboj

ę

tnej

J

ok

2

y

o

y

z

y

y

y

o

−

(

)

2

y

z

2

y

2

−

⋅

⌠




⌡

d

y

o

y

w

y

y

y

o

−

(

)

2

y

w

2

y

2

−

⋅

⌠




⌡

d

−

















⋅

:=

J

ok

2.65

10

10

×

mm

4

⋅

=

moment bezwładno

ś

ci układu "

ś

ruby-kołnierz":

J

c

J

os

J

ok

+

:=

Sprwadzono napr

ęż

enia dla II sytuacji obliczeniowej w styku segmentów I i II.

napr

ęż

enie w najbardziej wyt

ęż

onej

ś

rubie

σ

sr

1.3 M

II

2

⋅

r

s

y

o

+

(

)

⋅

J

c

:=

σ

sr

20.1 MPa

⋅

=

<

0.8 f

d

⋅

232 MPa

⋅

=

Napr

ęż

enia w spoinach obwodowych pachwinowych ł

ą

cz

ą

cych kołnierz z blach

ą

trzonu

najmniejsza grubo

ść

blachy

t

min

t

n

s

t

k

−

:=

t

min

6 mm

⋅

=

przyj

ę

ta grubo

ść

spoin

0.2 g

b

⋅

3.2 mm

⋅

=

<

a

s

5 mm

⋅

:=

<

0.7 t

min

⋅

4.2 mm

⋅

=

wska

ź

nik wytrzymało

ś

ci przekroju spoin

W

s

π

32

D

d

a

s

+

(

)

4

D

d

4

−

D

d

⋅

:=

W

s

3869116.83 mm

3

⋅

=

napr

ęż

enia w spoinach od zginania

τ

n

1.3 M

II

2

⋅

W

s

:=

τ

n

112.02 MPa

⋅

=

<

f

d

290 MPa

⋅

=

napr

ęż

enia w spoinie od

ś

cinania

τ

o

1.3 P

2

⋅

a

s

2

π

⋅

D

d

2

⋅













⋅

:=

τ

o

1.24 MPa

⋅

=

<<

f

d

290 MPa

⋅

=

wypadkowe napr

ęż

enia w spoinach

τ

τ

n

2

τ

o

2

+

:=

τ

112.02 MPa

⋅

=

Styki pozostałych segmentów wykonano jak styk segmentów I i II.

13. Zakotwienie trzonu w fundamencie.

Komin jest posadowiony na stopie kołowej wykonanej z betonu B20

przyj

ę

to

ś

ruby M30 klasy 8.8 o no

ś

no

ś

ci na rozci

ą

ganie

S

Rt

303 kN

⋅

:=

pole przekroju

ś

ruby

A

s

561 mm

2

⋅

:=

moduł spr

ęż

ysto

ś

ci betonu

E

b

27 10

3

⋅

MPa

⋅

:=

szeroko

ść

pier

ś

cienia stopy

b

k

40 cm

⋅

:=

promie

ń

ś

rodkowy pier

ś

cienia stopy

r

D

d

2

:=

liczba

ś

rub na pbwodzie komina

n

2

π

⋅

r

⋅

b

k

:=

n

11

=

n > 8

przyj

ę

ta liczba

ś

rub

n

8

:=

obliczeniowy moment zginaj

ą

cy w styku trzonu ze stop

ą

M

o

1.3 M

II

1

⋅

:=

M

o

243.86 m kN m

⋅

⋅

=

obliczeniowa siła

ś

ciskaj

ą

ca

N

o

1.1 N

II

1

⋅

g

⋅

:=

N

o

153.63 kN

⋅

=

zast

ę

pcza szeroko

ść

pier

ś

cienia w strefie rozci

ą

ganej

b

z

n A

s

⋅

2

π

⋅

r

⋅

:=

b

z

0.1 cm

⋅

=

ϕ

M

o

r N

o

⋅

:=

ϕ

6.8

=

K

100 E

⋅

b

z

⋅

b

k

E

b

⋅

:=

K

1.94

=

k

ą

t strefy docisku odczytany z nomogramu

α

36 deg

⋅

:=

waro

ść

współczynnika

ν

odczytana z nomogramu

ν

30

:=

napr

ęż

enia dociskowe pod stop

ą

σ

d

N

o

1

cos

α

( )

−

(

)

⋅

2 b

k

⋅

r

⋅

1

sin

α

( )

α

cos

α

( )

⋅

−

0.01 K

⋅

sin

α

( )

π

α

−

(

) cos

α

( )

⋅

+

[

]

⋅

−

⋅

:=

σ

d

1.83 MPa

⋅

=

napr

ęż

enia w

ś

rubach

σ

a

E

σ

d

⋅

E

b

1

cos

α

( )

+

1

cos

α

( )

−

⋅

:=

σ

a

131.3 MPa

⋅

=

obliczeniowa siła rozci

ą

gaj

ą

ca

ś

rub

ę

N

s

σ

a

A

s

⋅

:=

N

s

73.66 kN

⋅

=

<

S

Rt

303 kN

⋅

=

kN

10

3

newton

⋅

:=

MPa

10

6

Pa

⋅

:=

s

sec

:=

W

watt

:=

lat

yr

:=

v

v s

⋅

m

:=

T

e.

T

e

lat

:=

H

H

m

:=

D

D

d

m

:=

v

v

H

:=

v

H.

H

m s

1

−

⋅

:=

z

i

z

i

m

:=

H

H

m

:=

D

D

d

m

:=

v

H.

v

H

m s

1

−

⋅

:=

z

i

z

i

m

:=

ρ

p

ρ

p

m

3

−

kg

⋅

:=

i

1 n

s

..

:=

α

kor

0.85

:=