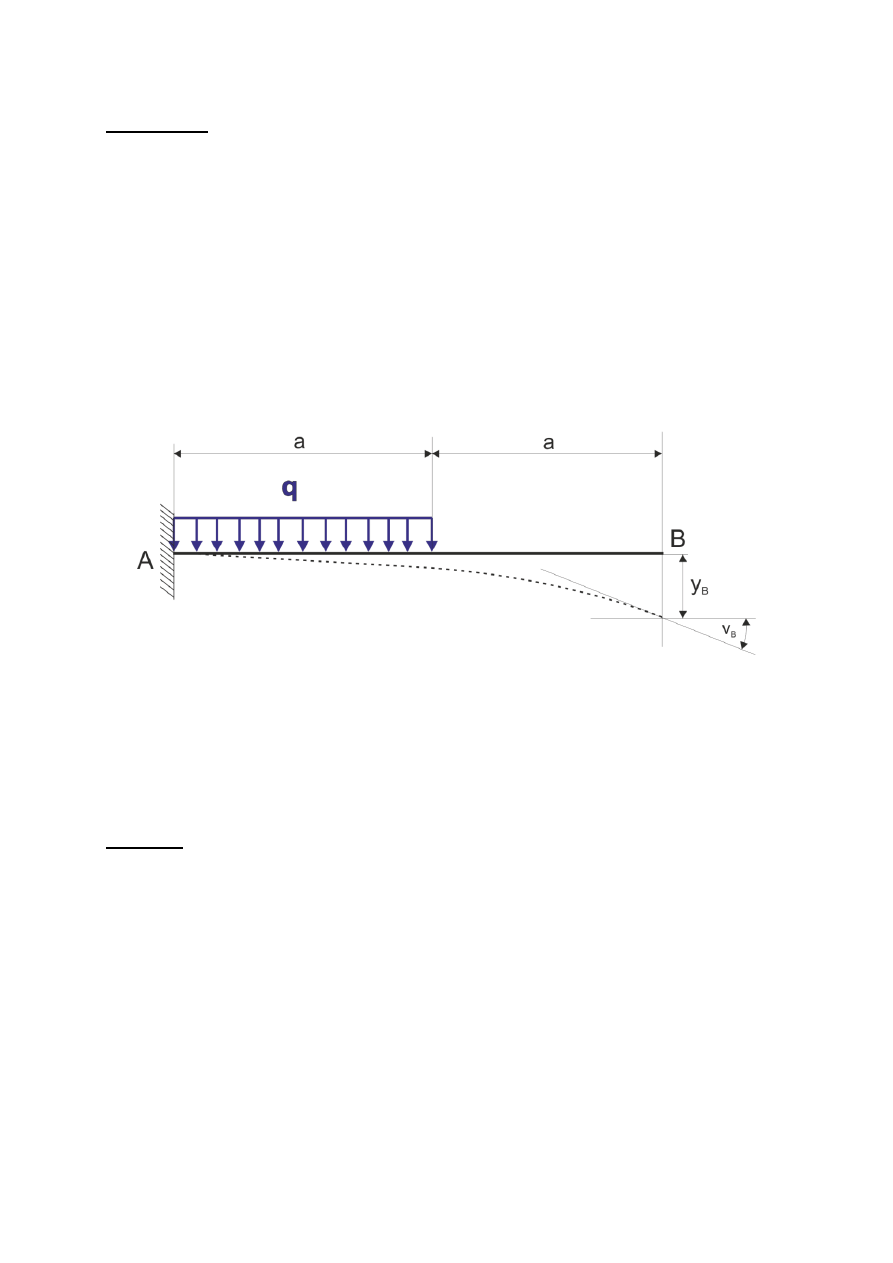
Zadanie 8

Twierdzenie CASTIGLIANO (omówić + wzorki)

Wyznaczyć dla belki pokazanej na rysunku, obciążonej obciążeniem ciągłym q,
przemieszczenia w punkcie B:

 y

B

ugięcie w punkcie B



v

B

kąt ugięcia (kat obrotu) w punkcie B

Zaliczenie:

Opracowanie ZADANIA przesłać w formie elektronicznej (np. word, pdf) w terminie 2 tygodni po
wygłoszonym referacie na adres:

[e-mail]

plik zapisać w postaci:

Nazwa Grupy_Nazwisko1Pierwsza litera imienia_ Nazwisko2Pierwsza litera imienia_zadanie numer.doc, np.

M1_PaczosP_TomczykT_ZAD1.doc

TEORIA

Energię sprężystą dowolnego układu można przedstawić w postaci kwadratowej funkcji jednorodnej
sił obciążających układ.

𝑉 =

1
2

∑ ∑ 𝛿

𝑖𝑘

𝑃

𝑖

𝑃

𝑘

𝑛

𝑘=1

𝑛

𝑖=1

,

gdzie:

𝛿

𝑖𝑘

− liczby wpływowe.

Siły zewnętrzne

𝑃

𝑖

, czyli

𝑃

1

, 𝑃

2

, … , 𝑃

𝑛

przyjmujemy jako zmienne niezależne i różniczkujemy

powyższe wyrażenie cząstkowo względem dowolnej siły zewnętrznej

𝑃

𝑖

.

𝜕𝑉

𝜕𝑃

𝑖

=

1
2

𝑃

1

(

𝛿

1𝑖

+ 𝛿

𝑖1

)

+

1
2

𝑃

2

(

𝛿

2𝑖

+ 𝛿

𝑖2

)

+ ⋯ + 𝑃

𝑖𝛿

𝑖𝑖

+

1
2

𝑃

𝑛

(

𝛿

𝑛𝑖

+ 𝛿

𝑖𝑛

)

Ponieważ zgodnie z twierdzeniem Maxwella o wzajemności przemieszczeń jest

𝛿

1𝑖

= 𝛿

𝑖1

,

𝛿

2𝑖

+ 𝛿

𝑖2

,

𝛿

𝑛𝑖

+ 𝛿

𝑖𝑛

więc wyrażenie przyjmuje postać:

𝜕𝑉

𝜕𝑃

𝑖

= 𝑃

1

𝛿

𝑖1

+ 𝑃

2

𝛿

𝑖2

+ ⋯ + 𝑃

𝑖

𝛿

𝑖𝑖

+ ⋯ + 𝑃

𝑛

𝛿

𝑖𝑛

Prawa strona tego wyrażenia to przemieszczenie

𝑢

𝑖

punktu i układu w kierunku działania siły

zewnętrznej

𝑃

𝑖

.

Przyjmując kolejno

𝑖 = 1,2, … , 𝑛 otrzymamy ostatecznie:

𝝏𝑽

𝝏𝑷

𝒊

= 𝒖

𝒊

− 𝑻𝒘𝒊𝒆𝒓𝒅𝒛𝒆𝒏𝒊𝒆 𝑪𝒂𝒔𝒕𝒊𝒈𝒍𝒊𝒂𝒏𝒐

Pochodna cząstkowa energii sprężystej względem dowolnej zewnętrznej siły uogólnionej jest równa
przemieszczeniu uogólnionemu w punkcie działania tej siły.

Siła uogólniona jest to siła skupiona lub moment zewnętrzny, a odpowiadające przemieszczenia
uogólnione to przemieszczenia liniowe punktu działania siły lub momentu.

Postać ogólna twierdzenia Castigliano może być stosowana w także tych przypadkach kiedy
obciążenie jest typu złożonego i znane są podstawowe siły wewnętrzne rozważanego układu
sprężystego, jak:

M – moment gnący M = M(x)

T – siła tnąca, poprzeczna, ścinająca T = T(x)

N – siła normalna N=N(x)

M

s

– moment skręcający M

s

= M

s

(x)

Energia sprężysta odkształcenia dla pojedynczego pręta o długości l wynosi:

𝑉 = 𝑉

𝑧𝑔𝑖𝑛

+ 𝑉

𝑟𝑜𝑧𝑐/ś𝑐𝑖𝑠𝑘

+ 𝑉

ś𝑐𝑖𝑛

+ 𝑉

𝑠𝑘𝑟ę𝑐

𝑉 =

1
2

∫

𝑀

2

𝑑𝑥

𝐸𝐼

𝑙

0

+

1
2

∫

𝑁

2

𝑑𝑥

𝐸𝐴

+ 𝑘

′

1
2

∫

𝑇

2

𝑑𝑥

𝐺𝐴

+

𝑙

0

𝑙

0

1
2

∫

𝑀

𝑠

2

𝑑𝑥

𝐺𝐼

0

𝑙

0

Po wykorzystaniu powyższego wyrażenia na energię sprężystą wzór Castigliano przyjmie postać
ogólną dla pojedynczego pręta o długości

𝑙 :

𝜕𝑉

𝜕𝑃

𝑖

= 𝑢

𝑖

=

∫ [

𝑀

𝐸𝐼

∙

𝜕𝑀
𝜕𝑃

𝑖

+

𝑁

𝐸𝐴

∙

𝜕𝑁

𝜕𝑃

𝑖

+ 𝑘

′

∙

𝑇

𝐺𝐴

∙

𝜕𝑇

𝜕𝑃

𝑖

+

𝑀

𝑠

𝐺𝐼

0

∙

𝜕𝑀

𝑠

𝜕𝑃

𝑖

]

𝑑𝑥

𝑙

0

W przypadku gdy chcemy obliczyć kąt obrotu (kąt ugięcia) belki to obciążeniem zewnętrznym jest
𝑀

𝑖

. Twierdzenie Castigliano przyjmuje postać:

𝜕𝑉

𝜕𝑀

𝑖

= 𝜗

𝑖

=

∫ [

𝑀

𝐸𝐼

∙

𝜕𝑀

𝜕𝑀

𝑖

+

𝑁

𝐸𝐴

∙

𝜕𝑁

𝜕𝑀

𝑖

+ 𝑘

′

∙

𝑇

𝐺𝐴

∙

𝜕𝑇

𝜕𝑀

𝑖

+

𝑀

𝑠

𝐺𝐼

0

∙

𝜕𝑀

𝑠

𝜕𝑀

𝑖

]

𝑑𝑥

𝑙

0

W przypadku rozwiązywania belek, w których dominujące jest zginanie najistotniejszy jest pierwszy
składnik uwzględniający energię zginania. Pozostałe składniki można pominąć i twierdzenie
Castigliano przyjmie postać:

𝑢

𝑖

=

𝜕𝑉

𝜕𝑃

𝑖

=

1

𝐸𝐼

∫

𝑀(𝑥)

𝜕𝑀(𝑥)

𝜕𝑃

𝑖

𝑙

0

𝑑𝑥 − 𝑼𝒈𝒊ę𝒄𝒊𝒆

𝜗

𝑖

=

𝜕𝑉

𝜕𝑀

𝑖

=

1

𝐸𝐼

∫

𝑀(𝑥)

𝜕𝑀(𝑥)

𝜕𝑀

𝑖

𝑙

0

𝑑𝑥 − 𝑲ą𝒕 𝒖𝒈𝒊𝒆𝒄𝒊𝒂

WAŻNE! W miejscu, w którym wyznaczamy przemieszczenie musi znajdować się siła uogólniona,
natomiast jeśli nie występuje, to dodajemy w tym miejscu dodatkową, fikcyjną, siłę, której wartość
wynosi 0.

𝑃

𝐹

= 0

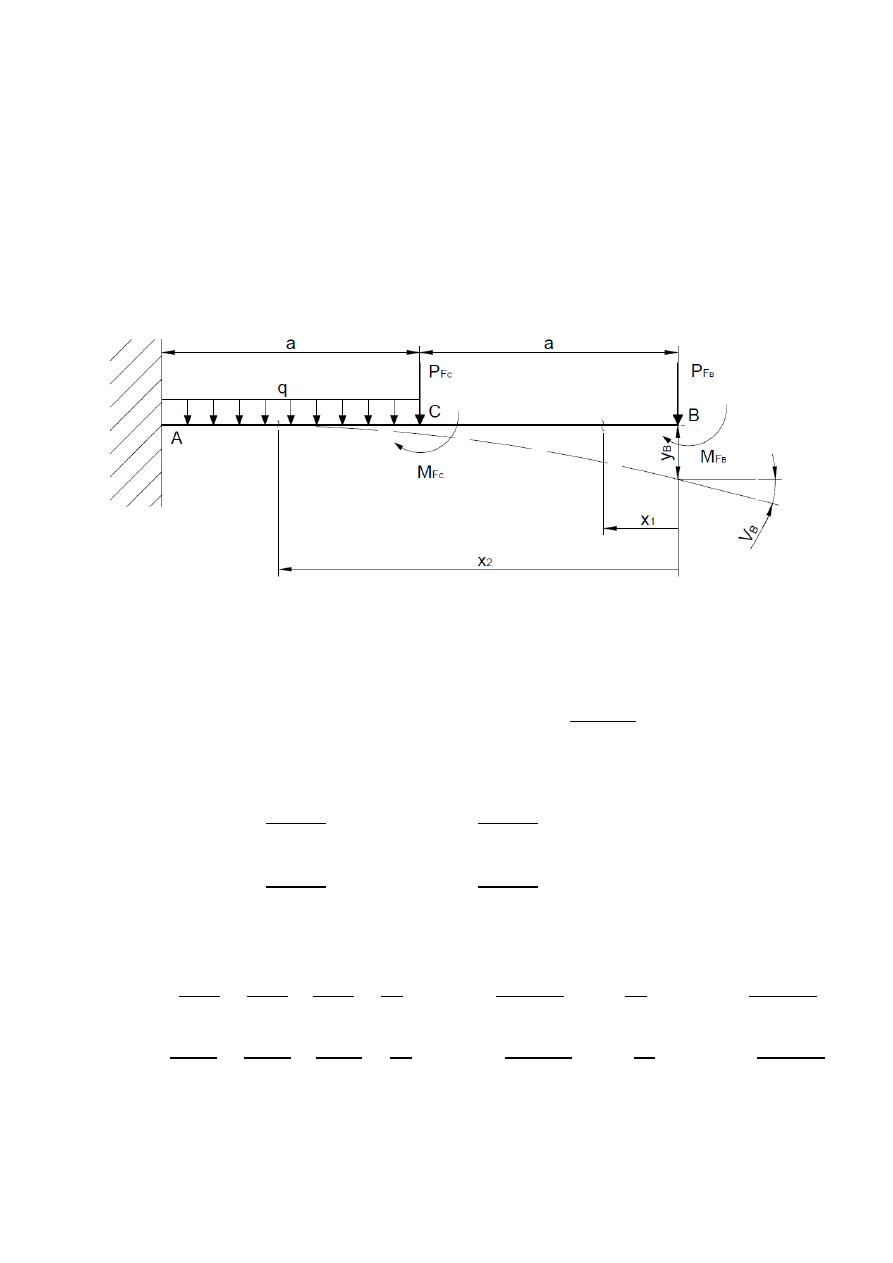
ROZWIĄZANIE:

W tym zadaniu wprowadziliśmy dodatkową siłę i moment w punkcie C. Dzięki temu pojawiły się one
w równaniu momentów i możliwe jest wykorzystanie tego równania w celu obliczenia ugięcia i kąta
skręcenia w tym punkcie w sposób analogiczny do przedstawionego przez nas rozwiązania dla punktu
B.

𝑀(𝑥

1

) = −𝑃

𝐹

𝐵

𝑥

1

− 𝑀

𝐹

𝐵

𝑀(𝑥

2

) = −𝑃

𝐹

𝐵

𝑥

2

− 𝑃

𝐹

𝐶

(𝑥

2

− 𝑎) − 𝑞(𝑥

2

− 𝑎)

𝑥

2

− 𝑎

2

− 𝑀

𝐹

𝐵

− 𝑀

𝐹

𝐶

𝜕𝑀(𝑥

1

)

𝜕𝑃

𝐹𝐵

= −𝑥

1

𝜕𝑀(𝑥

1

)

𝜕𝑀

𝐹𝐵

= −1

𝜕𝑀(𝑥

2

)

𝜕𝑃

𝐹𝐵

= −𝑥

2

𝜕𝑀(𝑥

2

)

𝜕𝑀

𝐹𝐵

= −1

{

𝑦

𝐵

=

𝜕𝑉

𝜕𝑃

𝐹

𝐵

=

𝜕𝑉

1

𝜕𝑃

𝐹

𝐵

+

𝜕𝑉

2

𝜕𝑃

𝐹

𝐵

=

1

𝐸𝐼

∫ 𝑀(𝑥

1

)

𝜕𝑀(𝑥

1

)

𝜕𝑃

𝐹

𝐵

𝑑𝑥

1

+

1

𝐸𝐼

∫ 𝑀(𝑥

2

)

𝜕𝑀(𝑥

2

)

𝜕𝑃

𝐹

𝐵

𝑑𝑥

2

2𝑎

𝑎

𝑎

0

𝑉

𝐵

=

𝜕𝑉

𝜕𝑀

𝐹

𝐵

=

𝜕𝑉

1

𝜕𝑀

𝐹

𝐵

+

𝜕𝑉

2

𝜕𝑀

𝐹

𝐵

=

1

𝐸𝐼

∫ 𝑀(𝑥

1

)

𝜕𝑀(𝑥

1

)

𝜕𝑀

𝐹

𝐵

𝑑𝑥

1

+

1

𝐸𝐼

∫ 𝑀(𝑥

2

)

𝜕𝑀(𝑥

2

)

𝜕𝑀

𝐹

𝐵

𝑑𝑥

2

2𝑎

𝑎

𝑎

0

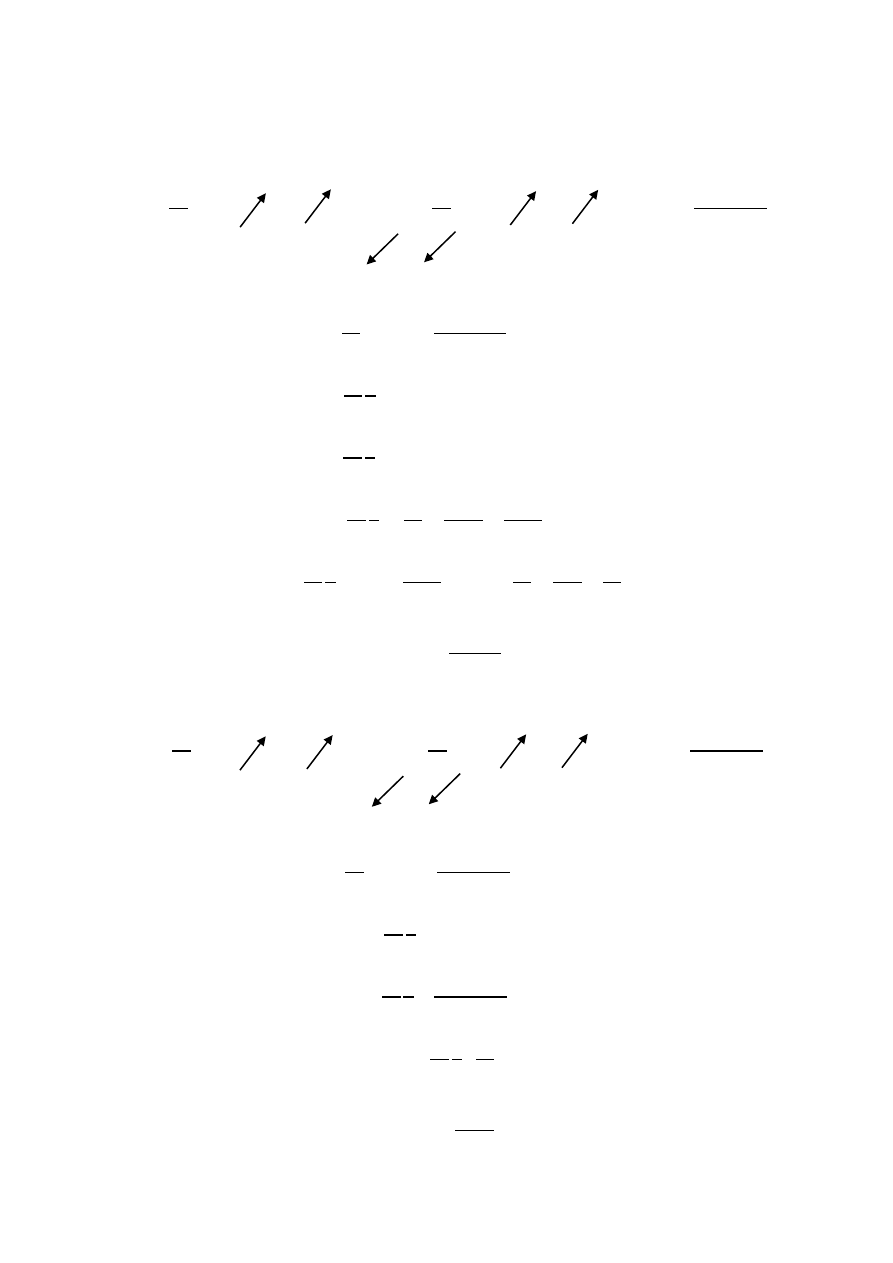
𝑦

𝐵

=

1

𝐸𝐼

∫ (−𝑃

𝐹

𝐵

𝑥

1

−

𝑎

0

𝑀

𝐹

𝐵

)(−𝑥

1

)𝑑𝑥

1

+

1

𝐸𝐼

∫ (−𝑃

𝐹

𝐵

𝑥

2

−

2𝑎

𝑎

𝑃

𝐹

𝐶

(𝑥

2

− 𝑎) − 𝑞

(𝑥

2

− 𝑎)

2

2

−𝑀

𝐹

𝐵

− 𝑀

𝐹

𝐶

)(−𝑥

2

)𝑑𝑥

2

𝑦

𝐵

=

1

𝐸𝐼

∫ (−𝑞

(𝑥

2

− 𝑎)

2

2

) (−𝑥

2

)𝑑𝑥

2

2𝑎

𝑎

𝑦

𝐵

=

1

𝐸𝐼

𝑞
2

∫ (𝑥

2

2

− 2𝑥

2

𝑎 + 𝑎

2

)𝑥

2

𝑑𝑥

2

2𝑎

𝑎

𝑦

𝐵

=

1

𝐸𝐼

𝑞
2

∫ (𝑥

2

3

− 2𝑥

2

2

𝑎 + 𝑥

2

𝑎

2

)𝑑𝑥

2

2𝑎

𝑎

𝑦

𝐵

=

1

𝐸𝐼

𝑞
2

[(

𝑥

2

4

4

−

2𝑥

2

3

𝑎

3

+

𝑥

2

2

𝑎

2

2

)|

2𝑎

𝑎

]

𝑦

𝐵

=

1

𝐸𝐼

𝑞
2

(4𝑎

2

−

16𝑎

4

3

+ 2𝑎

4

−

𝑎

4

4

+

2𝑎

4

3

−

𝑎

4

2

)

𝑦

𝐵

=

7𝑞𝑎

4

24𝐸𝐼

𝑉

𝐵

=

1

𝐸𝐼

∫ (−𝑃

𝐹

𝐵

𝑥

1

−

𝑎

0

𝑀

𝐹

𝐵

)(−1)𝑑𝑥

1

+

1

𝐸𝐼

∫ (−𝑃

𝐹

𝐵

𝑥

2

−

2𝑎

𝑎

𝑃

𝐹

𝐶

(𝑥

2

− 𝑎) − 𝑞

(𝑥

2

− 𝑎)

2

2

−𝑀

𝐹

𝐵

− 𝑀

𝐹

𝐶

)(−1)𝑑𝑥

2

𝑉

𝐵

=

1

𝐸𝐼

∫ (−𝑞

(𝑥

2

− 𝑎)

2

2

) (−1)𝑑𝑥

2

2𝑎

𝑎

𝑉

𝐵

=

1

𝐸𝐼

𝑞
2

∫ (𝑥

2

− 𝑎)

2

𝑑𝑥

2

2𝑎

𝑎

𝑉

𝐵

=

1

𝐸𝐼

𝑞
2

[(

(𝑥

2

− 𝑎)

3

3

)|

2𝑎

𝑎

]

𝑉

𝐵

=

1

𝐸𝐼

𝑞
2

(

𝑎

3

3

)

𝑉

𝐵

=

𝑞𝑎

3

6𝐸𝐼

0

0

0

0

0

0

0

0

0

0

0

0

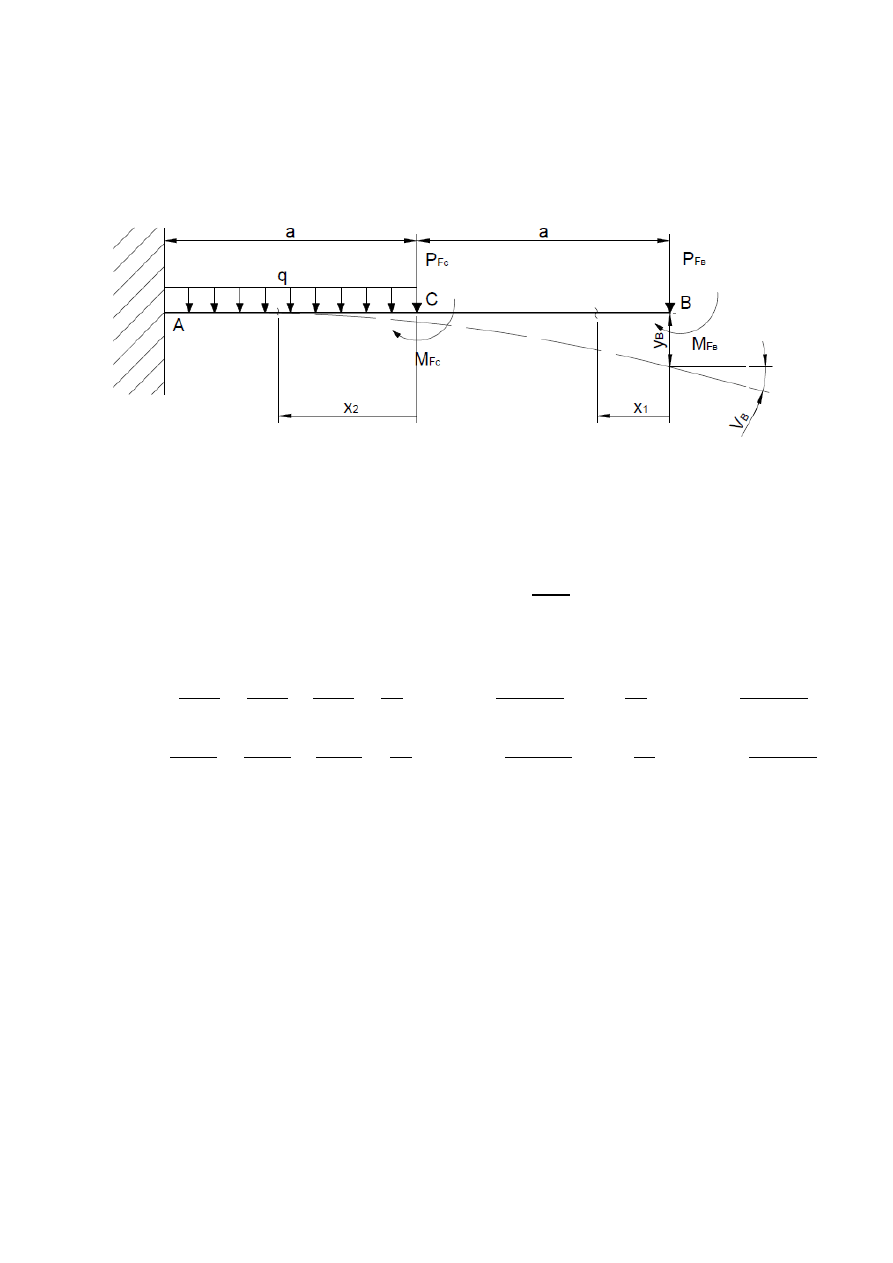
WARIANT II

𝑀(𝑥

1

) = −𝑃

𝐹

𝐵

𝑥

1

− 𝑀

𝐹

𝐵

𝑀(𝑥

2

) = −𝑃

𝐹

𝐵

(𝑥

2

+ 𝑎) − 𝑃

𝐹

𝐶

𝑥

2

−

𝑞𝑥

2

2

2

− 𝑀

𝐹

𝐵

− 𝑀

𝐹

𝐶

{

𝑦

𝐵

=

𝜕𝑉

𝜕𝑃

𝐹

𝐵

=

𝜕𝑉

1

𝜕𝑃

𝐹

𝐵

+

𝜕𝑉

2

𝜕𝑃

𝐹

𝐵

=

1

𝐸𝐼

∫ 𝑀(𝑥

1

)

𝜕𝑀(𝑥

1

)

𝜕𝑃

𝐹

𝐵

𝑑𝑥

1

+

1

𝐸𝐼

∫ 𝑀(𝑥

2

)

𝜕𝑀(𝑥

2

)

𝜕𝑃

𝐹

𝐵

𝑑𝑥

2

𝑎

0

𝑎

0

𝑉

𝐵

=

𝜕𝑉

𝜕𝑀

𝐹

𝐵

=

𝜕𝑉

1

𝜕𝑀

𝐹

𝐵

+

𝜕𝑉

2

𝜕𝑀

𝐹

𝐵

=

1

𝐸𝐼

∫ 𝑀(𝑥

1

)

𝜕𝑀(𝑥

1

)

𝜕𝑀

𝐹

𝐵

𝑑𝑥

1

+

1

𝐸𝐼

∫ 𝑀(𝑥

2

)

𝜕𝑀(𝑥

2

)

𝜕𝑀

𝐹

𝐵

𝑑𝑥

2

𝑎

0

𝑎

0