5. LINIE WPŁYWU W USTROJACH STATYCZNIE WYZNACZALNYCH
SPOSÓB STATYCZNY
5.1 INFROMACJE OGÓLNE
a konstrukcję działają obok obciążeń stałych jak na przykład ciężar własny również obciążenia,
których położenie może ulegać zmianie. Takimi obciążeniami są miedzy innymi obciążenia
użytkowe, technologiczne itp. Stad wynika potrzeba wyznaczania wielkości statycznych dla
różnych usytuowań obciążeń zmiennych szczególnie, gdy chcemy wyznaczyć wielkości ekstremalne.
Typowymi przykładami są mosty obciążone pojazdami, których położenie zmienia się oraz obciążenia
belki suwnicowej zależne od położenia suwnicy itd. Stąd ważnym zagadnieniem praktycznym statyki
budowli jest wyznaczenie linii wpływu wielkości statycznych, które pozwalają rozwiązywać problemy
związane ze zmiennością położenia obciążenia.
Linią wpływu wielkości statycznej Z (reakcji, sił przekrojowych jak momenty zginające, siły tnące i
osiowe) nazywamy wykres (dokładnie wykres funkcji) ilustrujący zależność wielkości Z od położenia
czynnej siły jednostkowej na ustalonym torze tej siły. Będziemy przyjmowali, że siła jednostkowa P=1
jest pionowa (w przypadku sił pod kątem wystarczy obrócić rysunek tak, aby siła była pionowa). Linią
przerywaną zaznaczamy tor przesuwania się siły (rys. 5.1).
Rys. 5.1
Można wyznaczać linie wpływu od jednostkowego momentu, ale nie będzie to przedmiotem niniejszego
wykładu. Wymiar rzędnych linii wpływu ustalamy następująco:
Stosujemy dwie metody wyznaczania linii wpływu: statyczną i kinematyczną. Wpierw zostanie
przedstawiona metoda statyczna.
Zanim przejdziemy do wyznaczania linii wpływu podamy ważne twierdzenie:
N
• dla układów statycznie wyznaczalnych wielkość statyczna jest liniową funkcją położenia siły
jednostkowej
• dla ustalonej tarczy.
Wynika to z faktu, że w równaniach równowagi występuje liniowa funkcja położenia siły
jednostkowej. Stąd wynika twierdzenie:
Linie wpływu wielkości statycznej dla ustrojów statycznie wyznaczalnych składają się z odcinków
prostych.
WNIOSEK 1
Linia wpływu wielkości statycznej dla każdej tarczy ustroju statycznie wyznaczalnego jest odcinkiem
prostej.
WNIOSEK 2
Dla każdej tarczy wystarczy wyznaczyć dwie rzędne linii wpływu dla dwóch różnych położeń siły
jednostkowej. Rzędne te z reguły wyznaczamy w pewnych punktach charakterystycznych dla danego
ustroju.
5.2 BELKI PROSTE
PRZYKŁAD
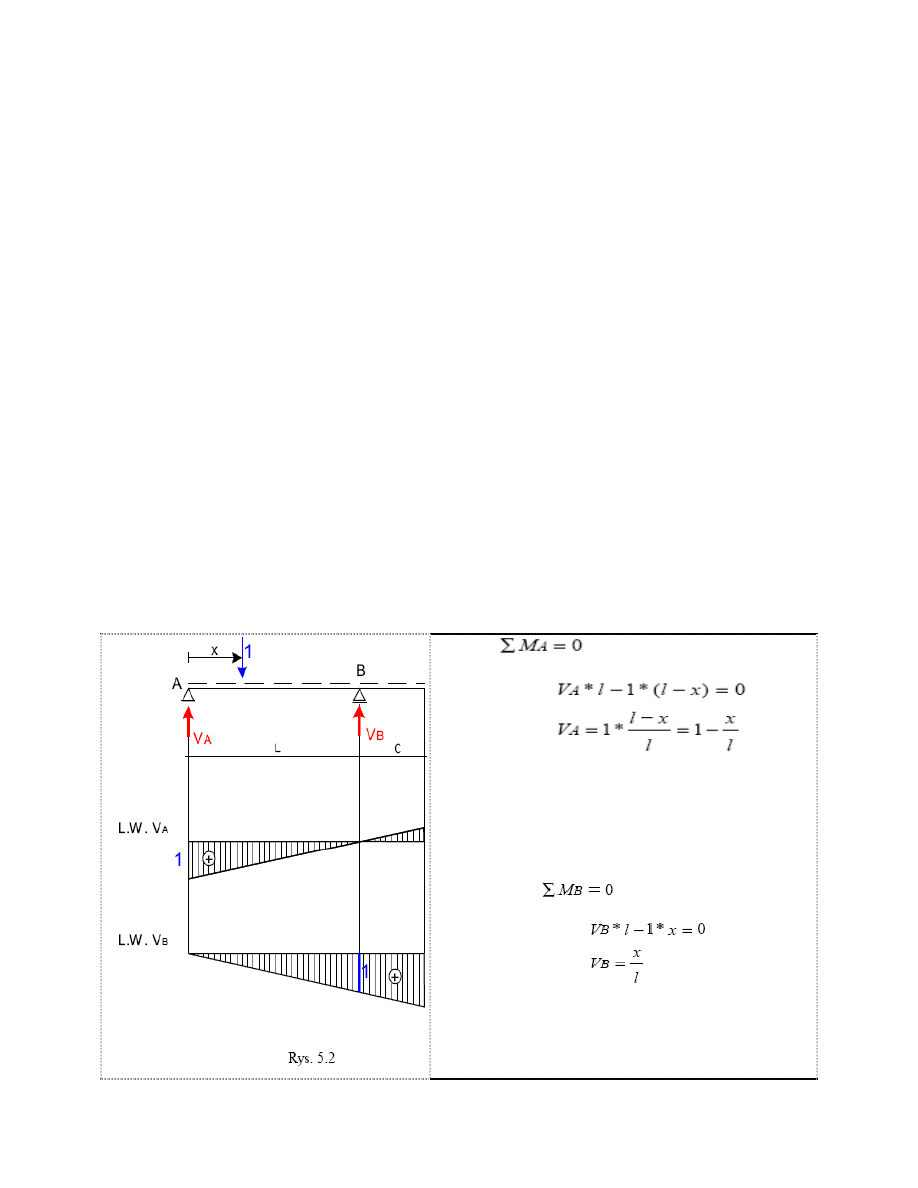
Belka swobodnie podparta.
Linia wpływu V
A
określona jest powyższą zależnością.
Można jednak ją wyznaczyć stawiając siłę w punkcie A
otrzymując V
A
=1 oraz w punkcie B otrzymując V
A
=0 i
następnie łącząc te dwie rzędne.
Gdy siła stoi w punkcie A V
B
=0, gdy siła jest w punkcie
B wtedy V
B
=1. Następnie otrzymujemy linię wpływu
łącząc dwie rzędne.
W dalszej części wykładu z reguły linię wpływu wyznaczać będziemy wyznaczając rzędną w
charakterystycznych punktach.
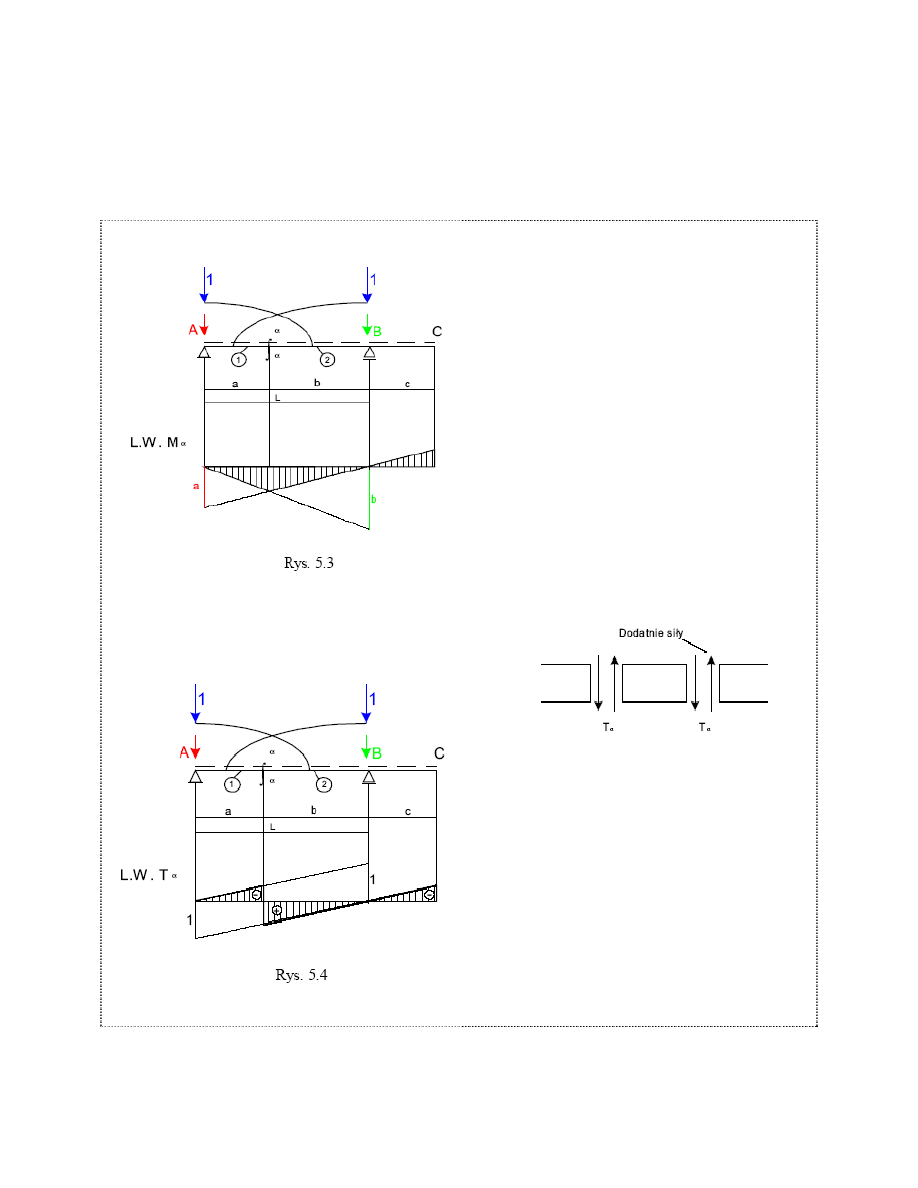
Dla powyższej belki wyznaczyć linię wpływu (L.W.) momentu M
α
i siły tnącej T
α
w przekroju α-α.
Linia wpływu momentu w przekroju α-α.
Linia wpływu siły tnącej w przekroju c α – α
Punktami charakterystycznymi są podpory A i B.
Przekrój α-α dzieli belkę na dwie tarcze: (A- α)=1
;(α -C)=2. Dla tarczy 1, gdy siła stoi nad podporą w
punkcie A M
α
=0, a gdy stoi na „fajce” nad
punktem B to M
α
=b. Dla tarczy 2, gdy siła stoi nad
podporą w punkcie B M
α
=0, gdy na „fajce” nad
punktem A to M
α
=a.
Rzędne odkładamy po stronie włókien
rozciąganych.
Znakowanie sił tnących:
Dla tarczy 1 = (A - α )siłę stawiamy w punkcie A,
gdzie T
α
= 0 oraz na ”fajce” w punkcie B, gdzie
T
α
= -1.
Dla tarczy 2 = (α - B) w punkcie A na „fajce”,
gdzie siła tnąca T
α
= 1 oraz w punkcie B, gdzie
T
α
= 0.
WNIOSEK 1
Dla momentu w miejscu przekroju linia wpływu ma załamanie.
WNIOSEK 2
Dla siły tnącej linia wpływu ma skok, a dwie sąsiednie gałęzie są równoległe.
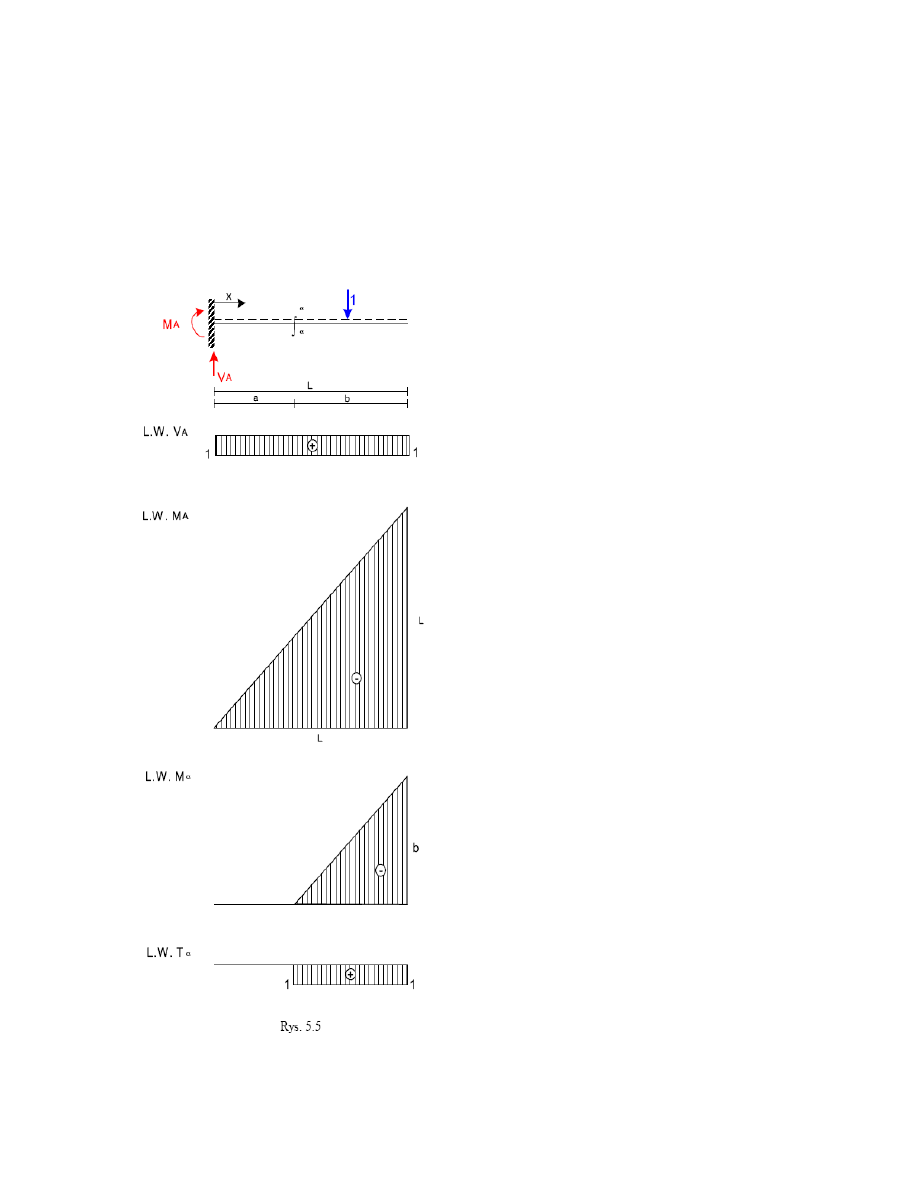
PRZYKŁAD
Wspornik
Linia wpływu V
A
V
A
– 1 = 0
V
A
= 1
Linia wpływu M
A
M
A
+ 1*x=0
M
A
= -x
Linia wpływu M
α
Dla 0
≤ x ≤ a
M
α
= 0
Dla a
≤ x ≤ l
M
α
= -1*(x-a)
Linia wpływu T
α
Dla 0
≤ x ≤ a
T
α
= 0
Dla a
≤ x ≤ l
T
α
= 1
WNIOSEK
Zauważmy, że linie wpływu momentów i sił tnących mają cechy charakterystyczne jak załamanie dla
momentu i skok dla siły tnącej.
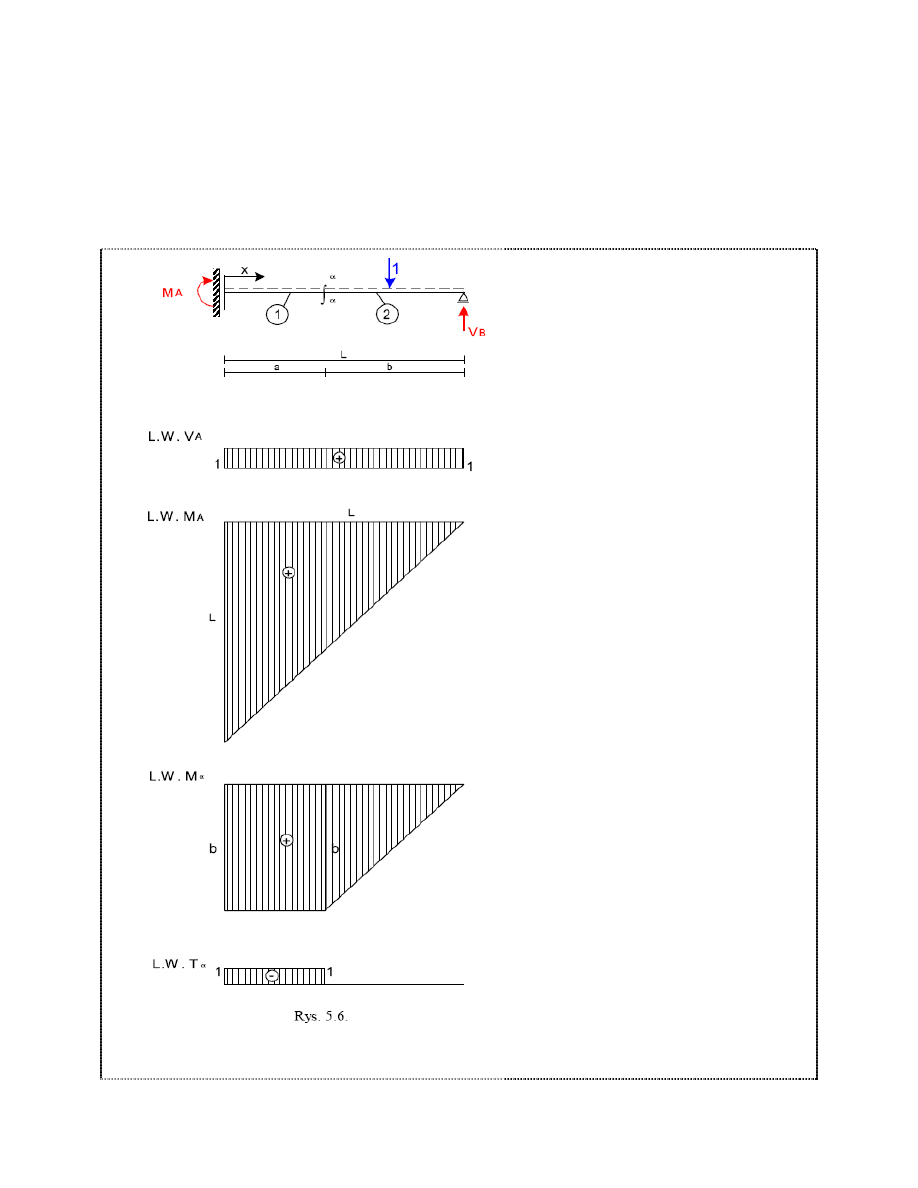
PRZYKŁAD
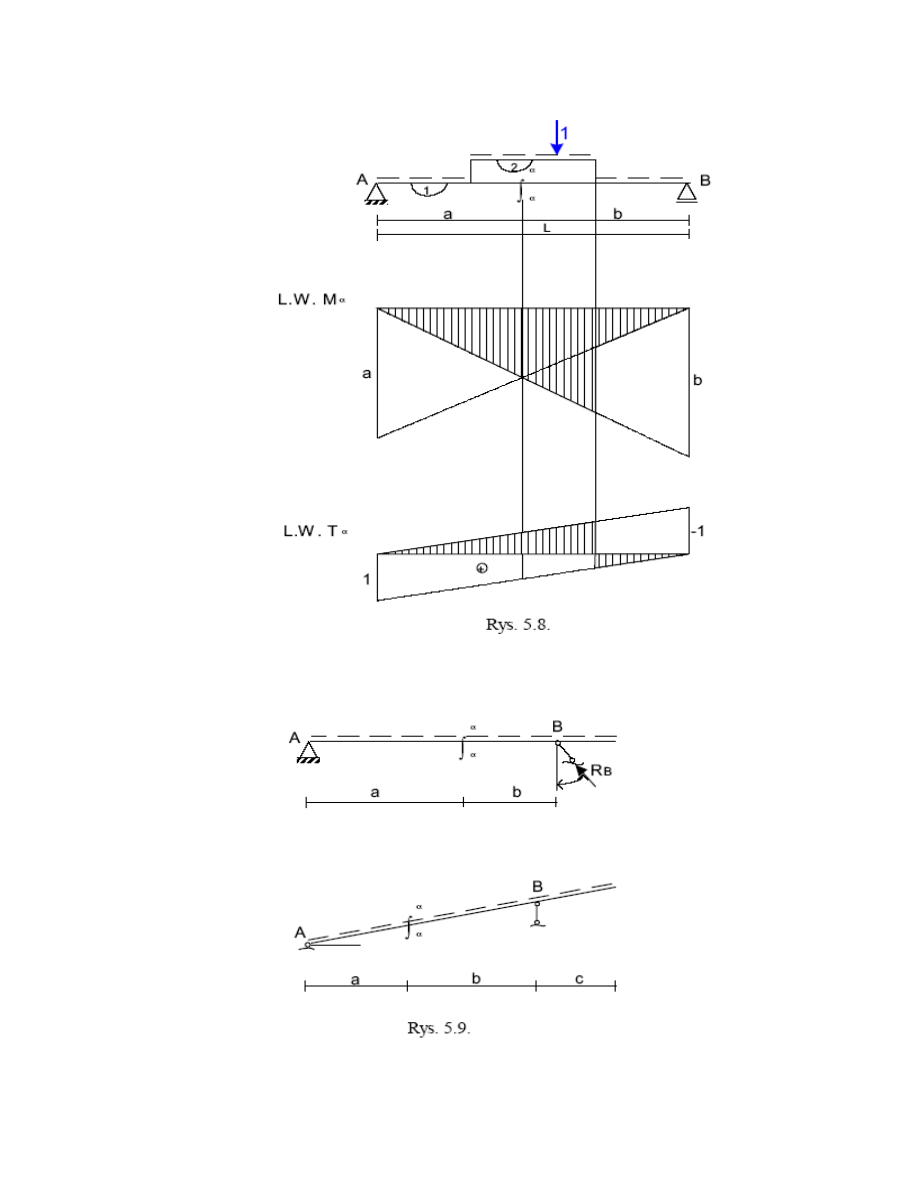
Belka z łyżwą
Linia wpływu reakcji podporowej V
B
ΣY=0
V
B
– 1 = 0
V
B
= 1
Linia wpływu momentu M
A
ΣM
A
=0
M
A
– 1*(L – x) = 0
M
A
= L – x
Linia wpływu momentu M
α
Siła stoi nad podporą B
M
α
= 0
Siła stoi w miejscu przekroju α- α
V
B
= 1 oraz M
α
= 1*b
Linia wpływu dla siły tnącej T
α
Gdy siła stoi na tarczy 1 wówczas V
B
= 1
oraz
T
α
= - V
B
= - 1
Gdy siła stoi na tarczy 2 wówczas
T
α
= - 1 + V
B
= 0
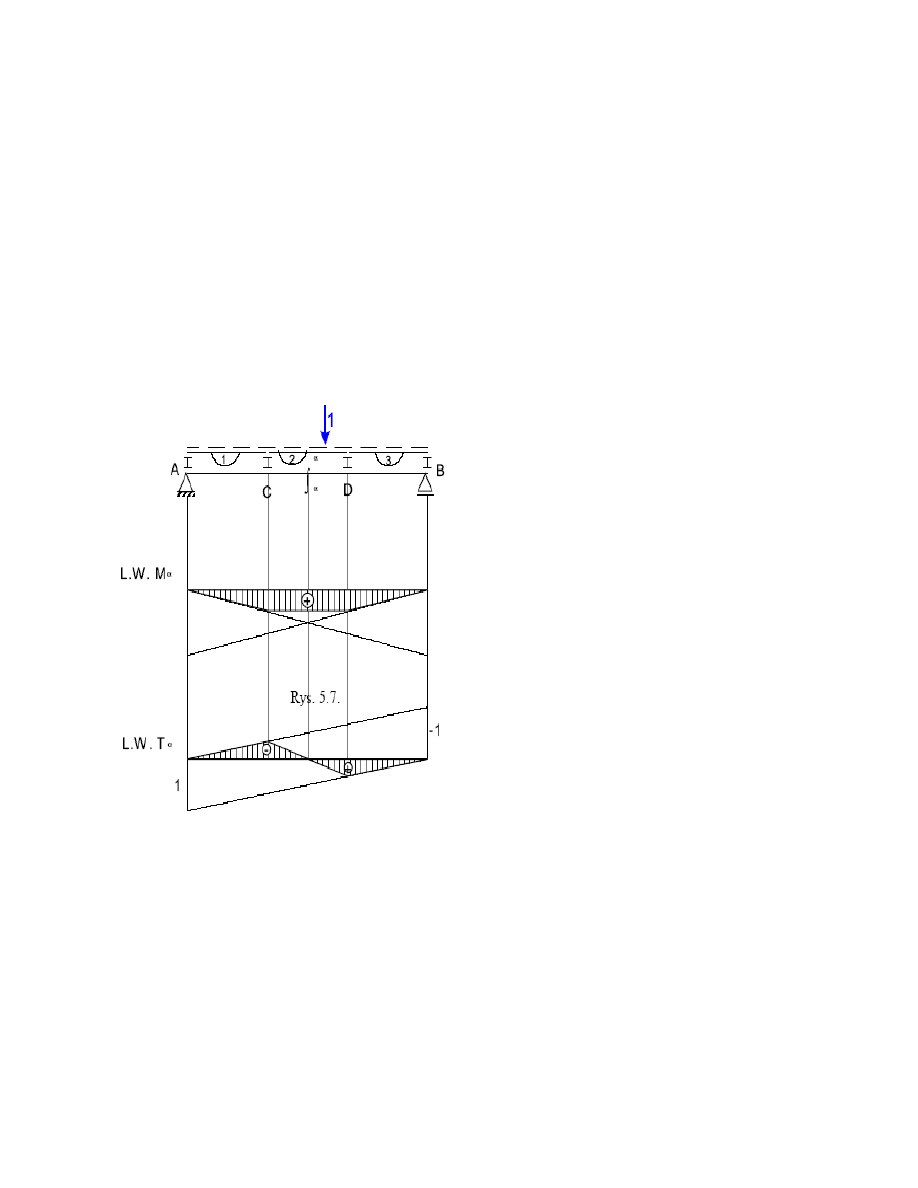
WNIOSEK
Dla momentu linia wpływu ma załamanie rzędnych w przekroju α-α, a dla sił tnących odpowiednio skok.
Bardzo często mamy sytuację, że obciążenie nie działa bezpośrednio na daną belkę, ale jest przekazywane
w sposób pośredni. Na przykład na belki główne, dla których chcemy wyznaczyć linie wpływu obciążenie
może być przekazywane poprzez podłużnice i poprzecznie. Wyznaczymy linię wpływu momentu i siły
tnącej dla belki jak na powyższym rysunku. Wykonujemy to w ten sposób, że wyznaczamy linię wpływu
jakby siła poruszała się bezpośrednio po belce, a następnie uwzględniamy fakt, że jest przekazywane
pośrednio.
PRZYKŁAD
Gdy siła porusza się po podłużnicy 2 przekazywana
jest w punktach C i D na belkę co powoduje
zmniejszenie ekstremum wartości.
Tutaj został cięty skok linii wpływu, gdyż
obciążenie przekazywane jest w punktach C i D z
podłużnicy na belkę.
PRZYKŁAD
Rozpatrzmy belkę z dodatkowym wspornikiem. Początkowo wykonujemy linię wpływu jakby tego
wspornika nie było, a następnie uwzględnimy do jakiego miejsca jest ważna każda tarcza.
Zadania do samodzielnego rozwiązania