1

Wprowadzenie do Teorii Algorytmów

(Introduction to Algorithms Theory)

Prof. Dr.habil. Alexander Prokopenya

Szkoła Główna Gospodarstwa Wiejskiego w Warszawie

Katedra Zastosowań Informatyki

Cele kursu:
zapoznanie studentów

z metodami konstrukcji, analizy kosztów oraz poprawności algorytmów,
z efektywnymi algorytmami rozwiązywania popularnych zagadnień;

nabycie przez studentów umiejętności konstruowania i analizy prostych algorytmów.

Metody dydaktyczne:
Wykłady (30 h) – przekazywanie wiedzy teoretycznej z przedmiotu z wykorzystaniem pomocy
dydaktycznych: komputer, rzutnik multimedialny.
Ćwiczenia (15 h) – rozwiązywanie problemów związanych z projektowaniem algorytmów oraz
analizą ich kosztów i poprawności.

Forma i warunki zaliczenia przedmiotu:

Wykłady

:

ZALICZENIE KOLOKWIUMU

pisemnego.

Ćwiczenia: zaliczenie na ocenę, na podstawie sumy punktów uzyskanych podczas 2 prac
kontrolnych; warunkiem do zaliczenia jest zdobycie co najmniej 50% od maksymalnej liczby
pkt.


Literatura podstawowa.
1. (CLR) Cormen Th.H., Leiserson Ch.E., Rivest R.L. Wprowadzenie do algorytmów.
Warszawa: Wydawnictwa Naukowo-Techniczne, 2004.
2. (DPV) Dasgupta S., Papadimitriu C., Vazirani U. Algorytmy. Warszawa, Wydawnictwo
Naukowe PWN, 2010.
3. (BDR) Banachowski L., Diks K., Rytter W. Algorytmy i struktury danych. Warszawa:
Wydawnictwa Naukowo-Techniczne, 2003.
4. (DLMRSS) Dańko A., Lan Le T., Mirkowska G., Rembelski P., Smyk A., Sydow M.
Algorytmy i struktury danych - zadania. Warszawa: Wydawnictwo PJWSTK, 2006.
5. (AHU) Aho A.V., Hopcroft J.E., Ullman J.D. Algorytmy i struktury danych. Gliwice: Hekion,
2003.

Literatura uzupełniająca
6. Knuth D. Sztuka programowania. Tom 1: Algorytmy podstawowe. Tom 2: Algorytmy semi-
numeryczne, Tom 3: Sortowanie i wyszukiwanie. Warszawa: WNT, 2002.
7. Lipski W. Kombinatoryka dla programistów. Warszawa: WNT, 2004.
8. Wirth N. Algorytmy+struktury danych=programy. Warszawa: WNT, 2004.

9. Materiały publikowane w sieci Internet:

http://wazniak.mimuw.edu.pl/ ; http://edu.pjwstk.edu.pl/wyklady/

2

Wykład 1.

Wprowadzenie. Podstawowe zasady analizy algorytmów

Projektowanie i analiza algorytmów są podstawa informatyki. Niniejszy wykład

stanowi przegląd najważniejszych problemów teoryi algorytmów: pojęcie specyfikacji a l-
gorytmu, poprawności i kosztu algorytmu. Na konkretnych przykładach będziemy śledzili
proces przejścia od problemu i jego specyfikacji do gotowego rozwiązania w postaci po-
prawnego programu.

1. Czym jest algorytm?

Algorytm – w matematyce oraz informatyce to skończony, uporządkowany ciąg jasno zdefinio-
wanych czynności, koniecznych do wykonania pewnego zadania.
[http://pl.wikipedia.org/wiki/Algorytm]

Nieformalnie, algorytm jest pewną ściśle określoną procedura obliczeniową, która dla

właściwych danych wejściowych „produkuje” żądane dane wyjściowe zwane wynikiem dziłania
algorytmu. Algorytm jest więc ciągiem kroków obliczeniowych prowadzących do przekształca-
nia danych wejściowych w wyjściowe.

Słowo algorytm często łączone z imieniem greckiego matematyka Euklidesa (365-300

p.n.e.) i jego słynnym przepisem na obliczanie największego wspólnego dzielnika dwóch liczb a
i b:

)

,

( b

a

NWD

.

Specjaliści zajmujący się historią matematyki odnaleźli najbardziej prawdopodobne źró-

dło słowa „algorytm”: termin ten pochodzi od nazwiska perskiego pisarza-matematyka Abu
Ja’far Mohammed ibn Musa al-Khowarizmi (IX wieku n.e.). Jego zasługą jest dostarczenie kla-
rownych reguł wyjaśniających krok po kroku zasady operacji arytmetycznych wykonywanych
na liczbach dziesiętnych: metody dodawania, odejmowania, mnożenia, dzielenia liczb, oblicza-
nia pierwiastków kwadratowych, oblicznia kolejnych cyfr rozwinięcia dziesiętnego liczby



.

Przykład 1. (Dodawanie liczb)

Weiście: dwie liczby całkowite x i y,

0

,



y

x

.

Wyjście: liczba całkowita

y

x



a) System dziesiętny :

2

4

5

1

7

2

albo

5

9

1

2

8

3

7

1

7

5

4

;

b) System binarny:

0

1

0

1

0

1

1

1

1

1

0

0

1

1

0

1

1

0

albo

1

1

0

0

1

0

0

1

0

0

0

1

0

1

0

1

0

0

1

1

0

1

1

0

1

0

0

1

0

0

1

1

1

0

0

0

c) Liczby rzymskie:

XXXXII

XV

XXVII





- w jaki sposób dodawać?

Przykład 2. (algorytm Euklidesa – obliczanie największego wspólnego dzielnika)
Weiście: dwie liczby całkowite x i y,

0

,



y

x

.

Wyjście: liczba całkowita

)

,

(

y

x

nwd

While

y

x



do

if

y

x



then

y

x

x





else

x

y

y





od

Wynik: y;

3

56



x

,

35



y

,

)

7

,

7

(

)

14

,

7

(

)

14

,

21

(

)

35

,

21

(

)

35

,

56

(

)

,

(











y

x

Przykład 3. (problem sortowania, Rys. 1)
Weiście: ciąg n liczb

n

a

a

a

a

,...,

,

,

3

2

1

.

Wyjście: permutacja

n

a

a

a

a

'

,...,

'

,

'

,

'

3

2

1

ciągu wejściowego taka, że

n

a

a

a

a

'

...

'

'

'

3

2

1









.

Rys. 1. Sortowanie talii kart za pomocą sortowania przez wstawianie

(Source: CLR)

Każdy algorytm:



posiada dane wejściowe (w ilości większej lub równej zero) pochadzące z dobrze zde-

finiowanego zbioru (np. algorytm Euklidesa operuje na dwóch liczbach całkowitych);



produkuje pewien wynik (niekoniecznie numeryczny);



jest precyzyjnie zdefiniowany (każdy krok algorytmu musi być jednoznacznie określo-

ny);



jest skończony (wynik algorytmu musi zostać „kiedyś” dostarczony – mając algorytm A

i dane wejściowe D powinno być możliwe precyzyjne określenie czasu wykonania

)

( A

T

).

Algorytm można przedstawić w postaci programu komputerowego albo zrealizować

sprzętowo. Jedynym wymaganiem jest precyzja opisu wynikającej z niego procedury oblicze-
niowej.

2. Język algorytmów

Jaki jest najlepszy język do opisu algorytmu?

Jest to przykład problemu nierozstrzygalnego. Niewątpliwie język ojczysty jest najlepszym języ-
kiem potocznym, a ulubiony język programowania jest najlepszym językiem do implementacji
algorytmu.

Język, którym będziemy opisywać algorytmy, jest gdzieś pomiędzy tymi językami – ję-

zyk potoczny nie wystarcza, a konkretny język programowania może spowodować, że "prosty"
algorytm się zrobi nieczytelny. Będziemy używać, o ile się da, nieformalnych konstrukcji pro-
gramistycznych, a w przypadkach bardzo prostych będziemy się starali pisać algorytm w pseu-
dojęzyku Pascalopodobnym, który zawiera instrukcję przypisania oraz instrukcję złożenia, wa-
runkową i pętli.

4

1. Przypisanie wartości zmiennej:

zmienna := wartość

2. Operatory zapisywane są za pomocą powszechnie używanych w matematyce symboli
(

1

:





i

i

,

2

mod

: n

i



,

2

:

div

n

i



).

3. Instrukcja warunkowa:

if warunek then
ciąg instrukcji-1
else
ciąg instrukcji-2
fi

Blok else może zostać pominięty:

if warunek then
ciąg instrukcji
fi

4. Pętla while:

while warunek do
ciąg instrukcji
od

5. Pętla for:

for zmienna = wart_pocz to wart_konc step krok do
ciąg instrukcji
od

Opuszczenie fragmentu step oznacza przyjęcie kroku równego 1.
6. W pętlach lub procedurach będziemy używać instrukcji exit, która przerywa działanie pętli,
lub instrukcji return pozwalającej przerywać wykonanie funkcji lub procedury i wrócić do in-
strukcji następującej po jej wywołaniu.
7. Dostęp do tablic uzyskuje się przez podanie nazwy i indeksu (np. A[i] jest i-tym elementem
tablicy A). A[1..j] oznacza podtablicę zawierającą elementy A[1], A[2], …, A[j]. Aby określić
liczbę elementów w tablicy A piszemy length(A).
8. Dopuszczalne jest zapisanie niektórych operacji za pomocą opisu słownego.

9. Symbol // oznacza, że reszta wiersza jest komentarzem. Komentarze, specyfikujące zachowa-
nie fragmentów programu, są bardzo pomocne przy uzasadnianiu semantycznej poprawności
programu.

Z dokładnością do ortografii, są to znane instrukcje z popularnych języków pr o-

gramowania (Pascal, C, C++, Java). Symbole „do – od”, „if – then else - fi” pełnią jedynie
rolę nawiasów, podobnie jak klamry „{ }” albo „begin - end”. Na ogół, nie będziemy się
zajmować deklaracjami zmiennych, chyba że przy omawianiu konkretnych implementacji,
lub, gdy deklaracje typu zmiennych są konieczne do zrozumienia działania algorytmu.
Będziemy natomiast zakładali, że każdy algorytm ma predefiniowaną zmienną result, któ-
ra służy do zapamiętania wyników algorytmu. Jej typ będzie zależyć od konkretnej sytu a-
cji i od konkretnego algorytmu.

Instrukcje składania, warunkowa i instrukcja pętli są podstawowymi metodami

konstruowania algorytmów. Dodatkowo, dopuszczać będziemy instrukcję wywołania
wcześniej zdefiniowanej procedury lub funkcji. Takie wywołanie zapiszemy w postaci:

nazwa_algorytmu(parametry_aktualne).

5

Przykład 4. (sortowanie przez wstawianie)

INSERTION-SORT(A)
1

for j := 2 to length(A) do

2

key := A[j]

3

// Wstaw A[j] w posortowany ciąg A[1..j-1]

4

i := j-1

5

While i > 0 and A[i] > key

6

do A[i+1] := A[i]

7

i := i-1 od

8

A[i+1] := key od

3. Analiza algorytmów

Analiza algorytmów polega na określeniu zasobów, jakie są potrzebne do jego wykonania. Za-
sobem zasadniczym jest dla nas czas obliczeń, jednakże innymi zasobami mogą być: pamięć,
szerokość kanalu komunikacyjnego lub układy logiczne. Zwykle analizowanie kilku algorytmów
dla tego samego problemu prowadzi do wyboru najoptymalniejszego z nich. Będziemy przyj-
mować dalej, że naszym podstawowym modelem obliczeń jest jednoprocesorowa maszyna o do-
stępie swobodnym do pamięci (RAM od ang. Random Access Machine), a naszy algorytmy są
realizowane jako programy komputerowe. W modelu RAM instrukcje są wykonywane jedna po
drugiej (sekwencyjnie).

3.1. Poprawność algorytmu

Przez poprawność algorytmu rozumiemy to, że dla dowolnych danych wejściowych daje on ta-
kie odpowiedzi, jakich oczekujemy. Żeby ustalić poprawność algorytmu, musimy jasno sformu-
łować intencje, podać tzw. jego specyfikację.

Specyfikacją algorytmu nazywać będziemy parę własności:





wk

wp,

, gdzie wp jest

warunkiem początkowym, a wk warunkiem końcowym. Intuicyjnie, warunek początkowy to ten,
który mają spełniać dane początkowe, a warunek końcowy to ten, który ma być spełniony po
wykonaniu algorytmu. Ogólnie, oba warunki powinny opisywać zależności między zmiennymi
przed i po wykonaniu algorytmu.

W przykładzie 4 dla sortowania przez wstawianie mamy na wejściu ciąg n liczb

n

a

a

a

a

,...,

,

,

3

2

1

. Naturalnym warunkiem początkowym będzie założenie niepustości ciągu: nie

można sortować pusty ciąg. Możemy go zapisać w postaci:

}

0

{





n

wp

. Warunek końcowy,

natomiast, powinien charakteryzować oczekiwany wynik i może mieć postać:

}

'

'

),

(

|

'

,...,

'

{

1

1









i

i

n

a

a

i

a

a

wk

. Algorytm rozwiązujący ten problem możemy zapisać w posta-

ci:
INSERTION-SORT(A)
1

if length(A) = 0 then exit // sprawdzenie waruneku n>0

2

for j := 2 to length(A) do

3

key := A[j]

4

i := j-1

5

while i > 0 and A[i] > key

6

do A[i+1] := A[i]

7

i := i-1 od

8

A[i+1] := key od

Warto zauważyć, że dla każdego niepustego ciągu liczb

n

a

a

a

a

A

,...,

,

,

3

2

1



algorytm zatrzy-

muje się i wydaje posortowany ciąg liczb, czyli po wykonaniu algorytmu warunek końcowy

}

'

'

),

(

|

'

,...,

'

{

1

1









i

i

n

a

a

i

a

a

wk

jest spełniony. Ten warunek wk wydaje się być rozsądnym z

6

punktu widzenie badanego problemu. Jest jednak jasne, że dla jednego algorytmu można zapro-
ponować wiele różnych par postaci





wk

wp,

, nie każda jest jednak dla nas interesująca, np.:

specyfikacja postaci

}

0

{





n

wp

,

}

{

n

j

wk





Chociaż opisuje własności zmiennych występujących w algorytmie INSERTION-SORT, nie da-
je nam dostatecznej informacji o tym, czego mamy się spodziewać po wynikach i co właściwie
robi ten algorytm. Specyfikacja ma precyzować problem, ma umożliwić odpowiedź na pytanie,
czy algorytm rozwiązuje postawiony problem, czy nie. Specyfikacja ma opisać co ma robić al-
gorytm, jednak bez wskazywania, jak ma to robić.

Definicja. Całkowita poprawność algorytmu.
Powiemy, że algorytm Alg działający w pewnej strukturze danych Str jest całkowicie poprawny
ze względu na warunek początkowy wp i warunek końcowy wk wtedy i tylko wtedy, gdy dla
wszystkich danych spełniających warunek początkowy wp w strukturze Str, algorytm kończy
obliczenie i jego wyniki spełniają warunek końcowy wk.

Podkreślmy jeszcze raz, że jeśli algorytm Alg jest całkowicie poprawny ze względu na

specyfikację





wk

wp,

, to warunek początkowy daje gwarancję, że algorytm zakończy obli-

czenie. Tak właśnie jest w poprzednim przykładzie: algorytm INSETION-SORT zatrzymuje się
dla dowolnych danych. Rzeczywiście, zmienna j, kontrolująca pętlę for, przyjmuje jako swoje
wartości kolejne liczby naturalne, a parametr n też jest liczbą naturalną. Zatem po skończonej
liczbie kroków zmienna j przyjmie wartość n. Dla każdej wartości j ilość kroków w wewnętrznej
pętli „while” nie przekracza

1



j

)

0

(

j

i





.

Łatwo zauważyć, że nie są tu istotne wartości elementów ciągu, ani ich typy. To samo

rozumowanie możemy powtórzyć dla ciągów o elementach z dowolnej liniowo uporządkowanej
przestrzeni, byle tylko n było liczba naturalną. Z tego powodu możemy stwierdzać, że algorytm
INSERTION-SORT

jest

całkowicie

poprawny

ze

względu

na

specyfikację

1

1

'

'

),

(

|

'

,...,

'

;

0









i

i

n

a

a

i

a

a

n

w każdej strukturze danych, w której relacja porównywania

elementów „



” jest relacją liniowego porządku.

Dowodzenie poprawności dla wielu algorytmów jest bardzo skomplikowane. Będziemy

postępowali zgodnie z ideą Floyda opisów programów. Skorzystamy przy tym ze strukturalnej
budowy algorytmu. Aby udowodnić poprawność algorytmu postaci {P1;P2;} ze względu na spe-
cyfikację





wk

wp,

, będziemy się starali znaleźć taką własność pośrednią



, że algorytm {P1}

jest poprawny ze względu na specyfikację







,

wp

, a algorytm {P2} jest poprawny ze względu

na specyfikację





wk

,



.

Dla analizy algorytmów zawierających pętli może być stosowana metoda niezmienników

Hoare.

Definicja. Niezmiennik

Powiemy że formuła lub warunek



jest niezmiennikiem pętli {while



do P od} w strukturze

Str, jeżeli z tego że formuła

)

(







jest spełniona przed wukonaniem programu P (tzn. treści

pętli) wynika, że formuła



jest spełniona po wykonaniu programu P w strukturze Str.

Przykład 5.
Problem: Znaleźć największy wspólny dzielnik dwóch danych liczb naturalnych x, y. Niech spe-
cyfikacja poszukiwanego algorytmu ma postać:

}

0

{







y

x

wp

,

)}

,

,

)(

(

|

,

),

,

(

|

{

1

1

result

z

z

m

y

z

n

x

z

result

m

y

result

n

x

m

n

result

wk

























.

7

Warunek początkowy gwarantuje, że x i y nie są równocześnie równe 0, a warunek końcowy, że
uzyskany wynik (wartość zmiennej result) jest dzielnikiem zarówno x jak i y, oraz każdy inny
wspólny dzielnik x i y ma mniejszą od niego wartość. Znany wszystkim algorytm Euklidesa
rozwiązuje postawiony w tym przykładzie problem.

NWD(x,y)

1

if x*y = 0 then result := x + y else // jeżeli jedna z liczb x, y jest równa 0, to NWD

// tych dwóch liczb jest równy drugiej z nich

2

while x



y do

// NWD(x,y) = k

3

if x > y then

4

x := x – y

// NWD(x,y) = k

5

else

6

y := y – x fi

// NWD(x,y) = k

7

od

8

result := y

// jeżeli x = y, to NWD(x,y) = k = x = y

Niezmiennikiem pętli w tym algorytmie jest formuła

k

y

x

NWD



)

,

(

. Uzasadnienie:

)

,

(

)

,

(

y

y

x

NWD

y

x

NWD





, gdy

y

x



oraz

)

,

(

)

,

(

x

x

y

NWD

y

x

NWD





, gdy

x

y



. Zatem

niezależnie od tego, którą część instrukcji warunkowej wykonamy, największy wspólny dzielnik
nowych wartości zmiennych x i y jest taki sam, jak liczb przypisanych tym zmiennym przed wy-
konaniem programu.

Nie na wiele przyda nam się niezmiennik, jeżeli nie jest on prawdziwy przed wykona-

niem programu. Jeżeli jednak jest prawdziwy przed wejściem do pętli i pozostaje prawdziwy po
każdej iteracji, to, o ile algorytm się zatrzyma, uzyskane wartości zmiennych również go spełnia-
ją. Pozwala nam to często zrozumieć co robi program i uzasadnić jego częściową poprawność.

Wróćmy na chwilę do przykładu poprzedniego. Niech k będzie największym wspólnym

dzielnikiem danych liczb naturalnych x i y. Jeżeli x*y = 0, to jedna z liczb x lub y musi być ze-
rem, ale wtedy k jest równe sumie tych liczb. Jeżeli obie liczby x i y są różne od zera i przed
wykonaniem pętli mamy

k

y

x

NWD



)

,

(

, to własność ta nie zmienia się w kolejnych iteracjach

pętli. W momencie wyjścia z pętli mamy

)

)

,

(

(

y

x

k

y

x

NWD







, z czego wynika, że zmienna

result ma wartość k, a więc wartość największego wspólnego dzielnika danych liczb. Pozostaje
jeszcze pytanie, czy ten algorytm zatrzymuje się dla wszystkich danych spełniających warunek
początkowy. Zauważmy, że suma (x + y) jest w tym algorytmie zawsze liczbą naturalną różną
od zera. Co więcej, wartość tej sumy jest w każdym następnym kroku równa większej z wartości
x i y w kroku poprzednim. Zatem ciąg wartości sum (x + y) jest ściśle malejący, a więc nie może
być nieskończony. To dowodzi, że po skończonej liczbie kroków algorytm Euklidesa zatrzyma
się.

3.2. Koszt algorytmu

Podstawowymi miarami kosztu algorytmu są czas i pamięć.
Jak mierzyć czas? Oczywiście chcemy by miara była niezależna od komputera, na którym reali-
zowany będzie algorytm. Jest oczywiste, że realizacja tego samego algorytmu na różnych kom-
puterach dla tych samych danych, nie musi zająć tyle samo czasu. Zatem informacja, ile jedno-
stek czasu wymaga wykonanie algorytmu dla konkretnych danych, na konkretnym komputerze,
niewiele mówili o samym algorytmie. Miara kosztu algorytmu powinna zależeć od typu proble-
mu i rodzaju rozwiązania, a nie od komputera, na którym realizujemy obliczenia. Czas działania
algorytmu dla konkretnych danych wejściowych jest wyrażony liczbą wykonanych prostych
operacji lub „kroków”, np.

a) Liczbą instrukcji;

8

b) Liczbą operacji arytmetycznych;
c) Liczbą porównań wykonanych w trakcie realizacji algorytmu
d) Liczbą wywołań rekurencyjnych procedur, itd.

Jest dogonne zrobienie założenia, że operacja elementarna jest maszynowo niezależna. Na razie
przyjmujemy, że do wykonania jednego wiersza naszego programu wymagamy stalego czasu.
Wykonanie jednego wiersza programu nie musi trwać tyle co wykonanie innego wiersza. My
zakładamy, że każde wykonanie i-tego wiersza wymaga czasu

i

c , przy czym

i

c jest stała. Taki

punkt widzenia jest zgodny z przyjętym modelem RAM i odzwierciedla sposób implementacji
naszego programu na nowoczesnych komputerach.

W prowadzonych poniżej rozważaniach wyrażenie opisujące czas działania algorytmu

INSERTION-SORT otrzymamy z wyniku uproszczenia skomplikowanej formuly, w której wy-
korzystuje się koszty

i

c , czyniąc go bardziej zwięzlym i łatwiejszym do przekształceń. Ta

uproszczająca notacja pozwala łatwo rozpatrzywać, które z algorytmów są bardziej efektywne.

Rozpoczynamy od prezentacji procedury INSERTION-SORT z podanym „kosztem”

każdej instrukcji i liczbą jej wykonań. Dla każdego

n

j

,...,

3

,

2



, gdzie

)

(A

length

n



, niech

j

t

będzie liczbą sprawdzeń warunku wejścia do pętli while w wierszu 5 dla danej wartości j.

INSERTION-SORT(A)

koszt

Liczba wykonań

2

for j := 2 to n do

1

c

n

3

key := A[j]

2

c

1



n

4

i := j – 1

3

c

1



n

5

while i > 0 and A[i] > key

4

c





n

j

j

t

2

6

do A[i+1] := A[i]

5

c







n

j

j

t

2

)

1

(

7

i := i – 1 od

6

c







n

j

j

t

2

)

1

(

8

A[i+1] := key od

7

c

1



n

Czas działania algorytmu jest sumą czasów wykonania poszczególnych instrukcji; jeśli instruk-
cja wykonuje się w czasie

i

c i jest powtarzana n razy, to mamy w sumie czas

n

c

i



. Aby obli-

czyć czas działania

)

(n

T

procedury INSERTION-SORT, sumujemy iloczyny kosztów i liczby

wykonań, otrzymując

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(

)

(

7

2

6

2

5

2

4

3

2

1





































n

c

t

c

t

c

t

c

n

c

n

c

n

c

n

T

n

j

j

n

j

j

n

j

j

.

Czas działania algorytmu może się jednak różnić nawet dla danych o tym samym rozmiarze. W
procedurze INSERTION-SORT na przykład najlepszy przypadek (optymistyczny) występuje
wówczas, gdy wejściowa tablica jest już posortowana. Dla każdego

n

j

,...,

3

,

2



stwierdzamy, że

key

i

A



]

[

w wierszu 5, gdy i ma początkową wartość

1



j

. Zatem

1



j

t

dla

n

j

,...,

3

,

2



, a

minimalny czas działania wynosi

1

7

4

3

2

1

7

4

3

2

1

)

1

)(

(

)

1

(

)

1

(

)

1

(

)

1

(

)

(

c

n

c

c

c

c

c

n

c

n

c

n

c

n

c

n

c

n

T

































.

Ten czas działania można wyrazić jako

b

an



dla stalych a, b zależnych od kosztów

i

c poje-

dynczych instrukcji; jest to zatem funkcja liniowa względem n.

Jeśli tablica jest posortowana w porządku odwrótnym – to znaczy w porządku malejącym

– mamy do czynienia z przypadkiem najgorszym (pesymistycznum). Musimy porównać każdy

9

element

]

[ j

A

z każdym elementem podtablicy

]

1

..

1

[



j

A

, a więc

j

t

j



dla

n

j

,...,

3

,

2



. Zau-

ważmy, że

1

2

)

1

(

2











n

n

j

n

j

,

2

)

1

(

)

1

(

2











n

n

j

n

j

.

Wnioskujemy zatem, że czas działania procedury INSERTION-SORT wynosi



































































)

1

(

2

)

1

(

2

)

1

(

1

2

)

1

(

)

1

(

)

1

(

)

(

7

6

5

4

3

2

1

n

c

n

n

c

n

n

c

n

n

c

n

c

n

c

n

c

n

T

)

(

2

2

2

)

(

2

7

4

3

2

7

6

5

4

3

2

1

6

5

4

2

c

c

c

c

n

c

c

c

c

c

c

c

c

c

c

n









































.

Ten pesumistyczny czas działania można przedstawić jako

c

bn

an





2

dla stałych a, b, c, które

znowu zależą od kosztów

i

c ; jest to zatem funkcja kwadratowa względem n.

W typowych sytuacjach, takich jak sortowanie przez wstawianie, czas działania algoryt-

mu jest ustalony dla określonych danych wejściowych, natomiast w dalszych rozdzialach poka-
żemy algorytmy probabilistyczne, których czasy działania mogą być różne dla tych samych da-
nych wejściowych.

3.3. Złożoność pesymistyczna i średnia

Czas działania algorytmu zależy od danych wejściowych. Złożoność algorytmu może być rozu-
miana w sensie złożoności najgorszego przypadku lub złożoności średniej. Złożoność najgorsze-
go przypadku nazywamy złożonością pesymistyczną – jest to maksymalna złożoność dla danych
tego samego rozmiaru n albo górna granica możliwego czasu działania algorytmu dla każdych
danych wejściowych. Dla niektórych algorytmów pesymistyczny czas działania występuje dosyć
często. Zdarza sie tak na przykład przy wyszukiwaniu w bazie danych informacji której w tej
bazie nie ma. W praktyce ważniejsza może się okazać złożoność średnia lub oczekiwana. W tym
przypadku

)

(n

T

jest średnią (oczekiwaną) wartością złożoności dla wszystkich problemów roz-

miaru n. Tego typu złożoność zależy istotnie od tego, jaka się pod tym kryje przestrzeń probabi-
listyczna danych wejściowych. Z reguły zakładamy, że wszystkie dane wejściowe tego samego
rozmiaru mogą się pojawić z tym samym prawdopodobieństwem. Jednakże jest to często mało
realistyczne założenie. Przestrzeń probabilistyczna danych wejściowych może być bardzo skom-
plikowana. Prowadzić to może do bardzo trudnych analiz.

Definicja.
Niech D(n) będzie zbiorem danych rozmiaru n dla pewnego problemu P oraz Alg niech będzie
algorytmem rozwiązującym ten problem. Pesymistyczną złożoność czasową oznaczamy przez
W(Alg,n), a średnią (oczekiwaną) złożoność czasową przez A(Alg,n). Wielkości te są zdefinio-
wane następująco:

W(Alg,n) = max{T(Alg,d): d



D(n)} A(Alg,n) =



{p(d)



T(Alg,d): d



D(n)}

gdzie d jest egzemplarz danych ze zbioru D(n), p(d) jest prawdopodobieństwem wystąpienia da-
nych d, T(Alg,d) liczbą operacji dominujących, wykonanych przez algorytm Alg dla danych d.

Jeżeli wartość T(Alg,d) jest taka sama dla wszystkich danych d z klasy D(n), to złożoność

pesumistyczna jest równa złożoności średniej i mówimy po prostu o złożoności czasowej algo-
rytmu o wielkości T(Alg, n).

5. Notacje asymptotyczne

10

Kiedy rozmiar danych weiściowych n staje się bardzo duży, powstaje problem porównywania
efektywności i złożoności różnych algorytmów. Ten problem można rozwiązać na podstawie
rzędu wielkości funkcji czyli ich zachowaniu asymptotycznym. Dla dostatecznie dużych danych
weiściowych stałe współczynniki i mniej znaczące składniki we wzorze na czas działania są
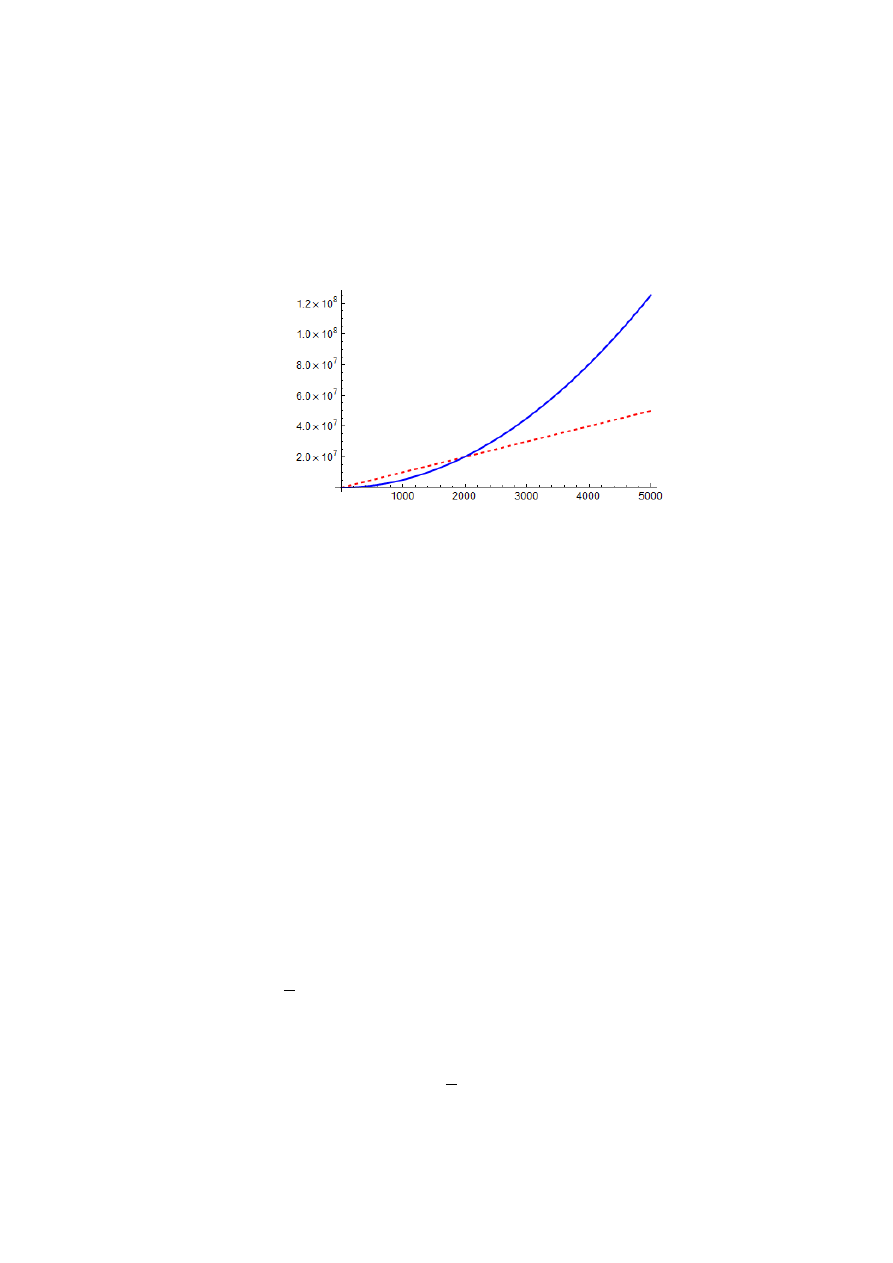
zdominowane przez rozmiar samych tych danych. Na przykład, złożoność optymistyczna algo-
rytma sotrowania przez wstawianie

b

an

n

T





)

(

1

będzie mniejsza niż złożoność pesymistyczna

e

dn

cn

n

T







2

2

)

(

dla dowolnych stalych a, b, c, d, e, jesli rozmiar danych weiściowych n staje

się duży (Rys. 1).

Rys. 1. Funkcji

5000

10000

)

(

1





n

n

T

,

n

n

n

T

100

5

)

(

2

2





Kiedy dla dostatecznie dużych danych wejściowych liczymy jedynie rząd wielkości czasu dzia-
łania algorytmu, wtedy zajmujemy się asymptotyczną złożonościa algorytmów. Oznacza to, że
interesuje nas, jak szybko wzrasta czas dzialania algorytmu, gdy rozmiar danych wejściowych
dąży do nieskończoności. Zazwyczaj dla dostatecznie dużych danych najlepszy jest algorytm
asymptotycznie bardziej efektywny. Zwykle staramy sie podać jak najprostszą funkcję charakte-
ryzującą rząd wielkości W(Alg,n) i A(Alg,n), na przykład n,

n

n log

,

2

n ,

3

n .

Będziemy używać następujących oznaczeń dla rzędów wielkości funkcji.

Definicja.
Dla danej funkcji

)

(n

g

oznaczamy przez

))

(

(

n

g



zbior funkcji





)

(

)

(

)

(

0

,

),

0

,

,

(

:

)

(

))

(

(

2

1

0

0

2

1

n

g

c

n

f

n

g

c

n

n

n

c

c

n

f

n

g



















.

Funkcja

)

(n

f

należy do zbioru

))

(

(

n

g



, jeśli istnieją dodatnie stałe

1

c oraz

2

c takie, że funkcja

może być „wstawiona między”

)

(

1

n

g

c

i

)

(

2

n

g

c

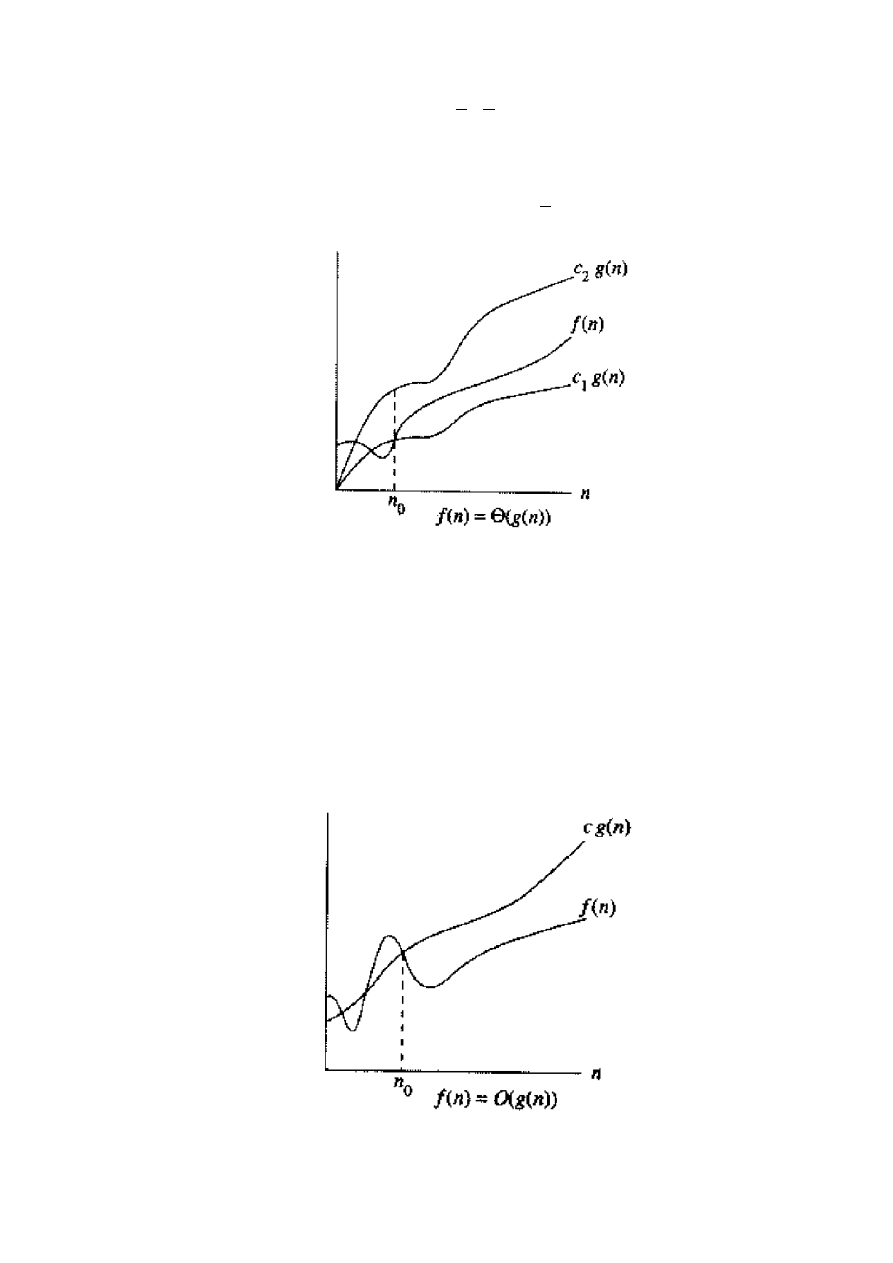
dla dostatecznie dużych n. (Rys. 2). Chociaż

))

(

(

n

g



jest zbiorem, piszemy

))

(

(

)

(

n

g

n

f





, żeby wyrazić, że

)

(n

f

jest elementem

))

(

(

n

g



. Dla wszystkich wartości n większych od

0

n wartość

)

(n

f

znajduje się między

)

(

1

n

g

c

i

)

(

2

n

g

c

. Inaczej mówiąc, dla wszystkich

0

n

n



funkcja

)

(n

f

jest równa

)

(n

g

z dokładnością

do stalego współczynnika. Mówimy, że

)

(n

g

jest asymptotycznie dokładnym oszacowaniem dla

)

(n

f

. Na przykład,

)

(

3

2

1

2

2

n

n

n







, co oznacza że można pominąć składniki niższych rzę-

dów. To można latwo udowodnić, używając formalnych definicji. W tym celu musimy znalezć
dodatnie stałe

1

c ,

2

c oraz

0

n takie, że

2

2

2

2

1

3

2

1

n

c

n

n

n

c







dla każdego

0

n

n



. Dzieląc powyższą zależność przez

2

n , otrzymujemy

11

2

1

3

2

1

c

n

c







.

Prawa strona jest prawdziwa dla każdej wartości

1



n

, gdy wybierzemy

2

/

1

2



c

. Podobnie,

lewa strona jest prawdziwa dla każdej wartości

7



n

, gdy wybierzemy

14

/

1

1



c

. Wybierając

14

/

1

1



c

,

2

/

1

2



c

oraz

7

0



n

, możemy sprawdzić, że

)

(

3

2

1

2

2

n

n

n







.

Rys. 2. Za pomocą notacji



szacuje się funkcję z dokładnością do stalego współczynnika. Pi-

szemy

))

(

(

)

(

n

g

n

f





, jeśli istnieją dodatnie stałe

0

n ,

1

c ,

2

c takie, że na prawo od

0

n wartość

)

(n

f

leży zawsze między

)

(

1

n

g

c

i

)

(

2

n

g

c

.

Definicja.
Dla danej funkcji

)

(n

g

oznaczamy przez

))

(

(

n

g

O

zbior funkcji





)

(

)

(

0

,

),

0

,

(

:

)

(

))

(

(

2

0

0

n

g

c

n

f

n

n

n

c

n

f

n

g

O















.

Notacja



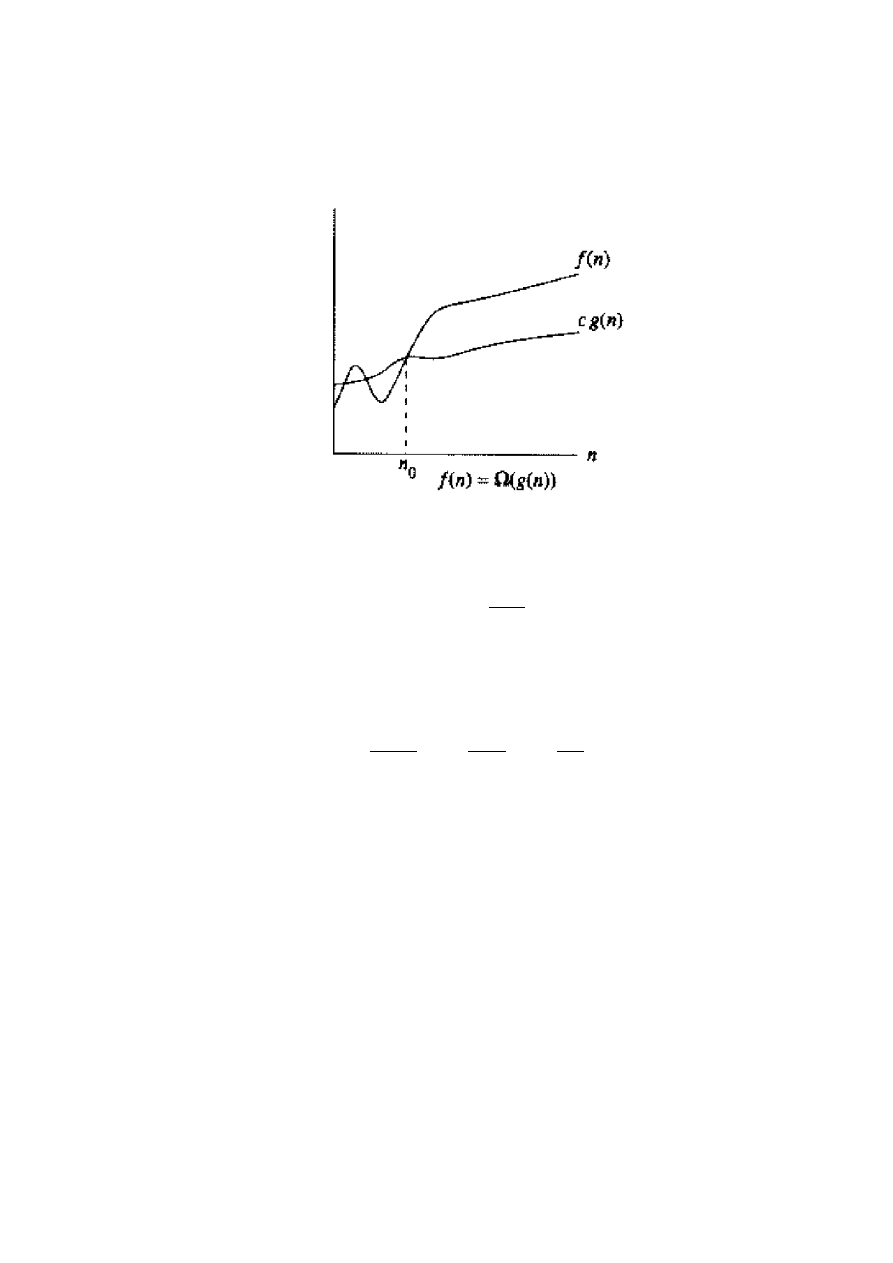
asymptotycznie ogranicza funkcję od góry oraz od dołu. Kiedy mamy tylko asympto-

tyczną granicę górną, używamy notacji O (Rys. 3).

Rys. 3. Notacja O daje górne organiczenie funkcji z dokladnością do stalego współczynnika.

12

Definicja.
Dla danej funkcji

)

(n

g

oznaczamy przez

))

(

(

n

g



zbior funkcji





)

(

)

(

0

,

),

0

,

(

:

)

(

))

(

(

0

0

n

f

n

cg

n

n

n

c

n

f

n

g

















.

Notacja



asymptotycznie ogranicza funkcję od dołu (Rys. 4).

Rys. 4. Notacja



daje dolne organiczenie funkcji z dokladnością do stalego współczynnika.

Rzędy wielkości dwóch funkcji

)

(n

f

i

)

(n

g

mogą być porównane przez obliczenie gra-

nicy

)

(

)

(

lim

n

g

n

f

E

n







.

Jeśli





E

, to

))

(

(

)

(

n

f

O

n

g



, ale nie

))

(

(

)

(

n

g

O

n

f



.

Jeśli

0





c

E

, to

))

(

(

)

(

n

g

n

f





.

Jeśli

0



E

, to

))

(

(

)

(

n

g

O

n

f



, ale nie

))

(

(

)

(

n

f

O

n

g



.

Na przykład stosując regułę de L’Hospitala, otrzymujemy

0

2

ln

/

1

lim

2

ln

ln

lim

log

lim

2



















n

n

n

n

n

n

n

n

n

,

czyli

)

(

log

2

n

O

n

n



, ale nie

)

log

(

2

n

n

O

n



.

Większość rozważanych algorytmów ma złożoność czasową proporcjonalną do jednej z

podanych tu funkcji:

n

log

– złożoność logarytmiczna

n – złożoność liniowa
n

n

log

– złożoność liniowo-logarytmiczna

2

n – złożoność kwadratowa

3

n ,

4

n ,... – złożoności wielomianowe

n

n

n

2

log

log

2



– złożoność podwykładnicza

n

2

– złożoność wykładnicza

n

2

!

n

– złożoność wykładnicza

!

n