PRZEMIANY ENERGETYCZNE

dr in

ż

. Andrzej Wawszczak

andrzej.wawszczak@p.lodz.pl

PODSTAWOWE POJ

Ę

CIA

układ jednostek SI:

– jednostki podstawowe (

m

, 

kg

, 

mol

, 

s

, 

K

, 

A

, 

cd

);

– jednostki pochodne (

N

, 

Pa

, 

J

, 

W

); 

wielokrotno

ś

ci –

M

mega, 

k

kilo, 

m

mili ... , 

.

.

.

PODSTAWOWE WIELKO

Ś

CI FIZYCZNE STOSOWANE W TERMODYNAMICE

wielko

ść

 fizyczna

–

warto

ść

 liczbowa

i 

jednostka miary

– np.

12

kg

,

15

m

, 

34

s

.

masa

–

1

kg

, kilogram, ( 

G

lub 

m

),

siła

–

1

N

=

1

kg·m/s

2

, niuton, ( 

F

),

ilo

ść

 substancji

–

1

mol

, mol, ( 

n

), 

temperatura

–

1

K

(bezwzgl

ę

dna), kelwin, ( 

T 

= 

t

+ 

273,15

) lub 

1

ºC

, stopie

ń

 celcjusza, ( 

t

= 

T

–

273,15

), 

ci

ś

nienie

–

1

Pa

, paskal, ( 

p

), 

obj

ę

to

ść

–

1

m

3

, metr sze

ś

cienny, ( 

V

), 

obj

ę

to

ść

 w warunkach normalnych

–

1

m

n

3

, normalny metr sze

ś

cienny, ( 

V

n

) 

– jest to obj

ę

to

ść

 gazu najcz

ęś

ciej przy: 

t

= 

0

°

C

, 

p

= 

101325

Pa

,

– jest to obj

ę

to

ść

 gazu najcz

ęś

ciej przy: 

t

= 

0

°

C

, 

p

= 

101325

Pa

,

energia

–

1

J

, = 1 

N·m

, d

ż

ul, ( 

E

), 

1

kWh

= 

3600

kJ

, kilowatogodzina,

praca

–

1

J

, d

ż

ul, ( 

L

),

ciepło

–

1

J

, d

ż

ul, ( 

Q

),

strumie

ń

 masy

–

1

kg/s

, kilogram na sekund

ę

, ( 

G

lub 

m

),

strumie

ń

 obj

ę

to

ś

ci

–

1

m

3

/s

, metr sze

ś

cienny na sekund

ę

, ( 

V

), 

moc

(

strumie

ń

 energii

) –

1

W

= 

1

J/s

, wat, ( 

P

= 

E

),

wielko

ś

ci fizyczne wła

ś

ciwe

oznaczane mał

ą

 liter

ą

 

– odniesione do masy –

v

, 

u

, 

s

, 

i

, 

q

... ,

– odniesione do mola – (

Mv

), (

Mu

), (

Ms

), (

Mi

), (

Mq

).

.

.

.

.

równanie bilansu substancji:

G

d

= 

∆

G

u

+ G

w

G

d

- masa substancji doprowadzonej do układu

G

w

- masa substancji wyprowadzonej z układu

∆

G

u

- przyrost masy substancji w układzie, 

∆

G

u

= G

d

- G

w

analogicznie: 

n

d

= 

∆

n

u

+ n

w

V

nd

= 

∆

V

nu

+ V

nw

warunek ci

ą

gło

ś

ci strugi w przewodzie (kanale):

ρρρρ

⋅⋅⋅⋅

⋅⋅⋅⋅

====

w

A

G

&

v

G

G

w

A

V

⋅⋅⋅⋅

====

ρρρρ

====

⋅⋅⋅⋅

====

&

&

warunek ci

ą

gło

ś

ci strugi w przewodzie (kanale):

gdzie: A – pole powierzchni przekroju kanału [ m

2

], 

ρ

– g

ę

sto

ść

, [ kg/m

3

]

v – obj

ę

to

ść

 wła

ś

ciwa, [ m

3

/kg ]

TERMICZNE RÓWNANIE STANU GAZÓW DOSKONAŁYCH I PÓŁDOSKONAŁYCH

Ogólna posta

ć

 termicznego rownania stanu:

F(p,T,v)=0

Gaz doskonały

– umowny gaz, ktorego drobiny nie przyci

ą

gaj

ą

 si

ę

 wzajemnie, s

ą

 

niesko

ń

czenie małe i sztywne (brak drga

ń

 wewn

ą

trz drobin).

Gaz półdoskonały

– ró

ż

ni si

ę

 od doskonałego tym, 

ż

e atomy w drobinach powi

ą

zane s

ą

 

spr

ęż

y

ś

cie, wyst

ę

puj

ą

 drgania wewn

ą

trz drobin. 

Wi

ę

kszo

ść

 gazów wyst

ę

puj

ą

cych w urz

ą

dzeniach cieplnych traktowa

ć

 mo

ż

na jako 

doskonałe lub półdoskonałe (za wyj

ą

tkiem gazow pod wysokim ci

ś

nieniem i pary – np. 

pary wodnej – do obliczania parametrow tych czynnikow nale

ż

y stosowa

ć

 rownania 

stanu gazow rzeczywistych, wykresy (wykresy parowe) lub tablice (tablice parowe)).

Dla dowolnej ilo

ś

ci gazu doskonałego lub półdoskonałego zale

ż

no

ść

 opisuj

ą

c

ą

 stan 

czynnika w sposób wystarczaj

ą

cy wyra

ż

a równanie stanu Clapeyrona:

czynnika w sposób wystarczaj

ą

cy wyra

ż

a równanie stanu Clapeyrona:

p · V = G · R · T

lub dla obj

ę

to

ś

ci wła

ś

ciwej:

p · v = R · T

p · V = n · (MR) · T

(MR) = 8,314 kJ/(kmol·K) – uniwersalna stała gazowa,
M – masa molowa, kg/kmol, liczbowo masa molowa jest równa masie atomowej, 
G – masa substancji, kg,
n – ilo

ść

 substancji, kmol,

V – obj

ę

to

ść

 substancji, m

3

.

Przeliczenie na warunki normalne:

[ V ] = [ m

3

]

[ p ] = [ Pa ]

[ T ] = [ K ]

T

p

V

10

696

,

2

T

p

V

 

101325

15

.

273

T

T

p

p

V

V

3

n

n

n

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

====

⋅⋅⋅⋅

⋅⋅⋅⋅

====

−−−−

PIERWSZA ZASADA TERMODYNAMIKI

Sposoby doprowadzania energii do układu:

praca mechaniczna

, 

ciepło

.

CIEPŁO DOPROWADZONE DO UKŁADU ( 

∆

Q

)

JEST RÓWNE SUMIE PRZYROSTU ENERGII WEWN

Ę

TRZNEJ UKŁADU ( 

∆

U

) 

ORAZ PRACY WYKONANEJ PRZEZ TEN UKŁAD ( 

∆

L

).

∆

Q = 

∆

U + 

∆

L

lub dla wielko

ś

ci wła

ś

ciwych

∆

q = 

∆

u + 

∆

l

∆

q = 

∆

u + 

∆

l

ENTALPIA

I = U + p · V  

lub dla wielko

ś

ci wła

ś

ciwych 

i = u + p · v 

[ Q ] = [ U ] = [ L ] = [ I ] = [ J ] lub [ kJ ],

[ V ] = [ m

3

]

[ p ] = [ Pa ]

[ q ] = [ u ] = [ l ] = [ i ] = [ J/kg ] lub [ kJ/kg ],

[ v ] = [ m

3

/kg ]

U

jest energi

ą

 wewn

ę

trzn

ą

 układu natomiast (

p · V

) to t.zw. praca przetłaczania. 

Pierwsz

ą

 zasad

ę

 termodynamiki mo

ż

na równie

ż

 zapisa

ć

 wykorzystuj

ą

c entalpi

ę

:

∆

Q = 

∆

I - V ·

∆

p

lub dla wielko

ś

ci wła

ś

ciwych

∆

q = 

∆

i - v ·

∆

p

CIEPŁO WŁA

Ś

CIWE

(pojemno

ść

 cieplna)

Ilo

ść

 ciepła potrzebna do podniesienia temperatury 1 kg ciała o 

∆

t mo

ż

na wyrazi

ć

 

wzorem:

∆

q = c ·

∆

t

gdzie:

c - współczynnik proporcjonalno

ś

ci zale

ż

ny od cieplnych wła

ś

ciwo

ś

ci ciała, 

nazywamy ciepłem wła

ś

ciwym, [ c ] = [ kJ/(kg·K) ].

Wielko

ść

 ta zale

ż

y nie tylko od rodzaju ciała i zakresu temperatur, w którym ciało jest 

ogrzewane lub ochładzane. Dla gazów ciepło wła

ś

ciwe mo

ż

e mie

ć

 wiele warto

ś

ci, 

zale

ż

nie od sposobu doprowadzania ciepła. 

W termodynamice szczególne znaczenie ma ciepło wła

ś

ciwe je

ż

eli doprowadzi si

ę

 

ciepło do czynnika termodynamicznego przy stałej obj

ę

to

ś

ci (c = c

v

) oraz przy stałym 

ci

ś

nieniu (c = c

p

). 

Dla gazów doskonałych ró

ż

nica ciepła wła

ś

ciwego przy stałym ci

ś

nieniu i przy stałej 

obj

ę

to

ś

ci jest wielko

ś

ci

ą

 stał

ą

i równ

ą

 indywidualnej stałej gazowej R:

c

p

- c

v

= R

oraz wykładnik adiabaty:

v

p

c

c

====

κκκκ

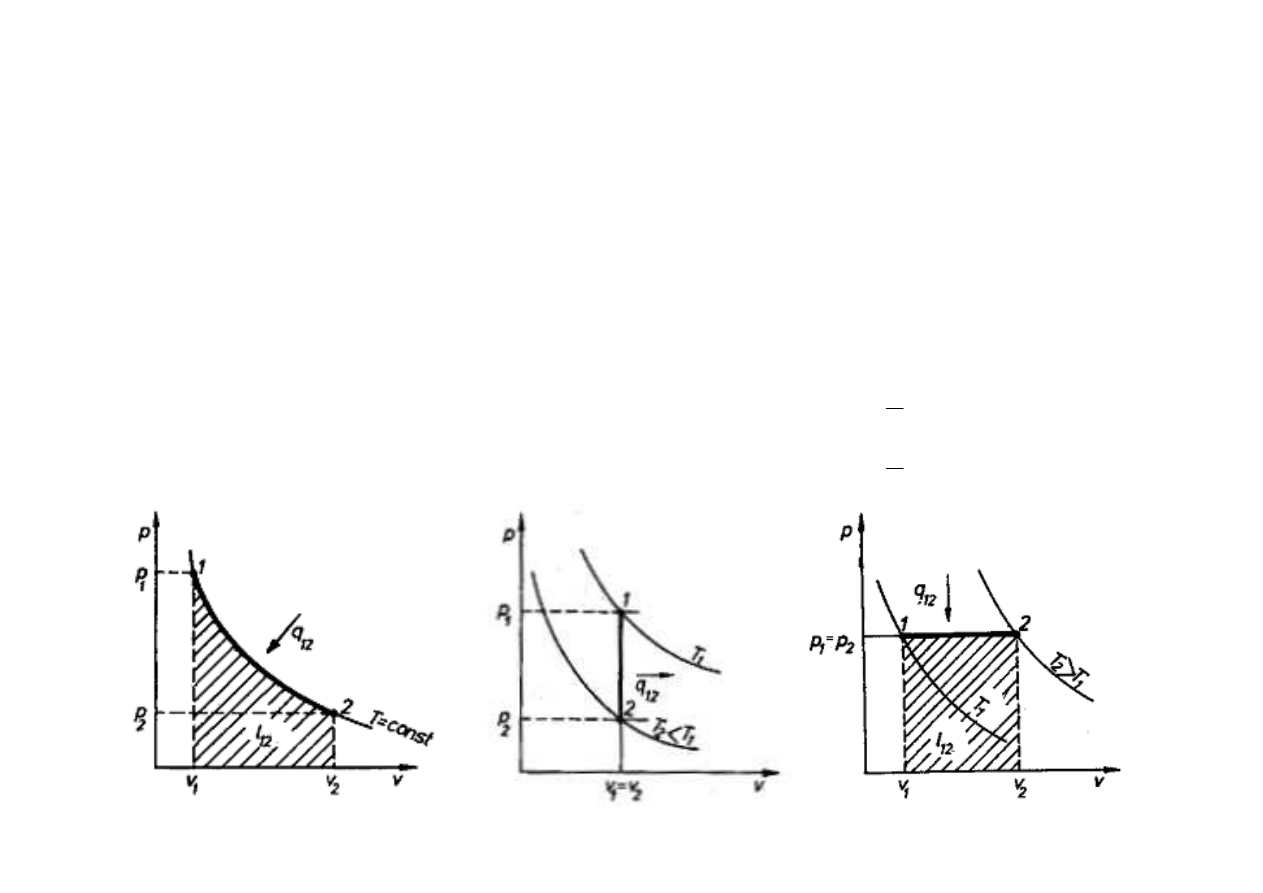
PRZEMIANY TERMODYNAMICZNE

układ (p-v)

Je

ż

eli w prostok

ą

tnym układzie współrz

ę

dnych na osi odci

ę

tych odło

ż

y si

ę

 obj

ę

to

ść

 

1 kg ciała podlegaj

ą

cego przemianie, a na osi rz

ę

dnych odpowiadaj

ą

ce tej obj

ę

to

ś

ci 

wła

ś

ciwej

v

ci

ś

nienie 

p

tej przemiany, to ka

ż

demu stanowi ciała odpowiada pewien 

punkt. Podczas przemiany termodynamicznej, czyli podczas zmian stanu układu, 
punkty te utworz

ą

lini

ę

, tzw.

krzyw

ą

 przemiany

. 

przemiana izotermiczna

(przy stałej temperaturze) – T = const:

p · v = const

przemiana izochoryczna

(przy stałej obj

ę

to

ś

ci) – v = const:

const

T

p

====

v

przemiana izobaryczna

(przy stałym ci

ś

nieniu) – p = const:

const

T

v

====

IZOTERMA

IZOCHORA

IZOBARA

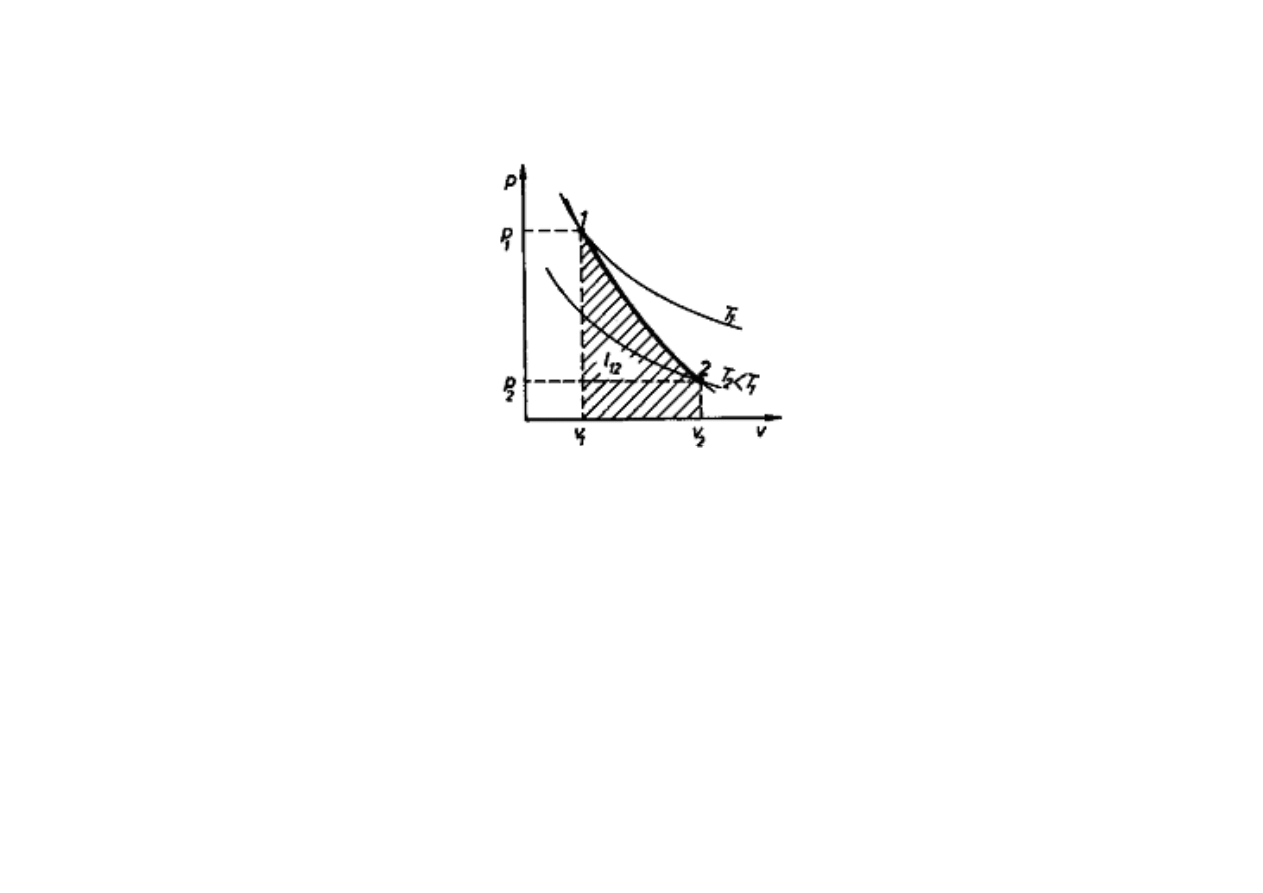
przemiana adiabatyczna

(bez wymiany ciepła) –

∆

q = 0:

p · v 

κ

= const

ADIABATA

Przemiana odbywaj

ą

ca si

ę

 bez wymiany ciepła z otoczeniem nosi nazw

ę

 

adiabatycznej, a krzywa przedstawiaj

ą

ca t

ę

 przemian

ę

 nazywa si

ę

 adiabat

ą

. 

Dla adiabaty praca techniczna równa si

ę

 ró

ż

nicy entalpii na pocz

ą

tku i ko

ń

cu 

przemiany:

l

12

= i

1

– i

2

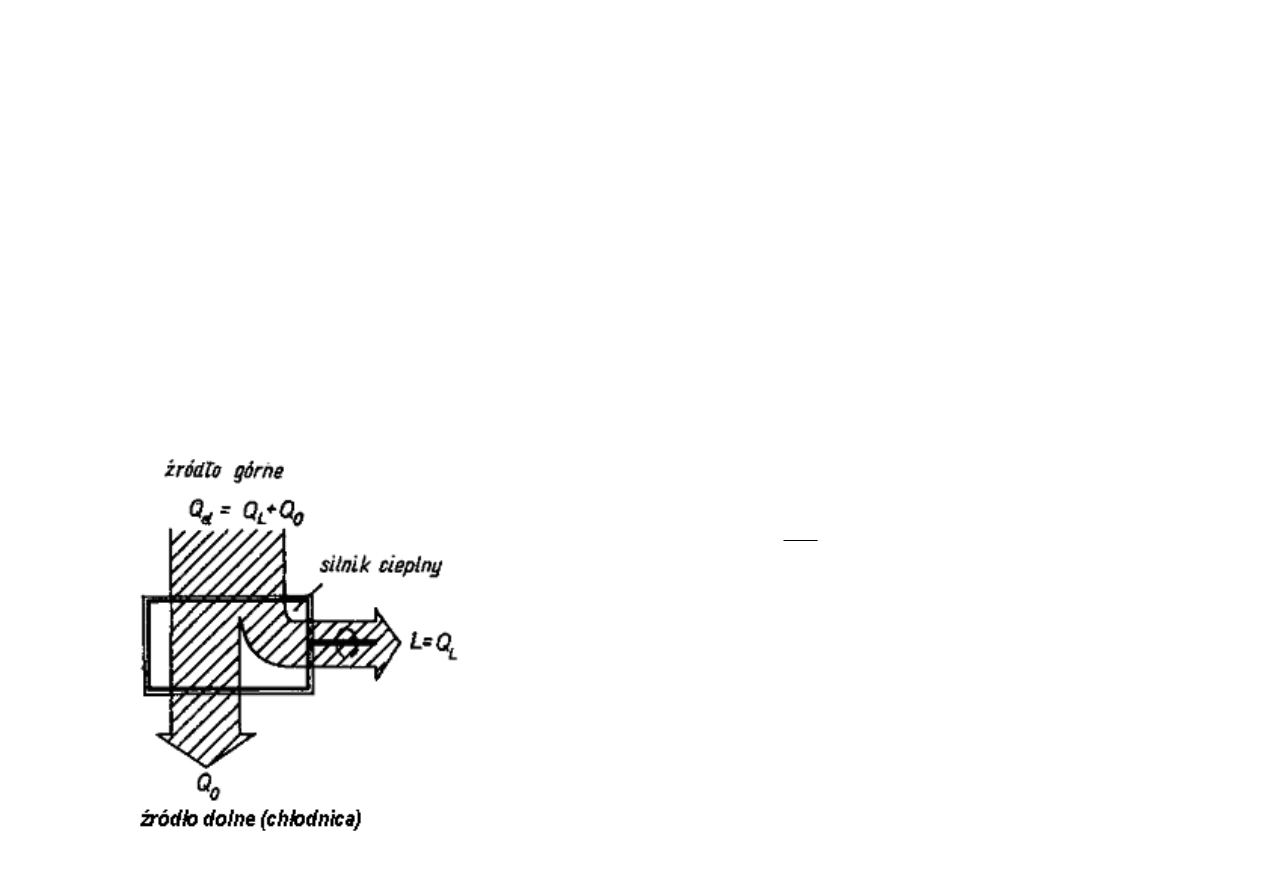
DRUGA ZASADA TERMODYNAMIKI

SILNIK CIEPLNY

Silnik cieplny

jest to układ, który w pewnych warunkach mo

ż

e zamienia

ć

 ciepło na 

prac

ę

. Czynnik termodynamiczny podczas odbywaj

ą

cych si

ę

 przemian czerpie ciepło ze 

ź

ródła gor

ą

cego (górnego) o wy

ż

szej temperaturze T

1

(np. palenisko, komora spalania, 

itp.), dzi

ę

ki czemu rozpr

ęż

a si

ę

 (zwi

ę

ksza swoj

ą

 obj

ę

to

ść

) i nast

ę

pnie oddaje ciepło do 

ź

ródła zimnego (dolnego) o ni

ż

szej temperaturze T

2

(np. skraplacz lub otaczaj

ą

ca 

atmosfera), wobec czego kurczy si

ę

 i mo

ż

e wróci

ć

 do stanu pierwotnego, wykonuj

ą

c 

obieg zamkni

ę

ty

. Miar

ą

 jako

ś

ci silnika b

ę

dzie stosunek wykonanej pracy zewn

ę

trznej L 

do dostarczonego ciepła Q

d

, nazywany 

sprawno

ś

ci

ą

 silnika cieplnego

( 

η

):

d

d

Q

L

====

ηηηη

Pierwsza zasada termodynamiki mówi, 

ż

e zu

ż

ywaj

ą

c 

pewn

ą

 ilo

ść

 ciepła jeste

ś

my w stanie otrzyma

ć

 

prac

ę

 i odwrotnie, zu

ż

ywaj

ą

c prac

ę

 – wywi

ą

zujemy 

ciepło. Zjawiska te, odwrotne wzgl

ę

dem siebie, 

ró

ż

ni

ą

 si

ę

 jednak bardzo istotnie mi

ę

dzy sob

ą

. 

Je

ż

eli pewien zasób pracy mechanicznej L, z zachowaniem wszelkich ostro

ż

no

ś

ci 

maj

ą

cych na celu unikni

ę

cie rozproszenia si

ę

 ciepła w formie przewodzenia, 

promieniowania itp., da si

ę

 zamieni

ć

 całkowicie na ciepło i ilo

ś

ciowo otrzymamy Q

d

= L 

ciepła, to zjawisko odwrotne odbywa si

ę

 w nieco odmiennych warunkach. Mianowicie, 

je

ż

eli w jakim

ś

 układzie cieplnym zachodz

ą

 specjalne warunki termodynamiczne 

umo

ż

liwiaj

ą

ce w ogóle zamian

ę

 ciepła na prac

ę

, co nie zawsze ma miejsce, to zu

ż

ywaj

ą

c 

Q

d

= Q

L

+ Q

O

ciepła mo

ż

na zamieni

ć

 na prac

ę

, mimo wszelkich zabiegów i stara

ń

, 

zaledwie cz

ęść

 tej ilo

ś

ci, a mianowicie Q

L

, otrzymuj

ą

c jedynie L = Q

L

pracy. Reszta, to 

jest Q

O

, jest dla tej zamiany stracona – pozostaje wprawdzie w formie ciepła, ale nie 

daj

ą

cego si

ę

 ju

ż

 w tym układzie przetworzy

ć

 na prac

ę

. To spostrze

ż

enie nie obala 

pierwszej zasady termodynamiki, równowa

ż

no

ść

 pracy i ciepła sw

ą

 moc utrzymuje, gdy

ż

 

przy przemianie ciepła na prac

ę

 zniknie w układzie dokładnie tyle ciepła, ile otrzymanej 

zostało pracy, ale jednocze

ś

nie cz

ęść

 ciepła, nie zamieniwszy si

ę

 w prac

ę

, ujdzie do 

ź

ródła dolnego jako ciepło z obni

ż

on

ą

 temperatur

ą

 (gazy wydechowe, spaliny, para 

wylotowa, skropliny itd.). Tak wi

ę

c chc

ą

c otrzyma

ć

 drog

ą

 przemiany termodynamicznej 

pewn

ą

 ilo

ść

 pracy L, trzeba doprowadzi

ć

 nie tylko równowa

ż

n

ą

 temu ilo

ść

 ciepła Q

L

= L, 

ale poza tym jeszcze ilo

ść

 Q

O

, to znaczy nale

ż

y doprowadzi

ć

 Q

d

= Q

L

+ Q

O

cho

ć

 ilo

ść

 

ciepła Q

O

nie bierze udziału w przemianie ciepła na prac

ę

. 

Niemo

ż

liwa jest wi

ę

c praca silnika cieplnego przy jednym tylko 

ź

ródle ciepła. Silnik taki 

pozwalałby przetwarza

ć

 dowolne ilo

ś

ci ciepła na równowa

ż

ne mu i praktycznie 

nieograniczone ilo

ś

ci energii mechanicznej, cho

ć

by z ciepła otoczenia, w ogóle ze 

ź

ródeł 

ciepła bez spadku temperatury, byłoby to tzw perpetum mobile drugiego rodzaju.

Silnik taki nie wytwarzałby pracy z niczego, zatem mo

ż

liwo

ść

 jego istnienia nie przeczy 

pierwszej zasadzie termodynamiki, przeczy natomiast drugiej zasadzie termodynamiki. 

Istnieje kilka równowa

ż

nych sformułowa

ń

 drugiej zasady termodynamiki. M. Planck 

Istnieje kilka równowa

ż

nych sformułowa

ń

 drugiej zasady termodynamiki. M. Planck 

głosił: 

Jest niemo

ż

liwe skonstruowanie periodycznie działaj

ą

cej maszyny, której 

działanie polegałoby tylko na podnoszeniu ci

ęż

arów i równoczesnym ochładzaniu 

ź

ródła 

ciepła

. R. Clausius  twierdził natomiast:

Ciepło nie mo

ż

e samorzutni przej

ść

 od ciała o 

temperaturze ni

ż

szej do ciała o temperaturze wy

ż

szej.

Przez samorzutny przebieg 

zjawiska rozumie si

ę

 tu taki przebieg, któremu nie towarzysz

ą

 

ż

adne zmiany w ciałach 

otaczaj

ą

cych rozpatrywany układ. 

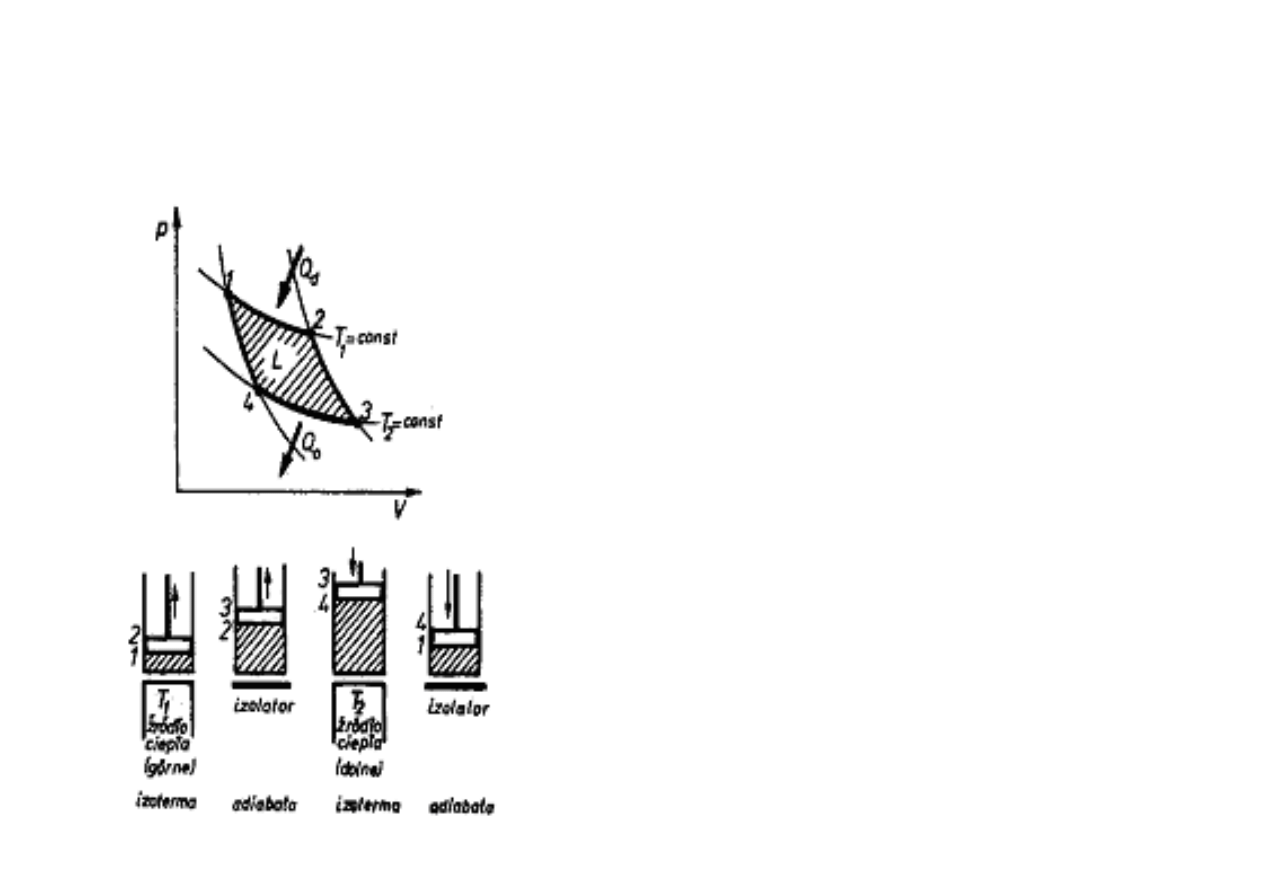
OBIEG CARNOTA

W 1824 roku francuski in

ż

ynier S. Carnot prz

ę

dstawił obieg termodynamiczny 

teoretyczny, który słu

ż

y j

ą

ko obieg porównawczy dla wszystkich obiegów 

rzeczywistych.  

Obieg Carnota składa si

ę

 z dwóch izoterm i dwóch 

adiabat. Czynnik pobiera ciepło Q

d

z górnego 

ź

ródła 

w stałej temperaturze T

1

(izotermicznie). Z chwil

ą

 

odci

ę

cia dopływu ciepła (punkt 2) czynnik rozpr

ęż

a 

si

ę

 dalej, ale ju

ż

 bez doprowadzenia ciepła, czyli 

adiabatycznie, a

ż

 do stanu 3, kiedy uzyska 

temperatur

ę

 dolnego 

ź

ródła ciepła T

2

. Teraz oddaje 

ciepło Q

O

izotermicznie, a

ż

 do stanu 4, sk

ą

d dzi

ę

ki 

spr

ęż

eniu adiabatycznemu, zostanie doprowadzony 

spr

ęż

eniu adiabatycznemu, zostanie doprowadzony 

do stanu pierwotnego 1. Mo

ż

na udowodni

ć

, 

ż

e obieg 

Carnota jest obiegiem odwracalnym. Praca L 
wykonana przy takim obiegu wyrazi si

ę

 na wykresie 

(p-v) polem 1-2-3-4. 

Sprawno

ść

 obiegu b

ę

dzie wyra

ż

ała si

ę

 zale

ż

no

ś

ci

ą

:

d

O

d

O

d

d

C

Q

Q

1

Q

Q

Q

Q

L

−−−−

====

−−−−

====

====

ηηηη

1

2

1

2

1

C

T

T

1

T

T

T

−−−−

====

−−−−

====

ηηηη

Jest to maksymalna sprawno

ść

, jak

ą

 mo

ż

na osi

ą

gn

ąć

 w obiegu termodynamicznym 

realizowanym w zakresie mi

ę

dzy temperatur

ą

 górnego 

ź

ródła T

1

i dolnego 

ź

ródła T

2

. 

Sprawno

ść

 ta jest tym wi

ę

ksza, im mniejszy jest stosunek T /T , tzn. im wy

ż

sza jest 

Sprawno

ść

 ta jest tym wi

ę

ksza, im mniejszy jest stosunek T

1

/T

2

, tzn. im wy

ż

sza jest 

temperatura górnego 

ź

ródła ciepła i jednocze

ś

nie im ni

ż

sza jest temperatura dolnego 

ź

ródła ciepła (chłodnicy).

Przykładowo: 
Temperatura górnego 

ź

ródła (kocioł parowy) t

1

= 400ºC ( T

1

= 673 K ), temperatura 

dolnego 

ź

ródła (otoczenie) t

2

= 20ºC ( T

2

= 293 K ) to

η

C

= 0.565 .

Temperatura górnego 

ź

ródła (geotermia) t

1

= 80ºC ( T

1

= 353 K ), temperatura dolnego 

ź

ródła (otoczenie) t

2

= 20ºC ( T

2

= 293 K ) to

η

C

= 0.17 .

Z wzoru na sprawno

ć

 

η

C

obiegu Carnota wynika równo

ść

:

czyli tzw. ciepło zredukowane:

W odwracalnej (idealnej) przemianie termodynamicznej ciepło zredukowane 
zale

ż

y tylko od skrajnych stanów czynnika, nie zale

ż

y od „drogi” przemiany.

Dla bardzo małych ilo

ś

ci przekazywanego ciepła:

Pewn

ą

 miar

ą

 nieodwracalno

ś

ci przemian (wszystkie przemiany rzeczywiste) jest 

parametr termodynamiczny 

entropia 

S, którego zmian

ę

 mo

ż

na opisa

ć

 

1

2

d

O

T

T

Q

Q

====

1

d

2

O

T

Q

T

Q

====

1

d

2

O

T

Q

T

Q

∆∆∆∆

====

∆∆∆∆

parametr termodynamiczny 

entropia 

S, którego zmian

ę

 mo

ż

na opisa

ć

 

zale

ż

no

ś

ci

ą

:

oraz dla wielko

ś

ci wła

ś

ciwych:

Jednostka entropii:

[ S ] = [ kJ/K ]

Jednostka entropii wła

ś

ciwej:

[ s ] = [ kJ/(kg·K) ]

T

Q

S

∆∆∆∆

====

∆∆∆∆

T

q

s

∆∆∆∆

====

∆∆∆∆

Poj

ę

cie entropii daje mo

ż

liwo

ść

 okre

ś

lenia kierunku przebiegu wszelkich zjawisk 

przyrody, obejmuj

ą

cych dostateczn

ą

 liczb

ę

 cz

ą

stek materii. Mo

ż

na łatwo udowodni

ć

, 

ż

e suma przyrostów entropii wszystkich ciał uczestnicz

ą

cych w zjawisku 

odwracalnym jest równa zeru, natomiast suma entropii wszystkich ciał 
uczestnicz

ą

cych w zjawisku nieodwracalnym, stale zwi

ę

ksza si

ę

 w czasie trwania 

zjawiska.

Uwzgl

ę

dniaj

ą

c równania opisuj

ą

ce pierwsz

ą

 zasad

ę

 termodynamiki, mo

ż

na do 

wyra

ż

enia opisuj

ą

cego zmian

ę

 entropii wprowadzi

ć

 parametry stanu czynnika. 

Otrzymuje si

ę

 wówczas dwa równania ró

ż

niczkowe zupełne, słuszne dla wszelkich 

przemian, zarówno odwracalnych jak i nieodwracalnych. Równania te to tzw. 

przemian, zarówno odwracalnych jak i nieodwracalnych. Równania te to tzw. 

to

ż

samo

ś

ci termodynamiczne

:

T

p

v

i

s

T

v

p

u

s

∆∆∆∆

⋅⋅⋅⋅

−−−−

∆∆∆∆

====

∆∆∆∆

∆∆∆∆

⋅⋅⋅⋅

++++

∆∆∆∆

====

∆∆∆∆

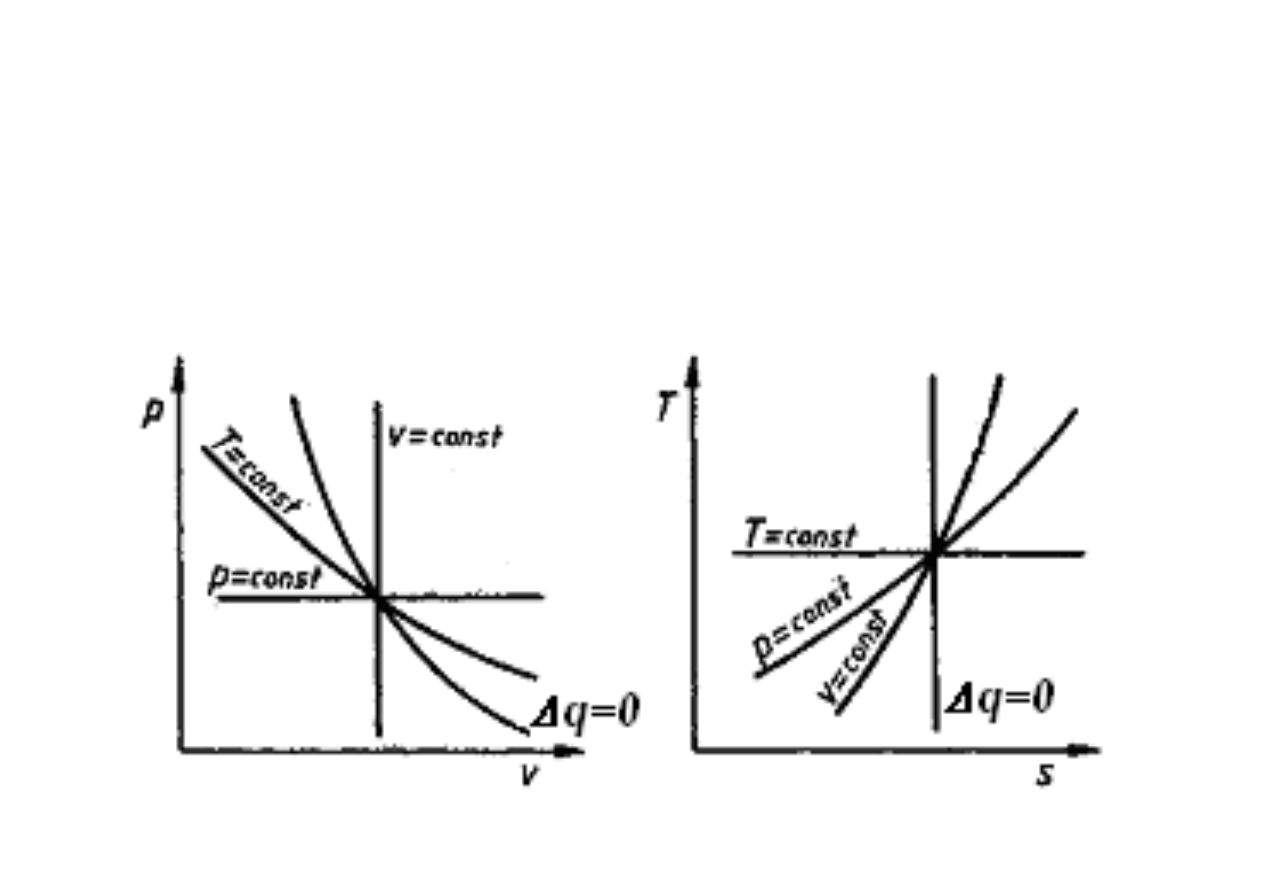
PRZEMIANY TERMODYNAMICZNE

układ (T-s)

Je

ż

eli w prostok

ą

tnym układzie współrz

ę

dnych na osi odci

ę

tych odło

ż

y si

ę

 entropi

ę

1 kg ciała podlegaj

ą

cego przemianie, a na osi rz

ę

dnych odpowiadaj

ą

ce tej entropii

wła

ś

ciwej s ci

ś

nienie p tej przemiany, to ka

ż

demu stanowi ciała odpowiada pewien 

punkt. Podczas przemiany termodynamicznej, czyli podczas zmian stanu, punkty te 
utworz

ą

lini

ę

, tzw. krzyw

ą

 przemiany. 

PARA WODNA

Praktyczne wykorzystanie i techniczna realizacja w elektrowni parowej procesu 
przetwarzania ciepła na energi

ę

 mechaniczn

ą

 wymaga znajomo

ś

ci podstawowych 

wła

ś

ciwo

ś

ci czynnika roboczego, tj. wody i pary wodnej. Wła

ś

ciwo

ś

ci te s

ą

 okre

ś

lone 

przez podstawowe parametry termodynamiczne: 

• ci

ś

nienie p, 

• temperatur

ę

 T lub t, 

• obj

ę

to

ść

 V lub obj

ę

to

ść

 wła

ś

ciw

ą

 v.

W analizach teoretycznych i w praktycznych obliczeniach technicznych bardzo s

ą

 

przydatne jeszcze dwa parametry termodynamiczne:

przydatne jeszcze dwa parametry termodynamiczne:

• entalpia I lub entalpia wła

ś

ciwa i,

• entropia S lub entropia wła

ś

ciwa s.

Entalpia wła

ś

ciwa jest ilo

ś

ci

ą

 ciepła niezb

ę

dn

ą

 do doprowadzenia 1 kg czynnika od 

punktu pocz

ą

tkowego przemiany do pewnego punktu ko

ń

cowego przy p = const. 

Entropia nie ma interpretacji fizycznej, wprowadzenie jej jako poj

ę

cia o charakterze 

matematycznym pozwala m.in. na przedstawienie obiegów termodynamicznych za 
pomoc

ą

 przejrzystych i wygodnych w u

ż

ytkowaniu wykresów. Powszechnie u

ż

ywane 

terminy: entalpia i entropia odnosz

ą

 si

ę

 najcz

ęś

ciej do entalpii i entropii wła

ś

ciwej 

(dla 1 kg czynnika).

Dla gazów rzeczywistych, w tym pary wodnej, równania stanu maj

ą

 w zapisie 

matematycznym znacznie bardziej skomplikowan

ą

 posta

ć

 ni

ż

 równanie stanu dla 

gazów doskonałych (Clapeyrona). Do oblicze

ń

 praktycznych i potrzeb kontroli pracy 

elektrowni parowych stosowa

ć

 mo

ż

na tablice pary wodnej lub opracowane na ich 

podstawie wykresy. Istniej

ą

 równie

ż

 stosunkowo łatwo dost

ę

pne w Internecie programy 

typu „kalkulator termodynamiczny” lub t.zw. biblioteki rozszerzaj

ą

ce mo

ż

liwo

ś

ci innych 

typu „kalkulator termodynamiczny” lub t.zw. biblioteki rozszerzaj

ą

ce mo

ż

liwo

ś

ci innych 

programów obliczeniowych, takich jak np. Excel. 

Przy analizie zjawisk termodynamicznych zwi

ą

zanych z par

ą

 wodn

ą

 jako czynnikiem 

roboczym powszechne zastosowanie znalazły wykresy T-s (temperatura-entropia) i i-s 
(entalpia-entropia). Wykres T-s pary wodnej umo

ż

liwia przedstawienie na nim, w postaci 

pewnego konturu, obiegu cieplnego elektrowni. 

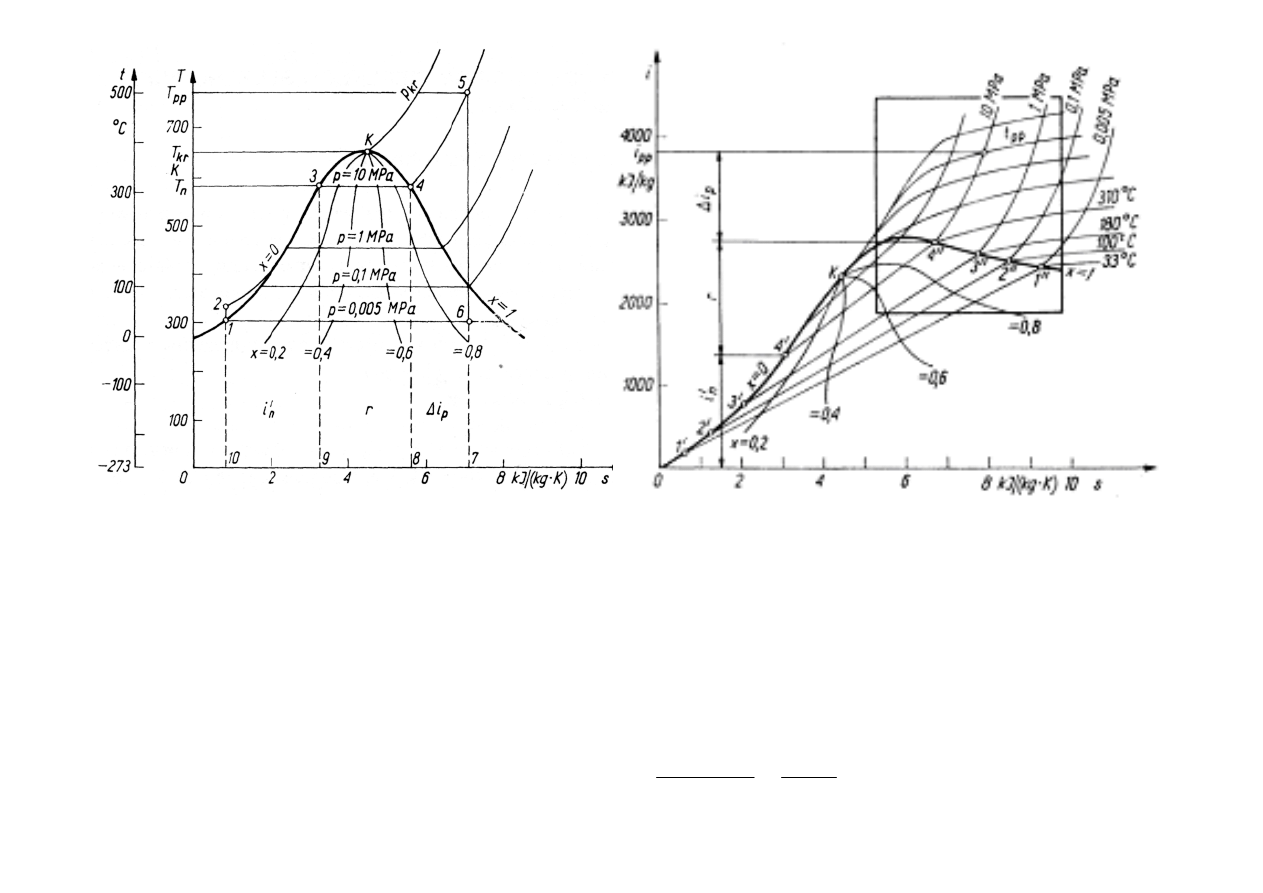
Punkt K na krzywej granicznej odpowiada 

parametrom krytycznym

pary wodnej, 

okre

ś

laj

ą

cym stan fizyczny, w którym ciecz staje si

ę

, bez doprowadzenia ciepła, par

ą

 

such

ą

 nasycon

ą

. Parametry tego stanu dla cieczy i pary suchej s

ą

 takie same: 

p

kr

= 22,064 MPa, T

kr

= 647,096 K (t

kr

= 373,946), v

kr

= 3,106 dm

3

/kg, 

ρρρρ

kr 

= 0.322 kg/dm

3

, 

i

kr

= 2084,26 kJ/kg, s

kr

= 4,40696 kJ/(kg·K), ciepło parowania r = 0.

Na lewo od punktu krytycznego znajduje si

ę

 linia x=0, wody w stanie nasycenia, na 

prawo linia x=1, pary suchej nasyconej. Mi

ę

dzy tymi liniami jest obszar pary nasyconej 

wilgotnej z liniami x o stałej wilgotno

ś

ci: 

i

i

i

i

m

m

m

x

x

p

w

p

′′′′

−−−−

′′′′′′′′

′′′′

−−−−

====

++++

====

Natomiast ciepło parowania r = i”- i’ .

Wykres T-s dla wody

Wykres i-s dla wody

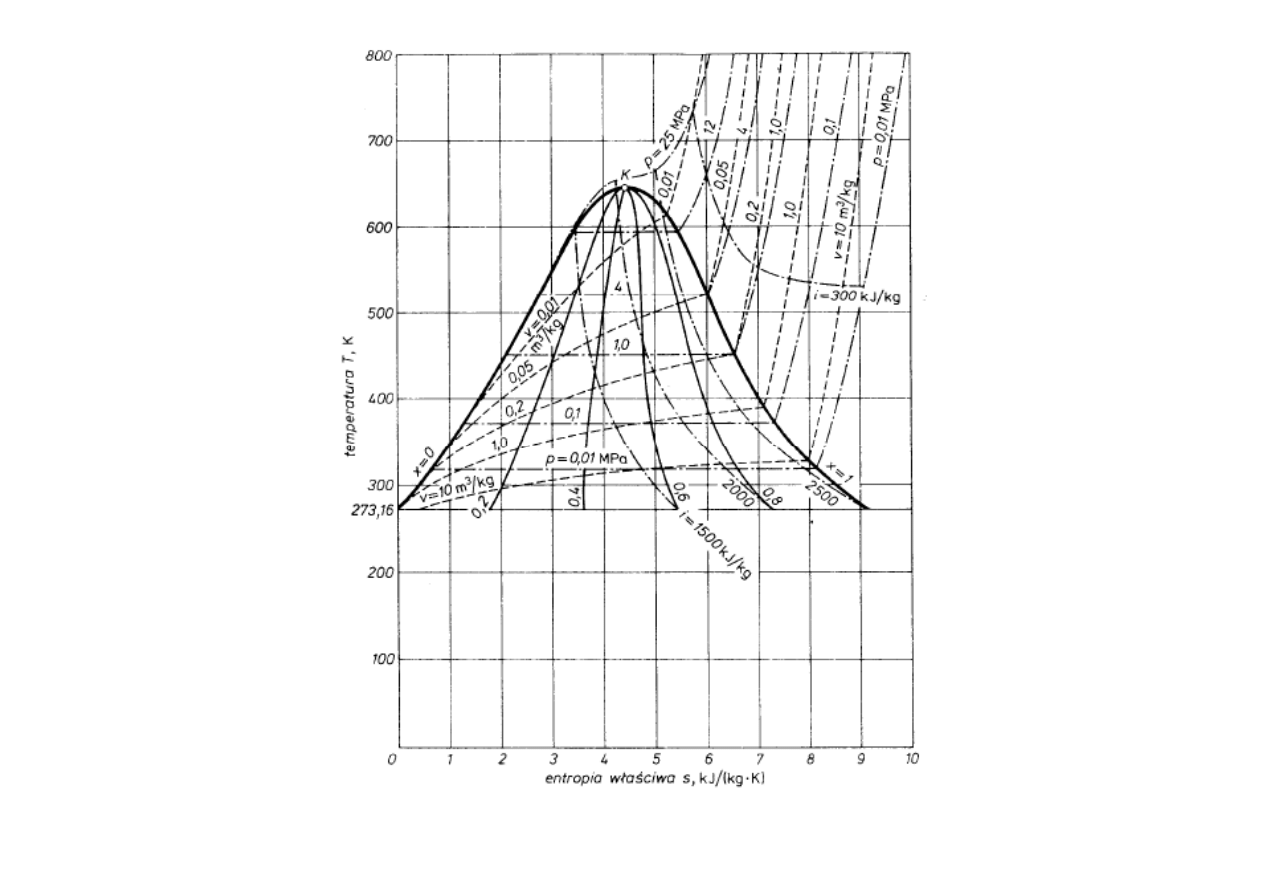
Wykres T-s pary wodnej

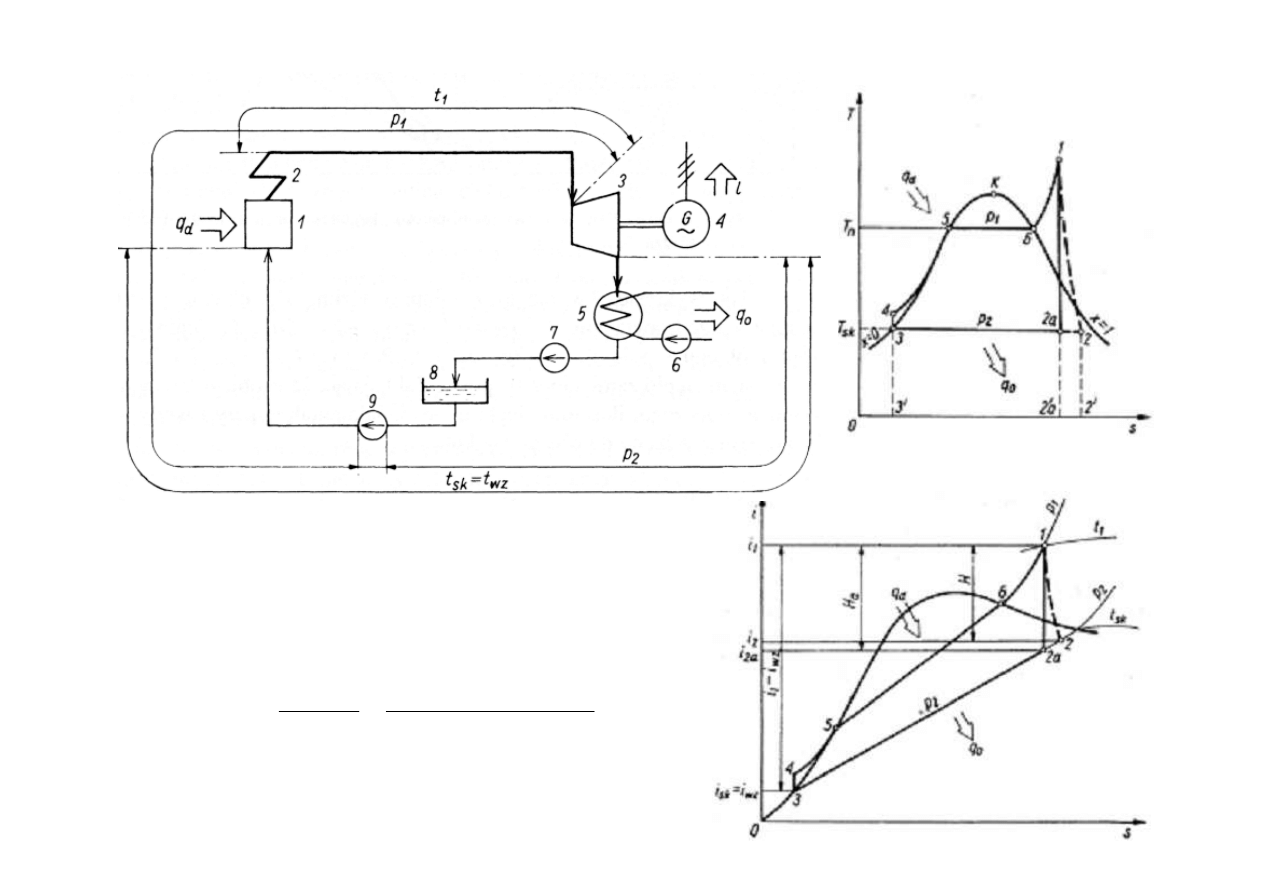
OBIEG CIEPLNY ELEKTROWNI PAROWEJ

1 - kocioł; 2 - przegrzewacz pary; 3 - turbina; 
4 - pr

ą

dnica (generator); 5 - skraplacz; 6 - pompa 

wody chłodz

ą

cej; 7 - pompa skroplin; 8 - zbiornik 

wody zasilaj

ą

cej; 9 - pompa wody zasilaj

ą

cej. 

Sprawno

ść

 teoretyczna obiegu Rankine’a:

(i

wz

- i

sk

) – praca na pompowanie wody do kotła.

((((

)))) ((((

))))

wz

1

sk

wz

a

2

1

d

o

d

t

i

i

i

i

i

i

q

q

q

−−−−

−−−−

−−−−

−−−−

====

−−−−

====

ηηηη

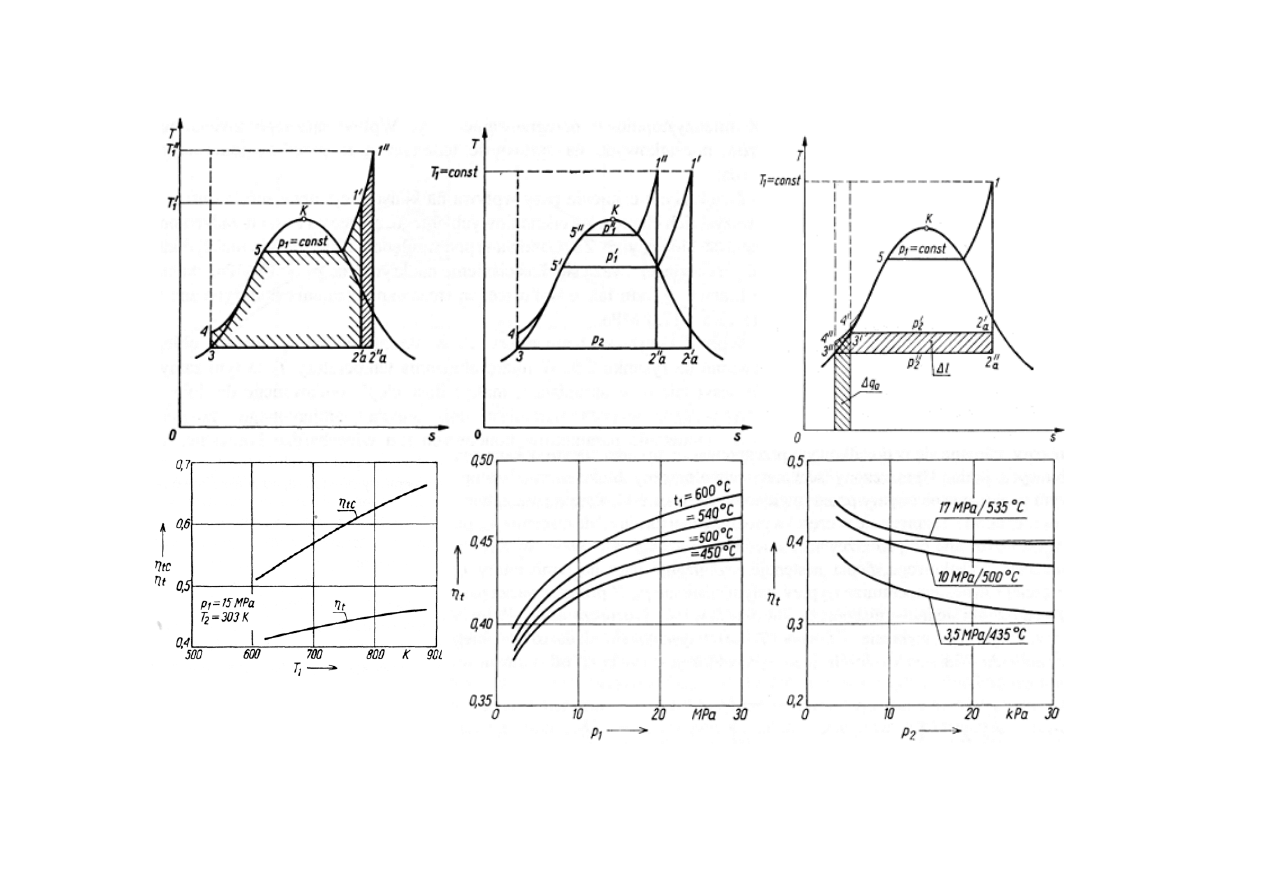
ZWI

Ę

KSZENIE SPRAWNO

Ś

CI OBIEGU CIEPLNEGO 

ELEKTROWNI KONDENSACYJNEJ

zwi

ę

kszenie temperatury T

1

przed turbin

ą

zwi

ę

kszenie ci

ś

nienia p

1

przed turbin

ą

zmniejszenie temperatury T

2

(ci

ś

nienia p

2

)

w skraplaczu turbiny

η

tc

– sprawno

ść

 obiegu Carnota

η

t

– sprawno

ść

 obiegu Rankine’a

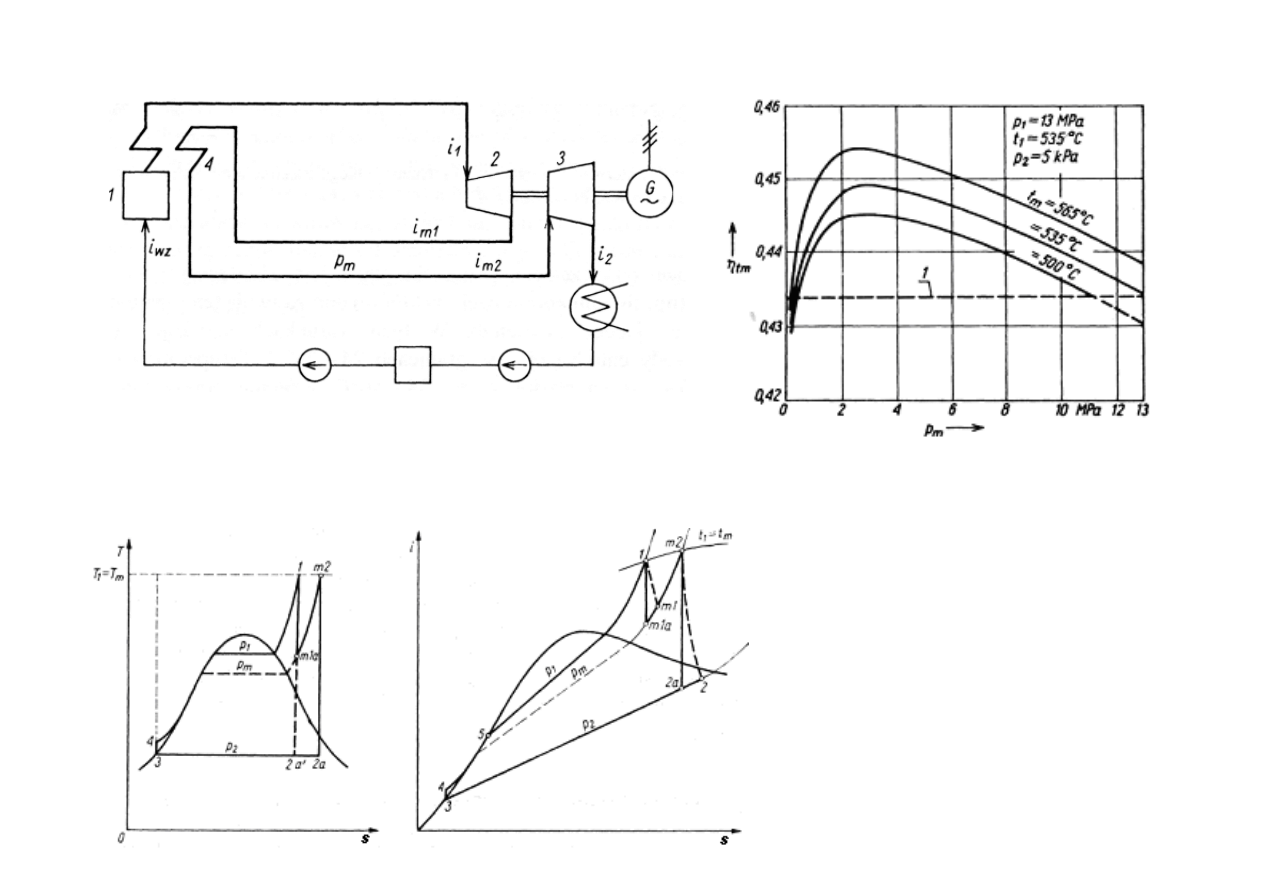
MI

Ę

DZYSTOPNIOWY PRZEGRZEW

Schemat obiegu cieplnego elektrowni z 
mi

ę

dzystopniowym przegrzewaniem pary: 1 - kocioł; 

mi

ę

dzystopniowym przegrzewaniem pary: 1 - kocioł; 

2 - cz

ęść

 wysokopr

ęż

na turbiny; 3 ~ cz

ęść

 niskopr

ęż

na 

turbiny; 4 - mi

ę

dzystopniowy przegrzewacz pary

Zale

ż

no

ść

 sprawno

ś

ci teoretycznej 

obiegu z mi

ę

dzystopniowym 

przegrzewaniem pary od ci

ś

nienia 

p

m

przy ró

ż

nych warto

ś

ciach 

temperatury t

m 

1 - sprawno

ść

 teoretyczna bez 

przegrzewania mi

ę

dzystopniowego

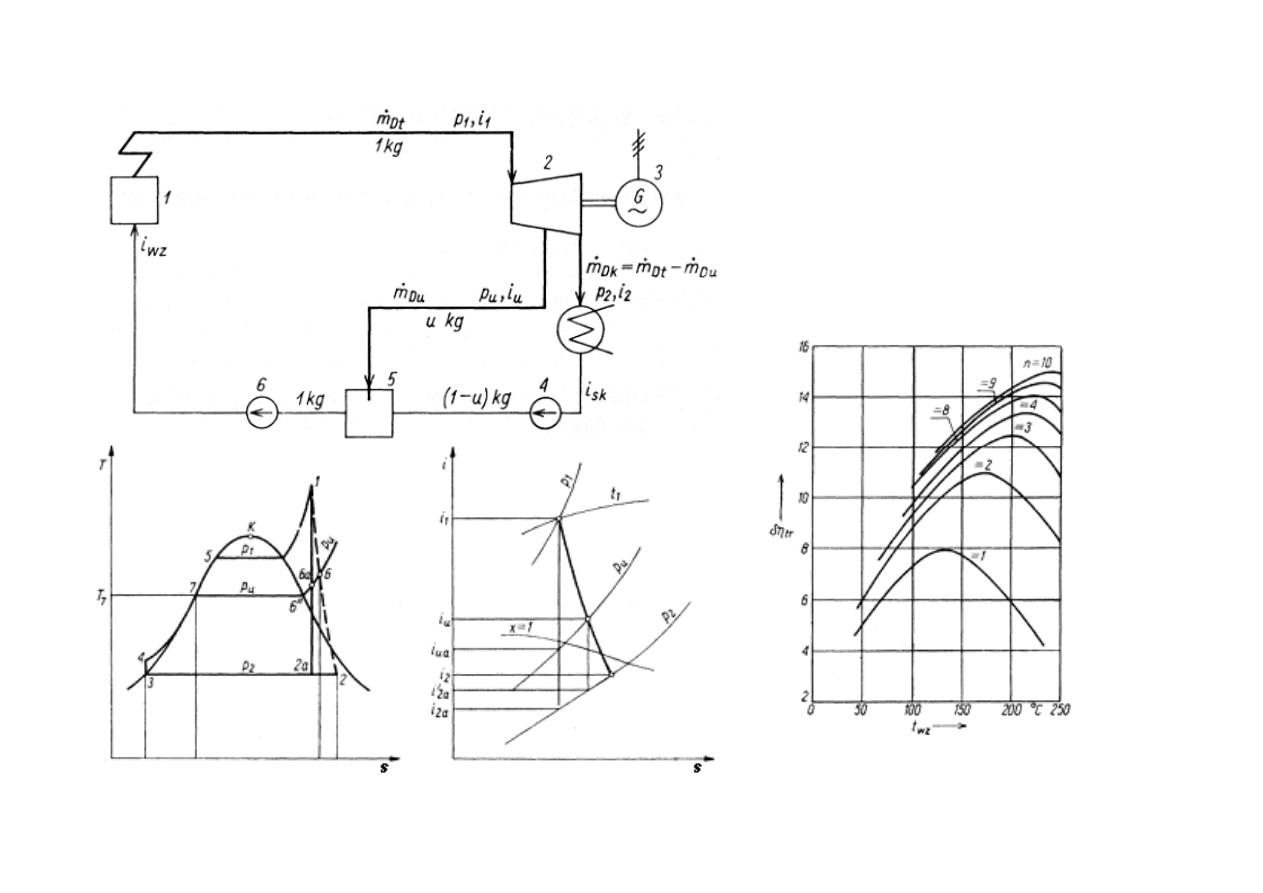
REGENERACYJNY PODGRZEW WODY ZASILAJ

Ą

CEJ

Schemat obiegu cieplnego 
elektrowni z jednostopniowym 
regeneracyjnym podgrzewaniem 
wody zasilaj

ą

cej

1- kocioł; 2 - turbina; 3 - pr

ą

dnica; 

4 - pompa skroplin; 
5 - podgrzewacz mieszankowy; 
6 - pompa wody zasilaj

ą

cej

obieg Rankine’a

rozpr

ęż

anie w turbinie

Wzgl

ę

dny przyrost sprawno

ś

ci obiegu 

w zale

ż

no

ś

ci od liczby podgrzewaczy 

regeneracyjnych n, twz – temperatura 

wody zasilaj

ą

cej kocioł. 

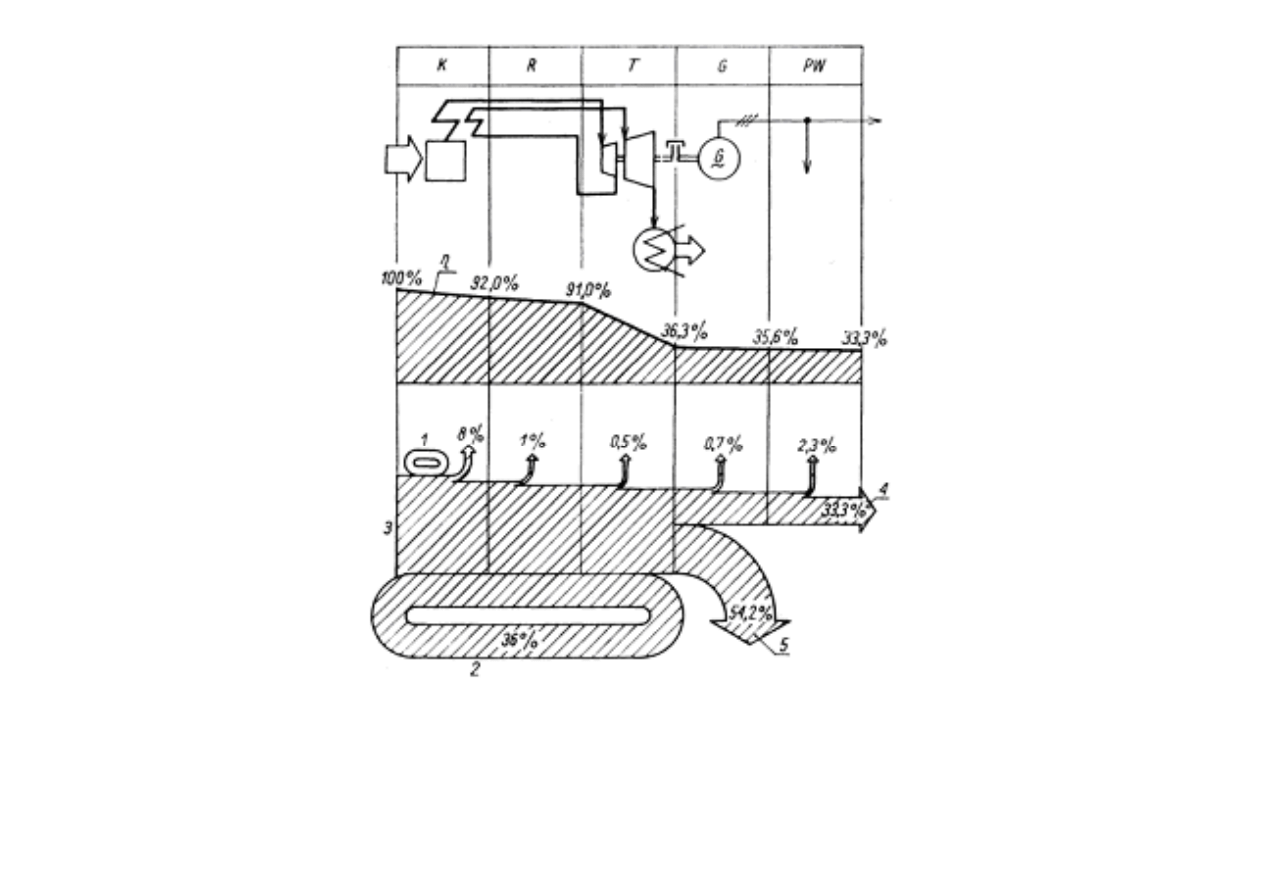
Przykładowy zmiany sprawno

ś

ci przemiany energii i bilans energetyczny strumieniowy 

(Sankeya) elektrowni parowej kondensacyjnej na umiarkowane parametry pary 
K - kocioł; R - ruroci

ą

gi; T— turbina; G — pr

ą

dnica; PW - potrzeby własne; 

1

podgrzewacz powietrza; 2 - regeneracyjne podgrzewanie wody zasilaj

ą

cej; 

3 - energia chemiczna paliwa; 4 - energia u

ż

yteczna netto; 5 - straty w skraplaczu

KOGENERACJA

ENERGIA 

PALIWA

ENERGIA 

ELEKTRYCZNA

CIEPŁO

STRATA

URZ

Ą

DZENIE 

PRZETWARZAJ

Ą

CE

CIEPŁO

Koszt produkcji u

ż

ytecznego produktu ubocznego nale

ż

y oceni

ć

 na podstawie 

kosztów mo

ż

liwych do unikni

ę

cia w całym procesie produkcji dzi

ę

ki zastosowaniu 

tego produktu ubocznego w procesie kogeneracji. Wytworzenie tego produktu 
ubocznego zast

ę

puje produkowanie go w wyspecjalizowanym procesie. Na 

przykład, wykorzystanie elektryczno

ś

ci z elektrociepłowni zast

ę

puje cz

ęść

 energii 

elektrycznej produkowanej w elektrowniach. Ponadto, istnieje ju

ż

 czysto 

ekonomiczna zasada podziału kosztów w procesach kogeneracji, jest to tak zwana 

zasada unikania wydatków

. 

OBIEGI CIEPLNE ELEKTROCIEPŁOWNI

Mała sprawno

ść

 obiegów kondensacyjnych jest wynikiem przede wszystkim 

odprowadzania du

ż

ych ilo

ś

ci ciepła z wod

ą

 chłodz

ą

c

ą

 skraplacz. Ciepło to ze wzgl

ę

du 

na stosunkowo nisk

ą

 temperatur

ę

 no

ś

nika (25

÷

38)

°

C ma niezwykle ograniczone 

mo

ż

liwo

ś

ci zastosowania, poniewa

ż

 do celów grzewczych s

ą

 wymagane temperatury 

mo

ż

liwo

ś

ci zastosowania, poniewa

ż

 do celów grzewczych s

ą

 wymagane temperatury 

(70

÷

150)

°

C, a do celów technologicznych w zakładach przemysłowych jeszcze wy

ż

sze.

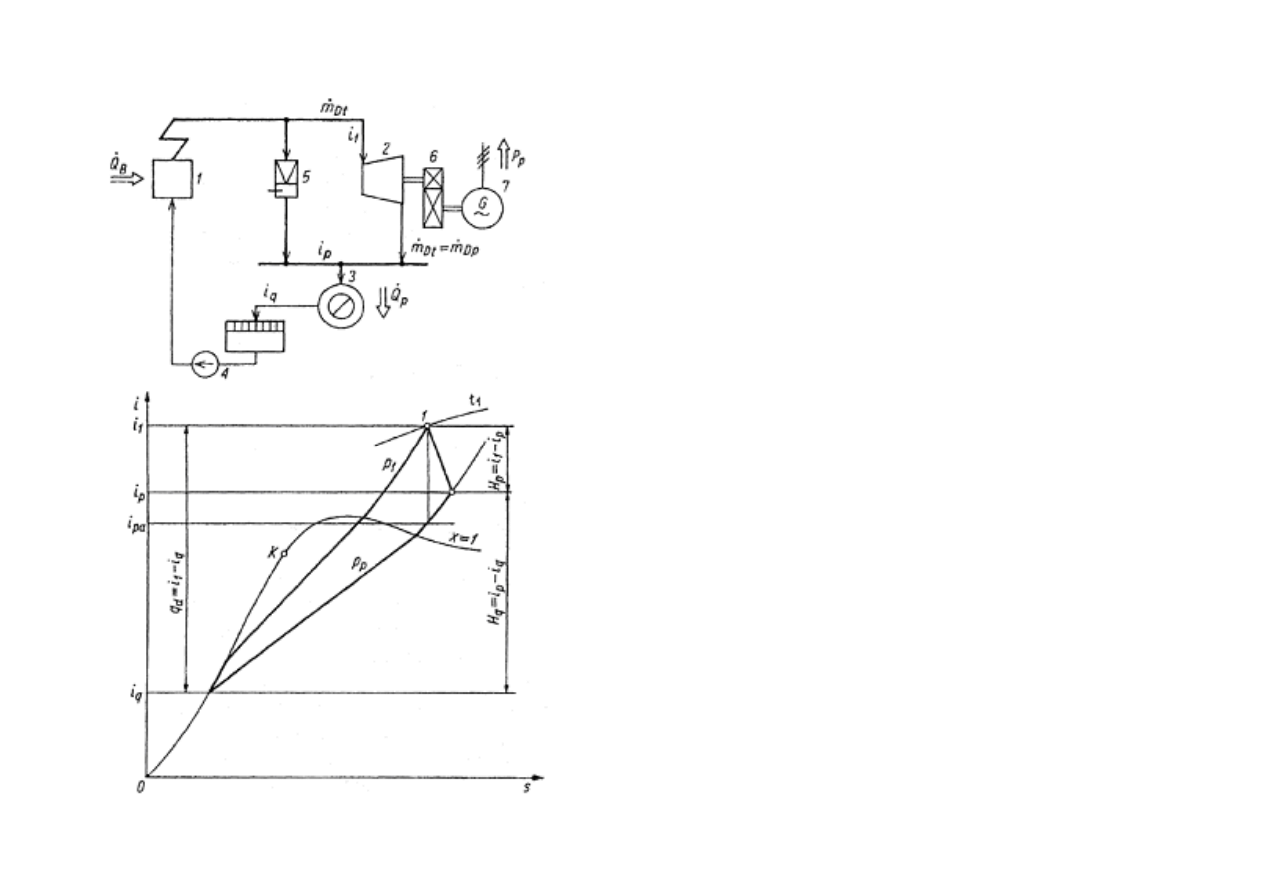
Aby dostosowa

ć

 parametry pary wylotowej z 

turbiny do potrzeb odbiorców ciepła, ogranicza si

ę

 

rozpr

ęż

anie pary w turbinie, podwy

ż

szaj

ą

c tym 

samym ko

ń

cowe ci

ś

nienie pary. W ten sposób 

turbozespół kondensacyjny przekształca si

ę

 w 

przeciwpr

ęż

ny, a ze strumienia pary rozpr

ęż

aj

ą

cego 

si

ę

 w turbinie od ci

ś

nienia pocz

ą

tkowego p

1

do 

ci

ś

nienia ko

ń

cowego, tzw. przeciwci

ś

nienia p

2

= p

p

, 

cz

ęść

 energii odpowiada-j

ą

ca spadkowi entalpii 

H

p

= i

1

- i

p

jest zamieniona na energi

ę

 elektryczn

ą

, a 

pozostała cz

ęść

 H

q

= i

p

- i

q

(i

q

- entalpia skroplin z pary wylotowej o ci

ś

nieniu 

p

p

) mo

ż

e by

ć

 całkowicie wykorzystana do celów 

grzewczych. Jest to najprostszy obieg 

grzewczych. Jest to najprostszy obieg 
ciepłowniczy realizuj

ą

cy skojarzone wytwarzanie 

energii elektrycznej i ciepła.

W układzie z turbin

ą

 przeciwpr

ęż

n

ą

, strumie

ń

 pary 

m

Dt

= m

Dp

, o parametrach p

1

, t

1

i entalpii i

1

, rozpr

ęż

a 

si

ę

 w turbinie przeciwpr

ęż

nej 2 do ci

ś

nienia p

p

. 

Nast

ę

pnie jest kierowany do odbiorników ciepła 3, 

gdzie oddaje ciepło skraplania, po czym jest 
tłoczony w postaci skroplin przez pomp

ę

 4 do 

kotła 1. Wyst

ę

puj

ą

ca w układzie stacja redukcyjno-

schładzaj

ą

ca 5 stanowi rezerw

ę

 zasilania 

odbiorców ciepła w przypadku odstawienia turbiny 
lub jej uzupełnienie (tzw. szczytowe 

ź

ródło ciepła).

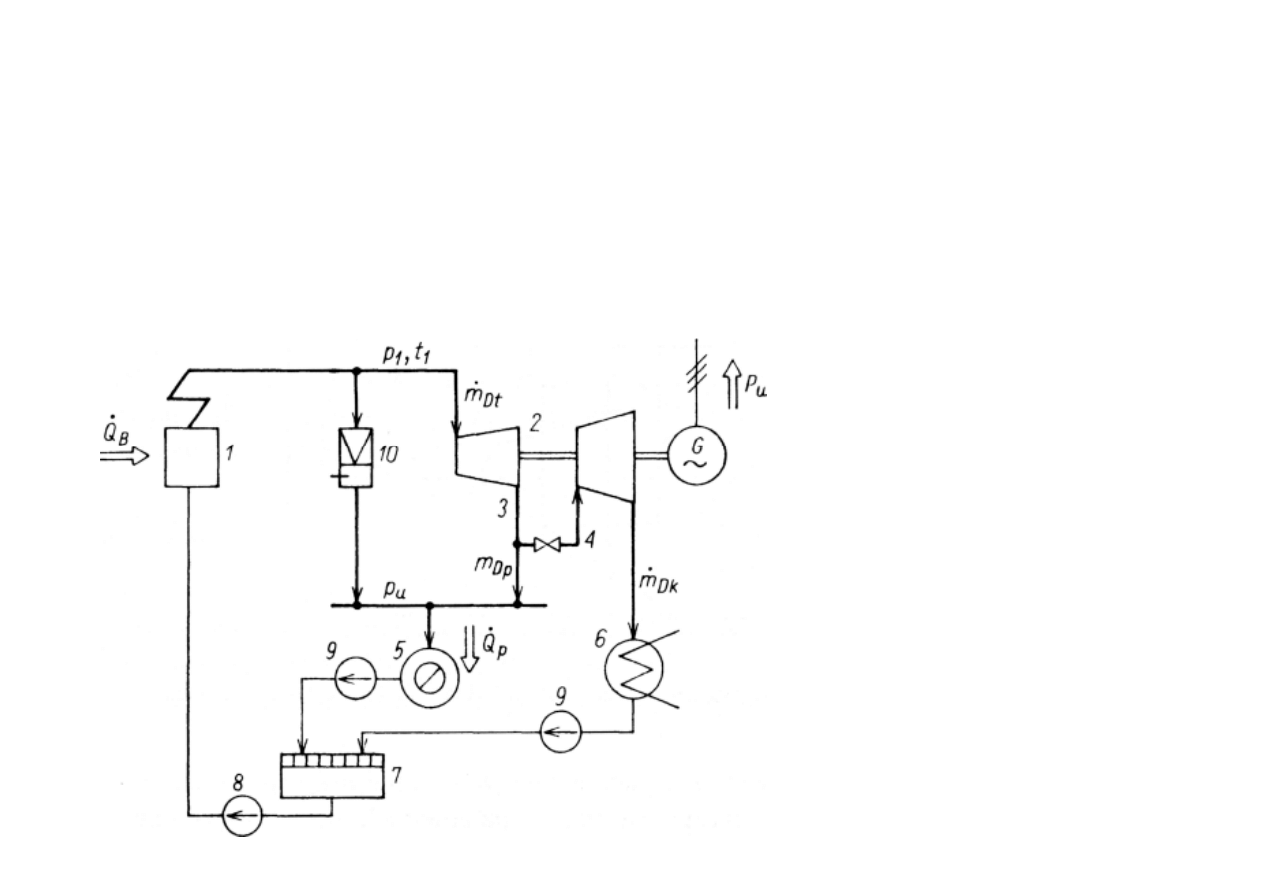
Ś

cisłe powi

ą

zanie wytwarzanej mocy elektrycznej z nat

ęż

eniem poboru pary do celów 

ciepłowniczych jest wad

ą

 turbiny przeciwpr

ęż

nej. Nie ma jej układ z turbin

ą

 

upustowo-

kondensacyjn

ą

, w którym cz

ęść

 strumienia pary jest pobierana z tzw. upustu 

regulowanego przy ci

ś

nieniu wymaganym przez odbiorniki ciepła, pozostała za

ś

 cz

ęść

 

strumienia rozpr

ęż

a si

ę

 do ci

ś

nienia panuj

ą

cego w skraplaczu turbiny. Najcz

ęś

ciej 

stosuje si

ę

 turbiny z jednym, rzadziej z dwoma upustami pary o ró

ż

nych ci

ś

nieniach,

w przypadku szczególnym liczba upustów mo

ż

e by

ć

 wi

ę

ksza. Je

ż

eli z wylotu turbiny 

upustowej jest pobierana równie

ż

 para do celów ciepłowniczych, to turbina taka nosi 

wówczas nazw

ę

 turbiny upustowo-przeciwpr

ęż

nej. 

Schemat obiegu ciepłowniczego 
z turbin

ą

 upustowo-kondensacyjn

ą

: 

1 - kocioł; 2 - turbina; 3 - upust; 
4 - zawór mi

ę

dzy cz

ęś

ci

ą

 wysoko-

i niskopr

ęż

n

ą

 turbiny; 5 - odbiornik 

ciepła; 6 - skraplacz; 7 - zbiornik 
skroplin; 8 - pompa wody zasilaj

ą

cej 

kocioł; 9 - pompy skroplin; 
10 - stacja redukcyjno-schładzaj

ą

ca. 

Charakterystycznym wska

ź

nikiem cieplno-elektrycznym elektrociepłowni, okre

ś

laj

ą

cym 

stosunek energii elektrycznej wytworzonej w obiegu do ciepła odprowadzonego do 
odbiorników z wylotu lub upustu turbiny, jest tzw. wska

ź

nik skojarzenia:

p

p

Q

E

====

σσσσ

gdzie:

E

p

- energia elektryczna wytworzona przez strumie

ń

pary przeciwpr

ęż

nej lub

upustowej w okre

ś

lonym czasie, kWh; Q

p

- ciepło odprowadzone z turbiny

do odbiorników w tym samym czasie, GJ.

Warto

ść

wska

ź

nika skojarzenia zale

ż

y od parametrów pocz

ą

tkowych oraz parametrów

pary odbieranej do celów ciepłowniczych, a tak

ż

e od układu technologicznego

elektrociepłowni i zawiera si

ę

w granicach od ok. 30 kWh/GJ (0,11 MW

c

/MW

t

) - dla

turbin przeciwpr

ęż

nych na małe parametry pocz

ą

tkowe i stosunkowo du

ż

e parametry

ko

ń

cowe) do ok. 150 kWh/GJ (0,55 MW

c

/MW

t

) - dla bloku ciepłowniczego BC-100.

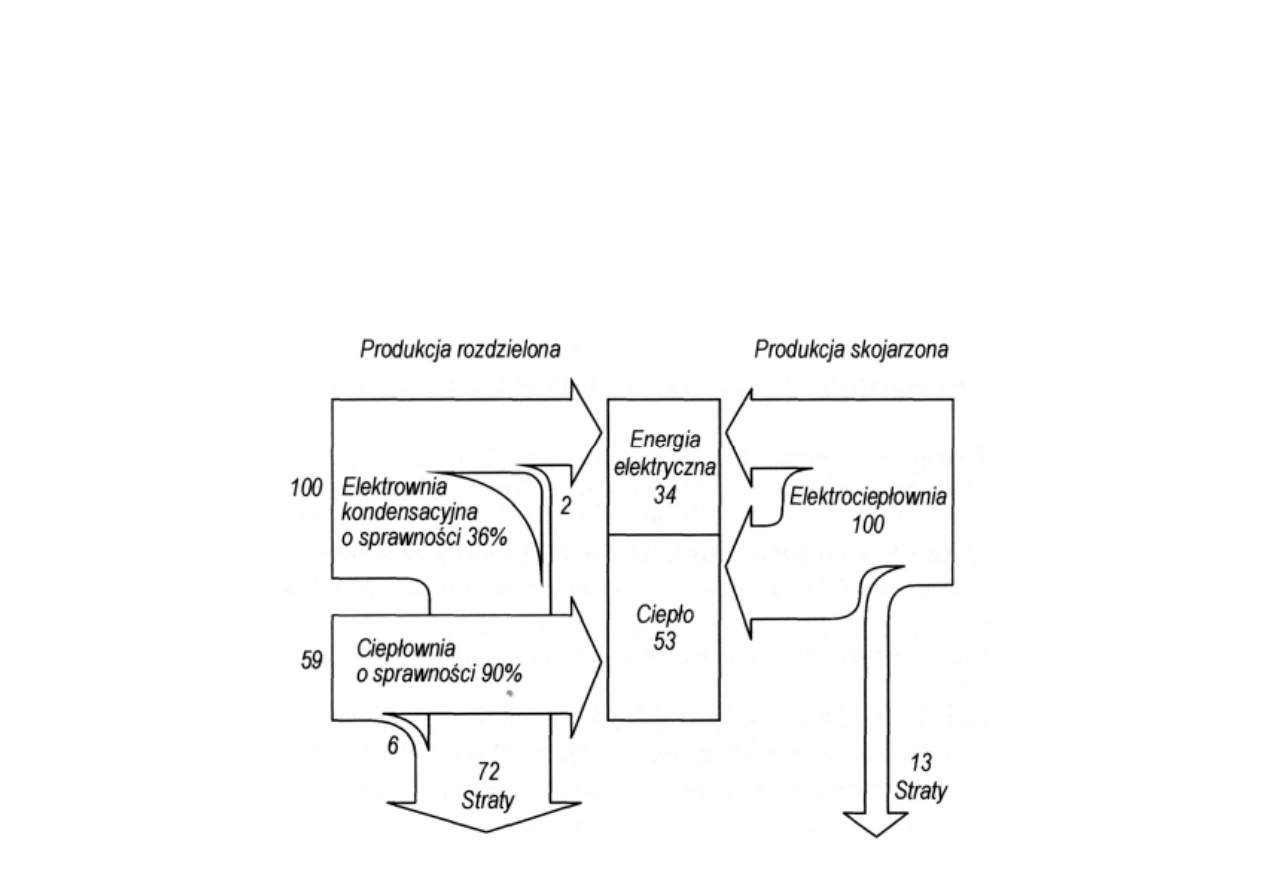
Głównym efektem ekonomicznym skojarzonego wytwarzania energii elektrycznej i ciepła 
w elektrociepłowni jest oszcz

ę

dno

ść

 paliwa w stosunku do układu niezale

ż

nego 

(rozdzielonego) wytwarzania obu postaci energii, składaj

ą

cego si

ę

 z zast

ę

pczej 

elektrowni kondensacyjnej i zast

ę

pczej ciepłowni (kotłowni). Dla tych samych strumieni 

oddawanych energii (odpowiednio 34 jednostki energii elektrycznej i 53 jednostki ciepła) 
w układzie rozdzielonym nale

ż

y zu

ż

y

ć

 159 jednostek energii chemicznej paliwa, czyli o 59 

jednostek wi

ę

cej ni

ż

 w elektrociepłowni. Sprawno

ść

 ogólna procesu skojarzonego 

wynosi w przedstawionym przykładzie 87%, a procesów rozdzielonych 54,7%. 

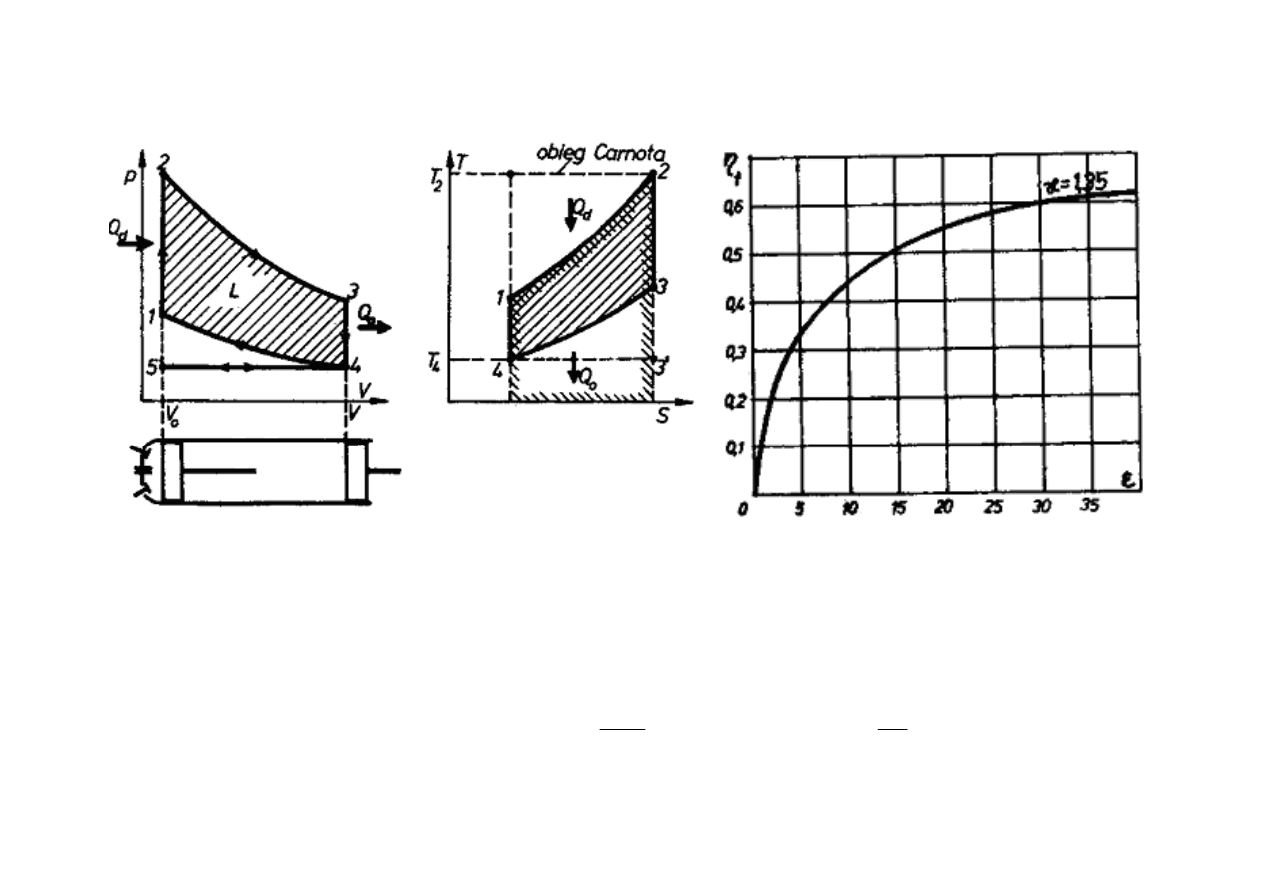
SILNIK SPALINOWY 

Ś

REDNIOPR

ĘŻ

NY

z zapłonem iskrowym (Otto)

W silnikach spalinowych czynnikiem roboczym s

ą

 spaliny wytwarzane wewn

ą

trz 

samego silnika w wyniku spalania paliwa. Obieg Otto, jest obiegiem porównawczym 
(teoretycznym) silnika spalinowego tłokowego z zapłonem iskrowym. 

Sprawno

ść

 teoretyczna obiegu Otto 

η

t

zale

ż

y od stopnia spr

ęż

ania 

ε

: 

κ

– wykładnik adiabaty

1

t

1

1

−−−−

κκκκ

εεεε

−−−−

====

ηηηη

0

V

V

====

εεεε

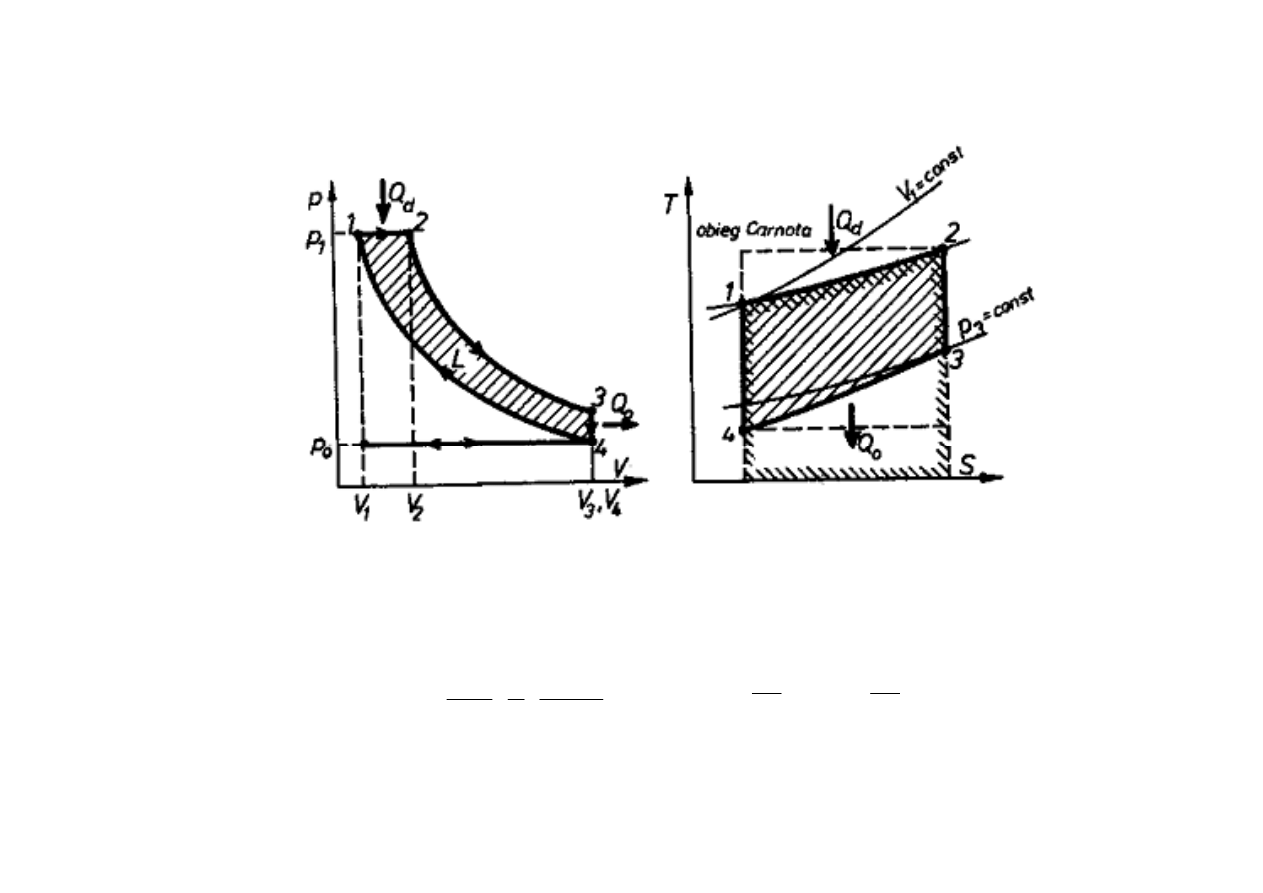
SILNIK SPALINOWY WYSOKOPR

ĘŻ

NY

z samoczynnym zapłonem (Diesela)

Obieg Diesela jest obiegiem porównawczym dla silnika wysokopr

ęż

nego z 

samoczynnym zapłonem. Do powietrza, które w wyniku spr

ęż

onia do bardzo wysokiego 

ci

ś

nienia, posiada wysok

ą

 temperatur

ę

, jest wtryskiwane paliwo, które ulega 

samozapłonowi. Sprawno

ść

 teoretyczna obiegu Diesela 

η

t

zale

ż

y od stopnia spr

ęż

ania 

ε

: 

1

1

1

1

1

1

t

−−−−

ϕϕϕϕ

−−−−

ϕϕϕϕ

⋅⋅⋅⋅

κκκκ

⋅⋅⋅⋅

εεεε

−−−−

====

ηηηη

κκκκ

−−−−

κκκκ

1

2

1

3

V

V

,

V

V

====

ϕϕϕϕ

====

εεεε

W silnikach Diesela osi

ą

ga si

ę

 sprawno

ść

 

η

t

= (0,52

÷

0,64) i s

ą

 to najwy

ż

sze sprawno

ś

ci 

spo

ś

ród wszystkich typów spalinowych silników cieplnych. 

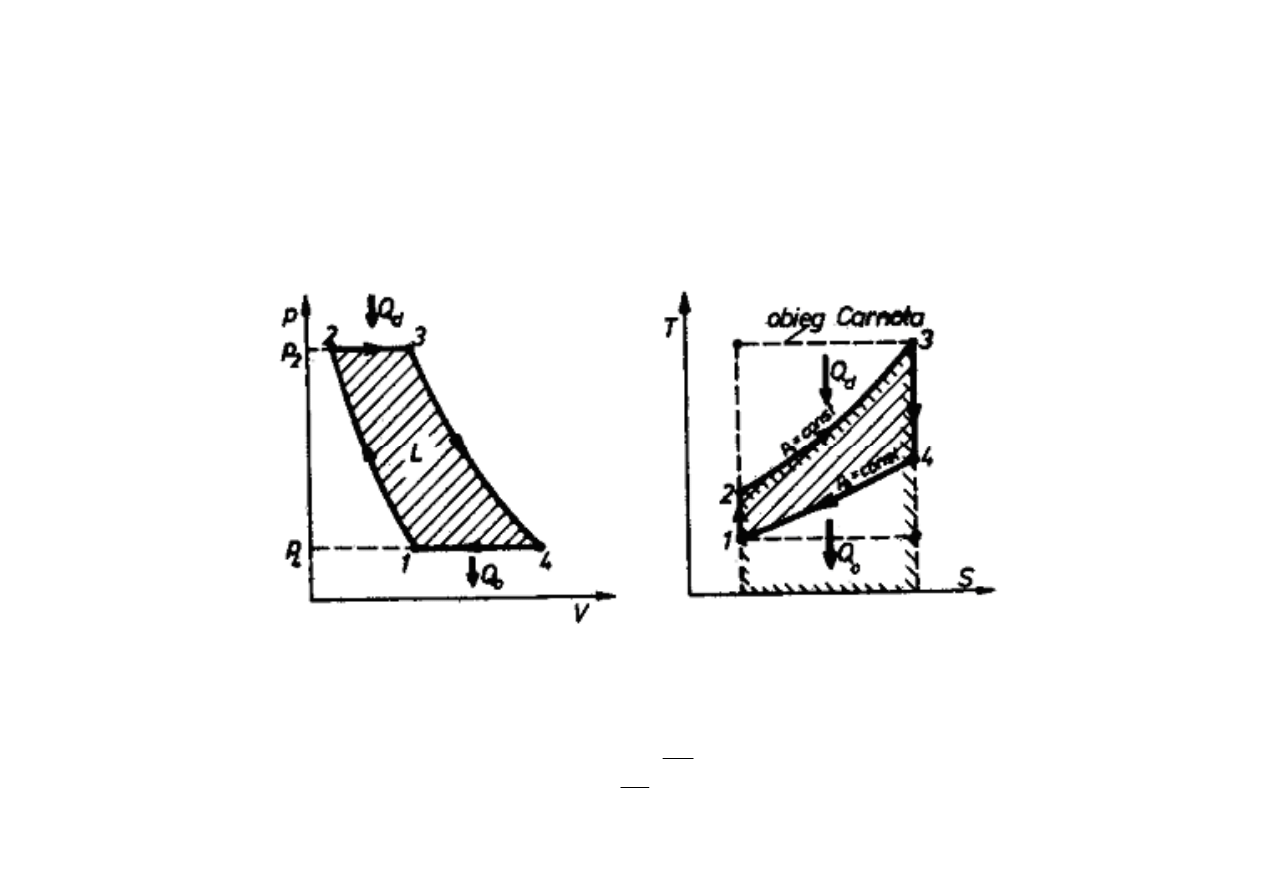
OBIEGI Z TURBINAMI GAZOWYMI

Ze wzgl

ę

du na posuwisto-zwrotny ruch tłoka pr

ę

dko

ść

 obrotowa silników tłokowych 

jest tym mniejsza, im wi

ę

ksza jest moc silnika. Konsekwencj

ą

 tego jest du

ż

y ci

ęż

ar 

jednostkowy silnika i ograniczona moc maksymalna.  Powoduje to stopniowe 
wypieranie silników tłokowych przez silniki turbinowe w zakresie du

ż

ych mocy. Obiegi 

porównawcze tego typu silników wywodz

ą

 si

ę

 z obiegu Joule’a.

Sprawno

ść

 teoretyczna obiegu Joule’a 

η

t 

zale

ż

y od stosunku ci

ś

nie

ń

, przy których 

doprowadza (p

2

) i odprowadza si

ę

 (p

1

) ciepło:

κκκκ

−−−−

κκκκ













−−−−

====

ηηηη

1

2

1

t

p

p

1

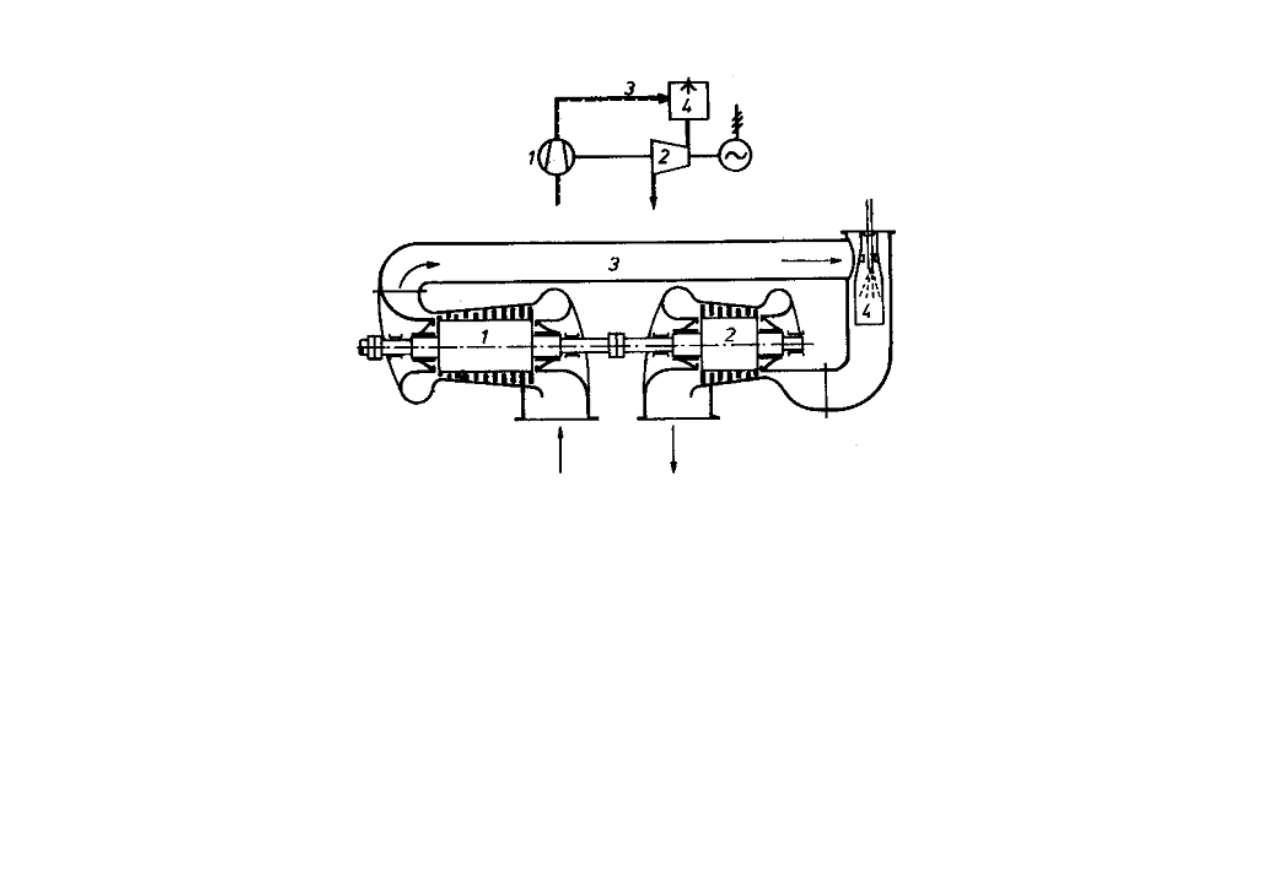
Istotn

ą

 wad

ą

 silników turbogazowych jest konieczno

ść

 stosowania spr

ęż

arki 

zu

ż

ywaj

ą

cej znaczn

ą

 cz

ęść

 mocy turbiny. Aby uzyska

ć

 moc zespołu wynosz

ą

c

ą

 

10 MW, nale

ż

y zainstalowa

ć

 turbin

ę

 o mocy około 40 MW, z czego około 30 MW 

zu

ż

ywa spr

ęż

arka. Ta cecha silników turbogazowych przyczynia si

ę

 do zwi

ę

kszenia 

nakładów inwestycyjnych i ograniczenia maksymalnej mocy jednego agregatu. Wady 
tej nie ma elektrownia parowa, w której tylko nieznaczna cz

ęść

 mocy wytworzonej w 

turbozespole zostaje zu

ż

yta do nap

ę

dy pompy wody zasilaj

ą

cej i innych urz

ą

dze

ń

 

pomocniczych.

1 - spr

ęż

arka powietrza, 2 - turbina gazowa, 3 - doprowadzenie powietrza do komory 

spalania, 4 - komora spalania.

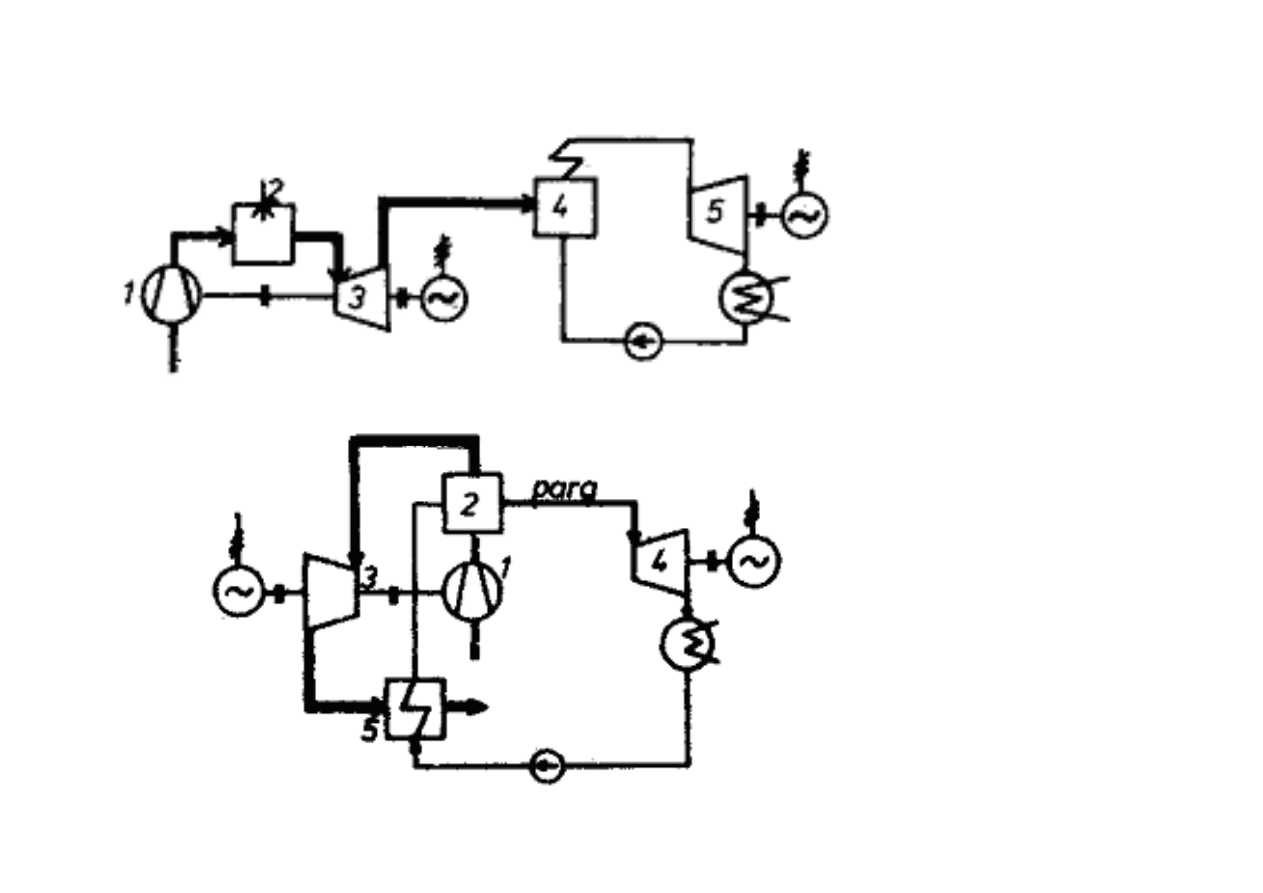
UKŁADY GAZOWO-PAROWE

1 - spr

ęż

arka, 

2 - komora spalania, 
3 - turbina gazowa, 
4 – kocioł odzyskowy, 
5 - turbina parowa

1 - spr

ęż

arka, 

2 - kocioł parowy, 
3 -turbina gazowa, 
4 - turbina parowa, 
5 - wymiennik ciepła. 

EGZERGIA

Ilo

ść

 energii nie jest dostatecznym miernikiem jej praktycznej przydatno

ś

ci. Ciepło 

dostarczane przez czynnik grzejny jest tym cenniejsze, im wy

ż

sza jest jego temperatura. 

Ciepło zawarte w otoczeniu jest ogromne lecz jest ono zupełnie nieu

ż

yteczne jako 

ź

ródło 

energii nap

ę

dowej procesów cieplnych. 

Konieczne jest wi

ę

c wprowadzenie wielko

ś

ci charakteryzuj

ą

cej energi

ę

 pod wzgl

ę

dem 

jej jako

ś

ci. T

ą

 wielko

ś

ci

ą

 jest 

Egzergia

– miara u

ż

yteczno

ś

ci energii. 

Do okre

ś

lenia wielko

ś

ci egzergi nale

ż

y uwzgl

ę

dni

ć

 2 zasad

ę

 termodynamiki oraz wpływ 

otaczaj

ą

cej przyrody na przebieg procesów realizowanych przez układy 

termodynamiczne. Procesy te mog

ą

 by

ć

 realizowane tylko dzi

ę

ki temu, 

ż

e dysponujemy 

bogactwami naturalnymi, które nie s

ą

 w równowadze termodynamicznej z otaczaj

ą

c

ą

 

przyrod

ą

. 

przyrod

ą

. 

Typowe bogactwa naturalne to: paliwa chemiczne, substancje zdolne do reakcji  
j

ą

drowych, strumienie wody o du

ż

ej energii kinetycznej lub potencjalnej, 

promieniowanie słoneczne itp. Materia traci swoj

ą

 przydatno

ść

 energetyczn

ą

, gdy 

zostanie sprowadzona do stanu równowagi termodynamicznej z otaczaj

ą

c

ą

 przyrod

ą

, z 

jej składnikami nie nale

żą

cymi do bogactw naturalnych. Otaczaj

ą

ca przyroda narzuca 

wi

ę

c naturalny punkt zerowy przy ocenie praktycznej przydatno

ś

ci energii. Jako miernik 

tej przydatno

ś

ci przyj

ę

to maksymaln

ą

 zdolno

ść

 do wykonania pracy i nazwano t

ę

 

wielko

ść

 egzergi

ą

.

Analiz

ę

 egzergetyczn

ą

 najwygodniej jest przeprowadzi

ć

 w formie bilansu. Składnikiem 

zamykaj

ą

cym bilans jest wewn

ę

trzna strata egzergii, wywołana przez przemiany 

nieodwracalne.

Egzergia nie podlega prawu zachowania. W ka

ż

dym rzeczywistym (nieodwracalnym) 

procesie wyst

ę

puj

ą

 straty egzergii. Straty egzergii s

ą

 spowodowane takimi procesami 

jak; tarcie, przepływ ciepła przy sko

ń

czonej ró

ż

nicy temperatur oraz dyfuzja substancji 

przy sko

ń

czonej ró

ż

nicy st

ęż

e

ń

. Szczególnie du

ż

e straty egzergii wyst

ę

puj

ą

 przy 

spalaniu. I wła

ś

nie w takich procesach gdzie spalanie odgrywa rol

ę

 dominuj

ą

c

ą

 

(procesy hutnicze , procesy energetyczne i cieplne ) bardzo wa

ż

na rol

ę

 pełni poj

ę

cie 

egzergii .  

W energetyce nale

ż

y tak realizowa

ć

 procesy, aby straty egzergii były jak najmniejsze. 

Im bardziej bowiem proces zbli

ż

ony jest do odwracalnego, tym mniejsze zu

ż

ycie 

ś

rodków nap

ę

dowych jest potrzebne do osi

ą

gni

ę

cia zamierzonego celu.

Chc

ą

c zbada

ć

 mo

ż

liwo

ś

ci poprawy jako

ś

ci procesu energetycznego nale

ż

y wyznaczy

ć

 

straty egzergii wyst

ę

puj

ą

ce w poszczególnych cz

ęś

ciach urz

ą

dzenia realizuj

ą

cego ten 

straty egzergii wyst

ę

puj

ą

ce w poszczególnych cz

ęś

ciach urz

ą

dzenia realizuj

ą

cego ten 

proces, a nast

ę

pnie poznanie przyczyn wyst

ę

powania tych strat (szczególnie tych 

najwi

ę

kszych). 

Zmniejszenie strat egzergii wi

ąż

e si

ę

 z reguły ze zwi

ę

kszeniem nakładów 

inwestycyjnych. Zmniejszenie strat egzergii w wymienniku ciepła mo

ż

na uzyska

ć

 przez 

zwi

ę

kszenie powierzchni wymiany ciepła (wi

ę

kszy i dro

ż

szy wymiennik). Opłacalno

ść

 

takiego sposobu zmniejszenia strat egzergii powinna by

ć

 sprawdzona rachunkiem 

ekonomicznym. Analiza egzergetyczna wyja

ś

nia mo

ż

liwo

ś

ci poprawy procesu 

cieplnego, dopiero jednak analiza ekonomiczna okre

ś

li celowo

ś

ci realizacji tej poprawy.

Egzergia

– maksymalna praca, jak

ą

 otwarty układ termodynamicznie mo

ż

e wykona

ć

 w 

otoczeniu przechodz

ą

c do stanu równowagi z otoczeniem. Otoczenie traktuje si

ę

 jako 

niesko

ń

czenie du

ż

y zbiornik nieu

ż

ytecznej energii i materii o stałej temperaturze. W 

procesie odwrotnym mo

ż

na uzyska

ć

 maksymaln

ą

 energi

ę

. 

Ogólne sformułowanie poj

ę

cia egzergii:

B = I + T

0

·S  lub dla wielko

ś

ci wła

ś

ciwych  b = i + T

0

· s

gdzie:

B, b – egzergia,
I, i – entalpia,
T – temperatura otoczenia,
S, s – entropia.

Egzergia ró

ż

nych no

ś

ników energii:

Energia elektryczna jest równowa

ż

na pracy mechanicznej,  tak wi

ę

c z definicji 

egzergia pr

ą

du elektrycznego równa jest energii tego pr

ą

du, czyli: B/Q = 1.

egzergia pr

ą

du elektrycznego równa jest energii tego pr

ą

du, czyli: B/Q

el

= 1.

W przypadku paliw egzergia jest w przybli

ż

eniu równa zawartej w nich energii, czyli:

B/Q

p

≈

1 , przy czym głównym składnikiem Q

p 

jest ciepło spalania paliwa. 

Wielkie ró

ż

nice mog

ą

 wyst

ą

pi

ć

 w przypadku ciepła. Egzergia zbiorników ciepła lub 

strumieni ciepła jest zawsze ni

ż

sza od ich energii. Egzergia maleje w miar

ę

 jak 

temperatura no

ś

nika ciepła zbli

ż

a si

ę

 do temperatury otoczenia.

Sprawno

ść

 egzergijn

ą

 elektrowni cieplnej wyra

ż

a stosunek energii wyprodukowanej 

przez elektrownie do egzergii chemicznej paliwa:

gdzie:

E

e

– energia elektryczna, kJ; G

B

– ilo

ść

 paliwa, kg; 

b

ch

– egzergia chemiczna paliwa wła

ś

ciwa, kJ/kg.

dla w

ę

gla kamiennego:

b

ch

≈

W

d

+ r·w = (1 – w) · W

s

W

d

– warto

ść

 opałowa w

ę

gla, kJ/kg,

r – ciepło parowania wody, kJ/kg,
w – wilgotno

ść

 w

ę

gla,

W

s

– ciepło spalania w

ę

gla, kJ/kg,

ch

B

e

b

b

G

E

⋅⋅⋅⋅

====

ηηηη

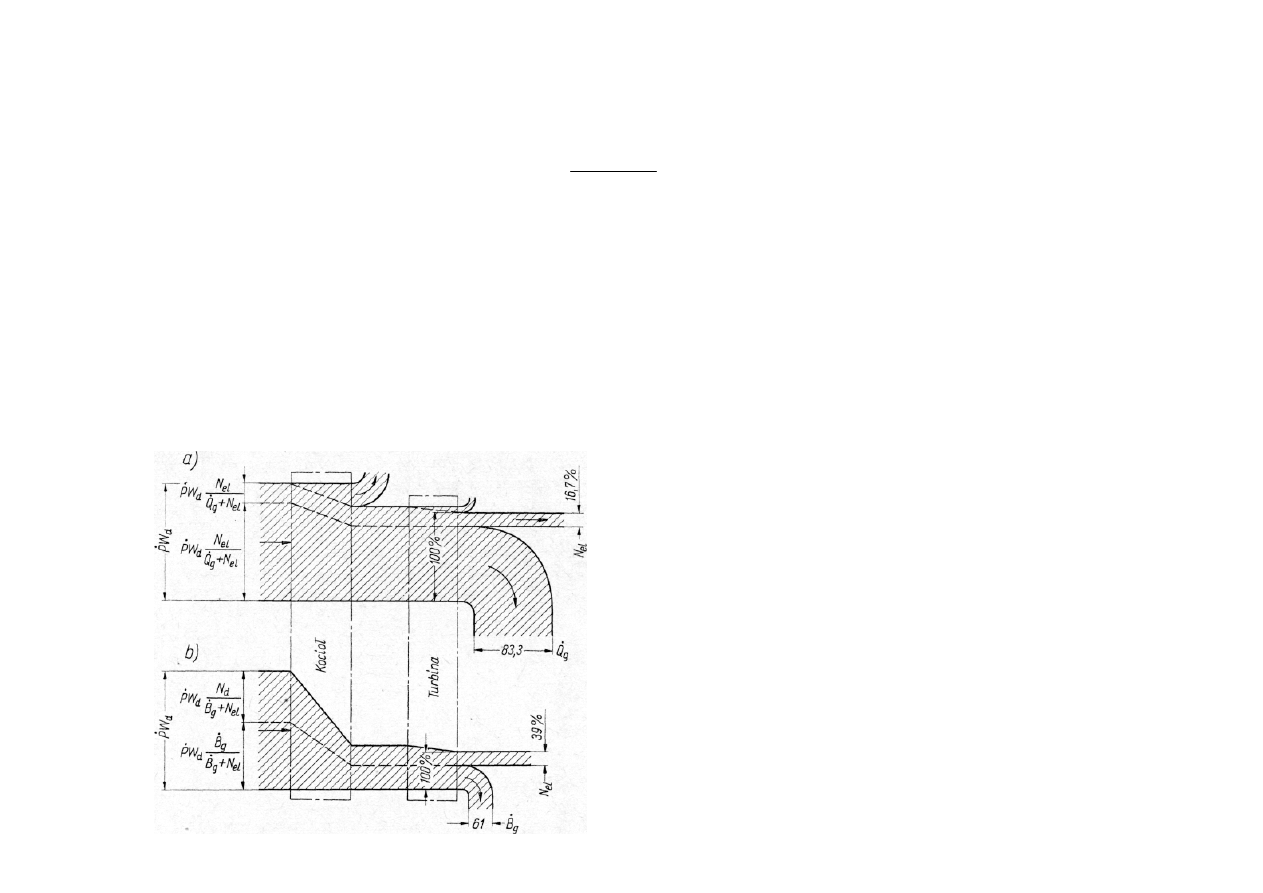
Bilans elektrociepłowni: a) energijny, b) egzergijny.