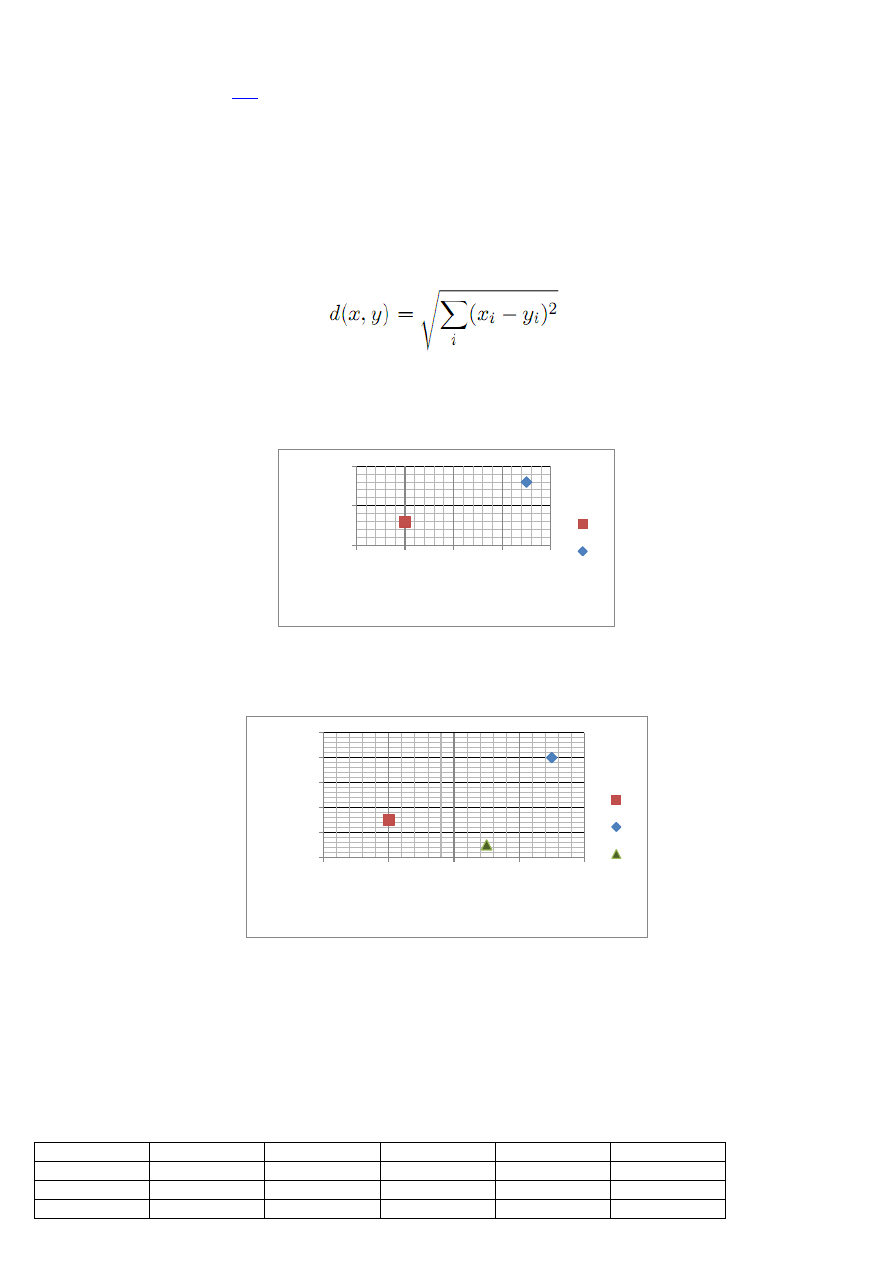
Laboratorium z analizy skupieo.
Analiza skupieo, grupowanie (
ang.
Cluster analysis) –jest metodą tzw. klasyfikacji bez nadzoru (ang. unsupervised learning). Jest to
metoda dokonująca grupowania elementów we względnie jednorodne klasy. Podstawą grupowania w większości algorytmów jest
podobieostwo pomiędzy elementami – wyrażone przy pomocy funkcji (metryki) podobieostwa bądź odległości. Poprzez grupowanie
można również rozwiązad problemy z gatunku odkrywania struktury w danych oraz dokonywanie uogólniania. Grupowanie polega
na wyodrębnianiu grup (klas, podzbiorów).
Grupujemy te obiekty które są do siebie podobne. Często zamiast podobieostwa mierzy się odległości między obiektami. Istnieją
różne miary podobieostwa czy odległości. Powinny byd one wybierane konkretnie dla typu danych analizowanych: inne są bowiem
miary typowo dla danych binarnych, inne dla danych nominalnych a inne dla danych numerycznych
Zadania do wykonania:
Oblicz odległośd punktu A o współrzędnych (2,3) do punktu B o współrzędnych (7,8).
D (A,B) = pierwiastek ((7-2)
2
+ (8-3)
2
) = pierwiastek (25 + 25) = pierwiastek (50) = 7.07
Mając dane punkty: A(2,3), B(7,8) oraz C(5,1) oblicz odległości między punktami:
D (A,B) = pierwiastek ((7-2)
2
+ (8-3)
2
) = pierwiastek (25 + 25) = pierwiastek (50) = 7.07
D (A,C) = pierwiastek ((5-2)
2
+ (3-1)
2
) = pierwiastek (9 + 4) = pierwiastek (13) = 3.60
D (B,C) = pierwiastek ((7-5)
2
+ (3-8)
2
) = pierwiastek (4 + 25) = pierwiastek (29) = 5.38
Wszystko jest dużo bardziej jasne gdy mamy punkty na płaszczyźnie. Gdy jednak liczba wymiarów się zwiększa zadanie stanowi
większy problem. Wyobraźmy sobie, że nie mamy 2 zmiennych opisujących każdy obiekt, ale tych zmiennych jest np. 5:
{v1,v2,v3,v4,v5} i że obiekty opisane tymi zmiennymi to 3 punkty: A, B i C:
V1
V2
V3
V4
V5
A
0.7
0.8
0.4
0.5
0.2
B
0.6
0.8
0.5
0.4
0.2
C
0.8
0.9
0.7
0.8
0.9
A
B
0
5
10
0
2
4
6
8
y
x
A
B
A
B
C
0
2
4
6
8
10
0
2
4
6
8
y
x
A
B
C
Policzmy teraz odległośd między punktami:
D (A,B) = pierwiastek ((0.7-0.6)
2
+ (0.8-0.8)
2
+ (0.4-0.3)
2
+ (0.5-0.4)
2
+ (0.2-0.2)
2
) = pierwiastek (0.01 + 0.01 + 0.01) = pierwiastek
(0.03) = 0.17
D (A,C) = pierwiastek ((0.7-0.8)
2
+ (0.8-0.9)
2
+ (0.4-0.7)
2
+ (0.5-0.8)
2
+ (0.2-0.9)
2
) = pierwiastek (0.01 + 0.01 + 0.09 + 0.09 + 0.49) =
pierwiastek (0.69) = 0.83
D (B,C) = pierwiastek ((0.6-0.8)
2
+ (0.8-0.9)
2
+ (0.5-0.7)
2
+ (0.4-0.8)
2
+ (0.2-0.9)
2
) = pierwiastek (0.04 + 0.01 + 0.04+0.16 + 0.49) =
pierwiastek (0.74) = 0.86
Szukamy najmniejszej odległości, bo jeśli te dwa punkty są najbliżej siebie, dla których mamy najmniejszą odległości ! A więc
najmniejsza odległośd jest między punktami A i B !
Metody grupowania
Grupowanie jako jedna z metod pozyskiwania wiedzy, a tym samym eksploracji danych, jest ściśle uwarunkowana źródłem danych
oraz oczekiwaną postacią rezultatów.
Algorytmy analizy skupieo dzieli się na kilka podstawowych kategorii:
metody hierarchiczne – algorytm tworzy dla zbioru obiektów hierarchię klasyfikacji, zaczynając od takiego podziału, w
którym każdy obiekt stanowi samodzielne skupienie, a koocząc na podziale, w którym wszystkie obiekty należą do jednego
skupienia. Istnieją dwa rodzaje metod hierarchicznych:
o procedury aglomeracyjne (ang. agglomerative) – tworzą macierz podobieostw klasyfikowanych obiektów, a
następnie w kolejnych krokach łączą w skupienia obiekty najbardziej do siebie podobne,
o procedury deglomeracyjne (ang. divisive) – zaczynają od skupienia obejmującego wszystkie obiekty, a następnie w
kolejnych krokach dzielą je na mniejsze i bardziej jednorodne skupienia aż do momentu, gdy każdy obiekt stanowi
samodzielne skupienie.
grupa metod k-średnich (ang. k-means), w której grupowanie polega na wstępnym podzieleniu populacji na z góry założoną
liczbę klas. Następnie uzyskany podział jest poprawiany w ten sposób, że niektóre elementy są przenoszone do innych klas,
tak, aby uzyskad minimalną wariancję wewnątrz uzyskanych klas. Podstawowy algorytm (J. MacQueen, 1967):
o losowy wybór środków (centroidów) klas (skupieo),
o przypisanie punktów do najbliższych centroidów,
o wyliczenie nowych środków skupieo,
o powtarzanie algorytmu aż do osiągnięcia kryterium zbieżności (najczęściej jest to krok, w którym nie zmieniła się
przynależnośd punktów do klas);
metody rozmytej analizy skupieo (ang. fuzzy clustering), wśród których najbardziej znaną jest metoda c-średnich (c-means).
Metody rozmytej analizy skupieo mogą przydzielad element do więcej niż jednej kategorii. Z tego powodu algorytmy
rozmytej analizy skupieo są stosowane w zadaniu kategoryzacji (przydziału jednostek do jednej lub wielu kategorii). Metody
rozmytej analizy skupieo różnią się pod tym względem od metod klasycznej analizy skupieo, w których uzyskana klasyfikacja
ma charakter grupowania rozłącznego, którego wynikiem jest to, że każdy element należy do jednej i tylko jednej klasy.
ALGORYTM K-MEANS (K-ŚREDNICH)
Inicjalizacja – wykonad wstępny podział obiektów na k – skupieo (wybór k – wiele możliwości). Przebieg algorytmu (4 kroki):
1) Dla każdego skupienia obliczyć jego centroid
2) Rozważa się kolejno obiekty i przydziela do najbliższego centroidu
3) Jeżeli nie osiągnięto stabilizacji (obiekty przenoszą się między skupieniami)
wyznacza się nowe, poprawione centroidy.
4) Kroki 2 i 3 powtarza się aż do osiągnięcia stabilizacji (obiekty znajdą się we
właściwych skupieniach) cel: minimalna odległość wewnątrz skupień, maksymalna –
między skupieniami.
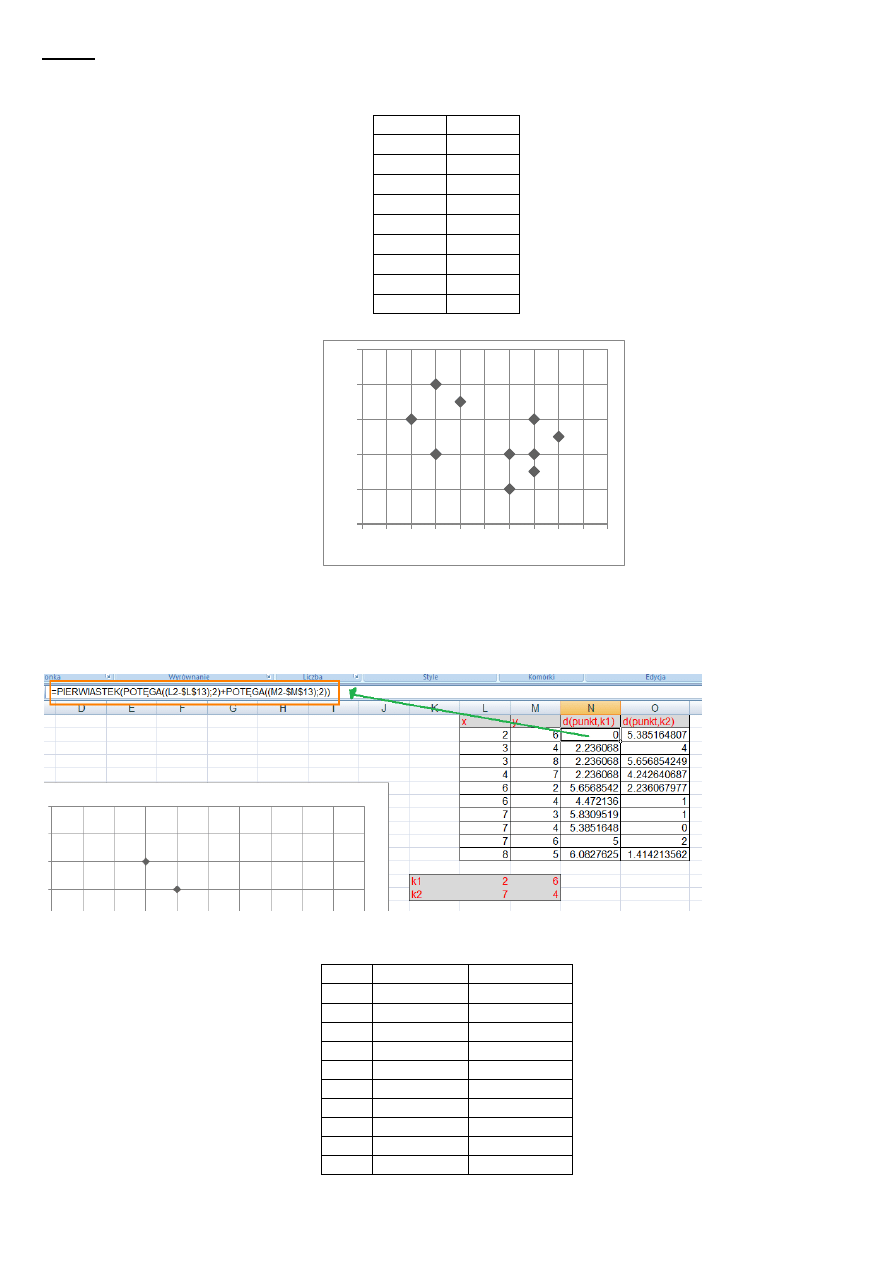
Przykład
Krok 0 – inicjalizacja obiektów
2
6
3
4
3
8
4
7
6
2
6
4
7
3
7
4
7
6
8
5
Krok 1 – wybór liczby skupieo: k=2
Wybór zalążków skupieo (środków, centrów)
K1 = (2,6)
K2 = (7,4)
Krok 2 – przydziel obiekty do skupieo
punkt K1
K2
1
0
5.385164807
2
2.23606798
4
3
2.23606798
5.656854249
4
2.23606798
4.242640687
5
5.65685425
2.236067977
6
4.47213595
1
7
5.83095189
1
8
5.38516481
0
9
5
2
10
6.08276253
1.414213562
0
2
4
6
8
10
0
1
2
3
4
5
6
7
8
9 10
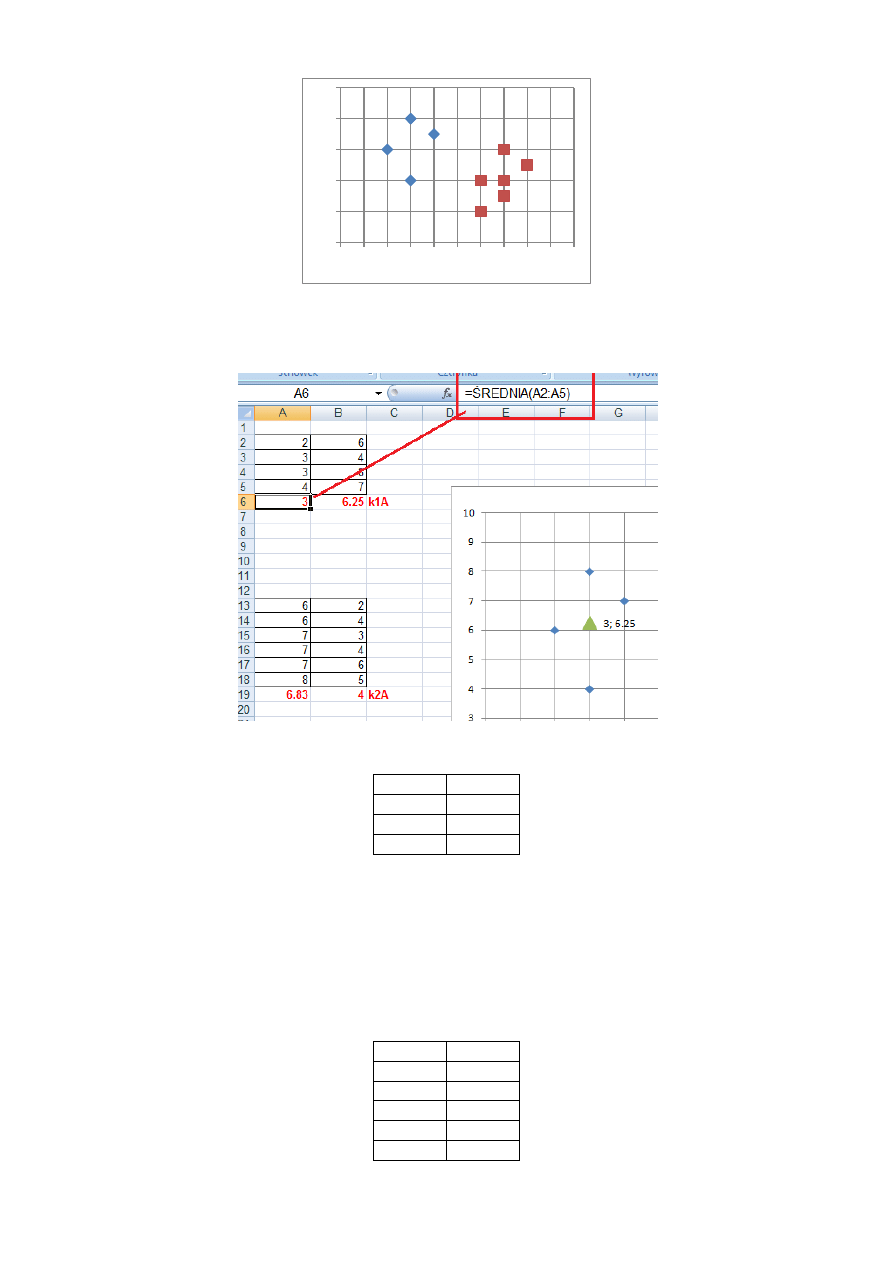
Czyli widzimy ze punkty 1,2,3 i 4 mają mniejsze odległości od punktu K1, zaś punkty 5,6,7,8,9,10 mają bliżej do punktu K2.
Krok 3 – wylicz nowe środki grup
A wiec wiedząc, że do skupienia pierwszego, którego poprzednio środkiem był punktu K1(2,6) zostały przydzielone punkty:
2
6
3
4
3
8
4
7
Reprezentantem takiego skupienia, a więc nowym zalążkiem grupy będzie punkt będący tzw. środkiem ciężkości grupy. Obliczamy
jako wartośd średnią z wartości punktów tworzących grupę, a więc osobno liczymy wartośd średnią dla 1 kolumny, i osobno – dla
drugiej kolumny.
Średnia dla współrzędnej x (1 kolumny) będzie wyliczona jako: (2 + 3 + 3 + 4 )/4 = 12/4 = 3
Średnia dla współrzędnej y (2 kolumny) będzie wyliczona jako: (6 + 4 + 8 +7)/4 = 25/4 = 6.25
Zaś do skupienia drugiego, punkty:
6
2
6
4
7
3
7
4
7
6
8
5
Średnia dla współrzędnej x (1 kolumny) będzie wyliczona jako: (6 + 6 +7 + 7 + 7 + 8 )/6 = 41/6 = 6,83
0
2
4
6
8
10
0
1
2
3
4
5
6
7
8
9 10
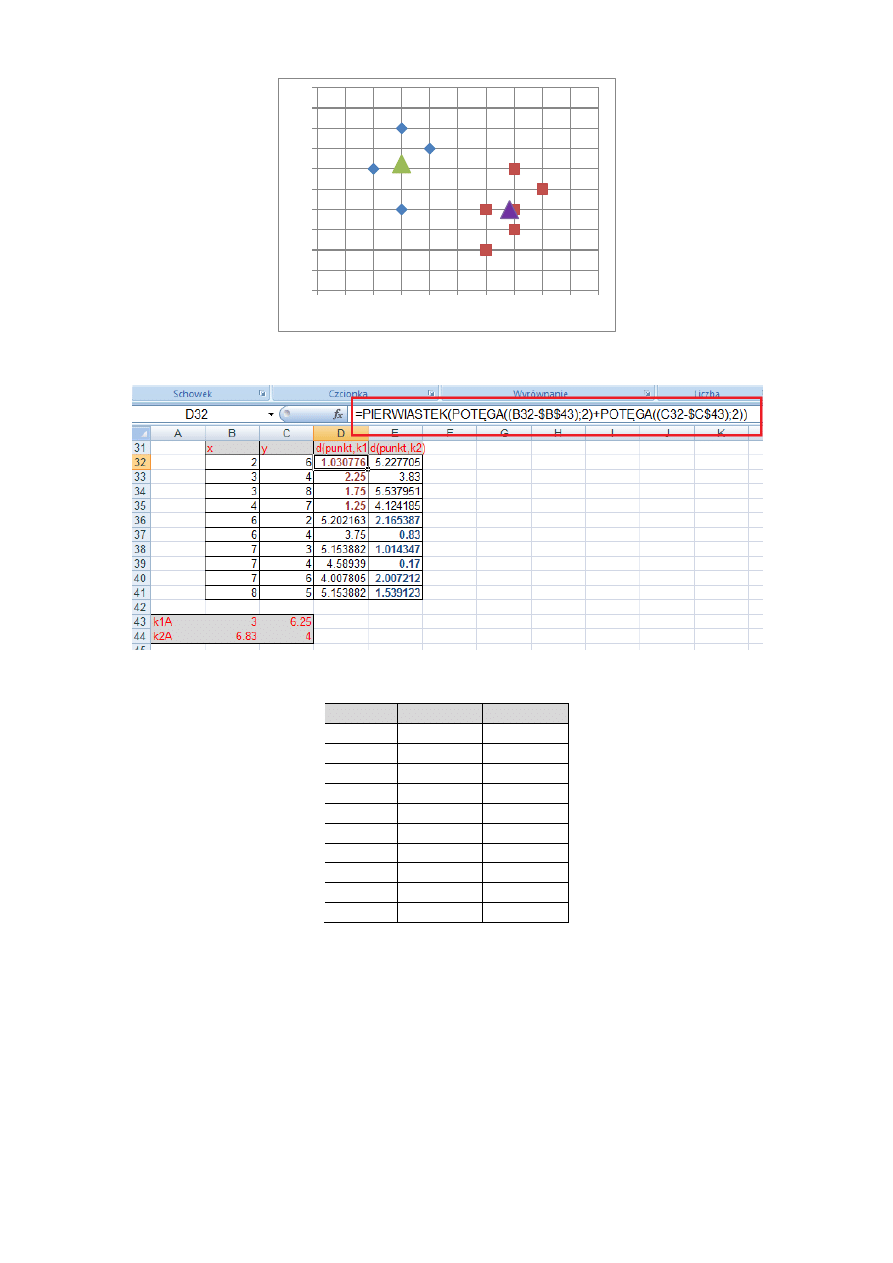
Średnia dla współrzędnej y (2 kolumny) będzie wyliczona jako: (2 + 4 + 3 + 4 + 6 + 5)/6 = 24/6 = 4
Krok 4. Ponownie przydziel obiekty do najbliższych im skupieo
d(punkt,k1A)
d(punkt,k2A)
1
1.03
5.23
2
2.25
3.83
3
1.75
5.54
4
1.25
4.12
5
5.20
2.17
6
3.75
0.83
7
5.15
1.01
8
4.59
0.17
9
4.01
2.01
10
5.15
1.54
A więc – co już zaznaczono kolorami – znów punkty 1,2,3,4 mają bliżej do środka K1A niż K2A, a punkty 5,6,7,8,9,10 bliżej do K2A niż
K1A.
Skoro żaden z punktów nie zmienił grupy, czyli ta iteracja nie różni się niczym od poprzedniej, algorytm grupowania zostaje
zakooczony. Nie ma bowiem sensu liczyd nowych środków skupieo i dalej sprawdzad przydział do grup, gdyż środki (zalążki) będą
takie same !
3; 6.25
6.83; 4
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
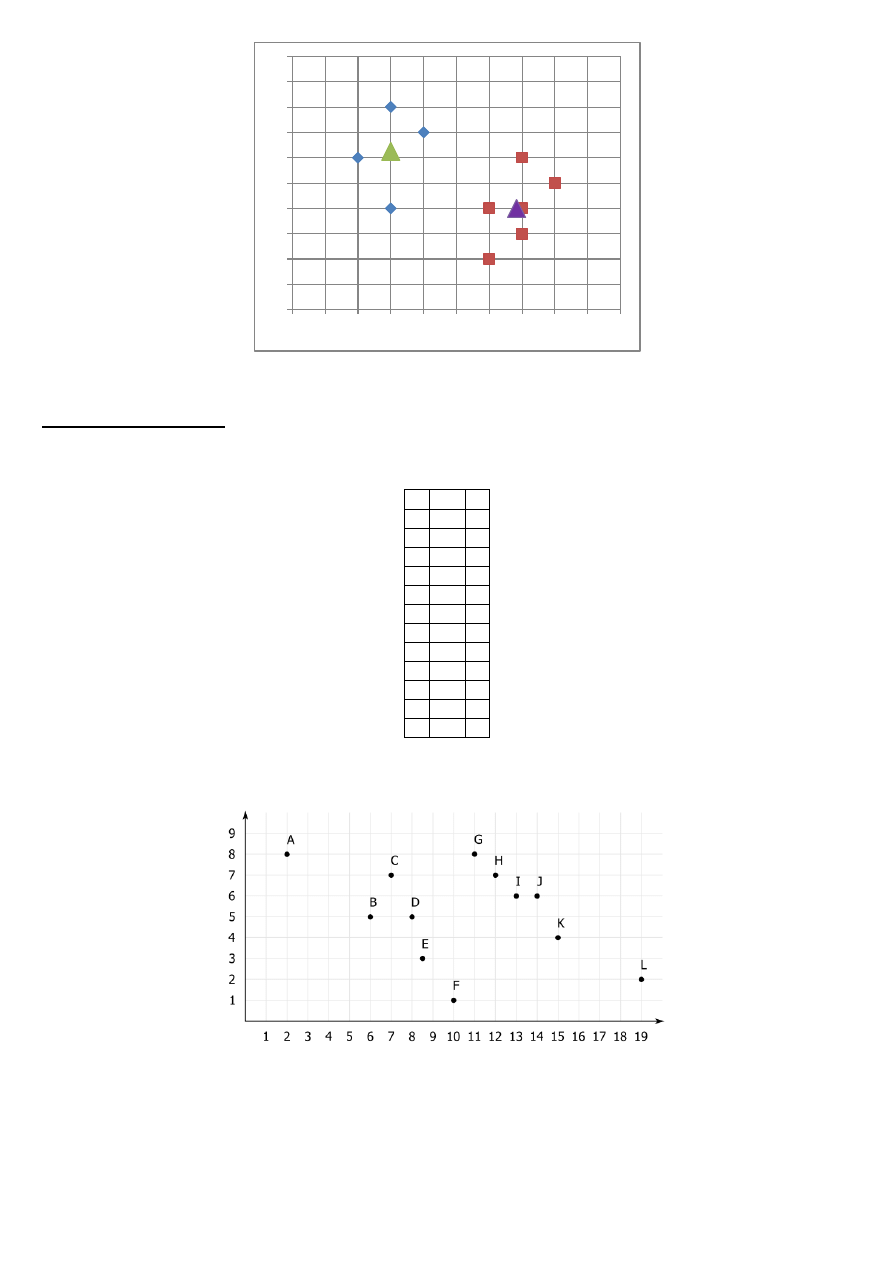
Zadanie 1 (za pomocą Excela)
Mając 10 punktów:
x
y
A 2
8
B 6
5
C 7
7
D 8
5
E 8.5 3
F
10
1
G 11
8
H 12
7
I
13
6
J
14
6
K 15
4
L
19
2
Rozkład punktów na płaszczyźnie
Losowy wybór centroidów
V1 = (5,6)
v2=(12,4)
3; 6.25
6.83; 4
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
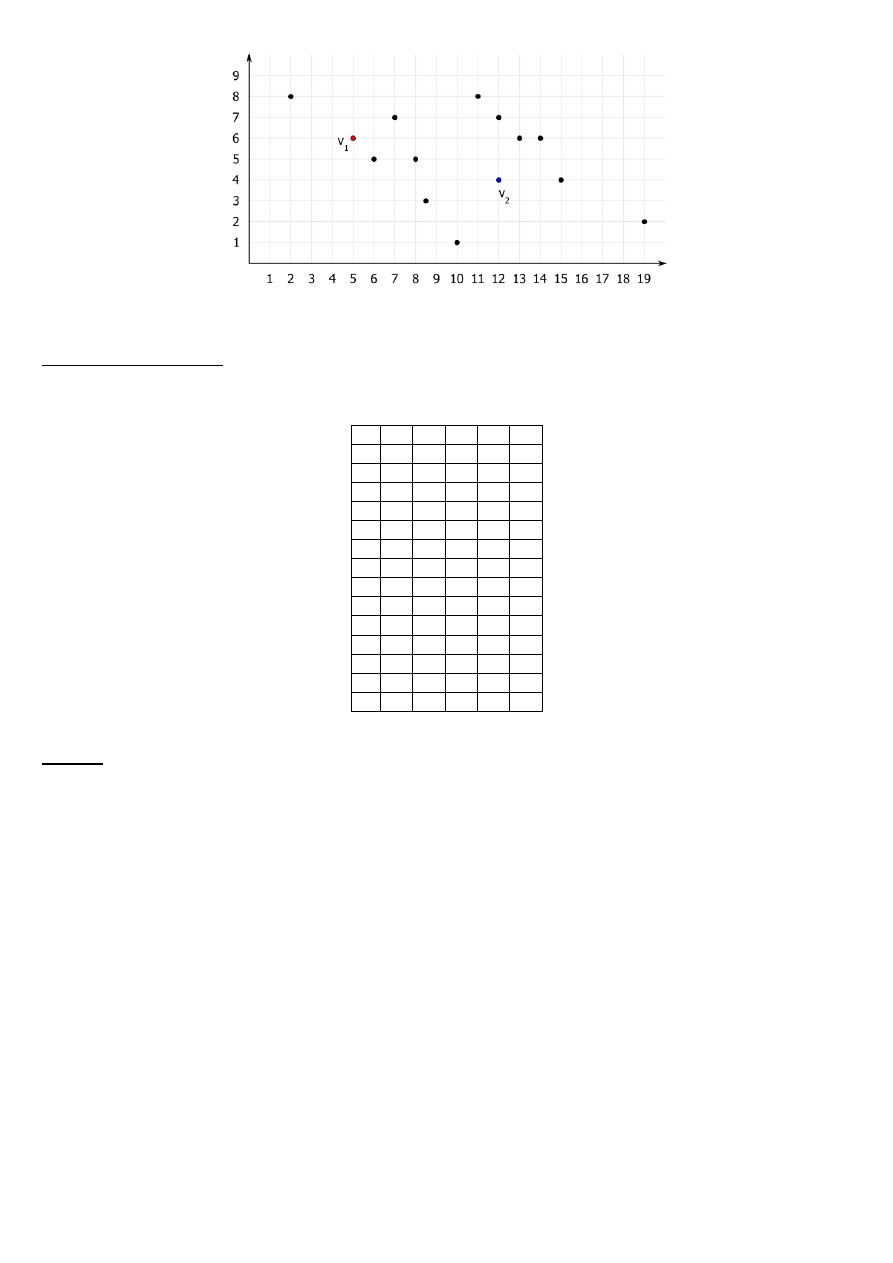
Wykonaj grupowanie algorytmem k-średnich.
Zadanie 2 (za pomocą Rattle)
Przeprowadź grupowanie dla następujących danych:
V1 V2 V3 V4 V5
A
7
8
5
4
2
B
6
8
5
4
2
C
8
9
7
8
9
D
6
7
7
7
8
E
1
2
5
3
4
F
3
4
5
3
5
G
7
8
8
6
6
H
8
9
6
5
5
I
2
3
5
6
5
J
1
2
4
4
2
K
3
2
6
5
7
L
2
5
6
8
9
M 3
5
4
6
3
N
3
5
5
6
3
Zadanie 3
Dla wybranego przez siebie zbioru danych do analizy z repozytorium Machine Learning Repository dokonaj grupowania danych
algorytmem k-średnich, dla danych numerycznych.
Spróbuj różnych konfiguracji liczby skupieo, sprawdź też czy w opisie zbioru na stronie źródłowej jest informacja o liczbie klas
(skupieo) bowiem niektóre zbiory mają taką informację. Wówczas jeśli liczba klas została określona np. na 5, to spróbuj dokonad
grupowania gdy k=5, ale również k=4 i k=6 i zinterpretuj wyniki. Jeśli w zbiorze nie ma określonej liczby skupieo, wybierz 3 możliwe
konfiguracje i też zinterpretuj wyniki.