Bennett

1. Pobierz plik:

bennett.zip

(346 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program bennett.exe.

Program Bennett tworzy tekst, dla którego prawdopodobieństwa występowania trójek
sąsiednich liter są takie same, jak dla tekstu wzorcowego. Po uruchomieniu programu pojawia
się ramka, do której należy wpisać:

1. Input file - Nazwę pliku zawierającego tekst wzorcowy.
2. Output file - Nazwę pliku, w którym pragniemy zapisać wytworzony tekst.
3. Character file - Nazwę pliku, w którym znajduje się lista liter (znaków).

Wszystkie ta nazwy można także wprowadzić za pomocą opcji Znajdź... (Browse...). Na
zakończenie należy także wpisać pierwsze dwie litery tekstu oraz liczbę znaków
w tworzonym pliku.

W katalogu Bennett umieściliśmy teksty Pana Tadeusza i Hamleta, które można
wykorzystać do generowania "podróbek" tych dzieł. Znajdują się tam także pliki zawierające
wszystkie litery alfabetu polskiego LiteryWin.txt i alfabetu łacińskiego Letters.txt.
Wszystkie teksty polskie są zapisane w kodzie Windows. Podajemy także przykładowe teksty
wygenerowane za pomocą programu Bennett.

Widok ekranu programu Bennett

Bentley

1. Pobierz plik:

bentley.zip

(156 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program bentley.exe.

Program Bentley rysuje kryształek płatka śniegu według następującego przepisu: wzrost
kryształka następuje w miejscu, które posiada dokładnie jednego sąsiada, zawierającego już
kryształek lodu.

Widok ekranu programu Bentley

Buffon

1. Pobierz plik:

buffon.zip

(98 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program buffon.exe.

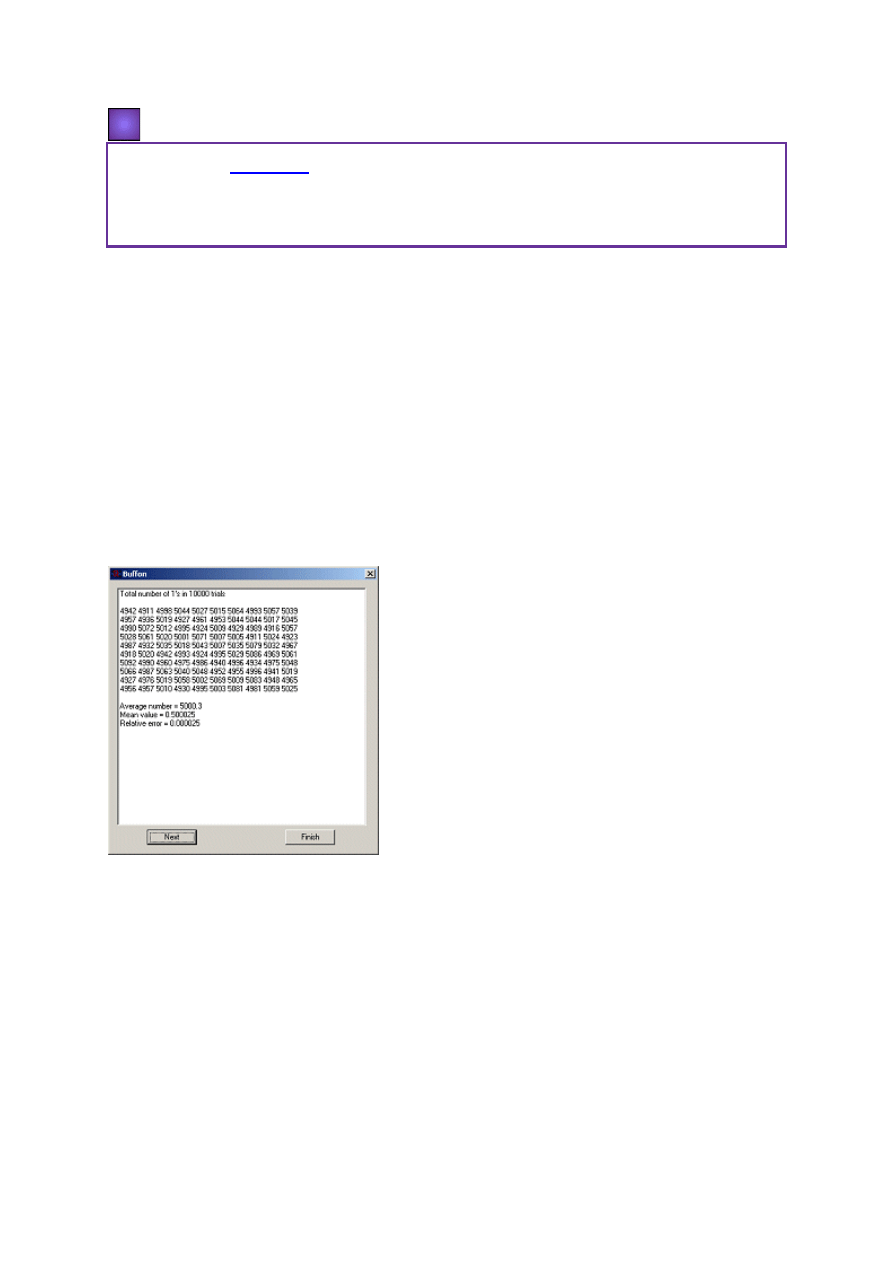
Program Buffon służy do generowania wyników rzutu monetą. Po uruchomieniu podaje on
najpierw wyniki uzyskiwane przy rzucaniu monetą 5 kolejek po 100 razy. Wyrzucenie orła
symbolizuje jedynka. Podane są liczby otrzymanych orłów Sum i obliczona jest wartość
średnia Mean value i błąd względny Relative error dla każdej kolejki. Następnie podane jest
podsumowanie tych wyników dla wszystkich kolejek. Na kolejnych ekranach,
uruchamianych przez kliknięcie na Next, podawane są wyniki dla 100 kolejek po 10 000
rzutów i dla 100 kolejek po 100 000 rzutów każda. Przy każdym uruchomieniu programu
zmienia się zarodek (zmiana ta jest innym rezultatem odczytu wewnętrznego zegara),
wykorzystywany przez komputer do zapoczątkowania procesu generacji ciągu liczb
przypadkowych. Każda kolejka rzutów jest zatem nieco inna.

Głównym celem tego programu jest przekonanie czytelnika, że przy powiększaniu liczby
rzutów średnie wartości dążą do 1/2, a błąd względny maleje.

Widok ekranu programu Buffon

Cantor

1. Pobierz plik:

cantor.zip

(152 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program cantor.exe.

Program Cantor służy do generowania figur fraktalnych:

1. Sierpinski Carpet (Dywan Sierpińskiego)
2. Christmas Tree (Choinka)
3. Dragon (Smok)
4. Cantor Maze (Labirynt Cantora)
5. Tree (Drzewo)
6. Kielek Tree (Drzewo Kiełka)
7. Barnsley Leaf (Liść Barnsleya).

Wybór figury następuje przez otworzenie menu Fractal i kliknięcie na wybraną nazwę.

Widok ekranu programu Cantor

Conway

1. Pobierz plik:

conway.zip

(1379 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program conway.exe.

Program Conway po uruchomieniu wymaga podania początkowej generacji bakterii albo
poprzez zaznaczenie położenia bakterii myszą na planszy, albo poprzez wczytanie jednego
z plików o rozszerzeniu ljf. Pliki te znajdują się w podkatalogu Ljf. Po naciśnięciu klawisza
F5 program rysuje następną generację bakterii. Po naciśnięciu kombinacji klawiszy Ctrl+F5
program rysuje kolejne generacje bez zatrzymywania się po każdym kroku. Opcje te dostępne
są także z menu Run.

Program Conway ma następujące dodatkowe opcje:

1. Zapisywanie w pliku widocznej na ekranie generacji File -> Save oraz File -> Save

As.

2. Zmiana liczby pól na planszy File -> Properties -> General.
3. Zmiana warunków brzegowych na planszy. Włączenie opcji File -> Properties ->

Conditions -> Torus powoduje, że plansza staje się zamknięta. Górny brzeg
utożsamiamy z dolnym brzegiem, zaś prawą krawędź z lewą krawędzią planszy
i powstaje powierzchnia o topologii dętki. Obiekty przekraczające granicę planszy
pojawiają się po przeciwnej stronie.

4. Zmiana reguł gry.

A. Można zmienić całkowicie reguły gry wymyślone przez Conwaya. W tym celu

należy przejść do File -> Properties -> Conditions i podać inne wartości
w odpowiednich polach. Według przyjętej konwencji 101 oznacza urodziny,
zaś 102 śmierć. Liczby te dla standardowej wersji Gry w życie zostały
umieszczone w polach o numerach 2 i 3, co oznacza, że dotyczą sytuacji, gdy
komórka ma 2 lub trzech sąsiadów.

B. Włączenie opcji File -> Properties -> Conditions -> 4 Neighbors powoduje,

że brane są pod uwagę tylko 4 sąsiednie komórki, a nie wszystkie 8.

W dodatku do programu Conway załączamy także instalacyjną wersję programu Life32
napisanego przez Johana G. Bontesa, posiadającego więcej opcji i przykładowych
konfiguracji (w katalogu Lif).

Widok ekranu programu Conway

Ehrenfest

1. Pobierz plik:

ehrenfest.zip

(157 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program ehrenfest.exe.

Program Ehrenfest służy do ilustracji problemu nieodwracalności procesów dotyczących
dużej liczby przypadkowo poruszających się obiektów. Zgodnie z tekstem w książce można
sobie wyobrażać, że proces ten polega na przeskokach pcheł z jednego psa na drugiego lub
na przemieszczaniu się molekuły z jednej połowy naczynia do drugiej. W chwili początkowej
wszystkie pchły (molekuły) są na jednym psie (w jednej połowie naczynia). Po uruchomieniu
programu należy wpisać liczbę obiektów (Number of fleas) oraz czas trwania procesu
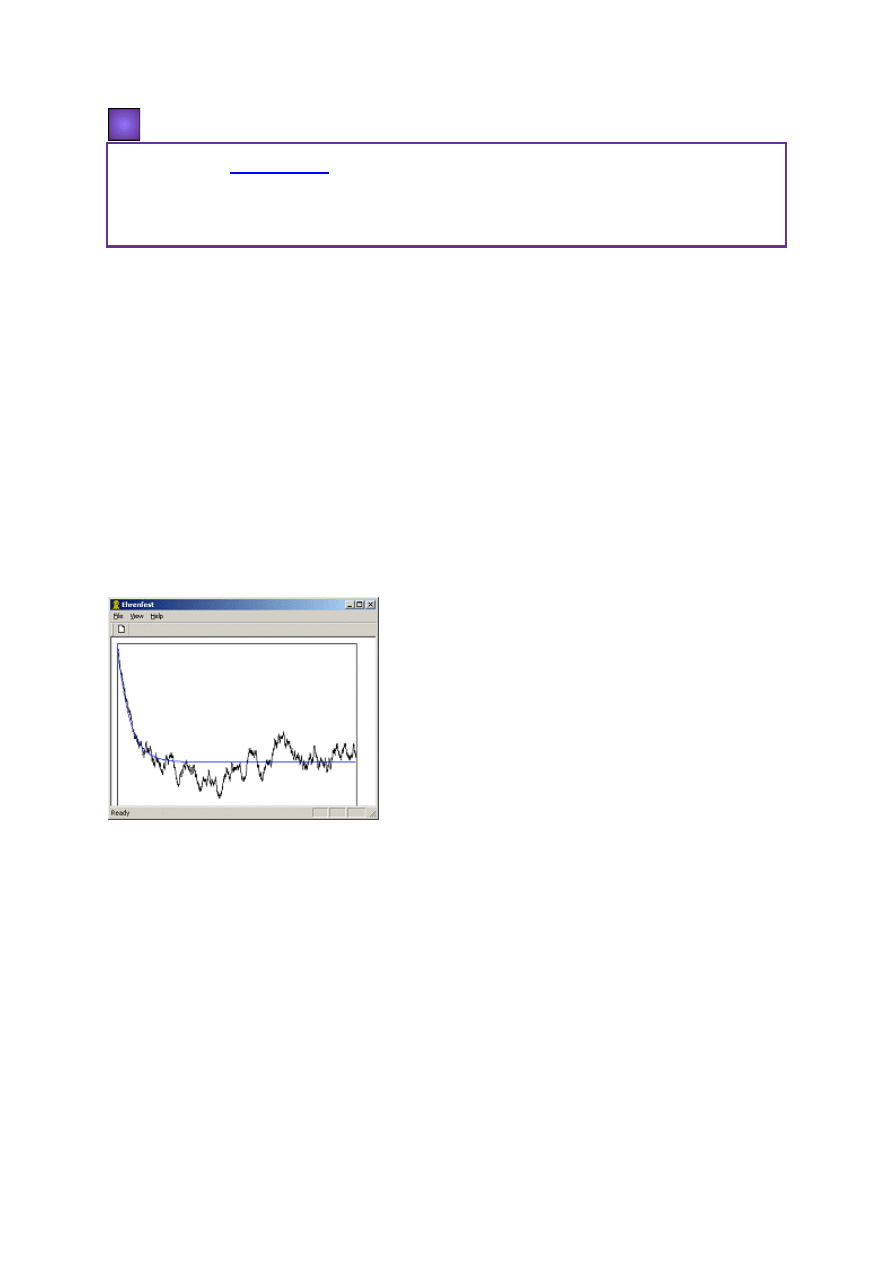
(Time). Program rysuje zależność od czasu liczby pcheł na pierwszym psie. Na zakończenie

narysowany zostaje wykres funkcji wykładniczej exp(

-

x)+1/2. Funkcja ta doskonale opisuje

początkowy przebieg procesu, tym lepiej, im większa liczba pcheł. Dla czasów dłuższych
występują fluktuacje wokół wartości 1/2, tym wyraźniejsze, im mniejsza jest liczba pcheł.
Zgodnie z rachunkiem prawdopodobieństwa możliwe jest ponowne znalezienie się
wszystkich pcheł na jednym psie, ale jest to niesłychanie mało prawdopodobne dla dużej
liczby pcheł. Ehrenfest tłumaczył za pomocą tego modelu zjawisko nieodwracalności
procesów fizycznych.

Widok ekranu programu Ehrenfest

Holland

1. Pobierz plik:

holland.zip

(160 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program holland.exe.

Program Holland służy jako ilustracja działania algorytmów genetycznych. Program znajduje
maksimum funkcji f(x) wykorzystując prosty algorytm genetyczny z twardą selekcją, opisany
w tekście. Użyta w tym programie funkcja ma postać f(x) = x (1 + sin(a x)). Wartości
parametru a odpowiadające różnym liczbom maksimów to: 4,7; 11; 17,5; 23,5. Po
uruchomieniu programu należy podać:

1. W jakim tempie chcemy obserwować działanie programu: opcja Slow lub Fast.
2. Liczbę maksimów badanej funkcji.
3. Liczbę generacji (dla funkcji z jednym maksimum wystarcza już czasem 100).

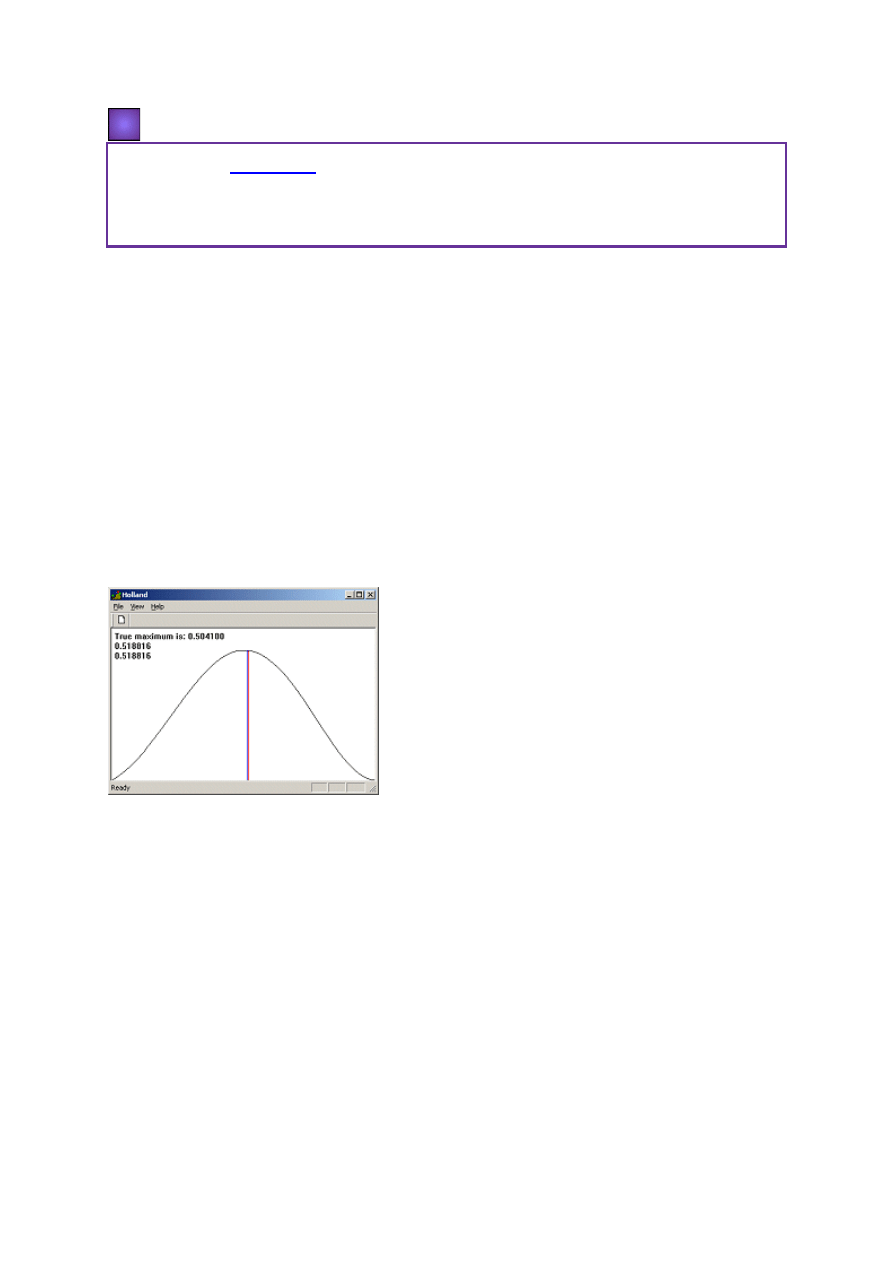
Na początku program rysuje wykres funkcji i wypisuje poprawną wartość argumentu
w punkcie maksimum oraz zaznacza (linia niebieska) punkt startu. Następnie program
zaznacza (linie czerwone) na wykresie i wypisuje wartości kolejnych wartości argumentu x,
przy których następuje zamiana gorszego genu na lepszy.

Widok ekranu programu Holland

Hopfield

1. Pobierz plik:

hopfield.zip

(166 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program hopfield.exe.

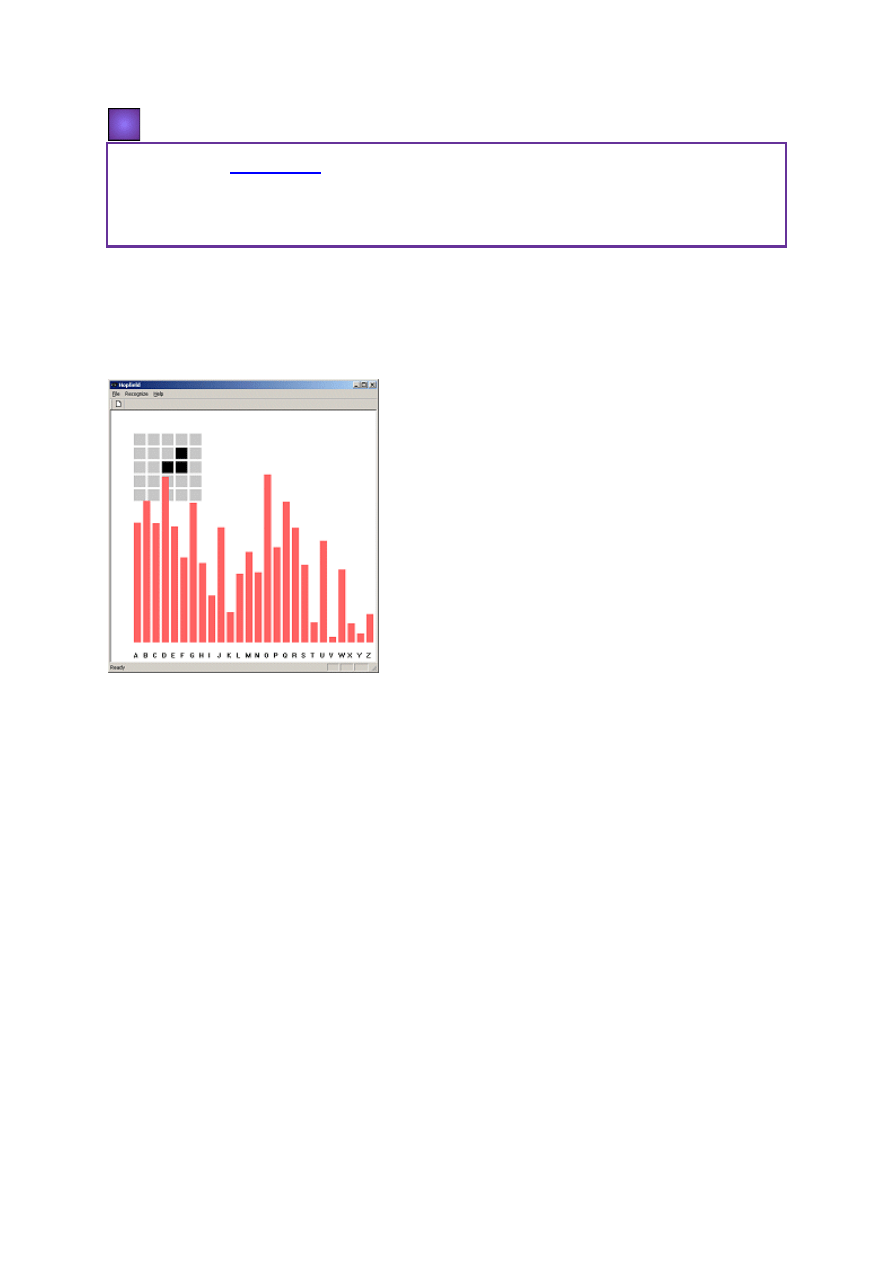
Program Hopfield służy jako ilustracja działania bardzo prostej sieci neuronowej:
perceptronu. Perceptron w tym programie został "wytrenowany" na wzorcach liter podanych
w pliku Patterns.in. Program próbuje dopasować podany wzór do tych wzorców i podaje
wykres odległości podanego wzoru od wszystkich wzorców liter.

Widok ekranu programu Hopfield

Huffman

1. Pobierz plik:

huffman.zip

(161 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program huffman.exe.

Program Huffman służy do generowania drzewa pytań określającego najlepszą strategię. Po
uruchomieniu należy wpisać ciąg wartości, które określają prawdopodobieństwa "znalezienia
skarbu" w danej komórce. Prawdopodobieństwa te podajemy w postaci zbioru liczb
naturalnych. Są to więc jedynie prawdopobieństwa względne. Program normuje te względne
prawdopodobieństwa do jedności.

Widok ekranu programu Huffman

Julia

1. Pobierz plik:

julia.zip

(7 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program julia.exe.

Program Julia koloruje na czerwono, zielono i niebiesko obszary na płaszczyźnie zespolonej
współrzędnych (x,y), które są dorzeczami (zbiorami przyciągania) trzech atraktorów - trzech
pierwiastków z jedności. Atraktory te występują we wzorach iteracyjnych określonych
następująco:

x

n+1

= 2 x

n

/3 + (x

n

2

-

y

n

2

)/3(x

n

2

+ y

n

2

)

2

,

y

n+1

= 2 y

n

/3

-

2x

n

y

n

/3(x

n

2

+ y

n

2

)

2

.

Dorzecza tych atraktorów są zbiorami fraktalnymi, ale w skali pokazanej na ekranie widać
początkowo tylko zarysy tych zbiorów. Klikając jednak myszą na dowolnie wybrany punkt
na ekranie, można uzyskać powiększony obraz wokół tego punktu. Powtarzając tę operacje
wielokrotnie, można uzyskać coraz to lepszy wgląd we fraktalną naturę tych zbiorów.

Widok ekranu programu Julia

Mandelbrot

1. Pobierz plik:

mandelbrot.zip

(8 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program mandelbrot.exe.

Program Mandelbrot służy do generowania obrazów fraktalnych powstałych w wyniku
iteracji punktów płaszczyzny o współrzędnych (x,y) określonej wzorami:

x

n+1

= x

n

2

-

y

n

2

+ x

0

y

n+1

= 2 x

n

y

n

+ y

0

Po uruchomieniu programu pojawia się obraz przedstawiający żuka Mandelbrota. Obraz ten
i wszystkie następne powstają w następujący sposób:

Program Mandelbrot wybiera systematycznie początkowe punkty płaszczyzny o
współrzędnych (x

0

, y

0

) i oblicza kolejne iteracje według podanych wzorów. Jeżeli

współrzędne punktu rosną nieograniczenie, to punkt ten zaznaczany kolorem; jeżeli
współrzędne pozostają ograniczone, to punkt ten zaznaczany jest na czarno. Powstaje tylko
pytanie: jak poznać, czy punkt ucieka do nieskończoności? Okazuje się, że kryterium jest
bardzo proste. Każdy punkt, który przekroczył okrąg o środku w (0, 0) i promieniu 2, ucieknie
do nieskończoności. Liczba iteracji potrzebnych do przekroczenia tego okręgu zależy jednak
od punktu startowego (x

0

, y

0

) i na obrazach kolor punktu zależy od tej liczby.

Kliknięcie myszą w dowolnym miejscu obrazu prowadzi do wygenerowania otoczenia tego
punktu z podwojoną rozdzielczością. W menu Properties można dokładnie ustawiać
wszystkie opcje.

Widok ekranu programu Mandelbrot

Pasteur

1. Pobierz plik:

pasteur.zip

(167 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program pasteur.exe.

Program Pasteur ilustruje zjawisko rozprzestrzeniania się epidemii (lub rozwój innego
podobnego procesu).

Początkowo można ustawić parametry, czyli długość choroby (Illness duration), początkową
odporność osobników (Initial defense level), początkowy procent chorych (Initial
percentage...) oraz siłę wirusa podczas poszczególnych dni trwania choroby (Virus
strength...). Następnie można symulować działanie choroby, naciskając F5, a za pomocą +

i

-

na klawiaturze numerycznej odpowiednio zwiększać i zmniejszać odporność osobników.

Widok ekranu programu Pasteur

Poe

1. Pobierz plik:

poe.zip

(104 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program poe.exe.

Program Poe oblicza statystykę występowania znaków w danym pliku. Po uruchomieniu
programu pojawia się ramka z trzema polami, w które trzeba wpisać:

1. Input file - Nazwę pliku zawierającego badany tekst.
2. Output file - Nazwę pliku, w którym pragniemy zapisać dane statystyczne dla

badanego tekstu.

3. Character file - Nazwę pliku, w którym znajduje się lista liter (znaków), które

chcemy uwzględnić przy obliczaniu statystyki.

Wszystkie te nazwy można także wprowadzić za pomocą opcji Znajdź... (Browse...).

Po kliknięciu na OK program zapisuje do pliku Output file liczbę wszystkich pojedynczych
znaków oraz liczbę par znaków. W nawiasach podane są kody ASCII uwzględnianych
znaków. Program oblicza także entropię informacyjną, o której piszemy w rozdziale 5
"Modelowania rzeczywistości".

Widok ekranu programu Poe

Sierpinski

1. Pobierz plik:

sierpinski.zip

(158 kB)

2. Rozpakuj go (używajac np. programu WinZip lub Windows Commander) do dowolnego
katalogu.
3. Uruchom program sierpinski.exe.

Program Sierpinski służy do generowania fraktalnych figur, będących wynikiem
przypadkowego błądzenia na płaszczyźnie, opartego na następującej zasadzie:

Wybieramy liczbę wierzchołków n określającą wielobok foremny (trójkąt, kwadrat, pięciobok
itd.) i podajemy jedną liczbę k określającą długość kroku błądzenia. Błądzenie odbywa się
według następującej zasady: Rozpoczynamy w losowo wybranym punkcie płaszczyzny.
W celu wyznaczenia kierunku i odległości kolejnego kroku losujemy numer wierzchołka
i posuwamy się w kierunku wylosowanego wierzchołka o kd , gdzie d jest odległością
aktualnego punktu płaszczyzny od wylosowanego wierzchołka. W zależności od tego, czy d <
1, czy też d > 1, nie dochodzimy do wierzchołka, bądź go przekraczamy.

A oto interesujące kombinacje liczb n oraz k:

n = 3, k = 1/2; n = 3, k = 3/2; n = 4, k = 4/3; n = 5, k = 4/3; n = 5, k = 1,38; n = 6, k = 4/3; n =
9, k = 3/4.

Widok ekranu programu Sierpinski