POLITECHNIKA
WROCŁAWSKA
LABORATORIUM FIZYKI
Wykonał:
Jelonek Michał
Grupa
I
Ćw. nr
31
Prowadzący
Mgr inż. Ewa
Stefaniak
Sprawdzanie prawa
Stefana-Boltzmanna
Data wykonania
18.10.2002
Data oddania
25.10.2002
Ocena
1. WSTĘP TEORETYCZNY
Emitancja energetyczna M(T) jest to iloraz mocy (czyli strumienia
energii)
∆φ wypromieniowanej w zakresie całego widma z powierzchni
∆S rozciągłego źródła tego promieniowania, przez wielkość tej
powierzchni. W granicy jest to pochodna mocy wypromieniowanej
φ
względem powierzchni źródła promieniowania. Emitancja
elektromagnetyczna jest funkcją temperatury T.
]
*
[
)
(
2
−
=
m
W
dS
d
T
M
φ
Natężenie napromieniowania E jest to stosunek mocy (czyli strumienia
energii)
∆φ promieniowania pochłoniętego przez element powierzchni ∆S
do wielkości tej powierzchni. W granicy, jest to pochodna mocy
φ
promieniowania padającego względem powierzchni S.
dS
d
E
φ
=
Współczynnik absorpcji A(T) jest ilorazem strumienia energii
φ
a
promieniowania zaabsorbowanego przez dane ciało do strumienia
energii
φ
i
promieniowania padającego na nie. Jest on funkcją
temperatury.
1
)
(
0
........
..........
)
(
<
<
=
T
A
T
A
i
a
φ
φ
1
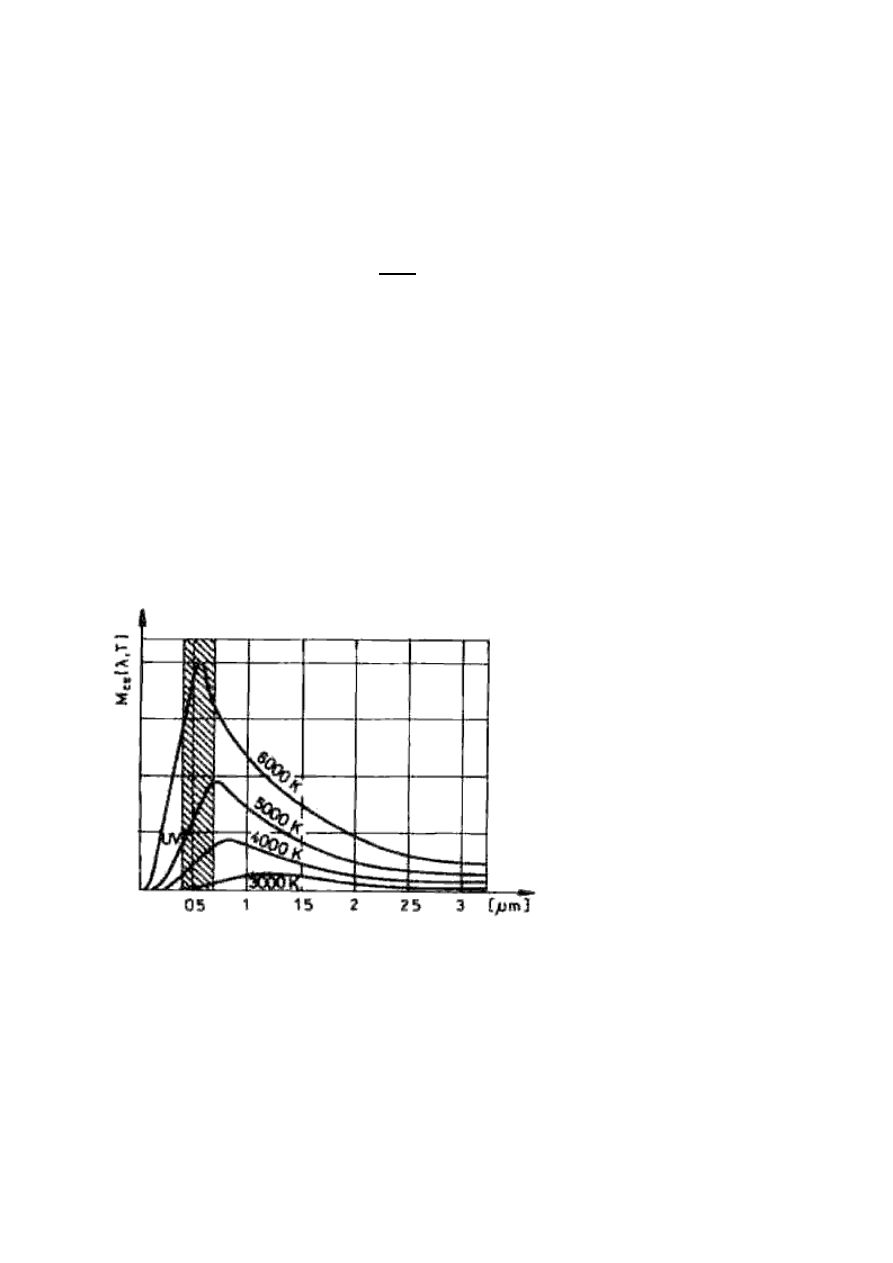
Promieniowanie termiczne ciała doskonale czarnego. Ciało
doskonale czarne to takie, które całkowicie pochłania padające na nie
promieniowanie elektromagnetyczne. Gęstość monochromatyczną
emitancji ciała doskonale czarnego opisuje równanie Plancka:
1
2
5
1
1
exp
)
,
(
−
−
−
=
T
C
C
T
M
CZ
λ
λ
λ
gdzie :
C
1
= 3,74*10
-16
[ W*m
2
]
C
2
= 0,0144 [ m*K ]
λ - długość fali
T – temperatura bezwzględna
Rozkład Plancka monochromatycznej gęstości emitancji energetycznej
ciała doskonale czarnego w różnych temperaturach prezentuje poniższy
wykres :
Emitancja ciała doskonale czarnego. Aby obliczyć emitancję ciała
doskonale czarnego w interesującym nas przedziale
∆λ należy całkować
w tym przedziale funkcję M
CZ
(
λ,T) po dλ. Całkując M
CZ
(
λ,T) po
wszystkich długościach fal :
∫
∞
=
0
)
,
(
)
(
λ
λ
d
T
M
T
M
CZ
CZ
2
otrzymuje się prawo Stefana-Boltzmanna :
4
)
(
T
T
M
CZ
σ
=
gdzie
σ = 5,67*10
-8
[ W*m
-2
*K
-4
] ( stała Stefana-Boltzmanna ).
Całkowita moc emitowana w postaci promieniowania przez ciało
doskonale czarne o powierzchni S (całkowita energia emitowana w
jednostce czasu – strumień energii
φ
C
) zgodnie z prawem Stefana-
Boltzmanna jest proporcjonalna do czwartej potęgi jego temperatury
wyrażonej w kelwinach.
Modelem ciała doskonale czarnego jest wnęka z małym otworem.
Promieniowanie wpadające do takiej wnęki zanim ją opuści ulega
wielokrotnemu odbiciu. Przy każdym z odbić część energii
promieniowania zostaje przekazana ściankom wnęki.
Zasada działania piroelektrycznego detektora promieniowania
podczerwonego.
Zjawisko piroelektryczne polega na generowaniu na powierzchni
niektórych kryształów, spolaryzowanych ceramik lub folii ładunków
elektrycznych pod wpływem zmian temperatury. Ładunek elektryczny
∆q
generowany na powierzchni S
K
kryształu, na skutek zmiany jego
temperatury o
∆T określony jest równaniem :
T
S
q
K
∆
=
∆
γ
współczynnik
γ nosi nazwę współczynnika piroelektrycznego.
3
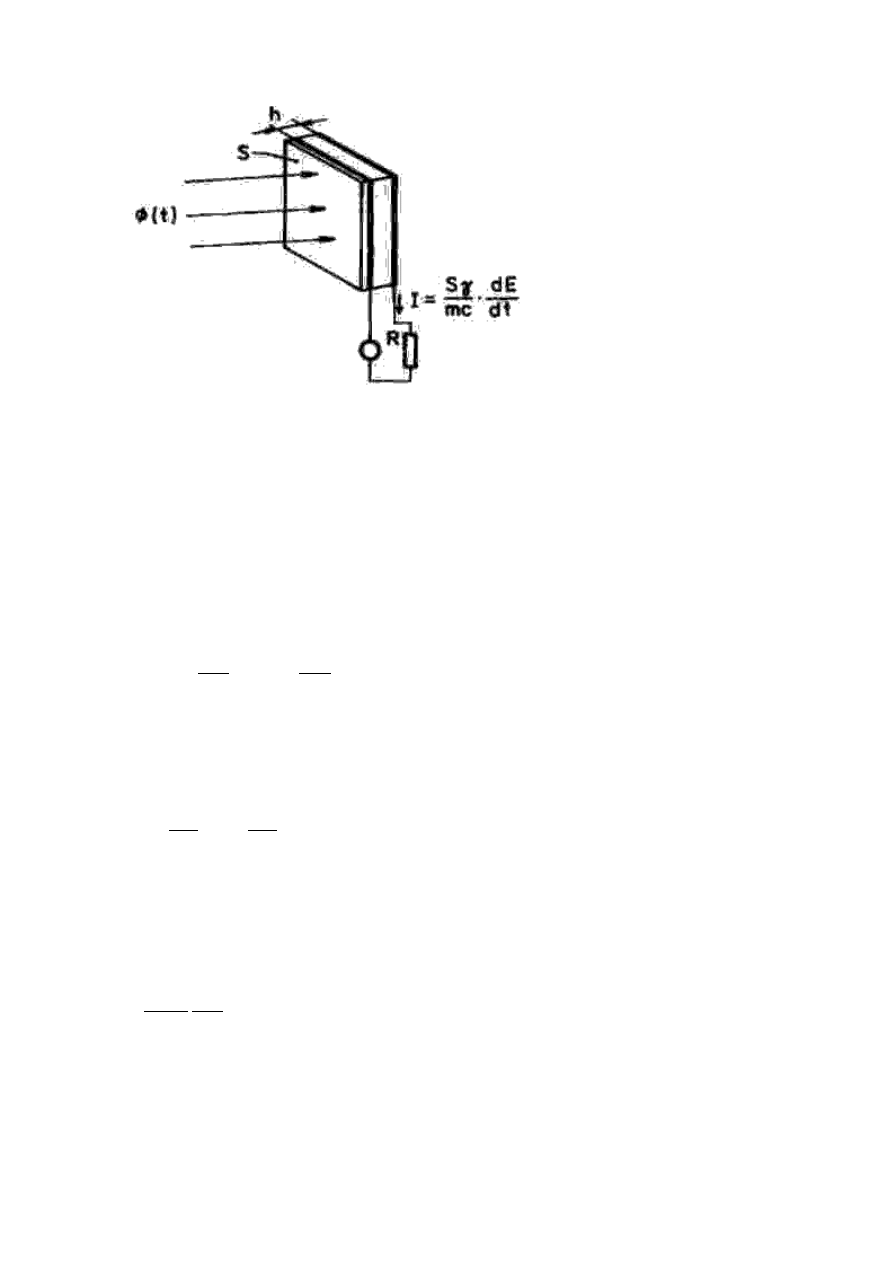
Rozpatrzmy cienką płytkę o grubości h i polu powierzchni S
K
wyciętą z piroelektryka (płytka musi być odpowiednio zorientowana -
zjawisko piroelektryczne obserwowane jest tylko w ściśle określonych
kierunkach krystalograficznych (zależnych od symetrii kryształu). Na
płytkę napylone są elektrody zwarte opornikiem R. Na jedną z elektrod
naniesiona jest dodatkowo warstwa absorbująca promieniowanie. Jeżeli
temperatura płytki ranieni się o
∆T, to na jej powierzchni S
K
pojawi się
ładunek
∆q, określony powyższym równaniem. Zmiana temperatury o ∆T
w czasie
∆t, powoduje przepływ prądu o natężeniu
dt
dT
S
t
q
I
K
γ
=
∆
∆
=
Jeżeli kryształ jest ogrzewany przez zmieniający się w czasie strumień
energii promieniowania
Φ(t), to z bilansu energii wynika, że
dt
dT
mc
dt
dE
t
=
=
Φ )
(
gdzie E to energia zgromadzona w krysztale , m jest masą , c – ciepłem
właściwym , dT średnią zmianą temperatury kryształu.
Po podstawieniu otrzymujemy :
dt
dE
mc
S
I
K
γ
=
z równania tego wynika, że natężenie prądu płynącego przez opór
obciążenia detektora jest proporcjonalne do powierzchni detektora,
wartości współczynnika piroelektrycznego oraz strumienia energii
4
absorbowanego przez kryształ, a odwrotnie proporcjonalne do
pojemności cieplnej kryształu (iloczynu mc), natomiast nie zależy od
składu spektralnego promieniowania, które pada na detektor. Jeżeli
kryształ byłby ogrzewany przez stały (niezależny od czasu) strumień
energii promieniowania, to po pewnym czasie temperatura kryształu
uległaby ustaleniu (energia absorbowana byłaby równa energii traconej).
Natężenie prądu generowanego przez detektor jest proporcjonalne do
szybkości zmian temperatury, dlatego strumień promieniowania
padający na detektor powinien być modulowany. Modulatorem jest
obracająca się tarcza z odpowiednio wyciętymi otworami, umieszczona
na drodze wiązki promieniowania docierającej do detektora :
.
Jeżeli pomiędzy źródłem promieniowania i detektorem znajduje się
wycięcie w tarczy modulatora, kryształ jest ogrzewany (temperatura
kryształu rośnie), natomiast w czasie gdy wiązka jest przesłaniana przez
modulator kryształ stygnie.
Piroelektryczne detektory promieniowania podczerwonego są
stosowane w wielu dziedzinach techniki. Na nich opierają swe działanie
np. kamery termowizyjne czy noktowizory. Wykorzystywane są w
medycynie do diagnozowania stanów chorobowych (wyższa
temperatura) , w budownictwie do wykrywania nieszczelności budynków,
a także ( choć nielegalnie ) na polowaniach (noktowizory).
5
2. CEL ĆWICZENIA
Celem ćwiczenia jest sprawdzenie prawa Stefana-Boltzmanna, w tym
celu należy wyznaczyć związek między mocą emitowaną przez model
ciała doskonale czarnego a jego temperaturą.
3. ZASADA POMIARU ORAZ UKŁAD POMIAROWY
Wyposażenie stanowiska :
- Piroelektryczny detektor promieniowania podczerwonego typ
DP-1C
- Regulator temperatury wraz z modelem ciała doskonale
czarnego
Układ pomiarowy :
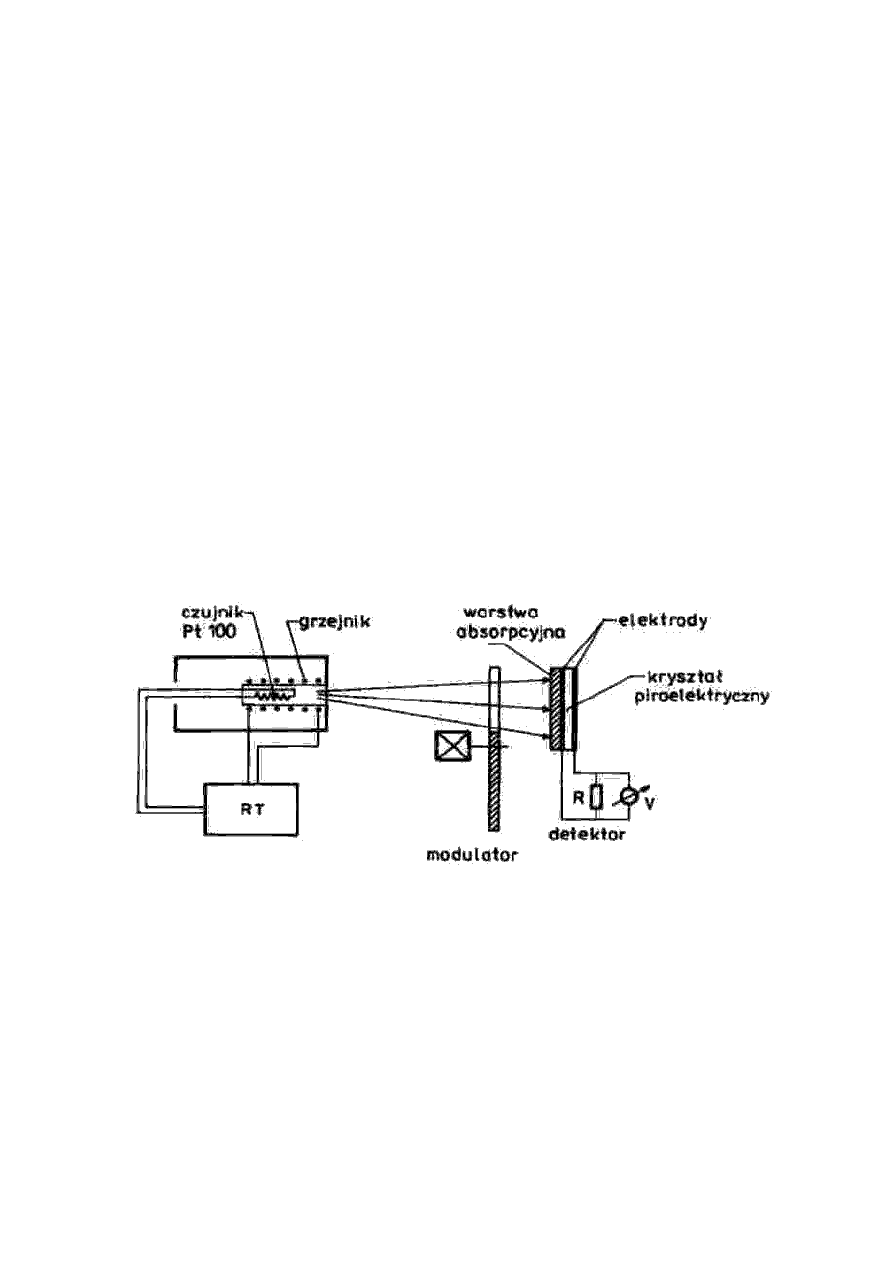
Układ pomiarowy składa się z modelu ciała doskonale czarnego,
którym jest grzejnik umieszczony w obudowie z małym otworem,
regulatora temperatury, modulatora oraz piroelektrycznego detektora
promieniowania podczerwonego. Źródłem promieniowania, jest model
ciała doskonale czarnego, którego temperatura jest stabilizowana za
pomocą regulatora temperatury RT współpracującego z platynowym
czujnikiem temperatury (Pt-100). Strumień energii padający na element
powierzchni detektora jest proporcjonalny do strumienia energii
emitowanej przez model ciała czarnego. Jeżeli temperatura ciała
6
czarnego nie jest zbyt wysoka, to zgodnie ze wzorem Plancka większość
energii emitowana jest w postaci promieniowania podczerwonego.
Aby wyznaczyć zależność mocy emitowanej przez model ciała
czarnego od jego temperatury powinniśmy dysponować detektorem
promieniowania, który reaguje na całkowitą moc padającego na ten
detektor promieniowania, niezależnie od jego składu spektralnego. W
ćwiczeniu korzystamy z piroelektrycznego detektora promieniowania
podczerwonego, który spełnia wymieniony warunek.
4. POMIARY
Wyznaczaliśmy zależność mocy promieniowania padającego na
detektor emitowanego przez model ciała doskonale czarnego , od
temperatury tego ciała (temperaturę można było regulować
potencjometrem grzejnika). Promieniowanie było „po drodze”
modulowane przez obracający się modulator. Układ pomiarowy
przedstawiłem w pierwszym punkcie sprawozdania.
5. WYNIKI POMIARÓW :
temperatura [K]
ustawiona odczytana średnia
I
min
I
max
I
0
log(T)
−
−
0
min
max
2
log
I
I
I
- 523
523
93
94
7
2,72
1,94
- 553
553
116
117
7
2,74
2,04
- 583
583
138
139
7
2,76
2,12
- 613
613
173
174
7
2,79
2,22
- 643
643
196
197
7
2,81
2,28
- 673
673
230
231
7
2,83
2,35
712 703
707,5
253
254
7
2,85
2,39
744 733
738,5
303
304
7
2,87
2,47
780 763
771,5
357
358
7
2,89
2,54
814 793
803,5
412
413
7
2,90
2,61
849 823 836
464
465
7
2,92
2,66
7
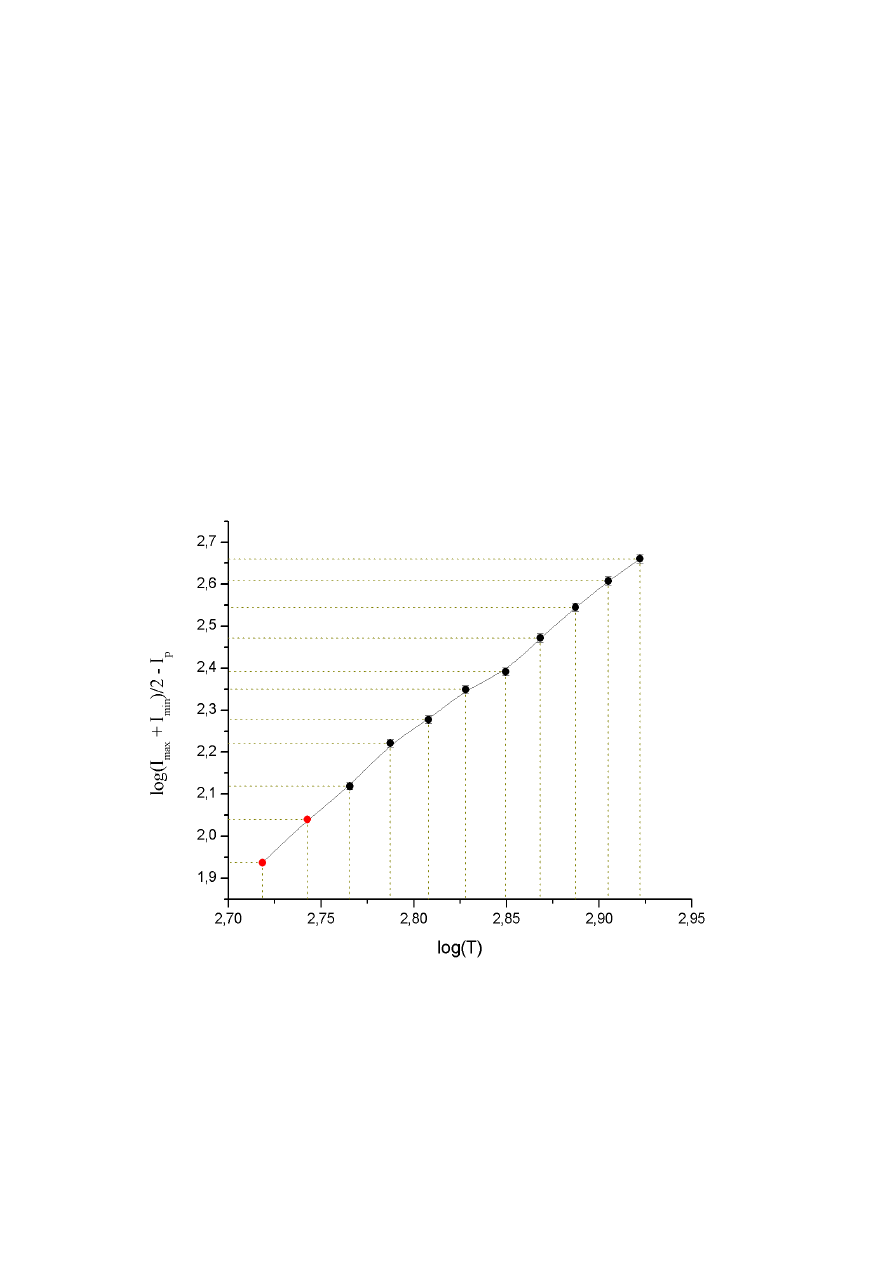
6. OPRACOWANIE WYNIKÓW
Prawo Stefana-Boltzmanna można zapisać w postaci :
α
σ
T
S
M
=
gdzie S
σ to wartość stała , a α traktujemy jako wielkość nieznaną , której
wartość chcemy wyznaczyć.
Należy więc sporządzić wykres zależności logarytmu natężenia
prądu (odczytanego z detektora) od logarytmu temperatury ciała
doskonale czarnego (wyniki obliczeń i wzory w tabelce w punkcie
poprzednim):
Wykorzystując regresję liniową możemy wyznaczyć tangens
nachylenia wykresu (prostej będącej najlepiej dopasowaną do
zaznaczonych na wykresie punktów). Jest on równocześnie wartością
szukanego wykładnika potęgowego
α.
8
Wartość współczynnika obliczyłem korzystając z formuły REGLINP
programu Microsoft Excel
2000 oraz z programu Microcal ORIGIN
6.0 .
Wartość ta wynosi :
3,4847
=
α
z błędem bezwzględnym :
0,014
=
∆
α
i względnym :
%
0,4
=
δα
7. PODSUMOWANIE I WNIOSKI
Rzeczywista wartość wykładnika
α (zgodnie z prawem Stefana-
Boltzmanna) wynosi 4 (bo całkowita moc emitowana w postaci
promieniowania przez ciało doskonale czarne jest proporcjonalna do
czwartej potęgi jego temperatury). Otrzymana przeze mnie wartość
3,4847
±0,014 nieco różni się od tej którą otrzymać powinienem. Różnicę
tę można jednak wytłumaczyć nie dość „sterylnymi” warunkami podczas
wykonywania ćwiczenia. Wykorzystany detektor piroelektryczny był
bardzo wrażliwy – nawet za bardzo. Reagował na wszelkie drgania (nie
chodzi tu o poruszenie aparatury ale o zwykłe chodzenie kolegów po
sali) , bardzo drastycznie zmienił wyniki podczas zmiany oświetlenia
(nastąpiło to w połowie wykonywania naszych pomiarów na prośbę
kolegów czy też koleżanek którzy nie mogli wykonać swojego ćwiczenia
z optyki przy włączonym oświetleniu) . Źródeł błędu należy też szukać w
modelu ciała doskonale czarnego , a dokładnie w potencjometrze
służącym do ustawiania temperatury i w niezależnym czujniku
platynowym. Odczyt temperatury z potencjometru i z wyświetlacza różnił
się nawet o 21
° !!! , w dodatku różnica ta nie była stała (rosła wraz ze
wzrostem temperatury) . Z tego powodu od pomiaru 6-go za temperaturę
modelu ciała doskonale czarnego musiałem przyjąć średnią z wartości
ustawionej i odczytanej. Kolejnym problemem było to, że po ustaleniu
9
się temperatury modelu wskazania detektora oscylowały wokół
zwiększającej się , a nie stałej wartości. Oznacza to że średnie
wskazanie detektora rosło wraz z biegiem czasu , pomimo stałej
temperatury modelu. Otrzymane wyniki (wykres i obliczony
współczynnik) w znacznym stopniu spełniają prawo Stefana-Boltzmanna,
a niewielkie odchylenie spowodowane jest prawdopodobnie błędami
opisanymi powyżej. Komfort wykonywania ćwiczenia jak i
zminimalizowanie wpływu czynników zewnętrznych poprawiłoby nakrycie
przyrządów np. skrzynią z materiału nie przepuszczającego światła i
wyprowadzenie na zewnątrz tylko wyświetlacza detektora , czujnika
temperatury i potencjometru. Wyniki poprawiłoby by również precyzyjne
ustawienie w jednej linii modelu ciała i detektora (w ćwiczeniu
ustawiliśmy je „na oko”). Tak zabudowany układ można by dodatkowo
ochronić przed wstrząsami lepiej niż , tak jak w ćwiczeniu zastosowanie
podkładki pod mysz komputerową pod detektorem.
10