4.1 Równanie falowe Schrödingera
4.2 Obserwable, stany stacjonarne,
warto
ś
ci
ś
rednie
4.3 Niesko
ń
czona studnia potencjału
4.4 Sko
ń
czona studnia potencjału
4.5 Trójwymiarowa niesko
ń
czona
studnia potencjału
4.6 Degeneracja
4.7 Oscylator harmoniczny
4.8 Bariery i tunelowanie
4.9 Studnia potencjału
0
Rozdział 4
Równanie Schrödingera
Erwin Schrödinger (1887-1961)
Wnikliwa analiza procesu obserwacji w fizyce atomowej wykazała,
ż
e
cz
ą
steczki subatomowe nie maj
ą
znaczenia jako pojedyncze jednostki,
ale mog
ą
by
ć
rozumiane wył
ą
cznie w kontek
ś
cie przygotowanego
eksperymentu i dokonanego pomiaru.
- Erwin Schrödinger
Przygotowanie Marek Szopa, na podstawie Rick Trebino, Georgia Tech, www.physics.gatech.edu/frog/lectures
Opinie o mechanice kwantowej
My
ś
l
ę
,
ż
e
ś
miało mo
ż
na
powiedzie
ć
,
ż
e nikt nie rozumie
mechaniki kwantowej. Je
ś
li nie
musisz nie zadawaj sobie
pytania: "Ale jak to mo
ż
e tak
by
ć
?", bo zabrniesz w
ś
lep
ą
uliczk
ę
, z której nikt jeszcze nie
uciekł. Nikt nie wie, jak mo
ż
e tak
by
ć
.
- Richard Feynman
Richard Feynman (1918-1988)
Ci, którzy spotkawszy si
ę
po raz
pierwszy z mechanik
ą
kwantow
ą
nie s
ą
w szoku, prawdopodobnie
nie rozumiej
ą
jej..
- Niels Bohr
( )
( )
( )
2
2
2
,
,
,
2
x t
x t
i
V
x t
t
m
x
∂Ψ
∂ Ψ
= −
+ Ψ
∂
∂
ℏ
ℏ
4.1: Równanie falowe Schrödingera
Jednowymiarowe równanie falowe Schrödingera, zale
ż
ne od czasu,
dla cz
ą
stek o energii E poruszaj
ą
cych si
ę
w potencjale
V
:
gdzie
V = V(x,t)
gdzie
i
jest pierwiastkiem kwadratowym z -1.
Równanie Schrodingera jest FUNDAMENTALNYM równaniem
Mechaniki Kwantowej.
Porównajmy je z równaniem falowym dla elektromagnetyzmu:
2
2
2
2
2
1
0
v
x
t
∂ Ψ
∂ Ψ
−
=
∂
∂
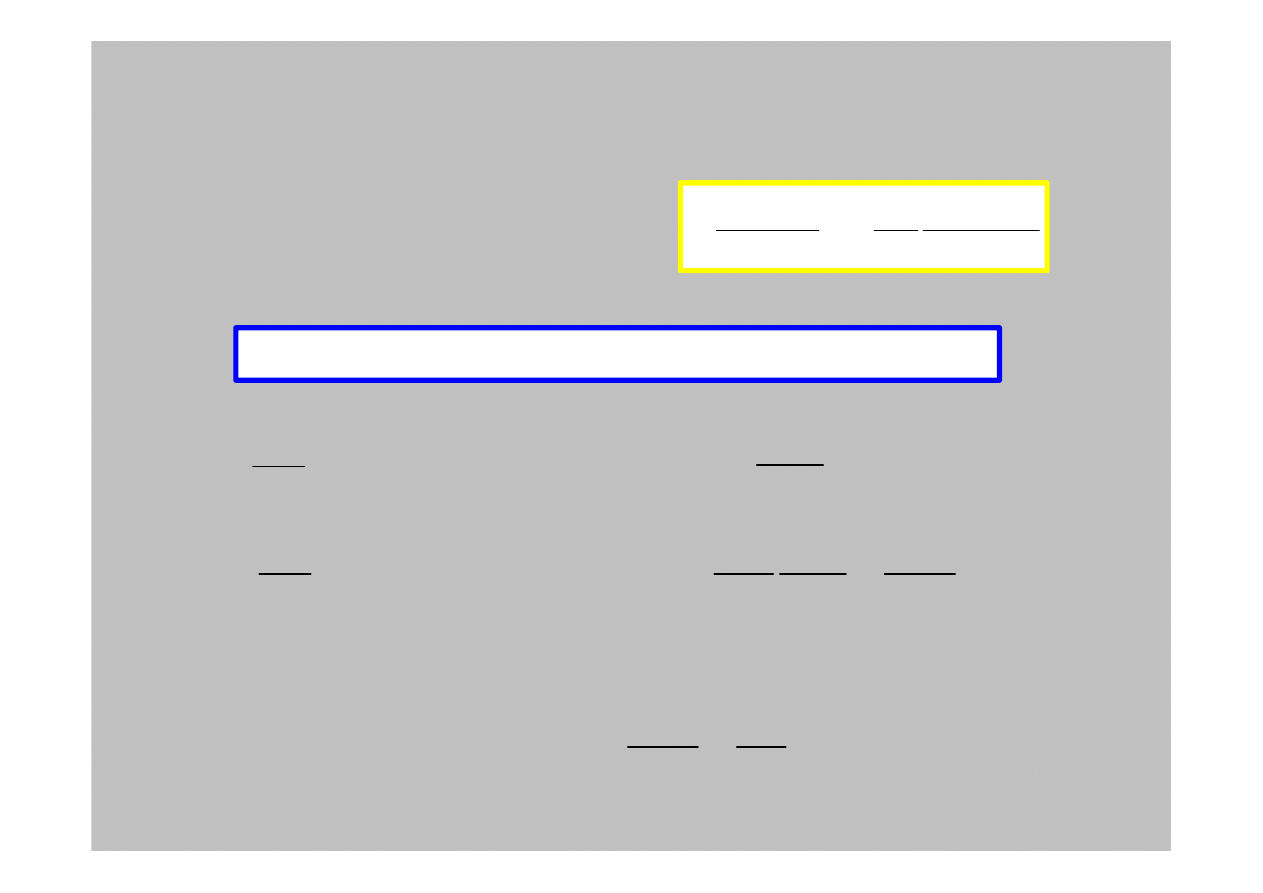
Rozwi
ą
zanie ogólne równania falowego
Schrödingera dla
V
= 0
Sprawd
ź
my rozwi
ą
zanie:
(
)
i kx
t
i Ae
i
t
ω
ω
ω
−
∂Ψ = −
= − Ψ
∂
2
2
2
k
x
∂ Ψ = − Ψ
∂
( )(
)
i
i
i
t
ω
ω
∂Ψ =
−
Ψ =
Ψ
∂
ℏ
ℏ
ℏ
2
2
2
2
2
2
2
k
m
x
m
− ∂ Ψ =
Ψ
∂
ℏ
ℏ
Równanie jest spełnione je
ś
li:
2
2
2
2
2
k
p
h
E
m
m
ω
ν
=
= =
=
ℏ
ℏ
Co oznacza,
ż
e
całkowita energia jest
energi
ą
kinetyczn
ą
.
( )
( )
2
2
2
,
2
,
x
t
x
m
t
t
x
i
∂
Ψ
∂
−
=
∂
Ψ
∂
ℏ
ℏ
)]
sin(
)
[cos(
)
,
(
)
(
t
kx
i
t
kx
A
Ae
t
x
t
kx
i
ω
ω
ω
−
+
−
=
=
Ψ
−
(
)
( , )
[cos(
)
sin(
)]
i kx
t
x t
Ae
A
kx
t
i
kx
t
ω
ω
ω
−
Ψ
=
=
−
+
−
Ogólne rozwi
ą
zanie równania falowego
Schrödingera dla
V
= 0
W pró
ż
ni (kiedy
V
= 0), ogólna posta
ć
funkcji falowej jest:
funkcja ta opisuje fal
ę
poruszaj
ą
c
ą
si
ę
w kierunku x. Amplituda
fali mo
ż
e w ogólno
ś
ci by
ć
liczb
ą
zespolon
ą
.
Funkcja falowa równie
ż
nie musi by
ć
rzeczywista.
W ogólnym przypadku jest ona funkcj
ą
zespolon
ą
.
Tylko mierzalne fizycznie wielko
ś
ci takie jak
prawdopodobie
ń
stwo, p
ę
d i energia musz
ą
by
ć
rzeczywiste.
Prawdopodobie
ń
stwo i normalizacja
Prawdopodobie
ń
stwo
P(x) dx
znalezienia cz
ą
stki mi
ę
dzy
x
i
x + dx
jest
dane równaniem:
wielko
ść
Ψ
∗
Ψ
nazywamy
g
ę
sto
ś
ci
ą
prawdopodobie
ń
stwa
.
Prawdopodobie
ń
stwo znalezienia cz
ą
stki mi
ę
dzy
x
1
a
x
2
jest dane
równaniem
Funkcja falowa musi by
ć
znormalizowana
, wi
ę
c prawdopodobie
ń
stwo
znalezienia cz
ą
stki mi
ę
dzy gdziekolwiek na osi musi by
ć
=1
dx
t
x
t
x
dx
x
P
)
,
(
)
,
(
)
(
Ψ
Ψ
=
∗
∫
Ψ
Ψ
=
∗
2
1
x
x
dx
P
∫
∞
∞
−
∗
=
Ψ
Ψ
1
)
,
(
)
,
(
dx
t
x
t
x
Warunki jakie musz
ą
spełnia
ć
funkcje falowe
Warunki na funkcje falowe:
1. W celu unikni
ę
cia niesko
ń
czonych prawdopodobie
ń
stw, funkcja
falowa musi by
ć
wsz
ę
dzie sko
ń
czona.
2. Funkcja falowa musi by
ć
jednowarto
ś
ciowa.
3. Funkcja falowa musi by
ć
dwukrotnie ró
ż
niczkowalna. Oznacza to,
ż
e ona i jej pochodna musz
ą
by
ć
ci
ą
głe. (Wyj
ą
tkiem od tej reguły
jest przypadek, gdy potencjał V jest niesko
ń
czony.)
4. W celu normalizacji, funkcja falowa musi d
ąż
y
ć
do zera jak
x
d
ąż
y
do (plus, minus) niesko
ń
czono
ś
ci.
Rozwi
ą
zania, które nie spełniaj
ą
tych wła
ś
ciwo
ś
ci z reguły nie
odpowiadaj
ą
rozwi
ą
zaniom akceptowalnym fizycznie.
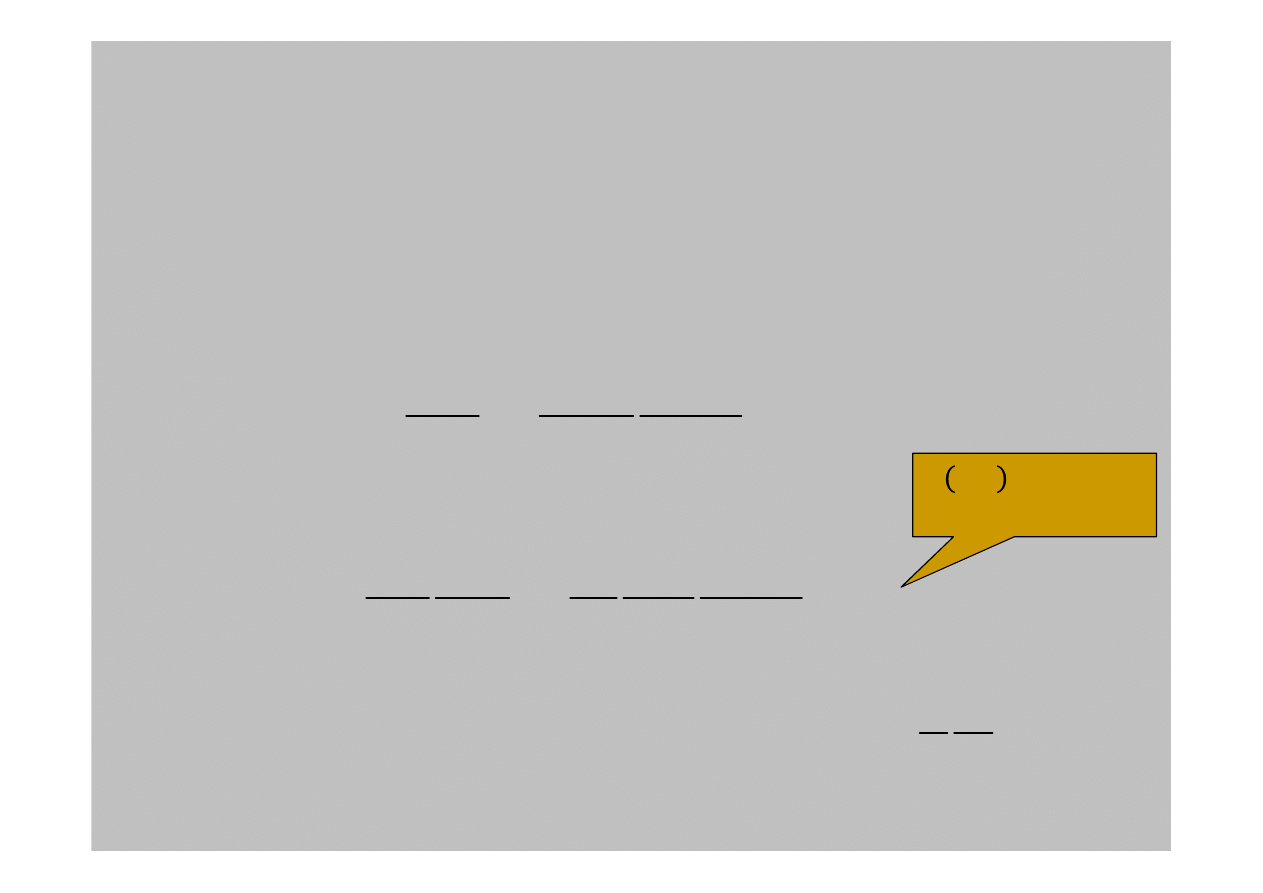
W wielu przypadkach potencjał nie zale
ż
y explicite od czasu.
Zale
ż
no
ś
ci od czasu i poło
ż
enia w równaniu Schrödingera mog
ą
by
ć
wówczas rozdzielone. Niech:
co daje:
Po podzieleniu przez
ψ
(x) f(t)
:
Bezczasowe równanie falowe Schrödingera
Lewa strona zale
ż
y tylko od
t
, a prawa tylko od
x
.
Ka
ż
da strona musi wi
ę
c by
ć
równa stałej. Dla
strona zale
ż
nej od czasu otrzymujemy:
)
(
)
(
)
,
(
t
f
x
t
x
ψ
=
Ψ
)
(
)
(
)
(
)
(
2
)
(
)
(
)
(
2
2
2
t
f
x
x
V
x
x
m
t
f
t
t
f
x
i
ψ
ψ
ψ
+
∂
∂
−
=
∂
∂
ℏ
ℏ
)
(
)
(
)
(
1
2
)
(
)
(
1
2
2
2
x
V
x
x
x
m
t
t
df
t
f
i
+
∂
∂
−
=
∂
ψ
ψ
ℏ
ℏ
B
t
df
f
i
=
∂
1
ℏ
,
=
-
nie zale
ż
y od
Mno
żą
c obie strony przez
f(t)/iħ
:
To równanie ró
ż
niczkowe jest łatwe do rozwi
ą
zania:
Bezczasowe równanie falowe Schrödingera
Przypomnijmy rozwi
ą
zanie dla cz
ą
stki swobodnej:
W którym
f(t) = exp(-i
ω
t)
, wi
ę
c:
ω
= B / ħ
lub
B = ħ
ω
, co oznacza,
ż
e:
B = E
!
Mno
żą
c przestrzenn
ą
cz
ęść
równ. Schrödingera przez
ψ
(x)
, otrzymujemy:
/
( )
e
iEt
f t
−
=
ℏ
/
f
B f i
t
∂ =
∂
ℏ
/
/
( )
e
e
Bt i
iBt
f t
−
=
=
ℏ
ℏ
(
)
( , )
e
i kx
t
x t
ω
−
Ψ
=
Stał
ą
przed
f(t)
mo
ż
emy zignorowa
ć
,
gdy
ż
jej warto
ść
b
ę
dzie okre
ś
lona z
warunku normalizacji
)
(
)
(
)
(
)
(
2
2
2
2
x
E
x
x
V
dx
x
d
m
ψ
ψ
ψ
=
+
−
ℏ
Bezczasowe równanie falowe Schrödingera
Równanie to jest znane jako
bezczasowe
(niezale
ż
ne od czasu)
równanie falowe Schrödingera
, i na równi z pełnym równaniem
falowym Schrödingera jest fundamentalnym równaniem mechaniki
kwantowej
Równanie to ma posta
ć
równania własnego
,
gdzie:
ˆ
H
E
ψ
ψ
=
2
2
2
ˆ
2
H
V
m x
∂
= −
+
∂
ℏ
jest
operatorem energii
.
ˆ
H
)
(
)
(
)
(
)
(
2
2
2
2
x
E
x
x
V
dx
x
d
m
ψ
ψ
ψ
=
+
−
ℏ
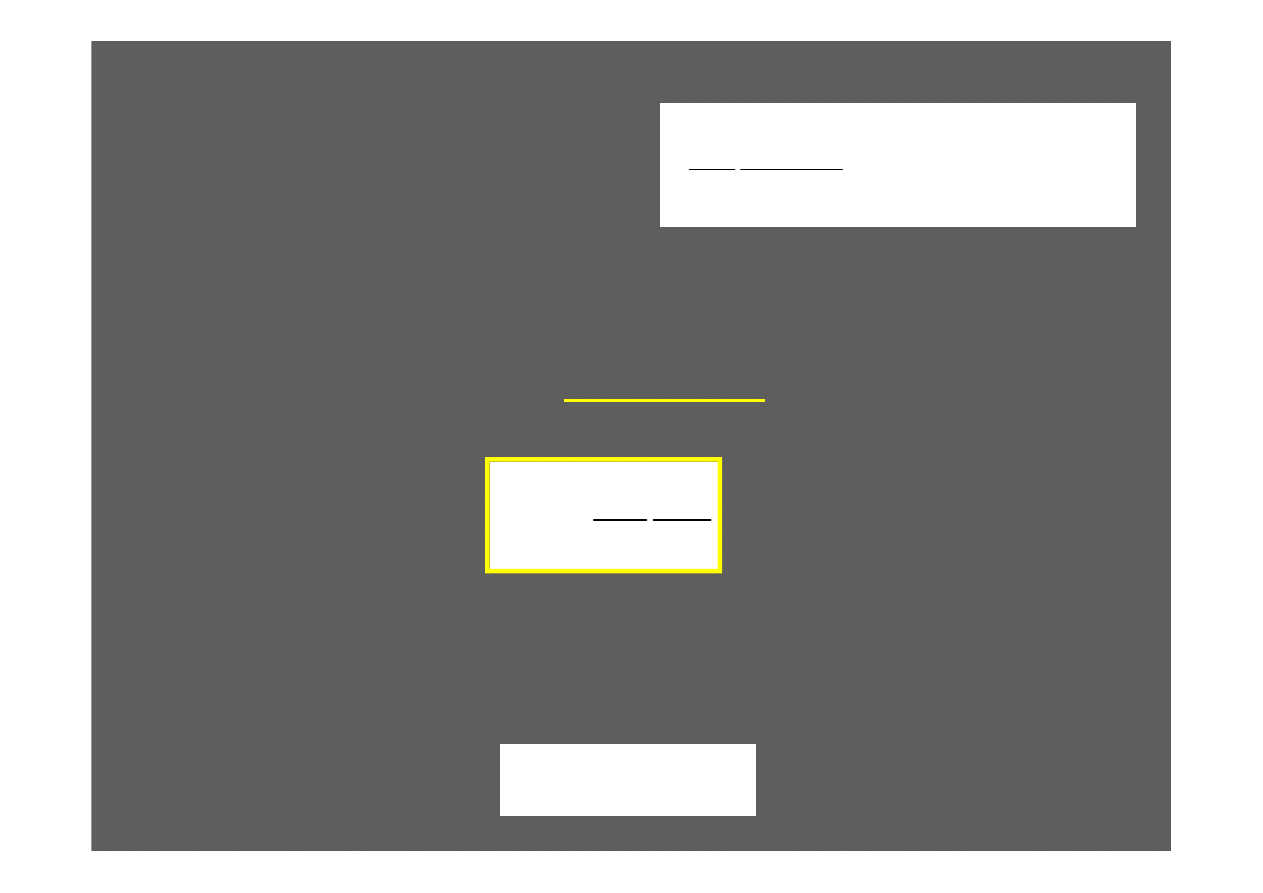
4.2: Obserwable
Operatory odgrywaj
ą
w mechanice kwantowej wa
ż
n
ą
rol
ę
.
Wszystkie wielko
ś
ci mierzalne maj
ą
odpowiadaj
ą
ce im
operatory które nazywamy obserwablami.
Operatorem energii kinetycznej jest:
2
2
2
2
K
m x
∂
= −
∂
⌢
ℏ
Inne operatory s
ą
na ogół prostsze, zazwyczaj zawieraj
ą
operacje
mno
ż
enia, dodawania.
Operator energii potencjalnej jest po prostu mno
ż
eniem przez
V(x)
.
)
(
)
(
)
(
)
(
2
2
2
2
x
E
x
x
V
dx
x
d
m
ψ
ψ
ψ
=
+
−
ℏ
( )
( ) ( )
V
x
V x
x
ψ
ψ
=
Stany stacjonarne
Załó
ż
my,
ż
e mamy funkcj
ę
falow
ą
postaci:
G
ę
sto
ść
prawdopodobie
ń
stwa tej funkcji jest równa:
Jest to rozkład prawdopodobie
ń
stwa niezale
ż
ny od czasu.
Taki stan, (reprezentowany przez fal
ę
stoj
ą
c
ą
) nazywamy
stanem
stacjonarnym
.
*
*
( )
( )
i t
i t
x e
x e
ω
ω
ψ
ψ
−
Ψ Ψ =
2
( )
x
ψ
=
t
i
e
x
t
x
ω
ψ
−
=
Ψ
)
(
)
,
(
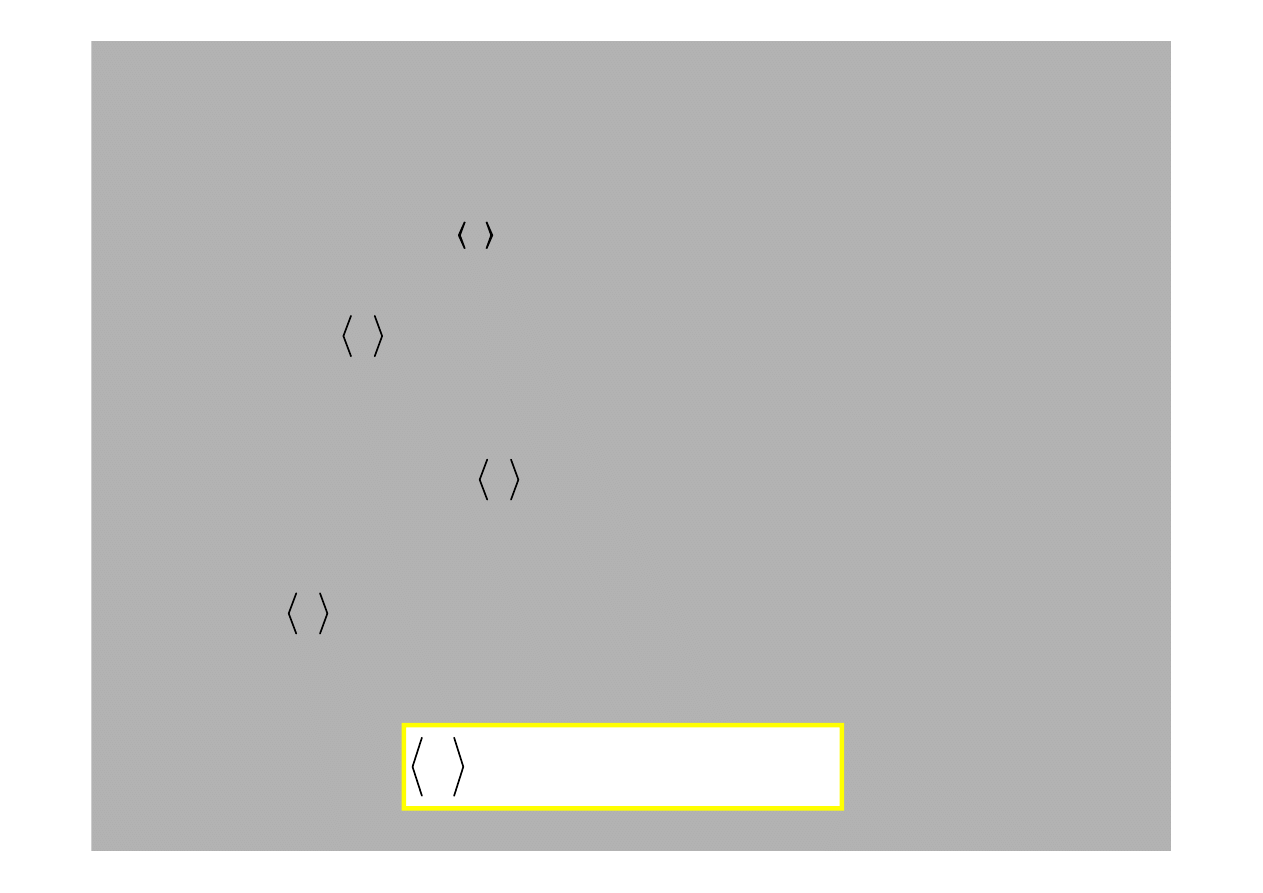
Warto
ś
ci
ś
rednie obserwabli
W mechanice kwantowej cz
ę
sto obliczamy warto
ś
ci oczekiwane.
Warto
ść
oczekiwana
jest
ś
redni
ą
wa
ż
on
ą
tej wielko
ś
ci.
Ogólnie rzecz bior
ą
c, warto
ść
oczekiwan
ą
jest:
Je
ś
li zmienna mo
ż
e przyjmowa
ć
niesko
ń
czenie wiele warto
ś
ci oraz
jest ci
ą
gła to:
1 1
2
2
N
N
i
i
i
x
P x
P x
P x
P x
=
+
+ +
=
∑
⋯
( )
x
P x x dx
=
∫
*
*
( )
( )
( )
( )
x
x
x x dx
x x
x dx
= Ψ
Ψ
=
Ψ
Ψ
∫
∫
W mechanice kwantowej:
Warto
ść
oczekiwana dowolnej obserwabli
zale
ż
nej od w
stanie
jest :
*
( )
( )
( )
x
x
x dx
Ψ
=
Ψ
Ψ
∫
A
A
Notacja Bra-Ket
*
( )
( )
( )
|
|
x
x
x dx
Ψ
= Ψ
Ψ
≡
Ψ
Ψ
∫
A
A
A
Poprzednie równanie jest na tyle wa
ż
ne,
ż
e fizycy maj
ą
dla niego
specjalna notacj
ę
.
Całe to wyra
ż
enie jest rozumiane jako “bracket” czyli nawias
Wyra
ż
enie
〈 |
nazywamy
bra
podczas gdy
| 〉
nazywamy
ket
.
Warunek normalizacji w tej notacji jest:
|
1
Ψ Ψ =
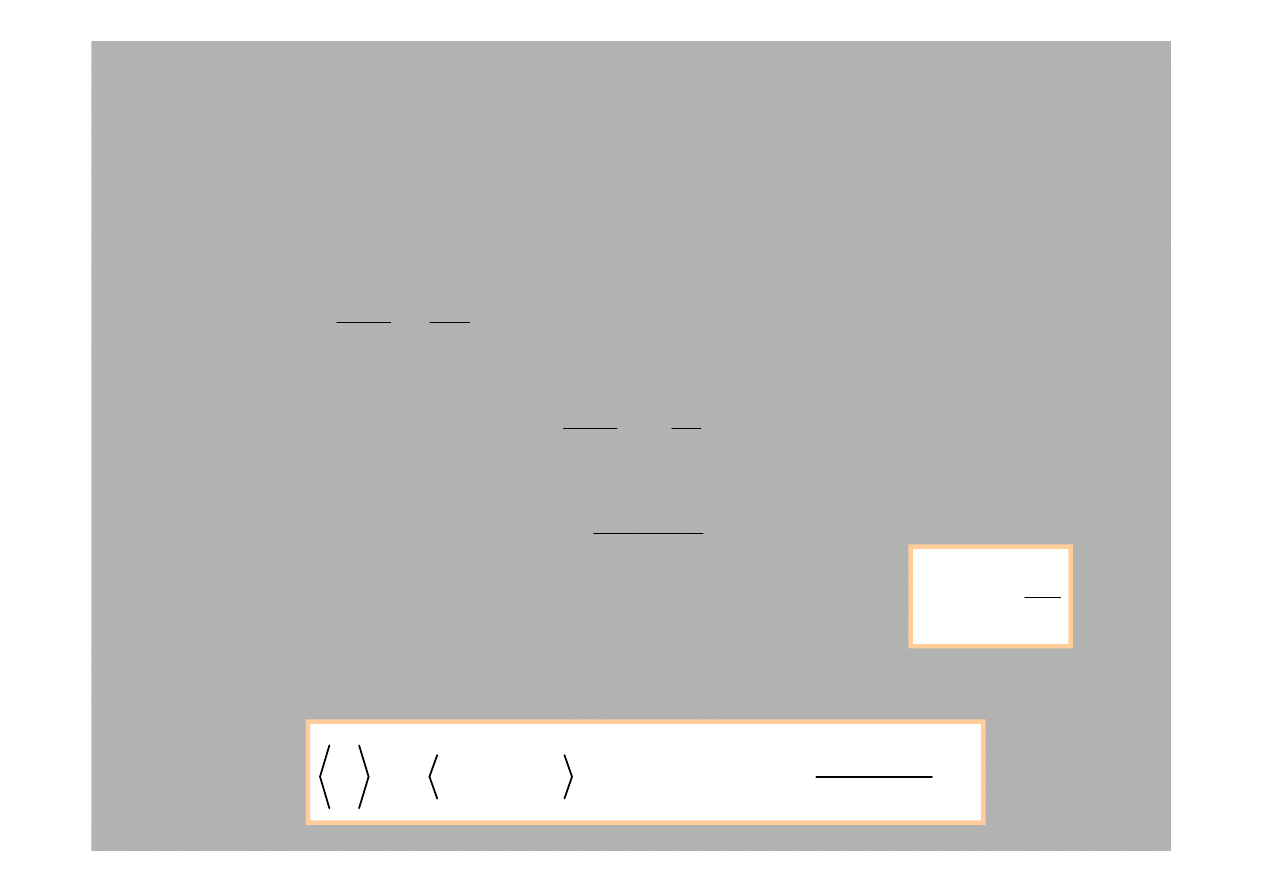
Aby znale
źć
warto
ść
oczekiwan
ą
, musimy najpierw wyrazi
ć
poprzez i . Rozwa
ż
my pochodn
ą
funkcji falowej cz
ą
stki swobodnej
wzgl
ę
dem :
ale
k = p / ħ
wi
ę
c mamy
mno
żą
c obie strony przez
− ℏ
To sugeruje,
ż
e operatorem p
ę
du powinni
ś
my nazwa
ć
Warto
ś
ci
ą
oczekiwan
ą
p
ę
du w stanie
Ψ
jest wi
ę
c
Operator p
ę
du
Ψ
=
=
∂
∂
=
∂
Ψ
∂
−
−
ik
ike
e
x
x
t
kx
i
t
kx
i
)
(
)
(
]
[
ω
ω
Ψ
=
∂
Ψ
∂
ℏ
p
i
x
( , )
ˆ[ ( , )]
( , )
x t
p
x t
i
p
x t
x
∂Ψ
Ψ
= −
= Ψ
∂
ℏ
x
i
p
∂
∂
−
=
ℏ
ˆ
*
( , )
ˆ
|
|
( , )
x t
p
p
i
x t
dx
x
∞
−∞
Ψ
∂Ψ
= Ψ
Ψ = −
Ψ
∂
∫
ℏ
Operatorem poło
ż
enia jest mno
ż
enie przez
x
.
Operator energii: Pochodna po czasie funkcji falowej cz
ą
stki
swobodnej jest:
Podstawiaj
ą
c
ω
=
Ε
/
ħ
mamy
[
, ] = ℏ
,
Operatorem energii jest wi
ę
c:
Warto
ś
ci
ą
oczekiwan
ą
energii w stanie
Ψ
jest:
Operatory poło
ż
enia i energii
Ψ
−
=
−
=
∂
∂
=
∂
Ψ
∂
−
−
ω
ω
ω
ω
i
e
i
e
t
t
t
kx
i
t
kx
i
)
(
)
(
]
[
t
i
E
∂
∂
=
ℏ
ˆ
*
( , )
( , )
x t
E
i
x t
dx
x
∞
−∞
Ψ
∂Ψ
=
Ψ
∂
∫
ℏ
Podstawiaj
ą
c operatory:
:
+
:
Operatorowa posta
ć
równania Schrödingera
2
2
p
E
K
V
V
m
= + =
+
Energia całkowita jest:
E
i
t
∂Ψ
Ψ =
∂
ℏ
2
2
1
2
2
p
V
i
V
m
m
x
∂
Ψ + Ψ =
−
Ψ + Ψ
∂
ℏ
2
2
p
E
V
m
⇒
Ψ =
Ψ + Ψ
2
2
2
2
V
m
x
∂ Ψ
= −
+ Ψ
∂
ℏ
2
2
2
2
i
V
t
m
x
∂Ψ
∂ Ψ
= −
+ Ψ
∂
∂
ℏ
ℏ
mamy:
Czyli pełne równanie falowe Schrodingera
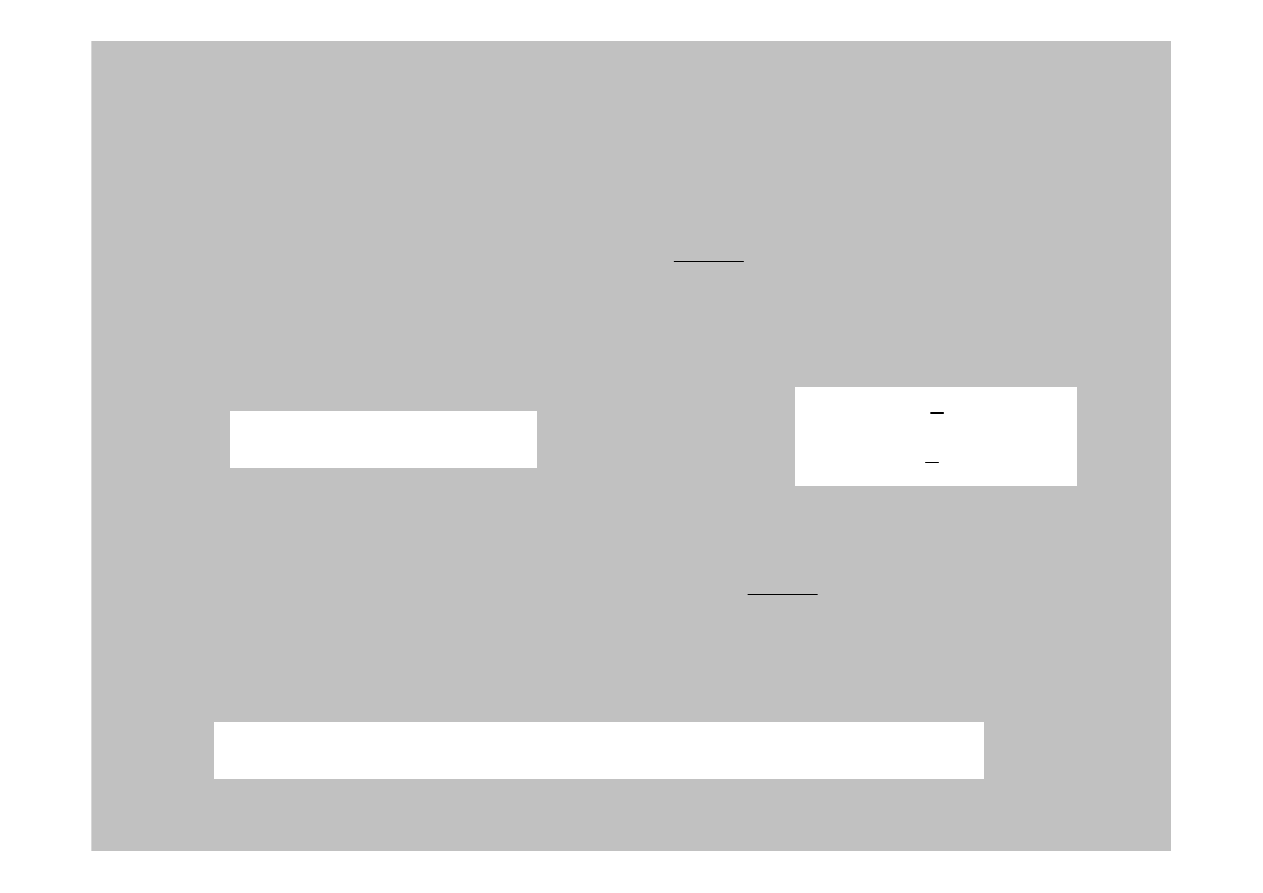
Dwa rozwi
ą
zania równa
ń
ró
ż
niczkowych
2
2
2
d
k
dx
ψ
ψ
=
Rozwa
ż
my równanie ró
ż
niczkowe:
Jako,
ż
e
k
2
jest dodatnie, rozwi
ą
zaniem równania jest:
( )
kx
kx
x
Ae
Be
ψ
−
=
+
ɶ
ɶ
2
2
2
d
k
dx
ψ
ψ
= −
Teraz rozwa
ż
my inne równanie ró
ż
niczkowe:
Poniewa
ż
stała -
k
2
jest ujemna, rozwi
ą
zaniem jest:
( )
albo
sin(
)
cos(
)
ikx
ikx
x
Ae
Be
A
kx
B
kx
ψ
−
=
+
+
ɶ
ɶ
k
jest rzeczywiste
1
2
1
2
cosh(
)
(
)
sinh(
)
(
)
kx
kx
kx
kx
kx
e
e
kx
e
e
−
−
=
+
=
−
Mo
ż
na te
ż
te
rozwi
ą
zania
zapisa
ć
jako:
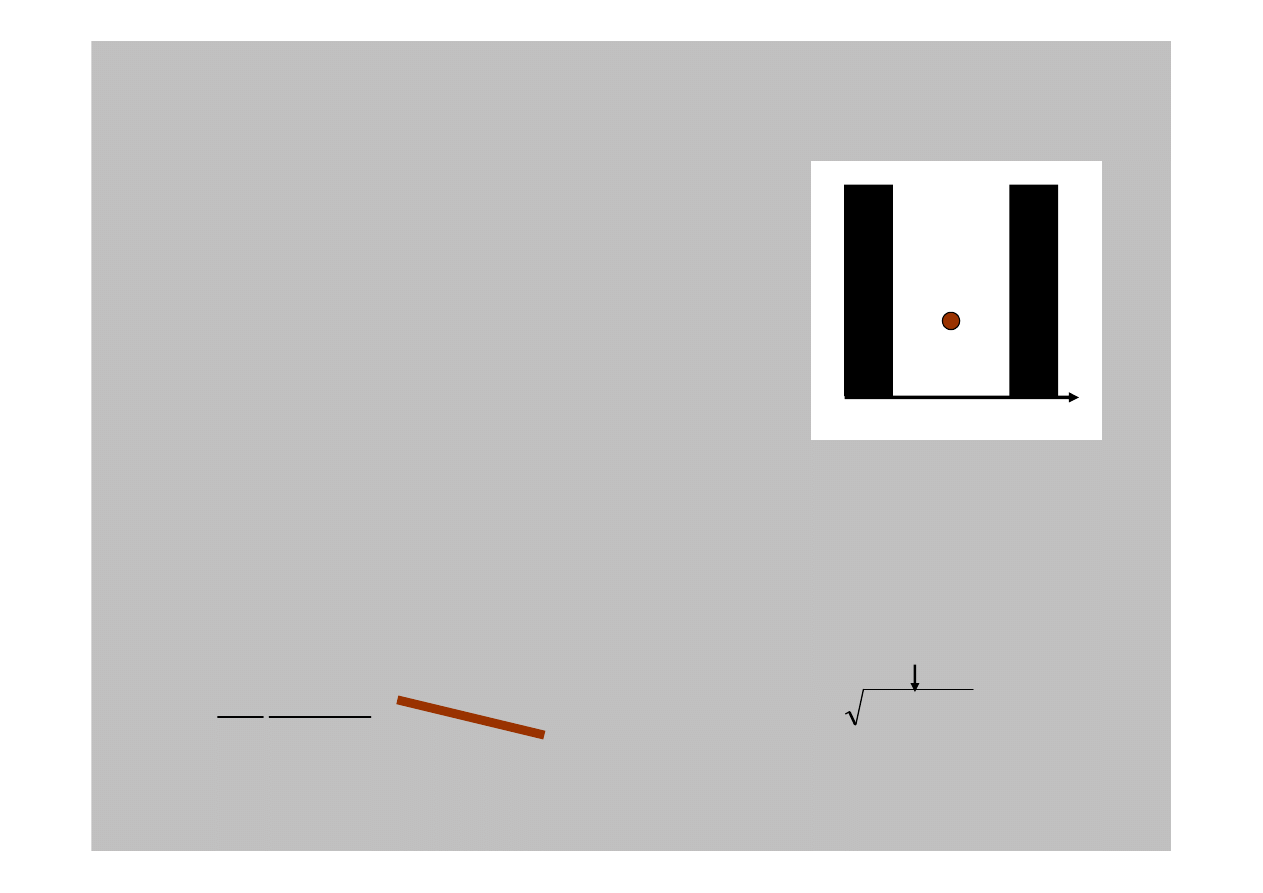
Najprostszym przykładem tego systemu jest
cz
ą
stka uwi
ę
zione w pudełku o niesko
ń
czenie
twardych
ś
cianach których cz
ą
stka nie mo
ż
e
przenikn
ąć
. Potencjał ten nazywany jest równie
ż
niesko
ń
czon
ą
prostok
ą
tn
ą
studni
ą
:
W obszarze gdzie potencjał jest niesko
ń
czony funkcja falowa musi by
ć
równa zeru.
W obszarze zerowego potencjału (wewn
ą
trz studni), bezczasowe
równanie Schrödingera mo
ż
na zapisa
ć
jako:
Ogólne rozwi
ą
zanie tego równania:
!
= "sin & + 'cos & *
ψ
ψ
ψ
2
2
2
2
2
k
mE
dx
d
−
=
−
=
ℏ
)
(
)
(
)
(
)
(
2
2
2
2
x
E
x
x
V
dx
x
d
m
ψ
ψ
ψ
=
+
−
ℏ
2
/
2
ℏ
mE
k
=
4.3: Niesko
ń
czona prostok
ą
tna studnia potencjału
x
0
L
gdzie
Energia jest tylko kinetyczna
i dlatego dodatnia
0,
( )
0
0
x
x
L
V x
x
L
∞
≤
≥
=
<
<
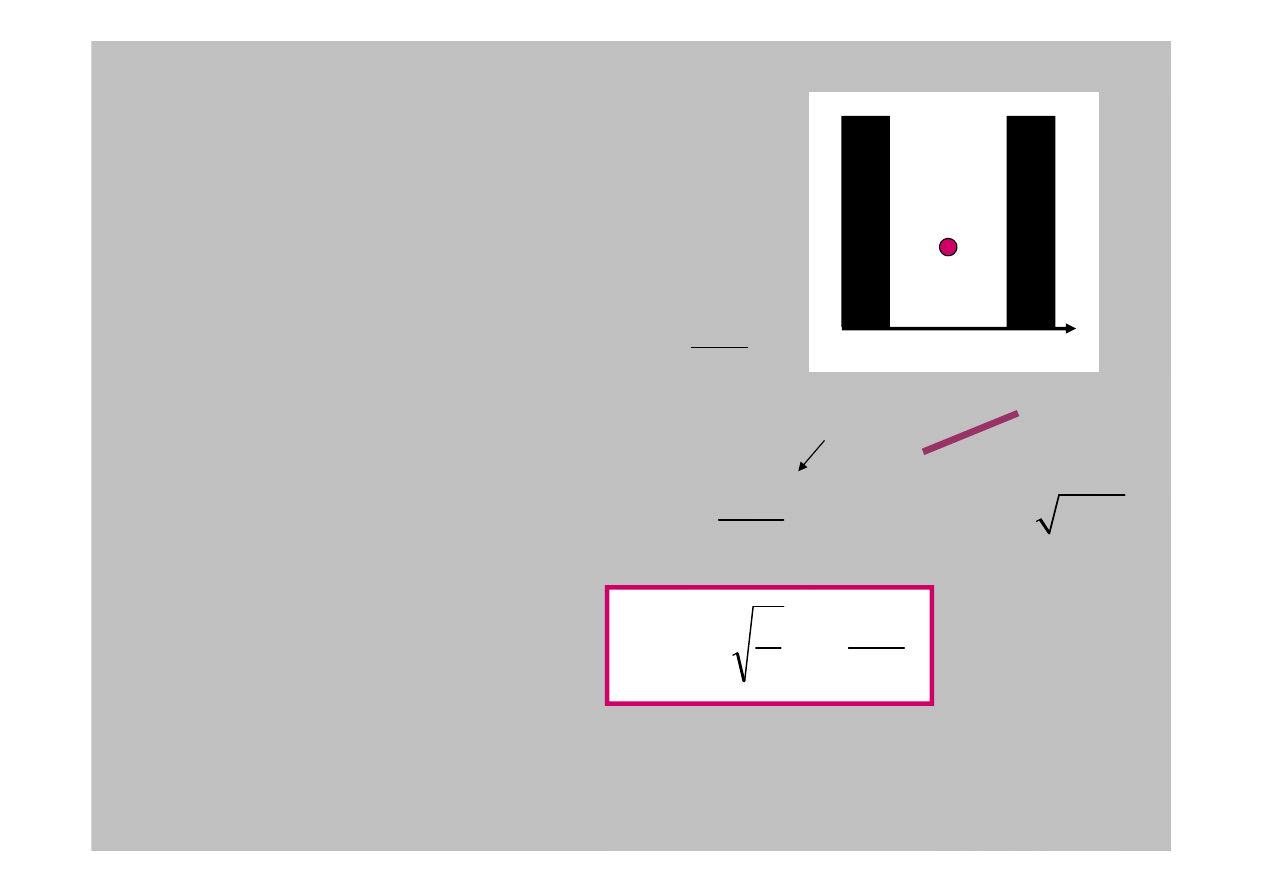
Warunki brzegowe potencjału stanowi
ą
,
ż
e
funkcja falowa musi by
ć
równa zeru w punktach
= 0
oraz
= +
. Aby tak mogło by
ć
dla musi
by
ć
,
ż
e
kL = n
π
dla całkowitych
,
.
Funkcja falowa jest wi
ę
c:
Normalizuj
ą
c j
ą
:
Otrzymamy znormalizowan
ą
funkcj
ę
falowa:
Taka sama funkcja opisuje drgaj
ą
c
ą
strun
ę
umocowan
ą
na obu
ko
ń
cach!
=
L
x
n
A
x
n
π
ψ
sin
)
(
Kwantowanie
⇒
x
0
L
2 /
A
L
=
⇒
½
−
½ cos(2n
π
x/L)
*
( )
( )
1
n
n
x
x dx
ψ
ψ
∞
−∞
=
∫
2
2
0
sin
1
L
n x
A
dx
L
π
=
∫
=
L
x
n
L
x
n
π
ψ
sin
2
)
(
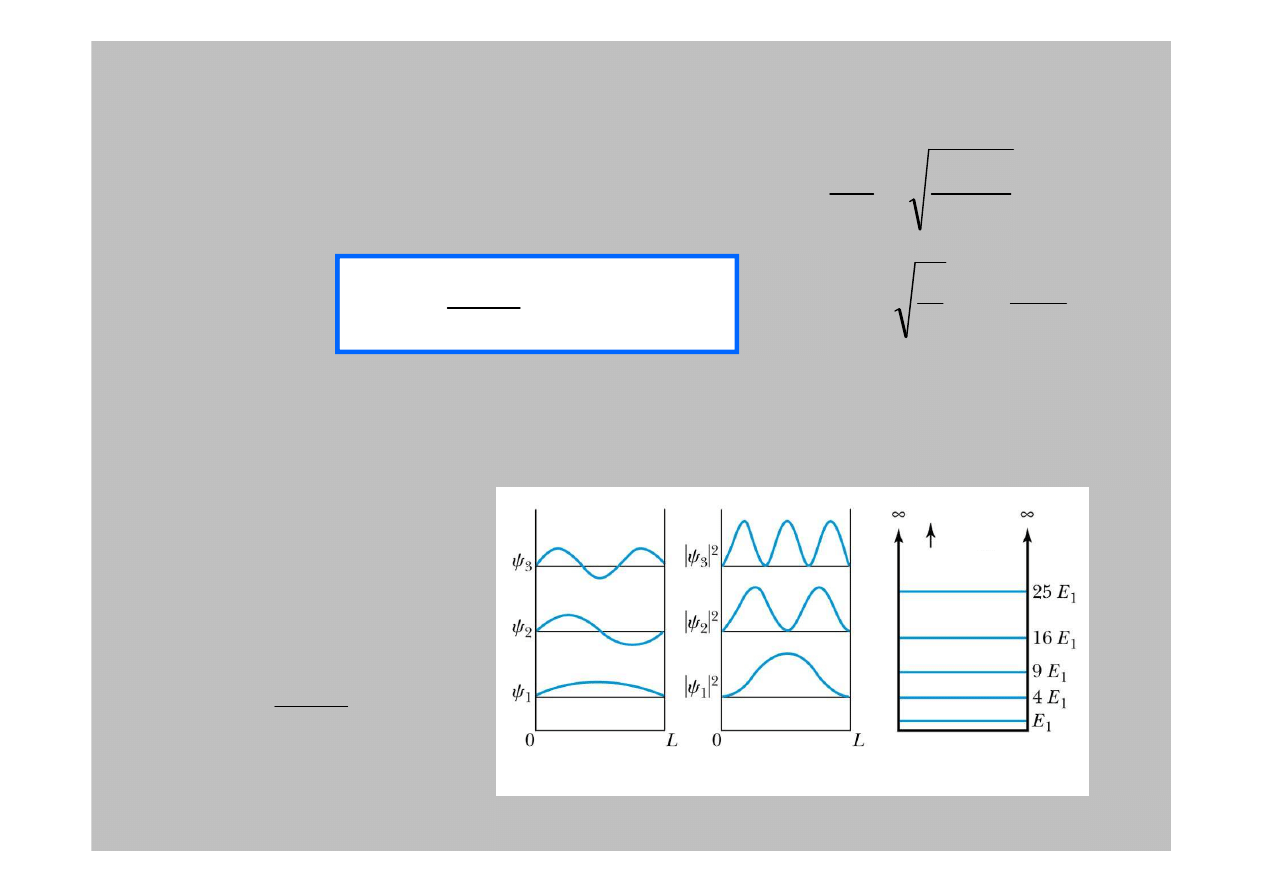
Skwantowana energia
Skwantowana liczba falowa wynosi wi
ę
c:
Co oznacza
energi
ę
:
Zauwa
ż
my,
ż
e energia zale
ż
y od liczby naturalnej
,
. St
ą
d energia jest
skwantowana i niezerowa.
Przypadek szczególny
gdy
n = 1
nazywamy
stanem podstawowym.
2
2
ℏ
n
n
mE
L
n
k
=
=
π
3,...)
2,
1,
(n
2
2
2
2
2
=
=
mL
n
E
n
ℏ
π
2
2
2
1
2mL
E
ℏ
π
=
Energia
Poło
ż
enie
=
L
x
n
L
x
n
π
ψ
sin
2
)
(
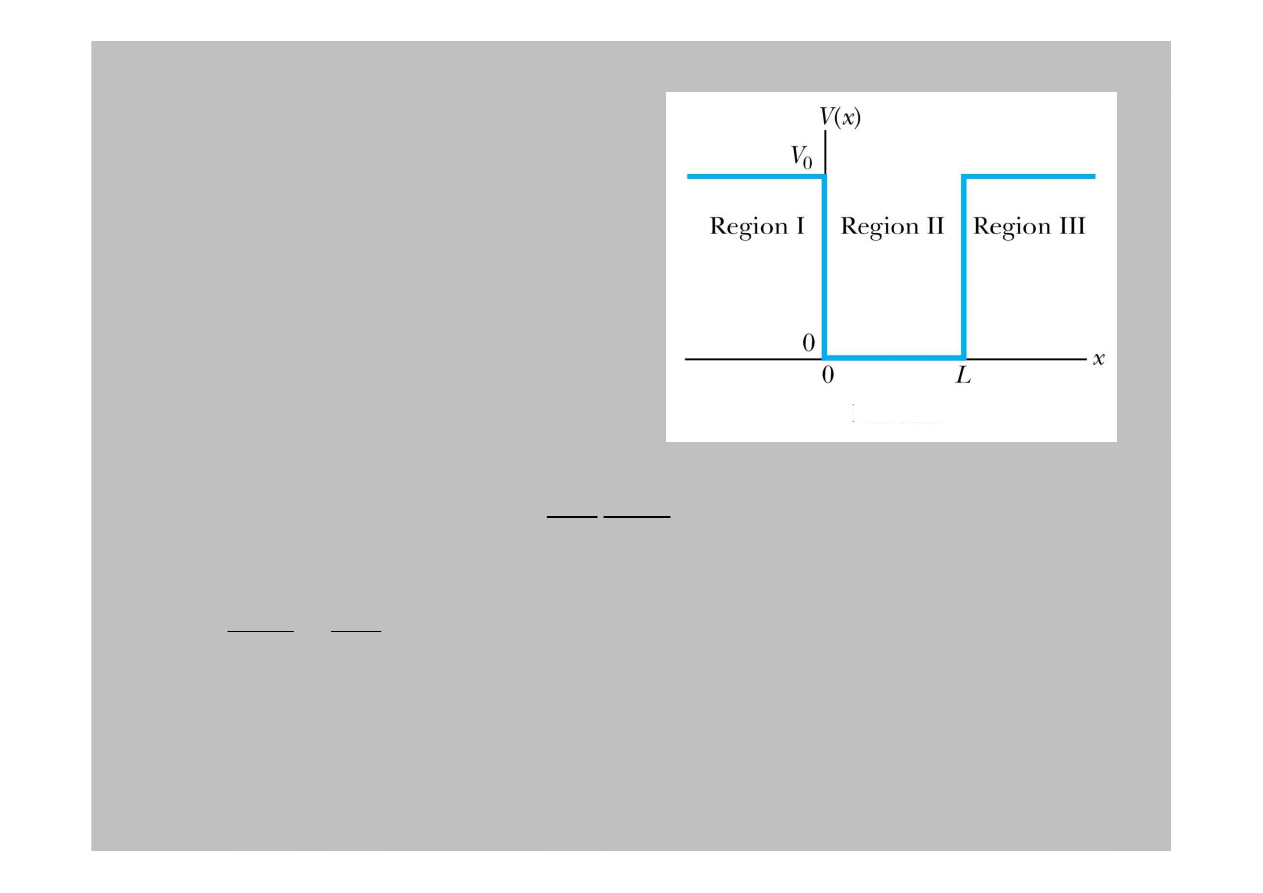
4.4: Sko
ń
czona
prostok
ą
tna studnia
potencjału
Sko
ń
czona prostok
ą
tna studnia
jest dana przez potencjał:
Bior
ą
c pod uwag
ę
,
ż
e funkcja
falowa musi by
ć
zero w (minus,
plus) niesko
ń
czono
ś
ci mamy:
Równanie Schrödingera
na zewn
ą
trz studni w
obszarach
I
i
III
jest:
gdzie:
2
2
0
2
2
d
V
E
m dx
ψ
ψ
ψ
−
+
=
ℏ
2
2
0
2
2
2
(
)
d
m
V
E
dx
ψ
ψ α ψ
⇒
=
−
=
ℏ
Załó
ż
my:
E < V
0
0
0
0
Region I
( )
0 0
Region II
Region III
V
x
V x
x
L
V
x
L
≤
=
<
<
≥
I
III
Region I,
0
( )
Region III,
( )
x
x
x
x
Ae
x
L
x
Be
α
α
ψ
ψ
−
<
=
>
=
2
0
2
/
)
(
2
ℏ
E
V
m
−
=
α
Poło
ż
enie
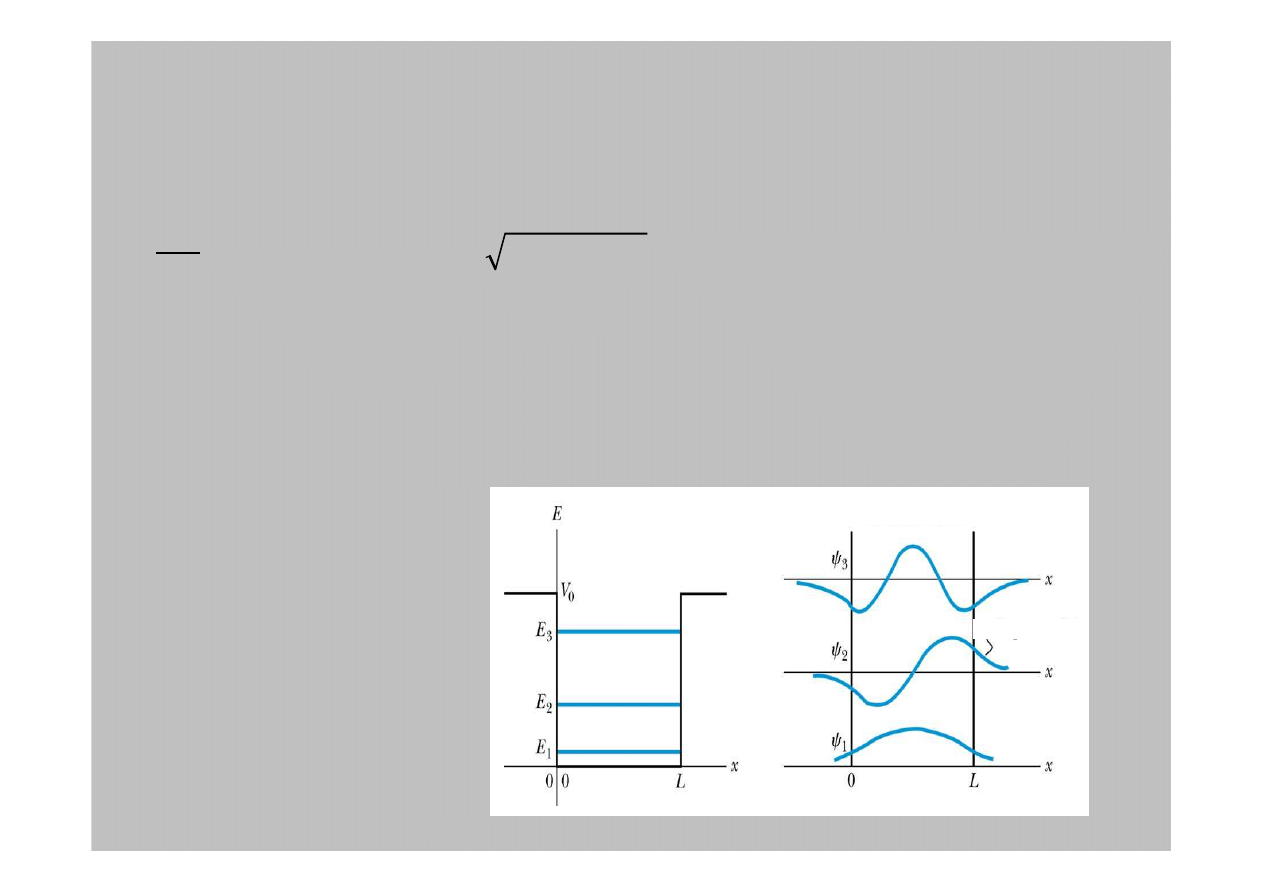
Wewn
ą
trz studni, gdzie potencjał
V
jest zero, równanie falowe jest
-
.
/
-
.
= −&
0
!
gdzie
& =
22 ) ℏ
0
⁄
(tak jak dla niesko
ń
czonej studni).
Rozwi
ą
zaniem tu jest:
Warunki brzegowe
wymagaj
ą
aby:
tzn. aby w miejscu
sklejenia obszarów
funkcja i jej pochodna
były ci
ą
głe
.
Zauwa
ż
my,
ż
e funkcja
falowa poza studni
ą
nie
jest równa zeru.
Rozwi
ą
zania dla sko
ń
czonej prostok
ą
tnej
studni potencjału
II
( )
sin
cos
Region II, 0
x
A
kx
B
kx
x
L
ψ
=
+
< <
I
II
II
III
dla
0
dla
x
x
L
ψ
ψ
ψ
ψ
=
=
=
=
oraz
I
II
II
III
'
' dla
0
'
'
x
x
L
ψ
ψ
ψ
ψ
=
=
=
=
oraz
dla
Funkcja falowa
E
n
e
rg
ia
Ekspotencjalna
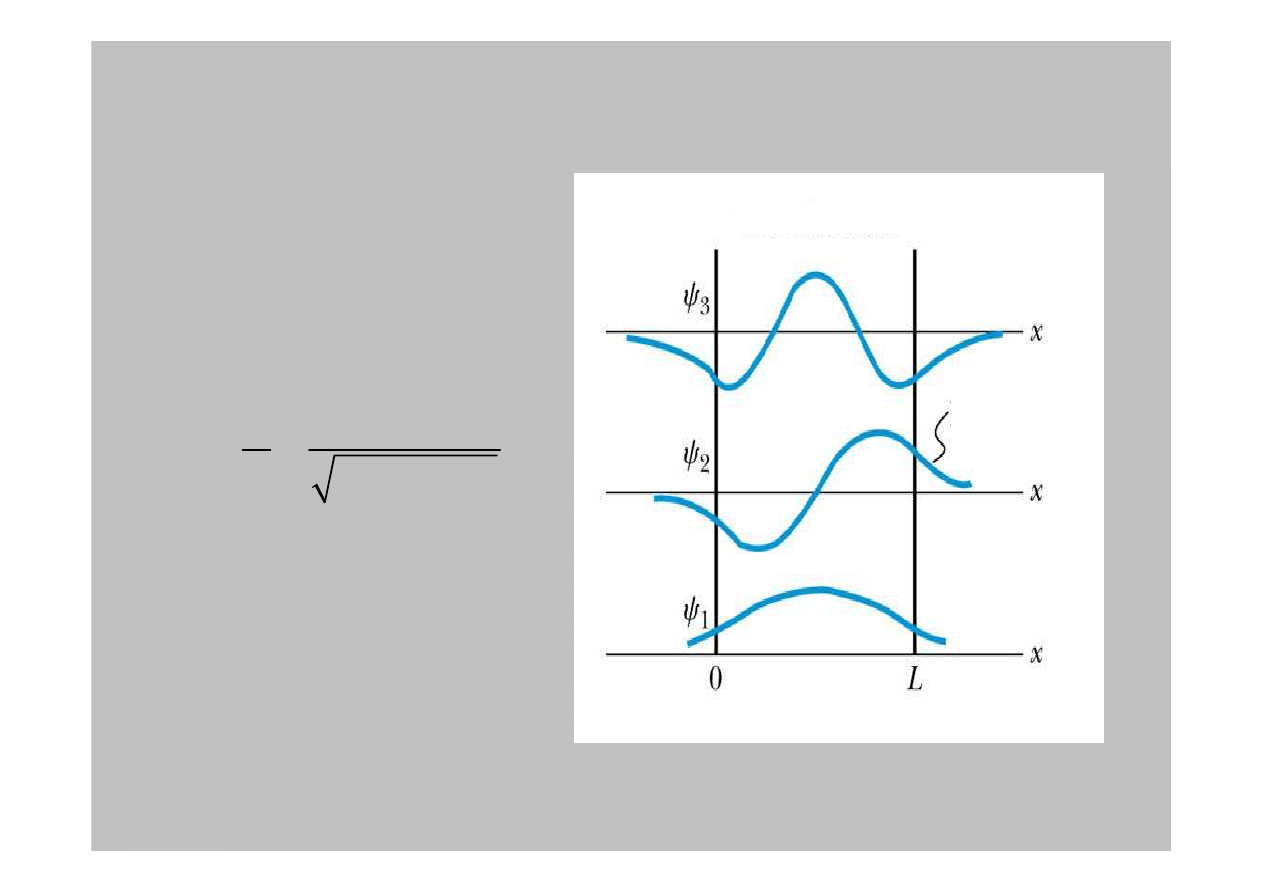
Cz
ą
stki wnikaj
ą
do
ś
ciany!
Gł
ę
boko
ść
wnikania to
odległo
ść
od
ś
cianki
studni powy
ż
ej której
prawdopodobie
ń
stwo
znalezienia cz
ą
stki
znacz
ą
co maleje. Jest to:
Gł
ę
boko
ść
penetracji
jest proporcjonalna do
stałej Plancka.
Uzyskane zjawisko jest
sprzeczne z fizyk
ą
klasyczn
ą
!
0
1
2 (
)
x
m V
E
δ
α
≈ =
−
ℏ
Funkcja falowa
Ekspotencjalna
I
III
Region I,
0
( )
Region III,
( )
x
x
x
x
Ae
x
L
x
Be
α
α
ψ
ψ
−
<
=
>
=
Funkcja falowa zale
ż
y od trzech wymiarów przestrzennych.
Tak jak dodaje si
ę
składowe wektora, tak aby zdefiniowa
ć
trójwymiarowy
operator p
ę
du dodajmy do siebie trzy przestrzenne składowe p
ę
du :
gdzie
4.5: Trójwymiarowa, niesko
ń
czona
studnia potencjału
Tak wi
ę
c trójwymiarowe równanie falowe Schrödingera ma posta
ć
:
2
2
2
2
ˆ
ˆ
ˆ
ˆ
x
y
z
p
p
p
p
=
+
+
x
i
p
x
∂
∂
−
=
ψ
ψ
ℏ
ˆ
y
i
p
y
∂
∂
−
=
ψ
ψ
ℏ
ˆ
z
i
p
z
∂
∂
−
=
ψ
ψ
ℏ
ˆ
ψ
ψ
ψ
ψ
ψ
E
V
z
y
x
m
=
+
∂
∂
+
∂
∂
+
∂
∂
−
2
2
2
2
2
2
2
2
ℏ
2
2
lub
2
V
E
m
ψ ψ
ψ
−
∇ +
=
ℏ
Trójwymiarowa, niesko
ń
czona
studnia potencjału
2
2
2
2
2
,
,
2
2
2
2
x
y
z
y
x
z
n n n
x
y
z
n
n
n
E
m
L
L
L
π
=
+
+
ℏ
Kiedy
=
0
łatwo znale
źć
rozwi
ą
zanie:
(
)
2
2
2
2
2
2
,
,
2
x
y
z
x
y
z
n n n
E
n
n
n
mL
π
=
+ +
ℏ
Kiedy wi
ę
c mamy cz
ą
stk
ę
w sze
ś
ciennym pudle:
( , , )
sin(
) sin(
) sin(
)
x
y
z
x y z
A
k x
k y
k z
ψ
=
/
x
x
x
k
n
L
π
=
gdzie:
/
y
y
y
k
n
L
π
=
/
z
z
z
k
n
L
π
=
oraz:
,
,
( , , )
sin(
/
) sin(
/
) sin(
/
)
x
y
z
n n n
x
x
y
y
z
z
x y z
A
n x L
n y L
n z L
ψ
π
π
π
=
4.6: Degeneracja
Widzimy,
ż
e dwie ró
ż
ne funkcje falowe mog
ą
mie
ć
t
ą
sam
ą
energi
ę
.
Trójwymiarowe równanie falowe Schrödingera wprowadza trzy
liczby kwantowe energii. Tej samej energii mog
ą
odpowiada
ć
ró
ż
ne
zestawy liczb kwantowych.
Je
ś
li istnieje wi
ę
cej ni
ż
jedna funkcja falowa dla danej energii, to taki
stan kwantowy nazywamy
zdegenerowanym
.
Degeneracja jest wynikiem szczególnych własno
ś
ci energii
potencjalnej, która opisuje system. Zaburzeniem energii potencjalnej
mo
ż
na usun
ąć
degeneracj
ę
.
we
ź
my 10, 4, 3 oraz 8, 6, 5:
ale:
10,4,3
8,6,5
E
E
=
1 0 , 4 , 3
8 , 6 , 5
ψ
ψ
≠
(
)
2
2
2
2
2
2
,
,
2
x
y
z
x
y
z
n n n
E
n
n
n
mL
π
=
+ +
ℏ
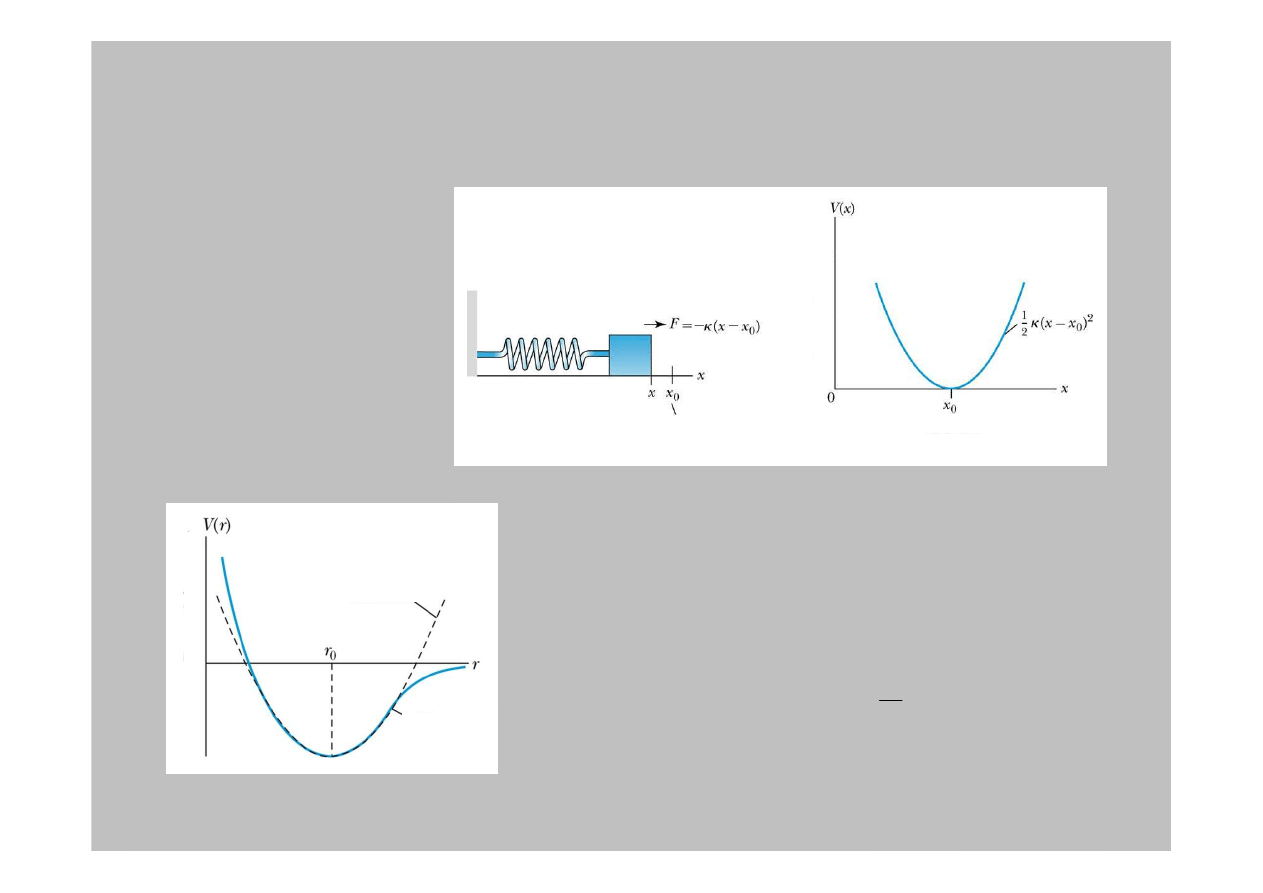
4.7: Prosty oscylator harmoniczny
Prosty oscylator
harmoniczny opisuje
wiele fizycznych
sytuacji od spr
ęż
yny,
poprzez cz
ą
steczki
dwuatomowe do sieci
krystalicznych
Rozwi
ń
my potencjał w szereg
Taylora:
...
)
(
2
1
)
(
)
(
2
0
2
0
1
0
+
−
+
−
+
=
x
x
V
x
x
V
V
x
V
Poło
ż
enie
równowagi
Poło
ż
enie
E
n
e
rg
ia
p
o
te
n
c
ja
ln
a
Prosty ruch
harmoniczny
Molekuła
dwuatomowa
E
n
e
rg
ia
p
o
te
n
c
ja
ln
a
Niech
4
0
=
56
ℏ
.
oraz
7 =
058
ℏ
.
, co daje:
We
ź
my pod uwag
ę
wyrazy
drugiego rz
ę
du rozwini
ę
cia
Taylora potencjału:
Prosty oscylator
harmoniczny
gdzie przyj
ę
li
ś
my
x
0
= 0
2
1
0
2
( )
(
)
V x
x
x
κ
=
−
Podstawiaj
ą
c to do
równania Schrödingera:
)
(
)
(
)
(
)
(
2
2
2
2
x
E
x
x
V
dx
x
d
m
ψ
ψ
ψ
=
+
−
ℏ
2
2
2
2
2
2
2
2
2
2
d
m
x
mE
m x
E
dx
ψ
κ
κ
ψ
ψ
= −
−
= −
+
ℏ
ℏ
ℏ
(
)
ψ
β
α
ψ
2
2
2
2
−
=
x
dx
d
E
n
e
rg
ia
p
o
te
n
cj
a
ln
a
Poło
ż
enie
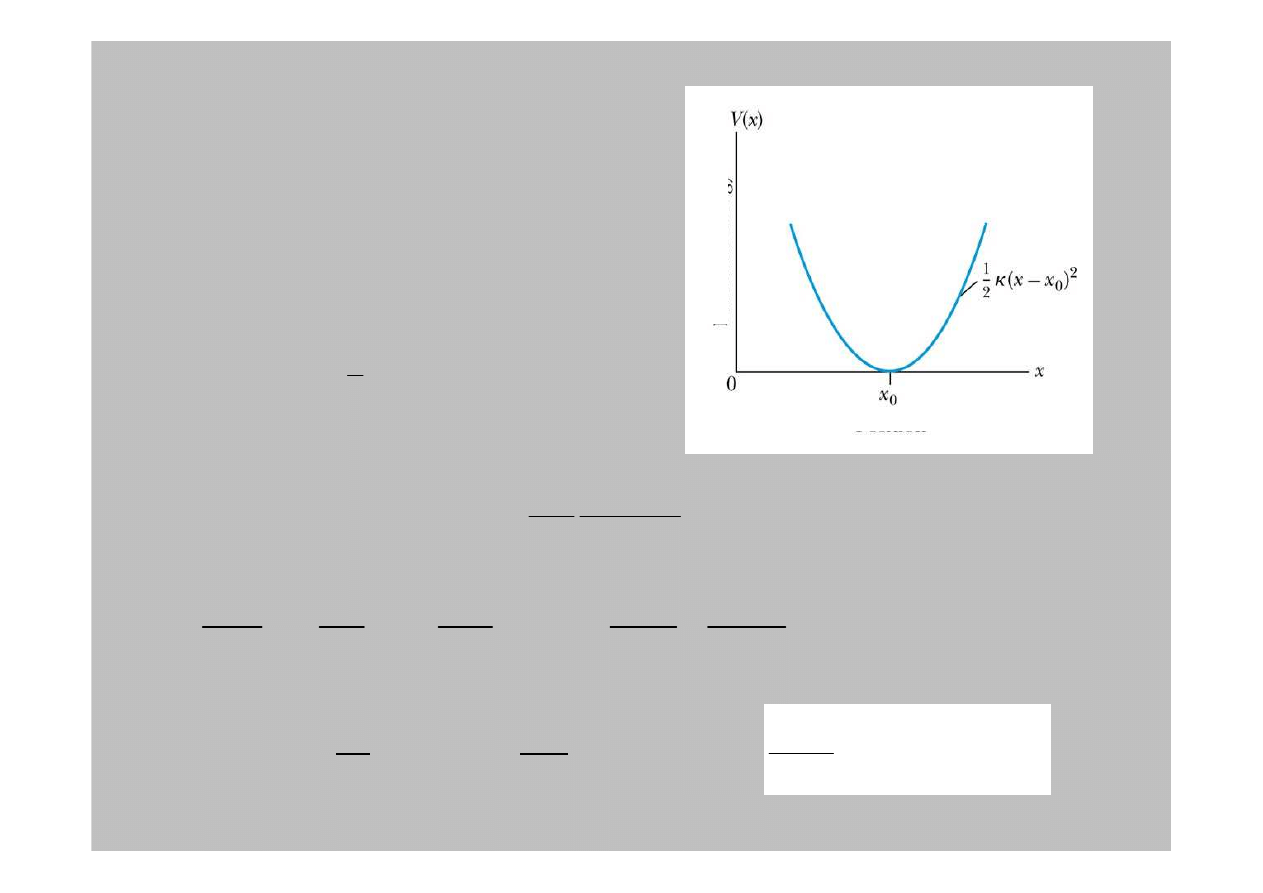
Jest to paraboliczna studnia potencjału
paraboliczna
studnia potencjału
Paraboliczna
studnia potencjału
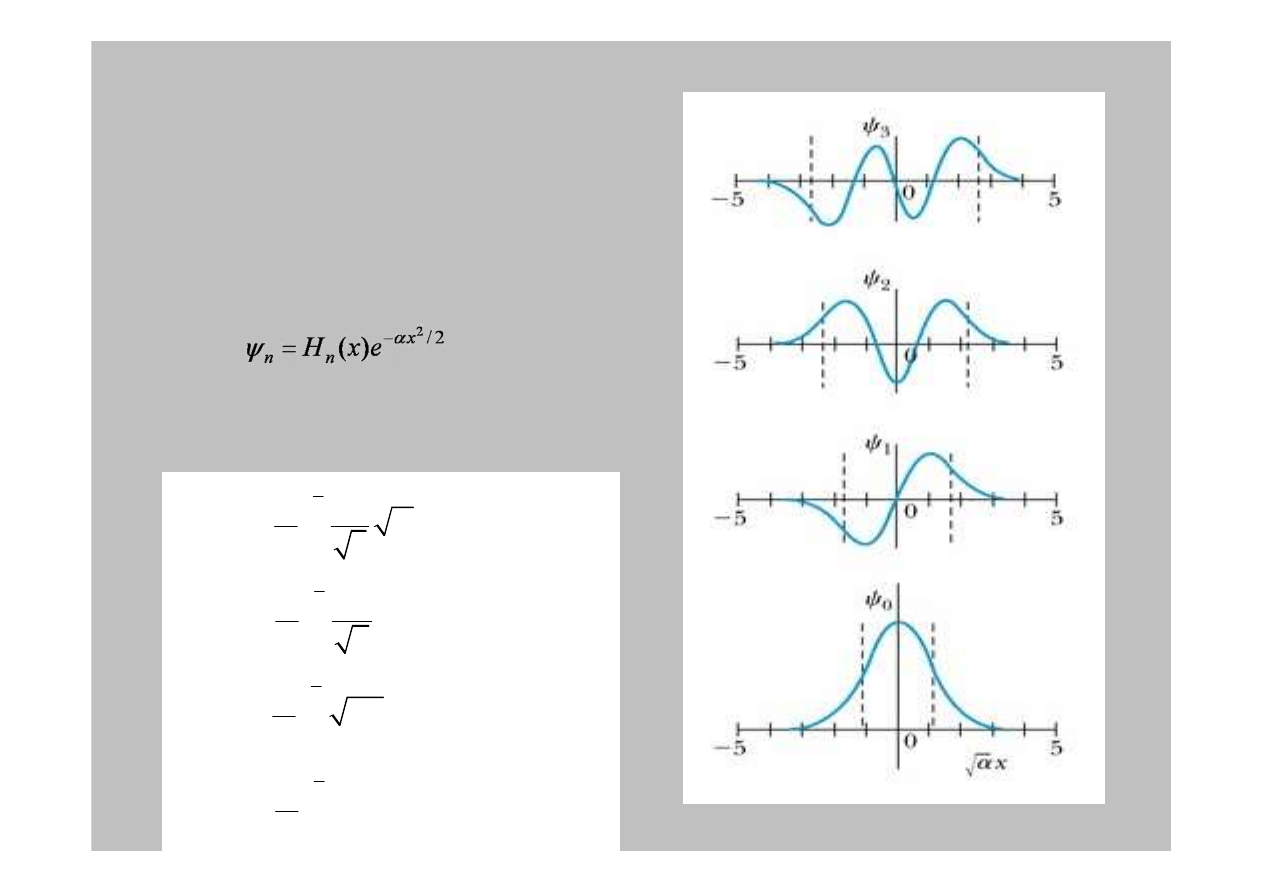
Funkcjami falowymi s
ą
gdzie
H
n
(x)
to
wielomiany Hermite’a
rz
ę
du
n
.
2
2
2
2
1
4
2
/ 2
3
1
4
2
/ 2
2
1
4
/ 2
1
1
4
/ 2
0
1
( )
(2
3)
3
1
( )
(2
1)
2
( )
2
( )
x
x
x
x
x
x
x
e
x
x
e
x
xe
x
e
α
α
α
α
α
ψ
α
α
π
α
ψ
α
π
α
ψ
α
π
α
ψ
π
−
−
−
−
=
−
=
−
=
=
Funkcje falowe
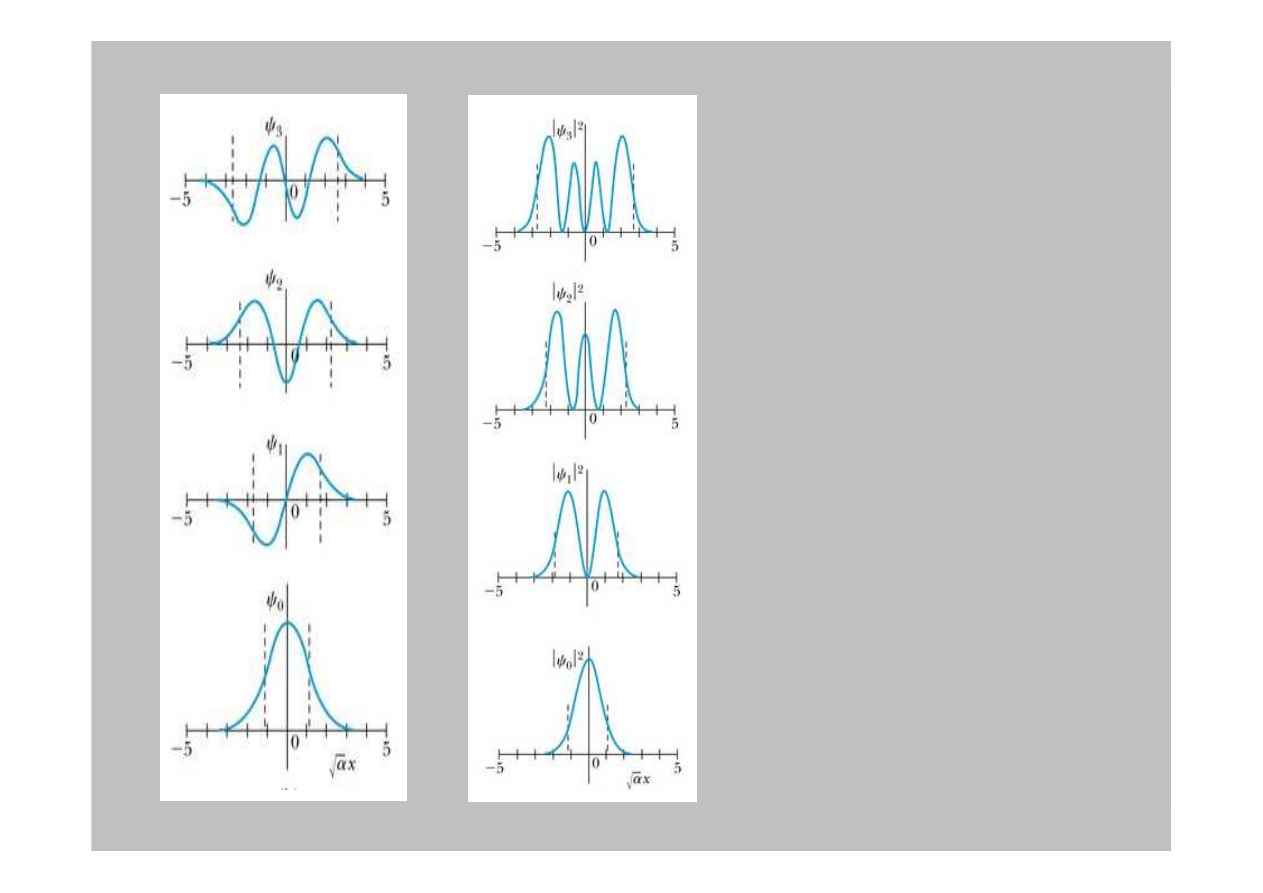
Paraboliczna
studnia potencjału
Klasycznie,
prawdopodobie
ń
stwo
znalezienia masy jest
najwi
ę
ksze na ko
ń
cach
studni a najmniejsze w
centrum.
Kwantowo najwi
ę
ksze
prawdopodobie
ń
stwo
znalezienia cz
ą
stki w
najni
ż
szym stanie energii
jest w centrum studni
potencjału.
⇔
⇔
⇔
⇔
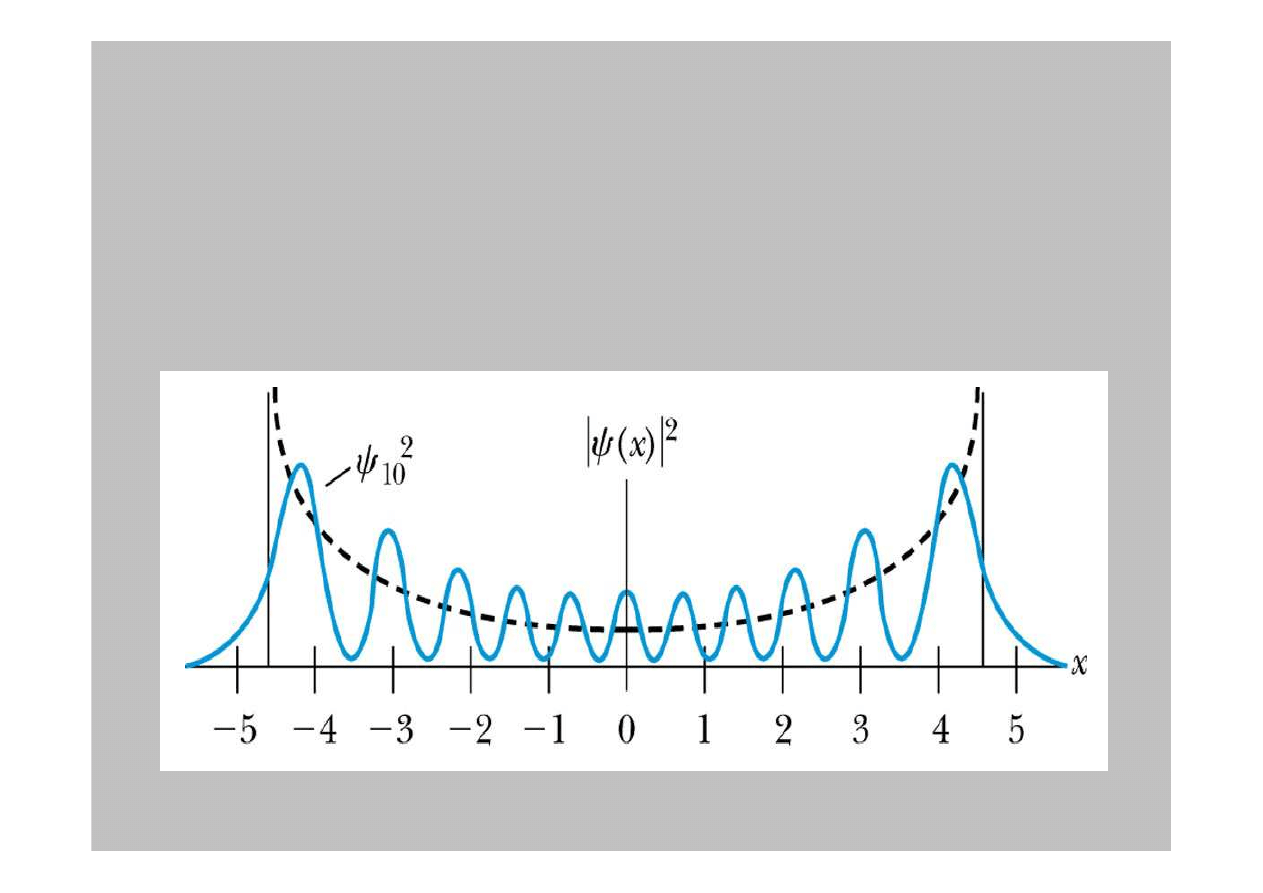
Dalsza analiza studni parabolicznej
Kiedy jednak liczby kwantowe rosn
ą
, rozwi
ą
zanie zbli
ż
a si
ę
do
wyniku klasycznego. Na tym przykładzie prostego oscylatora
harmonicznego widzimy
ż
e Zasada Korespondencji jest spełniona.
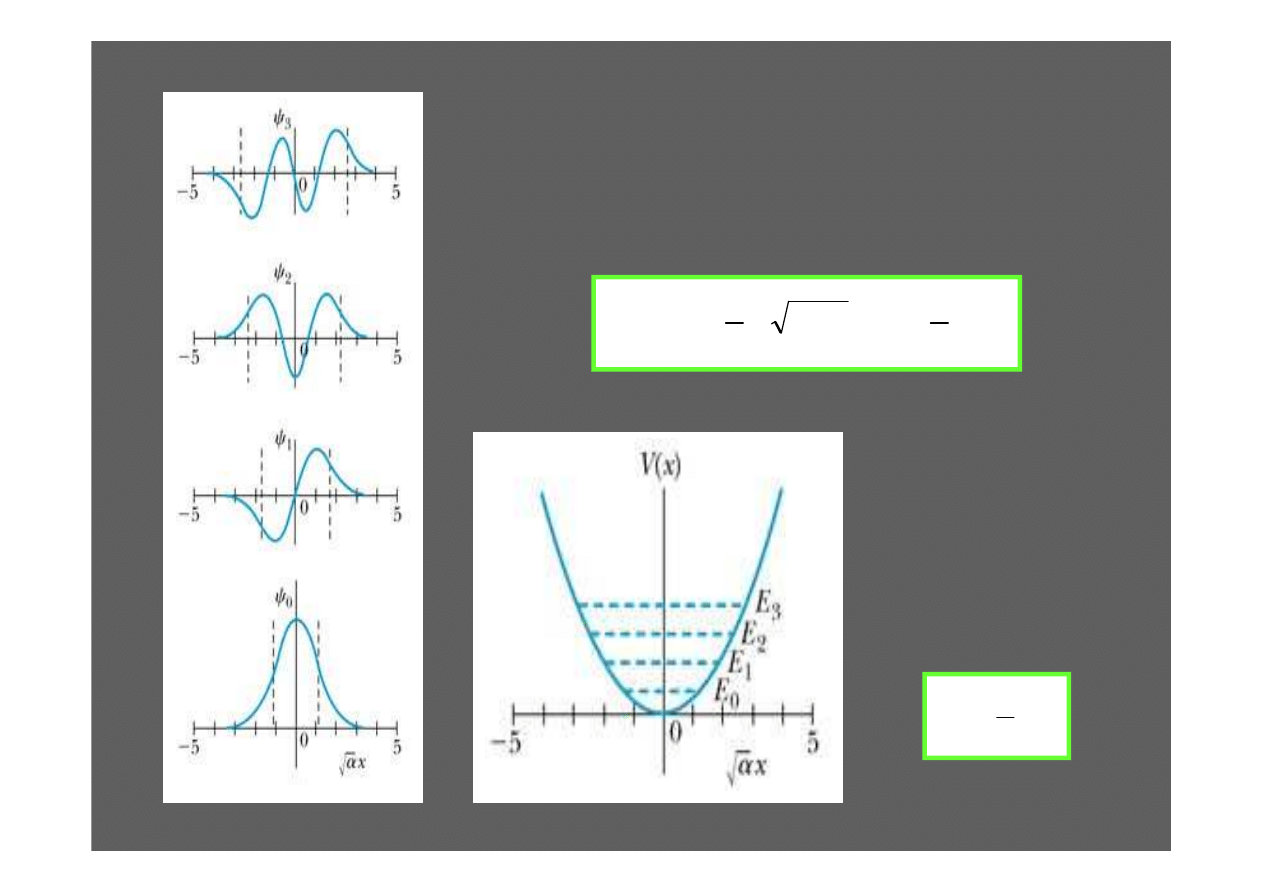
Paraboliczna studnia
potencjału
Poziomy energetyczne s
ą
dane
przez:
Energia stanu
podstawowego
jest nazywana
granic
ą
Heisenberga:
ω
κ
ℏ
ℏ
)
2
1
(
/
)
2
1
(
+
=
+
=
n
m
n
E
n
ω
ℏ
2
1
0
=
E
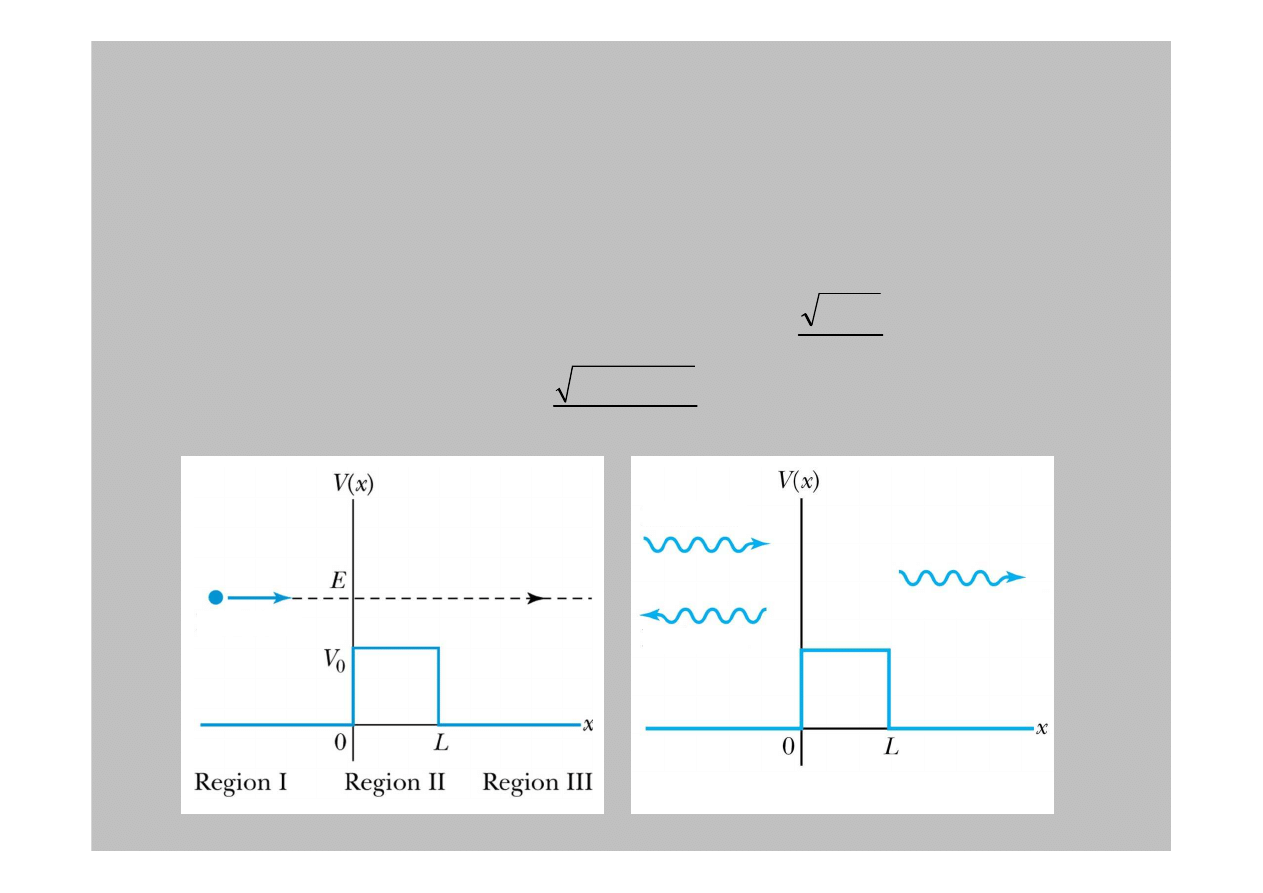
4.8: Bariery potencjału i tunelowanie
Rozwa
ż
my cz
ą
stk
ę
o energii E zbli
ż
aj
ą
c
ą
si
ę
do bariery potencjału o
wysoko
ś
ci
V
0
, poza któr
ą
potencjał wsz
ę
dzie jest zero.
Najpierw rozwa
ż
my przypadek kiedy energia cz
ą
stki jest wi
ę
ksza od
potencjalnej bariery.
W obszarach
I
i
III
, liczby falowe s
ą
:
W obszarze bariery za
ś
:
ℏ
mE
k
k
2
III
I
=
=
0
II
0
2 (
)
gdzie
m E V
k
V
V
−
=
=
ℏ
Padaj
ą
ca
Odbita
Przepuszczona
Cz
ą
stka
Odbicie i przej
ś
cie
Funkcja falowa b
ę
dzie składa
ć
si
ę
z fali padaj
ą
cej, fali odbitej oraz fali
która przeszła barier
ę
.
Potencjały oraz równania falowe Schrödingera dla trzech obszarów s
ą
:
Wszystkie
trzy stałe s
ą
ujemne tzn.:
Sinusy i kosinusy
we wszystkich
obszarach
Jako,
ż
e fala porusza si
ę
od lewej strony mo
ż
na zidentyfikowa
ć
rozwi
ą
zania:
Odpowiednie rozwi
ą
zania s
ą
:
2
I
I
2
2
2
II
0
II
0
2
2
2
III
III
2
2
2
R egion I (
0)
0
0
2
(
)
0
R egion II (0
)
2
0
R egion III (
)
0
d
m
x
V
E
dx
d
m
E
V
x
L
V
V
dx
d
m
E
x
L
V
dx
ψ
ψ
ψ
ψ
ψ
ψ
<
=
+
=
+
−
=
< <
=
+
=
>
=
ℏ
ℏ
ℏ
I
I
II
II
I
I
I
II
III
R egion I (
0)
R egion II (0
)
R egion III (
)
ik x
ik x
ik x
ik x
ik x
ik x
x
Ae
Be
x
L
C e
D e
x
L
Fe
G e
ψ
ψ
ψ
−
−
−
<
=
+
< <
=
+
>
=
+
I
I
I
I
II
III
(padająca)
(odbita)
(przepuszczona)
ik x
ik x
ik x
Ae
Be
Fe
ψ
ψ
ψ
−
=
=
=
Fala padaj
ą
ca
Fala odbita
Fala, która przeszła
2
2
2
d
k
dx
ψ
ψ
= −
Prawdopodobie
ń
stwa odbicia i przej
ś
cia
Prawdopodobie
ń
stwa odbicia cz
ą
stki
R
, oraz przej
ś
cia
T
s
ą
:
Poniewa
ż
cz
ą
stka musi si
ę
odbi
ć
lub przej
ść
:
R + T = 1
Po zastosowaniu warunków brzegowych
dla x = 0
, and
x = L
, uzyskujemy
prawdopodobie
ń
stwo przej
ś
cia:
Zauwa
ż
my,
ż
e prawdopodobie
ń
stwo przej
ś
cia mo
ż
e by
ć
nawet
równe 1.
2
*
I
2
*
I
2
*
III
2
*
I
(odbita)
(padająca)
(przekazana)
(padająca)
B B
R
A A
F F
T
A A
ψ
ψ
ψ
ψ
=
=
=
=
1
0
2
2
0
)
(
4
)
(
sin
1
−
−
+
=
V
E
E
L
k
V
T
II
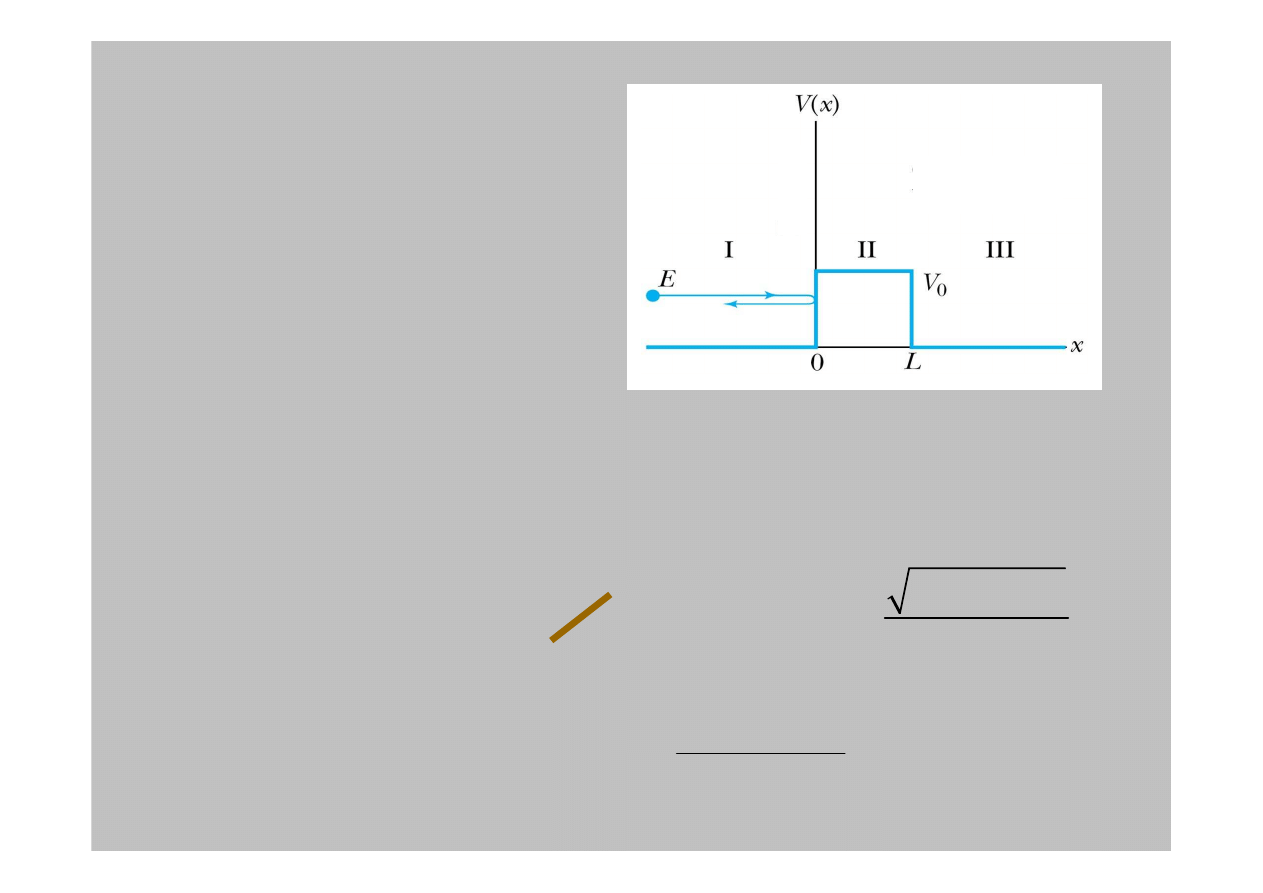
Wynik mechaniki kwantowej jest jedn
ą
z najbardziej
niezwykłych cech współczesnej fizyki.
Istnieje sko
ń
czone
prawdopodobie
ń
stwo,
ż
e cz
ą
stka przenika przez barier
ę
i pojawia
si
ę
po drugiej stronie!
Funkcja falowa w
obszarze
II
jest:
Współczynnik przej
ś
cia dla
tunelowania jest:
Tunelowanie
Teraz rozwa
ż
my sytuacj
ę
, w
której klasyczna cz
ą
stka nie
ma wystarczaj
ą
cej ilo
ś
ci
energii do pokonania bariery
potencjału,
E < V
0
.
0
II
2 (
)
gdzie
x
x
m V
E
Ce
De
κ
κ
ψ
κ
−
−
=
+
=
ℏ
1
0
2
2
0
)
(
4
)
(
sinh
1
−
−
+
=
E
V
E
L
V
T
κ
Zjawisko
klasyczne
E
n
e
rg
ia
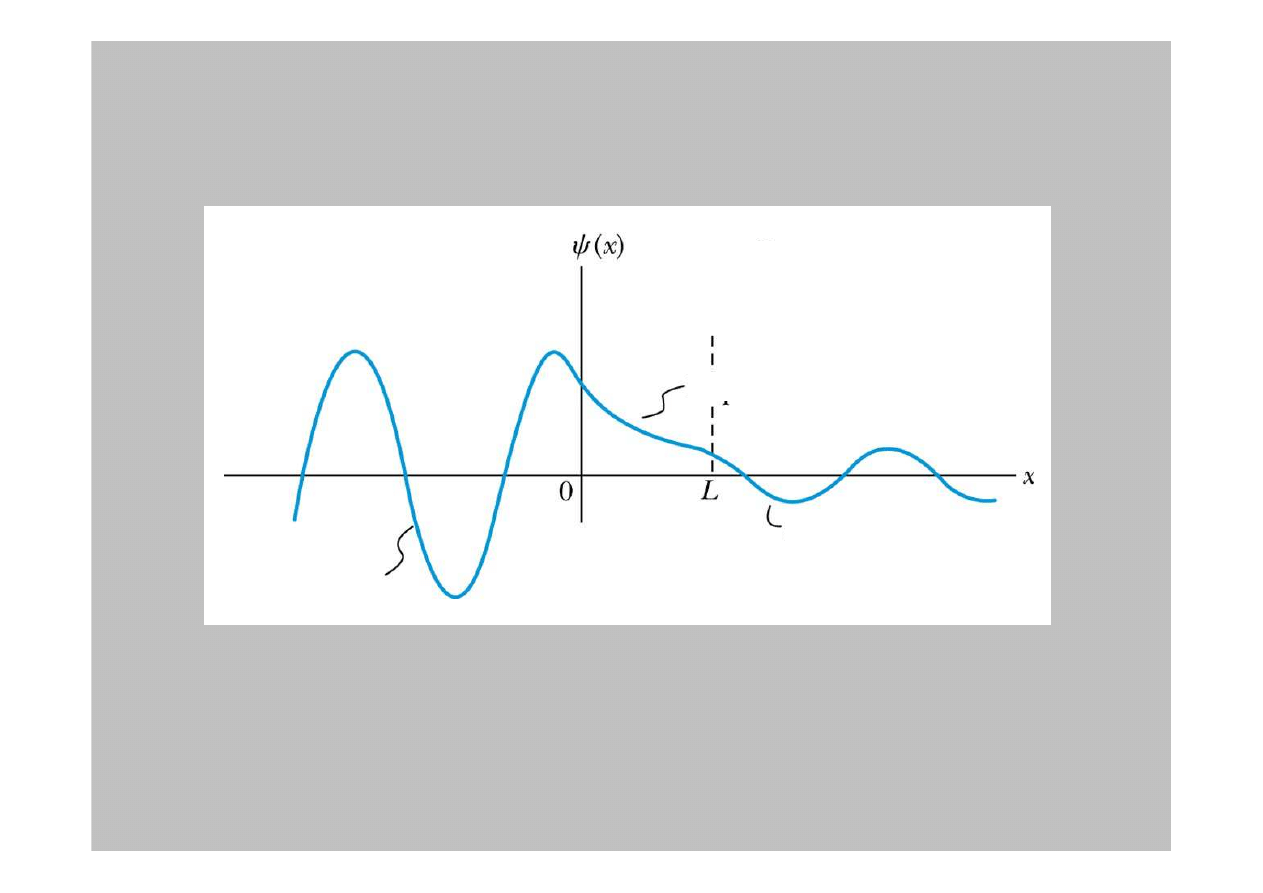
Tunnelownie funkcji falowej
To naruszenie fizyki klasycznej jest dozwolone przez zasad
ę
nieokre
ś
lono
ś
ci. Cz
ą
stka mo
ż
e narusza
ć
klasyczne zachowanie
o
∆
E
przez krótki czas,
∆
t
~
ħ /
∆
E.
Zjawisko
kwantowe
Sinusoidalnie
Sinusoidalnie
Ekspotencjalnie
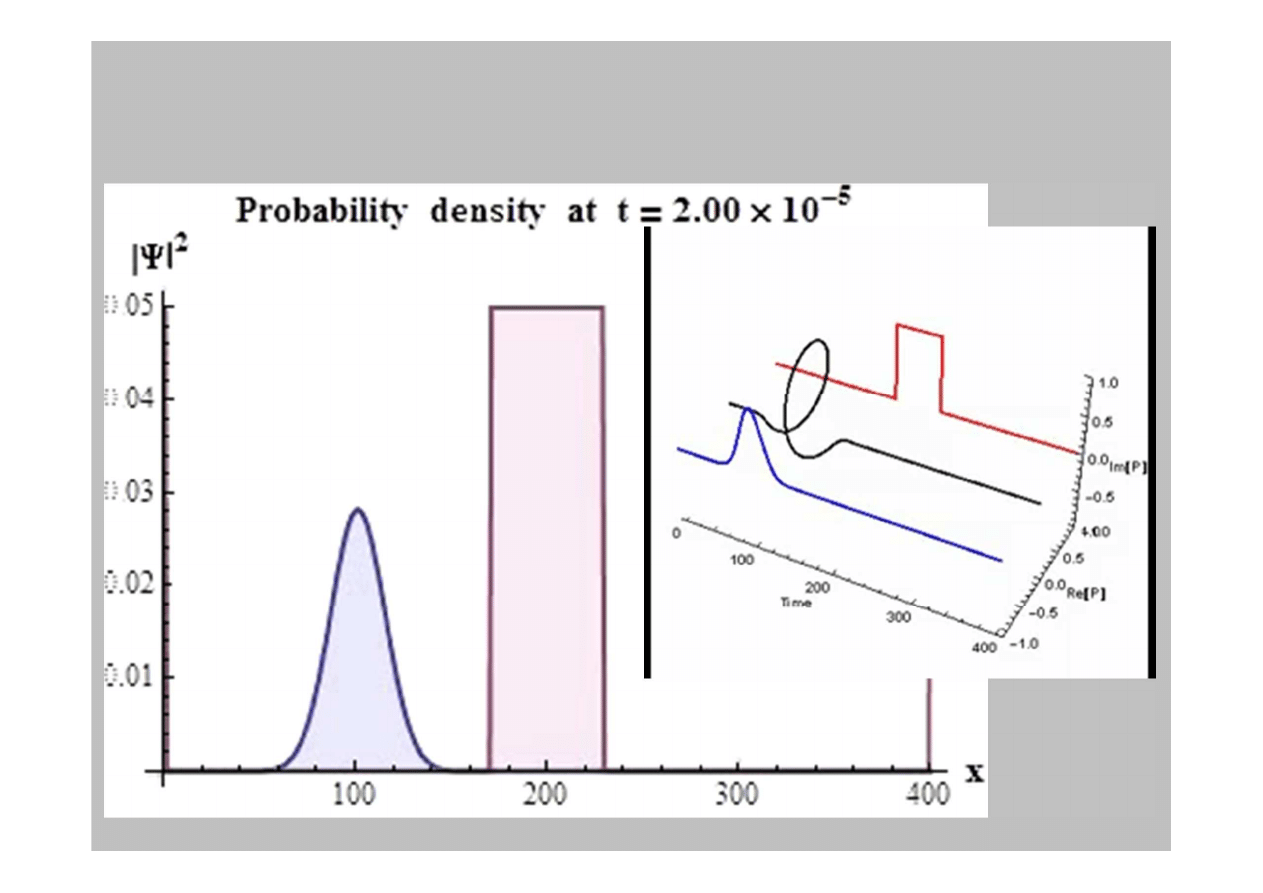
Ewolucja funkcji falowej i g
ę
sto
ś
ci
prawdopodobie
ń
stwa w czasie
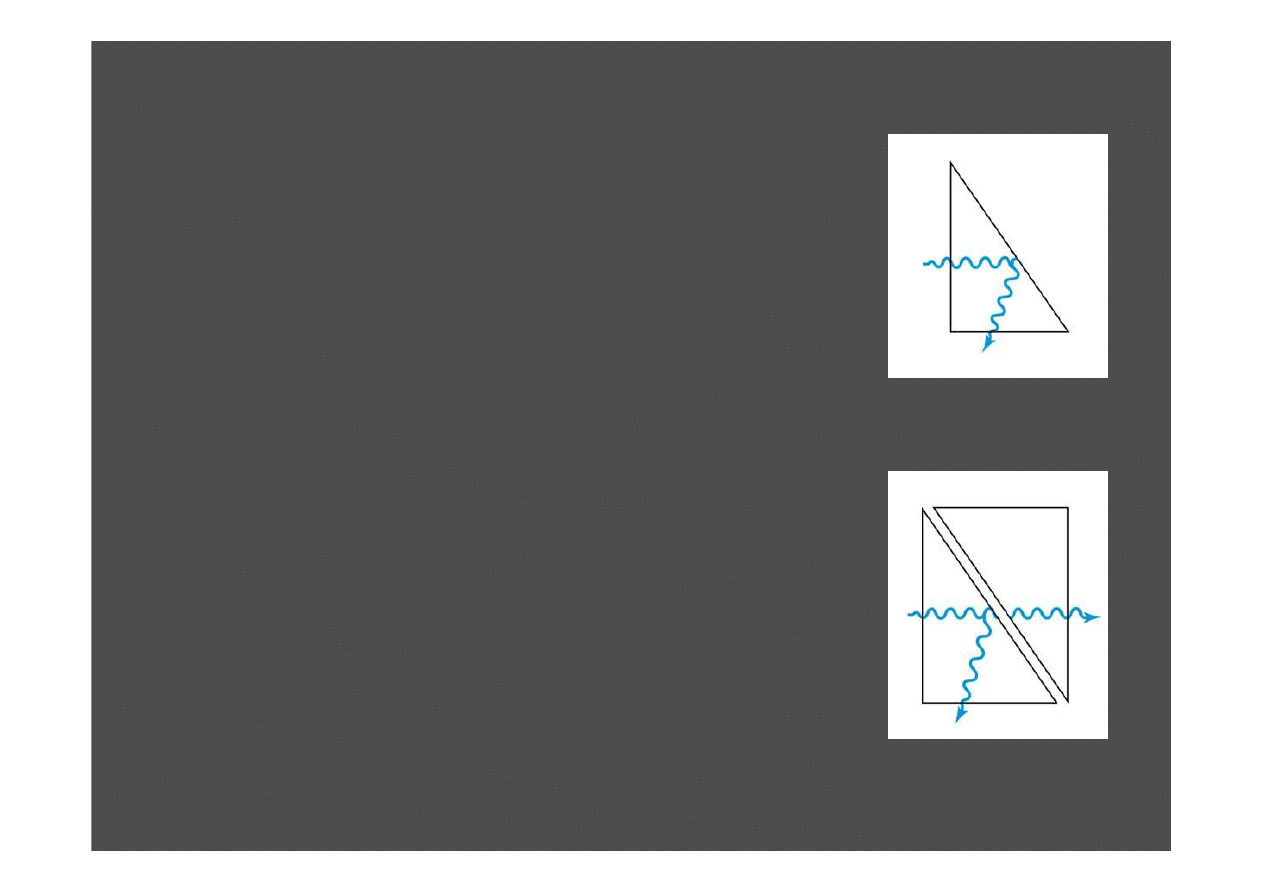
Analogia do optyki falowej
Je
ś
li
ś
wiatła przechodz
ą
ce przez pryzmat
szklany odbija si
ę
od wewn
ę
trznej powierzchni
pod k
ą
tem wi
ę
kszym od k
ą
ta krytycznego,
zachodzi całkowite wewn
ę
trzne odbicie.
Jednak pole elektromagnetyczne tu
ż
za
pryzmatem nie jest dokładnie zero. Jak
pokazuj
ą
eksperymenty, je
ś
li umie
ś
ci
ć
kolejny
pryzmat bardzo blisko pierwszego, to fala
elektromagnetyczna (
ś
wiatło) pojawia si
ę
w
równie
ż
w drugim pryzmacie. Sytuacja jest
analogiczna do opisanego wy
ż
ej tunelowania.
Efekt ten został zaobserwowany przez
Newtona i mo
ż
e by
ć
wykonany, za pomoc
ą
dwóch pryzmatów i lasera. Intensywno
ść
drugiej wi
ą
zki
ś
wiatła zmniejsza si
ę
ekspotencjalnie, kiedy odległo
ść
mi
ę
dzy
pryzmatami wzrasta.
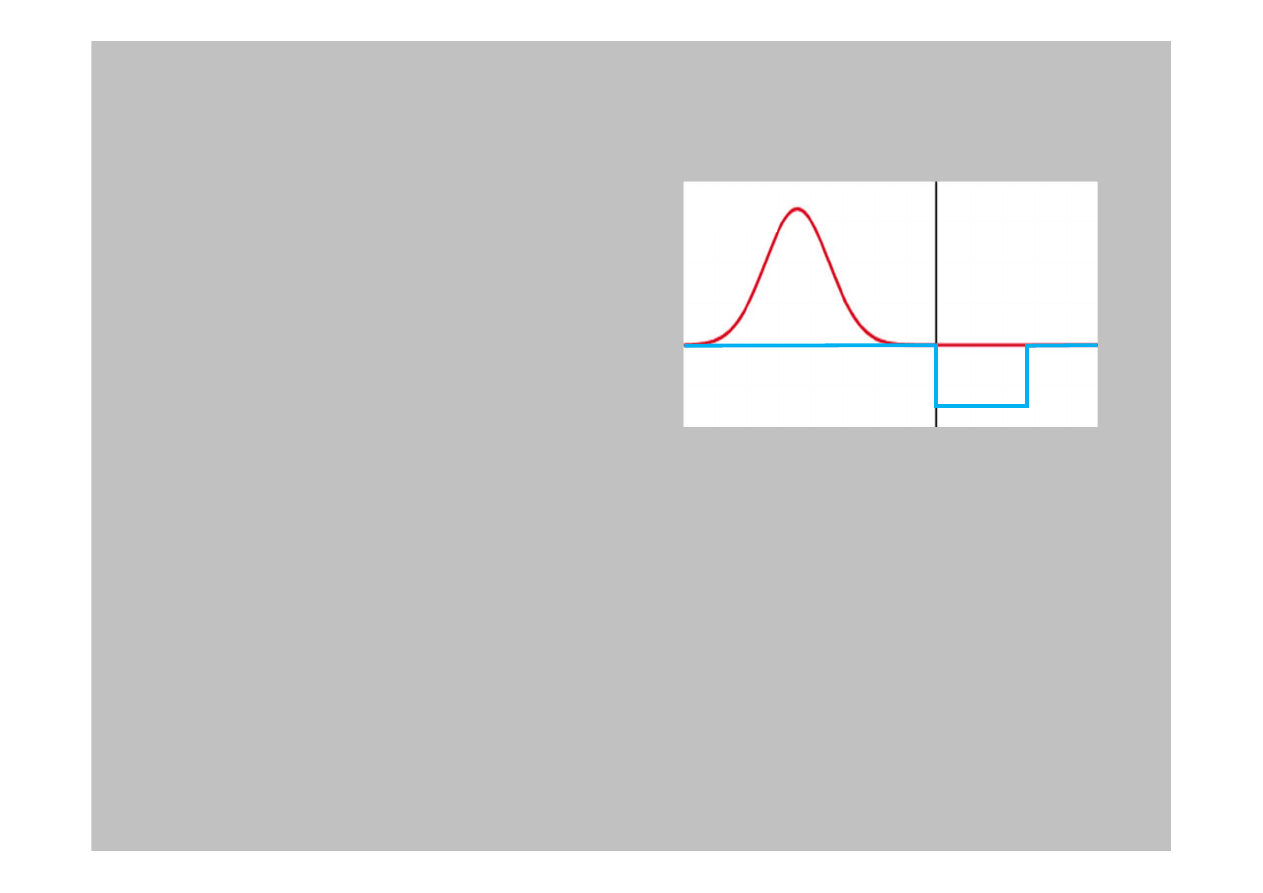
4.9: Studnia potencjału
9
:)
Rozwa
ż
my cz
ą
stk
ę
przechodz
ą
c
ą
przez studnie potencjału a nie barier
ę
.
Klasycznie, cz
ą
stka ta powinna
przyspieszy
ć
w rejonie studni gdy
ż
:
K = mv
2
/ 2 = E + V
0
Kwantowomechanicznie, fala ulegnie odbiciu i transmisji a jej długo
ść
wewn
ą
trz studni zmniejszy si
ę
.
Gdy szeroko
ść
studni potencjału jest dokładnie równa połowie lub
całkowitej wielokrotno
ś
ci długo
ś
ci fali, fala odbita b
ę
dzie w przeciwfazie lub
w fazie fali padaj
ą
cej odpowiednio, czego skutkiem b
ę
dzie wygaszenie lub
rezonans.
Wygaszenie b
ą
d
ź
wzmocnienie fal mo
ż
e spowodowa
ć
całkowite przej
ś
cie
; =
0, = = 1)
lub całkowite odbicie
; = 1, = =
0
. Je
ś
li, na przykład, na
prawym brzegu studni
= +
fala biegn
ą
ca w prawo jest w przeciwfazie
do fali odbitej, efektem b
ę
dzie zerowa amplituda (brak cz
ą
stki) wewn
ą
trz
studni.
= 0
= −
?
0
+
Cz
ą
stka o
energii E
Przykładowe rozwi
ą
zania równania falowego
Schrödingera dla jednowymiarowych pól potencjalnych
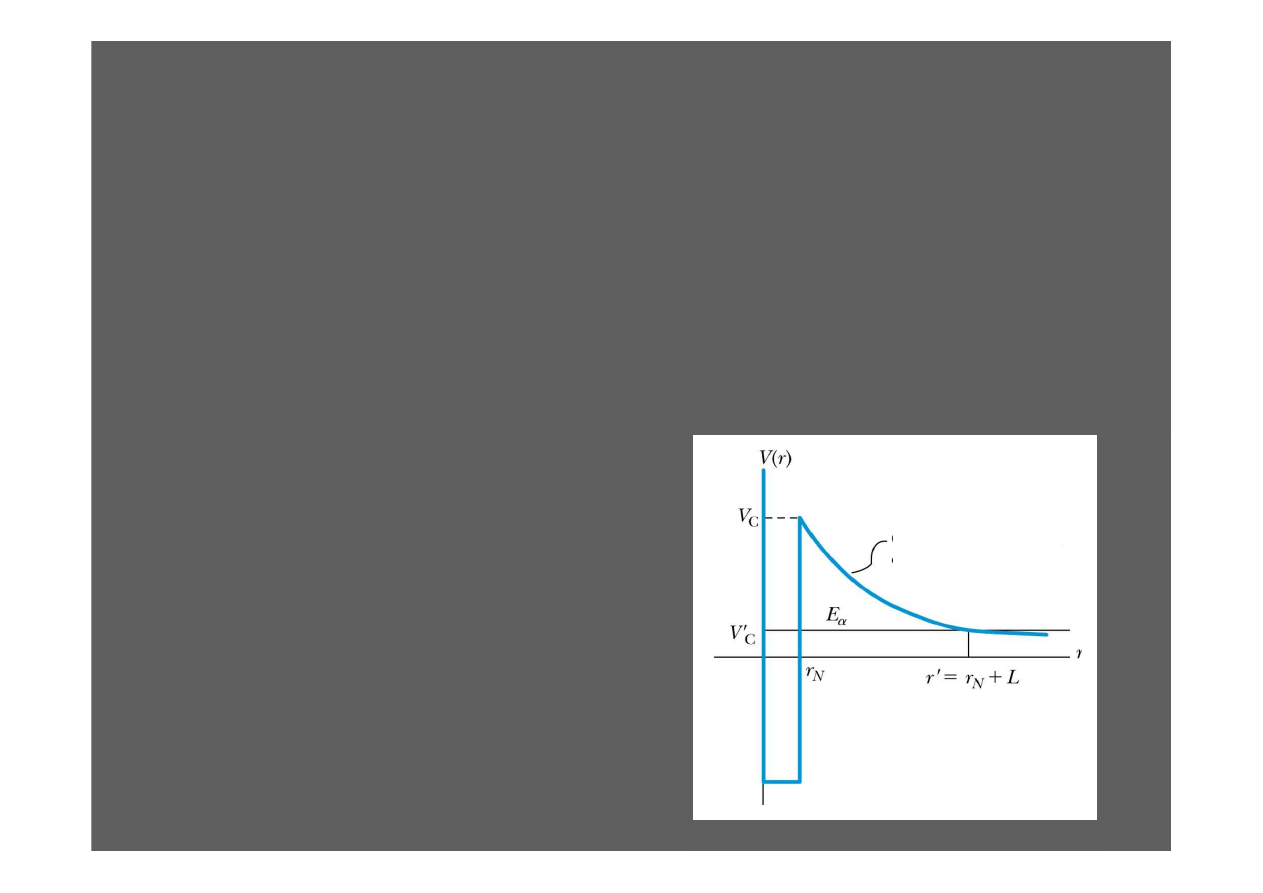
Rozpad Alfa
Zjawisko tunelowania wyja
ś
nia rozpad alfa, ci
ęż
kich j
ą
der
promieniotwórczych.
Wewn
ą
trz j
ą
dra, cz
ą
stka alfa czuje silne, krótkozasi
ę
gowe
przyci
ą
ganie j
ą
drowe, oraz Kulombowsk
ą
sił
ę
odpychaj
ą
c
ą
.
Oddziaływanie j
ą
drowe jest silniejsze wewn
ą
trz j
ą
dra a wypadkowy
potencjał mo
ż
e by
ć
opisany za pomoc
ą
studni potencjału.
Poza promieniem j
ą
dra dominuje
siła Kulomba.
Bariera potencjalna na granicy
j
ą
drowej jest kilka razy wi
ę
ksza
ni
ż
energia cz
ą
stki alfa.
W mechanice kwantowej, jednak
cz
ą
stka alfa mo
ż
e tunelowa
ć
przez
barier
ę
. Jest to obserwowane jako
zjawisko
rozpadu promieniotwórczego
..
Energia
potencjalna
Kulomba
Promie
ń
E
n
e
rg
ia