5.14. Ścisłe wyrównanie sieci kątowo-liniowej z wykorzystaniem programu
komputerowego
B. Przykłady
W prezentowanym przykładzie należy wyznaczyć współrzędne płaskie trzech
punktów (1201, 1202 i 1203) sieci kątowo-liniowej nawiązanej do trzech punktów (1001,
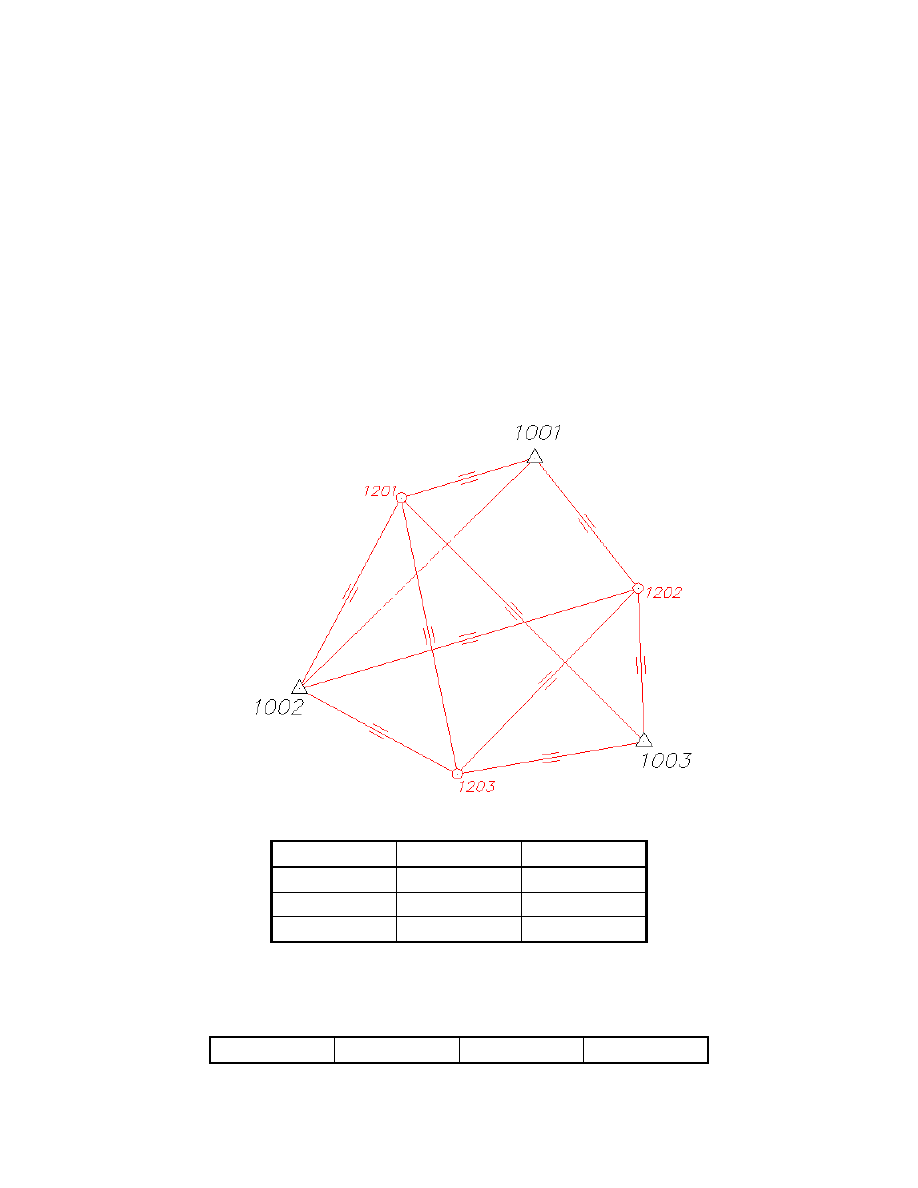
1002 i 1003) traktowanych jako bezbłędne (rys. 5.46). Dane są współrzędne punktów
nawiązania – tabela 5.33, zredukowane długości boków wraz z błędami (liczonymi z
równania dalmierza) – tabela 5.34 oraz kierunki i średnie błędy – tabela 5.35. Błąd dla
kierunków przyjęto jako wartość średnią z błędów wyliczonych w wyrównaniu
stacyjnym.
Rys. 5.46. Szkic sieci kątowo-liniowej
Nr
X [m]
Y [m]
1001
5406466.10
4553637.15
1002
5405901.58
4553061.64
1003
5405772.45
4553903.80
Tab. 5.33. Współrzędne punktów nawiązania
Początek
Koniec
Długość d [m]
Błąd m
d
[m]
1
1001
1202
406.240
0.007
1001
1201
341.142
0.006
1002
1201
529.291
0.008
1002
1202
862.903
0.009
1002
1203
438.089
0.007
1003
1201
841.542
0.009
1003
1202
375.061
0.007
1003
1203
463.401
0.007
1201
1203
689.120
0.008
1202
1203
633.167
0.008
Tab. 5.34. Zredukowane długości boków wraz z błędami
Stanowisko
Cel
Kierunek K [
g
]
Błąd m
k
[
g
]
1202
0.0000
0.0009
1002
93.1513
0.0009
1001
1201
124.1424
0.0009
1201
0.0000
0.0009
1001
19.4999
0.0009
1202
50.5108
0.0009
1002
1203
100.3901
0.0009
1203
0.0000
0.0009
1201
61.0418
0.0009
1003
1202
108.3541
0.0009
1001
0.0000
0.0009
1003
68.5445
0.0009
1203
105.6528
0.0009
1201
1002
149.5110
0.0009
1003
0.0000
0.0009
1203
51.6846
0.0009
1002
84.1601
0.0009
1202
1001
159.9983
0.0009
1002
0.0000
0.0009
1201
55.7544
0.0009
1202
117.6451
0.0009
1203
1003
157.6046
0.0009
Tab. 5.35. Kierunki wraz z błędami
2
Realizacja przykładu
Prace rozpoczynamy od wprowadzenia do bazy danych współrzędnych punktów
nawiązania (rys. 5.47).
Rys. 5.47. Współrzędne punktów nawiązania wprowadzone do bazy
Następnie wybieramy z menu Wyrównanie – Kierunki i wprowadzamy do
poszczególnych okien wartości kierunków wraz z błędami dla wszystkich stanowisk.
Jeżeli pomierzone kierunki zostały w wyniku transmisji zaimportowane z instrumentu do
programu WinKalk i znajdują się w menu Rejestrator, wówczas możemy przenieść je
bezpośrednio do wyrównania poprzez funkcję
. W menu
Edycja Kierunków mamy możliwość wydrukowania raportu z wprowadzonych
kierunków, założenia nowego stanowiska oraz przejścia pomiędzy istniejącymi
stanowiskami za pomocą przycisków
. Możemy także wybrać, czy
wprowadzamy w tym oknie tylko kierunki, czy także długości poszczególnych celowych
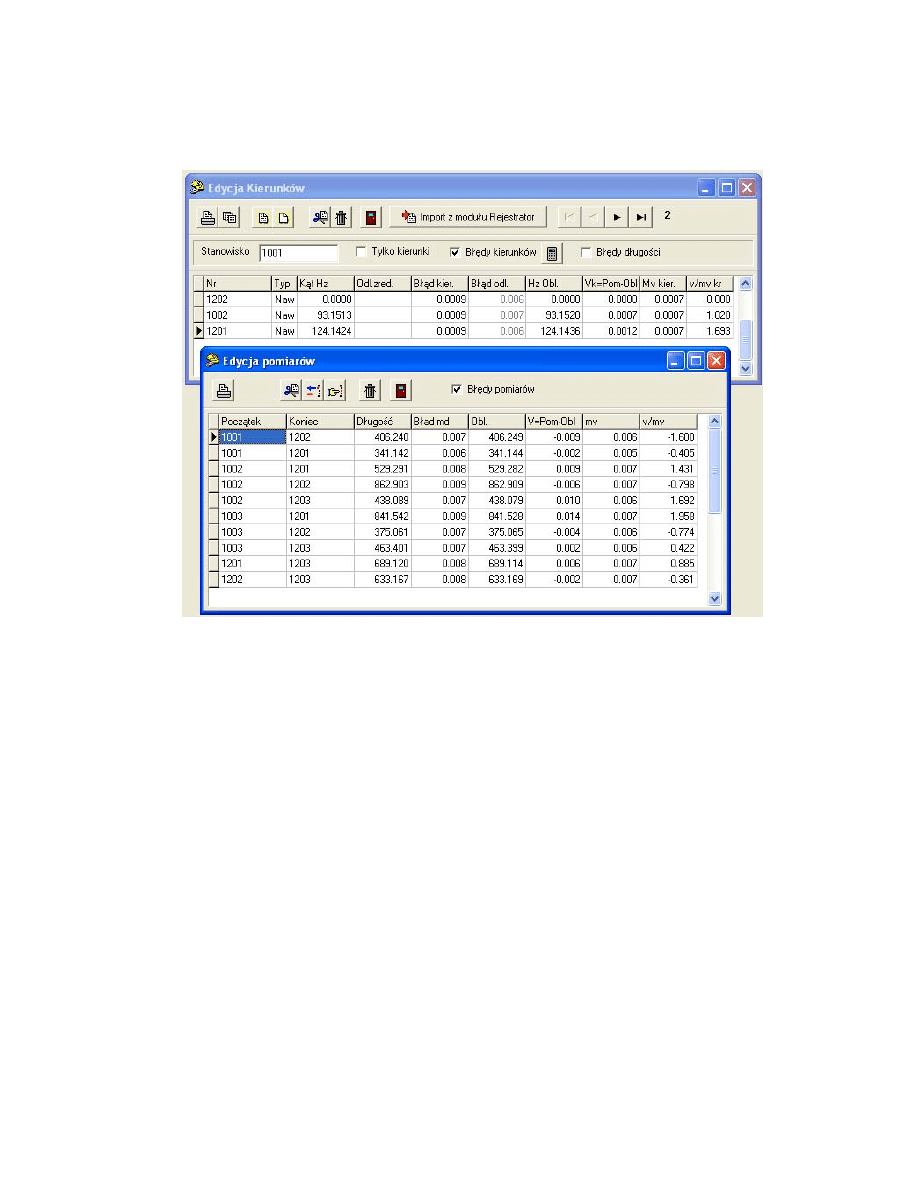
wraz z błędami. Na rysunku 5.48 zaprezentowano wygląd okna dialogowego Edycja
Kierunków wraz z wprowadzonymi danymi dla stanowiska 1002.
3
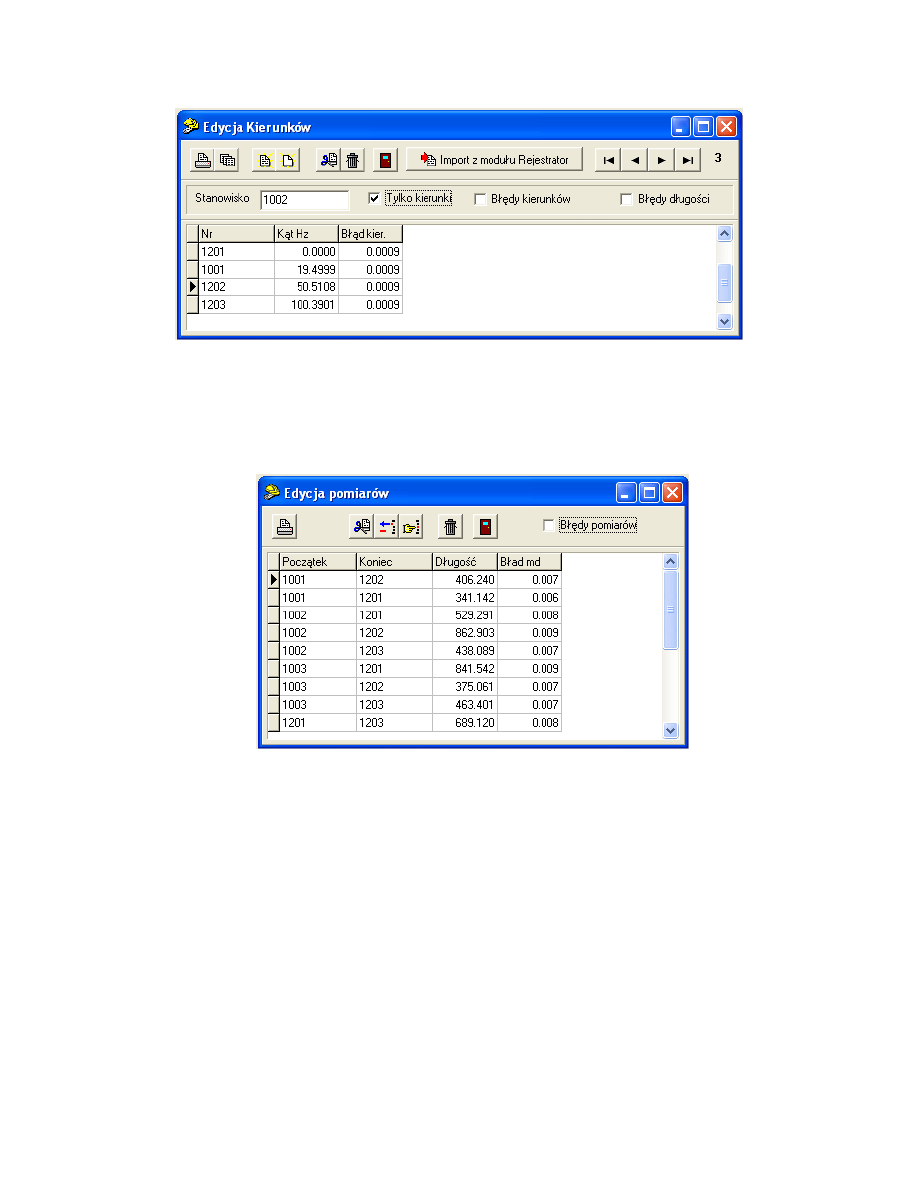
Rys. 5.48. Edycja kierunków – kierunki wraz z błędami dla stanowiska 1002
Chcąc wprowadzić długości boków, wybieramy z menu Wyrównanie – boki i wpisujemy
długości wraz z błędami do otwartego okna (rys. 5.49).
Rys. 5.49. Edycja pomiarów – długości wraz z błędami
W tym momencie mamy wprowadzone do programu wszystkie dane wyjściowe i
możemy przystąpić do obliczeń. Do wyrównania potrzebujemy jeszcze współrzędnych
przybliżonych punktów wyznaczanych, które możemy obliczyć na kilka sposobów.
Często stosowane są obliczenia przybliżonych współrzędnych punktów łączonych w
system ciągu poligonowego lub wyznaczanie współrzędnych pojedynczych punktów
wcięciami. Jeżeli dysponujemy dużą liczbą obserwacji nadliczbowych w sieci, możliwe
jest także wyznaczenie współrzędnych przybliżonych szukanych punktów poprzez
skorzystanie z funkcji Wyrównanie – Współrzędne przybliżone. Wybieramy tą funkcję
dla naszego przykładu i dysponując już wszystkimi danymi możemy przystąpić do
4
pierwszej iteracji wyrównania. Z menu wybieramy Wyrównanie – Obliczenia (sieć
płaska); program przygotowuje i rozwiązuje układy równań oraz charakterystykę m
0
i
prosi o potwierdzenie, czy wykonać obliczenia charakterystyk dokładności. Na
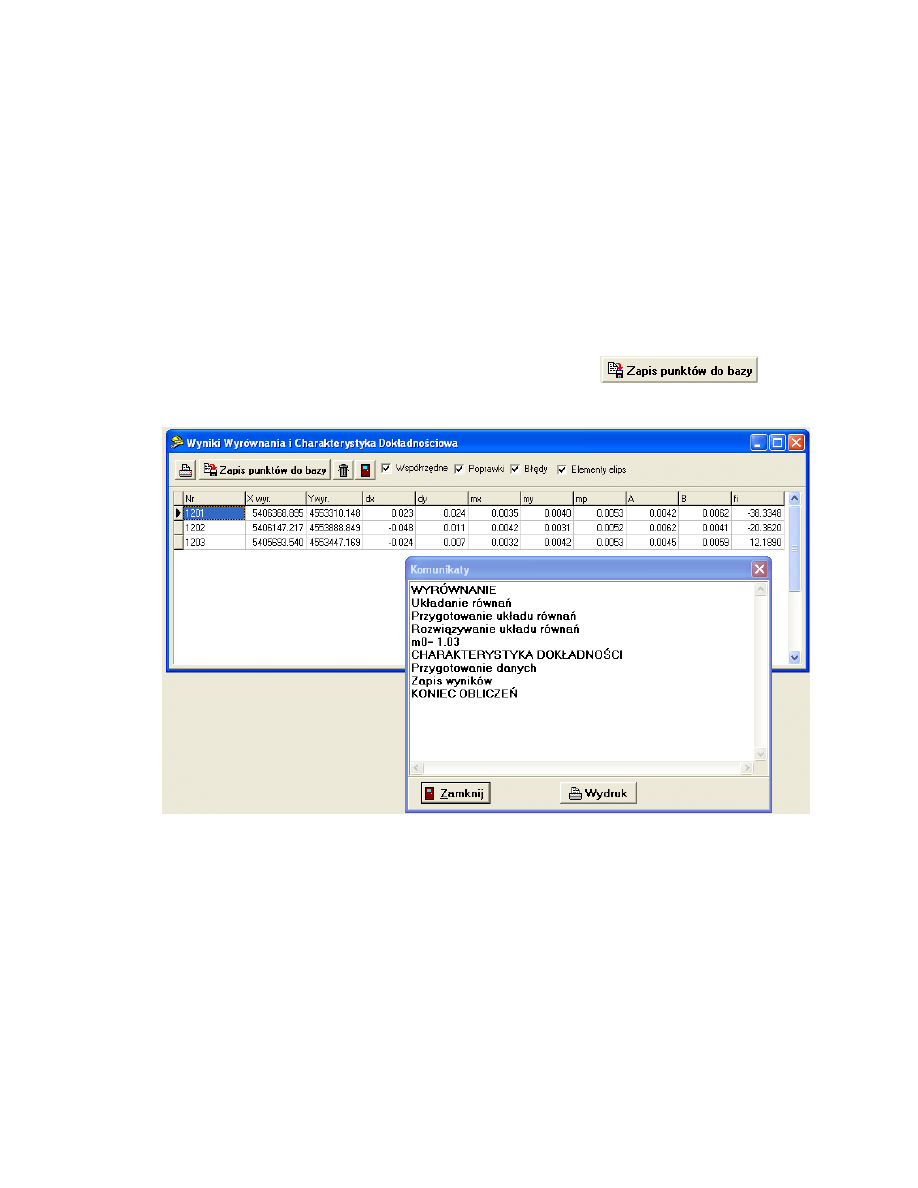
zakończenie procesu pojawi się okno z komunikatami oraz panel Wyniki Wyrównania i
Charakterystyka Dokładnościowa (rys. 5.50). W tym oknie wyświetlane są współrzędne
wyrównane, poprawki dx i dy oraz błędy współrzędnych. Możliwa jest także prezentacja
elementów elips błędów. Wyrównane współrzędne możemy zapisać do bazy danych jako
punkty stałe (jeżeli jesteśmy usatysfakcjonowani wynikami wyrównania) lub przybliżone
(jeżeli chcemy wykonać koleją iterację) korzystając z przycisku
. W
prezentowanym przykładzie druga iteracja nie wpłynęła na wyrównane wartości.
Rys. 5.50. Okno dialogowe Wyniki Wyrównania i Charakterystyka Dokładnościowa
wraz z Komunikatami
Po wykonaniu wyrównania istnieje możliwość podglądu i wydruku szkicu sieci wraz z
naniesionymi elipsami błędów w skali (Wyrównanie – Szkic sieci) oraz analiza
poprawionych wartości kierunków (kątów) i długości. Pomocnym narzędziem jest
zestawienie w kolumnach wartości poprawek do obserwowanych wielkości i błędów tych
poprawek a także ich wzajemnego stosunku (rys. 5.51). Ostania kolumna pozwala nam w
5
szybki sposób zidentyfikować obserwacje, dla których wartość poprawki w znaczny
sposób przekracza jej błąd, czyli identyfikować błędy grube w obliczeniach.
Rys. 5.51. Kierunki i boki wraz z poprawkami i błędami
6