Jerzy Winczek,
Politechnika Częstochowska
IMiPKM

ŚRODKI CIĘŻKOŚCI

1. Wprowadzenie

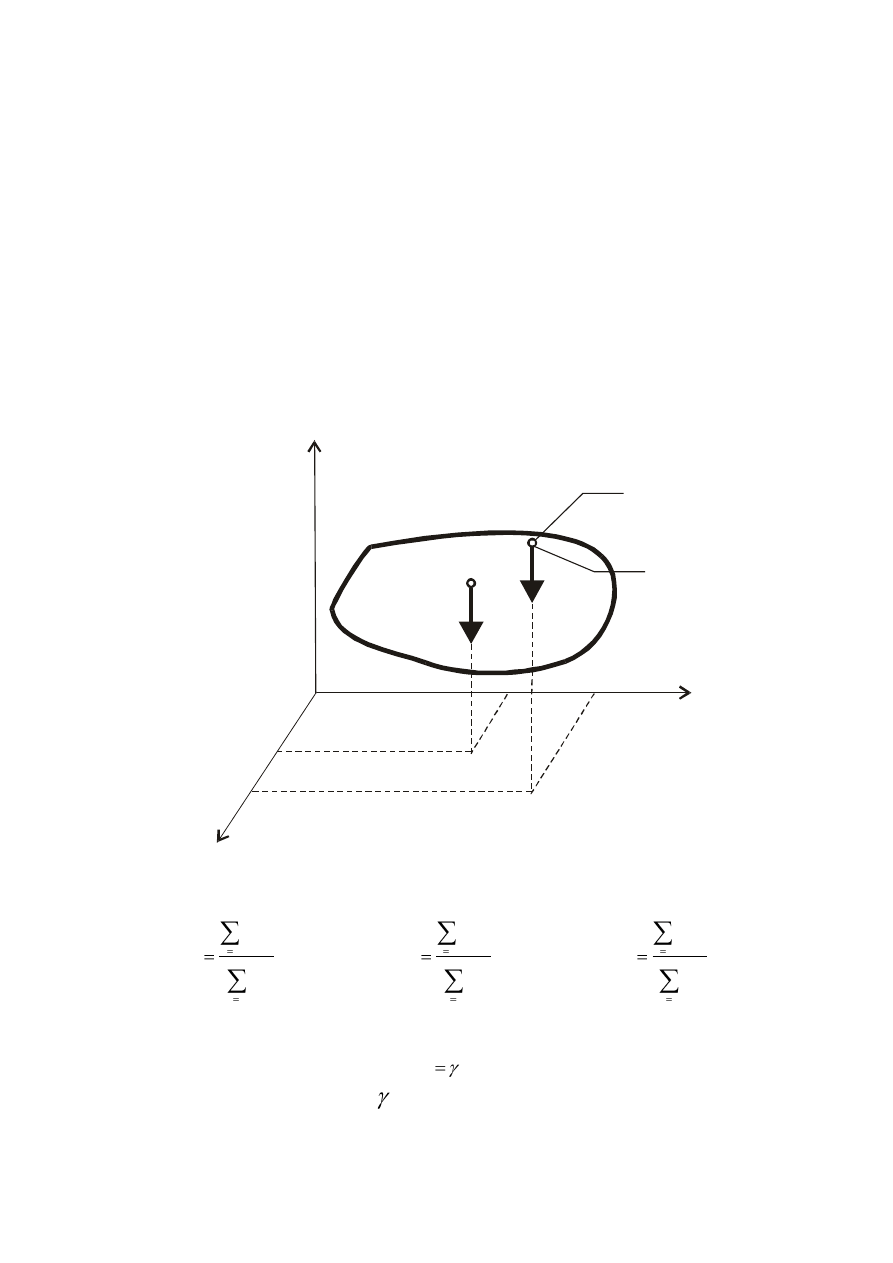
Dowolne ciało sztywne możemy uważać za zbiór bardzo dużej liczby cząstek na które
działają siły ciężkości. Siły te są skierowane do środka ziemi. Ponieważ wymiary ciał, z
którymi mamy do czynienia w mechanice są znikomo małe z promieniem kuli ziemskiej (ok.
6370 km), możemy uważać, że siły ciężkości przyłożone do tychże cząstek są równoległe.
Środek sił równoległych w odniesieniu do sił ciężkości nazywamy środkiem ciężkości.

2. Wzory ogólne

c

V

A

y

z

x

x

y

z

c

i

G

G

i

x

i

y

c

c

i

z

i

i

Jeżeli całe ciało podzielimy na n małych objętości to współrzędne środka ciężkości
określimy wzorami:

n

i

i

n

i

i

i

C

G

G

x

x

1

1

,

n

i

i

n

i

i

i

C

G

G

y

y

1

1

,

n

i

i

n

i

i

i

C

G

G

z

z

1

1

,

gdzie

i

G

jest siłą ciężkości cząsteczki o współrzędnych

i

i

i

z

y

x

,

,

. Wartość siły ciężkości

działającej na cząsteczkę

i

wynosi

i

i

i

V

G

,

gdzie

i

V

jest objętością cząsteczki, a

i

oznacza jej ciężar właściwy.

Wówczas zapisujemy:

n

i

i

i

n

i

i

i

i

C

V

V

x

x

1

1

n

i

i

i

n

i

i

i

i

C

V

V

y

y

1

1

n

i

i

i

n

i

i

i

i

C

V

V

z

z

1

1

3. Środek ciężkości bryły.

Przy założeniu jednorodności rozpatrywanego ciała, to znaczy, że ciężar właściwy jest
jednakowy dla każdej cząsteczki i wynosi , otrzymujemy:

V

V

x

x

n

i

i

i

C

1

V

V

y

y

n

i

i

i

C

1

V

V

z

z

n

i

i

i

C

1

,

gdzie przez V oznaczono całkowita objętość ciała.


4. Środek ciężkości figury płaskiej

W przypadku figury płaskiej, której grubość jest stała i znikomo mała w porównaniu z
pozostałymi wymiarami, możemy tak obracać osiami układu współrzędnych, by figura ta
znalazła się w płaszczyźnie

y

x,

, jak na rysunku.

c

A

y

x

x

(x , y )

G

G

i

y

c

c

i

i

i

Wówczas wzory na współrzędne środka ciężkości figury płaskiej przyjmą postać:

A

A

x

x

n

i

i

i

C

1

A

A

y

y

n

i

i

i

C

1

,

gdzie przez

i

A

oznaczono pola powierzchni figur elementarnych, a przez

A

całkowite pole

powierzchni figury płaskiej.

Oznaczając momenty statyczne odpowiednio przez

x

S

i

y

S

mamy:

n

i

i

i

y

A

x

S

1

- moment statyczny względem osi

y

,

n

i

i

i

x

A

y

S

1

- moment statyczny względem osi x .

Przy tych oznaczeniach wzory na współrzędne środka ciężkości figury płaskiej możemy
zapisać w następującej postaci:

A

S

x

y

C

A

S

y

x

C

.

Jeżeli figura ma oś symetrii to środek masy figury znajduje się na tej osi.

Moment statyczny figury płaskiej względem osi przechodzącej przez jej środek masy jest
równy zero.

Wzory szczegółowe dla podstawowych figur płaskich:

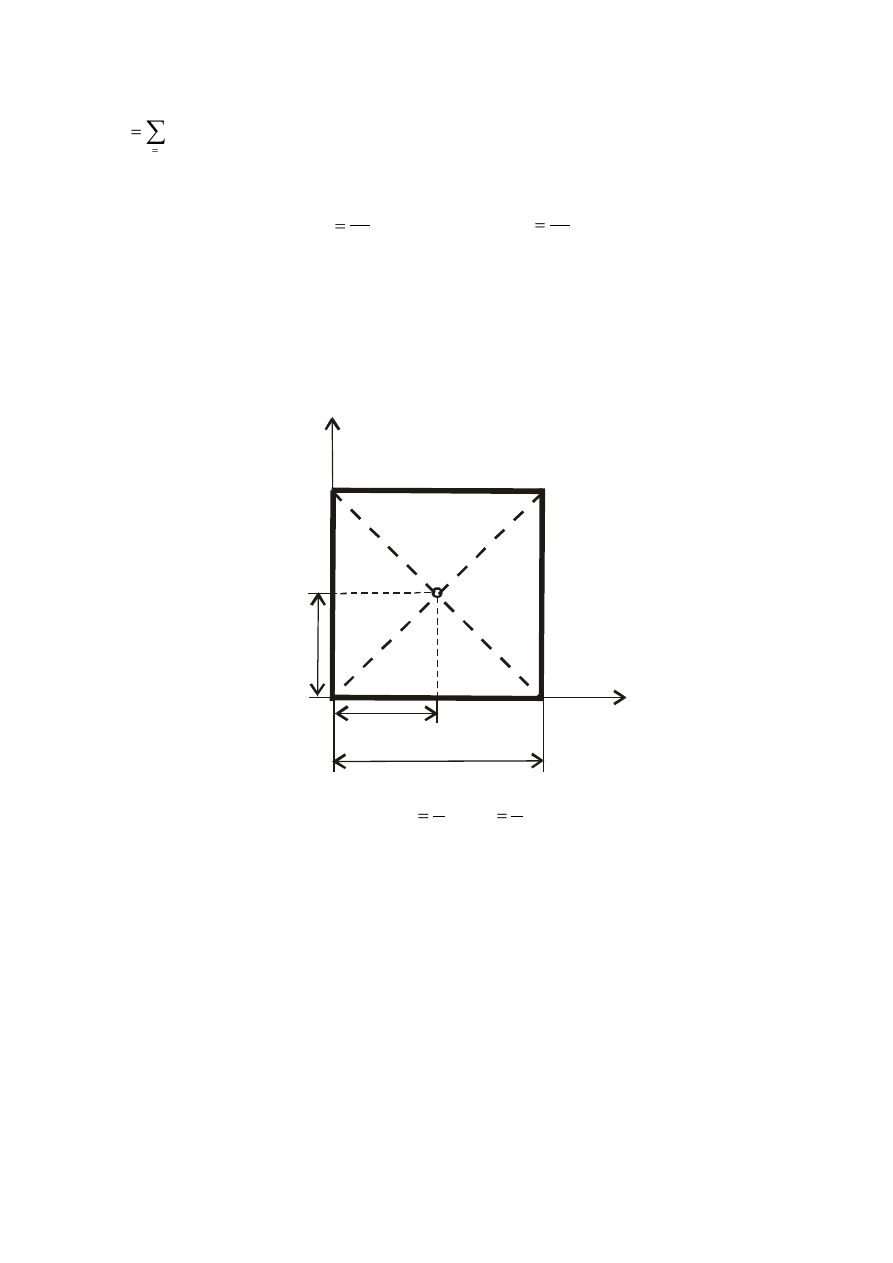
- kwadrat o boku a

c

y

x

x

y

c

c

a

2

a

x

C

,

2

a

y

C

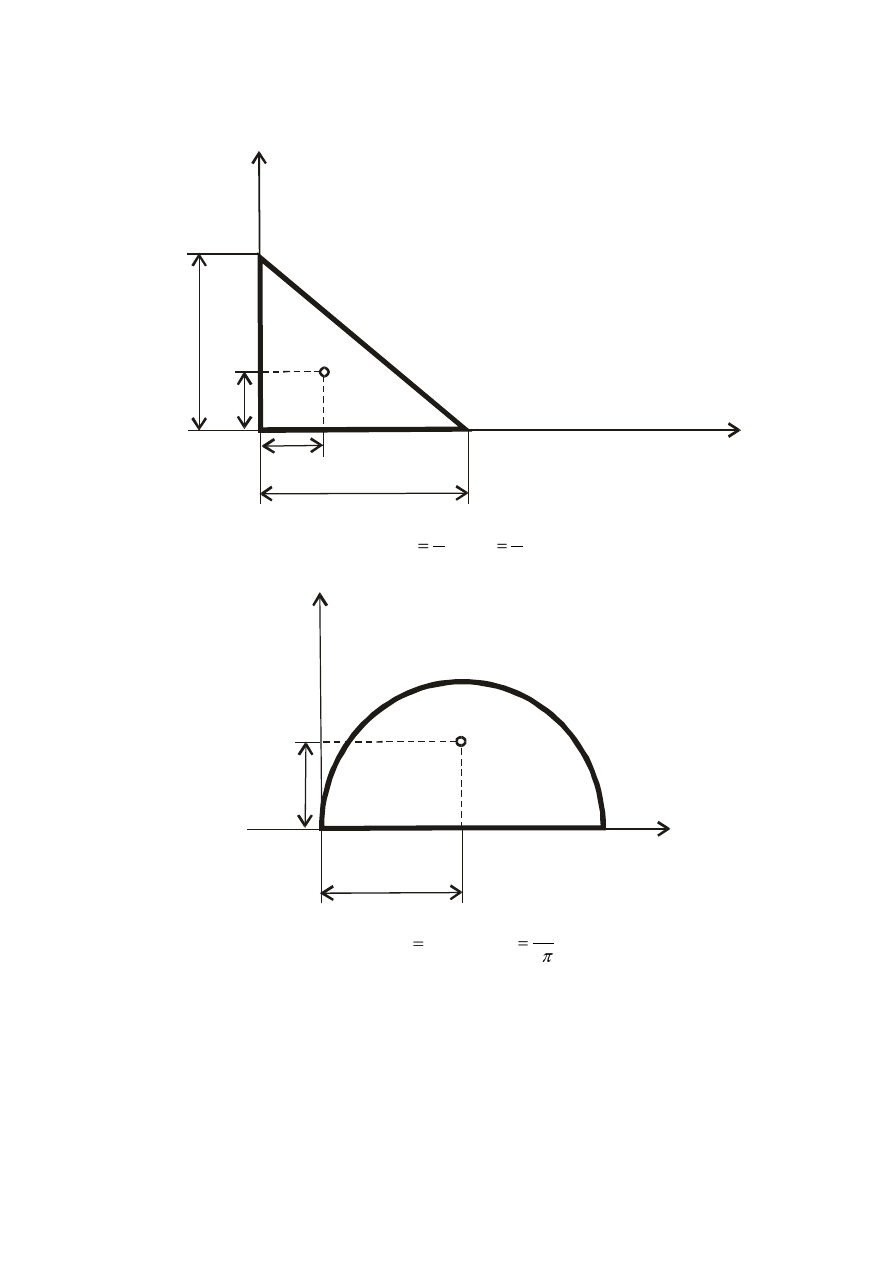
- trójkąt

c

y

x

x

y

c

c

h

a

3

a

x

C

,

3

h

y

C

- półkole:

c

y

x

x

y

c

c

=r

-

r

x

C

,

3

4r

y

C

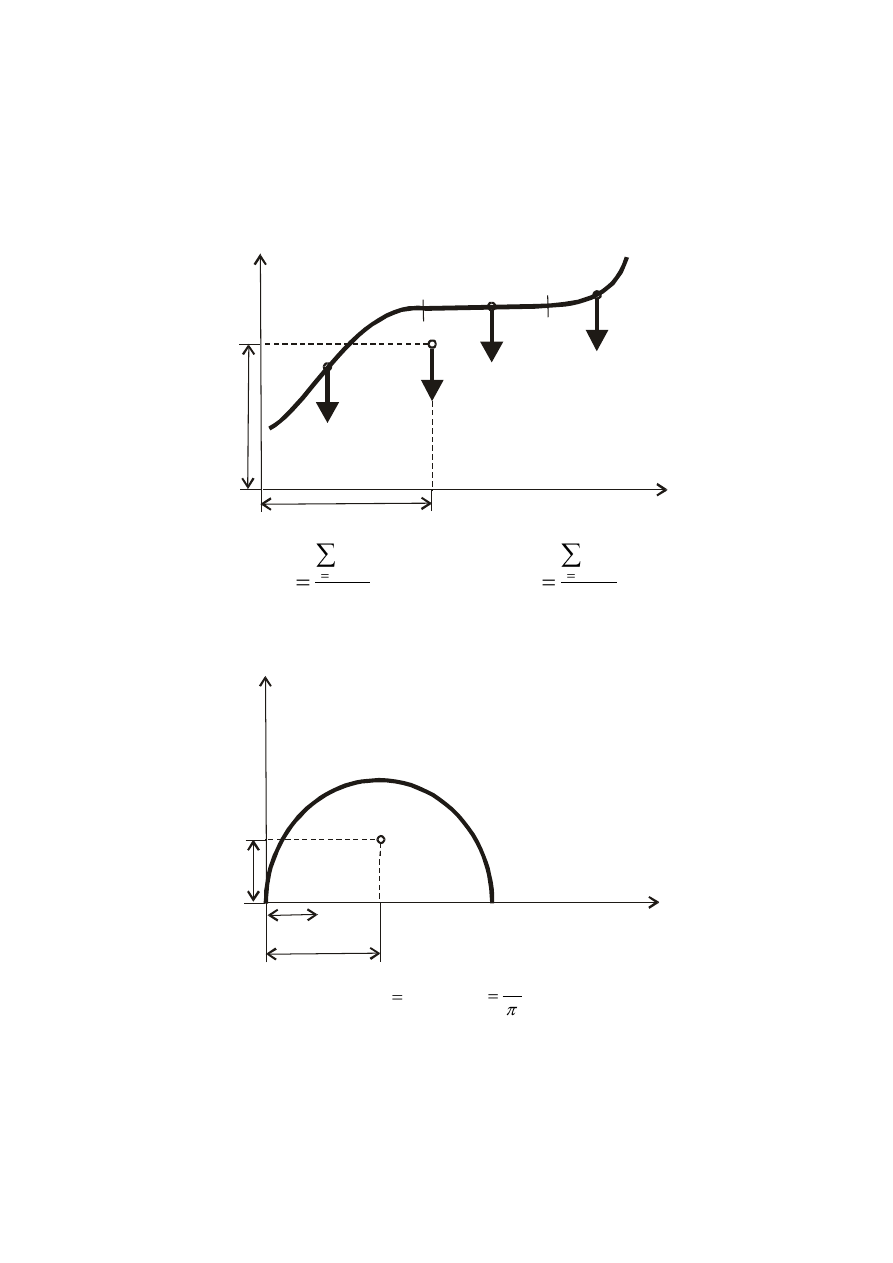
4. Środek ciężkości linii materialnej

Jednorodną linią materialną nazywamy ciało jednorodne o stałym przekroju poprzecznym,
którego długość jest znacznie większa od wymiarów przekroju poprzecznego, na przykład
drut czy długi pręt.
Wzory położenia środka ciężkości linii na płaszczyźnie są następujące:

c

y

x

x

G

G

2

y

c

c

G

n

G

1

c

c

c

n

n

1

2

l

l

l

2

1

l

l

x

x

n

i

i

i

C

1

l

l

y

y

n

i

i

i

C

1

,

Wzory na współrzędne środka masy półokręgu:

c

y

x

x

y

c

c

r

r

x

C

,

r

y

C

2

Literatura obowiązkowa:

1. J. Misiak, Zadania z mechaniki ogólnej. Statyka WN-T, Warszawa 2009
2. J. Nizioł: Metodyka rozwiązywania zadań z mechaniki, WNT Warszawa 2006
3. M. Niezgodziński, T. Niezgodziński: Zbiór zadań z mechaniki ogólnej, PWN

Warszawa 2003

4. J. Leyko; J. Szmelter: Zbiór zadań z mechaniki ogólnej, PWN Warszawa 1976 (t. 1)
5.

http://www.plan-rozwoju.pcz.pl/wyklady/mechatronika/Zadania_z_mechaniki.pdf

6.

http://www.przeklej.pl/plik/giergiel-gluch-lopata-zbior-zadan-z-mechaniki-metodyka-
rozwiazan-pdf-0018mv34540i?err=referr

Literatura dodatkowa:

1. F.P.Beer, E. Russell Johnston: Vector Mechanics for Engineers. McGraw-Hill

Publishing Company, 2004

2. I. W. Mieszczerski: Zbiór zadań z mechaniki. PWN Warszawa 1969
3.

http://psych.iteffect.pl/archive/ukw/Mechanika/cw1_2Mech.pdf

4.

http://www.matthewz.republika.pl/zad5.htm

5.

http://www.matthewz.republika.pl/statyk14.htm

6.

http://www.youtube.com/watch?v=j_Kz13JidA0

7.

www.tzc.net/lectures/statykawyklad6.doc

8.

http://www.youtube.com/watch?v=vYbBakL9Cj8