Rok LXXV 2007 nr 8

17

MATERIAŁY KONFERENCYJNE 8 SPE-2007

Metody poprawy jakości energii elektrycznej

– kształtowanie prądu źródła

Marian Pasko, Marcin Maciążek, Dawid Buła

Artykuł stanowi kontynuację tematyki związanej

z metodami analizy i poprawy jakości energii elektrycznej.

Poprzedni artykuł (WE nr 4/07) prezentował przyczyny

pogorszenia jakości energii elektrycznej oraz konsekwencje

tego faktu.

Autorzy w swojej działalności naukowej zajmują się metodami

pomiaru i eliminacji wyższych harmonicznych z przebiegów

prądów i napięć, dlatego szerzej zostanie przedstawiony

właśnie ten obszar metod poprawy jakości energii.

Metody kształtowania prądu źródła

W metodach kształtowania prądu źródła (eliminacji wyższych har-

monicznych) możemy wyróżnić dwa podstawowe bloki tematyczne.

Pierwszy dotyczy syntezy dwójników kompensacyjnych, natomiast

drugi – wykorzystania energoelektronicznych układów kluczujących.

Proces syntezy układów liniowych przeprowadza się z reguły

w dwóch etapach:

●

pierwszy (etap aproksymacji) polega na określeniu transmitancji

dwójnika spełniającego warunki realizowalności w danej klasie,

●

drugi – przyporządkowuje danej transmitancji konkretny układ

realizowalny fizycznie.

Niejednoznaczność rozwiązania tego problemu (teoretycznie istnieje

nieskończona liczba rozwiązań układowych danego procesu syntezy) po-

woduje, że zagadnienia te są trudne. Brak jest przy tym jednoznacznych

kryteriów określających optymalne rozwiązanie postawionego problemu.

Teoria dotycząca syntezy dwójników kompensujących i metod po-

prawy jakości energii elektrycznej przy ich wykorzystaniu jest bar-

dzo obszerna. Mimo wielu publikacji poruszających te zagadnienia

[1÷14], nie doczekała się ona jednoznacznego rozwiązania.

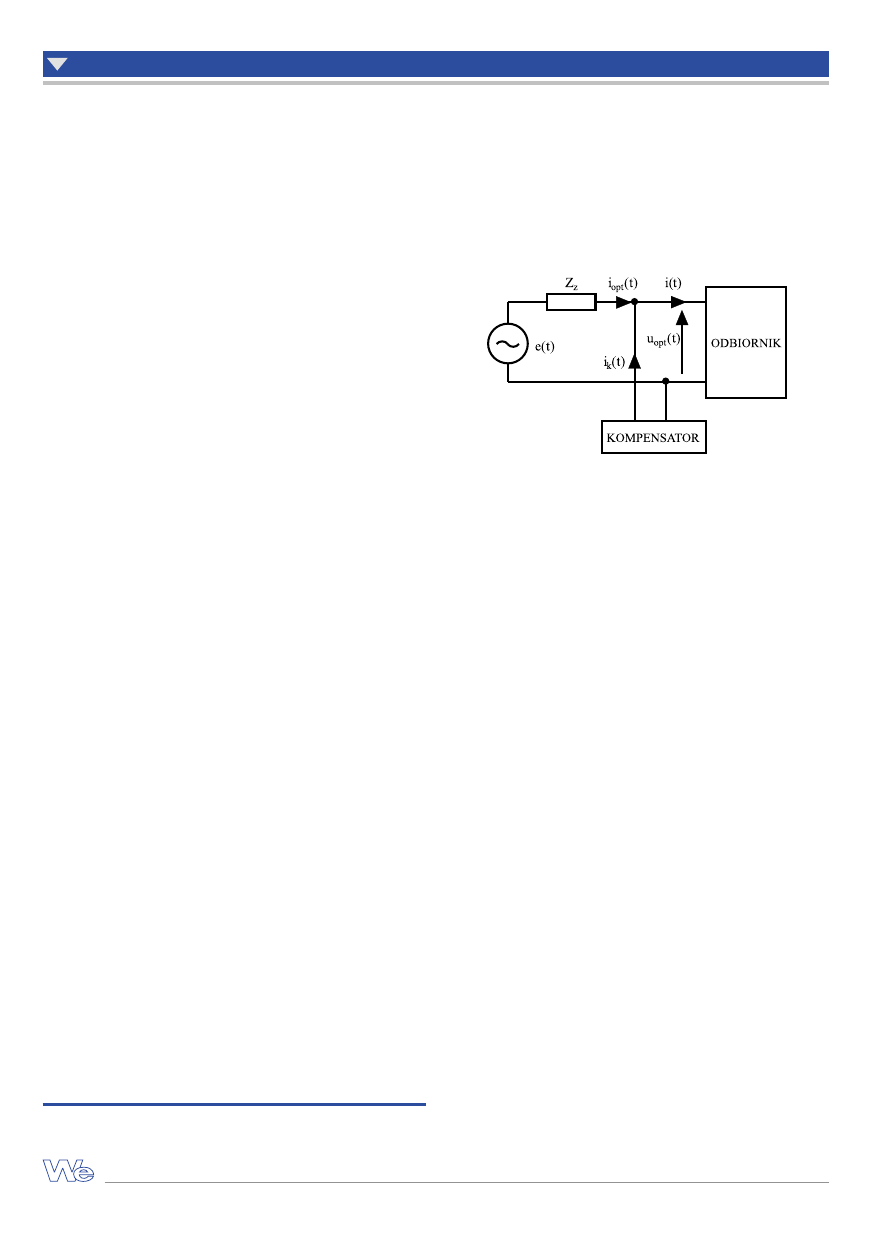
Zasadę działania kompensacji przy wykorzystaniu dwójników

ilustruje rysunek 1: pomiędzy źródłem a odbiornikiem znajduje się

równolegle włączony kompensator.

Przez kompensator rozumiemy tutaj dwójnik o takich właściwoś-

ciach, że dołączenie go do wybranych węzłów obwodu optymalizuje

stan pracy tego układu ze względu na przyjęte kryterium, powodując

np. że straty energii elektrycznej na wybranych elementach obwodu

lub zawartość wyższych harmonicznych w wybranych przebiegach

prądów i napięć w obwodzie są minimalne.

W metodzie tej wykorzystuje się ortogonalne rozkłady prądu

źródła na prąd aktywny (który jako pierwszy zdefiniował S. Fryze

[15]) i dodatkowe składowe (różne w poszczególnych podejściach).

Rozkłady te proponowali w swoich teoriach m.in. Shepherd i Zakik-

hani [16], Kusters i Moore [17] oraz Czarnecki [2].

Należy jednak nadmienić, że rozkłady ortogonalne są słuszne dla

układów zasilanych z idealnych źródeł. Dla układów zasilanych ze

źródeł o niezerowej impedancji wewnętrznej, układy ortogonalne

zawodzą [18]. Dlatego w późniejszych latach zaproponowano do

opisu właściwości energetycznych i energetyczno-jakościowych po-

dejście optymalizacyjne.

Ideę tej koncepcji (która była przedmiotem wielu publikacji, m.in.

na kolejnych konferencjach IC-SPETO), która zrodziła się w Insty-

tucie Elektrotechniki Teoretycznej i Przemysłowej w 1985 roku,

można przedstawić w postaci ciągu postulatów [3]:



Do opisu właściwości energetycznych obwodów z przebiegami

niesinusoidalnymi wykorzystuje się wyłącznie prądy, napięcia, ich

wartości skuteczne, moc chwilową i moc czynną P.



Przez prąd optymalny obwodu rozumie się prąd otrzymany jako

rozwiązanie zadania optymalizacji przy narzuconych warunkach

ubocznych.



Zdefiniowany dla obwodu optymalizacyjny wskaźnik jakości po-

winien umożliwiać ocenę:

– właściwości energetycznych przebiegów na podstawie ich warto-

ści skutecznych i strat mocy czynnej,

– zniekształcenie przebiegów od żądanego przebiegu sinusoidalnego.



Wyróżniony zbiór prądów optymalnych określa stan optymalny

układu w żądanym sensie.



Optymalny stan pracy układu realizuje się za pomocą obwodów

modyfikujących (kompensatorów).

Szczegółowe omówienie tego podejścia oraz przykładowe rozwią-

zania można znaleźć w pracach [3, 6, 9] oraz w materiałach konfe-

rencyjnych IC-SPETO.

Drugi z bloków tematycznych dotyczy kompensacji dynamicznej

przy wykorzystaniu energetycznych filtrów aktywnych (EFA). Są

to układy energoelektroniczne pełniące funkcje źródeł dodawczych

napięciowych lub prądowych, przeznaczone do kompensacji odchy-

Prof. dr hab. inż. Marian Pasko, dr inż. Marcin Maciążek, mgr inż. Dawid

Buła – Wydział Elektryczny Politechniki Śląskiej, Gliwice

Rys. 1. Ilustracja zasady kompensacji równoległej z wykorzystaniem dwójnika

kompensującego

18

Rok LXXV 2007 nr 8

MATERIAŁY KONFERENCYJNE 8 SPE-2007

leń wartości chwilowych napięć i prądów linii zasilających od prze-

biegów sinusoidalnych [8].

Równoległe układy EFA umożliwiają np.:

– kompensację składowych biernych prądu odbiornika o częstotli-

wości podstawowej,

– symetryzację obciążenia widzianego z zacisków sieci,

– filtrację wyższych harmonicznych prądu, praktycznie niezależną

od impedancji sieci i na poziomie nieosiągalnym dla filtrów bier-

nych LC.

Dodatkowo układy te charakteryzują się większymi możliwościami

i lepszymi parametrami dynamicznymi niż kompensatory tradycyj-

ne [13, 19, 20].

W przypadku aktywnej filtracji równoległej układ EFA jest ste-

rowanym źródłem prądu dodawczego, przyłączonym równolegle

do odbiornika. Suma prądu filtru i prądu linii zasilającej daje w re-

zultacie prąd pobierany przez odbiornik. Efektem tego działania

w idealnym przypadku jest prąd o przebiegu sinusoidalnym w li-

nii zasilającej, natomiast wszystkie niepożądane składowe prądu

przepływają wyłącznie w układzie odbiornik – źródło sterowane

prądu dodawczego, nie obciążając tym samym źródła zasilania.

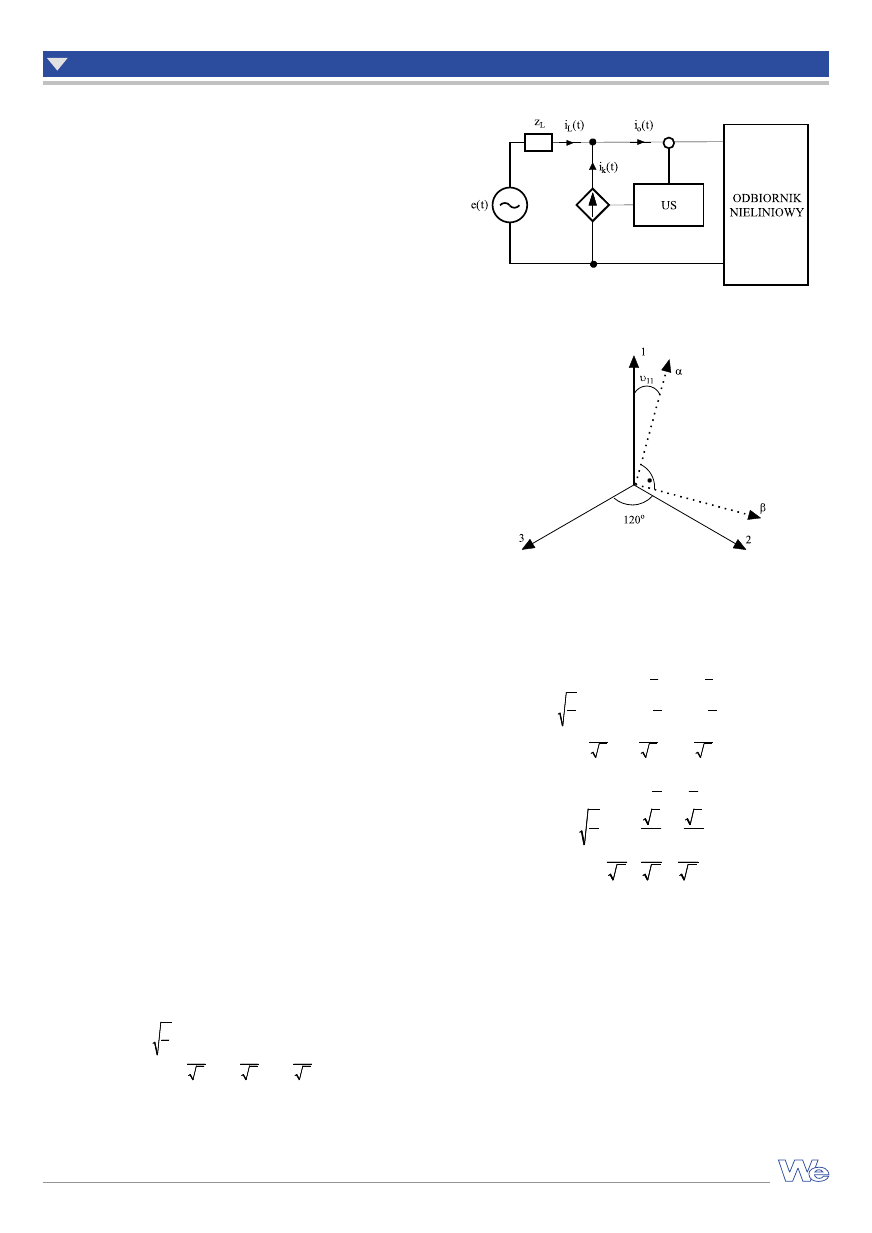
Zasada działania tego sposobu kompensacji została zilustrowana

na rysunku 2.

Ograniczeniem takiej metody kompensacji jest fakt, że rów-

noległe filtry aktywne spełniają swoją funkcję jedynie dla tych

odbiorników nieliniowych, które można traktować jako źródła

wyższych harmonicznych prądu. Można je także stosować do

eliminacji przesunięcia fazowego pomiędzy prądem i napięciem

w przypadku obciążenia odbiornikiem liniowym (wprowadzają-

cym to przesunięcie).

W systemach równoległej filtracji aktywnej jako sterowane źródło

prądu stosuje się falowniki napięcia (Voltage Source Inverter). Fa-

lowniki te są sterowane przy wykorzystaniu metod modulacji szero-

kości impulsów w taki sposób, aby ich prądy wyjściowe nadążały za

przebiegami wzorcowymi.

Najczęściej obecnie stosowana teoria mocy (w obszarze popra-

wy jakości energii elektrycznej przy wykorzystaniu EFA) została

zaprezentowana w Japonii w 1983 r. Teoria mocy chwilowej, zapro-

ponowana przez H. Akagiego oraz A. Nabae, nie ma cech ogólnej

teorii mocy. Nie może wyjaśnić wielu zjawisk fizycznych [21], ale

charakteryzuje się wieloma zaletami [22÷26], z których najważniej-

sza jest możliwość wyznaczenia prądu optymalnego (w zadanym

sensie) z minimalnym opóźnieniem, przy zastosowaniu podstawo-

wych operacji matematycznych [27].

Teoria ta bazuje na skalarnej transformacji napięć fazowych [u

L1

, u

L2

,

u

L3

]

T

oraz prądów obciążenia [i

oL1

, i

oL2

, i

oL3

]

T

z trójfazowego układu

naturalnego 1-2-3, do układu współrzędnych prostokątnych α-β-0

(rys. 3). Transformację tę przeprowadza się, przeliczając wartości

chwilowe według wzoru

(1)

gdzie: υ

1x

– kąt przesunięcia pomiędzy osią x naturalnego układu

trójfazowego a osią α układu prostokątnego (rys. 3).

















































−

−

−

=





















3

2

1

0

β

α

F

F

F

F

F

F

2

1

2

1

2

1

sin υ

sinυ

sinυ

cosυ

cosυ

cosυ

13

12

11

13

12

11

3

2

















































−

−

−

=





















3

2

1

0

β

α

F

F

F

F

F

F

2

1

2

1

2

1

sin υ

sinυ

sinυ

cosυ

cosυ

cosυ

13

12

11

13

12

11

3

2

W przypadku, gdy osie 1 i α pokrywają się, tzn. gdy υ

11

= 0, ma-

cierz transformacji przyjmuje postać

(2)

czyli

(3)

Dla układu trójfazowego o napięciach fazowych [u

L1

, u

L2

, u

L3

]

T

i prądach fazowych [i

oL1

, i

oL2

, i

oL3

]

T

, moc chwilowa [23], wyrażona

przez chwilowe wartości prądów i napięć fazowych, w układzie

1-2-3 może być zapisana

(4)

Po przetransformowaniu napięć i prądów fazowych z układu

naturalnego 1-2-3 do układu współrzędnych prostokątnych α-β-0

według wzoru (3), moc chwilowa – ze względu na ortogonalność

transformacji – zachowuje niezmienność formy przy posłużeniu się

napięciami i prądami w nowym układzie współrzędnych, tzn.

(5)





















































π

−

π

−

−

π

π

=





















3

2

1

0

β

α

F

F

F

0

0

F

F

F

2

1

2

1

2

1

3

2

3

4

3

2

3

4

sin

sin

sin

cos

cos

cos

3

2





















































π

−

π

−

−

π

π

=





















3

2

1

0

β

α

F

F

F

0

0

F

F

F

2

1

2

1

2

1

3

2

3

4

3

2

3

4

sin

sin

sin

cos

cos

cos

3

2

2

1

2

1

2

1

2

3

2

3

0

2

1

2

1

1

3

2

3

2

1

0

























































−

−

−

=





















F

F

F

F

F

F

β

α

2

1

2

1

2

1

2

3

2

3

0

2

1

2

1

1

3

2

3

2

1

0

























































−

−

−

=





















F

F

F

F

F

F

β

α

oL3

L3

oL2

2

1

oL

L1

u

i

u

p

i

u

i

L

+

+

=

oL3

L3

oL2

2

1

oL

L1

u

i

u

p

i

u

i

L

+

+

=

0

0

β

β

α

α

i

u

i

u

i

u

p

+

+

=

0

0

β

β

α

α

i

u

i

u

i

u

p

+

+

=

Rys. 2. Ilustracja zasady kompensacji równoległej z wykorzystaniem EFA

Rys. 3. Transformacja układu 1-2-3 do układu α-β-0

Rok LXXV 2007 nr 8

19

MATERIAŁY KONFERENCYJNE 8 SPE-2007

Ze względu na to, że w większości przypadków przekazywanie

energii odbywa się z symetrycznego źródła napięcia o przebiegu

sinusoidalnym za pomocą linii trójprzewodowej, w macierzy trans-

formacji można pominąć elementy u

0

, i

0

, a także chwilową moc

składowej zerowej.

Jeżeli przez p

α

i p

β

oznaczymy chwilowe moce w osiach α i β, to

moc chwilową można zapisać

(6)

gdzie:

i

αp

– chwilowy prąd czynny w osi α,

i

βp

– chwilowy prąd czynny w osi β,

i

αq

– chwilowy prąd reaktancyjny w osi α,

i

βq

– chwilowy prąd reaktancyjny w osi β,

p

αp

– chwilowa moc czynna w osi α,

p

αq

– chwilowa moc reaktancyjna w osi α,

p

βp

– chwilowa moc czynna w osi β,

p

βq

– chwilowa moc reaktancyjna w osi β.

Składowe te nie mają interpretacji w tej teorii mocy.

Przy takiej dekompozycji suma składowych mocy

(7)

Składowe te (nazywane chwilowymi mocami reaktancyjnymi) zno-

szą się wzajemnie i nie uczestniczą w przekazywaniu energii ze

źródła do odbiornika.

Suma pozostałych dwóch składowych (zwanych chwilowymi mo-

cami czynnymi)

(8)

jest zgodna z typową interpretacją mocy chwilowej stosowaną w ob-

wodach trójfazowych, a jej wartość średnia jest mocą czynną P.

Zupełnie inne podejście należy natomiast zastosować do mocy

biernej. Konwencjonalna moc bierna jest definiowana w dziedzinie

częstotliwości (C.I. Budeanu) i jako taka nie powinna być w żaden

sposób porównywana z wartościami otrzymywanymi w dziedzinie

czasu. Autorzy teorii mocy chwilowej [23] wprowadzili zupełnie

nowe pojęcie – chwilowej mocy urojonej (jednostka tej mocy z ana-

logii do var została oznaczona jako vai, czyli wolt-amper-urojony).

Chwilową moc urojoną wyliczamy, korzystając ze wzoru [23, 28]

(9)

Wartości określonej wzorem (9) nie należy utożsamiać z konwen-

cjonalnym rozumieniem pojęcia mocy biernej znanym z elektro-

techniki (stosowanym dla układów z przebiegami sinusoidalnymi).

Składową tą traktuje się jako element niepożądany, który należy wy-

eliminować z układu, natomiast nie ma ona interpretacji fizykalnej.

Główną zaletą zastosowania współrzędnych prostokątnych α-β

jest możliwość prostego zapisu równań wynikowych dla prądów fa-

zowych. Prąd źródła układu trójfazowego trójprzewodowego, prze-

transformowany do układu α-β, można zapisać w postaci

q

p

q

p

q

p

q

p

p

p

p

p

q

u

u

u

u

p

u

u

u

u

q

u

u

u

u

p

u

u

u

u

i

u

i

u

i

u

i

u

p

p

p

β

β

α

α

β

α

α

β

β

α

β

β

β

α

β

α

β

α

α

α

β

β

β

β

α

α

α

α

β

α

+

+

+

=

=

+

+

+

+

+

−

+

=

=

+

+

+

=

+

=

2

2

2

2

2

2

2

2

q

p

q

p

q

p

q

p

p

p

p

p

q

u

u

u

u

p

u

u

u

u

q

u

u

u

u

p

u

u

u

u

i

u

i

u

i

u

i

u

p

p

p

β

β

α

α

β

α

α

β

β

α

β

β

β

α

β

α

β

α

α

α

β

β

β

β

α

α

α

α

β

α

+

+

+

=

=

+

+

+

+

+

−

+

=

=

+

+

+

=

+

=

2

2

2

2

2

2

2

2

0

=

+

βq

αq

p

p

0

=

+

βq

αq

p

p

p

p

p

p

p

β

α

+

=

p

p

p

p

p

β

α

+

=

α

β

β

α

i

u

i

u

q

−

=

α

β

β

α

i

u

i

u

q

−

=

(10)

Dla symetrycznego źródła napięcia zasilania

(11)

Jednym z zadań optymalizacji może być eliminacja niekorzyst-

nych składowych prądu źródła, tak by prąd źródła był prądem ak-

tywnym [15]. Zadanie to można zrealizować przy wykorzystaniu

filtru aktywnego.

Z zależności (10) można wyznaczyć prądy kompensatora (filtru ak-

tywnego), eliminujące niekorzystne składowe (wybrane lub wszyst-

kie) poza składową stałą chwilowej mocy czynnej (pożądaną), wg

wzoru

12)

W zależności od tego, którą składową chcemy wyeliminować,

w miejsce p

k

i q

k

należy wstawić wielkości z tabeli.

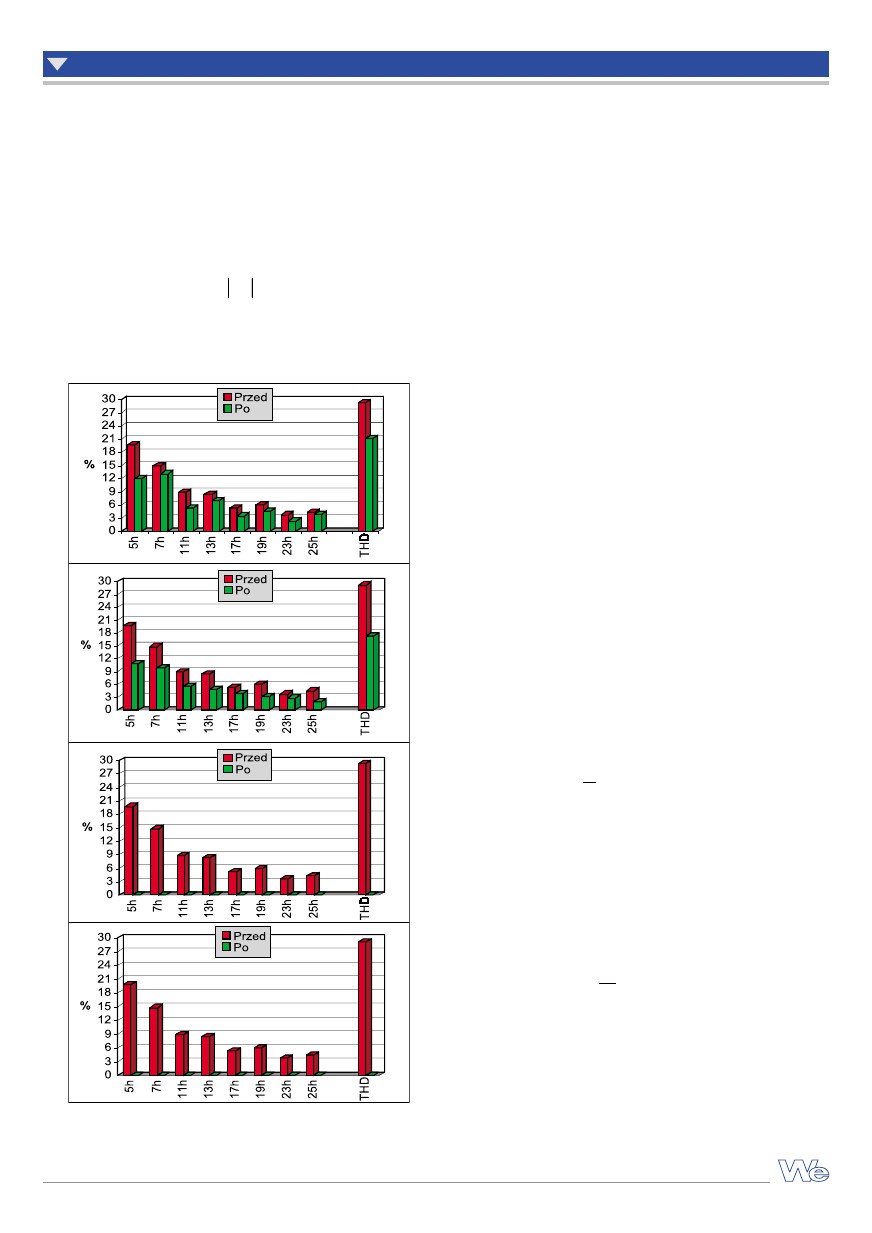
Na rysunku 4 pokazano widma procentowej zawartości wyższych

harmonicznych (w stosunku do harmonicznej podstawowej), przed

i po optymalizacji, z wykorzystaniem teorii mocy chwilowej, dla

różnych przypadków eliminacji składowych (tab.). Wyniki te doty-

czą pierwszej fazy układu trójfazowego trójprzewodowego, obcią-

żonego sterowanym sześciopulsowym prostownikiem energoelek-

tronicznym z obciążeniem rezystancyjnym.

Teoria mocy chwilowej ma jednak istotne ograniczenia stosowa-

nia. Nie należy jej stosować w układach z niesymetrycznym bądź

też odkształconym napięciem zasilania.

W przypadku, gdy odbiornik nieliniowy jest zasilany ze źródła

napięcia odkształconego okresowego, po kompensacji w prądzie

źródła pozostaną odkształcenia wywołane wyższymi harmoniczny-

mi napięcia zasilającego. Odkształcenia te są spowodowane niepo-

prawnym wyliczeniem prądów optymalnych, a tym samym również

prądów kompensujących.

Jednym z poważniejszych ograniczeń teorii mocy chwilowej

była jej stosowalność jedynie w układach symetrycznych. Wyniki

przeprowadzonych symulacji przy zasilaniu układu napięciem od-

kształconym (zawierającym dodatkowo udział piątej harmonicz-

nej), jak też napięciem niesymetrycznym dowodzą, że teoria mocy





















+

+













−

+

=













~

_

~

_

2

2

1

q

q

p

p

u

u

u

u

u

u

i

i

α

β

β

α

β

α

β

α





















+

+













−

+

=













~

_

~

_

2

2

1

q

q

p

p

u

u

u

u

u

u

i

i

α

β

β

α

β

α

β

α

const

3

=

=

+

2

1

L

2

β

2

α

E

u

u

const

3

=

=

+

2

1

L

2

β

2

α

E

u

u

























−

+

=













k

k

q

p

u

u

u

u

u

u

i

i

α

β

β

α

β

α

β

α

2

2

1

























−

+

=













k

k

q

p

u

u

u

u

u

u

i

i

α

β

β

α

β

α

β

α

2

2

1

Zestawienie niekorzystnych składowych mocy chwilowej

Eliminowana składowa prądu źródła

p

k

q

k

Składowa związana z chwilową mocą urojoną

0

q

Składowa kolejności przeciwnej i wyższe harmoniczne

p

~

q

~

Składowa związana ze składową stałą chwilowej mocy urojonej

0

q

–

Składowe związane z chwilową mocą urojoną i wyższymi

harmonicznymi

p

~

q

Składowa kolejności przeciwnej

p

2ω

q

2ω

Składowe związane z wyższymi harmonicznymi

p

h

q

h

Składowa związana ze składową zmienną chwilowej mocy

czynnej

p

~

0

20

Rok LXXV 2007 nr 8

MATERIAŁY KONFERENCYJNE 8 SPE-2007

chwilowej nie nadaje się do stosowania w układach sterowania EFA

pracujących z takimi warunkami zasilania. Główną przyczyną tych

ograniczeń jest postać macierzy transformacji stosowana w tej teorii

mocy chwilowej, a w szczególności zmienna wartość normy warto-

ści chwilowej wektora napięcia (14) w przypadkach, gdy napięcie

zasilania jest niesymetryczne bądź odkształcone okresowe.

Dla układu zasilanego symetrycznym trójfazowym napięciem si-

nusoidalnym

(13)

natomiast dla układu zasilanego napięciem odkształconym

(14)

const

3

2

1

2

2

=

=

+

L

β

α

E

u

u

const

3

2

1

2

2

=

=

+

L

β

α

E

u

u

const

≠

+

2

β

2

α

u

u

const

≠

+

2

β

2

α

u

u

Ponieważ układy z niewielkimi asymetriami zasilania występują

dosyć często, dlatego potrzebne było inne podejście do wyznacza-

nia wartości chwilowych prądów optymalnych dla takich układów.

W 1995 roku Komatsu i Kawabata [29÷31] zaprezentowali teorię

mocy chwilowej zwaną extension pq.

W teorii tej zaproponowano ogólniejsze podejście kompen-

sacyjne, zapewniające poprawną pracę układu sterowania za-

równo przy niesymetriach, jak i odkształceniach napięcia za-

silającego. Chwilowe moce – czynna i bierna – zdefiniowane

są wzorami

(15)

(16)

gdzie: napięcia poprzeczne (prostopadłe) e’

L1

, e’

L2

, e’

L3

uzyskuje się

poprzez przesunięcie napięć fazowych e

L1

, e

L2

, e

L3

oddzielnie dla

każdej z faz o kąt π/2.

Dodatkowo dla układów trójfazowych, trójprzewodowych (takie

układy występują najczęściej) można – zgodnie z I prawem Kir-

chhoffa – zapisać

(17)

Uwzględniając wzór (17), można zredukować wzory (15), (16) do

postaci

(18)

Wzór ten umożliwia określenie energetycznego stanu układu

(wyznaczenie wartości mocy chwilowych p, q). Jego prze-

kształcenie pozwala na wyznaczenie wartości chwilowych prą-

dów fazowych źródła przy znajomości wartości mocy chwilo-

wych p, q

(19)

gdzie:

(20)

Analizując postać wzoru (19), można zauważyć podobieństwo do

analogicznego wzoru w teorii mocy „pq”

(21)

gdzie:

(22)

Można przy tym wykazać, że teoria ta jest równoważna teorii

„pq” w obszarze układów zasilanych napięciami symetrycznymi,

tzn. gdy

(23)

3

3

2

2

1

1

L

L

L

L

L

L

def

i

e

i

e

i

e

p

+

+

=

3

3

2

2

1

1

L

L

L

L

L

L

def

i

e

i

e

i

e

p

+

+

=

3

'

3

2

'

2

1

'

1

L

L

L

L

L

L

def

i

e

i

e

i

e

q

+

+

=

3

'

3

2

'

2

1

'

1

L

L

L

L

L

L

def

i

e

i

e

i

e

q

+

+

=

0

3

2

1

=

+

+

L

L

L

i

i

i

0

3

2

1

=

+

+

L

L

L

i

i

i

























−

−

−

−

=













2

1

'

3

'

2

'

3

'

1

3

2

3

1

L

L

L

L

L

L

L

L

L

L

i

i

e

e

e

e

e

e

e

e

q

p

























−

−

−

−

=













2

1

'

3

'

2

'

3

'

1

3

2

3

1

L

L

L

L

L

L

L

L

L

L

i

i

e

e

e

e

e

e

e

e

q

p





























−

−

−

−

∆

=













q

p

e

e

e

e

e

e

e

e

i

i

L

L

L

L

L

L

L

L

L

L

3

1

'

1

'

3

2

3

'

3

'

2

2

1

1

2

1

3

L

L

L

i

i

i

−

−

=





























−

−

−

−

∆

=













q

p

e

e

e

e

e

e

e

e

i

i

L

L

L

L

L

L

L

L

L

L

3

1

'

1

'

3

2

3

'

3

'

2

2

1

1

2

1

3

L

L

L

i

i

i

−

−

=

)

)(

(

)

)(

(

3

2

'

3

'

1

'

3

'

2

3

1

L

L

L

L

L

L

L

L

e

e

e

e

e

e

e

e

−

−

−

−

−

=

∆

)

)(

(

)

)(

(

3

2

'

3

'

1

'

3

'

2

3

1

L

L

L

L

L

L

L

L

e

e

e

e

e

e

e

e

−

−

−

−

−

=

∆

























−

∆

=













q

p

u

u

u

u

i

i

α

β

β

α

β

α

'

1

























−

∆

=













q

p

u

u

u

u

i

i

α

β

β

α

β

α

'

1

2

2

'

β

α

u

u +

=

∆

2

2

'

β

α

u

u +

=

∆

0

3

2

1

=

+

+

L

L

L

e

e

e

0

3

2

1

=

+

+

L

L

L

e

e

e

Rys. 4. Procentowa zawartość wyższych harmonicznych w prądzie źródła

przed i po optymalizacji

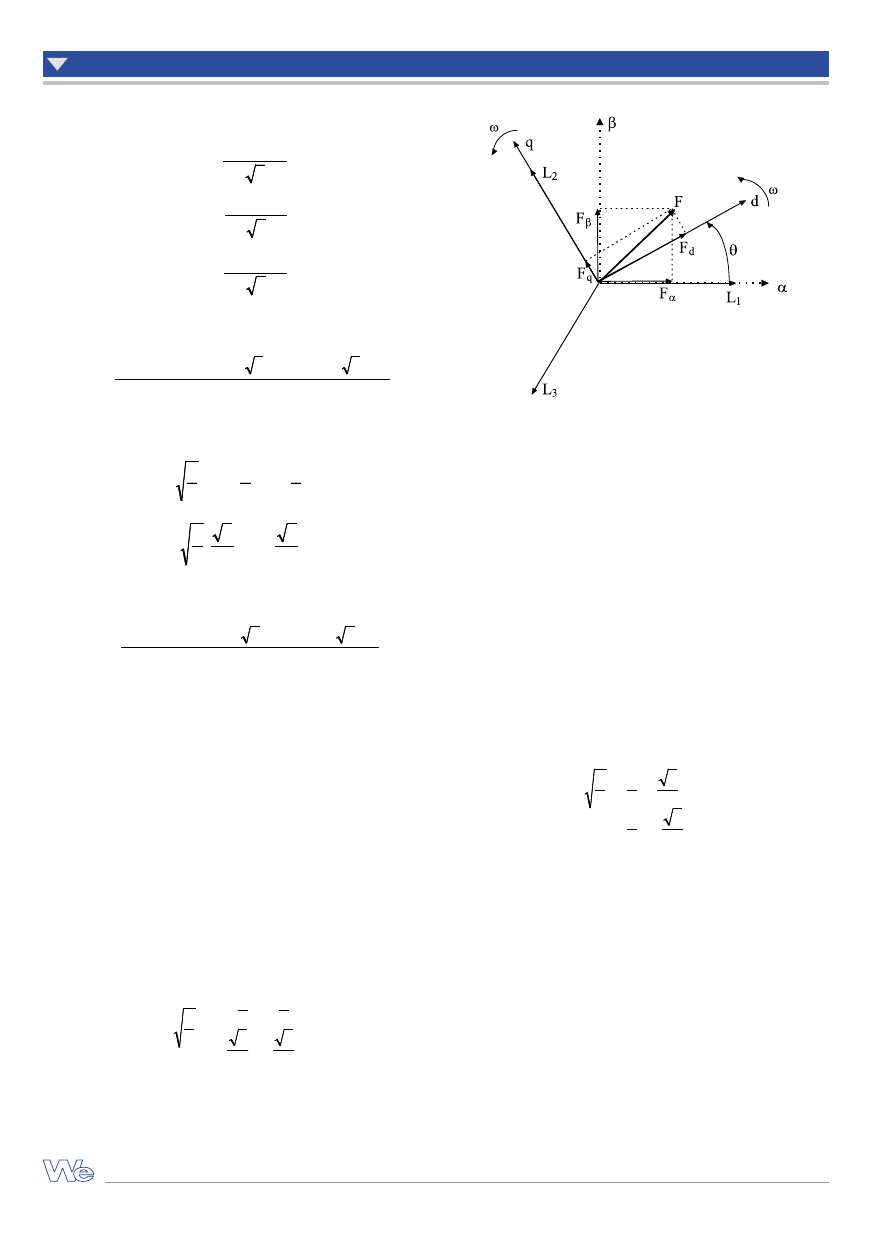
Rok LXXV 2007 nr 8

21

MATERIAŁY KONFERENCYJNE 8 SPE-2007

Wówczas napięcia poprzeczne można zapisać w postaci

(24)

(25)

(26)

a prąd fazowy w fazie L

1

można zapisać jako

(27)

Natomiast uwzględniając, że w teorii „pq”

(28)

(29)

prąd fazowy w fazie L

1

, w teorii „pq” można zapisać jako

(30)

Porównując wzory (27) i (30) widać, że są one identyczne.

Postępując podobnie z prądami w pozostałych fazach, otrzymano

równie zbieżne wyniki. Dowodzi to ogólniejszego podejścia kom-

pensacyjnego w teorii „extension pq”, a także równoważności tych

teorii w przypadku zasilania symetrycznego (i tylko w takim przy-

padku, gdyż tylko wtedy są prawdziwe zależności ze wzorów (24),

(25), (26)).

Kolejne z uogólnień teorii mocy chwilowej mogło znaleźć zastoso-

wanie w układach z zaszumionym bądź odkształconym okresowym

napięciem zasilania. W podejściu tym wykorzystuje się przekształ-

cenie [37] wektorów sygnałów wejściowych z naturalnego układu

trójfazowego 1-2-3 do układu współrzędnych wirujących d-q, jak to

przedstawiono na rysunku 5.

Przekształcenie to odbywa się w dwóch etapach. W pierwszym wek-

tory transformowane są z układu 1-2-3 do układu stacjonarnego α-β

analogicznie jak w metodzie Akagiego [23], tzn. wg zależności

(31)

Następnie wektory są transformowane do układu d-q, wirującego

z prędkością ω. Wartości w nowym układzie współrzędnych otrzy-

muje się z zależności

(32)

3

2

3

'

1

L

L

L

e

e

e

−

=

3

2

3

'

1

L

L

L

e

e

e

−

=

3

3

1

'

2

L

L

L

e

e

e

−

=

3

3

1

'

2

L

L

L

e

e

e

−

=

3

1

2

'

3

L

L

L

e

e

e

−

=

3

1

2

'

3

L

L

L

e

e

e

−

=

))

(

(

2

)

3

(

)

3

(

2

3

2

1

2

3

3

2

2

2

2

1

3

1

2

1

L

L

L

L

L

L

L

L

L

L

L

L

e

e

e

e

e

e

e

e

q

p

e

q

p

e

p

e

i

+

−

+

−

+

+

−

+

−

+

=

))

(

(

2

)

3

(

)

3

(

2

3

2

1

2

3

3

2

2

2

2

1

3

1

2

1

L

L

L

L

L

L

L

L

L

L

L

L

e

e

e

e

e

e

e

e

q

p

e

q

p

e

p

e

i

+

−

+

−

+

+

−

+

−

+

=

)

2

1

2

1

(

3

2

3

2

1

L

L

L

e

e

e

u

−

−

=

α

)

2

1

2

1

(

3

2

3

2

1

L

L

L

e

e

e

u

−

−

=

α

)

2

3

2

3

(

3

2

3

2

L

L

e

e

u

−

=

β

)

2

3

2

3

(

3

2

3

2

L

L

e

e

u

−

=

β

))

(

(

2

)

3

(

)

3

(

2

3

2

1

2

3

3

2

2

2

2

1

3

1

2

'

1

L

L

L

L

L

L

L

L

L

L

L

L

e

e

e

e

e

e

e

e

q

p

e

q

p

e

p

e

i

+

−

+

−

+

+

−

+

−

+

=

))

(

(

2

)

3

(

)

3

(

2

3

2

1

2

3

3

2

2

2

2

1

3

1

2

'

1

L

L

L

L

L

L

L

L

L

L

L

L

e

e

e

e

e

e

e

e

q

p

e

q

p

e

p

e

i

+

−

+

−

+

+

−

+

−

+

=













































−

−

−

=













3

2

1

β

α

F

F

F

F

F

2

3

2

3

0

2

1

2

1

1

3

2













































−

−

−

=













3

2

1

β

α

F

F

F

F

F

2

3

2

3

0

2

1

2

1

1

3

2

θ

α β

j

dq

e

F

F

−

>

−

>

−

=

θ

α β

j

dq

e

F

F

−

>

−

>

−

=

czyli

(33)

Transformacja ta w literaturze nazywana jest również transformacją

Parka.

Podobnie postępuje się przy transformacji odwrotnej, tzn. w pierw-

szej kolejności należy dokonać transformacji wektorów z układu

wirującego d-q do układu stacjonarnego α-β

(34)

Następnie z układu stacjonarnego α-β do układu naturalnego 1-2-3

(35)

Zaletą takiej transformacji jest to, że układ nie wymaga identyfi-

kacji stanu energetycznego poprzez wyznaczanie wartości chwilo-

wych mocy czynnej i biernej. Jeżeli przebieg funkcji cosθ pokry-

wa się z przebiegiem podstawowej harmonicznej napięcia fazy L

1

,

wtedy układ d-q wiruje synchronicznie z przebiegiem podstawowej

harmonicznej napięcia zasilającego. W takim układzie odniesienia

wielkości będące w fazie z podstawową harmoniczną napięcia zasi-

lającego, a więc i składowa aktywna prądu źródła, reprezentowane

są przez wartości stałe w czasie.

Wartość średnia składowej prądu w osi d (rys. 6) odpowiada wów-

czas składowej aktywnej prądu źródła w układzie współrzędnych

wirujących [38]. Dlatego wartości chwilowe prądów optymalnych

oraz prądów kompensujących można wyliczyć wprost ze znajomo-

ści składowych prądów fazowych w nowym układzie współrzęd-

nych (i

d

oraz i

q

), według zależności (36) (wynika to z faktu, że jedy-

ną pożądaną składową jest składowa stała składowej i

d

)

























−

=













β

α

θ

θ

θ

θ

F

F

F

F

q

d

cos

sin

sin

cos

























−

=













β

α

θ

θ

θ

θ

F

F

F

F

q

d

cos

sin

sin

cos

























−

=













q

d

F

F

F

F

θ

θ

θ

θ

β

α

cos

sin

sin

cos

























−

=













q

d

F

F

F

F

θ

θ

θ

θ

β

α

cos

sin

sin

cos













































−

−

−

=





















β

α

3

2

1

F

F

F

F

F

2

3

2

1

2

3

2

1

0

1

3

2













































−

−

−

=





















β

α

3

2

1

F

F

F

F

F

2

3

2

1

2

3

2

1

0

1

3

2

Rys. 5. Ilustracja przekształcenia z układu trójfazowego 1-2-3 do układu

wirującego d-q

22

Rok LXXV 2007 nr 8

MATERIAŁY KONFERENCYJNE 8 SPE-2007

(36)

gdzie: i

~

d

– składowa zmienna składowej prądu i

d

.

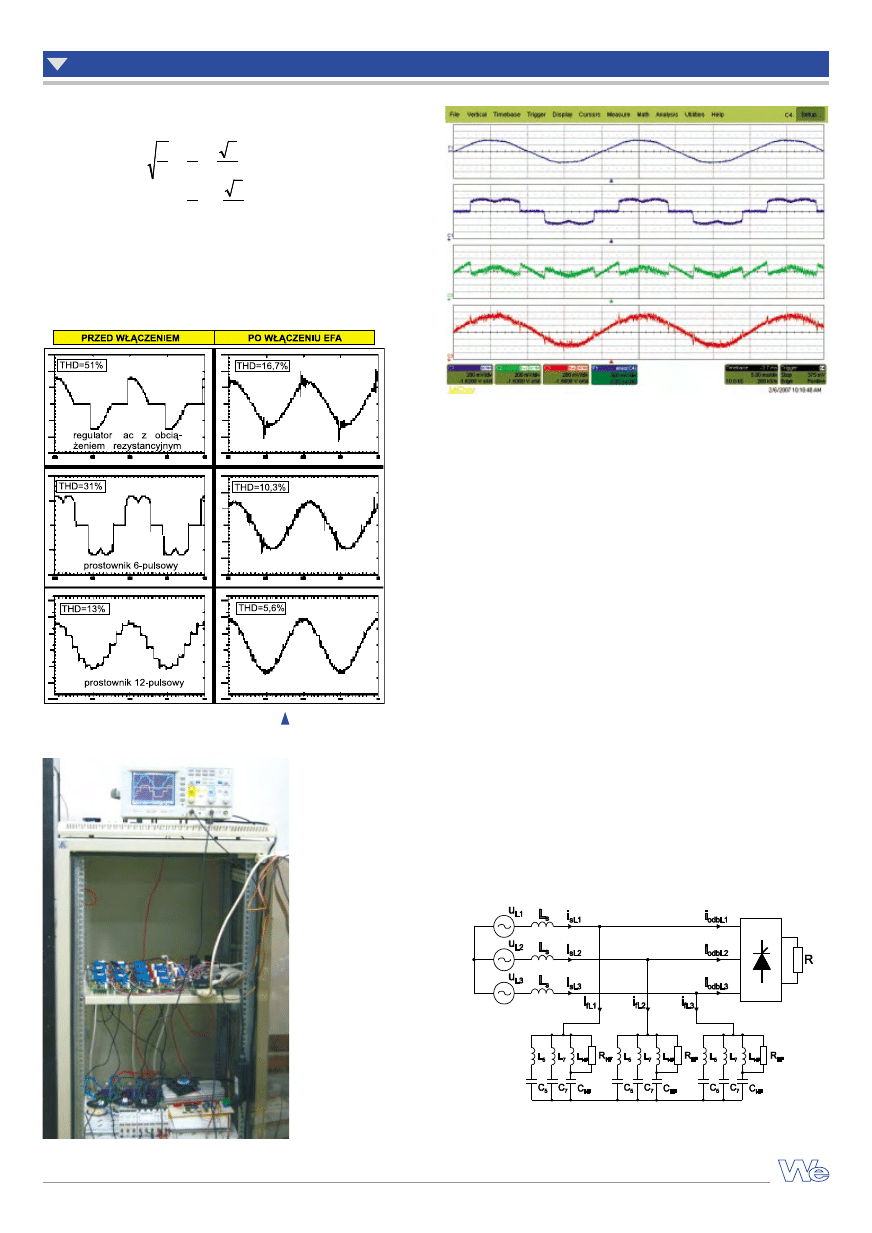
Na rysunku 6 [32] pokazano przykładowe przebiegi czasowe oraz

udział harmonicznych przed i po włączeniu do układu filtru aktywnego.





























−

































−

−

−

=





















q

d

kL

kL

kL

i

i

i

i

i

~

cos

sin

sin

cos

2

3

2

1

2

3

2

1

0

1

3

2

3

2

1

θ

θ

θ

θ





























−

































−

−

−

=





















q

d

kL

kL

kL

i

i

i

i

i

~

cos

sin

sin

cos

2

3

2

1

2

3

2

1

0

1

3

2

3

2

1

θ

θ

θ

θ

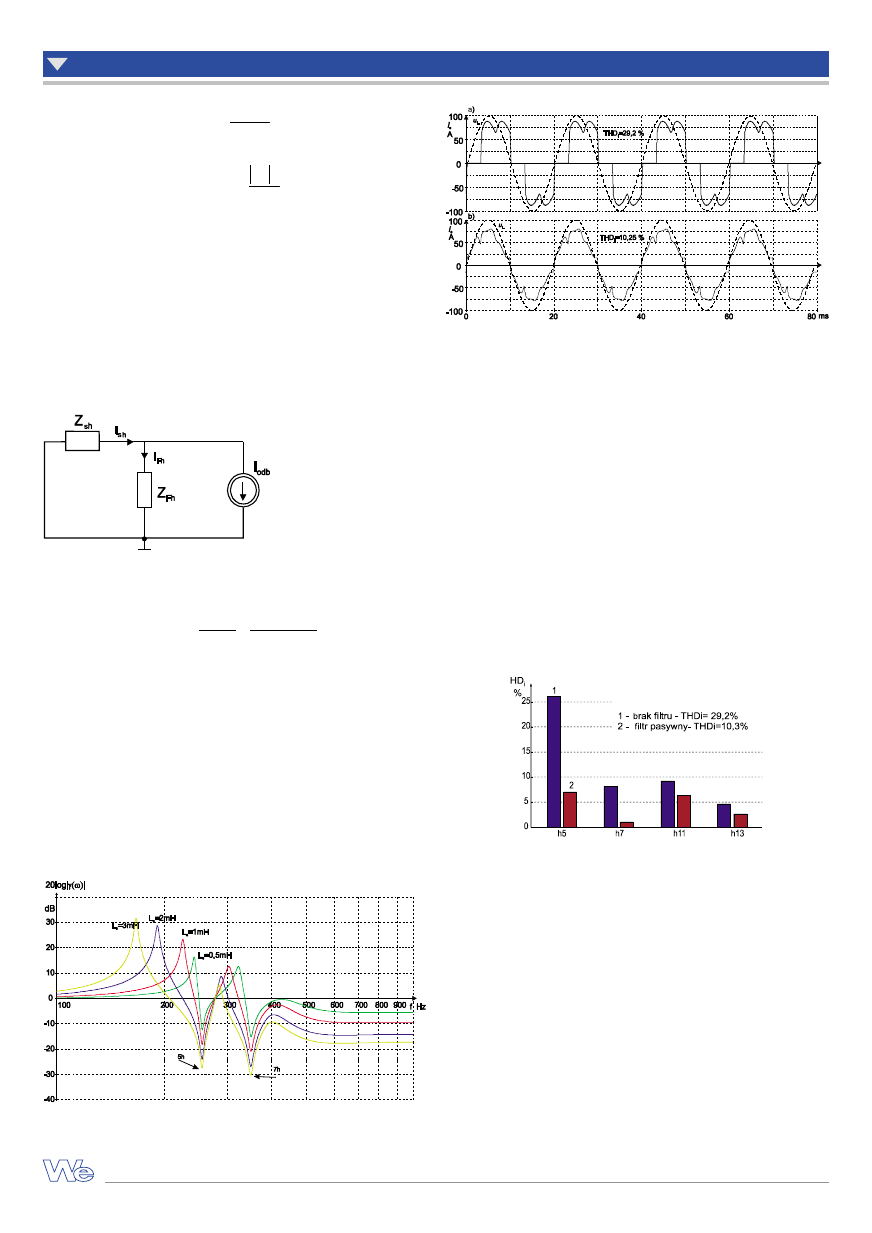
Na rysunku 7 pokazano energetyczny filtr aktywy opracowany przez

autorów artykułu w ramach projektu badawczego 3T10A04926, na-

tomiast na rysunku 8 – przykładowe przebiegi prądu i napięcia.

Rezonansowe filtry LC

Tradycyjnym sposobem redukcji wyższych harmonicznych sieci

zasilającej są rezonansowe filtry LC. Filtry te budowane są zazwy-

czaj w postaci gałęzi szeregowo połączonych kondensatorów i dła-

wików, których częstotliwość rezonansowa jest dostrojona do czę-

stotliwości wyższej harmonicznej prądu odbiornika. Liczba gałęzi

jest zależna od liczby filtrowanych harmonicznych.

Dla podstawowej harmonicznej filtry te pobierają moc bierną

pojemnościową, dlatego – przy odpowiednim doborze pojemności

– realizują także kompensację mocy biernej podstawowej harmo-

nicznej (odbiornik o charakterze indukcyjnym). Przykładową struk-

turę filtrów, podłączoną do układu źródło – odbiornik, pokazano na

rysunku 9. Elementy L

HF

, C

HF

oraz R

HF

w tym przypadku tworzą filtr

dla harmonicznych powyżej 7.

Dobór elementów LC przeprowadza się na podstawie warunku

rezonansu napięć oraz wymaganej reaktancji filtru dla podstawowej

harmonicznej, wynikającej z mocy biernej

Rys. 6.

Przebiegi czasowe

oraz zawartość

wyższych

harmonicznych

przed i po włączeniu

filtru aktywnego

Rys. 7.

Energetyczny

filtr aktywny

opracowany

przez autorów artykułu

w ramach

projektu badawczego

Rys. 8. Przebieg napięcia, prądu odbiornika, prądu filtru i prądu źródła,

w przypadku gdy odbiornik jest prostownikiem sześciopulsowym o obciążeniu

rezystancyjnym

Rys. 9.

Przykładowy układ 3-fazowy z podłączonym filtrem rezonansowym LC

Rok LXXV 2007 nr 8

23

MATERIAŁY KONFERENCYJNE 8 SPE-2007

(37)

(38)

gdzie:

L

h

, C

h

– wartości elementów dla poszczególnych harmonicznych,

|U

1

| – wartość skuteczna napięcia na filtrze dla pierwszej harmo-

nicznej,

Q

1

– moc bierna podstawowej harmonicznej,

Z – impedancja filtru.

Dla częstotliwości rezonansowej filtry mają niską impedancję, co

powoduje bocznikowanie prądów o danej częstotliwości. Jednofa-

zowy model, dla wyższych harmonicznych, układu z filtrem rezo-

nansowym przedstawiono na rysunku 10.

h

h

h

C

L

2

1

ω

=

h

h

h

C

L

2

1

ω

=

1

1

Q

U

Z

2

}

{

Im

−

=

1

1

Q

U

Z

2

}

{

Im

−

=

Efektywność filtracji zależy od impedancji (indukcyjności) sieci

i dla sieci o większej impedancji jest lepsza. Widoczne są tutaj także

efekty rezonansów równoległych (maksima) z siecią, co może być

problemem przy pojawieniu się w sieci częstotliwości, dla których

te rezonanse zachodzą.

Na rysunku 12 przedstawiono przebiegi prądu sieci dla przykła-

dowego układu z filtrem rezonansowym LC (rys. 9). Widoczna jest

tutaj znaczna poprawa współczynnika całkowitej zawartości harmo-

nicznych prądu sieci, a przebieg prądu (zbliżony do sinusoidy) jest

w fazie z napięciem fazowym, co świadczy o kompensacji mocy

biernej.

Procentową zawartość wyższych harmonicznych w prądzie sieci

przed i po użyciu filtru pasywnego LC pokazano na rysunku 13.

Właściwości układu opisuje współczynnik tłumienia wyższych har-

monicznych prądu odbiornika

(39)

gdzie: Z

Fh

– impedancja filtru, Z

sh

– impedancja sieci.

Analizując zależność (39), widać wyraźny wpływ impedancji sieci na

właściwości filtrujące układu, co jest jedną z podstawowych wad rezonan-

sowych filtrów LC. Na rysunku 11 przedstawiono charakterystykę często-

tliwościową modułu współczynnika tłumienia wyższych harmonicznych

dla różnych wartości indukcyjności sieci. Dla wybranych harmonicznych

(w tym przypadku 5. i 7.) współczynnik tłumienia wyższych harmonicz-

nych prądu odbiornika osiąga minimum, co powoduje zmniejszenie za-

wartości tych częstotliwości w prądzie źródła. Tłumienie wyższych har-

monicznych realizowane jest przez filtr wyższych harmonicznych HF.

sh

Fh

Fh

odbh

sh

Z

Z

Z

I

I

γ(ω)

+

=

=

sh

Fh

Fh

odbh

sh

Z

Z

Z

I

I

γ(ω)

+

=

=

Symetryzacja obciążenia

Przeprowadzenie symetryzacji układu stanowi poprawę warun-

ków pracy źródła, rozumianą jako zapewnienie równomiernego ob-

ciążenia poszczególnych faz układu oraz kompensację mocy biernej

dla każdej rozpatrywanej harmonicznej. W zakresie symetryzacji

można wyróżnić następujące kierunki:

– symetryzacja z wykorzystaniem jedynie dwójników LC [33],

– symetryzacja z wykorzystaniem dwójników LC i filtrów aktyw-

nych (EFA) [34],

– symetryzacja z wykorzystaniem jedynie filtrów aktywnych [35],

– symetryzacja z wykorzystaniem dwójników LC o zmiennych pa-

rametrach [36].

Rys. 11. Charakterystyka częstotliwościowa modułu współczynnika tłumienia

wyższych harmonicznych dla różnych przypadków impedancji sieci zasilającej

Rys. 10.

Jednofazowy

schemat zastępczy

analizowanego układu

Rys. 12. Przebieg prądu sieci na tle przebiegu napięcia sieci: a) przed

zastosowaniem pasywnego filtru LC, b) po zastosowaniu pasywnego filtru LC

Rys. 13. Porównanie zawartości wyższych harmonicznych przed włączeniem

i po włączeniu filtru

MATERIAŁY KONFERENCYJNE 8 SPE-2007

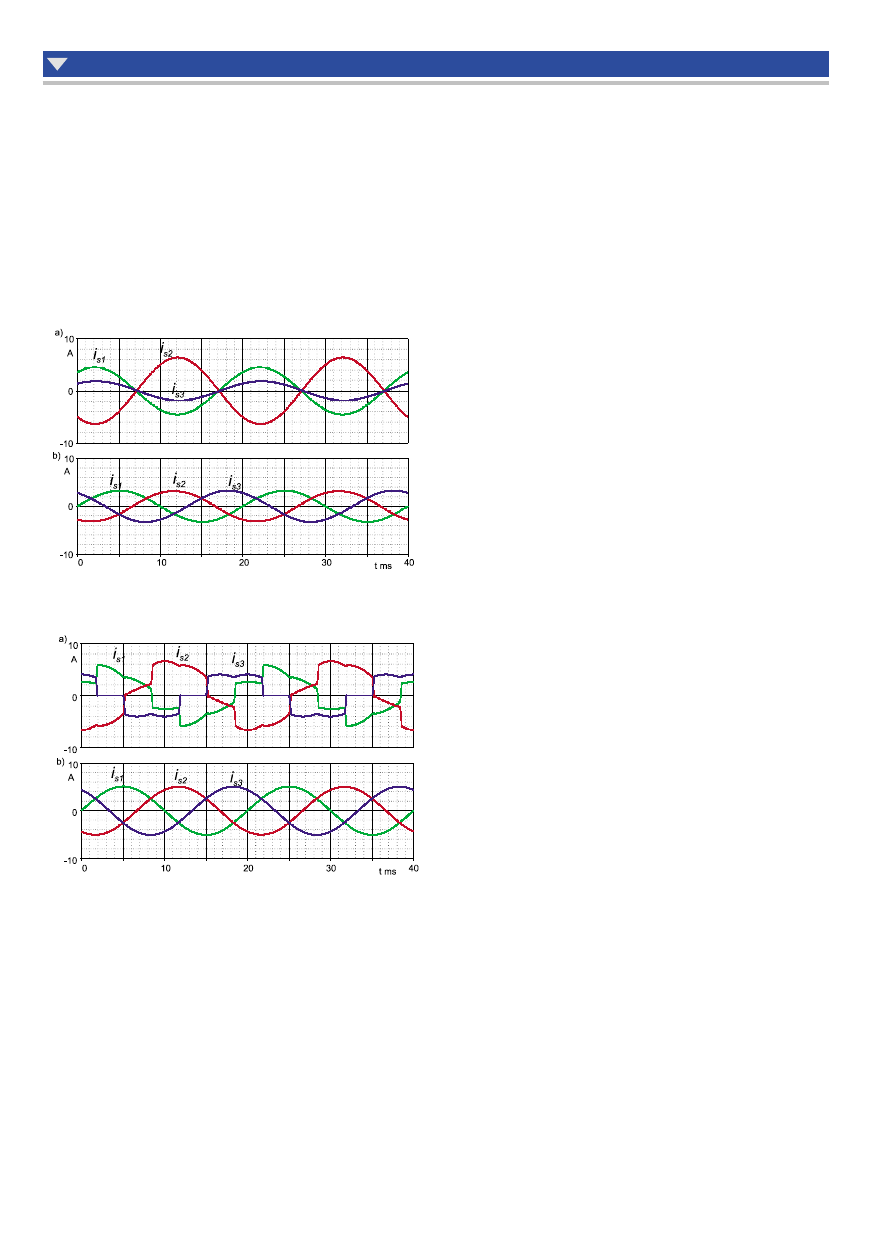
Przykładowy wynik symetryzacji dla odbiornika liniowego nie-

symetrycznego, przy zasilaniu źródłem symetrycznym sinusoidal-

nym przedstawiono na rysunku 14. Należy zwrócić uwagę, że po

symetryzacji wartości skuteczne prądów są mniejsze, przez co mniej

obciążają źródła oraz mniejsze są straty mocy czynnej na impedan-

cjach źródeł (linii).

Na rysunku 15 pokazano przykładowe przebiegi dla omawianego

układu EFA w przypadku obciążenia sieci odbiornikiem nielinio-

wym niesymetrycznym. Układ zasilany jest w tym przypadku ze

źródła symetrycznego sinusoidalnego.

Rys. 14. Przebiegi prądów sieci dla odbiornika niesymetrycznego liniowego:

a) przed symetryzacją, b) po symetryzacji

LITERATURA

[1] Emanuel A.E.: Suggested definition of reactive power nonsinusoidal systems. Proc.

IEEE 1974 nr 7

[2] Czarnecki L.S.: Interpretacja, identyfikacja i modyfikacja właściwości energetycz-

nych obwodów jednofazowych z przebiegami odkształconymi. Zeszyty Naukowe

Politechniki Śląskiej, Elektryka 1984 z. 91

[3] Pasko M.: Dobór kompensatorów optymalizujących warunki pracy źródeł napięć

jednofazowych i wielofazowych z przebiegami okresowymi odkształconymi. Ze-

szyty Naukowe Politechniki Śląskiej, Elektryka 1994 z. 135

[4] Czarnecki L.S.: Moce i kompensacja w obwodach z okresowymi przebiegami prą-

du i napięcia. Część 8. Równoważenie i kompensacja mocy biernej liniowych od-

biorników trójfazowych. Jakość i Użytkowanie Energii Elektrycznej 2001 tom VII

z. 1

[5] Pasko M.: Modification of three-phase systems with nonsinusoidal waveforms for

optimization of source current shape. Archiwum Elektrotechniki 1995 tom XLIV,

z.1

[6] Pasko M., Walczak J.: Optymalizacja energetyczno-jakościowych właściwości

obwodów elektrycznych z przebiegami okresowymi niesinusoidalnymi. Zeszyty

Naukowe Politechniki Śląskiej, Elektryka 1996 z. 150

[7] Siwczyński M.: Teoria uniwersalnych globalnie pasywnych obwodów kompensa-

cyjnych. Jakość i Użytkowanie Energii Elektrycznej 2000 tom VI

[8] Strzelecki R., Supronowicz H.: Współczynnik mocy w systemach zasilania prądu

przemiennego i metody jego poprawy. Oficyna Wydawnicza Politechniki Warszaw-

skiej, Warszawa 2000

[9] Walczak J.: Optymalizacja energetyczno-jakościowych właściwości obwodów

elektrycznych w przestrzeniach Hilberta. Zeszyty Naukowe Politechniki Śląskiej,

Elektryka 1992 z. 125

[10] Pasko M., Maciążek M.: Algorytm numeryczny do wyznaczania struktur kompen-

satorów pasywnych i aktywnych w jednofazowych układach z przebiegami od-

kształconymi okresowymi. Zeszyty Naukowe Politechniki Śląskiej, Elektryka 2000

z. 167

[11] Maciążek M., Pasko M.: Komputerowo wspomagana optymalizacja stanów pracy

układów trójfazowych z przebiegami okresowymi odkształconymi. Jakość i Użyt-

kowanie Energii Elektrycznej 2001 tom VII, z. 1

[12] Maciążek M., Pasko M.: Algorytm numeryczny syntezy uniwersalnego dwójnika

kompensacyjnego. Konferencja „Zastosowania komputerów w elektotechnice”,

Poznań-Kiekrz 2002

[13] Maciążek M.: Zastosowanie nowych technik do identyfikacji, optymalizacji i mo-

dyfikacji stanu pracy układów elektrycznych z przebiegami okresowymi odkształ-

conymi. Praca doktorska, Politechnika Śląska, Gliwice 2003

[14] Pasko M., Dębowski K.: Symetryzacja układów trójfazowych wielofazowych za-

silanych ze źródeł napięć okresowych odkształconych. Wydawnictwo Politechniki

Śląskiej, Gliwice 2002

[15] Fryze S.: Moc czynna, bierna i pozorna w obwodach o przebiegach odkształconych

prądu i napięcia. Przegląd Elektrotechniczny 1931 nr 7 oraz 1932 nr 22

[16] Shepherd W., Zakikhani P.: Suggested definition of reactive power for nonsinusoi-

dal systems. Proc. IEE 1972 nr 9, 1973 nr 7

[17] Kusters N.L., Moore W.J.M.: On the definition of reactive power under nonsinuso-

idal conditions. IEEE Trans. Pow. Appl. Systems 1980 vol. 99

[18] Pasko M., Siwczyński M., Walczak J.: Dlaczego zawodzi ortogonalny rozkład prą-

du dla obwodów z przebiegami niesinusoidalnymi? Konferencja „Elektrotechnika

prądów niesinusoidalnych”, Zielona Góra 1995

[19] Maciążek M., Pasko M.: The algorithm of active power filter control in the case

of supply voltage unbalance. Konferencja „Zastosowania komputerów w elektro-

technice”, Poznań-Kiekrz 2002

[20] Pasko M., Maciążek M.: Algorytm sterowania filtrem aktywnym dla uzyskania

prądu czynnego źródła według koncepcji Fryzego. Zeszyty Naukowe Politechniki

Szczecińskiej, Elektryka 2003

[21] Czarnecki L.S.: Power properties of three-phase electric circuits and their misin-

terpretations by the instantaneous reactive power p-q theory. Przegląd Elektrotech-

niczny 2003 nr 12

[22] Afonso J., Couto C., Martins J.: Active Filters with Control Based on the p-q

Theory. IEEE Industrial Electronics Newsletter 2000 nr 3 http://sant.bradley.eduie-

news/00_3/newtech.pdf

[23] Akagi H., Kanazawa y., Nabae A.: Instantaneous Reactive Power Compensators

Comprising Switching Devices without Energy Storage Components. IEEE Tran-

sactions on Industry Applications 1984 nr 3

[24] Akagi H., Nabae A.: The p-q Theory in Three-Phase Systems under Non-Sinusoidal

Conditions. ETEP 1993 nr 3

[25] Hanzelka Z.: Zastosowanie wektorowej teorii mocy chwilowej do sterowania

energetycznych filtrów aktywnych. Międzynarodowa Konferencja „Jakość Energii

Elektrycznej”, Spała 1991

[26] Watanabae E. H., Aredes M.: Compensation of Non-Periodic Currents Using the

Instantaneous Power Theory. IEEE PES Summer Meeting, Seattle 2000

[27] Maciążek M., Pasko M.: Sterowanie filtrami aktywnymi przy wykorzystaniu teo-

rii mocy chwilowej (p-q). Zeszyty Naukowe Politechniki Śląskiej, Elektryka 2002

z. 182

Podobne zasady symetryzacji obowiązują również wtedy, gdy źród-

ło zasilania jest symetryczne, ale odkształcone [33].

Podsumowanie

W artykule przedstawiono metody kształtowania prądu źródła

(eliminacji wyższych harmonicznych). Dynamiczny wzrost liczby

odbiorników nieliniowych, w szczególności urządzeń powszechne-

go użytku, powoduje że problemy związane z obecnością wyższych

harmonicznych w przebiegach prądów i napięć będą się nasilać.

Dlatego prezentowane zagadnienia są ważne zarówno z punktu wi-

dzenia naukowego, jak i ekonomicznego.

Pracę wykonano w ramach projektu badawczego 3T10A04926

Rys. 15. Przebiegi prądów sieci dla odbiornika niesymetrycznego

nieliniowego: a) przed włączaniem układu EFA, b) po włączeniu układu EFA

Rok LXXV 2007 nr 8

25

MATERIAŁY KONFERENCYJNE 8 SPE-2007

[28] Cristaldi L., Ferrero A.: Mathematical Foundations of the Instantaneous Power

Concepts: An Algebraic Approach. ETEP 1996 nr 5

[29] Komatsu y., Kawabata T.: A control method of active power filter where system

voltage contains negative-phase-sequence component or zero-phase-sequence com-

ponent. PEDS 95, Singapore 1995

[30] Komatsu y., Kawabata T.: A control method for the active power filter in unsyme-

trical voltage systems. Int. J. Electronics 1999 nr 10

[31] Komatsu y., Kawabata T.: A control method for the active power filter in unsyme-

trical voltage systems. Proc. EPE’95, Sevilla 1995

[32] McGranaghan M.: Active filter design and specification for control of harmonics in

industrial and comercial facilities. Technical document from Dranetz BMI Home-

page url:http://www.dranetz-bmi.com

[33] Pasko M., Dębowski K.: Symmetrization of three-phase and multi-phase systems

supplied from sources of periodic nonsinusoidal voltages. Publishing House of Si-

lesian University of Technology, Gliwice 2002

[34] San-yi Lee, Chi-Jui Wu.: Combined compensation structure of a static VAr com-

pensator and an active filter for unbalanced three-phase distribution feeders with

harmonic distortion. Electric Power Systems Research 1998 nr 3

[35] Nedeljkovic D., Nastran J., Ambrozic V.: Symmetrization of line currents in three-

phase four-wire loads. Industrial Electronics 1999, IEEE Proc. 1999 vol. 2

[36] Chindris M., Cziker A., Stefanescu S.: Fuzzy logic controller for Steimetz symme-

trizing circuitry with variable reactor. IEEE Porto Power Tech Conference, Portugal

2001

[37] Bhattacharya S., Divan D.M., Banerjee B.: Synchronous Frame Hamonic Isolator

Using Active Series Filter. EPE 91 Conference Proceedings, Firenze, Italy 1991

[38] Piróg S.: Energetyczne filtry aktywne i kompensatory podstawowej harmonicznej

prądu biernego STATCOM sterowane we współrzędnych wirujących dq. Jakość

i użytkowanie energii elektrycznej 2001 t. VII, z. 1

Od Autorów: W numerze 4/07 WE (ss. 4-9) ukazała się pierwsza część tego

artykułu, przygotowywanego pierwotnie jako całość. Podczas podziału tekstu

niekonsekwentnie zostały rozdzielone poszczególne pozycje bibliografii. Poda-

jemy więc ponownie uporządkowany wykaz, uwzględniający numerację pozycji

zastosowaną w I części.

LITERATURA do I cz. (WE 4/07, s. 9)

[1] Jakość Energii Elektrycznej – słownik terminów. http://tsunami.kaniup.agh.edu.

pl/~lds/lista/slownik.htm

[3] Baranecki A., Płatek T., Niewiadomski M.: Harmoniczne prądu – problemy pomia-

rowe. Elektro info 2003 nr 7

[4] Hanzelka Z., Kowalski Z.: Kompatybilność elektromagnetyczna i jakość energii

w dokumentach normalizacyjnych. Jakość i Użytkowanie Energii Elektrycznej

1999 t. 5, z. 1

[5] http://www.electroportal.net

[6] Baranecki A., Niewiadomski M., Płatek T.: Odbiorniki nieliniowe – problemy i za-

grożenia. Wiadomości Elektrotechniczne 2004 nr 2

[7] International Electrotechnical Commission (IEC). Technical Committee. No. 25.

Working Group 7. Report: Reactive power and distortion power. Dec. 1979

[8] IEEE. The new IEEE standard dictionary of electrical and electronics terms. New

york: IEEE, 1992

[9] IEEE Working group on nonsinusoidal situations. Practical definitions for powers in

systems with nonsinusoidal waveforms and unbalanced loads: A discussion. IEEE

Trans. on Power Delivery 1996 nr 1

[10] IEEE Trial–use standard definitions for the measurement of electric power quanti-

ties under sinusoidal, nonsinusoidal, balanced or unbalanced conditions. IEEE std.

1459-2000, 21 June 2000

[12] http://www.electronic-circuits-diagrams.com

[13] Gawlik W.: H. M. Time Domain Modelling of Active Filters for Harmonic Compen-

sation. IEEE, PowerTech, Bologna 2003

[14] Filtracja i detekcja harmonicznych. Schneider Electric Polska. http://www.schnei-

der-electric.pl.

[15] Beniak R. i in.: Jakość energii elektrycznej – normalizacja, pomiary, przykłady.

Wiadomości Elektrotechniczne 2003 nr 4

[16] Rozporządzenie Ministra Gospodarki i Pracy z dnia 20 grudnia 2004 r. w sprawie

szczegółowych warunków przyłączenia podmiotów do sieci elektroenergetycz-

nych, ruchu i eksploatacji tych sieci. Dz.U. 2005 nr 2

[17] PN-EN 50160:2002/Ap1:2005 Parametry napięcia zasilającego w publicznych sie-

ciach rozdzielczych

[18] Pasko M., Maciążek M.: Zjawiska energetyczne w obwodach elektrycznych i ich

interpretacje. Wiadomości Elektrotechniczne 2005 nr 4

[19] Pasko M., Maciążek M.: Wkład elektrotechniki teoretycznej w poprawę jakości

energii elektrycznej. Wiadomości Elektrotechniczne 2004 nr 7–8

KONFERENCJE

Kilkuset energetyków odwiedzi w czerwcu przyszłego roku

Toruń i jego okolice. Sprawdzono już bazę hotelową, sale

pokazowe, obiekty techniczne, zapoznano się z walorami

turystycznymi miasta i okolic.

25 kwietnia odbyło się w Toruniu w Oddziale Koncernu Ener-

getycznego ENERGA SA spotkanie organizatorów przyszłorocznej

Międzynarodowej Konferencji Prac Pod Napięciem – ICOLIM.

Uczestnicy spotkania zapoznali się z miejscami i obiektami tech-

nicznymi, w których odbywać się będą w czerwcu 2008 r. prelek-

cje i pokazy zastosowania technologii prac pod napięciem (PPN).

Zapoznano się ponadto z bazą hotelową Torunia i jego walorami

turystycznymi.

Decyzja o wyborze Polski i Torunia na miejsce ICOLIM-u 2008

była dowodem uznania wkładu energetyków polskich, w tym Od-

działu Toruńskiego, w rozwój technologii PPN w eksploatacji sieci

elektroenergetycznych.

Konferencje Prac Pod Napięciem – ICOLIM – organizowane są

od roku 1992, co dwa lata w innym państwie. Służą one wymianie

wiedzy i doświadczeń w tej dziedzinie. Tradycyjnie w konferencji

uczestniczą przedstawiciele kilkudziesięciu krajów. Spoza Europy

na konferencji bywają: Amerykanie, Kanadyjczycy, Japończycy,

Argentyńczycy, Urugwajczycy, Tajlandczycy. Konferencje obejmu-

ją część teoretyczną i praktyczną – pokazy prac pod napięciem. Każ-

dej konferencji towarzyszą wystawy sprzętu i narzędzi stosowanych

w tej technologii.

Trwają przygotowania

do ICOLIM-u 2008 w Toruniu

Przedstawiciele Polski w towarzystwie członka Komitetu Organizacyjnego

Międzynarodowej Konferencj Prac Pod Napięciem ICOLIM – Gyorgy’ego

Felera (Węgry).

Od lewej: Zbigniew Michalski – KE ENERGA SA – Oddział w Toruniu,

Roman Kuczkowski – wiceprezes Polskiego Towarzystwa Rozdziału

Energii Elektrycznej w Poznaniu, Andrzej Pazda – dyrektor Biura PTPiREE

w Poznaniu, Gyorgy Feler – Komitet Organizacyjny ICOLIM-u – Węgry,

Krzysztof Dębczyński – dyrektor generalny KE ENERGA SA – Oddział

w Toruniu, Dariusz Lubera – prezes PTPiREE w Poznaniu, Krzysztof Dmoch

– dyrektor ds. dystrybucji KE ENERGA SA – Oddział w Toruniu