Analiza regresyjna

1. Zależność funkcyjna pewnej zmiennej y od zmiennej u - jednoznaczne przyporządkowanie każdej możliwej wartości u określonej wartości y: y=f(u).

W analizie statystycznej - ta zależność funkcyjna nieprzydatna. W analizie statystycznej - zależność stochastyczna pewnej zmiennej losowej Y od zmiennej losowej U: jednoznaczna zależność rozkładu prawdopodobieństwa zmiennej losowej Y od wartości u przybranej przez zmienną losową U.

W praktyce często interesuje nas nie cała dystrybuanta (gęstość prawdopodobieństwa), lecz jej moment I rzędu tj. wartość oczekiwana zmiennej losowej T przy warunku u.

Jeżeli wartość oczekiwana zmiennej losowej Y przy warunku u jest funkcją u

to mówimy o korelacji (współzależności) między zmiennymi Y i U.

Korelację między dwiema zmiennymi losowymi można przedstawić za pomocą wykresu punktowego korelacji zwanego również polem korelacji, nanosząc poszczególne obserwacje.

Korelację jako zależność stochastyczną charakteryzuje się analitycznie za pomocą zależności

,

zwanej regresją lub funkcją regresji.

Jeżeli interesuje nas zależność stochastyczna zmiennej losowej Y od zmiennej losowej U, to rozpatrujemy funkcję regresji zmiennej losowej Y względem zmiennej losowej U, czyli funkcję:

Funkcja regresji jest wyrazem zależności funkcyjnej tkwiącej w zalezności stochastycznej.

Funkcja regresji
, określona jako warunkowa wartość oczekiwana, nosi nazwę funkcji regresji I rodzaju lub teoretycznej funkcji regresji.

W praktyce na ogół nie jesteśmy w stanie wyrazić dokładnie funkcji regresji I rodzaju, gdyż zwykle dysponujemy tylko zbiorowością próbną pochodzącą za zbiorowości generalnej. Sporządzamy wykres punktowy i na podstawie smugi punktów wysuwamy hipotezę, że funkcja regresji należy do określonej klasy funkcji

liniowych względem parametrów (nieznanych) Θ₀, Θ₁, ..., Θ_K i poszukujemy najlepszych estymatorów tych parametrów w sensie określonego kryterium estymacji, np. najmniejszych kwadratów, największej wiarygodności, itp.

Otrzymana w ten sposób funkcja
nosi nazwę funkcji regresji II rodzaju lub empirycznej funkcji regresji.

W przypadku wielowymiarowym, gdy na wielkość Y, a ściślej na jej rozkład, wpływa wiele zmiennych losowych U₁, U₂, ..., U_S, przyjmujemy, że funkcja regresji należy do klasy funkcji

Z reguły przyjmujemy, że powyższa funkcja regresji jest liniowa względem nieznanych parametrów Θ₀, Θ₁, ..., Θ_K
gdzie

przy czym funkcje
, k=1,2,...K, są znane i w ogólnym przypadku mogą być nieliniowe.

3. Metoda najmniejszych kwadratów:

Model :

Obiekt:

- nieznane parametry (należy je estymować - oszacować).

Różnica między obiektem a jego modelem

interpretuje się jako błąd aproksymacji obiektu przez model; błąd ten powinien być jak najmniejszy. Stąd zadanie minimalizacji błędu
(lub sumy wartości bezwzględnych
albo sumy kwadratów
) względem wektora nieznanych parametrów, np.

Kwadratowe kryterium minimalizacji
-metoda najmniejszych kwadratów (MNK).

Kryterium minimalizacji funkcji „strat” według MNK

Stąd
-optymalny najmniejszo-kwadratowy estymator wektora

Optymalny najmniejszo - kwadratowy estymator nieznanych parametrów
modelu liniowego

4. Obciążenie estymatora:

jeśli:

1. klasa modelu należy do klasy obiektu, tj. dane wyjściowe generowane przez model i przez obiekt różnią się jedynie o zakłócenie
   ,

2. 
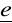
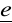
   jest wektorem zmiennych losowych stochastycznie niezależnych o stałej wariancji σ² i zerowej wartości oczekiwanej, tj.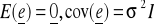
   ,

wówczas
, tzn. estymator
parametrów
jest nieobciążony.

W praktyce zakłócenia mają często charakter szumów skorelowanych (nie „białych”); wówczas estymator najmniejszokwadratowy
jest obciążony.

Macierz kowariancji estymatora
nieobciążonego

Elementy diagonalne macierzy
charakteryzują wariancję parametrów Θ_i, zaś elementy pozadiagonalne charakteryzują kowariancje odpowiednich parametrów Θ_i, Θ_j.

Dlatego też macierz
jest nazwana macierzą kowariancyjną. W rzeczywistości macierz
jest proporcjonalna do macierzy kowariancji estymatora
.

Jeśli
-osobliwa, to „wybuch” (niestabilność) estymatora. Występuje to, gdy kolejne wartości wejścia u_i, u_i+1 są sobie równe (lub bliskie siebie).

5. Badania istotności statystycznej modelu

Zakładamy, że zakłócenia
są wektorem niezależnych zmiennych losowych o wartości oczekiwanej
i wariancji σ².

Dla zbadania istotności statystycznej modelu konieczne jest jeszcze założenie o postaci rozkładu prawdopodobieństwa zakłóceń. Przyjmiemy w dalszym ciągu, że zakłócenia mają wielowymiarowy rozkład normalny:

Wielkość wyjściowa
ma również wielowymiarowy rozkład normalny typu:

.

Także estymator
nieznanych parametrów
ma wielowymiarowy rozkład normalny typu:

Współczynniki Θ_k (k=0,1,...,K) modelu są normalnymi zmiennymi losowymi o wartości oczekiwanej Θ_k i dyspersji
.

Zmienna unormowana

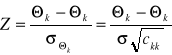
ma rozkład typu N(0,1).

W praktyce nie znamy często wariancji zakłóceń σ² i posługujemy się jej estymatorem s²

o rozkładzie chi kwadrat o N-K-1 stopniach swobody.

Zamiast zmiennej losowej Z tworzymy wówczas zmienna losową

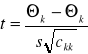
która ma rozkład Studenta o N-K-1 stopniach swobody. Można więc skonstruować przedział ufności na poziomie ufności 1-α dla tej zmiennej określony równością

czyli przy posługiwaniu się tablicą wartości krytycznych t_kryt rozkładu t Studenta o N-K-1 stopniach swobody na poziomie istotności α -równością

Po wyznaczeniu z tablic wartości krytycznej t_kryt podstawiamy do nierówności
zamiast t_N-K-1 wyrażenie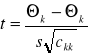
i przekształcamy tak, aby w środkowym członie występował parametr estymowany Θ_k.

Otrzymujemy:

Zależność ta określa przedział ufności dla parametru estymowanego Θ_k na poziomie ufności 1-α.

Dla duzych wartości stopni swobody N-K-1>30 zamiast rozkładu t Studenta można przyjmować rozkład normalny N(0,1) do wyznaczania wartości krytycznej t_kryt.

W praktyce duże znaczenie ma hipoteza zerowa typu:

H₀ : Θ_k=0, która przyjmuje, że między wyjściem obiektu y a danym wejściem u_k nie ma zależności liniowej. W tym przypadku obliczamy wartość

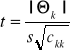
k=0,1,...,K

Jednocześnie wyznaczamy z tablic t Studenta wartość krytyczną t_kryt przy przyjętym poziomie istotności i liczbie stopni swobody N-K-1, spełniającą równość
. Jeżeli wartość obliczona zmiennej t spełnia warunek
to odrzucamy hipotezę zerową H₀ . W przypadku przeciwnym nie ma podstaw do odrzucenia hipotezy.

6. Metoda uogólnionych najmniejszych kwadratów - wejścia off-line

Metoda najmniejszej uogólnionej sumy kwadratów

Niech funkcja strat

gdzie W jest pewną funkcją „wagową”

Wówczas:

Jest to optymalny estymator wektora parametrów
według uogólnionych najmniejszych kwadratów.

Dobór
wynika z następującej zależności na macierz kowariancji zakłóceń
, jeśli są one skorelowane
.

Wprowadzenie macierzy wagowej
do funkcji strat
sprawia, że otrzymany estymator
jest nieobciążony ( estymator metodą NK byłby obciążony, gdyż zakłócenie
nie jest już wektorem niezależnych zmiennych losowych).

dla metody uogólnionych NK.

7. Estymator rekursywny (on-line) według metody najmniejszych kwadratów; nasycenie estymatora.

Estymator rekursywny wartości oczekiwanej:

k=1,2,...

warunki początkowe:

Trzeba wprowadzić element rekursywny i nadać mu wartość początkową.

Estymator off line najmniejszych kwadratów:

dla długości danych N

Estymator rekursywny metodą NK on-line

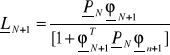
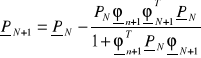
Warunki początkowe:

,

- macierz kowariancji

8. Estymator adaptacyjny według metody najmniejszych kwadratów; adaptacja przez zapominanie wykładnicze.

Estymacja adaptacyjna NK = rekursywna NK + mechanizm zapominania wykładniczego.

-> NK

-> adaptacyjna wersja NK

0<λ<1

λ - współczynnik zapominania wykładniczego, tłumi stare pomiary.

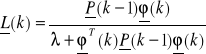
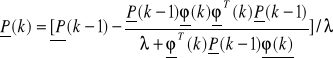
warunek początkowy

Przełączanie λ:

1. λ bliskie 1 jeśli mała zmiana parametrów w czasie

2. λ dalsze od 1 (np. 0,96) szybka zmiana parametrów w czasie

Estymator adaptacyjny stosuje się najczęściej w przypadku modeli dynamicznych.

Metoda najmniejszych kwadratów off line.

ogólnie

estymator off-line NK

1

4

---