Zamiana zmiennych w całce potrójnej

Tw. (o Zamianie zmiennych w całce potrójnej)

Jeżeli

1. odwzorowanie

przekształca wzajemnie jednoznacznie wnętrze obszaru regularnego
na wnętrze obszaru regularnego V

2. funkcje
są klasy C¹ na pewnym zbiorze otwartym zawierającym zbiór

3. jakobian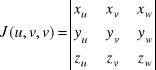
jest różny od zera wewnątrz obszaru

4. funkcja podcałkowa f jest ciągła na V

to

.

Współrzędne walcowe (cylindryczne)

Położenie punktu P w przestrzeni opisujemy trójką liczb
gdzie

r - odległość rzutu punktu P na płaszczyznę 0xy od początku układu współrzędnych,

- miara kąta między rzutem promienia wodzącego punktu P na płaszczyznę 0xy a dodatnim kierunkiem osi 0x
lub

Zależności między współrzędnymi kartezjańskimi a walcowymi punktu opisują wzory

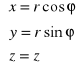
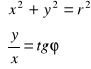
Wzór na zamianę współrzędnych kartezjańskich na współrzędne walcowe w całce potrójnej ma postać

Przykłady

1.

Opisać we współrzędnych walcowych obszary

a) walec o promieniu podstawy 2, którego osią symetrii jest oś 0z, ograniczony płaszczyznami
;

b) stożek ograniczony powierzchnią
i płaszczyzną
,
;

2.

a) Obliczyć objętość bryły ograniczonej powierzchnią paraboloidy obrotowej
i płaszczyzną
.

Współrzędne sferyczne

Położenie punktu P w przestrzeni opisujemy trójką liczb
gdzie

R- odległość punktu P od początku układu współrzędnych (długość promienia wodzącego punktu)

- miara kąta, jaki tworzy wektor wodzący punktu z dodatnim kierunkiem osi 0z,

- miara kąta między rzutem promienia wodzącego punktu P na płaszczyznę 0xy a dodatnim kierunkiem osi 0x,
lub

Zależności między współrzędnymi kartezjańskimi a walcowymi punktu opisują wzory

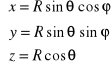
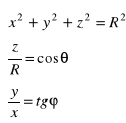
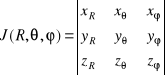
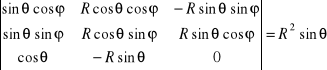
Wzór na zamianę współrzędnych kartezjańskich na współrzędne sferyczne w całce potrójnej ma postać

Przykład

1. Opisać we współrzędnych sferycznych obszary

a) kula o środku w początku układu współrzędnych i promieniu a,

b) kula o środku w punkcie
i promieniu a,

30

---