Wytrzymałość Materiałów 4

Zginanie belek z udziałem sił tnących

Wzór Żurawskiego (patrz strona 206 książka autora Jana Misiaka

z Statyka i Wytrzymałość

R_Az R_Ax P R_B Materiałów)

A x

x dx B

a

l

M

dM

T

M+dM N+dN

z dx x

z

M

₁ z₁ y

τ_z -z A_z

N dA τ_{z 1} b_z

*

Rys. 17 Określenie naprężeń stycznych w zginanej belce

∑P_ix = -N + τ_zb_zdx + N + dN = 0
(b)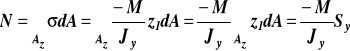

Różniczkując N po x mamy:

dN/dx = - (dM/dx)·(S_y/J_y) (c)

M T M+dM

∑M₀ = M- M- dM + Tdx = 0 0 x

T=dM /dx (d) dx T+dT

podstawiając (c) i (d) do (b) mamy:

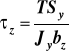
gdzie
(13)

Przykład 7

Określić rozkład naprężeń stycznych przy zginaniu belki o przekroju prostokątnym o wymiarach b×H (rys.18), oraz dobrać wartość H= 2h z warunku τ_max = 50 MPa. Wartość siły tnącej w rozpatrywanym przekroju wynosi T= 10⁴N, a stosunek 2h/b = 4.

dA=dydz₁ z A_z

z₁ 2h z h₁ y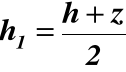
; H=2h

A_z = b(h-z)

b

Rys.18 Określenie naprężeń stycznych

Rozwiązanie

Moment statyczny pola A_z względem osi obojętnej z

S_y = A_zh₁ = b(h²-z²)/2 S_ymax = bh²/2 = bH²/8

Moment bezwładności pola przekroju względem osi y

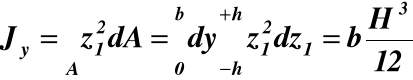
(14)

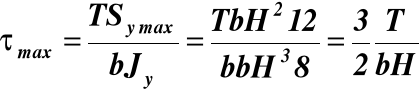
(c)

Podstawiając do (c) T = 10⁴ N, b = H/4,

τ_max = 50MPa otrzymujemy:

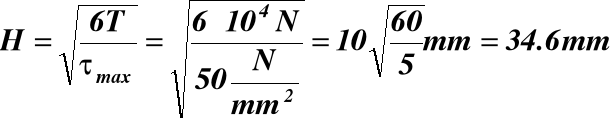
Odpowiedz: H = 34.6mm, b = H/4 = 34.6/4 = 8.6mm

Naprężenia średnie: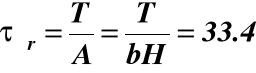
MPa

τ_max /τ_śr = 1.5

Stan czystego ścinania (Jan Misiak strona 181 książka SiWM)

γ τ s = γ ·1

a) z τ₂ b)

τ₃

τ τ

1 τ₁

o 1 0

x τ

1 τ₄

Rys.19 Parametry czystego ścinania

Warunki równowagi prostopadłościanu o wymiarach 1×1×1

∑P_x = τ₂×1×1−τ₄×1×1=0 τ₂ = τ₄

∑P_y = τ₃×1×1−τ₁×1×1=0 τ₁ = τ₃ τ_i = τ

∑M_o = τ₂×1×1×1−τ₃×1×1×1=0 τ₂ = τ₃

Energia odkształcenia w stanie czystego ścinania kostki

o wymiarach 1cm³ V₁ = L(praca) = τ · s / 2 = τγ / 2.

τ

tgα = τ/γ =G τ = G×γ (15)

τ_pl τ_spr

α

γ

Rys. 20 Wykres naprężeń τ w funkcji γ

G moduł sprężystości postaciowej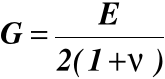

Skręcanie prętów (J. Misiak st.215 książka St. i Wyt. Mat.)

M_s dr

* r

s dA R_z

γ_r l α r

dα

τ_max dA r

dr

Rys.21 Skręcanie rd* dP

τ_r

dP = dAτ_r ; dM_s = rdP = rdAτ_r ; τ_r /τ_max = r/R_z ; (τ_max /R_z )= τ_r / r

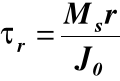
gdzie (16)

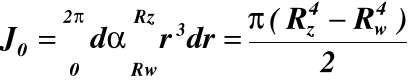
(17)

z rys.21 s = γ_r l = *r; τ_r = Gγ_r ; γ_r = τ_r /G; * = γ_r l /r

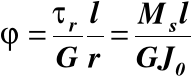
(18)

Przykład 8

Określić przebieg momentów skręcających w wale przedstawionym na rysunku 22.

M_A M_S M_B

a b

Rys.22

M_A1 = M_S M_S *₁ *₁

M_A2 = M_B
l = a+b *₂

M_B

*₁= M_S a /(GJ₀); *₂= M_B l /(GJ₀)

*₁+ *₂ = 0; M_S a + M_B l =0; M_B = M_S a l

M_A = M_A1 + M_A2 = M_S M_S a l = M_S b/l

M_A M_S

M_B

Rys.22a Wykres momentów skręcających

Przykład 9

Dla wału z rysunku 22 dobrać średnice tak aby współczynnik bezpieczeństwa n_e = 2. Dane τ_e = 125 MPa

τ_dop = τ_e /n_e = 125/2 = 62.5 MPa; M_s = 10⁴ Nm;
a = 1.2m,

b = 1.5m; R_z = R

Rozwiązanie

M_A = M_S (b/l) = 10⁴(1.5/2.7) = 5556 Nm

M_B = - M_S (a/l) = -10⁴(1.2/2.7) = -4444 Nm

M_max = M_A = 5556Nm

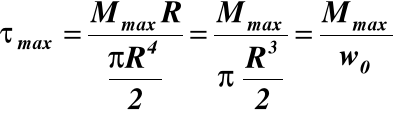
(19)

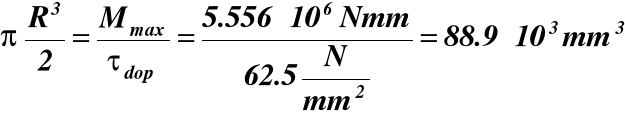
d = 2R = 76.8mm

22 WM

23WM

24WM

R_w

25WM

26WM

27WM

---