Równania drgań układu o n - stopniach swobody układamy korzystając z równania Lagrange'a drugiego rodzaju.
gdzie L= Ek - Ep
-masy
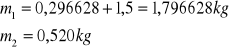
-współczynniki sprężystości
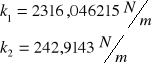
-współczynniki tłumienia
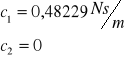
Przelicznik
![]()
Dla dwóch stopni swobody otrzymujemy równania
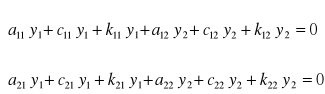
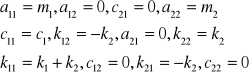
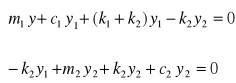
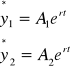
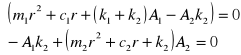
Δ=0
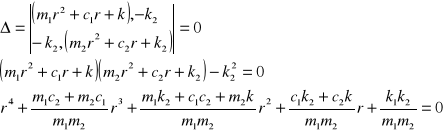
Przyjmując c2 =0 otrzymamy:
![]()
![]()
podstawiając dane otrzymamy:
![]()
Pierwiastków równania poszukujemy w zakresie liczb zespolonych. Do tego celu można użyć metody
Newtona, lub programu DERIVE. Ostatecznie pierwiastki równania mają postać:
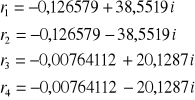
![]()
równania q1(t) i q2(t) możemy zapisać jako:
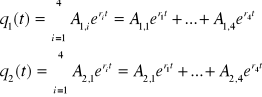
Obliczenie Aj,i przyjmując jako wartość niezależną
A1,i =A2,i*1,i/2,i
gdzie:
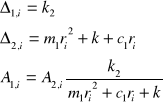
Podstawiając wartości liczbowe otrzymujemy:

![]()
Ogólnie mamy:
![]()
Ostatecznie podstawiając powyższy wzór otrzymujemy równania postaci:
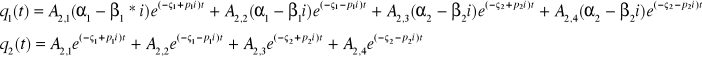
korzystając ze wzoru:
![]()
![]()
uzyskujemy postać powyższych funkcji względem nowych stałych C1 i C2 stosując następujące podstawienie stałych
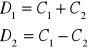
![]()
funkcje powyższe można zapisać w postaci
![]()
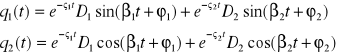
wartości D1,D2,ϕ,ϕ określamy wykorzystując warunki początkowe
ξ=5mm - wychylenie początkowe
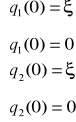
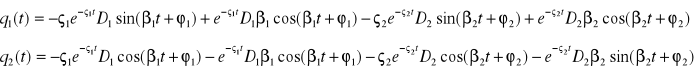
uwzględniając warunki i stosując podstawienia uzyskujemy układ równań
![]()
![]()
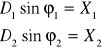
![]()
![]()
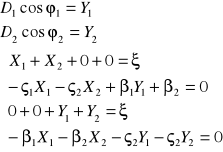
stąd![]()
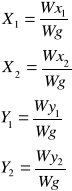

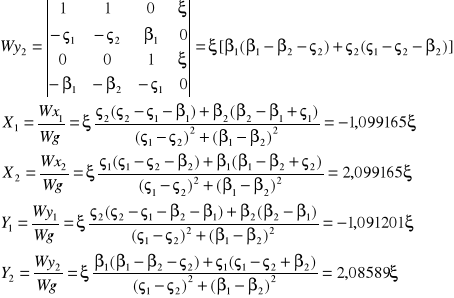
Wracając do podstawień wyznaczamy:
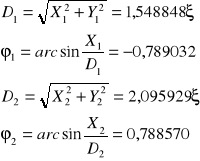
![]()
![]()
Ostateczna postać równań ruchu wygląda następująco:
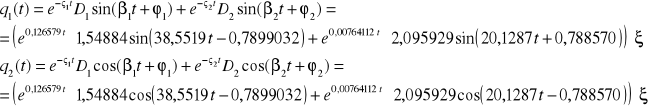
Wyszukiwarka
Podobne podstrony:
Drgania układu o n stopniach swobody
Drgania układu o n stopniach swobody
Lista zadań 4 Drgania o dwóch stopniach swobody (Równania Lagrange'a II rodzaju)
dobrucki,wprowadzenie do inżynierii akustyki, drgania układów o skończonej liczbie stopni swobody
Drgania mechaniczne, Badanie drgań własnych o jednym stopniu swobody, WSI Opole
Drgania mechaniczne, Badanie drgań własnych o jednym stopniu swobody1, WSI Opole
Drgania mechaniczne, Badanie drgań wymuszonych o jednym stopniu swobody na przykładzie wymuszonych b
Drgania mechaniczne, Badanie drgań własnych o dwóch stopniach swobody na przykładzie drgań belki wsp
Drgania mechaniczne, Badanie drgań wymuszonych o jednym stopniu swobody na przykładzie wymuszonych b
Drgania ukladu o jednym stopniu swobody v2011
Drgania układu o wielu stopniach swobody
Drgania wymuszone z tłumieniem układu o jednym stopniu swobody, wip, Drgania
Drgania Skrętne Układu o Wielu Stopniach Swobody
Drgania ukladu o jednym stopniu swobody v2011
Drgania Skrętne Układu o Wielu Stopniach Swobody
więcej podobnych podstron