SZEREGI LICZBOWE

Przez szereg liczbowy nieskończony oznaczony symbolem:

u₁+ u₂+ …+ u_n+ … lub

rozumiemy ciąg sum:

S₁ = u₁

S₂ = u₁+ u₂

...

S_n = u₁+ u₂+ u₃+ …+ u_n

...

Wyrazy ciągu {S_n} nazywamy sumami cząstkowymi szeregu

Jeżeli ciąg sum cząstkowych jest zbieżny, czyli ma skończoną granicę s, to mówimy, że szereg jest zbieżny, a liczbę s nazywamy sumą szeregu nieskończonego. Szereg, który nie jest zbieżny, nazywamy szeregiem rozbieżnym.

Jeżeli, szereg jest zbieżny, to na oznaczenie jego sumy s używa się zapisu:

u₁+ u₂+ …+ u_n+ …=s lub

Warunkiem koniecznym zbieżności każdego szeregu jest to, żeby jego wyraz ogólny u_n dążył do zera:

Jeżeli szereg (*) jest zbieżny i jego suma równa się s, a c jest liczbą stałą, to szereg (*c) jest zbieżny i jego suma jest równa cs; jeżeli szereg (*) jest rozbieżny, to przy c≠0 szereg (*) jest też rozbieżny.

Ważne szeregi !

1. szereg geometryczny

czyli a + aq + aq² +…+ aq^n-1 +…

jest zbieżny, gdy |q|<1, tzn. gdy -1<q<1, i wówczas suma jego wynosi:

Szereg geometryczny jest natomiast rozbieżny, gdy |q|≥1, tzn. gdy q≤-1 lub q≥1.

2. szereg harmoniczny

czyli

jest rozbieżny do ∞.

c) szereg harmoniczny rzędu α

czyli

gdzie α>0, jest dla α>1 zbieżny, a dla α≤1 jest rozbieżny. Dla α=1 otrzymujemy szereg podany poprzednio.

d) szeregi o wyrazach nieujemnych,

np.

czyli

e) szeregi przemienne, tzn. szeregi, w których wyrazy dodatnie i ujemne występują regularnie na przemian, np.

czyli

Szeregi o wyrazach nieujemnych

Kryterium porównawcze zbieżności szeregów.

Jeżeli dla szeregu (*) u_n, gdzie u_n ≥ 0, można wskazać taki szereg zbieżny (*) v_n, że począwszy od pewnego miejsca N (tzn. dla każdego n ≥ N) zachodzi nierówność u_n ≤ v_n, to szereg (*) u_n jest również zbieżny.

Kryterium porównawcze rozbieżności szeregów.

Jeżeli dla szeregu (*) u_n, można wskazać taki szereg rozbieżny (*) v_n, gdzie v_n ≥ 0, że począwszy od pewnego miejsca c zachodzi nierówność u_n ≥ v_n, to szereg (*) u_n jest również rozbieżny.

Kryterium d'Alemberta zbieżności szeregów.

Jeżeli w szeregu (*) u_n o wyrazach dodatnich począwszy od pewnego miejsca N (tzn. dla każdego n ≥ N) stosunek dowolnego wyrazu u_n+1 do poprzedzającego wyrazu u_n jest stale mniejszy od pewnej liczby p mniejszej od 1, tzn. jeżeli:

dla każdego n ≥ N,

to szereg (*) u_n jest zbieżny.

Kryterium d'Alemberta rozbieżności szeregów.

Jeżeli w szeregu (*) u_n o wyrazach dodatnich począwszy od pewnego miejsca N (tzn. dla każdego n ≥ N) stosunek dowolnego wyrazu u_n+1 do poprzedzającego wyrazu u_n jest nie mniejszy od jedności, tzn. jeżeli:

dla każdego n ≥ N,

to szereg (*) u_n jest rozbieżny.

Z podanych kryteriów d'Alemberta wynikają wnioski:

1. jeżeli

to szereg (*) u_n jest zbieżny

b) jeżeli

to szereg (*) u_n jest rozbieżny

c) jeżeli

to przypadek jest wątpliwy, należy wtedy stosować inne metody badania zbieżności szeregów.

Kryterium Cauchy'ego zbieżności szeregów.

Jeżeli dla szeregu (*) u_n o wyrazach nieujemnych istnieje taka liczba p<1, że począwszy od pewnego miejsca N (tzn. dla każdego n ≥ N) zachodzi nierówność:

to szereg (*) u_n jest zbieżny.

Kryterium Cauchy'ego rozbieżności szeregów.

Jeżeli dla szeregu (*) u_n dla nieskończenie wielu wartości n (niekoniecznie dla wszystkich) zachodzi nierówność:

to szereg (*) u_n jest rozbieżny.

Z podanych kryteriów Cauchy'ego wynikają wnioski:

1. jeżeli

to szereg jest zbieżny

2. jeżeli

to szereg jest rozbieżny

3. jeżeli

to przypadek jest wątpliwy.

Uwaga: Kryterium Cauchy'ego jest mocniejsze niż kryterium d'Alemberta.

Warunek konieczny zbieżności szeregów:

jest zbieżny wtedy, gdy

Twierdzenie (szereg harmoniczny)

[A] [B]

Jeśli a_n≤b_n to ze zbieżności szeregu [B] wynika zbieżność [A] (z rozbieżności [A] wynika rozbieżność [B]).

1. jeśli α>1 to szereg jest zbieżny

2. jeśli α≤1 to szereg jest rozbieżny.

Szeregi przemienne

Szereg (*) u_n nazywamy przemiennym, jeśli jego wyrazy są naprzemian dodatnie i ujemne.

Kryterium Leibniza zbieżności szeregów.

Jeżeli w szeregu przemiennym (*) u_n, począwszy od pewnego miejsca N bezwzględne wartości wyrazów szeregu dążą monotonicznie do zera, to znaczy, dla każdego n>N spełnione są warunki:

a) warunek konieczny zbieżności szeregów

b) szereg jest malejący

to szereg (*) u_n jest zbieżny.

Kryterium bezwzględnej zbieżności szeregów.

Jeżeli szereg (*) |u_n|, którego wyrazy są równe wartościom bezwzględnym wyrazów szeregu (*) u_n, jest zbieżny, to i szereg (*) u_n jest zbieżny.

Szereg (*) u_n nazywamy szeregiem bezwzględnie zbieżnym, jeżeli szereg (*) |u_n| jest zbieżny.

Szereg zbieżny, który nie jest bezwzględnie zbieżny, nazywamy szeregiem warunkowo zbieżnym.

GRANICE FUNKCJI

Mówimy, że liczba g jest granicą funkcji f(x) w punkcie x=c, co zapisujemy:

jeżeli istnieją granice lewostronna i prawostronna w punkcie x=c i obie są równe liczbie g tzn. jeżeli:

Mówimy, że liczba g jest granicą funkcji f(x) przy x →+∞, co zapisujemy:

jeżeli dla dowolnie obranej liczby ε>0 istnieje taka liczba N>0, żeby było |f(x)-g|<ε dla każdej wartości x>N.

Mówimy, że liczba g jest granicą funkcji f(x) przy x →-∞, co zapisujemy:

jeżeli dla dowolnie obranej liczby ε>0 istnieje taka liczba K>0, żeby było |f(x)-g|<ε dla każdej wartości x<-K.

Mówimy, że funkcja f(x) dąży do +∞ przy x→+∞, co zapisujemy:

jeżeli dla dowolnie obranej liczby M>0 istnieje taka liczba K>0, żeby było f(x)>M dla każdej wartości x>K.

Mówimy, że funkcja f(x) dąży do -∞ przy x→+∞, co zapisujemy:

jeżeli dla dowolnie obranej liczby M>0 istnieje taka liczba K>0, żeby było f(x)<M dla każdej wartości x>-K.

Twierdzenia o granicach

Jeżeli istnieją granice lim f(x) oraz lim g(x), to:

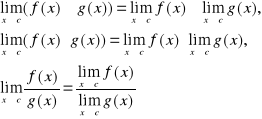
Ciągłość funkcji

Funkcję f(x) nazywamy funkcją ciągłą w punkcie x=c, jeżeli istnieje granica lim f(x) i jeżeli granica ta równa się f(c).

Zachodzą następujące twierdzenia dotyczące ciągłości funkcji:

1. suma dwóch funkcji ciągłych w punkcie x=c jest funkcją ciągłą w tym punkcie.

2. Iloczyn dwóch funkcji ciągłych w punkcie x=c jest funkcją ciągłą w tym punkcie.

3. Iloraz dwóch funkcji ciągłych w punkcie x=c takim, że dzielnik jest różny od zera, jest funkcją ciągłą w tym punkcie.

Jeżeli funkcja złożona (superponowana) f(g(x)) jest określona w pewnym otoczeniu punktu x=x₀ , funkcja g(x) jest ciągła w punkcie x=x_o, a funkcja f(u) jest ciągła w punkcie u=u_o, gdzie u₀=g(x₀), to funkcja złożona f(g(x)) jest ciągła w punkcie x=x₀.

---