dodatkowo
. Zatem oba sygnały x(t) i y(t) są identyczne, gdy jednocześnie:
oraz
.

5. „Przejście” sygnału przez układ liniowy

5.1. Sygnały zdeterminowane

5.1.2. Analiza w dziedzinie czasu - układ o jednym stopniu swobody

Weźmy pod uwagę najprostszy układ dynamiczny o jednym stopniu swobody (rys.28), opisany równaniem:

(57)

przy warunkach początkowych:

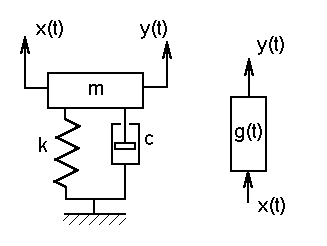
(57a)
i

Rys.28 Rys.29

Rozważymy ten układ w kategorii sygnałów zdeterminowanych. Jak wiadomo z teorii drgań rozwiązanie równania (57), przy warunkach początkowych (57a) może być przedstawione w postaci t.zw. „całki Duhamela”:

(58)

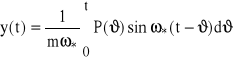
gdzie:
.

Całka ta „wiąże” sygnał wejściowy P(t) z sygnałem wyjściowym y(t) i opisuje tzw. „przejście” sygnału wejściowego przez układ. W dynamice układów często sygnał wejściowy jest oznaczany symbolem x(t) i w miejsce rys.28 stosujemy ogólniejszy, pokazany na rys.29. W przypadku, gdy sygnał wejściowy
, gdzie δ(t) jest „delta” funkcją Diraca zaś S jest wartością impulsu działającego na układ (przypominamy, że δ(t) bywa nazywany chwilowym impulsem jednostkowym, tj. równym jeden), to otrzymamy:

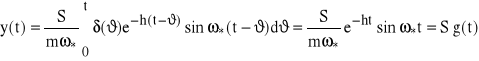
Funkcja g(t) osi nazwę charakterystyki impulsowej układu (rys.30) (danego układu przy danym wejściu x(t) i danym wyjściu y(t)). Charakterystyka impulsowa układu, dla t<0 jest tożsamościowo równa zero, zatem ściślej należy zapisać:

59. g(t) =
    

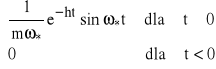
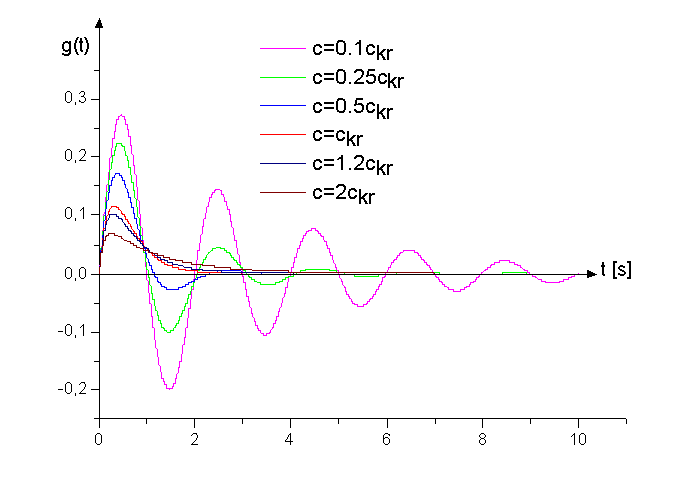
Rys.30. Charakterystyki impulsowe układu o jednym stopniu swobody

gdzie:
.

Ogólnie możemy więc napisać:

(60)

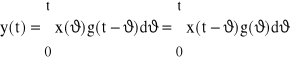
Rozwiązanie powyższe nazywamy rozwiązaniem w dziedzinie czasu.

5.1.2. Analiza w dziedzinie częstotliwości - układ o jednym stopniu swobody

Równanie (57) można również rozwiązać w dziedzinie częstotliwości. Aby takie rozwiązanie otrzymać należy dokonać transformaty Fouriera na składnikach po lewej i prawej stronie tego równania.

Najpierw jednak podamy kilka uwag na temat transformacji Fouriera.

Jeśli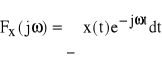
oraz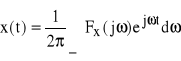
,
, to obie te operacje zapisujemy w skrócie:

Przytoczymy teraz niektóre własności transformacji Fouriera:

1) jeśli
oraz
, to

2) jeśli
, to

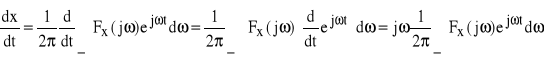
stąd

i podobnie

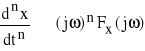
3) jeśli
, to

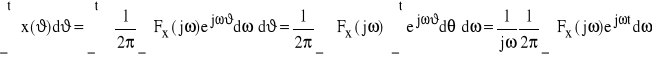
stąd

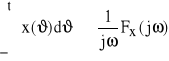
4) jeśli
, to

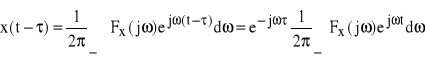
stąd

5) splotem funkcji x₁(t) i x₂(t) nazywamy:

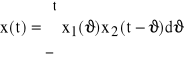
, przy czym ϑ≤ t

(zauważmy podobieństwo do (60)); jeśli
oraz
oraz
, to

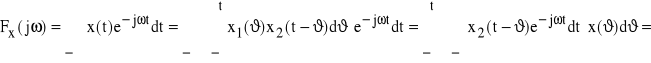
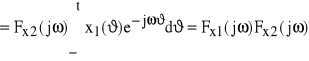
stąd

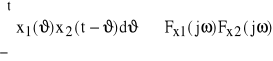
Wróćmy teraz do równania (57) i oznaczmy

(61)

Podstawmy P(t)≡x(t). Po podstawieniu powyższego do (57) mamy

lub

(62)

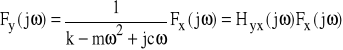
gdzie

(63)

=

=

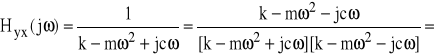
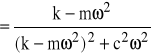
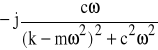
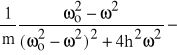
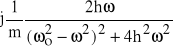
przy −∞<ω<∞ nosi nazwę transmitancji widmowej danego układu przy danym wejściu x(t) i danym wyjściu y(t). Transmitancja widmowa układu jest funkcją zespoloną. Możemy zapisać ją w dwóch postaciach:

(64)

gdzie:

(64a)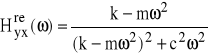
=

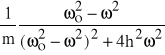
jest częścią rzeczywistą transmitancji, zaś

(64b)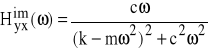

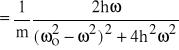
jest częścią urojoną transmitancji lub

(65)

gdzie:

(65a)

=
=
,

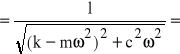
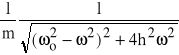
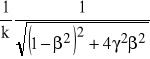
jest modułem transmitancji, zaś

(65b)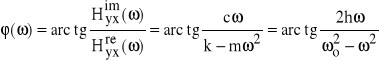
=

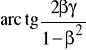
jest argumentem transmitancji.

Transmitancja układu bywa również nazywana: podatnością dynamiczną, admitancją, receptancją lub też przepustowością układu.

Zauważmy, że transmitancja H_yx(jω) jest transformatą Fouriera charakterystyki impulsowej g_yx(t)

(66)
,

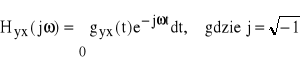
Istotnie:

,

,

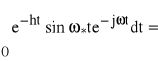
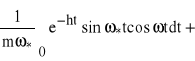
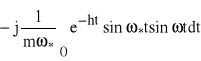
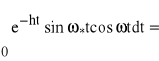
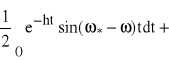
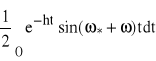
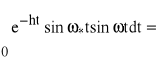
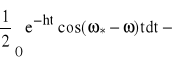
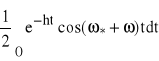
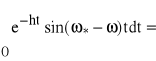
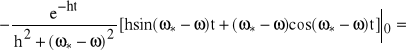
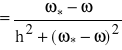
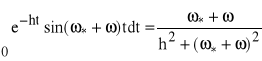
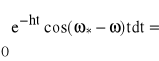
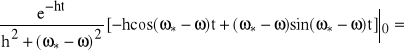
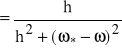
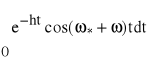
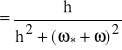
Część rzeczywista wynosi:

=

=
=

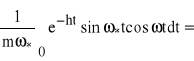
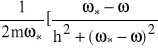
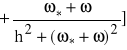
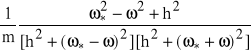
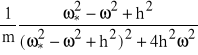
Część urojona wynosi:

=

=
=

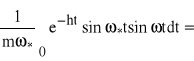
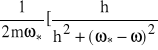
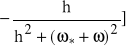
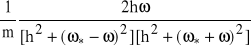
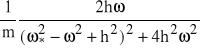
Stąd

=

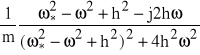
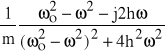
gdyż
. Wzór ten jest identyczny, jak (63).

Wykresy transmitancji układu liniowego o jednym stopniu swobody pokazano na rys.31.

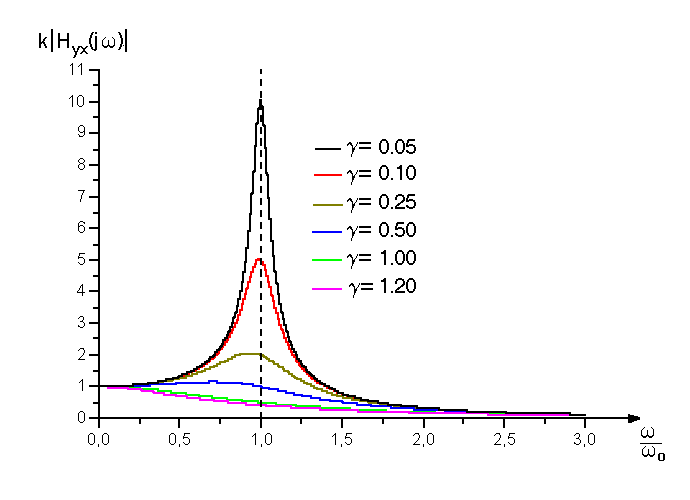
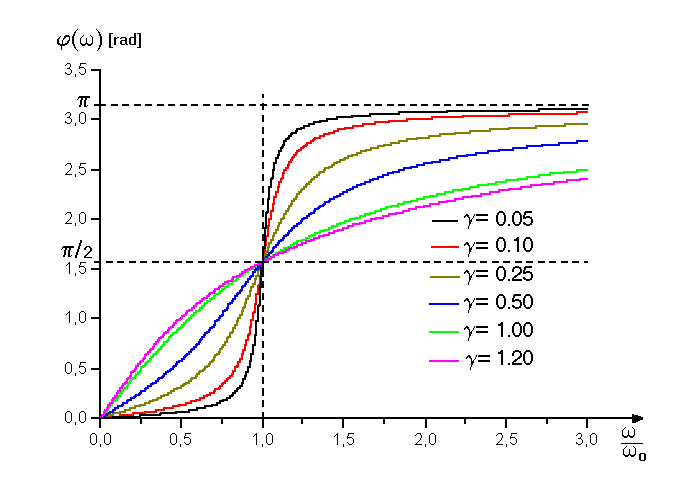
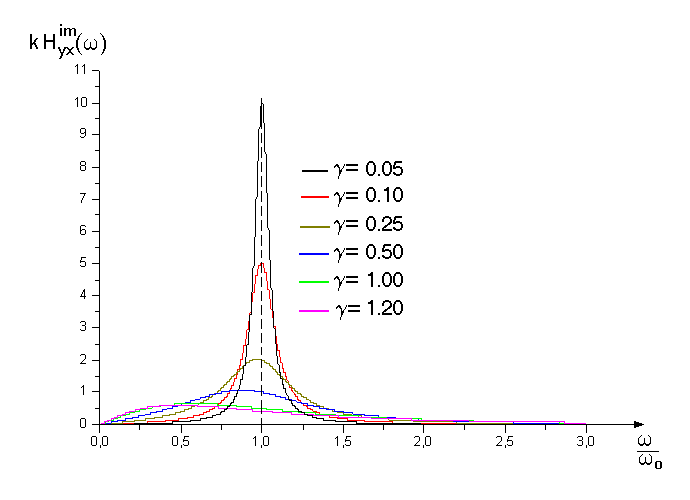
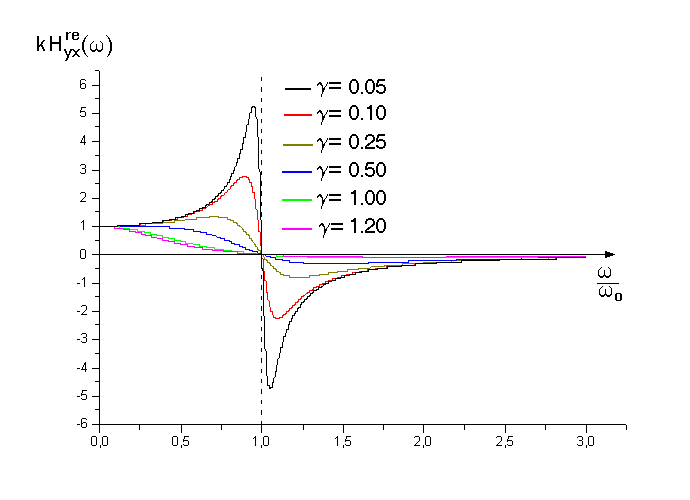
Rys.31. Transmitancje widmowe układu liniowego o jednym stopniu swobody.

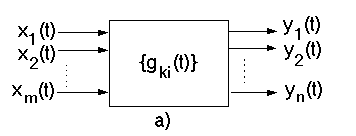
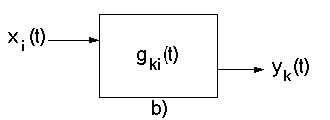
5.1.3. Analiza w dziedzinie czasu - układ liniowy o „n” stopniach swobody

(„n” sygnałów wyjściowych) poddany działaniu „m” sygnałów wejściowych (rys.32a).

Rys.32. Układy liniowe o „n” stopniach swobody - analiza w dziedzinie czasu.

Układ równań różniczkowych, opisujących ten układ można, przy m=n, zapisać w następującej postaci ogólnej:

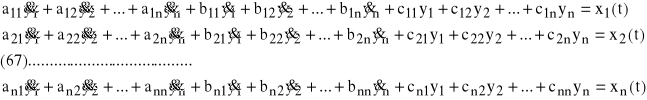
Oczywiście w konkretnych przypadkach nie muszą w tych równaniach występować wszystkie składniki, np. często się zdarza, że a_ik=a_ki=0. Powyższy układ równań można zapisać w skrócie. Niżej podamy dwa sposoby takiego zapisu.

Zapis w postaci sum (tzw. zapis „sumacyjny”)

(68)
i=1,2, ... ,n

Zapis macierzowy

(69)

gdzie:

,
,

,
,
,

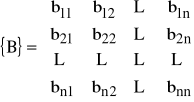
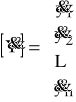
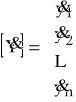
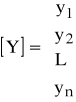
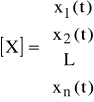
Rozważmy przypadek szczególny, gdy na układ działa jeden sygnał wejściowy x_i(t) i analizujemy tylko jeden sygnał wyjściowy y_k(t) (rys.32b). Wówczas możemy wykorzystać wzór (60), który tutaj przyjmie postać:

(70)

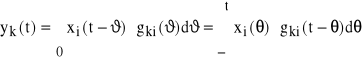
gdzie: i=1, 2, ... m, k=1, 2, ... n, zaś - jest charakterystyką impulsową układu przy „wejściu i” i „wyjściu k”, czyli odpowiedzią układu w p. „k” na sygnał wejściowy w p. „i” o postaci chwilowego impulsu jednostkowego δ(t). Oczywiście charakterystyka impulsowa będzie tu inna niż podana wzorem (59), bowiem inny jest tu układ. Trzeba ją wyznaczyć odrębnie.

Wzory powyższe dotyczą tzw. procesów ustalonych. Gdy chcemy uwzględnić procesy przejściowe należy we wszystkich tych wzorach w dolnej granicy całkowania podstawić „0”, zaś w górnej „t”:

(71)

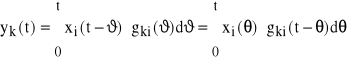
gdzie i=1, 2, ... m, k=1, 2, ... n.

Rozwiązanie to jest ważne przy zerowych warunkach początkowych układu.

Charakterystyka impulsowa podana wyżej dotyczy tzw. układów stacjonarnych, tj. takich które są opisywane układami zwyczajnych równań różniczkowych liniowych o stałych współczynnikach. W przypadku, gdy współczynniki tych równań są zmienne w czasie, to układ (liniowy) nazywamy układem niestacjonarnym. Dla układów niestacjonarnych charakterystyka impulsowa jest funkcją dwóch zmiennych: t i θ, czyli

- dla układów stacjonarnych
i jest funkcją jednej zmiennej t-θ lub ϑ,

- dla układów niestacjonarnych
i jest funkcją dwóch zmiennych.

Wyznaczenie
jest bardzo trudne.

Gdy uwzględnimy wszystkie sygnały wejściowe, to rozwiązanie y_k(t) otrzymamy metodą superpozycji, tj. jako sumę rozwiązań (70) lub (71) od wszystkich sygnałów wejściowych x_i(t):

(72)
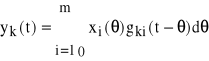
lub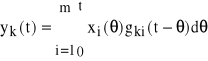

gdzie k=1, 2, ... , n.

5.1.4. Analiza w dziedzinie częstotliwości- układ liniowy o „n” stopniach swobody

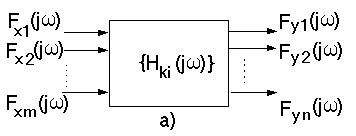
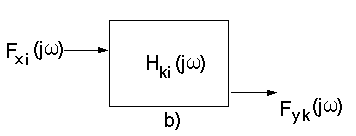
Schemat układu pokazano na rys.33a.

Rys.33. . Układy liniowe o „n” stopniach swobody - analiza w dziedzinie częstotliwości

Podobnie jak dla układu o jednym stopniu swobody poddajemy układ równań (67) transformacji Fouriera. Otrzymujemy:

(73)
, i=1,2, ... ,n

Stąd wyznaczamy
. W wyniku otrzymamy:

(74)

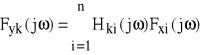
Wyznaczenie transmitancji
jest tu trudniejsze, gdyż należy rozwiązać układ równań (73). Jeśli zapiszemy równania (73) w postaci macierzowej:

(75)

gdzie

(76)

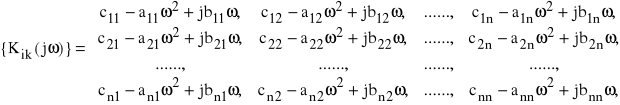
(76a)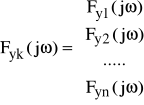
,

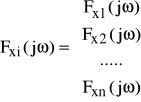
Macierz transmitancji wynosi:

(77)

W przypadku pojedynczego sygnału wejściowego (rys.33b) mamy:

78. 
    

gdzie:

(79)

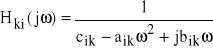
5.2. Sygnały losowe (stacjonarne i ergodyczne)

Analizy przeprowadzimy tu tylko dla sygnałów stacjonarnych i ergodycznych.

5.2.1. Analiza w dziedzinie czasu

Weźmy układ najprostszy, jak na rys.47. Jeśli sygnał wejściowy x(t) jest sygnałem traktowanym jako losowy, to przyjmujemy, że znamy jego charakterystyki losowe, jak wartość średnia m_x, wariancja
, funkcja korelacji własnej
. Odpowiedź układu jest wówczas otrzymana też w postaci charakterystyk losowych sygnału wyjściowego y(t). Wyznaczmy więc funkcję korelacji własnej sygnału wyjściowego y(t) dla dostatecznie długiej jego realizacji.

(80)

Korzystamy z rozwiązania (75)

(81)
,

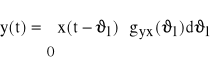
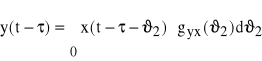
i podstawiamy do (80)

]}

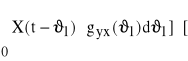
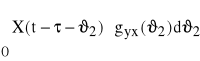
Operacje całkowania (a taką jest E{ }) są przemienne, a więc zmieniamy kolejność całkowania. Operacja E{ } dotyczy tylko funkcji losowych X(t), zaś charakterystyki impulsowe g_yx są funkcjami zdeterminowanymi. Stąd

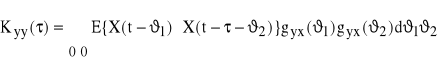
Pod znakiem całki mamy funkcję korelacji własnej sygnału wejściowego

Stąd

(82)

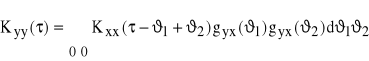
Wzór ten odpowiada wzorowi (75) dla sygnałów zdeterminowanych.

Funkcje korelacji dają jeszcze inne możliwości analizy „przepływu” sygnału wejściowego przez układ. Weźmy pod uwagę funkcję korelacji wzajemnej: wejście -wyjście

(83)

i podstawmy (81)

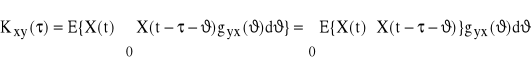
Skoro
, więc

(84)

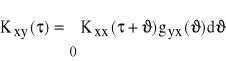
Podobnie możemy wyznaczyć

(85)

Stąd

(85)

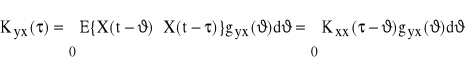
W przypadku układu o wielu stopniach swobody i wielu sygnałach wejściowych (rys.41) należy rozpatrywać dwa podstawowe przypadki: 1) gdy sygnały wejściowe są wzajemnie skorelowane, tj.
, 2) gdy sygnały wejściowe nie są wzajemnie skorelowane, tj.
(oczywiście
). Ten ostatni przypadek jest wprawdzie znacznie łatwiejszy do analizy, ale ma jedynie teoretyczne znaczenie (w rzeczywistości nie obserwujemy sygnałów nieskorelowanych). Dalej, dla ogólności rozważań, wyznaczymy nie funkcję korelacji własnej wybranego sygnału wyjściowego, lecz korelację wzajemną dwóch sygnałów wyjściowych
. Funkcja korelacji własnej obranego sygnału wyjściowego będzie tu szczególnym przypadkiem, gdy y_s=y_k. Wykorzystamy tu wzór (77), który przepiszemy do równoważnejpostaci

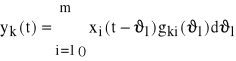
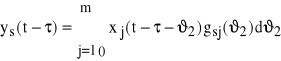
Stąd

=

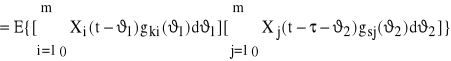
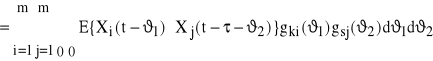
oraz

(86)

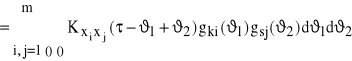
Gdyby sygnały wejściowe były nieskorelowane (jest to przypadek idealny), to

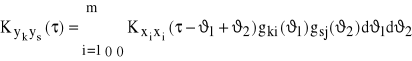
Podobnie możemy wyznaczyć korelacje wzajemne wybranych par sygnałów „wejście-wyjście”.

(87)

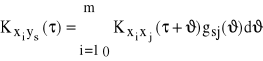
Gdyby sygnały wejściowe były nieskorelowane, to

(88)

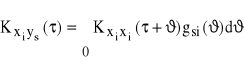
5.2.2. Analiza w dziedzinie częstotliwości

Analiza ta dotyczy tylko sygnałów stacjonarnych. Biorąc pod uwagę (73), dla układu liniowego o wielu stopniach swobody, zapisujemy

(89)

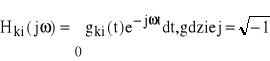
gdzie
jest transmitancją układu między wejściem „i” i wyjściem „k”.

Weźmy najpierw przypadek jednego sygnału wejściowego „i” i jednego sygnału wyjściowego „k”. Wówczas funkcja korelacji własnej sygnału y_k została wyznaczona wzorem (82)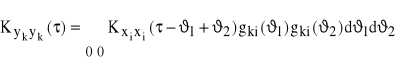

Widmowa gęstość mocy własnej sygnału wyjściowego jest transformatą Fouriera funkcji
i wynosi:

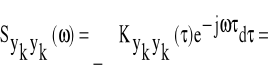
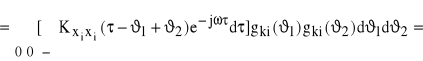
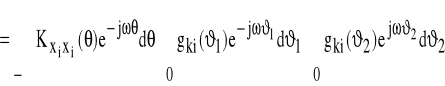
gdzie . Stąd

(90)

Wzajemna widmowa gęstości mocy sygnałów wejście „i” -wyjście „k” wynosi:

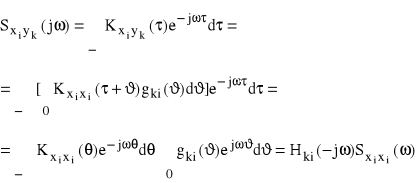
gdzie θ=τ+ϑ. Zatem

(91)

Biorąc pod uwagę, że

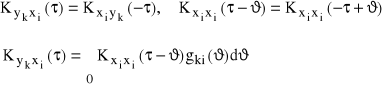
otrzymujemy:

(92)

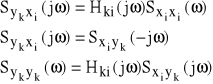
6. Zagadnienia podstawowe

6.1. Zagadnienia główne

Ogólnie zagadnienia dynamiki układów klasyfikujemy według następującego schematu (rys.34).

x( t ) układ y( t )

g_yx( t )

H_yx(jω)

Rys.34

47

J. W. Osiecki: Analiza sygnałów.

=F_x1(jω)

=F_x2(jω)e^-jωϑ

=

=

=

---