3. ANALIZA STRUKTURY ZBIOROWOŚCI

1. Istota analizy struktury

Jej celem jest ustalenie podobieństw i różnic między jednostkami badanej zbiorowości ze względu na interesującą nas cechę statystyczną.

Podobieństwa ustala się poprzez wyznaczenie przeciętnego poziomu wartości cechy u wszystkich jednostek badanych, różnice natomiast charakteryzujemy wielostronnie poprzez:

1. badanie dyspersji - określającej stopień zróżnicowania poszczególnych wartości cechy,

2. określenie kierunku i stopnia asymetrii - tj. wewnętrznego rozmieszczenia jednostek w zbiorowości statystycznej,

3. ustalenie koncentracji - czyli stopnia skupienia wartości cechy wokół przeciętnego poziomu tej cechy.

Analiza struktury oparta jest więc na porównaniu dyferencyjnym. Stosownie do tego zbudowane zostały odpowiednie parametry opisu statystycznego, które można ze względu na cel analizy podzielić na dwie grupy:

• miary zgodności, które pozwalają określić podobieństwa między porównywanymi zbiorowościami,

• miary zróżnicowania, przy pomocy których określamy istniejące różnice w struk-turze porównywanych zbiorów.

Ze względu natomiast na wartości teorio-poznawcze, parametry analizy struktury (tak miary zgodności jak i zróżnicowania) dzielą się na:

• parametry klasyczne - są to momenty i parametry uzyskane w drodze przekształceń na momentach. Charakteryzują się one tym, że obliczane są na podstawie wszystkich obserwacji. Z tych też względów nazywane są wyliczeniowymi.

• parametry pozycyjne - są to konkretne wielkości wyznaczone spośród zaobser-wowanych wartości zmiennej (cechy).

W związku z powyższym podziałem nasuwa się pytanie: kiedy należy posługiwać się parametrami klasycznymi a kiedy pozycyjnymi? W wyborze tym kierować się należy:

1. właściwościami przedmiotu badania (przez stwierdzenie postaci rozkładu empirycznego zmiennej),

2. właściwościami algebraicznymi parametrów analizy struktury,

przy czym wybór ten winien być zawsze poprzedzony rozpoznaniem postaci rozkładu zmiennej empirycznej. W tabeli 1 przedstawiono klasyfikację parametrów stosowanych w analizie struktury.

Tabela 1. KLASYFIKACJA PODSTAWOWYCH PARAMETRÓW

ANALIZY STRUKTURY

Parametry klasyczne	Parametry pozycyjne
I. MIARY POŁOŻENIA ( przeciętne )
1. Średnia arytmetyczna − 2. Średnia geometryczna − 3. Średnia harmoniczna − 4. Średnia kwadratowa −	1. Kwantyle: Kwartyle, w tym mediana − Me, Q1, Q3 Decyle, percentyle 2. Dominanta (Modalna) − D
II. MIARY DYSPERSJI ( zmienności )
1. Odchylenie przeciętne 2. Odchylenie standardowe − 3. Wariancja − 3. Współczynnik zmienności − Vx	1. Rozstęp (obszar zmienności) − R 2. Odchylenie ćwiartkowe − Q 3. Współczynnik zmienności − VQ
III. MIARY ASYMETRII
Współczynnik asymetrii (klasyczno − pozycyjny) - As (Ws)
Moment trzeci centralny standaryzowany − 3	Współczynnik asymetrii − As
IV. MIARY KONCENTRACJI (skupienia)
Moment czwarty centralny standaryzowany − 	-

Źródło: Opracowanie własne

Kryteria wyboru parametrów opisowych analizy struktury

Parametrami klasycznymi posługujemy się, gdy spełnione są dwa warunki:

1. warunek merytoryczny, który wymaga, by analizowana zbiorowość była jednorodna (w odniesieniu oczywiście do interesującej nas cechy). Wszystkie klasyczne parametry są ze swej istoty wielkościami abstrakcyjnymi. Zakłada się bowiem, że rozkład sumy wartości cechy na poszczególne jednostki zbiorowości jest równomierny, przez co świadomie godzimy się na pewną fikcję.

1. warunek formalny − odnosi się do zbiorowości przedstawionych w postaci szeregu rozdzielczego. Warunkiem stosowania miar klasycznych jest, by przedziały klasowe były równe oraz by wartości graniczne szeregu zostały ściśle określone (szereg powinien być obustronnie zamknięty). W praktyce statystycznej posługujemy się niekiedy parametrami odpowiednio przystosowanymi do nierównych przedziałów klasowych. Dają one jednak tylko przybliżony wynik dociekań. Podobnie w uza-sadnionych przypadkach, możemy również umownie określić wartości graniczne szeregu. Wymaga to jednak dobrej znajomości przedmiotu badania oraz pewności, że liczba jednostek w klasach krańcowych jest stosunkowo niewielka.

Parametrami pozycyjnymi posługujemy się, gdy:

1. nie możemy w konkretnej sytuacji posłużyć się parametrami klasycznymi tzn. gdy nie wystąpi co najmniej jeden z poprzednich, podstawowych warunków lub obydwa jednocześnie,

1. pragniemy uzyskać opis uzupełniający do parametrów klasycznych. Dotyczy to głównie obszernych zbiorowości posiadających rozkład łagodnie asymetryczny. Wówczas miary pozycyjne spełniają funkcję pomocniczą w stosunku do miar klasycznych.

Analiza struktury rozkładu zmiennej empirycznej winna być prowadzona zawsze w sposób kompleksowy. Oznacza to, że dla stwierdzenia podobieństw i różnic winniśmy się posługiwać odpowiednio dobranymi zespołami parametrów, które winny umożliwiać:

• ocenę przeciętnego poziomu wartości zmiennej,

• ustalenie stopnia rozproszenia tych wartości od poziomu przeciętnego,

• określenie kierunku rozproszenia, czyli zbadanie asymetrii rozkładu,

• ustalenie skupienia wartości cechy wokół średniej (tylko gdy stosujemy miary klasyczne - metodę momentów).

Charakterystyka podstawowych parametrów analizy struktury

1. Charakterystyka miar tendencji centralnej

W analizie struktury interesuje nas nie tylko rozkład częstości kategorii wyróżnionej zmiennej, ale najczęściej pytamy o to, co jest typowe, np. jaka jest typowa (przeciętna) płaca górników, nauczycieli, jakiej płci jest typowy student itp.

Na pytanie takie odpowiadamy stosując miary tendencji centralnej (przeciętnego poziomu).

Najczęściej stosowanymi miarami przeciętnego poziomu są:

• dominanta,

• mediana,

• kwartale,

• średnia arytmetyczna.

1. Dominanta

Dominanta, zwana również modalną, jest to „wartość” cechy, która występuje w zbiorowości najczęściej. Największą zaletą dominanty jest łatwość jej ustalenia i in-terpretacji. Dominanta nie zawsze jednak będzie dawać najlepszy opis danych, gdyż:

• kategoria występująca najczęściej może nie występować dużo częściej od innych kategorii,

• rozkład badanej cechy może nie mieć jednej, wyraźnej dominanty. Mówi się wtedy o rozkładzie wielomodalnym. Może też charakteryzować się równomierną liczebnością poszczególnych kategorii i w ogóle nie mieć dominanty.

• dominanta jest podatna na sposób kategoryzacji zmiennej i łączenie kategorii.

Pomimo tych wad, dominanta jest bardzo często używana miarą przeciętnego poziomu i można ją ustalać dla cechy jakościowej i ilościowej.

1. Mediana i kwartyle

Mediana, czyli kwartyl drugi (Me lub Q₂) jest kategorią cechy, która dzieli zbiorowość na dwie połowy, z których każda zawiera po 50% obserwacji. Walory mediany (poznawcze) rosną wraz ze wzrostem liczby obserwacji oraz liczby kategorii (wariantów) zmiennej. Mediana (wartość środkowa) wskazuje więc wartość środkowej obserwacji w bazie danych, uporządkowanej ze względu na badaną cechę.

Mediana jest odporna na wpływ obserwacji o skrajnych wartościach cechy, można ją obliczać nawet wówczas, gdy krańce rozkładu są otwarte.

Suma bezwzględnych wartości różnic pomiędzy wartościami danej zmiennej dla wszystkich obserwacji a medianą jest najmniejsza ze wszystkich sum bezwzględnych wartości różnic pomiędzy wartościami wszystkich obserwacji a jakąkolwiek stałą.

Podobny sens do mediany mają kwartyle: Q₁ oraz Q₃.

Kwartylem pierwszym (dolnym) Q₁ nazywamy taką wartość cechy (taką kategorię cechy), poniżej której leży 25% jednostek zbiorowości.

Kwartyl trzeci (górny) to taka wartość cechy, która dzieli zbiorowość na dwie części i to takie, że 75% jednostek ma wartości nie większe od Q₃.

Pomiędzy Q₁ i Q₃ leży 50% obserwacji, które można nazwać typowym obszarem zmienności.

1. Średnia arytmetyczna
   

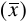
Średnia arytmetyczna jest najczęściej stosowaną klasyczną miarą tendencji centralnej.

Własności średniej są następujące:

• średnia jest obliczana na podstawie wszystkich obserwacji,

• dana zmienna (cecha) ma zawsze tylko jedną średnią,

• średnia bardzo dobrze nadaje się do porównywania dwóch lub większej liczby zbiorowości,

• suma odchyleń wszystkich wartości zmiennej od jej średniej arytmetycznej jest zawsze równa zero:

,

• suma kwadratów odchyleń wartości zmiennej od średniej arytmetycznej jest mniejsza niż suma kwadratów odchyleń od jakiejkolwiek innej stałej,

• średnia jest bardziej stabilna od innych miar tendencji centralnej,

• średnia może przyjmować wartości ułamkowe nawet wtedy, kiedy zmienna przyjmuje tylko wartości całkowite,

• średnia nie może być obliczana, jeśli skrajne kategorie zmiennej są otwarte,

• na wielkość średniej arytmetycznej silny wpływ mają skrajne wartości cechy.

Wyróżnia się średnią arytmetyczną:

• prostą - stosowaną w przypadku szeregów prostych (wyliczających),

• ważoną - stosowaną w przypadku danych pogrupowanych (szeregi roz-dzielcze).

Im rozkład zmiennej jest bardziej zbliżony do symetrycznego, tym większą wartość poznawczą ma średnia arytmetyczna. I odwrotnie, im rozkład jest bardziej asymetryczny, tym lepiej tendencję centralną wyraża mediana, a nie średnia arytmetyczna.

W przypadku rozkładów o stosunkowo dużej asymetrii najlepiej uwzględnić obydwa te parametry.

2. Charakterystyka miar dyspersji

Rozkłady empiryczne charakteryzują się nie tylko tendencją centralną, ale też określonym zróżnicowaniem (rozproszeniem). Możemy spotkać rozkłady o tej samej tendencji centralnej, ale o różnej zmienności. Do jej pomiaru stosuje się miary dyspersji.

2.1. Wariancja i odchylenie standardowe

Parametry te należą do najważniejszych miar statystycznych.

Interpretację merytoryczną posiada odchylenie standardowe
. Określa ono, o ile przeciętnie biorąc, poszczególne wartości cechy odchylają się +/- od średniej arytmetycznej. Posiada następujące właściwości:

• jest bardzo wrażliwe na wartości skrajne cechy,

• obliczamy je na podstawie wszystkich obserwacji,

• wyrażone jest w jednostkach miary analizowanej zmiennej,

• jest największe wówczas, gdy połowa obserwacji ma wartość maksymalną, a połowa minimalną. Wynosi ono wtedy:

,

Odchylenie standardowe wykorzystujemy do określania:

− typowego obszaru zmienności

− obszaru zmienności wynikającego z reguły 3
(trzech sigm)

,

Odchylenie standardowe służy też do standaryzacji zmiennych, która pozwala na wyeliminowanie wpływu jednostek miary na rozkład zmiennej. Standaryzację przeprowadza się według wzoru:

,

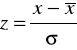
Zmienna standaryzowana ma średnią 0 i odchylenie standardowe równe 1.

Wariancja jest kwadratem odchylenia standardowego.

2.2 Klasyczny współczynnik zmienności

Dla porównania rozproszenia różnych zmiennych stosujemy względną miarę zmienności zwaną klasycznym współczynnikiem zmienności. Jest to miara niezmienna względem skali. Pozwala ustalić jaki procent średniej stanowi odchylenie standardowe. Współczynnik ten liczymy według wzoru:

Współczynnik ten wyrażamy najczęściej w % i im jest on większy, tym dyspersja rozkładu jest silniejsza. Umownie przyjmuje się, że:

− jeśli
% - dyspersja słaba,

− jeśli
% - dyspersja umiarkowana,

− jeśli
% - dyspersja silna,

− jeśli
% - dyspersja bardzo silna.

2.3 Odchylenie ćwiartkowe i pozycyjny współczynnik zmienności

Odchylenie ćwiartkowe stosujemy, gdy chcemy wyeliminować silny wpływ obserwacji skrajnych

Obliczamy je, korzystając z rozstępu ćwiartkowego:
, według wzoru:

.

Q informuje o tym, jakie jest przeciętne rozproszenie typowych obserwacji wokół mediany (wokół środka rozkładu).

Dla uniezależnienia pomiaru dyspersji od jednostek miary, w jakich wyrażona jest cecha stosujemy pozycyjny współczynnik dyspersji:

Pozycyjny współczynnik zmienności określa, jaką część (procent) mediany stanowi odchylenie ćwiartkowe.

Im jego wartość jest większa, tym dyspersja rozkładu jest silniejsza.

Do oceny dyspersji można też stosować miary oparte na decylach.

Czasami do pomiaru względnej dyspersji używa się współczynnika zmienności określonego wzorem:

.

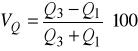
Jego interpretacja jest podobna jak współczynnika V_Me, mianowicie, im jego wartość jest większa, tym dyspersja badanej cechy jest silniejsza.

3. Miary asymetrii

Pozwalają one na określenie, jakie jednostki w zbiorowości przeważają: czy jednostki o wartościach cechy poniżej czy też powyżej tendencji centralnej.

Biorąc powyższe pod uwagę, wyróżnia się:

a) rozkład symetryczny, w którym taka sama liczba jednostek ma wartości cechy poniżej jak i powyżej średniej arytmetycznej. W rozkładzie tym trzy podstawowe miary przeciętne: średnia, mediana i dominanta są identyczne:

b) rozkład prawostronnie asymetryczny, w którym przeważają jednostki o wartościach cechy mniejszych od średniej arytmetycznej

c) rozkład lewostronnie asymetryczny, w którym występuje przewaga jednostek o wartościach cechy powyżej średniej arytmetycznej.

Do pomiaru natężenia i kierunku asymetrii służą współczynniki asymetrii. Najczęściej stosowane są:

• klasyczno - pozycyjny współczynnik asymetrii obliczany wg wzoru:

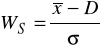
W_S=0 - rozkład symetryczny,

W_S>0 - rozkład prawostronnie asymetryczny,

W_S<0 - rozkład lewostronnie asymetryczny.

Jeśli przy tym : W_S
− to asymetria oceniana jest jako słaba, W_S
− asymetria umiarkowana,

W_S
− rozkład silnie asymetryczny.

Warto też wskazać, że w rozkładzie umiarkowanie asymetrycznym zachodzi następująca równość:

Wzór ten pozwala na ustalenie przybliżonej wartości jednej z trzech przeciętnych, jeśli dwie pozostałe są znane.

• pozycyjny współczynnik asymetrii liczymy korzystając ze wzoru:

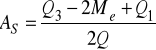
Miernik ten jest unormowany na przedziale
.

Przyjmuje wartość równą zero tylko wtedy, gdy rozkład jest symetryczny.

Przy jego interpretacji, jako punkt odniesienia uwzględniamy medianę, a nie średnią arytmetyczną.

• klasyczną miarą asymetrii jest standaryzowany trzeci moment centralny.

Najczęściej w oparciu o podane informacje o wartościach cechy liczymy moment trzeci centralny według wzoru:

,

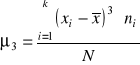
a następnie liczymy moment standaryzowany:

.

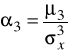
Interpretacja tego miernika jest identyczna jak wcześniej omówionego klasyczno-pozycyjnego współczynnika zmienności.

3. Miary koncentracji (skupienia)

Koncentrację wokół wartości średniej określa się mianem kurtozy. Jako względną miarę koncentracji stosuje się czwarty moment centralny wyrażony w jednostkach odchylenia standardowego.

Procedura jego liczenia jest podobna do procedury liczenia klasycznej miary asymetrii. Najpierw w oparciu o zebrane informacje liczymy czwarty moment centralny:

,

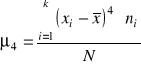
a następnie współczynnik koncentracji, według wzoru:

.

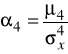
Interpretacja tego współczynnika jest następująca:

₄ < 3 − rozkład badanej cechy jest spłaszczony, tzn. o koncentracji wokół średniej mniejszej aniżeli w rozkładzie normalnym,

₄ = 3 − rozkład o koncentracji takiej jak w rozkładzie normalnym,

₄ > 3 − rozkład jest wysmukły, tzn. o koncentracji wokół średniej większej niż w rozkładzie normalnym.

Przykłady

Zadanie 1.

W przedsiębiorstwie „W” w Poznaniu przeprowadzono we wrześniu 2007 r. badanie wydajności pracy robotników (mierzonej w kg/godz.). Dla zatrudnionych 15 osób otrzymano następujące dane:

Nr kolejny	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Wydajność	17	17	15	20	17	18	20	17	16	18	19	19	17	21	16

1. Zdefiniuj zbiorowość, jednostkę i badaną cechę statystyczną,

2. Przeprowadź kompleksową analizę struktury robotników zatrudnionych w bada-nym przedsiębiorstwie według wydajności pracy.

Rozwiązanie:

ad a) Zbiorowość statystyczna to robotnicy zatrudnieni w przedsiębiorstwie „W” w Poznaniu we wrześniu 2007 r.

Jednostka statystyczna: robotnik tego przedsiębiorstwa.

Badana cecha: wydajność pracy - jest to cecha mierzalna, ciągła.

ad b) Jednostki porządkujemy rosnąco według wartości badanej cechy (kolumna 2 tabeli roboczej).

Tabela robocza do zadania 1.

Nr kolejny	xi
1	2	3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	15 16 16 17 17 17 17 17 18 18 19 19 20 20 21	7,84 3,24 3,24 0,64 0,64 0,64 0,64 0,64 0,04 0,04 1,44 1,44 4,84 4,84 10,24
Ogółem	267	40,40

Liczymy średnią arytmetyczną:

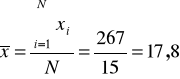
Przeciętna wydajność robotników tego przedsiębiorstwa wynosiła we wrześniu 2007 r. 17,8 kg/godz.

Ustalamy wartość dominanty :

Dominantę definiujemy jako poziom cechy, który występuje w zbiorowości najczęściej.

W naszym zadaniu najczęściej występuje wydajność 17 kg/godz., stąd też :

D = 17

Robotnicy badanego przedsiębiorstwa mieli najczęściej wydajność 17 kg/godz.

Ustalamy wartość mediany:

Mediana dzieli zbiorowość na dwie części w taki sposób, że połowa jednostek ma wartości od mediany mniejsze (w niektórych przypadkach: nie większe) a druga połowa większe (nie mniejsze).

W naszym zadaniu liczba jednostek w zbiorowości jest nieparzysta, czyli:

N = 2k-1 ; k = 1, 2,.....

stad:

W takim razie : Me = x_k

U nas: N = 15 czyli k = 8 wobec tego: Me = x₈ = 17 .

Połowa robotników miała wydajność nie większą niż 17 kg/godz.

Gdy liczba jednostek w zbiorowości jest parzysta, to N = 2k. Wtedy:

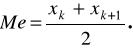
Liczymy odchylenie standardowe:

Odchylenie standardowe informuje nas, o ile przeciętnie różnią się jednostki badanej zbiorowości poziomem cechy od średniej arytmetycznej tej cechy.

W szeregu wyliczającym stosujemy następujące wzory:

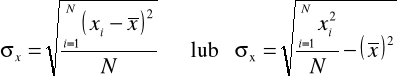
W naszym zadaniu wykorzystamy pierwszą wersję wzoru (potrzebne obliczenia wykonano w tabeli roboczej - kolumna 3):

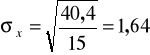
Robotnicy różnili się wydajnością od wydajności średniej przeciętnie o +/- 1,64 kg/godz.

Liczymy współczynnik zmienności:

Współczynnik ten informuje nas o dyspersji względnej, mówi więc, jaki procent średniej stanowi odchylenie standardowe .

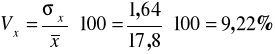
Zmienność robotników według wydajności jest niewielka, odchylenie standardowe stanowi zaledwie 9,22 % poziomu średniego.

Ustalamy asymetrię rozkładu wydajności pracy:

Wychodzimy tu z założenia, że w przypadku rozkładu o idealnej symetrii podstawowe trzy przeciętne są sobie równe, czyli:
. Jeżeli tak nie jest to rozkład jest asymetryczny. Stąd:

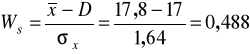
Rozkład wydajności pracy jest więc rozkładem o jeszcze umiarkowanej asymetrii prawostronnej (W_s < 0,5). Przeważają pracownicy o wydajności mniejszej niż średnia (17,8 kg/godz.).

W przypadku gdy analizujemy szereg szczegółowy liczący kilkadziesiąt obserwacji a zmienność cechy jest bardzo duża ( V_x > 70 % ) to wówczas konieczne staje się zastosowanie kwartyli.

Przy obliczaniu kwartyli dla szeregu szczegółowego można wyróżnić cztery przypadki:

• jeśli liczba obserwacji jest podzielna bez reszty przez cztery, czyli N = 4k (gdzie k - liczba naturalna), wtedy wartość kwartyla pierwszego i trzeciego oblicza się według wzorów:

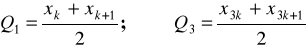
• jeśli liczba obserwacji jest podzielna przez cztery z resztą jeden, czyli N=4k+1, wtedy:

,

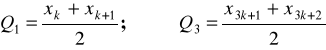
• jeśli liczba obserwacji jest podzielna przez cztery z resztą dwa, czyli N=4k+2, wtedy:

,

• jeśli liczba obserwacji jest podzielna przez cztery z resztą trzy, czyli N=4k+3, wtedy:

,

przy czym wszystkie wartości zmiennej są brane z szeregu uporządkowanego.

Zadanie 2.

Przeprowadzono badanie pracowników pewnej firmy w Kaliszu w lipcu 2007 r. według liczby dzieci na utrzymaniu. Zebrane dane pogrupowano i zbudowano następujący szereg rozdzielczy:

Liczba dzieci na utrzymaniu	Liczba pracowników
0	9
1	16
2	26
3	10
4	5
5	3
6	1
Ogółem	70

Źródło: dane umowne.

W oparciu o podane informacje:

1. Określ zbiorowość, jednostkę i badaną cechę statystyczną.

2. Przeprowadź kompleksową analizę struktury pracowników badanej firmy według liczby dzieci na utrzymaniu.

3. Analizowany szereg przedstaw graficznie.

Rozwiązanie:

ad a) Zbiorowość statystyczna: pracownicy pewnej firmy w Kaliszu w lipcu 2007r.

Jednostka statystyczna: jeden pracownik tej firmy.

Badana cecha: liczba dzieci na utrzymaniu - mierzalna, skokowa.

ad b) Jest to szereg rozdzielczy z przedziałami jednowariantowymi, jednomodalny. Stąd też możemy tu zastosować miary klasyczne, uzupełniając je przeciętnymi pozycyjnymi.

Tabela robocza do zadania 2:

Liczba dzieci na utrzymaniu − xi	Liczba pracowników − ni			kum ni
1	2	3	4	5
0 1 2 3 4 5 6	9 16 26 10 5 3 1	0 16 52 30 20 15 6	0 16 104 90 80 75 36	9 25 51 61 66 69 70
Ogółem	70	139	401	X

Liczymy średnią arytmetyczną:

Obliczenia cząstkowe zawarte są w kolumnie 3 w tabeli roboczej.

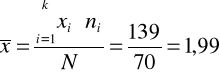
Przeciętnie pracownik badanej firmy miał na utrzymaniu dwoje dzieci.

Ustalamy wartość dominanty:

Maksymalna liczebność wynosi 26 - oznacza to, że najwięcej pracowników firmy miało dwoje dzieci, czyli D = 2.

Ustalamy wartość mediany:

W celu ustalenia wartości środkowej (mediany) musimy skumulować liczebności (patrz kolumna 5 tabeli roboczej).

N - jest liczbą parzystą, czyli N = 2k stąd: k = N/2 = 70/2 = 35

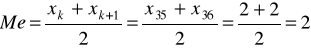
Połowa pracowników miała nie więcej niż dwoje dzieci, a druga połowa nie mniej niż dwoje.

Obliczamy odchylenie standardowe:

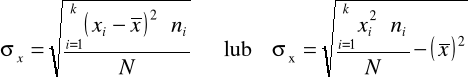
Stosujemy drugą wersję wzoru (obliczenia pomocnicze - kolumna 4 tabeli roboczej):

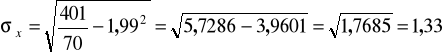
Pracownicy różnili się liczbą dzieci od średniej przeciętnie o +/- 1 dziecko (1,33).

Obliczamy współczynnik zmienności:

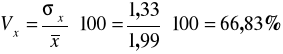
Zmienność pracowników według liczby dzieci na utrzymaniu jest duża, odchylenie stanowi 66,83 % średniej.

Ustalamy asymetrię rozkładu liczby dzieci:

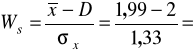
-0,0075

Rozkład liczby dzieci na utrzymaniu charakteryzuje się niewielką asymetrią lewostronną, co znaczy, że częściej liczba dzieci jest minimalnie większa od średniej.

ad c) Sporządzamy histogram

Źródło: Por. szereg rozdzielczy do zad.2.

Zadanie 3.

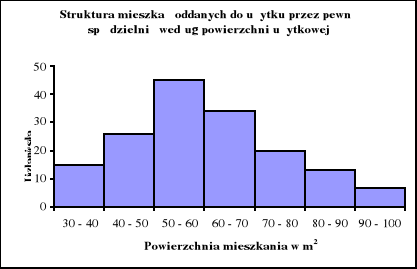
Przeprowadzono badanie mieszkań oddanych do użytku przez spółdzielnię mieszkaniową w Kaliszu w pierwszym półroczu 2007r. według powierzchni użytkowej w m². Zebrane informacje pogrupowano i zbudowano następujący szereg rozdzielczy.

W oparciu o podane informacje:

1. Określ zbiorowość, jednostkę i badaną cechę statystyczną.

2. Przeprowadź kompleksową analizę struktury mieszkań oddanych do użytku według ich powierzchni użytkowej.

3. Analizowany szereg przedstaw graficznie.

Powierzchnia użytkowa w m^2	Liczba mieszkań
30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 90 - 100	15 26 45 34 20 13 7
Ogółem	160

Źródło: dane umowne.

Rozwiązanie:

ad a) Zbiorowość - mieszkania oddane do użytku przez spółdzielnię mieszkaniową w Kaliszu w pierwszym półroczu 2007 r.

Jednostka - jedno mieszkanie.

Cecha statystyczna - powierzchnia użytkowa mieszkania w m² - cecha mierzalna, ciągła.

ad b) Szereg spełnia warunki pozwalające na stosowanie parametrów klasycznych (równe przedziały klasowe i jedno maksimum).

Wszystkie potrzebne obliczenia zawarte są w tabeli roboczej.

Liczymy średnią arytmetyczną

Ustalamy środki przedziałów klasowych - kolumna 3 tabeli roboczej, a następnie wykonujemy potrzebne obliczenia - kolumna 4.


.

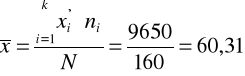
Przeciętna powierzchnia mieszkania oddanego do użytku przez tą spółdzielnię wynosi 60,31 m².

Pow. użytkowa w m^2 (x)	Liczba mieszkań (ni)				kum ni
1	2	3	4	5	6
30 - 40 40 - 50 50 - 60 60 - 70 70 - 80 80 - 90 90 - 100	15 26 45 34 20 13 7	35 45 55 65 75 85 95	525 1170 2475 2210 1500 1105 665	9610,84 6096.29 1270,02 747,07 4314,45 7923,14 8422,56	15 41 86 120 140 153 160
Ogółem	160	X	9650	38384,37	X

Wyznaczamy dominantę:

Największa liczebność wynosi 45, stąd :
.

Pojedynczą wartość dominanty obliczamy z tego przedziału stosując tzw. wzór interpolacyjny:




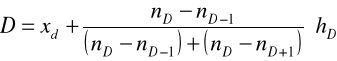
gdzie:

x_d - dolna granica przedziału, w którym jest dominanta,

n_D - największa liczebność,

n_D-1 - liczebność poprzedzająca największą,

n_D+1 - liczebność następna po największej,

h_D - rozpiętość przedziału z dominantą.

Podstawiamy:




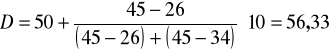
Najwięcej mieszkań oddanych do użytku w Kaliszu w I-ej połowie 2000 r. miało powierzchnię 56,33 m².

Obliczamy wartość mediany:

W celu ustalenia wartości środkowej (mediany) musimy skumulować liczebności (patrz kolumna 6).

N - jest liczbą parzystą, czyli N = 2k stąd: k = N/2 = 160/2 = 80




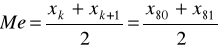
Jednostki 80 i 81 znajdują się w przedziale <50, 60>, z tego więc przedziału obliczamy wartość mediany stosując wzór interpolacyjny:




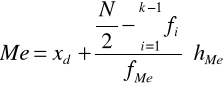
gdzie:

x_d - dolna granica przedziału, w którym jest mediana,


- liczebność skumulowana do przedziału poprzedzającego ten z medianą,

n_Me - liczebność w przedziale zawierającym medianę,

h_Me - rozpiętość przedziału zawierającego medianę.

Ustalamy poziom cechy u obu środkowych jednostek ( 80 i 81):







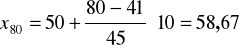
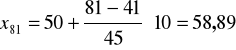
Ponieważ mediana to średnia z tych dwóch wartości, wobec tego mamy:




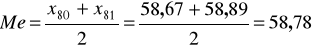
Oznacza to, że połowa mieszkań oddanych do użytku przez tą spółdzielnię miała powierzchnię mniejszą od 58,78 m² a połowa miała powierzchnię większą.

Łatwo zauważyć, że różnice w poziomach cechy u jednostek środkowych są minimalne. Dlatego też w przypadku gdy badamy liczne zbiorowości (N > 100) wystarczy ustalić wartość cechy dla pierwszej jednostki środkowej: N/2 i tą wartość uznać za medianę cechy.

Obliczamy odchylenie standardowe

Do wyboru mamy dwie wersje wzoru:




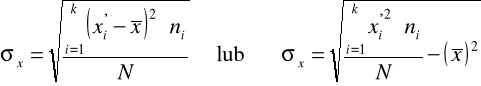
Stosujemy pierwszą wersję wzoru (obliczenia pomocnicze - kolumna 5 tabeli roboczej):




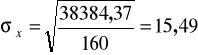
Mieszkania różniły się powierzchnią użytkową od powierzchni średniej przeciętnie o +/- 15,49 m².

Obliczamy współczynnik zmienności:




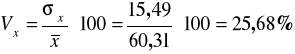
Zmienność mieszkań według powierzchni była nieduża, odchylenie standardowe stanowi 25,68% poziomu średniego.

Ustalamy asymetrię rozkładu powierzchni użytkowej badanych mieszkań:




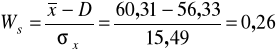
Rozkład powierzchni mieszkań oddanych do użytku charakteryzuje się małą asymetrią prawostronną, czyli częściej mieszkania miały powierzchnię nieco mniejszą od średniej.

Można tu jeszcze ustalić typowy obszar zmienności cechy:

Mamy wtedy:





.

Oznacza to, że około 2/3 mieszkań oddanych do użytku miało powierzchnię mieszczącą się w tym przedziale.


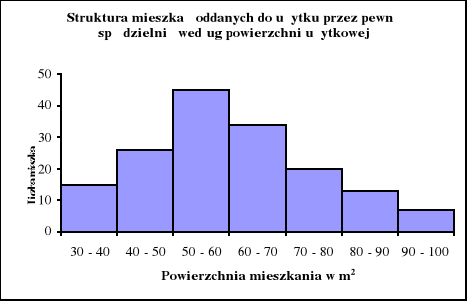
ad c) Sporządzamy histogram:

Źródło: dane z zadania 3.

Zadanie 4.

Przeprowadzono analizę indywidualnych gospodarstw rolnych w pewnej gminie w województwie wielkopolskim w czerwcu 2007 roku według powierzchni użytków rolnych w ha. Otrzymano następujący szereg rozdzielczy.

W oparciu o podane informacje:

1. Określ zbiorowość, jednostkę i badaną cechę statystyczną.

2. Przeprowadź kompleksową analizę struktury badanych gospodarstw według powierzchni użytków w ha.

3. Badany szereg przedstaw graficznie.

Powierzchnia użytków rolnych w ha	Odsetek gospodarstw
1,01 - 1,99 2,00 - 4,99 5,00 - 6,99 7,00 - 9,99 10,00 - 14,99 15,00 i więcej	15,2 36,0 23,5 15,8 7,1 2,4
Ogółem	100,0

Źródło: Dane umowne.

Rozwiązanie:

ad a) Zbiorowość statystyczna - indywidualne gospodarstwa rolne w jednej z gmin województwa wielkopolskiego w czerwcu 2007 roku,

jednostka statystyczna - pojedyncze gospodarstwo,

badana cecha - powierzchnia użytków w ha - cecha mierzalna, ciągła.

ad b) Przedziały klasowe mają różną rozpiętość, ostatni przedział jest otwarty - stąd też nie możemy stosować miar klasycznych. Musimy ograniczyć się do miar pozycyjnych.

Należy w tabeli skumulować liczebności:

Powierzchnia użytków w ha	Odsetek gospodarstw	Odsetek skumulowany
1,01 - 1,99	15,2	15,2
2,00 - 4,99	36,0	51,2
5,00 - 6,99	23,5	74,7
7,00 - 9,99	15,8	90,5
10,00 - 14,99	7,1	97,6
15,00 i więcej	2,4	100,0

Obliczamy wartość mediany:

Ponieważ liczebności są wyrażone w odsetkach, stąd N = 100 , w takim razie pozycja mediany to: N/2, czyli 50.

Tak więc mediana jest zawarta w przedziale <2,00 ; 4,99 >.

Korzystamy ze wzoru:




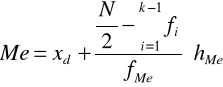
(objaśnienia do wzoru w poprzednim zadaniu).

Po podstawieniu otrzymujemy:




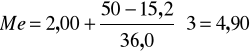
Połowa indywidualnych gospodarstw rolnych w badanym powiecie miała powierzchnię mniejszą od 4,9 ha, a połowa miała powierzchnię przekraczającą 4,9 ha.

Obliczamy kwartyle:

Kwartyl pierwszy dzieli zbiorowość na dwie części w ten sposób, że 25 % jednostek ma wartości mniejsze od tego kwartyla, a 75 % jednostek ma wartości od niego większe.

W przypadku gdy liczebności są wyrażone w odsetkach to kwartyl I ma pozycję N/4, czyli 25. Jest więc w przedziale < 2,00 ; 4,99 >.

Wzór interpolacyjny:




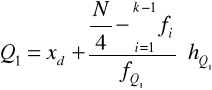
Po podstawieniu otrzymujemy:




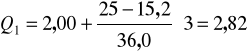
Tak więc, 25 % gospodarstw ma powierzchnię mniejszą od 2,82 ha a 75 % gospodarstw ma powierzchnię ponad 2,82 ha.

Kwartyl trzeci dzieli zbiorowość na dwie części w ten sposób, że 75 % jednostek ma wartości mniejsze od tego kwartyla a 25 % jednostek ma wartości od niego większe.

Pozycja kwartyla trzeciego to 3N/4, czyli w przypadku odsetek 75.

Kwartyl ten jest więc w przedziale <7,00 ; 9,99 >.

Wzór interpolacyjny:




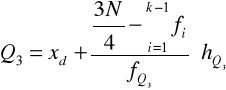
Po podstawieniu otrzymujemy:




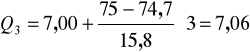
Znaczy to, że 75 % gospodarstw w badanej gminie miało powierzchnię poniżej 7,06 ha a tylko 25 % gospodarstw miało powierzchnię przekraczającą 7,06 ha.

Obliczamy odchylenie ćwiartkowe:




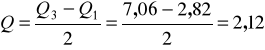
Przeciętne zróżnicowanie powierzchni w badanych gospodarstwach rolnych wynosi 2,12 ha.

Obliczamy pozycyjny współczynnik zmienności:




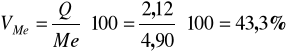
Zróżnicowanie powierzchni jest stosunkowo silne, odchylenie ćwiartkowe stanowi 43,3% mediany.

Obliczamy współczynnik asymetrii:




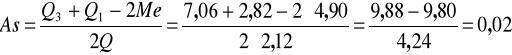
Rozkład powierzchni gospodarstw charakteryzuje się niewielką asymetrią prawostronną.

ad c) Sporządzamy wykres.

W tym przypadku nie można stosować histogramu, należy zastosować wykres powierzchniowy, np. wykres kołowy:




Źródło: Dane z zadania 4.

Zadanie 5.

Zebrano dane o stażu pracy pracowników pewnego przedsiębiorstwa w Poznaniu na koniec grudnia 2009 r. W oparciu o uzyskane informacje zbudowano następujący szereg rozdzielczy:

Staż pracy w latach	Liczba pracowników
0 - 4 4 - 8 8 - 12 12 - 16 16 - 20 20 - 24	9 14 36 29 18 8
Ogółem	114

Źródło: dane umowne.

W oparciu o podane informacje:

1. Określ zbiorowość, jednostkę i badaną cechę statystyczną.

2. Przeprowadź kompleksową analizę struktury pracowników tego przedsiębiorstwa według stażu pracy stosując metodę momentów.

Rozwiązanie:

ad a) Zbiorowość statystyczna - pracownicy badanego przedsiębiorstwa w Poznaniu według stanu z 31.12.2009.

jednostka statystyczna - pojedynczy pracownik

badana cecha - staż pracy wyrażony w latach - jest to cecha mierzalna, ciągła, najczęściej jednak wyrażana w pełnych latach.

ad b) Szereg spełnia warunki pozwalające na stosowanie parametrów klasycznych (równe przedziały klasowe i jedno maksimum).

Wszystkie potrzebne obliczenia zawarte są w tabeli roboczej:

Staż pracy w latach (x)	Liczba pracowników (ni)
1	2	3	4	5	6	7
0 - 4 4 - 8 8 - 12 12 - 16 16 - 20 20 - 24	9 14 36 29 18 8	2 6 10 14 18 22	18 84 360 406 324 176	900 504 144 116 648 800	-9000 -3024 -288 232 3888 8000	90000 18144 576 464 23328 80000
Ogółem	114	X	1368	3112	-192	212512

Liczymy średnią arytmetyczną

Ustalamy środki przedziałów klasowych - kolumna 3 tabeli roboczej, a następnie wykonujemy potrzebne obliczenia - kolumna 4.


.

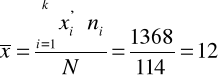
Przeciętny staż pracy pracowników tego przedsiębiorstwa wynosi 12 lat.

Obliczamy odchylenie standardowe

Do wyboru mamy dwie wersje wzoru:




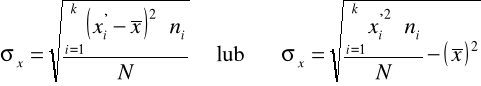
Stosujemy pierwszą wersję wzoru (obliczenia pomocnicze - kolumna 5 tabeli roboczej):




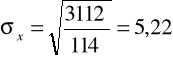
Pracownicy różnią się stażem pracy od stażu średniego przeciętnie o +/- 5,22 lat.

Obliczamy współczynnik zmienności:




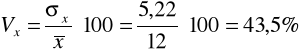
Zmienność pracowników według stażu pracy jest stosunkowo duża, bo odchylenie standardowe stanowi 43,5% poziomu średniego.

Ustalamy stopień asymetrii rozkładu stażu oracy:

Ponieważ mamy stosować metodę momentów musimy wyliczyć trzeci moment centralny i moment trzeci standaryzowany.

Moment trzeci centralny:




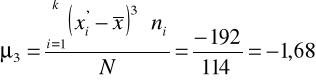
Moment trzeci standaryzowany:




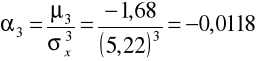
Rozkład stażu pracy charakteryzuje się niewielką asymetrią lewostronną.

Badamy koncentrację (skupienie) rozkładu badanej cechy

W tym celu liczymy czwarty moment centralny a czwarty moment centralny standaryzowany:

Moment czwarty centralny:




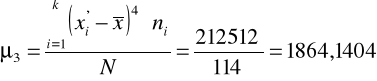
Moment czwarty standaryzowany:




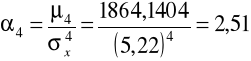
Rozkład stażu pracy jest lekko spłaszczony w stosunku do rozkładu normalnego.




---