1.1 Wyjaśnić pojęcia związane z błędem:

• liczba przybliżona a jest to liczba różniąca się nieznacznie od dokładnej liczby A i zastępująca ją w obliczeniach

• błąd bezwzględny Δ nazywamy wartość bezwzględną różnicy między wartością dokładną A a wartością przybliżoną a = | A-a |

• błąd względny δa liczby przybliżonej a nazywamy stosunek błędu bezwzględnego do modułu liczby A. δa=a/|a|

l .2 Wyprowadzić wzory na błąd bezwzględny i błąd względny wartości funkcji jednej i wielu zmiennych.

"Niech oszacowanie x będzie małe i niech i || <=x. Dla funkcji f określonej na przedziale [x-x,x+x] o wartościach rzeczywistych, klasy C^∞ mamy:

Ponieważ w porównaniu do pierwszego, pozostałe składniki powyższego rozwinięcia są małe, więc

Tak więc dla dostatecznie małego x, dobrymi przybliżeniami dla oszacowań błędu bezwzględnego i błędu względnego wartości funkcji są odpowiednio wielkości

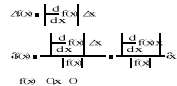
Przeprowadzając analogiczne rozumowanie błąd bezwzględny i względny dla funkcji wielu zmiennych definiujemy w następujący sposób

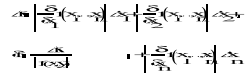
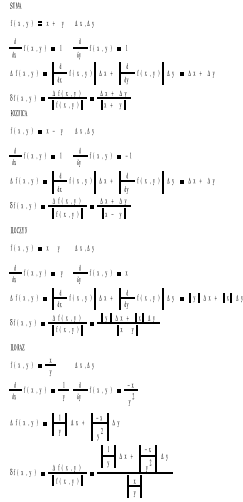
1.3 Wyprowadzić wzory na błąd bezwzględny i błąd względny działań arytmetycznych: suma, różnica iloczynu i ilorazu

1.4 Obliczyć błąd bezwzględny i błąd względny wartości funkcji f, gdy np. f(x)=xy² oraz x = 1, y = 2 oraz Δx = 0,1, Δy = 0.05

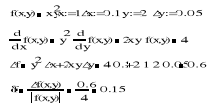
1.5

1.6 Co to jest: wskaźnik uwarunkowania zadania numerycznego -jest mnożnikiem, zależnym zwykle od danych zadania, określającym zmianę zaburzeń względnych danych (w sensie wartości bezwzględnych Iub norm tych zaburzeń). Oznaczany jest przez cond lub cond(x)

Podać ten wskaźnik dla zadania obliczania wartości funkcji jedej zmiennej y=f(x)

2. Rozwiązywanie układów równań liniowych.

1.7 Co to jest: wskaźnik uwarunkowania zadania numerycznego - jest mnożnikiem, zależnym zwykle od danych zadania, określającym zmianę zaburzeń względnych danych (w sensie wartości bezwzględnych lub norm tych zaburzeń). Oznaczany jest przez cond lub cond(x) Podać ten wskaźnik dla zadania rozwiązywania układów równań liniowych.

cond(A)=||A|| ||A^-1||

2. Rozwiązywanie równań nieliniowych i ich układów.

2.1 Na czym polegają metody iteracyjne rozwiązywania rozważanego obecnie zadania numerycznego (dla przypadku skalarnego). Zdefiniować wykładnik zbieżności takich metod. Podać ten wykładnik dla metody: siecznych, stycznych, bisekcji.

Metody iteracyjne polegają na tworzeniu ciągu kolejnych przybliżeń x_k, który zbiega do rozwiązania .

Wykładnik zbieżności metod-jest to największa liczba p (p≥1), że | e_k+1 | ≤ C*( | e_k | )^p, gdzie e_k=-x_k, zaś C jest stałą nieujemną zależną zazwyczaj od funkcji f (lub jej pochodnych). Wykładnik zbieżności dla metody:

• Siecznych: p=(l+√5 )/2 (p≈1.62) - zbieżność ponadliniowa

• Stycznych: p=2 - zbieżność ponadliniowa

• Bisekcii: p=l - metoda jest wtedy zbieżna liniowo

2.2 Dla równania skalarnego, omówić metodę

• siecznych - opis metody:

a)wybieramy dwa punkty startowe x₀ i x₁ z przedziału, w którym poszukujemy pierwiastka,

b)kolejne przybliżenia x_k+1, k=0,1,2,.. obliczamy ze wzoru: x_k+1=x_k-f(x_k)⋅{[(x_k-x_k-1)]/[f(x_k)-f(x_k-1)]}.

Warunki kończenia iteracji: l)  x_k+1-x_k≤ε, 2)  x_k+1-x_k≤ε⋅x_k+1, 3) f(x_k+1)≤ε.

Zapewniamy zbieżność metody gdy:

1) f jest funkcją klasy C² ([a,b])

2) f(a)*f(b)<0,

3) f'i f" nie zmieniają znaku w [a,b], wówczas zbieżność jest z wykładnikiem p= (1+√5)/2

• stycznych - opis metody:

a)wybieramy punkt startowy x_o z przedziału, w którym poszukujemy pierwiastka,

b)kolejne przybliżenia x_k+i, k=0,l,2,„ obliczamy ze wzoru: x_k+1=x_k-[f(x_k)/f1(_­x_k)]

f(x)=d/dxf(x)

Warunki kończenia iteracji są takie same jak w metodzie siecznych.

Zapewniamy zbieżność metody gdy:

l ) f jest funkcją klasy C

2) f(a)*f(b)<0,

3) f'i f" nie zmieniają znaku w [a,b], to przyjmując x_o takie, że f(x_o)f"(x_o)>0; zbieżność jest z wykładnikiem p=2

• bisekcji - opis metody:

a)dzielimy przedział [a,b] na połowę punktem x₁==(a+b)/2,

b)jeżeli f(x₁)=0, to x₁ jest pierwiastkiem i metodę kończymy,

c)jeżeli f(x₁)≠0 to wybieramy ten z podprzedziałów [a,x₁] lub [x₁,b], w którym funkcja zmienia znak.

W tej metodzie z góry można określić liczbę iteracji potrzebną do uzyskania dokładności 

Metoda ta jest liniowo zbieżna gdy wykładnik p=l i stała C=0,5.

2.3 Podać założenia dotyczące a)funkcji f, b)przedziału [a,b], c)punktów (punktu) startowych, zapewniające zbieżność do pierwiastka ciągu generowanego przez metodę:

• siecznych - f jest funkcją klasy C²[a,b]), f(a)*f(b)<0, na przedziale [a,b] f' i f "nie zmieniają znaku, punkty startowe x_o i x₁ wybieramy z przedziału w którym poszukujemy pierwiastka, przyjmując je tak by f(x_o)-f "(x_o)>0 i f(x₁)'-f"(x₁)>0

• stycznych - f jest funkcją klasy C²[a,b]), f(a)*f(b)<0, na przedziale [a,b] f' i f "nie zmieniają znaku, punkt startowy x_o wybieramy z przedziału w którym poszukujemy pierwiastka, przyjmujemy je takie by f(x_o)*f "( x_o)>0

• bisekcji - f jest funkcją ciągłą na przedziale [a,b], oraz f(a)*f(b)<0 (f zmienia znak w [a,b]), przedział [a,b] dzielimy na połowę punktem x₁=(a+b)/2, jeżeli f(x₁)=0 to x₁ jest szukanym pierwiastkiem, jeżeli f(x₁)=/0 wybieramy ten z podprzedziałów [a,x₁] lub [x₁,b] gdzie funkcja zmienia znak

2.4 Wyznaczyć pierwsze przybliżenie: np. w metodzie stycznych, gdy f(x) = 2x⁴-x² i punkt startowy x₀ = 1

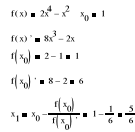
2.5 Czy można stosować metodę np. stycznych, gdy f(x) = e^x - x - 1 i punkt startowy x₀ = 1

??? 2.6 Omówić metodę Newtona dla układów równań

Zakłada się, że pochodne cząstkowe funkcji f_i(x_i ...x_n)=0, i=l ,2,..,n są ciągłe i macierz Jacobiego DF(x)=[(δ/ δ x_j)f_i(x)] i,j=l ,..,n jest nieosobliwa w pewnym otoczeniu pierwiastka α (F()=0). Jeżeli zostanie dobrany x^(o) dostatecznie blisko , to ciąg iteracyjny określony poprzez (metoda Newtona) x^(k+l)=x^(k)-[DF(x^(k))}^-1F(x^(k)), k=0, l,2,.. jest określony poprawnie (tzn.istnieją macierze odwrotne [DF(x^(k))]^-1 oraz jest zbieżny do . Jeżeli są dodatkowe założenia o F wówczas uzyskuje się zbieżność ponadliniową z wykładnikiem p=2.

Pojedynczy krok:, obliczamy F_k=F(x^(k)) i DF_k=F(x^(k)) rozwiązujemy układ równań liniowych, wyznaczając poprawkę p^(k): DF_kp^(k)=-F_k podstawiamy: x^(k+l)=x^(k)+p^(k)

3 Interpolacja,

3.1 Sformułować zadanie interpolacyjne Lagrange'a.

Zadanie interpolacyjne Lagrange'a polega na znalezieniu wielomianu L_n, stopnia nie wyższego niż n spełniającego warunki interpolacji L_n(x_i)=f(x_i) dla i=0,l,..,n. Wielomian L_n nazywamy wielomianem interpolacyjnym Lagrange'a funkcji f opartym na węzłach x₀,x₁,...,x_n.

3.2 Sformułować i udowodnić twierdzenie o jednoznaczności rozwiązania zadania interpolacyjnego Lagrange'a.

Zadanie interpolacyjne Lagrange'a polega na znalezieniu wielomianu L_n, stopnia nie wyższego niż n spełniającego warunki interpolacji L_n(x_i)=f(x_i) dla i=0,l,..,n.

Zadanie interpolacyjne Lagrange' a ma jednoznaczne rozwiązanie.

Dowód: Szukany wielomian zapiszemy w postaci:

** Zadanie interpolacji L_n(x_j)=y_i dla i=0,l,..,n prowadzi do układu n+1 równań liniowych Va=y z

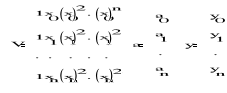
Macierz Vandermonde'a jest macierzą nieosobliwą dla układu różnych węzłów. Zatem układ Va=y ma dokładnie jedno rozwiązanie. Istnieje wielomian postaci ** i jest on wyznaczony jednoznacznie.

3.3 Podać warunek Lagrange'a dla funkcji f określonej następująco: np. f(1)=2, f(2)=3, f(3)=2

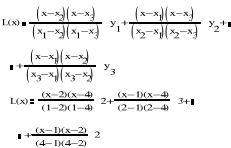
3.4 Zdefiniować iloraz różnicowy 1-go rzędu, 2-go rzędu i ogólnie k-go rzędu.

Wyznaczyć tablicę ilorazów różnicowych dla funkcji f określonej następująco: np. f(0)=1, f(1)=3, f(3)=2.

Ilorazami różnicowymi I rzędu nazywamy wyrażenia.

f_0,1=(y₁-y_o)/x₁-x_o,.. .f_n-l,n=(y_n-y_n-l)/x_n-x_n-l

Ilorazami różnicowymi II rzędu nazywamy wyrażenia.

f_0,1,2=(f_l,2-f_0,l)/x₂-x₀,...f_n-2,n-l,n=(f_n-l,n-f_n-2,n-l)/x_n-x_n-2

Ilorazami różnicowymi k-tego rzędu nazywamy wyrażenia

f_i,j+1,..,i+k=(f_i+1,..,i+k-f_i,..,i+k-1)/x_i+k-x_i

Wyznaczyć tablicę ilorazów różnicowych dla funkcji f określonej następująco: np. f(0)=1, f(1)=3, f(3)=2

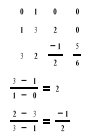
3.5 Podać wielomian interpolacyjny w postaci Newtona dla funkcji f określonej następująco: np. f(0)=1, f(2)=3, f(3)=2

3.6 Podać definicję funkcji sklejanej stopnia trzeciego.

Funkcją sklejaną stopnia 3 na przedziale <a,b> nazywamy funkcję, która:

a)jest wielomianem stopnia 3 na każdym przedziale <x_i,x_i+1>,

b)jest klasy C² na <a,b>

3.7 Sformułować zadanie interpolacji przy pomocy funkcji sklejanych stopnia trzeciego. Czym są dodatkowe warunki ?

Funkcję f(x) określoną na przedziale [a,b] nazywamy funkcją sklejaną stopnia trzeciego, jeżeli

• f(x) jest wielomianem stopnia co najwyżej trzeciego na każdym podprzedziale (x_i,x_i+1),i=0,l,..n-l

• f(x) jest funkcją klasy C²[a,b].

Punkty x_i są węzłami funkcji sklejanej.

Interpolacyjna funkcja sklejana stopnia trzeciego zależy od dwóch parametrów, wobec czego nakładane są najczęściej na węzłach krańcowych a i b dwa dodatkowe warunki. Mogą mieć one postać: f'(a+0)= i f'(b-0)= , ,-ustalone liczby rzeczywiste. Jeżeli funkcja f ma pochodne w punktach a i b oraz znane są ich wartości, to można je przyjąć jako liczby występujących po prawych stronach powyższych warunków. Jeżeli zaś znane są tylko wartości funkcji f w węzłach to mogą to być przybliżenia pochodnych.

3.8.

4. Aproksymacja średmokwadratowa dyskretna.

4.1 Sformułować zadanie aproksymacji średniokwadratowej dyskretnej.

Rozważyć przypadki aproksymacji typu wielomianowego i trygonometrycznego.

• Aproksymacja średniookwadratowa dyskretna:  = ( _o, _i,.., _m)→układ m+l funkcji

określonych na (a,b)

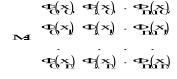
funkcja przybliżająca F_m(x)=Σ^m_j=0a_j-ϕ_j(x); współczynnik a_j dobieramy tak by wyrazenie: H(a_o,a₁,..,a_m)=Σⁿ_i=0(y_iF_m(x_i)² miało najmniejszą wartość. Wartości współczynników wyznaczamy z warunków zerowania się pochodnych (δ/δa_k)H=-2Σⁿ_i=0(y_i-F­_m(x_i))ϕ_k(x_i)=0 k=0,1,...,m otrzymujemy m+1 równań liniowych z niewiadomymi a_o,a₁,..,a_m

• Aproksymacja wielomianowa - Funkcje _j są wielomianami stopnia (j=0,l ,2,..m) kiedy F_m jest wielomianem stopnia co najwyżej m, wtedy funkcję optymalną F_m nazywamy m-tym wielomianem optymalnym.

• Aproksymacja trygonometryczna - Do aproksymacji stosujemy wielomiany trygonometryczne ( =(1, sin(x), cos(x), sin(2x),...,sin(kx), cos(kx)) 2k<=n wtedy:

F_2k+1(x)=a₀+Σ^k_j=1(a_jcos(j⋅k)+b_jsin(j⋅x))

rozważamy odcinek (0,2) na zbiorze równoodległych punktów: x_i=(2*i)/(n+1) i=0,l,..,n macierz Gramma jest diagonalna a_o=l /(n+1)Σⁿ_i=0y_i a_j=2/(n+1)Σⁿ_i=0y_icos(jx_i) bj=2/(n+1)Σⁿ_i=0y_isin(jx_i) j=1,..,k

4.2

4.3 Przyjmując, że G=M^TM jest macierzą Grama, podać postać macierzy M., gdy np. a) 2,x,x²,2^x są funkcjami bazowymi, b) aproksymacji dokonujemy na zbiorze {-1,0,2,3}.

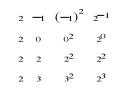
4.4 Omówić problem uwarunkowania zadania rozwiązywania układu równań normalnych.

H(a_o,a₁,..,a_m)-odchylenie średniokwadratowe, należy tak dobrać współczynniki "a_j" by odchylenie średniokwadratowe było jak najmniejsze.

Błąd średniokwadratowy: δ=√[1/(n+1)Σⁿ_i=0(y_i-F(x_i))²].

Gdy m=n rząd macierzy M jest równy n+1 to n-ta funkcja optymalna jest funkcją interpolującą funkcji f opartą na węzłach x, wtedy H=0 δ=0.

W przypadku (_j=x^j już dla niedużych m (m>5) układ jest równań normalnych, jest źle lub bardzo źle uwarunkowany (jednomiany); liczbę funkcji przybliżających=(m+l) ustalamy wyznaczając kolejne funkcje optymalne i kwadrat średniego błędu: (δm)²=Hm/n-m

Hm-odchylenie średniokwadratowe dla m-tej funkcji optymalnej Fm;

obliczenia prowadzi się aż (δm)² maleje w sposób istotny, wartość po której (δm)² już znacznie nie maleje wyznaczają układ funkcji przybliżających _o, ₁,.., _m

5. Całkowanie numeryczne.

5.1 Co to jest kwadratura ? Omówić rolę funkcji wagowej p.

Do przybliżonego obliczenia całki I(f) stosujemy wzory, zwane kwadraturami, w postaci:

przy czym współczynniki A_k nie zależą od funkcji f. Oczywiście x_i≠x_j dla i≠j. Współczynniki A_k i punkty x_k nazywamy odpowiednio współczynnikami i węzłami kwadratury S. Jeżeli funkcja f ma osobliwości utrudniające dobre przybliżenie to f(x)=F(x)*p(x) gdzie F(x) jest funkcją która może dobrze przybliżyć a p(x) ma wszelkie osobliwości funkcji podcałkowej utrudniające przybliżenie

5.2 Podać definicję rzędu kwadratury.

Mówimy, że kwadratura S jest rzędu r(r≥ l), jeżeli: I(W)=S(W) dla wszystkich wielomianów

W stopnia mniejszego niż r, istnieje wielomian W stopnia r taki, że I(W)≠S(W). Jedynym ze sposobów otrzymywania kwadratur S jest zastąpienie w całce I funkcji f funkcją interpolującą F. Wtedy:

gdzie funkcja interpolująca F jest np. interpolacyjnym wielomianem czy interpolacyjną funkcją sklejaną dla funkcji f. Jeżeli F jest wielomianem interpolacyjnym, to S nazywamy kwadraturą interpolacyjną.

Wykazać, że kwadratura postaci S(f)=2f(0), gdy a=-1, b=1 oraz p(x)=1, jest dokładna dla wielomianów pirwszego stopnia.

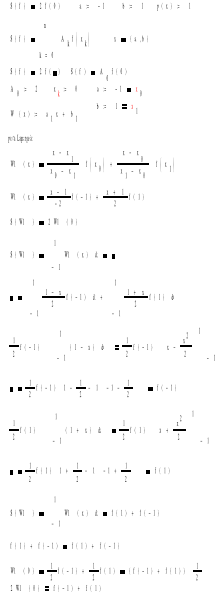
5.3 Omówić prosty i złożony wzór trapezów.

Niech F=L_n będzie wielomianem interpolacyjnym Lagrange'a

Wtedy

Jeżeli funkcję f zastąpimy wielomianem interpolacyjnym L opartym na węzłach a i b, to otrzymamy kwadraturę trapezów

Geometrycznie dla f≥0, przybliżamy pole między wykresem f i osią Ox polem trapezu o podstawach f(a) i f(b). Złożony wzór trapezów przy podziale przedziału [a,b] na n podprzedziałów o tej samej długości h=(b-a)/n jest postaci

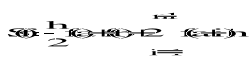
5.4 Omówić prosty i złożony wzór parabol.

Prosty: S(f)=(b-a)/6*(f(a)+f(b)+4f(a+b)/2) ∫^b_af(x)dx=h/3(f(x₀)+4f(x₁)+f(x₂);

aby osiągnąć lepszą dokładność można zwiększać liczbę węzłów n lub dzielić przedział na mniejsze części Złożony: dzielimy przedział całkowania <a,b> na m równych części o długości (b-a)/m=h , „m" musi być parzyste S(f)=h/2*[f(a)+f(b)+2Σ^m-1_i=1f(a+ih+h/2)]

5.5 Omówić błąd złożonego wzoru trapezów i złożonego wzoru parabol.

Błąd trapezów: E(f)=-[(b-a)³/12m²]*f⁽²⁾ () Błąd parabol: E(f)=-[(b-a)⁵/2880m⁴]*f⁽⁴⁾ ()

, > pewne punkty z przedziału (a,b); pochodna f⁽²⁾(x) oraz f⁽⁴⁾(x) jest ciągła na <a,b>

5.6 Omówić 2 - punktowa prosta i złożona kwadraturę Gaussa-Legendre'a.

Dla przedziału <-1,1> całkowania: S(f)=f(x_o)+f(x₁); dla dowolnego przedziału całkowania <a,b> → liniowa zmiana zmiennej całkowania t=[(a+b)/2]+[(b-a)/2]*x prosta ∫^b_af(t)=[(b-a)/2]∫¹_-1g(x)dx g(x)=f{[(a+b)/2]+[(b-a)/2]*x} S(f)=(b-a)/2*[f((a+b)/2+(b-a)/2-x_o)+f((a+b)/2+(b-a)/2*x₁)] złożona: dla równomiernego podziału przedziału całkowania na części (m) gdzie h=(b-a)/m S(f)=h/2Σ^m-l_i=0[f(a+ih+ht_o)+f(a+ih+ht₁] t_o=(1+x_o)/2 t1=(l+x₁)/2

-----------------------------------------------------------------

6. Rozwiązywanie zagadnień początkowych dla równań różniczkowych zwyczajnych.

6.1.Omówić metodę rozwijania w szereg potęgowy.

6.2. Omówić metody dyskretne. Wyjaśnić pojęcia: zbieżność i rząd metody dykretnej.

Metody dyskretne - przy ich pomocy można uzyskać przybliżone rozwiązanie tylko dla dyskretnych wartości x_i zmiennej niezależnej x, przyjmuje się, że punkty x_i są równoodległe, tzn. x_i=a+ih, i=0,l,2,..,n h=(b-a)/n gdzie h to krok całkowania. Największą liczbę całkowitą p taką, że dla dostatecznie małych h zachodzi nierówność |e_i(h)| ≤ ch^p dla każdego i=0,l,..,n(h), gdzie c jest niezależną od h, nazywa się rzędem metody.

6.3 Omówić jawną metodę Eulera.

Według tej metody y_i+1=y_i+hf(x_i,y_i), i=0,1,2,..,n-1 przy czym y_o=y_a

Metoda ta ma prostą interpretację geometryczną, oznaczamy punkty M_i=M_i(x_i,y_i), odcinek M_iM_i+1 ma w punkcie M_i zgodny z kierunkiem stycznej do rozwiązania, które przechodzi przez ten punkt, wielkość T_i, jest błędem metody który powstał przy przejściu od x_i do x_i+1, e_o=0, e₁=T_o zakłada się również że rozwiązanie dokładne y=y(x) jest klasy C²([a,b]). Rozwiązanie to spełnia równanie y(x_i+l)==y(x_i)+hf(x_i,y(x_i))+(1/2)h²y⁽²⁾ (_i), x_i<_i<x_i+1 stąd otrzymujemy: T_i=(1/2)h²y⁽²⁾ (_i) WYKRES

6.4 Dane jest zagadnienie początkowe y'=y+x, y(0)=1. Za pomocą jawnej metody Eulera obliczyć y₁ oraz y₂, gdy krok całkowania h=0.1.

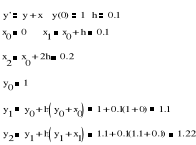
6.5. Dane jest zagadnienie początkowe y'=2y+x, y(1)=1 oraz metoda dyskretna (metoda Heuna rzędu 2-go) gdzie f_i=f(x_i,y_i). Obliczyć y_1­, gdy krok całkowania h=0.2.

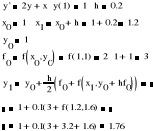
Opać metodę złożoną Simpsona.

W metodzie tej sumuje się kwadratury proste na mniejszych odcinkach, na które dzielimy przedział [a,b]. Złożony wzór parabol przy podziale przedziału [a,b] na n przedziałów o tej samej długości n=b-a/n ma postać:

Błąd złożony kwadratury Simpsona dla funkcji klasy C⁴(a,b) jest postaci

ρ - punkt z przedziału (a,b)

1.3? Podać sposób całkowania numerycznego dla funkcji danej w przedziale <a,b> wzorem: F(x) gdzie funkcja f(x) nie ma osobliwości w <a,b>

Funkcję takiej postaci całkujemy za pomocą kwadratury Gaussa-Czebyszewa funkcją wagową jest

, która posiada osobliwości na krańcach przedziału całkowania. Kwadratury Gaussa-Czebyszewa wyrażają się wzorem

gdzie

k=0,1,...,n

Węzły x_k (k=0,1,2,...,n) są pierwiastkami wielomianów Czebyszewa pierwszego rodzaju T_n+1(x)=cos((n+1)arccosx)

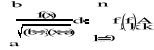
gdzie

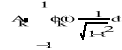
t_k - węzły czebyszewa

1.4? Sformułować zagadnienie aproksymacji funkcji f(x) (metodą najmniejszych kwadratów)

Niech φ=(φ₀, φ₁,... ,φ_n) będzie układem (m+1) f.określonych na przedziale [a,b]. Zakładamy, że rząd macierzy M=m+1

Będziemy rozważać zadanie aproksymacji linowej polegającej na przybliżeniu funkcji f kombinacjami linowymi funkcji φ_j­ (j=0,1,..,n) F_n(x)=Σ^m_j=0a_jφ_j(x) a_j dobieramy tak aby wyrażenie H(a₀,a₁,...,a_m) = Σⁿ_i=0(y_i-F(x_i))² było jak najbliżej węzłów tzn min H

Funkcję F_m, dla której H osiąga minimum nazywamy m-tą funkcją optymalną. Liczymy δH/δa_k­=0 k=0,1,...,m

F(x) = a₀+a₁x+…+a_mx^m

1.5? Sformułować twierdzenie o istnieniu I jednoznaczności wielomianu interpolacyjnego

Danych jest n+1 p'któw x₀,x₁,...,x_n z przedziału [a,b], które nazywamy węzłami oraz wartości funkcji w tych punktach y₀=f(­x­₀)...

Zadanie interpolacji - znalezienie funkcji interpolacyjnej F która pokrywa się z funkcją f w węzłach tzn F(x_i)=f(x_i) dla i=1,2,...,n

Funkcję F można przedstawić w postaci kombinacji liniowej F(x)=Σ_j=0ⁿa_jφ_j(x) gdzie a_j - współczynnik kombinacji liniowej

Σ_j=0ⁿa_jφ_j(x_i­)=y_i

jeżeli detA≠0 to układ ma jednoznaczne rozwiązanie

Tw. Istnieje jedyny wielomian stopnia ≤ n który n+1 węzłach pokrywa się z funkcją f(x) W_n(x)=f(x_i)=y_i

4

---